SỞ GD & ĐT THANH HÓA
KỲ THI KHẢO SÁT CÁC MÔN THI VÀO LỚP 10
TRƯỜNG THPT CHUYÊN LAM SƠN THPT CHUYÊN LAM SƠN
Năm học: 2024 – 2025 ĐỀ THI CHÍNH THỨC Môn thi: TOÁN
( Đề thi có 01 trang)
(Dành cho thí sinh thi vào chuyên Toán) Ngày thi: 07/4/2024
Thời gian làm bài:150 phút (không kể thời gian phát đề) 2 Câu 1  + 
. a) Cho x, y là các số hữu tỉ dương thỏa mãn 2 2 xy 1 x + y + =   2, chứng  x + y 
minh 1+ xy là số hữu tỉ. b) Cho biểu thức 8
P(x) = x −12x +12 + 3x . Gọi x là một nghiệm của 0 phương trình 2
x + x −1= 0. Tính giá trị P(x ).. 0
Câu 2. a) Giải phương trình: 2
3x - 2 + 5x -1 = x − x + 3. 3
x (3 + 2y) = 8
b) Giải hệ phương trình  2
xy(y + 3y + 3) = 4.
Câu 3. a) Giải phương trình nghiệm nguyên dương: 2 2
5(x + xy + y ) = 7(x + 2y).
b) Cho n là số nguyên dương và d là ước dương của 2 2n , chứng minh 2
n + d không phải là số chính phương.
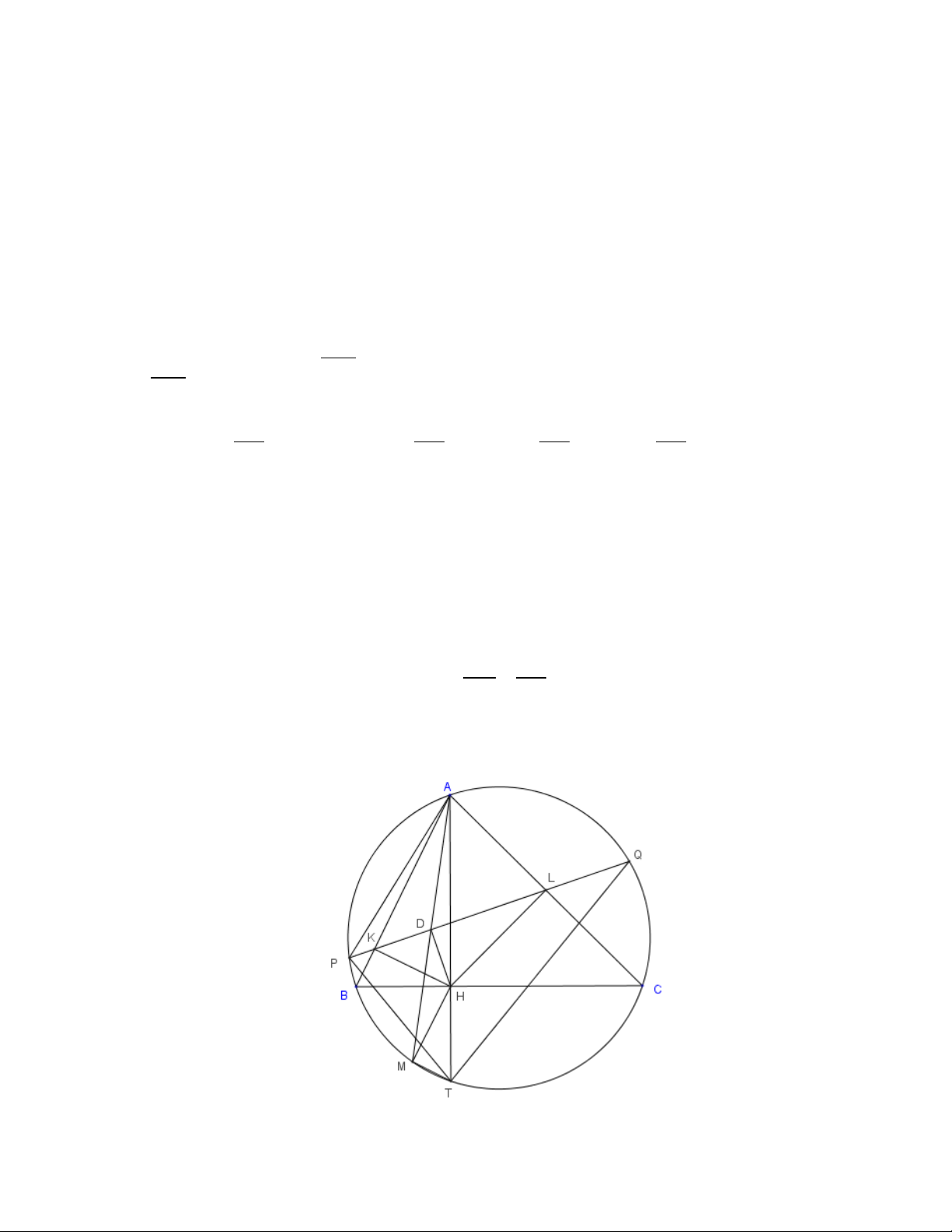
Câu 4. Tam giác nhọn không cân ABC nội tiếp đường tròn (O), đường cao
AH (H ∈ BC). Gọi K,L lần lượt là hình chiếu vuông góc của điểm H trên các
cạnh AB, AC. Đường thẳng KL cắt đường tròn (O) tại hai điểm P,Q ( P và B
cùng phía đối với AC ).
a) Chứng minh tứ giác BKLC nội tiếp đường tròn.
b) Chứng minh BC là tiếp tuyến của đường tròn ngoại tiếp tam giác P . HQ
c) AH cắt lại đường tròn (O) tại T (T ≠ ).
A Gọi D là hình chiếu vuông
góc của H lên K ;
L AD cắt đường tròn (O) tại M (M ≠ ). A Chứng minh  0 HMT = 90 .
Câu 5. Chứng minh rằng từ 6 số vô tỉ tùy ý ta có thể chọn được 3 số a, , b c sao cho cả 3 số a + ,
b b + c, c + a đều là số vô tỉ. Bài toán còn đúng không nếu ban đầu là 4 số?
………………………….. Hết …………………………
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:................................................................... Số báo danh:..........................
Chữ kí của giám thị số 1 : ……………………………………..….Chữ kí của giám thị số 2:………………
SỞ GD & ĐT THANH HÓA
KỲ THI KHẢO SÁT CÁC MÔN THI VÀO LỚP 10
TRƯỜNG THPT CHUYÊN LAM SƠN THPT CHUYÊN LAM SƠN
Năm học: 2024 - 2025 ĐỀ THI CHÍNH THỨC
Môn thi: Toán (chuyên Toán)
( Đề thi có 01trang) Ngày thi:
Thời gian làm bài:150 phút (không kể thời gian phát đề)
ĐÁP ÁN (Chuyên Toán) 2 2 Câu 1  +   +  . a) Ta có: 2 2 xy 1 x + y + = 2 xy 1  
2 ⇔ (x + y) − 2(xy + ) 1 + =   0 (0,25đ)  x + y   x + y  2 ⇔  xy +1 xy +1 xy +1 x + y − =  0 ⇔ x + y − = 0 ⇔ x + y =  (0,25đ)  x + y  x + y x + y
⇔ xy + = (x + y)2 1
⇔ 1+ xy = x + y (0,5đ) b) Ta có 2 2 4 2
x + x −1= 0 ⇒ x =1− x ⇒ x = x − 2x +1= (1− x ) − 2x +1= 2 − 3x . 0 0 0 0 0 0 0 0 0 0 8 2
⇒ x = 9x −12x + 4 0 0 0 (0,5đ) 2
Do đó P(x ) = 9x − 24x +16 + 3x = 4 − 3x + 3x , 0 0 0 0 0 0 (0,25đ) mà 2
4 − 3x = 3(1− x ) +1= 3x +1> 0.
P(x ) = 4 − 3x + 3x = 4. 0 0 0 Vậy 0 0 0 (0,5đ)
Câu 2. a) ĐK: x ≥ 2 / 3. Ta có: 2
3x-2 + 5x-1 = x − x + 3 ⇔ (x − 3x-2) + (x +1− 5x-1) 2
+ (x − 3x + 2) = 0 2 2
x − 3x+2 (x +1) − (5x-1) 2 ⇔ +
+ (x − 3x + 2) = 0 (0,5d) 3x-2 + x 5x-1 + (x +1)   2 1 1
⇔ (x − 3x + 2) + +1 =   0  3x-2 + x 5x-1 + (x +1)  Ta có: 1 1 + +1> 0, x ∀ ≥ 2 / 3 3x +1 + (x +1) 5x + 4 + (x + 2) Suy ra: 2
x − 3x + 2 = 0 ⇔ x =1, x = 2 (tm)
KL: x =1, x = 2. (0,5đ) 1  8  8 3 + 2y = 1+ 2 y +1 =  3 ( )  3
b) Từ hệ suy ra x ≠ 0. Hê  x  x ⇔  ⇔   3 2 4 y y y (  + + = y + )3 4 3 3 1 = +1  x  x  2  = 3 u  = 2v +  ( ) 1 1 Đặt u 
x ta được hệ phương trình:  (0,5đ)  3 v = 2u +  ( 1 2) v = y +1 3 3
⇒ u − v = v − u ⇔ (u − v)( 2 2 2( )
u + uv + v + 2) = 0 Vì 2 2
u + uv + v + 2 > 0, nênu = v u  = v = 1 − Từ (1) suy ra : 3
u − 2u −1= 0  ⇒  1± 5 u  = v =  2 Với u = v = 1
− ⇒ x = y = 2 − x = 5 −1 Với 1+ 5 u v  = = ⇒  5 −1 2 y =  2 x = − 5 −1 Với 1− 5 u v  = = ⇒  − 5 −1 (0,5đ) 2 y =  2
Câu 3. a) Từ giả thiết suy ra:
7(x + 2y)5 ⇒ (x + 2y)5 ⇒ x + 2y = 5m ⇒ x = 5m − 2y ( * m∈ )
Thay vào phương trình ta có:
( m − y)2 + ( m − y) 2 5 2 5
2 y + y − 7m = 0 2 2
⇔ 3y −15my + 25m − 7m = 0 (0,25d)
Phương trình (ẩn y)có nghiệm nên 2 ∆ = m − ( 2 m − m) 2 84 225 12 25
7 ≥ 0 ⇒ 75m − 84m ≤ 0 ⇔ 0 ≤ m ≤ (0,25đ) 75
Do m là số nguyên nên m = 0(loại), hoặc m =1 x = 5 − 2y x = 5 − 2y
Với m =1, ta được   ⇒ x y = (0,5đ) 3
 y −15y +18 = 0 ( y − 2  )( y − 3) ( , ) (1,2) 2 = 0
Nhận xét. Cũng có thể giải câu 3a) theo cách sau:
Giải phương trình nghiệm nguyên dương: 2 2
5(x + xy + y ) = 7(x + 2y).
Vì x, y ∈ *, ta có: 2 2 2 2
5(x + xy + y ) = 7(x + 2y) ⇔ 5(4x + 4xy + 4y ) = 28(x + 2y) 2
⇔ 15x + 5(x + 2y)2 = 28(x + 2y) ⇒ (x + y)2 < (x + y) 28 5 2 28
2 ⇒ x + 2y < 5 2
⇒ 3 ≤ x + 2y ≤ 5
Từ phương trình suy ra: 7(x + 2y)5 ⇒ (x + 2y)5 (vì (5;7) =1) x + 2y = 5
Dẫn đến x + 2y = 5 ⇒ 
⇔ (x, y) = (1,2) 2 2
x + xy + y = 7
Vật phương trình có nghiệm nguyên dương: (x, y) = (1,2) 2 2
n + d = m b) Giải sử 2
n + d là số chính phương, ta có  ( , m k ∈ *) 2
2n = d.k 2 2
n + d = m 2  2 ⇒ 2 n 2 2 2 2 2 2 2  ⇒ n + = m ⇒ n k + 2 2 n k = m k n (0,5đ)  = d k  k 2 2 2 2 2  mk k k  ⇒ + =  mk  mk  mk   vì k ∈ *  ⇒ ∈   *  ⇒ ∈ *  ⇒ là số chính n       n  n  n  phương 2
⇒ k + 2k là số chính phương. Nhưng ta có 2 2
k < k + 2k < (k + )2 1 nên vô lý,
dẫn đến giả sử sai. Vậy 2
n + d không chính phương. (0,5đ)
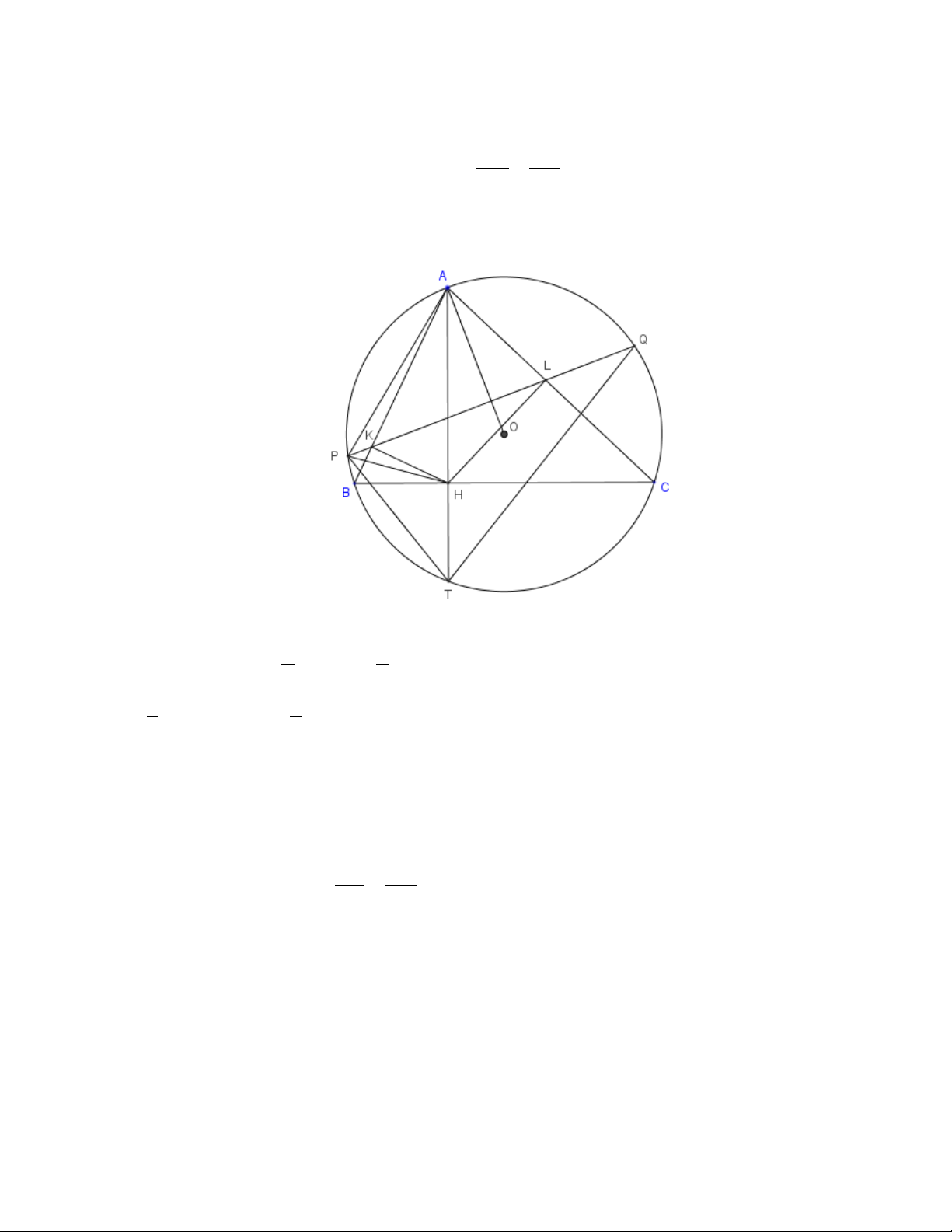
Câu 4. a) (Có nhiều cách để chứng minh tứ giá BKLC nội tiếp)
Ta có tam giác AHB vuông tại H và có đường cao là HK, nên 2
AH = AK.AB (1) (hệ
thức trong tam giác vuông). Tương tự ta có 2 AH = . AL AC (2). Từ(1) và (2) ta được . = . AK AL AK AB AL AC ⇒ = (3) (0,5đ) AC AB
Xét tam giác AKL và ACB có 
KAL chung và thỏa mãn (3), suy ra ∆  ∆ − − ⇒  =  AKL ACB(c g c)
AKL ACB, suy ra tứ giác BKLC nội tiếp. (0,5đ) 3 b) Từ  =  1 ⇒  1 =  +  ACB AKL sd APB (sdAQ sdPB) 2 2 1 ⇒  +  (sdAP sdPB) 1 =  + 
(sdAQ sdPB)⇒  = 
sd AP sd AQ ⇒ A là trung điểm cung PQ, 2 2
suy ra AP = AQ (4) (0,25đ)
Xét tam giác APK và tam giác ABP có 
PAB chung và  = 
APK ABP (hai góc nội tiếp
chắn hai cung bằng nhau), suy ra ∆  ∆ ( − ) AP AK APK ABP g g ⇒ = AB AP 2
⇒ AP = AK.AB (5)Từ (1), (5) và (4) suy ra AP = AH = AQ, (0,25đ)
suy ra A là tâm đường tròn ngoại tiếp tam giác PQH, mà AH ⊥ BC, nên BC là tiếp
tuyến của đường tròn ngoại tiếp tam giác PHQ. (0,5đ)
c) Xét hai tam giác APD và AMP có  PAM chung và  =  1 =  1 =  =  APD APQ sd AQ sd AP AMP, dó đó 2 2 AP AD 2 APD ∆  AM ∆
P(g − g) ⇒ = ⇒ AP = .
AD AM , (0,25đ) AM AP do đó 2 2 = = . AH AM AH AP AD AM ⇒ = AD AH Xét hai tam giác A ∆ HM và A ∆ DH có 
HAM chung và AH AM = , do đó AD AH AHM ∆  ADH ∆
(c − g − c) ⇒  = 
AMH AHD ⇒ AH là tiếp tuyến của đường tròn ngoại tiếp tam giác DHM, (0,5đ) Suy ra  =  0 = −  0 1 = −  +  THM HDM 90 MDP 90 (sdPM sdAQ) 0 1 = −  +  90 (sdPM sdAP) 2 2 0 1 = −  0 = −  0 = −  ⇒  +  0 = ⇒  0 90 sd APM 90 ATM 90 HTM THM HTM 90
HMT = 90 .(0,25đ) 2
Câu 5. Xét một số A bất kỳ trong 6 số đó, xét 5 tổng của A với 5 số còn lại. Ta thấy
trong 5 tổng này ít nhất có 3 tổng cùng là là số vô tỉ hoặc cùng là hữu tỉ.
*) Nếu có ít nhất 3 tổng là vô tỷ chẳng hạn A + B ; A + B ; A + B là vô tỉ, xét 3 số 1 2 3
B + B ;B + B ;B + B nếu có 1 số vô tỷ chẳng hạn B + B thì bộ 3 số ( , A B ,B thỏa 1 2 ) 1 2 1 3 3 2 1 2
mãn yêu cầu bài toán. Nếu không có số nào vô tỉ thì cả 3 số đó hữu tỉ, điều này dẫn đến
(B + B + B + B − B + B = 2B hữu tỉ , vô lý. (0,5đ) 1 2 ) ( 1 3) ( 3 2) 1
Trường hợp nếu có ít nhất 3 tổng là hữu tỉ chẳng hạn A + B ; A + B ; A + B hữu tỉ 1 2 3
Thì ta cũng lập luận như trên đối với bộ (B ,B ,B . 1 2 3 )
Vậy bài toán đã được chứng minh. (0,25đ) 4
Bài toán không còn đúng nếu ban đều là 4 số, chẳng hạn bộ 4 số sau:
{a,1+ a,1− a,− }
a với a vô tỉ không thể chọn được ra 3 số có tổng đôi một vô tỉ. nhau (0,25đ)
………………………………….. Hết ……………………………… 5
SỞ GD & ĐT THANH HÓA
KỲ THI KHẢO SÁT CÁC MÔN THI VÀO LỚP 10
TRƯỜNG THPT CHUYÊN LAM SƠN THPT CHUYÊN LAM SƠN
Năm học: 2024 - 2025 ĐỀ THI CHÍNH THỨC Môn thi: TOÁN
( Đề thi có 01 trang)
(Dành cho thí sinh thi vào lớp chuyên Tin học) Ngày thi: 07/4/2024
Thời gian làm bài:150 phút (không kể thời gian phát đề) 4 3 2
Câu 1. a) Tính giá trị của biểu thức
x − 6x − 2x +18x + 23 P(x) =
tại x = 19 − 8 3. 2 x − 8x +15
b) Cho x, y là các số hữu tỉ dương sao cho x − 2 3 là số hữu tỉ. Tính x .y 2 − y 3
Câu 2. a) Giải phương trình: 2
3x - 2 + 5x -1 = x − x + 3. 3 2 4x = y + 3
b) Giải hệ phương trình  . 3 2 4y = x + 3
Câu 3. a) Cho các số thực x, y khác 0, sao cho 1 x + và 1
y + là những số nguyên, y x chứng minh rằng 1 3 3 x y + là số nguyên. 3 3 x y
b) Giải phương trình nghiệm nguyên dương 6 3 4
x + 3x +1= y .
Câu 4. Tam giác nhọn không cân ABC nội tiếp đường tròn (O), đường cao AH (H ∈BC).
Gọi K,L lần lượt là hình chiếu vuông góc của điểm H trên các cạnh AB, AC.
Đường thẳng KL cắt đường tròn (O) tại hai điểm P,Q ( P và B cùng phía đối với AC ).
a) Chứng minh tứ giác BKLC nội tiếp đường tròn.
b) Chứng minh PQ vuông góc với A . O
c) AH cắt lại đường tròn (O) tại T (T ≠ ).
A Chứng minh H là tâm đường tròn
nội tiếp tam giác PT . Q
Câu 5. Các số thực dương x, y thỏa mãn: 3 3
x + y = x − y, chứng minh 2 2 x + y <1.
…………………………………….. Hết ……………………………………
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:................................................................ Số báo danh:...........................
Chữ kí của giám thị số 1 : ………………………….Chữ kí của giám thị số 2:……………
SỞ GD & ĐT THANH HÓA
KỲ THI KHẢO SÁT CÁC MÔN THI VÀO LỚP 10
TRƯỜNG THPT CHUYÊN LAM SƠN THPT CHUYÊN LAM SƠN
Năm học: 2024 - 2025 ĐỀ THI CHÍNH THỨC
Môn thi: Toán (cho chuyên Tin)
( Đề thi có 01 trang) Ngày thi: 07/4/2024
Thời gian làm bài:150 phút (không kể thời gian phát đề) ĐÁP ÁN
Câu 1. a) Ta có x = − = ( − )2 2 19 8 3 4
3 = 4 − 3 ⇒ 4 − x = 3 ⇒ x −8x +13 = 0. (0,5đ) Do đó 4 3 2 2 2
x − 6x − 2x +18x + 23 = (x − 8x +13)(x + 2x +1) +10 =10. Vậy P( − ) 10 19 8 3 = = 5. (0,5đ) 2 x (x−2 3)(2+ − y 3 2 3 ) b) Ta có = 2 2 − y 3 4 − 3y (0,5đ)
2x − 3.2y + (xy − 4) 3 =
, là số hữu tỉ khi xy = 4. (0,5đ) 2 4 − 3y Cách khác: Đặt x − 2 3 a = (  b − ay = a,b∈ ;  a,b ≠ 0)) 2 0
⇒ bx − 2a = (2b − ay) 3 ⇒  ⇒ xy = 4. 2 − y 3 b bx  − 2a = 0
Câu 2. a) ĐK: x ≥ 2 / 3. Ta có: 2
3x-2 + 5x-1 = x − x + 3 ⇔ (x − 3x-2) + (x +1− 5x-1) 2
+ (x − 3x + 2) = 0 2 2
x − 3x+2 (x +1) − (5x-1) 2 ⇔ +
+ (x − 3x + 2) = 0 (0,5d) 3x-2 + x 5x-1 + (x +1)   2 1 1
⇔ (x − 3x + 2) + +1 =   0  3x-2 + x 5x-1 + (x +1)  Ta có: 1 1 + +1> 0, x ∀ ≥ 2 / 3 3x +1 + (x +1) 5x + 4 + (x + 2) Suy ra: 2
x − 3x + 2 = 0 ⇔ x =1, x = 2 (tm)
KL: x =1, x = 2. (0,5đ) 3 2
4x = y + 3 (1)
b) Giải hệ phương trình:  3 2
4y = x + 3 (2). 1
Lấy phương trình (1) trừ phương trình (2) vế theo vế, ta được: x − y = 0 2 2
(x − y)(4x + 4y + 4xy + x + y) = 0 ⇔  2 2
4x + 4y + 4xy + x + y = 0. (0,25đ)
- Với x− y =0⇔ x= y, thay vào phương trình (1) ta được 3 2 2
4x − x − 3 = 0 ⇔ (x −1)(4x + 3x + 3) = 0 ⇔ x =1, (vì pt 2
4x + 3x + 3 = 0, có ∆ = 2
− 7 < 0, nên vô nghiệm)
Từ x =1⇒ y =1⇒ x = y =1 là nghiệm. (0,5đ)
- Từ phương trình (1) và (2) suy ra các vế trái của (1) và (2) dương, suy ra
x > 0, y > 0. Do đó phương rình 2 2
4x + 4y + 4xy + x + y = 0 vô nghiệm.
Vậy hệ phương trình đã cho có một nghệm x = y =1. (0,25đ)  
Câu 3. a) Từ giả thiết suy ra: 1  1  1  x +  y + = xy + +   2 là số nguyên 1 ⇒ xy +  y  x  xy xy
là số nguyên. (0,5đ) 3 3       Từ đó ta có 3 3 1 1 1 1 1 x y + = xy + =    xy + −  3x . y  xy + 3 3 ( )3 x y xy xy xy xy        3     1 1 =  xy + −  3 xy + là số nguyên (đpcm) (0,5đ) xy xy     
b) Giải phương trình nghiệm nguyên dương: 6 3 4
x + 3x +1= y (1) Đặt 3
z = x , phương trình (1) trở thành 2 4
z + 3z +1− y = 0 (2)
Phương trình (2) ẩn z có 4 ∆ = 5 + 4y .
Nếu phương trình (2) có nghiệm nguyên thì 4 2 *
∆ = + y = m m∈ ⇒ ( 2 m − y )( 2 5 4 ( ) 2
m + 2y ) = 5 (0,25) 2
m + 2y = 5 m = 3 ⇒  ⇒  ⇒ y = 1. ± (0,5đ) 2 2
m − 2y =1 y =1
Với y =1⇒ x = 0 (loại) Với y = 1 − (loại).
Vậy phương trình đã cho không có nghiệm nguyên dương. (0,25đ)
Cách khác: Vì x > 0, nên 3 2 6 3 4 3 2 6 3
(x +1) < x + 3x +1= y < (x + 2) = x + 4x + 4. (2) Mà 3 2 (x +1) và 3 2
(x + 2) là hai số chính phương liên tiếp, nên (2) suy ra 4 y không
chính phương (vô lý). Vây phương trinhg (1) vô nghiệm nguyên dương. 2
Câu 4. a) Ta có tam giác AHB vuông tại H và có đường cao là HK, nên 2
AH = AK.AB (1) (hệ thức trong tam giác vuông). Tương tự ta có 2 AH = . AL AC (2). Từ(1) và (2) ta được . = . AK AL AK AB AL AC ⇒ = (3) (0,5đ) AC AB
Xét tam giác AKL và ACB có 
KAL chung và thỏa mãn (3), suy ra ∆  ∆ ⇒  =  AKL ACB
AKL ACB, suy ra tứ giác BKLC nội tiếp. (0,5đ)
b) (Có nhiều cách để chứng minh PQ ⊥ AO , sau đây chỉ nêu một cách) Từ  =  1 ⇒  1 =  +  ACB AKL sd APB
(sdAQ sdPB) (0,25đ) 2 2 1 ⇒  +  (sdAP sdPB) 1 =  + 
(sdAQ sdPB)⇒  = 
sd AP sd AQ ⇒ A là trung điểm cung PQ, (0,5đ) 2 2 do đó PQ ⊥ . AO (0,25đ)
c) Từ A là trung điểm cung PQ, suy ra AP = AQ (4) và TA là phân giác  PT . Q
Xét tam giác APK và tam giác ABP có 
PAB chung và  = 
APK ABP (hai góc nội tiếp
chắn hai cung bằng nhau), suy ra AP AK 2 APK ∆  ABP ∆ (g − g) ⇒ =
⇒ AP = AK.AB (5) Từ (1), (5) và (4) suy ra AB AP AP = AH = . AQ (0,5đ)
Từ tam giác APH cân tại A, suy ra
 =  ⇒  +  =  +  =  +  =  +  ⇒  =  APH AHP
APQ QPH HPT HTP HPT ATQ HPT APQ QPH HPT,
suy ra PH là phân giác của  T . PQ (0,25đ)
Vậy H là giao điểm của hai đường phân giác trong trong tam giác TPQ, do đó H là
tâm đường tròn nội tiếp tam giác TPQ. (0,25đ)
Câu 5. Do x, y dương nên 3 3
x − y = x + y > 0 ⇒ x > y (0,25đ) 3
Do x, y dương nên 3 3 3 3
x − y = x + y > x − y (0,25đ) 3 3
⇒ x − y > x − y 2 2
⇒ x + xy + y <1 Suy ra 2 2
x + y <1 (đpcm) (0,5đ)
…………………………………….. Hết …………………………………… 4
Document Outline

• Đề thi KSCL vào 10(Toán chuyên Toán)
• ĐA -Toán chuyên
• Đề thioán cho chuyên Tin)
• ĐA-Toán cho chuyên Tin)