Đề khảo sát Toán thi vào 10 năm 2022 – 2023 phòng GD&ĐT Ba Đình – Hà Nội

UBND QUẬN BA ĐÌNH
ĐỀ KHẢO SÁT THI VÀO LỚP 10
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022-2023 Môn: TOÁN 9 ĐỀ CHÍNH THỨC Ngày kiểm tra: 29/4/2022
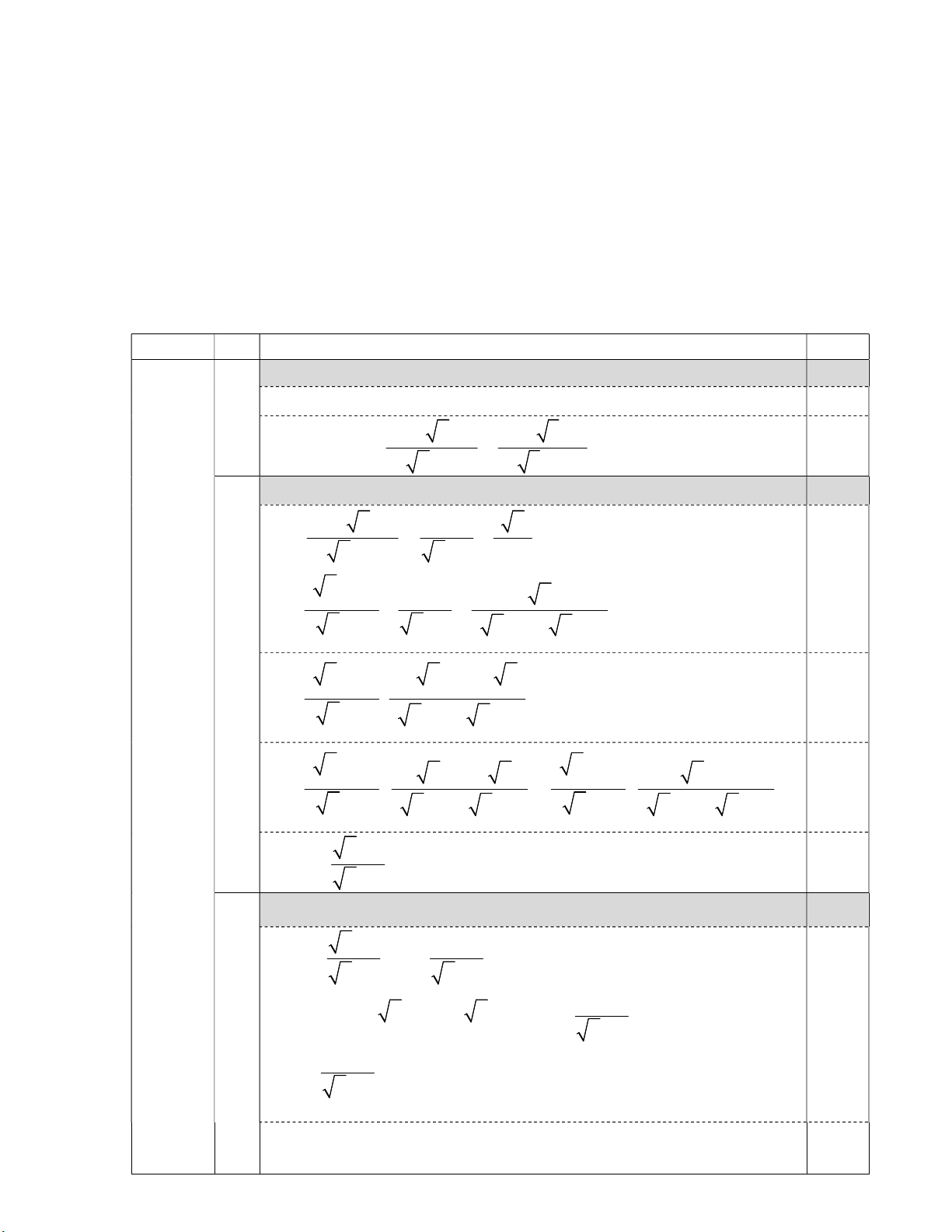
Thời gian làm bài: 120 phút (Đề thi gồm 01 trang) Bài I (2,0 điểm). x  2 x  1 2 x Cho biểu thức: A  ;B  
với x  0,x  1,x  4 . x  2 x  1 x  1
1) Tính giá trị của biểu thức A khi x  9.
2) Rút gọn biểu thức P  A B . .
3) Tìm tất cả giá trị của x để biểu thức P nhận giá trị là số nguyên âm. Bài II (2,0 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một đội sản xuất phải làm 10 000 khẩu trang trong một thời gian quy định. Nhờ cải tiến kĩ
thuật và tăng giờ làm nên mỗi ngày đội sản xuất được thêm 200 khẩu trang. Vì vậy, không những
đã làm vượt mức kế hoạch 800 khẩu trang mà còn hoàn thành công việc sớm hơn 1 ngày so với
dự định. Tính số khẩu trang mà đội sản xuất phải làm trong một ngày theo dự định.
2) Một thùng nước bằng tôn có dạng hình trụ với bán kính đáy là 0,2m và chiều cao
0, 4 m. Hỏi thùng nước này đựng đầy được bao nhiêu lít nước ? (Bỏ qua bề dày của thùng
nước, lấy   3,14 và làm tròn kết quả đến chữ số thập phân thứ hai). Bài III (2,5 điểm)  1  y2   6
1) Giải hệ phương trình x  1  . 2   y 3  5 x  1
2) Trên mặt phẳng tọa độ Oxy, cho parabol P  2
: y  x và đường thẳng
d : y  m  2x  m 2 .
a) Xác định tọa độ giao điểm d  và P  khi m  3  .
b) Tìm tất cả giá trị của m để d  cắt P  tại hai điểm phân biệt có hoành độ lần lượt 1 1 x x là x ,x thỏa mãn 1 2   . 1 2 x 4 1 x2 Bài IV (3 điểm)
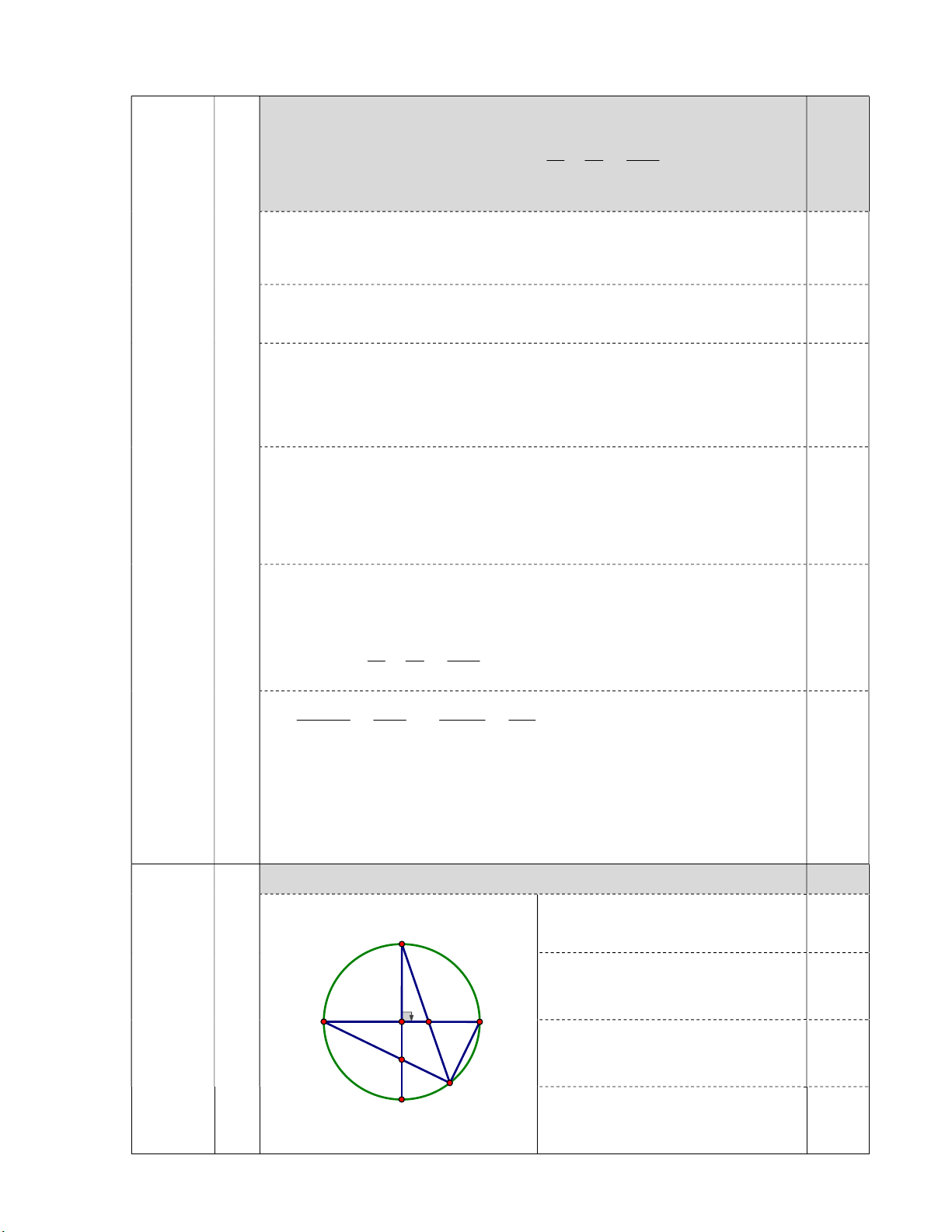
Cho đường tròn O;R có hai đường kính AB và CD vuông góc với nhau. Lấy
điểm I thuộc đoạn thẳng OB I  O,B. Gọi E là giao điểm của đường thẳng CI với
O E  C, H là giao điểm của hai đoạn thẳng AE và CD.
1) Chứng minh tứ giác OHEB là tứ giác nội tiếp. 2) Chứng minh AH AE  R2 . 2 . OH
3) Nếu I là trung điểm của đoạn thẳng OB. Tính tỉ số . OA
4) Tìm vị trí của I trên đoạn thẳng OB sao cho tích EAE . B E . C E
. D đạt giá trị lớn nhất.
Bài V (0,5 điểm). Giải phương trình: x2  x 4  1  x  1  x 2  4.
…….……………Hết…………………. 2 HƯỚNG DẪN CHẤM HƯỚNG DẪN CHUNG
+) Điểm toàn bài để lẻ đến 0,25.
+) Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm.
+) Các tình huống phát sinh trong quá trình chấm do Hội đồng chấm thi quy định, thống nhất bằng biên bản.
+) Chú ý: Bài IV ý 3 học sinh không cần vẽ lại hình. Bài Ý Đáp án Điểm
Tính giá trị của biểu thức A khi x  9. 0,5
Thay x  9 (TMĐK) vào biểu thức . A 0,25 1)
x  2 x  1 9  2 9  1 Tính được A    4. 0,25 x  2 9  2
Rút gọn biểu thức P  A B . . 1,0 x  2 x  1  2 x  P      x  2  x   1 x  1   2 x 1    0,25  2 x .   
x 2  x 1  x 1 x 1          2 x  1 2 x 1 2)  x  . 0,25
x  2  x 1 x 1 Bài I  2 2 x  1    x x x  1 2 2  2,0 điểm x  2     0,25
x  2  x 1 x 1
x  2  x 1 x  1 x  P  1  . 0,25 x  1
Tìm tất cả giá trị của x để biểu thức P nhận giá trị là số nguyên âm. 0,5 x  P  1 2 )   1  . x  1 x  1 2
Với x  0 thì x  0  x  1  1   2 0,25 3) x  1 2  1 
 1  P  1. Mà P nhận giá trị là số nguyên âm x  1  P  1.
)P  1  x  0 (TMĐK). 0,25
Vậy x  0 thì P nhận giá trị là số nguyên âm. 3
Tính số khẩu trang mà đội sản xuất phải làm trong một ngày theo dự định. 1,5
+) Gọi số khẩu trang mà đội sản xuất phải làm trong một ngày theo dự định là x (cái) x  0. 0,25 10 000
+) Thời gian làm theo dự định là: (ngày). x 0,25
+) Tổng số khẩu trang thực tế sản xuất là: 10 000  800  10 800 (cái).
+) Thực tế, mỗi ngày của đội sản xuất được số khẩu trang là: 10 800 x 0,25
 200 (cái), thời gian làm là: (ngày). x  200
+) Vì hoàn thành công việc sớm hơn 1 ngày so với dự định nên ta có 10 000 10 800 Bài II 0,25 phương trình:   1. 2,0 điểm x x  200
 10000x  200  1080 x 0  x x  200  8  0 x 0  2000 000  x2  20 x 0  x2  100 x 0  2 000 000  0 x   1000 0,25  x  2  000 
Đối chiếu điều kiện và kết luận số khẩu trang mà đội sản xuất phải làm
trong một ngày theo dự định là 1000 cái/ngày. 0,25
Hỏi thùng nước này đựng đầy được bao nhiêu lít nước ? 0,5
Thể tích nước là thể tích của thùng nước. 0,25
2) Thùng nước đựng đầy được số lít nước là: V   R2 h 2  V  m3 . . 3,14.0,2 .0,4 0,05024
 V  50,24lít. 0,25  1  y2   6
Giải hệ phương trình x  1  . 2 1,0   y 3  5 x  1 Điều kiện x  1. 0,25  1   y 2 2  6  y 4    12 7y  7 1) x 1    x 1       2 2 2 0,25          Bài III y 3 5 y 3 5 y 3 5 x     1 2,5 điểm x 1 x  1 y   1 y   1     1   0,25  x 5 4  x 1     4
Đối chiếu điều kiện và kết luận hệ phương trình có nghiệm    x y 5 ;   ;1. 0,25  4 
2) a) Xác định tọa độ giao điểm d  và P  khi m  3  . 1,5 4
b) Tìm tất cả giá trị của m để d  cắt P  tại hai điểm phân biệt có 1 1 x x
hoành độ lần lượt là x ,x thỏa mãn 1 2   . 1 2 x x 4 1 2
a) +) Phương trình hoành độ giao điểm của d  và P : 0,25
x2  m  x  m  x2 2 2  m  2x  m 2  0 1. +) Thay m  3  vào (1) ta được:
x2  x  6  0  x  3x  2  0 0,25 x   2  x  3   0,25
Tính được tọa độ hai giao điểm là 2;4;3;9. 2
b) +) Tính được   m  2 .
+) d  cắt P  tại hai điểm phân biệt  1 có hai nghiệm phân biệt 0,25     m  2 0 2  0  m  2. x   x  m  2
+) Lập luận áp dụng hệ thức Vi-et có: 1 2 x  x   m . 2  1 2 0,25 1 1 x x +) Biến đổi : 1 2  
(Điều kiện x ,x  0  m  0 ) x x 4 1 2 1 2 x  2  2 1 x2 x x12 m m     x x 4 2 4 1 2 m
 2  m  m2 m  0  m2  m  2  0 m  0 0,25 m   1   m  .   2 
Đối chiếu điều kiện và kết luận m  1  .
Chứng minh tứ giác OHEB là tứ giác nội tiếp. 1,0
+) Vẽ hình đúng đến câu 1. 0,25 C Bài IV +) Lập luận được  AEB  90 . 0,25 1) I O 3,0 điểm A B +) Tứ giác OHEB có 0,25 H   HEB HOB 180   , E D
mà hai góc ở vị trí đối nhau nên tứ 0,25
giác OHEB là tứ giác nội tiếp 5 Chứng minh AH AE  R2 . 2 . 1,0 +) Xét A  OH và A  EB có:   AEB  AOH  90 0,25  2) HAO chung  A  OH đồng dạng với A
 EB theo trường hợp góc – góc. 0,25 AH AO   0,25 AB AE  AH AE  AB AO  R2 . . 2 . 0,25 OH
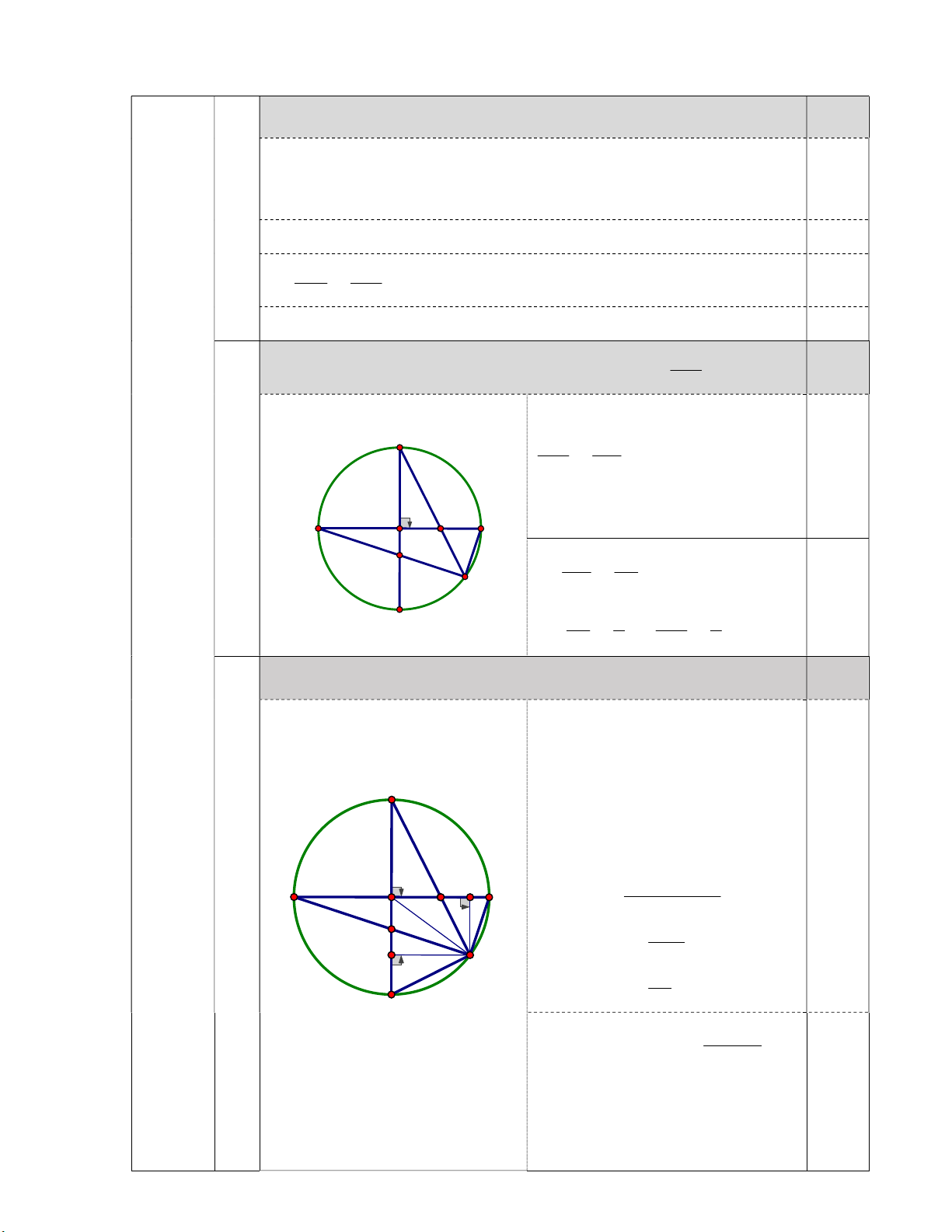
Nếu I là trung điểm của đoạn thẳng OB. Tính tỉ số . 0,5 OA +) A  OH đồng dạng với A  EB C OH EB  . OA EA 0,25 3)
+) Lập luận được EI là phân giác O I A B của  AEB. H EB IB   . E EA IA 0,25 D IB 1 OH 1 Mà    . IA 3 OA 3
Tìm vị trí của I trên đoạn thẳng OB sao cho tích EAE . B E . C E . D đạt 0,5 giá trị lớn nhất.
+) Kẻ EM,EN lần lượt vuông góc với AB,CD tại M,N. +) Lập luận được: C EAE . B E . C E . D  EM A . B E . N C . D  EM E . N. R2 4 . +) Ta có: 0,25 2 2 O I M EM  EN A B EM E . N  4) 2 H OE2  EM E . N  N E 2 R2  EM E . N  D 2 R2. R2  EAEB EC ED 4 . . .  2  EAE . B E . C E . D  R4 2 . 0,25 +) Dấu "  " xảy ra
 EM  EN  OE là phân giác của 
BOD  I là giao điểm của 6
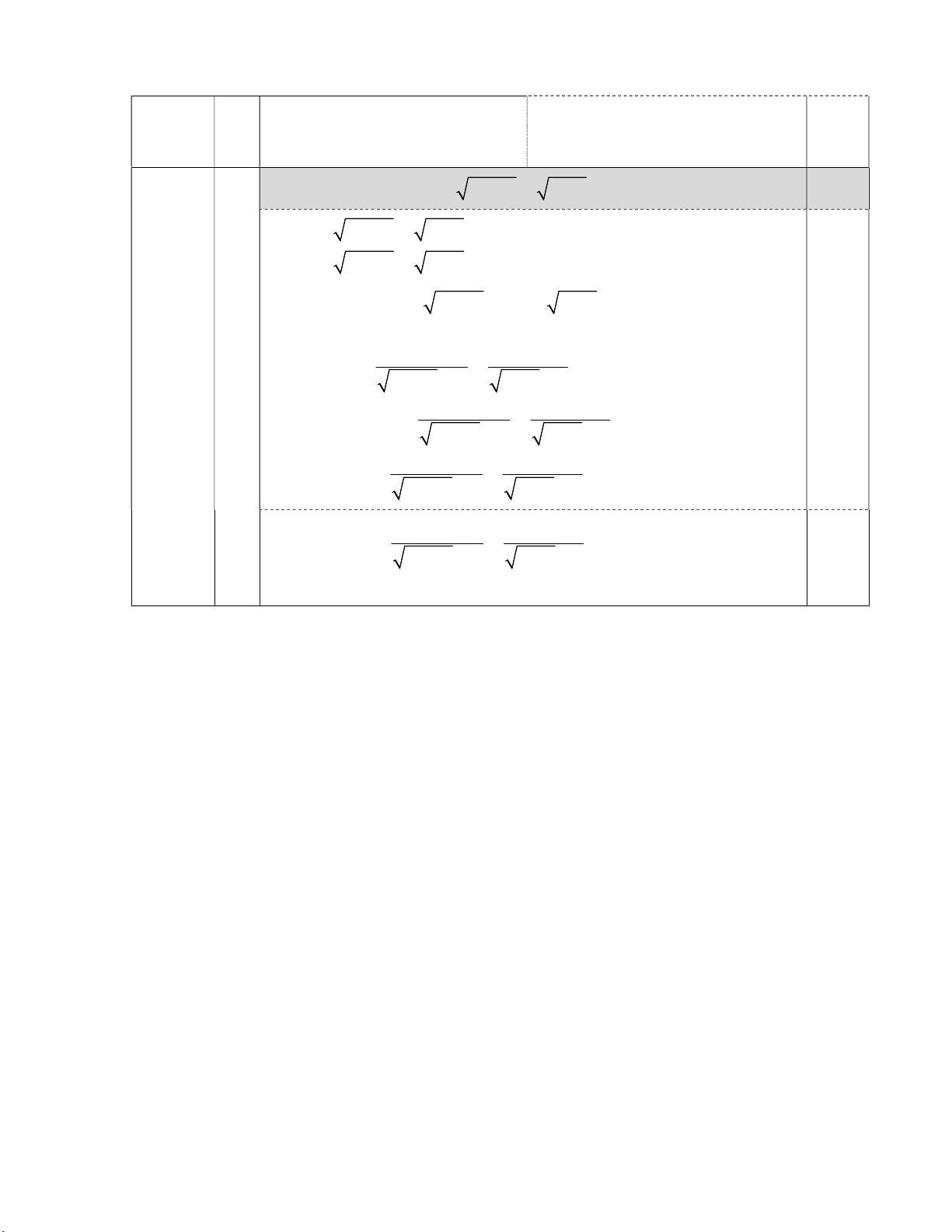
OB và CE với E là điểm chính giữa của cung BD. Kết luận. Giải phương trình: x2  x 4  1  x  1  x 2  4. 0,5 x2  x 4  1  x  1  x 2  4 Điều kiện x  1  x2  x 4  1  x  1  x 2  4  0  x2  x 4  4   x
4  1  3   x 1 1   x 2  4  0    2 x 4  8 x x  2 2    2x  2  0 0,25 Bài V x 4  1  3 x  1  1 0,5 điểm     x   x 4 1 2   2    2  0  x 4  1  3 x  1  1      x   x 4 1 2      0  x 4  1  3 x  1  1 4 1 Vì x  1  x  
 0  x  2  0  x  2. x 4  1  3 x  1  1 0,25
Đối chiếu điều kiện và kết luận.