Đề khảo sát Toán (Tin) vào 10 năm 2023 – 2024 trường chuyên Lam Sơn – Thanh Hóa

SỞ GD & ĐT THANH HÓA
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT
TRƯỜNG THPT CHUYÊN LAM SƠN CÁC MÔN THI VÀO LỚP 10 THPT CHUYÊN LAM SƠN NĂM HỌC 2023 - 2024 Môn: TOÁN
(Dành cho thí sinh thi vào lớp chuyên Tin)
Hướng dẫn chấm này gồm 04 trang Hướng dẫn chung:
1) Nếu học sinh giải cách khác với cách nêu trong HDC này mà đúng thì vẫn được điểm tối
đa của câu, ý tương ứng.
2) Trong câu hình, nếu học sinh không vẽ hình hoặc vẽ sai cơ bản thì không cho điểm câu đó. Câu Ý Nội dung Điểm
Cho hai số thực dương x, y thỏa mãn x  y  9 và xy  4 . Tính giá trị của biểu thức  x  y 2 2 (x  y ) P  . x x  y y 1  x  y 2 2 (x  y )  x  y(x y)(x y) (1,0đ) Ta có P   0,5 x x  y y
 x  yx xy  y
 x  y2 x  y(x y) x y2 xy(x y) (94).9 45      . 0,5
x  y x  xy  y x y xy 9  2 7 I (2,0đ)
Cho hai số thực a,b phân biệt thỏa mãn 2 2
a  2023a  b  2023b  c , với c là một số
thực dương. Chứng minh rằng 1 1 2023    0 . a b c 2
Theo bài ra ta có a,b là nghiệm của phương trình 2 x  2023x  c  0 . (1,0đ) a  b  2023 0,5
Do đó theo Hệ thức Vi-et, ta có  .  . a b  c 1 1 2023 a  b 2023 2023 2023 Suy ra        0 , đpcm. a b c ab c c c 0,5
Giải phương trình  x   x   2 5
2 1 x  3x 10   7 (1) Điều kiện: x  2 .
Phương trình (1) có thể viết lại thành:  x  5  x  21 x  5. x  2  7 0,25 a  x  5 Đặt  a  b  0thì 2 2
a  b  7 và phương trình trên trở thành: II 1 b   x  2 0,25 (2,0đ) (1,0đ) a b  ab 2 2 1
 a  b  a  b1 ab  a b  0     
a  b  a  b 1 a 0 1 1   do a  b 1   b  0 0,25 a  1  x  5 1 x  4(ktm)      b 1    x  2 1 x  3(tm)
Vậy phương trình đã cho có nghiệm duy nhất x  3. 0,25 3 3
2x - 7y  (x  y)(7  2xy)
Giải hệ phương trình  . 2 2 x  xy  y  7 3 3 3 3 2 2
2x - 7y  (x  y)(7  2xy)
2x - 7y  (x  y)(x  xy  y ) Ta có    0,25 2 2 2 2 x  xy  y  7 x  xy  y  7 3 3 3 3 3 3 2x  7y  x  y x  8y x  2y     2   0,25 2 2 2 2 x  xy  y  7 x  xy  y  7 2 7 y  7 (1,0đ) x  2  x  2y y  1    . 0,25 2 y 1   x  2  y  1
Vậy hệ phương trình có hai nghiệm  ; x y  2;  1 và  ; x y   2  ;  1 . 0,25
Giải phương trình nghiệm nguyên 2 2 2
xy  y  2x  xy  x y  2 y 1. Ta có 2 2 2 2 2 2
xy  y  2x  xy  x y  2y 1  xy  y  2x  xy  x y  2y  1   2 2 x y  xy    2
xy  y   2 x  y  1  xy  x  y  y  x  y  2 x  y  1 0,5
 x  y xy  y  2 1   1
Vì đây là phương trình nghiệm nguyên nên ta có: x  y  1  (*)       xy y 2 1 1   1 x  y  1     ** (1,0đ)
xy  y  2  1 x  1 y         x 1 y x 1 y  x  0; y  1 0,5 *      y   1 y   1 2 y  y 1  0   y 1  0  x  2; y  1  y  1  III x  1 y x  1 y x  1   y  x  2; y  1 (2,0đ) ( * * )       y    1 y   1 2 y  y  3  0  y  2y  3  0  x  2; y  3   y  3
Vậy tập nghiệm của hệ phương trình là S  
 0; 1,2; 1,2; 1,2; 3  .
Tìm các số nguyên dương a,b thỏa mãn: 2 a(ab 1)(a  ) b và 2 b(ab 1)(b  a) . Theo bài ra ta có: 2 2 2 2 2 (a  ) b | a(ab 1)  (a  ) b | ( b a  )
b  a(ab 1)  (a  b) | (b  a) (1). 0,25 Lại có: 2 2 2 2 2 2
(b  a) | b(ab 1)  (b  a) | b(ab 1)  a(b  a)  (b  a) | (a  ) b (2). (1,0đ) 0,25 Từ (1) và (2) ta suy ra: 2 2 | a  b | |  b  a |.
Ta xét hai trường hợp sau Trường hợp 1: 2 2 2 2
a  b  b  a  a  b  a  b  0  (a  b)(a  b 1)  0  b  a 1 0,25 (vì a  b  0 ).
Thay b  a 1 vào giả thiết ta thấy thỏa mãn. Trường hợp 2: 2 2 2 2
a  b  b  a  a  a  b  b .
Vì a là số nguyên dương nên 2 a  a . Suy ra 2 2 2
a  a  b  b  a  b  b  a nên 0,25 trường hợp này loại.
Vậy tất cả các cặp số (a;b) thỏa mãn là: (t;t 1) với t là số nguyên dương bất kì. Cho ba điểm ,
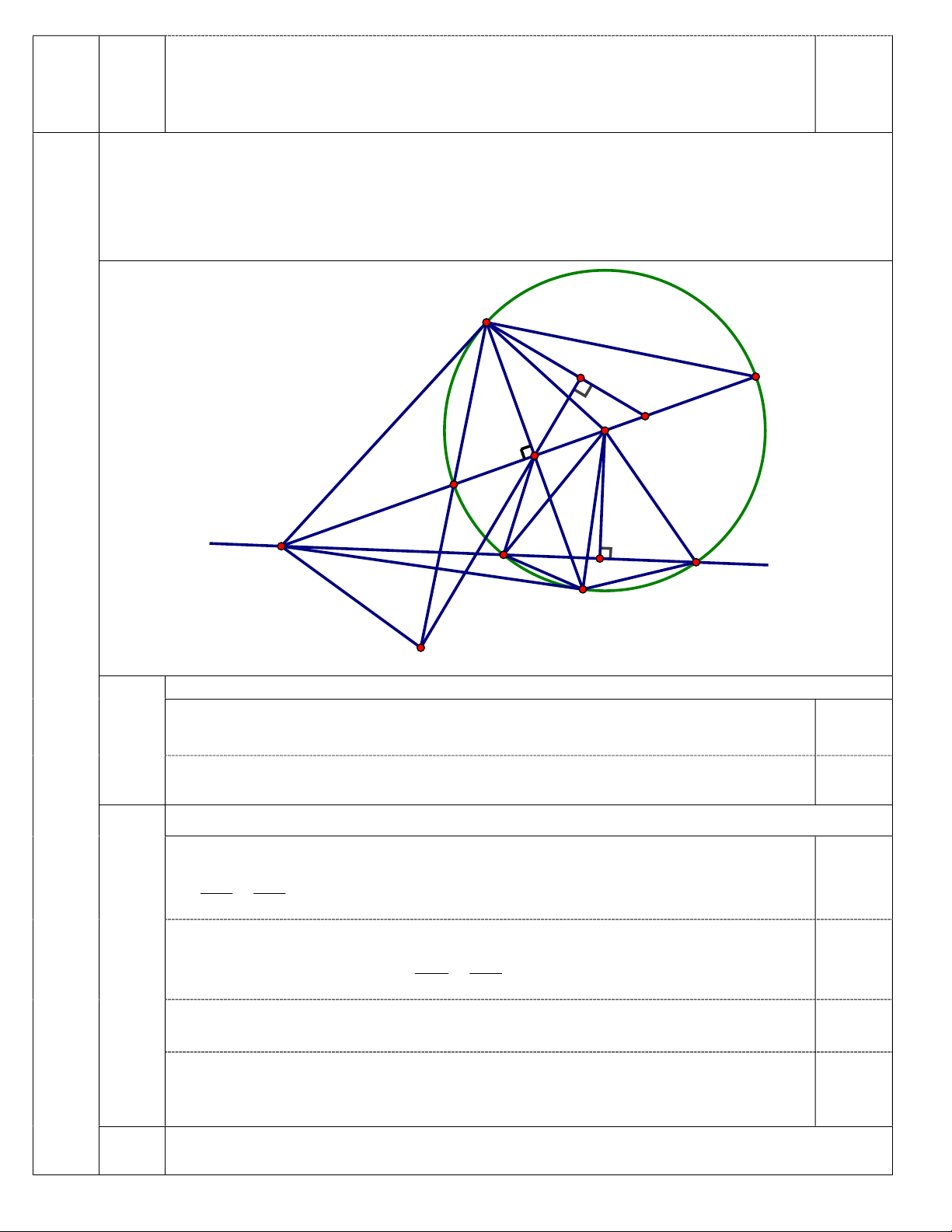
A B,C cố định nằm trên một đường thẳng d ( B nằm giữa A và C ). Vẽ đường
tròn tâm O thay đổi nhưng luôn đi qua B và C ( O không thuộc đường thẳng d ). Kẻ AM
và AN là các tiếp tuyến với đường tròn tâm O ( M , N là các tiếp điểm và N thuộc cung
nhỏ BC ). Đường thẳng AO cắt MN tại điểm H và cắt đường tròn tại các điểm P và Q ( P
nằm giữa A và Q ). Gọi I là trung điểm của BC . M F Q O D H P d A B I C N IV E (3,0đ)
Chứng minh rằng tứ giác AMOI nội tiếp.
Do AM là tiếp tuyến với đường tròn tâm O nên  0 AMO  90 . 1 0,5
(1,0đ) Do I là trung điểm của BC nên IO  BC . Suy ra  0 AIO  90 . Tứ giác AMOI có  AMO   0 0 0
AIO  90  90  180 nên nội tiếp (đpcm). 0,5
Gọi J là tâm đường tròn ngoại tiếp tam giác BHO . Chứng minh O, I, J thẳng hàng.
Ta có ABN đồng dạng với ANC (vì  ANB   ACN ,  CAN chung) AB AN 0,25   AB.AC = AN2. AN AC
Vì ANO vuông tại N, đường cao NH nên 2 AH.AO  AN . 2 AB AO 0,25 (1,0đ) Suy ra A . B AC  AH.AO hay  . AH AK Do đó A  BH A  OC . Suy ra  ABH   AOC hay  ABH   HOC . 0,25
Do đó tứ giác CBOH nội tiếp.
Vì J là tâm đường tròn ngoại tiếp tam giác BHO nên J cũng là tâm đường
tròn ngoại tiếp tứ giác CBOH . Do đó J nằm trên đường trung trực của đoạn 0,25
thẳng BC hay O, I, J thẳng hàng (đpcm). 3
Gọi D là trung điểm của HQ , từ H kẻ đường thẳng vuông góc với MD cắt đường thẳng
(1,0đ) MP tại E.Chứng minh P là trung điểm của ME .
Xét hai tam giác MHE và QDM , ta có:  EMH  
MQD (hai góc nội tiếp chắn hai cung bằng nhau). 0,25 Lại có  EDQ   MHD   0 HMD    0 HMD    0 90 90 FHD  90   PHE   EHM ME MH
Suy ra MHE đồng dạng QDM (g.g)   0,25 MQ DQ MP MH MH
PMH đồng dạng MQH (g.g)    0,25 MQ QH 2DQ MP 1 ME   .
 ME = 2 MP  P là trung điểm ME. 0,25 MQ 2 MQ
Cho 2023 hình chữ nhật có chiều rộng bằng 1 cm và chiều dài lần lượt bằng x cm, x cm, 1 2
, x cm. Biết rằng x , x ,, x là các số nguyên dương khác 1 thỏa mãn điều kiện 2023 1 2 2023 1 1 1   ...   88. x x x 1 2 2023
Chứng minh rằng trong 2023 hình chữ nhật này có ít nhất hai hình chữ nhật có diện tích bằng nhau.
Giả sử trong 2023 hình chữ nhật đã cho không có hai hình chữ nhật nào có diện
tích bằng nhau. Suy ra trong 2023 số nguyên dương x , x ,, x không có hai 1 2 2023 0,25
số nào bằng nhau. Không mất tính tổng quát, ta sắp xếp các số đó như sau: x  x  x  ...  x
 x  2, x  3, x  4,..., x  2024 . 1 2 3 2023 1 2 3 2023 1 1 1 1 1 1 1 1    ...    ... 0,25 V x x x x 2 3 4 2024 1 2 3 2023 (1,0đ) 2 2 2 2    ... 2 2 2 3 2 4 2 2024 0,25 (1,0đ)  1 1 1 1   2    ...     2  1 3  2 4  3 2023  2024 
 2 2  1  3  2  4  3 ...... 2024  2023  2 2024   1  88. 1 1 1 1 0,25     ...   88 , vô lí. x x x x 1 2 3 2023
Do đó trong 2023 hình chữ nhật này có ít nhất hai hình chữ nhật có diện tích bằng nhau.
------------ Hết ------------
Document Outline

• Doc1
• KSCL Chuyên Tin Lam Sơn