Đề khảo sát Toán vào 10 năm 2023 lần 3 phòng GD&ĐT Giao Thuỷ – Nam Định

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT LẦN 3 VÀO LỚP 10 THPT GIAO THỦY NĂM HỌC 2022 – 2023 Môn: Toán – lớp 9 THCS
(Thời gian làm bài: 120 phút) ĐỀ CHÍNH THỨC
Đề khảo sát gồm 02 trang.
Phần I: Trắc nghiệm (2,0 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm. 2023
Câu 1. Điều kiện xác định của biểu thức là 1 1 x A. x 1 B. x  1. C. x  1. D. x  1.
Câu 2. Cạnh huyền của một tam giác vuông có độ dài bằng 10m , hai cạnh góc vuông của
tam giác đó hơn kém nhau 2m . Độ dài hai cạnh góc vuông đó là A. 7m; 2 . m B. 6m; 4m. C. 6m;8m. D. 3m;1m.
Câu 3. Tìm tất cả các giá trị của m để phương trình 2
x 2x  m3  0 có hai nghiệm phân biệt. A. m  4. B. m  4. C. m  4. D. m  4.
Câu 4. Cho tam giác ABC vuông tại A nội tiếp đường tròn  ; O R, biết  0 ACB  60 . Độ
dài đoạn thẳng AB tính theo R là R R A. R . B. . C. . D. R 3. 2 3
Câu 5. Hàm số y  2  m x  2020 đồng biến trên  khi A. m  2. B. m  2 . C. m  2 . D. m  2 . 3 Câu 6. Cho A
 BC vuông tại A biết rằng cosB  . Tính sin C ? 5 4 2 1 3 A. sin C  . B. sin C  . C. sin C  . D. sinC  . 5 5 2 5
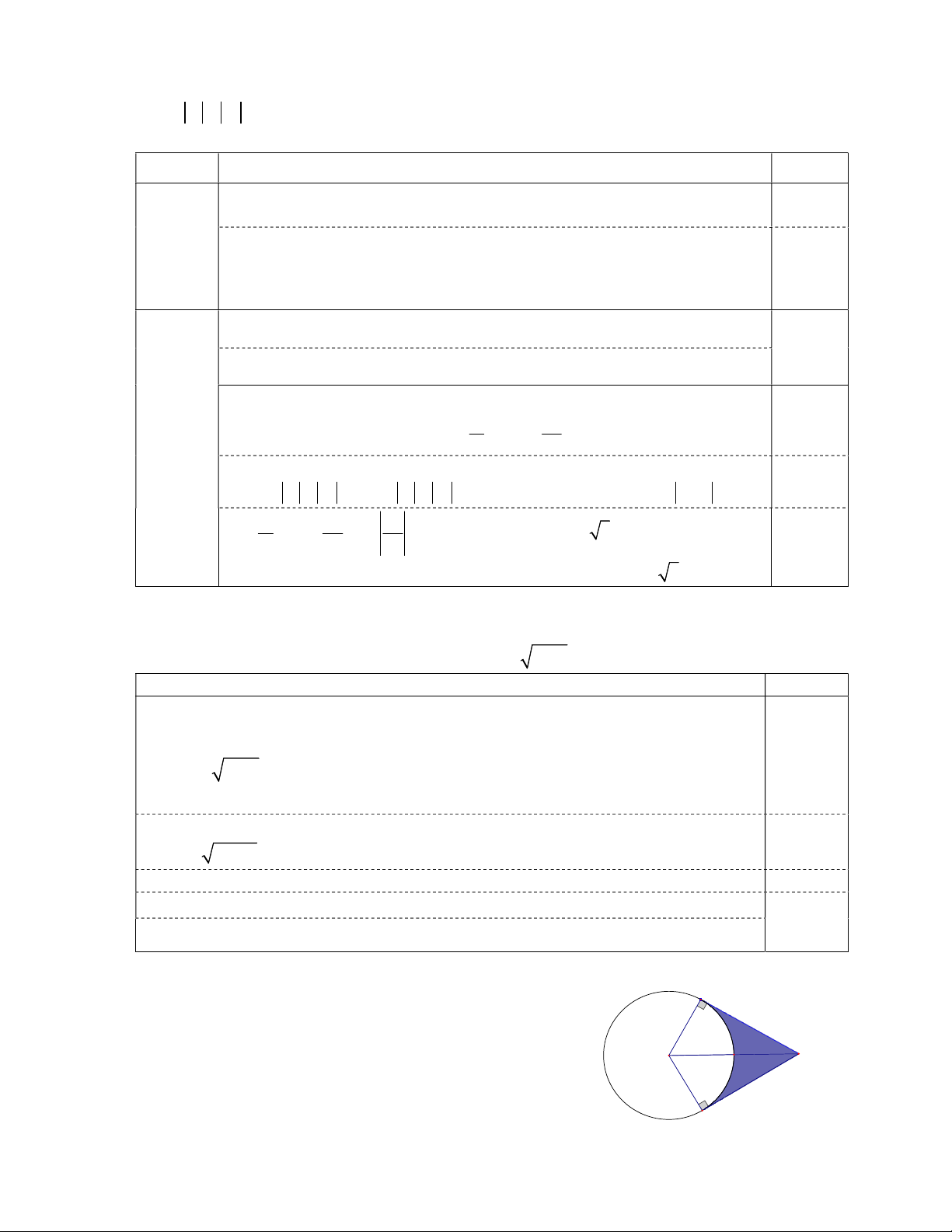
Câu 7. Đường ống nối hai bể cá trong một
thủy cung có dạng hình trụ, độ dài của
đường ống là 30m (Hình 86). Dung tích
của đường ống nói trên là 3 1950 m . Diện
tích đáy của đường ống là A. 2 65m . C. 2 50m . B. 2 60m . D. 2 80m .
Câu 8. Tất cả giá trị của m để hai đường thẳng y  5x  m 1 và y   2 3  2m  x 1song song với nhau là A. m  2  . B. m  2  . C. m  2 . D. m  0. Trang 1/2
Phần II: Tự luận (8,0 điểm) Câu 1. (1,5 điểm) 
1) Tính giá trị biểu thức Q      2 6 3 48 1 3 . 2 1  x  2 x  2 16  x  2
2) Tìm điều kiện xác định và rút gọn biểu thức P      : . x  2 x  2 4  x 8   Câu 2. (1,5 điểm).
1) Tìm toạ độ giao điểm của parabol 2
(P) : y  x và đường thẳng (d) : y 5x4. 2) Cho phương trình 2
2x mx3 0 (1) (với mlà tham số).
a) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị . m
b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm phân biệt x ; x 1 2 thỏa mãn x  x  3. 1 2 2 2 4x  y  4xy
Câu 3. (1,0 điểm). Giải hệ phương trình  2  x  y 1.  Câu 4. (3,0 điểm)
1. Cho đường tròn O;3cm. Từ điểm M nằm B
ngoài đường tròn O kẻ hai tiếp tuyến MA, MB
với đường tròn O (A, B là các tiếp điểm) sao O M cho  0
AOB 120 . Tính diện tích phần giới hạn bởi
hai tiếp tuyến MA, MB và cung nhỏ AB . A
2. Cho đường tròn (O) có dây AB không là đường kính, tiếp tuyến tại A và B cắt
nhau tại M. Vẽ cát tuyến MCD nằm giữa hai tia MA và MO, ( MC  MD ). Đoạn thẳng
MO cắt AB tại H và cắt (O) tại điểm I. Chứng minh: a) 2 MA  MC.MD và 2 MC.MD  OH.OM  MO .
b) Tứ giác OHCD nội tiếp và CI là tia phân giác của  HCM . Câu 5. (1,0 điểm) 1) Giải phương trình 2
(4x  3)x  (3  x) 3  2x . 2) Cho ,
x y là các số thực thỏa mãn đẳng thức 5
x  y  xy  . Tìm giá trị nhỏ nhất 4 của biểu thức 4 4 M  1 x  1 y .
-------------------Hết------------------
Họ và tên thí sinh: ……………………………………
Họ tên, chữ ký GT 1: ………………………………...
Số báo danh: …………………………………………...
Họ tên, chữ ký GT 2: …………………………………. Trang 2/2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT LẦN 3 GIAO THỦY
VÀO LỚP 10 THPT NĂM HỌC 2022-2023 Môn: Toán - Lớp 9 THCS ĐỀ CHÍNH THỨC
(Hướng dẫn chấm gồm 04 trang) I. Hướng dẫn chung
1. Học sinh giải theo cách khác, đúng cho điểm tối đa tương đương đáp án.
2. Điểm toàn bài là tổng điểm các câu, các ý không làm tròn.
II. Đáp án và thang điểm Phần I. Trắc nghiệm
Mỗi đáp án đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 Đáp án A C C D A D A B Phần II. Tự luận Câu 1. (1,5 điểm) 
1) Tính giá trị biểu thức Q      2 6 3 48 1 3 . 2 1  x  2 x  2 16  x  2
2) Tìm điều kiện xác định và rút gọn biểu thức P      : . x  2 x  2 4  x 8   Ý Nội dung Điểm Ta có  3 ( 2 1). 3 0,25 Q  48   1 32 6  4 3  1 2 3  3   1 2 1 2 1 (0,5 điểm)
 4 3  3 1 2 3  3  3  4 0,25 ĐKXĐ : x  0; x  4 0,25 2 2     x  2  x 2 16  x 2 P    : 0,25 2  x 4 x 2 x 4     8   (1,0 điểm)  
x  4 x  4  (x  4 x  4) 16 8 P  . x  4 0,25 x  2 8( x  2) 8 64 P  .  . x  4 0,25 x  2 x  4 Câu 2. (1,5 điểm).
1) Tìm toạ độ giao điểm của parabol 2
(P) : y  x và đường thẳng (d) : y 5x4 . 2) Cho phương trình 2
2x mx3 0(với m là tham số).
a) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị . m . Trang 1/4
b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x ; x thỏa 1 2 mãn x  x  3 . 1 2 Ý Nội dung Điểm
Phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d): 0,25 2 1 x  5x  4  0 (0,5
Nghiệm phương trình là x 1  ; x4
điểm) Với x 1 y 1; x 4 y 1  6 0,25
Toạ độ giao điểm 1;  1 ; 4;1  6 .
a) Phương trình có a  2;b  m  ;c  3  trong đó ac  2.( 3  )  6   0 0,25
Do đó phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m
b) Với mọi m phương trình luôn có 2 nghiệm phân biệt x ; x 1 2 2 0,25 Theo hệ thức viet ta có m 3 x  x  ; x .x  (1,0 1 2 1 2 2 2 điểm) Theo bài ra 2 2 2
x  x  3  ( x  x )  3  (x  x )  2x .x  2 x .x  9 0,25 1 2 1 2 1 2 1 2 1 2 m 3  3  2 2  ( )  2.( )  2.  9  m 12  m  2  3 2 2 2 0,25
Vậy tất cả giá trị m thỏa mãn yêu cầu bài toán là m  2  3 2 2 4x  y  4xy
Câu 3. (1,0 điểm). Giải hệ phương trình  2  x  y 1.  Nội dung Điểm
Điều kiện xác định: y  1; x   . 2 2 4x  y  4xy (I)  2  x  y 1 (II )  0,25 Ta có 2 2 2 2 2
4x  y  4xy  4x  4xy  y  0  (2x  y)  0  y  2x
Thay y  2x vào phương trình (II) ta được 2
2  x  2x 1  (2  x)  2x 1 (điều kiện x  2 ) 0,25
Giải phương trình ta được: x  1 (nhận); x  5 (loại) 0,25 Suy ra x  1; y = 2
Đối chiếu điều kiện, kết luận hệ phương trình đã cho có nghiệm  x; y  1; 2 0,25 . Câu 4. (3,0 điểm)
1. Cho đường tròn O;3cm. Từ điểm M nằm ngoài B đường tròn  
O kẻ hai tiếp tuyến MA, MB với đường tròn  
O (A, B là các tiếp điểm) sao cho  0 AOB 120 . Tính O M
diện tích phần giới hạn bởi hai tiếp tuyến MA, MB và cung nhỏ AB . A Trang 2/4 Nội dung Điểm Ta có A  OM vuông tại A và  0 AOM  60  AM  3 3cm Suy ra 1 9 3 2 S  AO.AM  cm 0,25 AOM 2 2 2 S  2S  9 3cm 0,25 AOBM AOM 2 2 R n 3 120
Diện tích hình quạt OAB là S    3 0,25 1 360 360
Diện tích phần tô đậm là S  S S  9 3 3 cm 0,25 AOBM  2 1 
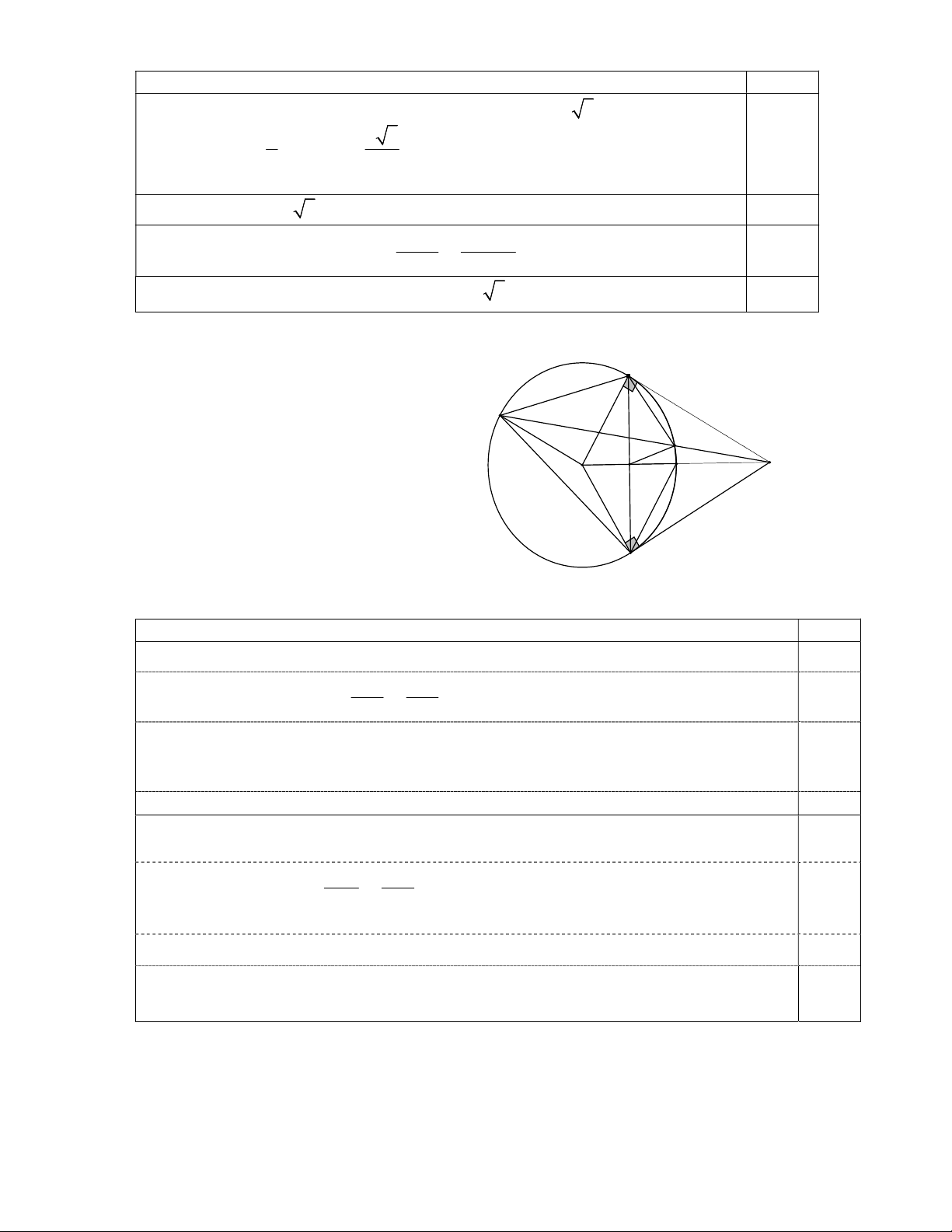
2. Cho đường tròn (O) có dây AB
không là đường kính, tiếp tuyến tại A và A
B cắt nhau tại M. Vẽ cát tuyến MCD
nằm giữa hai tia MA và MO, D
( MC  MD ). Đoạn thẳng MO cắt AB tại C
H và cắt (O) tại điểm I. Chứng minh: M a) 2 MA  MC.MD và O H I 2 MC.MD  OH.OM  MO .
b) Tứ giác OHCD nội tiếp và CI là tia phân giác của  HCM . B Nội dung Điểm a)  MAC 
 MDA (góc tạo bởi tia tiếp tuyến và dây bằng góc nội tiếp cùng chắn  AC ) 0,25 MA MC M  AC ∽ M  DA (g.g) 2    MA  MC.MD (1) 0,25 MD MA
MA, MB là 2 tiếp tuyến của (O) cắt nhau tại M nên MA = MB và OA = OB = bán 0,25
kính suy ra OM là đường trung trực của AB Suy ra O
 AM vuông tại A, có đường cao AH .Suy ra 2 OH.OM  OA 2 2 2
MC.MD  OH.OM  MA  OA  MO (đpcm) 0,25
b) Áp dụng hệ thức lượng trong O
 AM vuông, đường cao AH có: 2 MA  MH.MO . 0,25
Kết hợp với (1) suy ra: MH.MO  MC.MD MH MD MH.MO  MC.MD    M  HC ∽MDO ( .cg.c)   HCM   DOM MC MO 0,25
 Tứ giác OHCD nội tiếp (vì góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện)  HCM   DOM   DOA   AOI  2( DBA   ABI)  2 DBI 0,25
Tứ giác DCIB nội tiếp đường tròn (O) nên suy ra  DBI   ICM . 0,25 Suy ra  HCM  2
ICM  CI là tia phân giác của  HCM (đpcm). Trang 3/4 Câu 5. (1,0 điểm) 1) Giải phương trình 2
(4x  3)x  (3  x) 3  2x . 2) Cho ,
x y là các số thực thỏa mãn đẳng thức 5
x  y  xy  . Tìm giá trị nhỏ nhất 4 của biểu thức 4 4 M  1 x  1 y . Ý Nội dung Điểm Điều kiện 3 x  2 2 3  y
Đặt y  3  2x  y  0  x  2
Thay vào phương trình ta được 2 0,25 3  y 3 3 3 4x  3x  (3 
) y  8 x  y  6x  3y  0 1 2 (0,5 điểm) 2 2
(2x  y)(4 x  2xy  y )  3(2x  y)  0 2 2
 (2x  y)(4 x  2xy  y  3)  0  y  2x ( do 2 2 2 2
4 x  2xy  y  3  3x  (x  y)  3  0, x  , y )
Với y  2x ta có 3  2x =2x bình phương hai về và thử nghiệệm  0,25
lại nghiêm. Phương trình có nghiệm 1 13 4 2 Ta có 4 4  x   y   2 2 1 1 4
x  y  ,x, y     *
Chứng minh: Bình phương hai về của (*) ta được  x  y   x   x  y   x 2 4 4 2 2 4 4 2 2 2 (1 )(1 ) 2 2 y (1 )(1 ) 1 y 0,25 x  y 2 2 2  0 Ta có x y2 2 2  0  x  y  2xy 2  1   2 1 2 1 x
   0  x   x  2x      2x 2 4  4 2 2     (0,5 điểm) 1 1 1 2 2 y
    0  y   y  2y      2y 2 4  4 5 1 Cộng lại 2 2 2 2
3(x  y ) 1 2(x  y  xy)   x  y  2 2 0,25 1 17 Vậy 4 4
1 x  1 y  4   4 2 1 17 x  y  thì M  . 2 2 17
Vậy giá trị nhỏ nhất của M bằng 2
------------------------- Hết ------------------------ Trang 4/4
Document Outline

• 1. Đề Toán 9-Thi thử lần 3
• 2. Đáp an Toán 9-Thi thử lần 3