Đề khảo sát Toán vào lớp 10 năm 2025 – 2026 lần 4 trường Hoằng Sơn 1 – Thanh Hóa
Giới thiệu đến quý thầy, cô giáo và các em học sinh đề khảo sát chất lượng học sinh lớp 9 môn Toán tuyển sinh vào lớp 10 THPT năm học 2025 – 2026 lần 4 trường TH & THCS Hoằng Sơn 1, huyện Hoằng Hóa, tỉnh Thanh Hóa. Kỳ thi được diễn ra vào ngày 18 tháng 05 năm 2025. Đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm.
Chủ đề: Đề thi vào 10 môn Toán năm 2025-2026 122 tài liệu
Môn: Môn Toán 1.4 K tài liệu
Tác giả:
Preview text:
UBND HUYỆN HOẰNG HÓA
ĐỀ KHẢO SÁT HỌC SINH LỚP 9 THI VÀO
TRƯỜNG TH&THCS HOẰNG SƠN 1
LỚP 10 THPT NĂM HỌC 2025- 2026 Môn: Toán - LẦN 4 ĐỀ CHÍ NH THỨC Ngày khảo sát: 18/5/2025
Thời gian làm bài: 120 phút, không kể thời gian giao đề ĐỀ A (Đề gồm có 02 trang)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm, gồm 08 câu, mỗi câu 0,25 điểm). (x + 3)(x − 4)
Câu 1. Phương trình = 0 có nghiệm là: 2x + 6 A. x = 3
− B. x = 4 C. x = 3 và x = 4 − D. x = 3 − và x = 4 Câu 2. Biểu thức 2 4
4x y khi bỏ dấu căn có giá trị là: A. 2 2x y B. 2 2 − x y C. 2 2xy D. 2 2 x y
Câu 3: Kết luận nào sau đây là sai khi nói về đồ thị hàm số 𝑦𝑦 = 𝑎𝑎𝑥𝑥2(𝑎𝑎 ≠ 0).
A. Đồ thị hàm số nhận trục tung làm trục đối xứng.
B. Với a < 0thì đồ thị nằm phía dưới trục hoành và O(0;0) là điểm cao nhất của đồ thị.
C. Với a > 0thì đồ thị nằm phía trên trục hoành và O(0;0) là điểm cao nhất của đồ thị.
D. Với a > 0thì đồ thị nằm phía trên trục hoành và O(0;0) là điểm thấp nhất của đồ thị.
Câu 4. Bất phương trình 2024x − 2025 ≤ 0 có các hệ số ; a b lần lượt là:
A. a = 2024;b = 2025 B. a = 2025 − ; b = 2024
C. a = 2024;b = 2025 − D. a = 2024 − ; b = 2025 −
Câu 5. Cho tam giác ABC vuông tại A, AB = 3cm; BC = 5cm. Khẳng định nào sau đây là sai? A. 3 tanC = B. 4 sinC = C. 3 cosB = D. 4 tan B = 4 5 5 3
Câu 6. Cho đơờng tròn ( ;4
O cm)và đường thẳng d tiếp xúc với nhau. Gọi h là khoảng cách từ tâm
O đến đường thẳng d . Khẳng định nào sau đây là đúng:
A. h > 4cm B. h < 4cm C. h ≤ 4cm D. h = 4cm
Câu 7: Thời gian chạy cự ly 100m của các học sinh khối lớp 9 ở một trường THCS được giáo viên
Thể chất ghi lại trong bảng số liệu sau:
Thời gian (giây)
[13;15) [15;17) [17;19) [19; ) 21 Số học sinh 25 36 40 57
Thời gian hoàn thành của bạn Đăng là 14 giây. Thời gian chạy của bạn Đăng nằm trong nhóm số liệu nào? A. [13;15) B. [15;17) C. [17;19) D. [19; ) 21
Câu 8. Nam có 10 tấm thẻ cùng loại được đánh số từ 1 đến 10. bạn rút ngẫu nhiên một tấm thẻ. Xác
suất của biến cố: “Chữ số trên tấm thẻ được rút số chẵn” bằng: A. 3 B. 4 C. 5 D. 1 10 10 10 10
PHẦN II. TỰ LUẬN (8,0 điểm).
Câu 9. (1,5 điểm)
a) (0,75 điểm) Giải phương trình: 2
2x + 7x −9 = 0. + = b) 3 x y 6
(0,75 điểm) Giải hệ phương trình: . x − y = 2 − −
Câu 10. (1,0 điểm) Rút gọn biểu thức: 2 1 3 x 1 4 P = − + :
, với x ≥ 0 và x ≠ 1 x +1 x −1 x −1 x + 1
Câu 11. (1,0 điểm) Tìm m để phương trình: 2 2
x − 2(m −1)x + m − 4m + 5 = 0 có hai nghiệm 1 x , 2 x thỏa mãn điều kiện 2 2 1 x 2 x + 1x 2
x − 3 1x − 3 2 x = 0 .
Câu 12. (1 điểm) Một ca nô đi xuôi dòng trên một khúc sống từ bến Ađến bến B dài 40kmsau đấy lại
ngược dòng từ B về A. Thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 20 phút. Vận tốc của
dòng nơớc là 3km / h và vận tốc riêng của ca nô không đổi. Tính vận tốc riêng của ca nô.
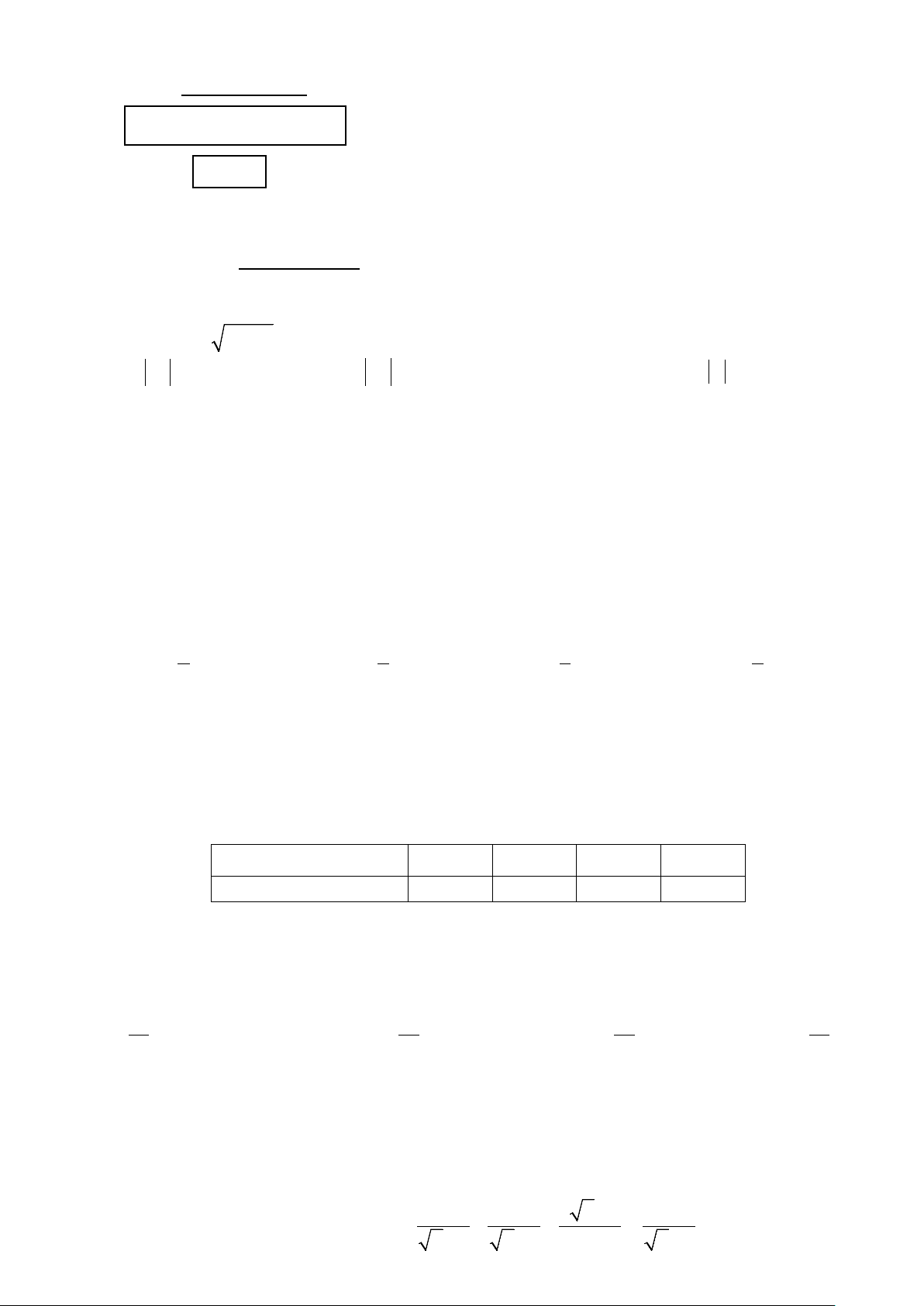
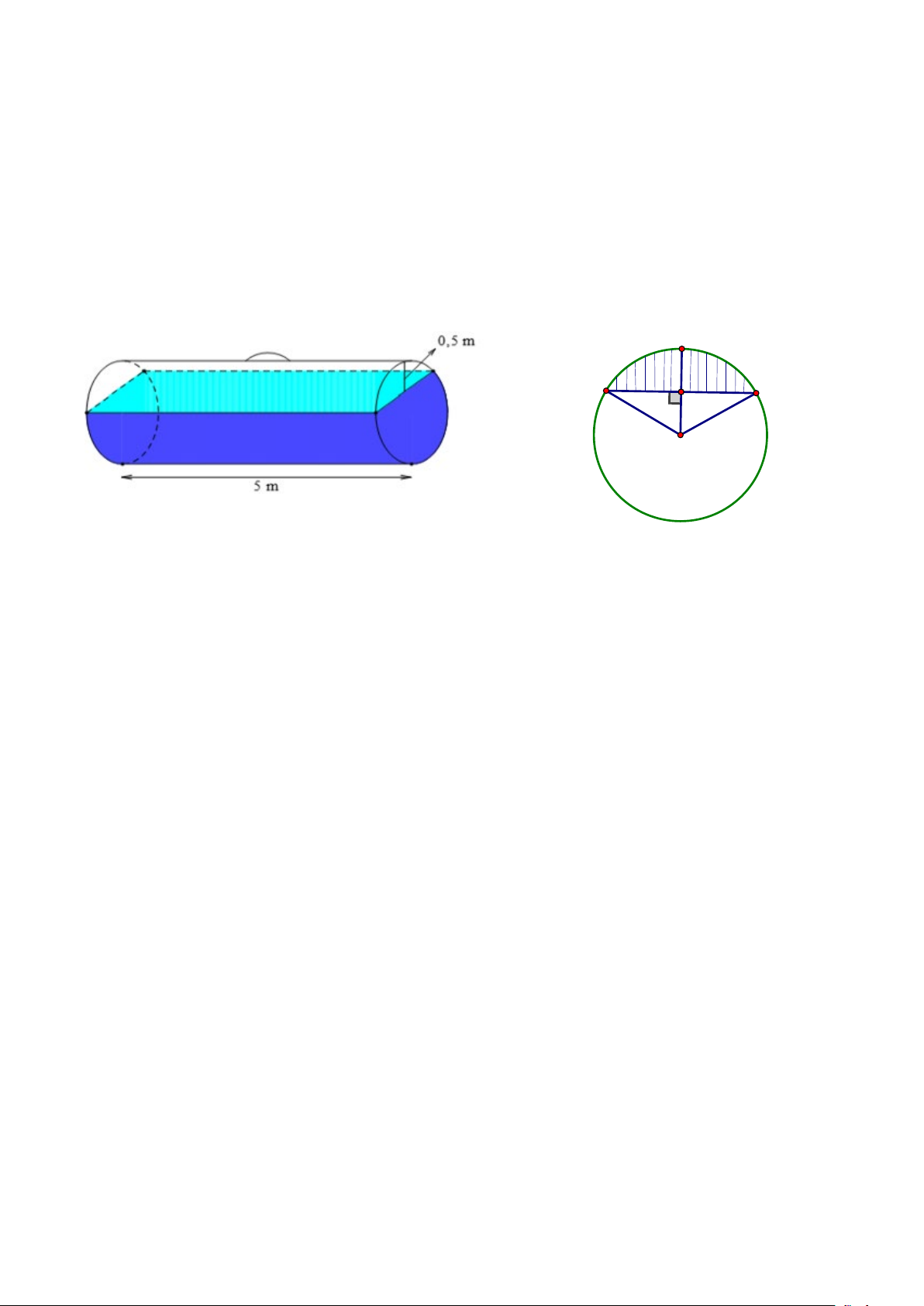
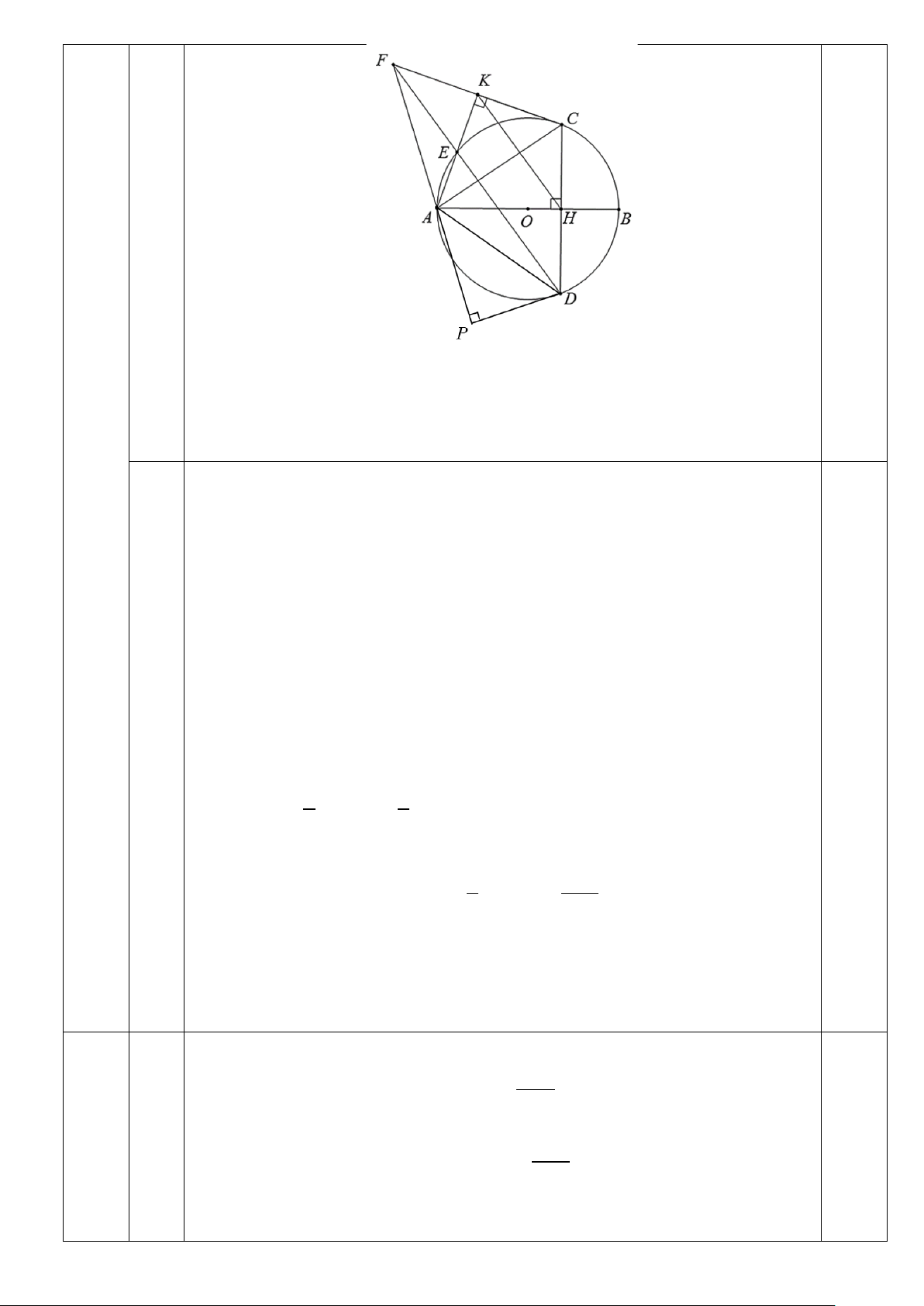
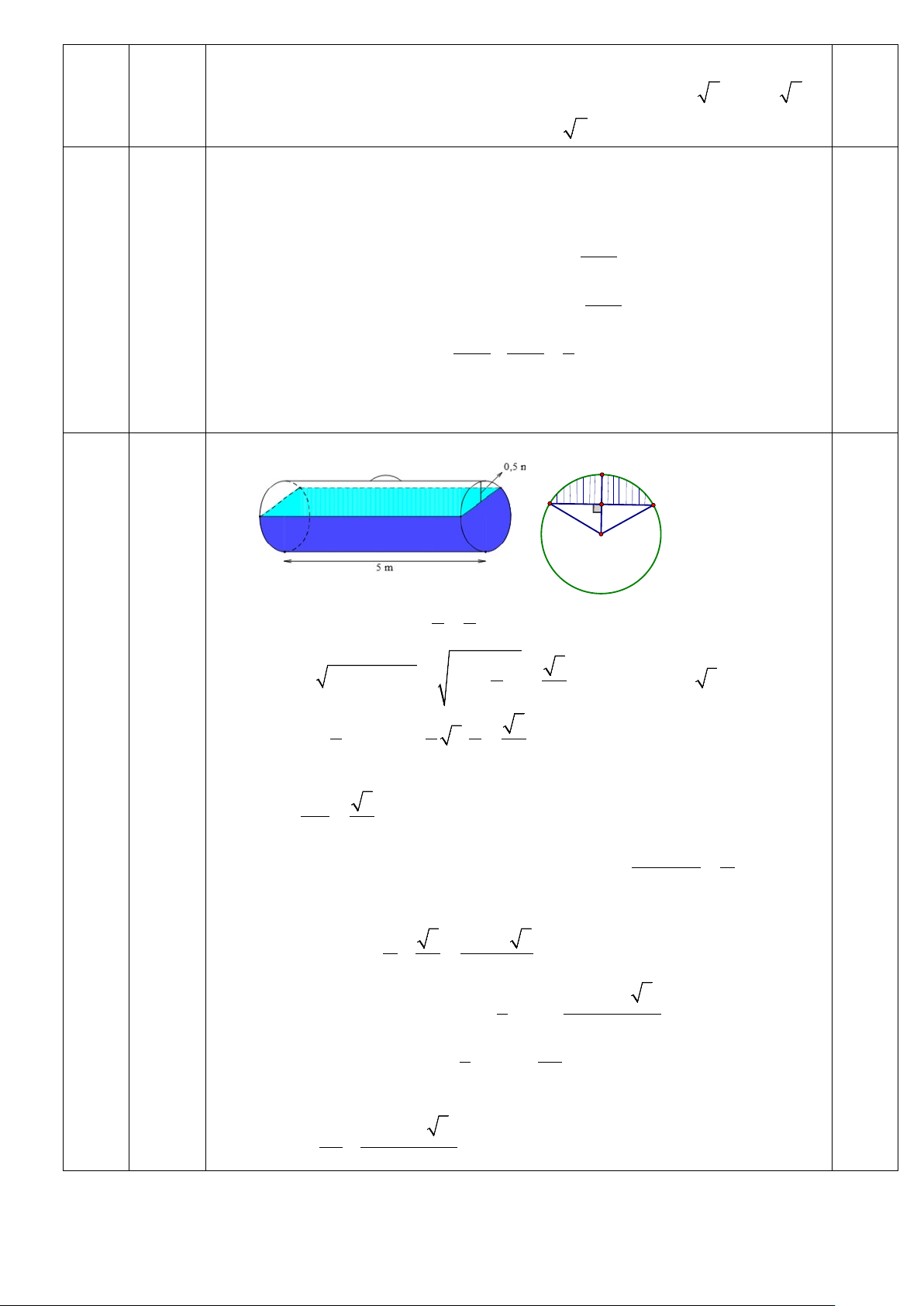
Câu 13. (1 điểm) Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là 5m, có bán
kính đáy 1m, với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng
với 0,5m của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (lấy π ≈ 3,14,
kết quả làm tròn đến chữ số thập phân thứ hai, theo 3
m ) Mặt đáy được minh họa như hình vẽ sau: C A B H O
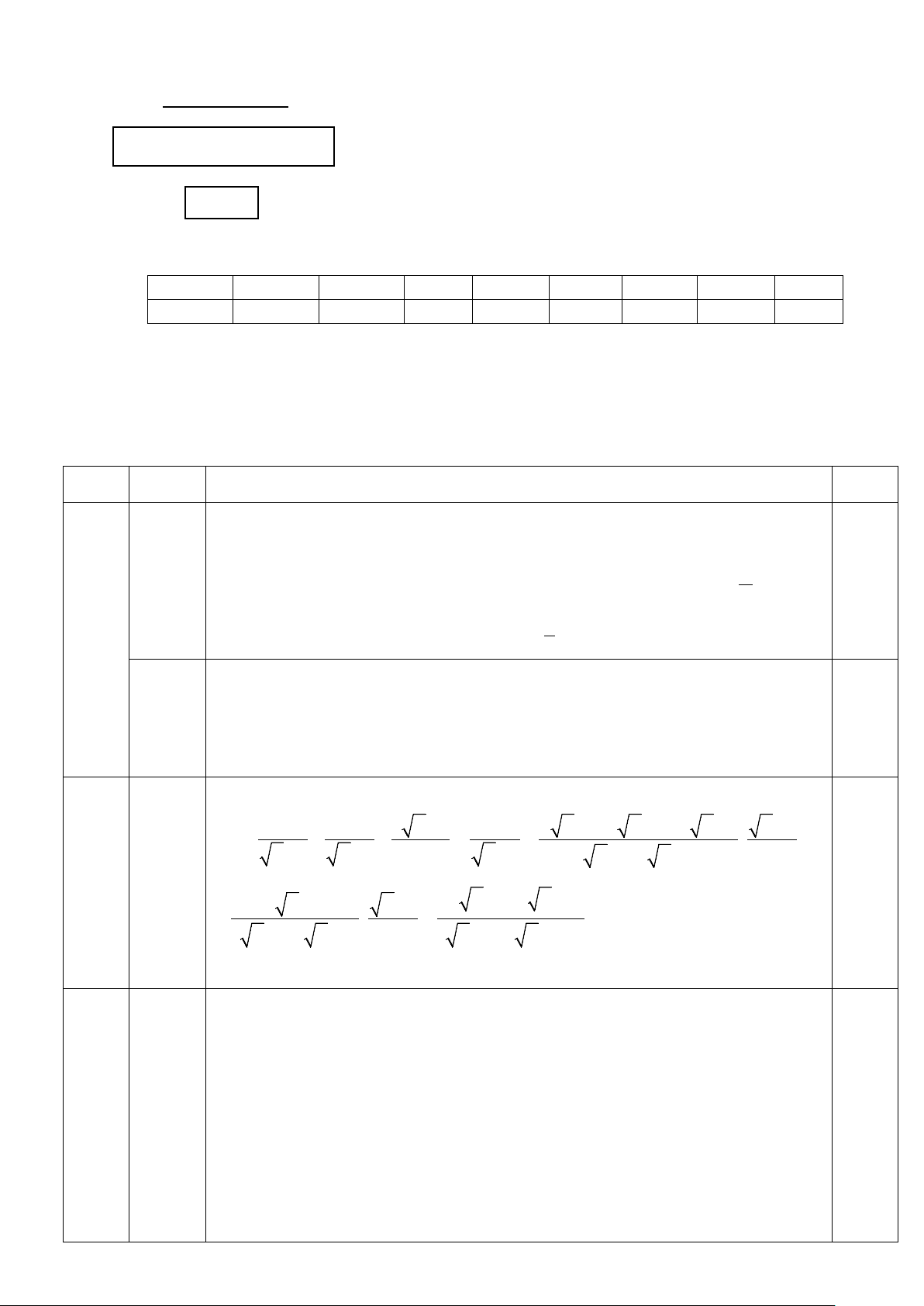
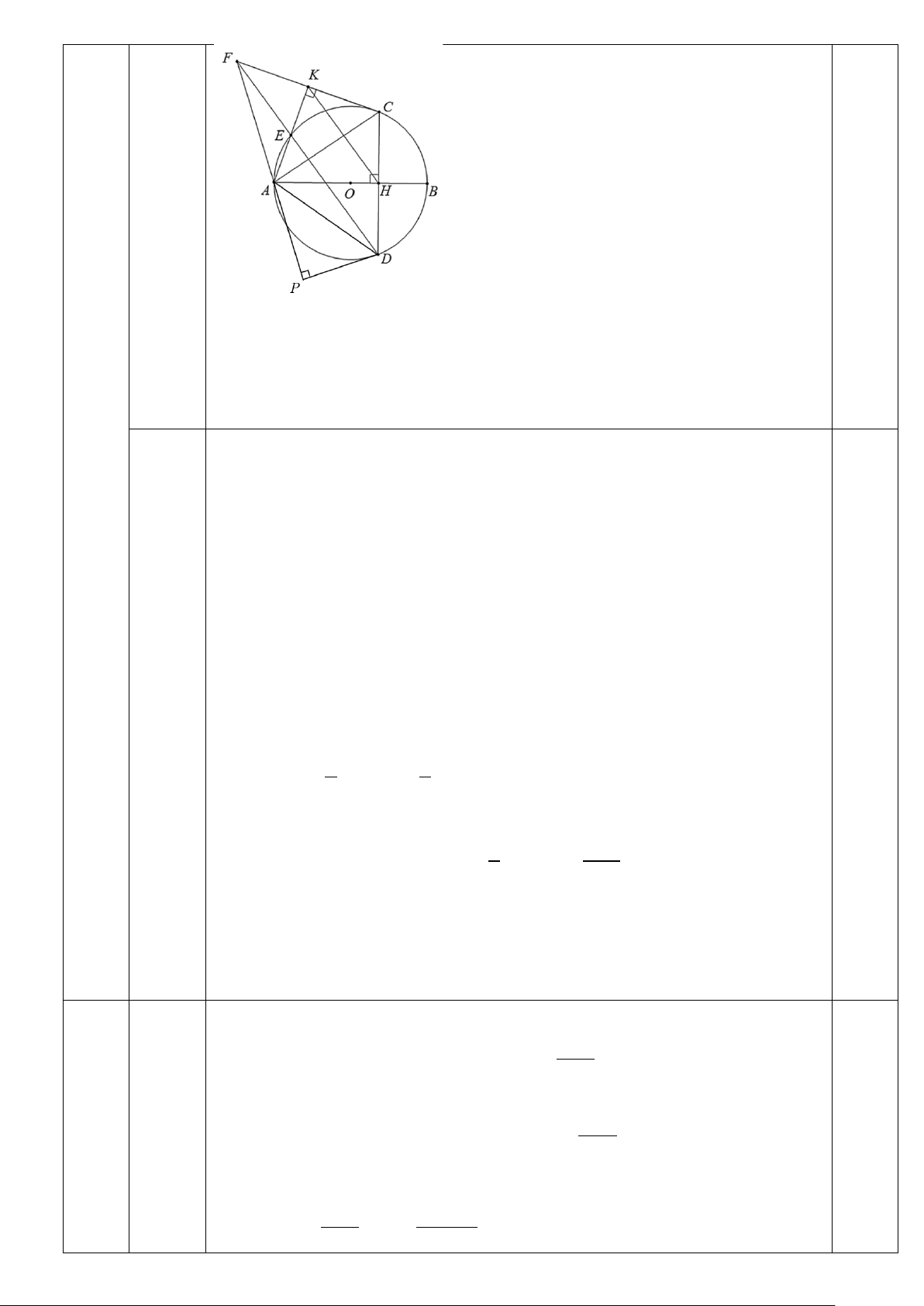
Câu 14. (2,0 điểm) ) Cho đường tròn (O) đường kính A .
B Gọi H là điểm nằm giữa O và . B Kẻ dây
CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông
góc với AE tại K. Đường thẳng DE cắt CK tại F.
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.
b) Chứng minh K là trung điểm CF. Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.
Câu 15. (0,5 điểm) Một người chạy bộ ngược chiều gió trên một quãng đường có độ dài là s km, với vận tốc
gió thổi là 6 km / h . Nếu vận tốc của người chạy khi không có gió là v ( km / h ) thì năng lượng tiêu hao của
người đó trong t giờ được cho bởi công thức 3
E v c v t , trong đó c là một hằng số, E được tính bằng
đơn vị Jun. Người đó cần chạy với vận tốc bao nhiêu km / h để năng lượng tiêu hao trong quá trình chạy là ít nhất?
------------------------Hết------------------------
Họ tên thí sinh: …………………………………. SBD: ……..
Chữ kí của giám thị 1:………………………Chữ kí của giám thị 2:……………………… UBND HUYỆN HOẰNG HÓA
ĐỀ KHẢO SÁT HỌC SINH LỚP 9 THI VÀO
TRƯỜNG TH&THCS HOẰNG SƠN 1
LỚP 10 THPT NĂM HỌC 2025- 2026 Môn: Toán - LẦN 3 ĐỀ CHÍ NH THỨC Ngày khảo sát: 11/5/2025
Thời gian làm bài: 120 phút, không kể thời gian giao đề ĐỀ B (Đề gồm có 02 trang)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm, gồm 08 câu, mỗi câu 0,25 điểm). (x + 3)(x − 4)
Câu 1. Phương trình = 0 có nghiệm là: 2x − 8 A. x = 3
− B. x = 4 C. x = 3 và x = 4 − D. x = 3 − và x = 4 Câu 2. Biểu thức 4 2
4x y khi bỏ dấu căn có giá trị là: A. 2 2 − x y B. 2 2x y C. 2 2x y D. 2 2 − x y
Câu 3: Kết luận nào sau đây là sai khi nói về đồ thị hàm số 𝑦𝑦 = 𝑎𝑎𝑥𝑥2(𝑎𝑎 ≠ 0).
A. Đồ thị hàm số nhận trục tung làm trục đối xứng.
B. Với a < 0thì đồ thị nằm phía dưới trục hoành và O(0;0) là điểm cao nhất của đồ thị.
C. Với a > 0thì đồ thị nằm phía trên trục hoành và O(0;0) là điểm thấp nhất của đồ thị.
D. Với a > 0thì đồ thị nằm phía trên trục hoành và O(0;0) là điểm cao nhất của đồ thị.
Câu 4. Bất phương trình 2025x − 2024 ≥ 0có các hệ số ; a b lần lượt là:
A. a = 2025;b = 2024 B. a = 2025;b = 2024 −
C. a = 2024;b = 2025 − D. a = 2024 − ; b = 2025 −
Câu 5. Cho tam giác ABC vuông tại A, AB = 3cm; BC = 5cm. Khẳng định nào sau đây là đúng? A. 4 tanC = B. 4 sinC = C. 3 cosB = D. 3 tan B = 3 5 5 4
Câu 6. Cho đơờng tròn ( ;6
O cm)và đường thẳng d tiếp xúc với nhau. Gọi h là khoảng cách từ tâm
O đến đường thẳng d . Khẳng định nào sau đây là đúng:
A. h < 6cm B. h > 6cm C. h = 6cm D. h ≥ 4cm
Câu 7: Thời gian chạy cự ly 100m của các học sinh khối lớp 9 ở một trường THCS được giáo viên
Thể chất ghi lại trong bảng số liệu sau:
Thời gian (giây)
[13;15) [15;17) [17;19) [19; ) 21 Số học sinh 25 36 40 57
Thời gian hoàn thành của bạn Bắc là 16 giây. Thời gian chạy của bạn Bắc nằm trong nhóm số liệu nào? A. [13;15) B. [15;17) C. [17;19) D. [19; ) 21
Câu 8. Nam có 10 tấm thẻ cùng loại được đánh số từ 1 đến 10. bạn rút ngẫu nhiên một tấm thẻ. Xác
suất của biến cố: “Chữ số trên tấm thẻ được rút số lẻ” bằng: A. 4 B. 5 C. 6 D. 3 10 10 10 10
PHẦN II. TỰ LUẬN (8,0 điểm).
Câu 9. (1,5 điểm)
a) (0,75 điểm) Giải phương trình: 2
2x −9x + 7 = 0. + = − b) 3 x y 6
(0,75 điểm) Giải hệ phương trình: . x − y = 2 −
Câu 10. (1,0 điểm) Rút gọn biểu thức: 2 1 3 y 1 4 Q = − + :
, với y ≥ 0 và y ≠ 1. y +1 y −1 y 1 − y + 1
Câu 11. (1,0 điểm) Tìm k để phương trình: 2 2
x − 2(k −1)x + k − 4k + 5 = 0 có hai nghiệm 1 x , 2 x thỏa mãn điều kiện 2 2 1 x 2 x + 1x 2
x − 3 1x − 3 2 x = 0 .
Câu 12. (1 điểm) Một ca nô đi xuôi dòng trên một khúc sống từ bến Ađến bến B dài 40kmsau đấy lại
ngược dòng từ B về A. Thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 20 phút. Vận tốc của dòng
nơớc là 3km / h và vận tốc riêng của ca nô không đổi. Tính vận tốc riêng của ca nô.
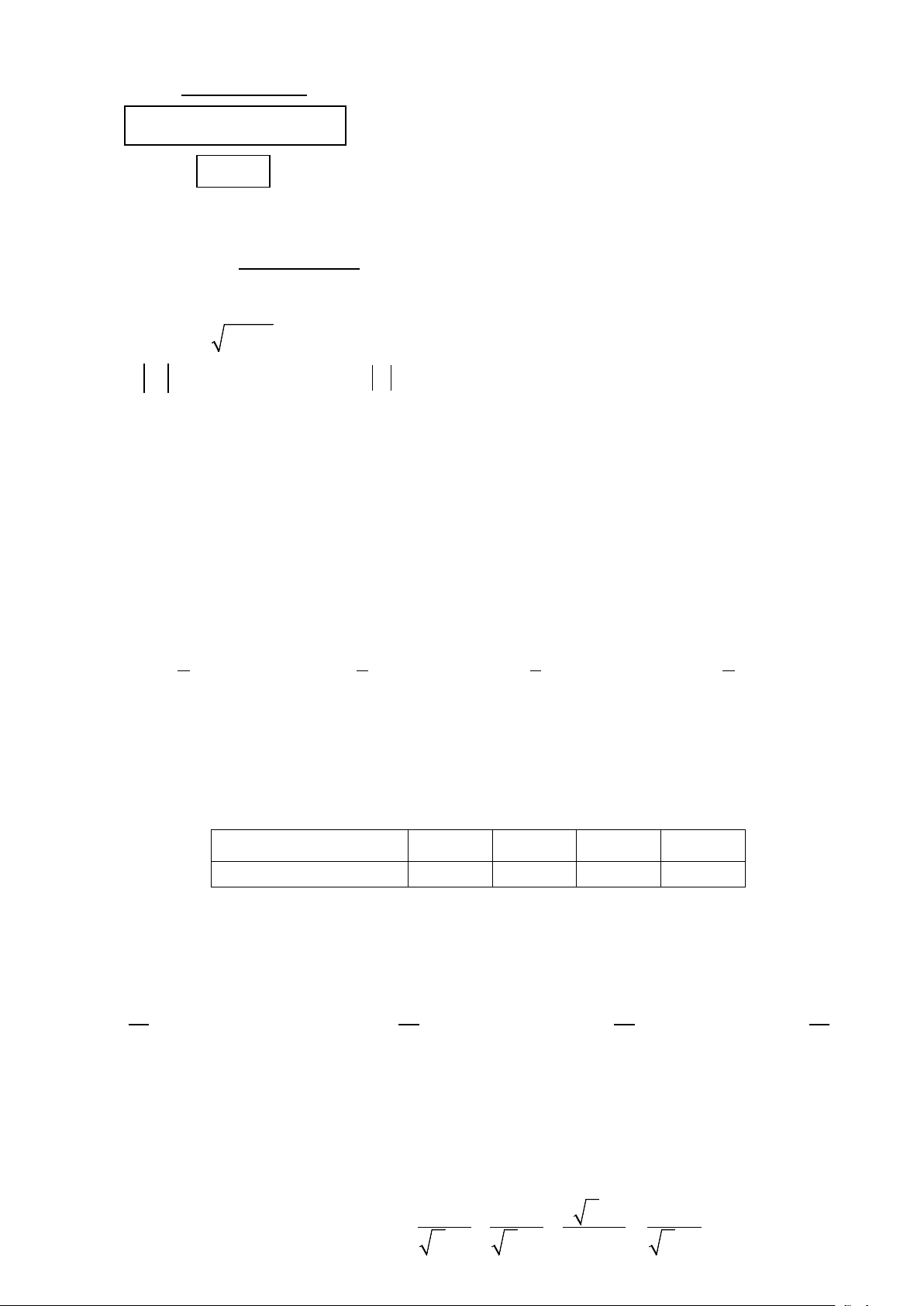
Câu 13. (1 điểm) Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là 5m, có bán
kính đáy 1m, với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng
với 0,5m của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (lấy π ≈ 3,14,
kết quả làm tròn đến chữ số thập phân thứ hai, theo 3 m )
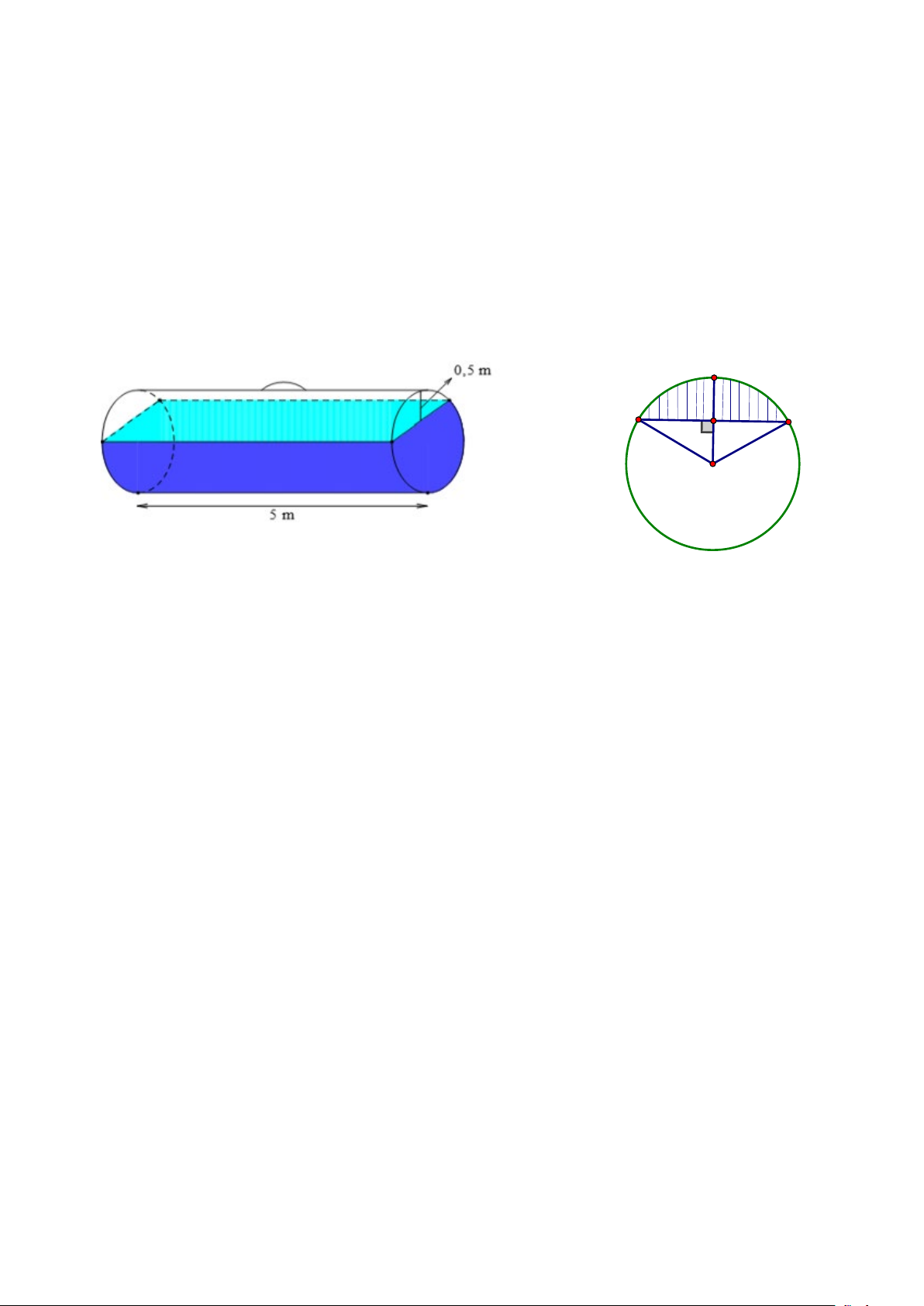
Mặt đáy được minh họa như hình vẽ sau: C A B H O
Câu 14. (2,0 điểm) ) Cho đường tròn (O) đường kính A .
B Gọi H là điểm nằm giữa O và . B Kẻ dây
CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông
góc với AE tại K. Đường thẳng DE cắt CK tại F.
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.
b) Chứng minh K là trung điểm CF. Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.
Câu 15. (0,5 điểm) Một người chạy bộ ngược chiều gió trên một quãng đường có độ dài là s km, với vận tốc
gió thổi là 6 km / h . Nếu vận tốc của người chạy khi không có gió là v ( km / h ) thì năng lượng tiêu hao của
người đó trong t giờ được cho bởi công thức 3
E v c v t , trong đó c là một hằng số, E được tính bằng
đơn vị Jun. Người đó cần chạy với vận tốc bao nhiêu km / h để năng lượng tiêu hao trong quá trình chạy là ít nhất?
------------------------Hết------------------------
Họ tên thí sinh: …………………………………. SBD: ……..
Chữ kí của giám thị 1:………………………Chữ kí của giám thị 2:……………………… UBND HUYỆN HOẰNG HÓA
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT HỌC SINH LỚP 9
TRƯỜNG TH&THCS HOẰNG SƠN 1
THI VÀO LỚP 10 THPT NĂM HỌC 2025- 2026 (LẦN 3) Môn: Toán ĐỀ CHÍNH THỨC Ngày khảo sát: 10/5/2025
(Hướng dẫn chấm gồm có 03 trang) ĐỀ A
PHẦN I - TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm) Mỗi câu đúng cho 0,25 điểm Câu 1 2 3 4 5 6 7 8 Đáp án B D C C B D A C
PHẦN II - TỰ LUẬN (8 điểm): Câu ý Nội dung Điểm 9 a Xét phương trình: 2
2x + 7x −9 = 0. 0,25
(1,5đ) (0,75 Phương trình có: a = 2; b = 7; c = 9 − 0,25 đ) 9
Vì a + b + c = 2 + 7 − 9 = 0 nên phương trình có 2 nghiệm là : x =1; x = − 1 2 2 0,25
Vậy Phương trình có tập nghiệm S = { 9 1;− 2} b 3 x + y = 6 4x = 4 x =1 x =1 0,5 Ta có: ⇔ ⇔ ⇔ (0,75 x − y = 2 − x − y = 2 − 1 − y = 2 − y = 3 0,25 đ)
Vậy hệ phương trình đã cho có nghiệm duy nhất: ( ; x y) = (1; 3) 10
Với x ≥ 0 và x ≠ 1 ta có: 0,25 (1,0đ) 2 1 3 x −1 4
2 x − 2 − x −1+ 3 x −1 x +1 P = − + : = ⋅ x +1 x −1 x 1 − x +1
( x + )1( x − )1 4 4( x − )1.( x x x + − + )1 4 4 1 = ( ⋅ = = 0,5 x + )1( x − )1
( x + )1.( x − ) 1 4 1 .4
Vậy P =1 với x ≥ 0 và x ≠1. 0,25 11 Xét phương trình 2 2
x − 2(m −1)x + m − 4m + 5 = 0 (m là tham số). (1,0đ)
Có : a = b = −(m − ) 2 1; '
1 ; c = m − 4m + 5 0,25
Ta có: ∆′ = (m − )2 − ( 2 1
1. m − 4m + 5) = 2m − 4
Phương trình đã cho có hai nghiệm 1x, 2x khi và chỉ khi ∆′ ≥ 0 ⇔ m ≥ 2 (*) 1 x + 2 x = 2(m − )1
Áp dụng hệ thức Vi-et, ta có : 0,25 2 1 x 2
x = m − 4m + 5 Theo đề bài 2 2 ⇔ + − = 1 x 2 x + 1x 2
x − 3 1x − 3 2 x = 0
( 1x 2x)( 1x 2x 3) 0
+Với 1x + 2x = 0 ta có 2(m −1) = 0 ⇔ m =1 0,25 +Với 1
x 2x = 3 ta có 2 2
m − 4m + 5 = 3 ⇔ m − 4m + 2 = 0 ⇔ m = 2 + 2;m = 2 − 2 . 0,25
Kết hợp với điều kiện (*) tìm được m = 2 + 2 12
Gọi vận tốc thực của ca nô là x (km/h,x>3). (1,0đ)
Vận tốc ca nô khi xuôi dòng từ A đến B và ngược dòng từ B về Alần lượt là : 0,25 x+3 (km/h) và x-3 (km/h)
Thời gian ca nô khi xuôi dòng từ A đến B là : 40 ( h). x + 3
Thời gian ca nô khi ngược dòng từ B về A là : 40 ( h). 0,5 x − 3
Theo bài ra ta có phương trình: 40 40 1 − = x − 3 x + 3 3
Giải phương trình ta được x = 27(tm);x = 27 − (l) . 1 2
Vậy vận tốc thực của ca nô là 0,25 27km / h 13
Mặt đáy được minh họa như hình vẽ (1,0đ) sau: C A B H O 0,25 Ta có: 1 1
HO = OC − CH = 1− = (m) 2 2 2 Ta có: 2 2 2 1 3
HB = OB − OH = 1 − =
⇒ AB = 2HB = 3 (m) 2 2 0,25 Ta có: 1 1 1 3 S = = = ( 2 m ) ∆ AB OH OAB . 3. 2 2 2 4 Tam giác HB 3 OHB có: = = ⇒ = ° ⇒ = sin HOB HOB 60
AOB 2HOB = 120° OB 2 2 Gọi π π
S là diện tích hình quạt tròn R .120 2 S = = m 1 OACB , ta có: 1 ( ) 360 3
Gọi S là diện tích hình viên phân giới hạn bởi dây AB và cung nhỏ AB , ta 2 0,25 có: π 3 4π − 3 3
S = S − S = − = ( 2 m ) 2 1 OA ∆ B 3 4 12 5(4π − 3 3 1 )
Thể tích phần dầu đã hút đi là: V = S .5 = ( 3 m ) 1 2 3 36
Thể tích của thùng dầu là: 1 2 5π V = π R .5 = ( 3 m ) 3 3
Thể tích dầu còn lại trong thùng là: 0,25 5 π (4π −3 3 5 )
V = V −V = − ≈ 4,21 ( 3 m 2 1 ) 3 36 14 1 (2,0đ) (1,0đ ) 0,25
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp. 0,5 Ta có AKC = AHC = 90 .°(gt) 0,25
Suy ra K, H cùng nằm trên đường tròn đường kính AC.
Vậy tứ giác AHCK nội tiếp.
2 b) Chứng minh K là trung điểm CF. Tìm vị trí của điểm E để diện tích tam
(1,0đ giác ADF lớn nhất. )
Vì AHCK là tứ giác nội tiếp nên = =
CHK CAK CAE (góc nội tiếp cùng chắn cung 0,25 KC). Tứ giác
ADCE nội tiếp nên =
CAE CDE (góc nội tiếp cùng chắn cung EC). Từ đó suy ra =
CHK CDE (đồng vị) nên HK // DE .
Do HK // DE , mà H là trung điểm CDnên HK là đường trung bình của
tam giác CDF nên K là trung điểm FC. 0,25
Tam giác AFC có AK là đường cao đồng thời cũng là trung tuyến nên là
tam giác cân tại A . Mặt khác tam giác ACD cân tại A nên AC = AD = AF.
Vẽ đường cao DP của tam giác ADF. Ta có 1 1 S = ⋅ = ⋅ . ∆ DP AF DP AC ADF 2 2 0,25
Do AC không đổi nên S
lớn nhất khi và chỉ khi DP lớn nhất. A ∆ DF 2
Ta có: DP ≤ AD = AC hay 1 AC S = ⋅ ≤ (không đổi). ∆ DP AC ADF 2 2
Dấu “=” xảy ra khi và chỉ khi P ≡ A tức là
DAF = 90° nên tam giác ADF
vuông cân tại A , suy ra
EDA = 45° mà = EBA EDA nên
EBA = 45° . Khi đó E 0,25
là điểm chính giữa cung A . B
Vậy diện tích tam giác ADF lớn nhất khi E là điểm chính giữa cung A . B 15
Vận tốc khi chạy ngược chiều gió là v6 km / h (0,5đ)
Thời gian chạy trên quãng đường s là: s t (giờ) v 6
Năng lượng tiêu hao của để chạy trên quãng đường s là: 0,25 3 s
E v c v ( Jun ), v 6 v6
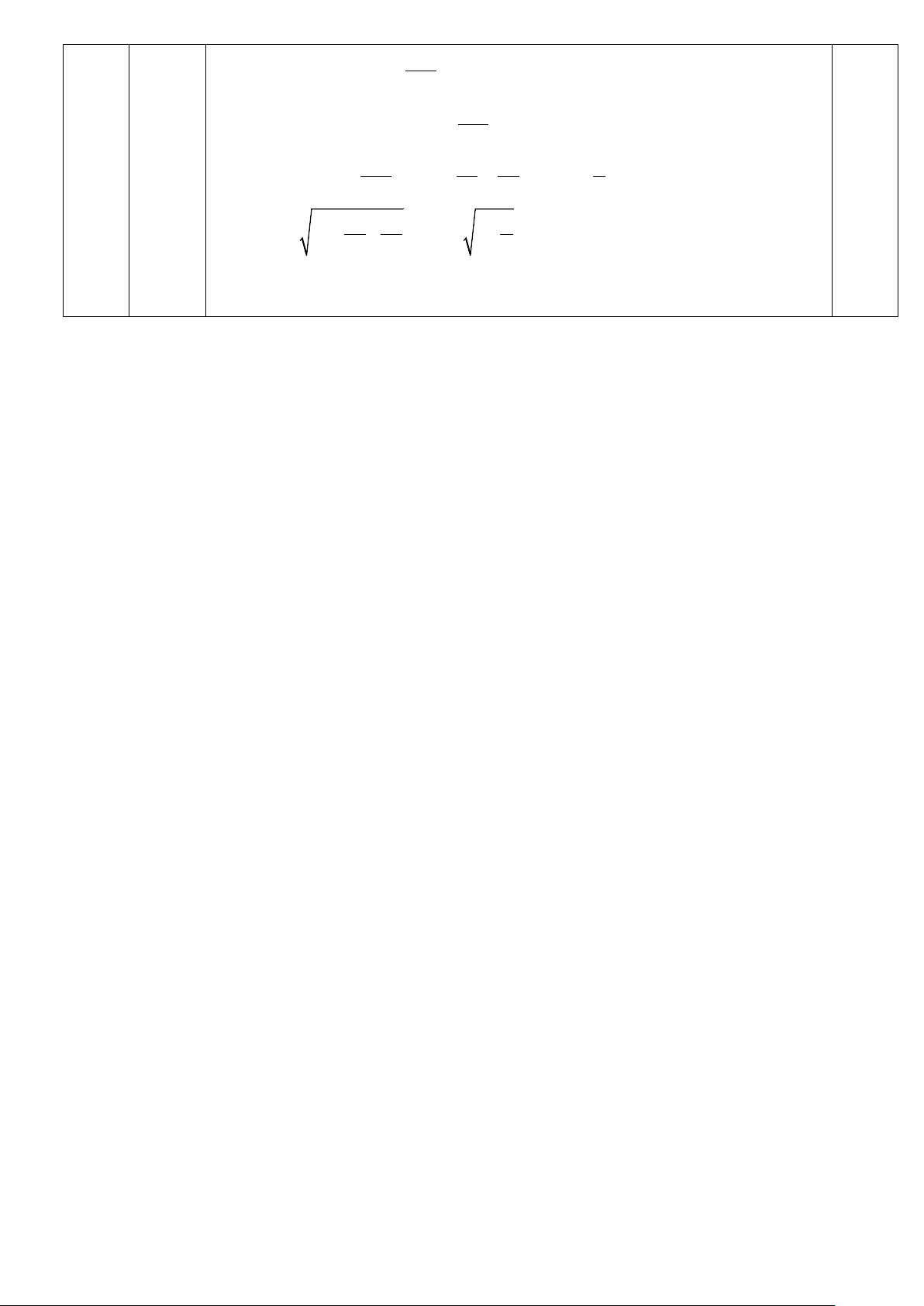
Đặt: a v6, suy ra: v a 6 a 0. Ta có: s a 63 3 c v s.c v6 a 2 216
s.c a 18a 108 a
Ev nhỏ nhất khi 2 216 a 18a nhỏ nhất a Ta có: 2 216 2 27 27 9 0,25 a 18a a 18 a a a a a 2 27 27 9 3 3 a
18 2 a 351 a a a
Dấu " " xảy ra khi a 3 hay v 9
Vậy người đó chạy với vận tốc 9 km / h thì năng lượng tiêu hao ít nhất.
Chú ý: + Học sinh làm cách khác đúng vẫn cho điểm tôi đa.
+ Bài hình không có hình hoặc vẽ hình sai thì không chấm. UBND HUYỆN HOẰNG HÓA
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT HỌC SINH LỚP 9 THI
VÀO LỚP 10 THPT NĂM HỌC 2025- 2026 (LẦN 2)
TRƯỜNG TH&THCS HOẰNG SƠN 1 Môn: Toán ĐỀ CHÍNH THỨC Ngày khảo sát: 10/5/2025
(Hướng dẫn chấm gồm có 03 trang) ĐỀ B
PHẦN I - TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm) Mỗi câu đúng cho 0,25 điểm Câu 1 2 3 4 5 6 7 8 Đáp án A B D B C C B B
Chú ý: + Học sinh làm cách khác đúng vẫn cho điểm tôi đa.
+ Bài hình không có hình hoặc vẽ hình sai thì không chấm.
PHẦN II - TỰ LUẬN (8 điểm): Câu ý Nội dung Điểm 9 a Xét phương trình: 2
2x −9x + 7 = 0. 0,25
(1,5đ) (0,75đ) Phương trình có: a = 2; b = 9; − c = 7 0,25
Vì a + b + c = 2 − 9 + 7 = 0 nên PT có 2 nghiệm là : 7 x =1;x = 1 2 2 0,25
Vậy Phương trình có tập nghiệm S = { 7 1; 2} b 3 x + y = 6 − = − = − = − 0,5 Ta có: 4x 4 x 1 x 1 ⇔ ⇔ ⇔ . (0,75đ) x − y = 2 x − y = 2 1 − − y = 2 − y =1 0,25
Vậy hệ phương trình đã cho có nghiệm duy nhất: ( ; x y) = ( 1 − ; ) 1 10
Với y ≥ 0 và y ≠1 ta có: 0,25 (1,0đ) 2 1 3 y −1 4
2 y − 2 − y −1+ 3 y −1 y +1 Q = − + : = ⋅ y +1 y −1 y 1 − y +1
( y + )1( y − )1 4 0,5 4( y − )1.( y y y + − + )1 4 4 1 = ( ⋅ = = y + )1( y − )1
( y + )1.( y − ) 1 4 1 .4 0,25
Vậy Q =1 với y ≥ 0 và y ≠1. 11 Xét phương trình 2 2
x − 2(k −1)x + k − 4k + 5 = 0 (m là tham số). (1,0đ)
Có : a = b = −(k − ) 2 1; '
1 ; c = k − 4k + 5 0,25
Ta có: ∆′ = (k − )2 − ( 2 1
1. k − 4k + 5) = 2k − 4
P. trình đã cho có hai nghiệm 1x, 2x khi và chỉ khi ∆′ ≥ 0 ⇔ k ≥ 2 (*) 1x + 2 x = 2(k − )1 0,25
Áp dụng hệ thức Vi-et, ta có 2 1 x 2
x = k − 4k + 5 Theo đề bài 2 2 1 x 2 x + 1x 2
x − 3 1x − 3 2
x = 0 ⇔ ( 1x + 2 x )( 1x 2 x − 3) = 0 +Với 0,25 1 x + 2
x = 0 ta có: 2(k −1) = 0 ⇔ k =1 +Với 1
x 2x = 3 ta có: 2 2
k − 4k + 5 = 3 ⇔ k − 4k + 2 = 0 ⇔ k = 2 + 2;k = 2 − 2 . 0,25
Kết hợp với điều kiện (*) tìm được k = 2 + 2 12
Gọi vận tốc thực của ca nô là x (km/h,x>3). (1,0đ)
Vận tốc ca nô khi xuôi dòng từ A đến B và ngược dòng từ B về Alần lượt 0,25
là : x+3 (km/h) và x-3 (km/h)
Thời gian ca nô khi xuôi dòng từ A đến B là : 40 ( h). x + 3
Thời gian ca nô khi ngược dòng từ B về A là : 40 ( h). 0,5 x − 3
Theo bài ra ta có phương trình: 40 40 1 − = x − 3 x + 3 3
Giải phương trình ta được x = 27(tm);x = 27 − (l) . 1 2
Vậy vận tốc thực của ca nô là 0,25 27km / h 13
Mặt đáy được minh họa như hình vẽ sau: C (1,0đ) A B H O Ta có: 1 1
HO = OC − CH = 1− = (m) 2 2 0,25 2 Ta có: 2 2 2 1 3
HB = OB − OH = 1 − =
⇒ AB = 2HB = 3 (m) 2 2 Ta có: 1 1 1 3 S = = = ( 2 m ) ∆ AB OH OAB . 3. 2 2 2 4 0,25 Tam giác OHB có HB 3 = = ⇒ = ° ⇒ = sin HOB HOB 60
AOB 2HOB = 120° OB 2 2 Gọi π π
S là diện tích hình quạt tròn R .120 2 S = = m 1 OACB , ta có: 1 ( ) 360 3
Gọi S là diện tích hình viên phân giới hạn bởi dây AB và cung nhỏ AB , ta 2 0,25 có: π 3 4π − 3 3
S = S − S = − = ( 2 m ) 2 1 OA ∆ B 3 4 12 5(4π − 3 3 1 )
Thể tích phần dầu đã hút đi là: V = S .5 = ( 3 m ) 1 2 3 36
Thể tích của thùng dầu là: 1 2 5π V = π R .5 = ( 3 m ) 3 3
Thể tích dầu còn lại trong thùng là: 0,25 5 π (4π −3 3 5 )
V = V −V = − ≈ 4,21 ( 3 m 2 1 ) 3 36 14 1 (2,0đ) (1,0đ)
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp. 0,25 Ta có AKC = AHC = 90 .°(gt)
Suy ra K, H cùng nằm trên đường tròn đường kính AC. 0,5
Vậy tứ giác AHCK nội tiếp. 0,25 2
b) Chứng minh K là trung điểm CF. Tìm vị trí của điểm E để diện tích
(1,0đ) tam giác ADF lớn nhất.
Vì AHCK là tứ giác nội tiếp nên = =
CHK CAK CAE (góc nội tiếp cùng chắn cung 0,25 KC). Tứ giác
ADCE nội tiếp nên =
CAE CDE (góc nội tiếp cùng chắn cung EC). Từ đó suy ra =
CHK CDE (đồng vị) nên HK // DE .
Do HK // DE , mà H là trung điểm CDnên HK là đường trung bình của
tam giác CDF nên K là trung điểm FC. 0,25
Tam giác AFC có AK là đường cao đồng thời cũng là trung tuyến nên là
tam giác cân tại A . Mặt khác tam giác ACD cân tại A nên AC = AD = AF.
Vẽ đường cao DP của tam giác ADF. Ta có 1 1 S = ⋅ = ⋅ . ∆ DP AF DP AC ADF 2 2 0,25
Do AC không đổi nên S
lớn nhất khi và chỉ khi DP lớn nhất. A ∆ DF 2
Ta có: DP ≤ AD = AC hay 1 AC S = ⋅ ≤ (không đổi). ∆ DP AC ADF 2 2
Dấu “=” xảy ra khi và chỉ khi P ≡ A tức là
DAF = 90° nên tam giác ADF
vuông cân tại A, suy ra
EDA = 45° mà = EBA EDA nên
EBA = 45° . Khi đó 0,25
E là điểm chính giữa cung A . B
Vậy diện tích tam giác ADF lớn nhất khi E là điểm chính giữa cung A . B 15
Vận tốc khi chạy ngược chiều gió là v6 km / h (0,5đ s )
Thời gian chạy trên quãng đường s là: t (giờ) v6
Năng lượng tiêu hao của để chạy trên quãng đường s là: 0,25 3 s
E v c v ( Jun ), v 6 v6 Đặt: a
v6 , suy ra: v a 6 a 0. Ta có: s a 63 3 c v s.c v6 a 2 216
s.c a 18a 108 a
Ev nhỏ nhất khi 2 216 a 18a nhỏ nhất a Ta có: 2 216 2 27 27 9 a 18a a 18 a a a a a 0,25 2 27 27 9 3 3 a
18 2 a 351 a a a
Dấu " " xảy ra khi a 3 hay v 9
Vậy người đó chạy với vận tốc 9 km / h thì năng lượng tiêu hao ít nhất.
Chú ý: + Học sinh làm cách khác đúng vẫn cho điểm tôi đa.
+ Bài hình không có hình hoặc vẽ hình sai thì không chấm.
Xem thêm: ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN
https://thcs.toanmath.com/de-thi-tuyen-sinh-lop-10-mon-toan
Document Outline
- ĐỀ - ĐA Toán 9( Lần 4)
- TUYEN SINH 10