Đề kiểm tra 1 tiết Giải tích 12 chương 1 năm 2019 – 2020 trường Chà Cang – Điện Biên

Ngay sau khi các em học sinh lớp 12 hoàn thành nội dung Giải tích 12 chương 1: ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số, trường THPT Chà Cang (Xã Chà Cang, Huyện Nậm Pồ, Điện Biên) đã tổ chức kỳ kiểm tra một tiết để đánh giá khả năng tiếp thu bài học của các em.

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

8 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/4 Mã đề 100
SỞ GD&ĐT ĐIỆN BIÊN
TRƯỜNG THPT CHÀ CANG
Đề chính thức
(Đề kiểm tra gồm 04 trang)
ĐỀ KIỂM TRA 1 TIẾT
Môn: Giải tích 12 – THPT
Năm học 2019 - 2020
Thời gian làm bài: 45 phút
(Không kể thời gian giao đề)
I. TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm).
Câu 1. Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
2;0
. B.
( ;1)
. C.
0;2
. D.
(3;1)
.
Câu 2. Cho hàm số
y f x
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
1
. B.
2
. C.
0
. D.
.
Câu 3. Hàm số
4
2 1
y x
đồng biến trên khoảng nào?
A.
1
;
2

. B.
1
;
2

. C.
0;

. D.
( ;0)
.
Câu 4. Tìm giá trị lớn nhất M của hàm số
3 1
3
x
y
x
trên đoạn
0;2
A.
1
3
M
. B.
1
3
M
. C.
5
M
. D.
5
M
.
Câu 5. Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
. B.
0
. C.
2
. D.
1
.
Câu 6. Tìm phương trình các đường tiệm cận đứng của đồ thị hàm số
2 1
3 1
x
y
x
A.
2
3
x
. B.
2
3
y
. C.
1
3
x
. D.
1
3
y
.
Câu 7. Giá trị lớn nhất của hàm số
3
( ) 3 2f x x x
trên đoạn
[ 3;3]
bằng
A.
16
. B.
20
. C.
0
. D.
4
.
MÃ ĐỀ 100
Trang 2/4 Mã đề 100
Câu 8. Cho hàm số
( )y f x
, có đạo hàm
2
'( ) 1,
f x x x R
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
(1; )
.
B. Hàm số nghịch biến trên khoảng
( ; ) 
.
C. Hàm số đồng biến trên khoảng
( ; ) 
.
D. Hàm số nghịch biến trên các khoảng
1;1
.
Câu 9. Cho đồ thị hàm số
2 3
1
x
y
x
. Mệnh đề nào sau đây đúng?
A. Đồ thị hàm số có đường tiệm cận đứng là
1x
.
B. Đồ thị hàm số có đường tiệm cận ngang là
2
x
.
C. Đồ thị hàm số có đường tiệm cận đứng là
1y
.
D. Đồ thị hàm số có đường tiệm cận ngang là
2
y
.
Câu 10. Hàm số nào dưới đây đồng biến trên khoảng
;
 
?
A.
1
3
x
y
x
. B.
3
y x x
. C.
1
2
x
y
x
. D.
3
3y x x
.
Câu 11. Tìm giá trị cực tiểu của đồ thị hàm số
3 2
2 3 2
y x x
.
A.
3
CT
y
. B.
2
CT
y
. C.
0
CT
y
. D.
1
CT
y
.
Câu 12. Cho hàm số
y f x
có bảng biến thiên như sau:
Số tiệm cận ngang của đồ thị hàm số đã cho là
A.
4.
. B.
1.
. C.
3.
. D.
2.
.
Câu 13. Cho hàm số
y f x
liên tục trên đoạn
1;3
và có đồ thị như hình bên. Gọi
M
và
m
lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3
. Giá trị của
M m
bằng
A.
0
. B.
1
. C.
4
. D.
.
Câu 14. Cho hàm số
( )f x
có bảng xét của đạo hàm như sau:
O
2
2
1
1
2
y
x
Trang 3/4 Mã đề 100
Số điểm cực trị của hàm số đã cho là
A.
. B.
2
. C.
4
. D.
1
.
Câu 15. Cho hàm số
( )y f x
có
lim ( ) 1
x
f x

và
lim ( ) 1
x
f x

. Khẳng định nào sau đây là
khẳng định đúng?
A. Đồ thị hàm số đã cho không có đường tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một đường tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng
1y
và
1y
.
D. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng
1x
và
1x
.
Câu 16. Tính tổng giá trị cực đại và giá trị cực tiểu của hàm số
3 2
3 2
y x x
.
A. 3. B. 2. C. 1. D. 0.
Câu 17. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
5
2
x
y
x
trên
2;1
.
Tính
2T M m
.
A.
14T
. B.
10
T
. C.
21
2
T
. D.
13
2
T
.
Câu 18. Đường tiệm cận ngang của đồ thị hàm số
2
2 1
4 3
x
y
x
A.
1y
. B.
2; 2y y
. C.
2y
. D.
1; 1y y
.
Câu 19. Cho hàm số
f x
có đạo hàm
2 3
'( ) ( 1)( 2) ( 3)
f x x x x
,
x
. Số điểm cực trị của hàm
số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 20. Đồ thị hàm số
2
2
4
x
y
x
có bao nhiêu đường tiệm cận.
A.
0
. B.
. C.
1
. D.
2
.
Câu 21. Tìm tham số m để đồ thị của hàm số
4 2
2( 1) 1
y x m x
có ba điểm cực trị?
A.
1
m
.
B.
1
m
. C.
1
m
. D.
1
2
m
.
Câu 22. Hàm số
3 2
1
1 1 2
3
y x m x m x
đồng biến trên tập xác định của nó khi
A.
4
m
. B.
2 1
m
. C.
2
m
. D.
4
m
.
Câu 23. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
3
x
y
x m
đồng biến trên khoảng
; 6
?
A.
2
. B.
6
. C. Vô số. D.
1
.
Câu 24. Hàm số
2
1
x m
y
x
đạt giá trị lớn nhất trên đoạn
0;1
bằng 1 khi:
A.
2
m
. B.
0
m
. C.
1
m
. D.
2
m
.
Trang 4/4 Mã đề 100
Câu 25. Cho hàm số
f x
, bảng xét dấu của
f x
như sau:
x
3
1
1
f x
0
0
0
Hàm số
3 2
y f x
nghịch biến trên khoảng nào dưới đây?
A.
4;
. B.
2;1
. C.
2;4
. D.
1;2
.
II. TỰ LUẬN (2,0 điểm).
Cho hàm số
3
12 1y x x
a) Xét tính đơn điệu của hàm số ;
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
0;3
.
-------------------------------- HẾT -----------------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm !
Họ và tên thí sinh: …………………………Số báo danh…………………….
Chữ ký cán bộ coi thi số 1……………….Chữ ký cán bộ coi thi số 2……………………
NGƯỜI RA ĐỀ TỔ TRƯỞNG CHUYÊN MÔN BAN GIÁM HIỆU
Trang 1/4 Mã đề 100
SỞ GD&ĐT ĐIỆN BIÊN
TRƯỜNG THPT CHÀ CANG
Đề chính thức
(Đề kiểm tra gồm 04 trang)
ĐỀ KIỂM TRA 1 TIẾT
Môn: Giải tích 12 – THPT
Năm học 2019 - 2020
Thời gian làm bài: 45 phút
(Không kể thời gian giao đề)
I. TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm).
Câu 1. Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
2;0
. B.
( ;1)
. C.
0;2
. D.
(3;1)
.
Câu 2. Cho hàm số
y f x
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
1
. B.
2
. C.
0
. D.
.
Câu 3. Hàm số
4
2 1
y x
đồng biến trên khoảng nào?
A.
1
;
2

. B.
1
;
2

. C.
0;

. D.
( ;0)
.
Câu 4. Tìm giá trị lớn nhất M của hàm số
3 1
3
x
y
x
trên đoạn
0;2
A.
1
3
M
. B.
1
3
M
. C.
5
M
. D.
5
M
.
Câu 5. Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
. B.
0
. C.
2
. D.
1
.
Câu 6. Tìm phương trình các đường tiệm cận đứng của đồ thị hàm số
2 1
3 1
x
y
x
A.
2
3
x
. B.
2
3
y
. C.
1
3
x
. D.
1
3
y
.
Câu 7. Giá trị lớn nhất của hàm số
3
( ) 3 2f x x x
trên đoạn
[ 3;3]
bằng
A.
16
. B.
20
. C.
0
. D.
4
.
MÃ ĐỀ 100
Trang 2/4 Mã đề 100
Câu 8. Cho hàm số
( )y f x
, có đạo hàm
2
'( ) 1,
f x x x R
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
(1; )
.
B. Hàm số nghịch biến trên khoảng
( ; ) 
.
C. Hàm số đồng biến trên khoảng
( ; ) 
.
D. Hàm số nghịch biến trên các khoảng
1;1
.
Câu 9. Cho đồ thị hàm số
2 3
1
x
y
x
. Mệnh đề nào sau đây đúng?
A. Đồ thị hàm số có đường tiệm cận đứng là
1x
.
B. Đồ thị hàm số có đường tiệm cận ngang là
2
x
.
C. Đồ thị hàm số có đường tiệm cận đứng là
1y
.
D. Đồ thị hàm số có đường tiệm cận ngang là
2
y
.
Câu 10. Hàm số nào dưới đây đồng biến trên khoảng
;
 
?
A.
1
3
x
y
x
. B.
3
y x x
. C.
1
2
x
y
x
. D.
3
3y x x
.
Câu 11. Tìm giá trị cực tiểu của đồ thị hàm số
3 2
2 3 2
y x x
.
A.
3
CT
y
. B.
2
CT
y
. C.
0
CT
y
. D.
1
CT
y
.
Câu 12. Cho hàm số
y f x
có bảng biến thiên như sau:
Số tiệm cận ngang của đồ thị hàm số đã cho là
A.
4.
. B.
1.
. C.
3.
. D.
2.
.
Câu 13. Cho hàm số
y f x
liên tục trên đoạn
1;3
và có đồ thị như hình bên. Gọi
M
và
m
lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3
. Giá trị của
M m
bằng
A.
0
. B.
1
. C.
4
. D.
.
Câu 14. Cho hàm số
( )f x
có bảng xét của đạo hàm như sau:
O
2
2
1
1
2
y
x
Trang 3/4 Mã đề 100
Số điểm cực trị của hàm số đã cho là
A.
. B.
2
. C.
4
. D.
1
.
Câu 15. Cho hàm số
( )y f x
có
lim ( ) 1
x
f x

và
lim ( ) 1
x
f x

. Khẳng định nào sau đây là
khẳng định đúng?
A. Đồ thị hàm số đã cho không có đường tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một đường tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng
1y
và
1y
.
D. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng
1x
và
1x
.
Câu 16. Tính tổng giá trị cực đại và giá trị cực tiểu của hàm số
3 2
3 2
y x x
.
A. 3. B. 2. C. 1. D. 0.
Câu 17. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
5
2
x
y
x
trên
2;1
.
Tính
2T M m
.
A.
14T
. B.
10
T
. C.
21
2
T
. D.
13
2
T
.
Câu 18. Đường tiệm cận ngang của đồ thị hàm số
2
2 1
4 3
x
y
x
A.
1y
. B.
2; 2y y
. C.
2y
. D.
1; 1y y
.
Câu 19. Cho hàm số
f x
có đạo hàm
2 3
'( ) ( 1)( 2) ( 3)
f x x x x
,
x
. Số điểm cực trị của hàm
số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 20. Đồ thị hàm số
2
2
4
x
y
x
có bao nhiêu đường tiệm cận.
A.
0
. B.
. C.
1
. D.
2
.
Câu 21. Tìm tham số m để đồ thị của hàm số
4 2
2( 1) 1
y x m x
có ba điểm cực trị?
A.
1
m
.
B.
1
m
. C.
1
m
. D.
1
2
m
.
Câu 22. Hàm số
3 2
1
1 1 2
3
y x m x m x
đồng biến trên tập xác định của nó khi
A.
4
m
. B.
2 1
m
. C.
2
m
. D.
4
m
.
Câu 23. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
3
x
y
x m
đồng biến trên khoảng
; 6
?
A.
2
. B.
6
. C. Vô số. D.
1
.
Câu 24. Hàm số
2
1
x m
y
x
đạt giá trị lớn nhất trên đoạn
0;1
bằng 1 khi:
A.
2
m
. B.
0
m
. C.
1
m
. D.
2
m
.
Trang 4/4 Mã đề 100
Câu 25. Cho hàm số
f x
, bảng xét dấu của
f x
như sau:
x
3
1
1
f x
0
0
0
Hàm số
3 2
y f x
nghịch biến trên khoảng nào dưới đây?
A.
4;
. B.
2;1
. C.
2;4
. D.
1;2
.
II. TỰ LUẬN (2,0 điểm).
Cho hàm số
3
12 1y x x
a) Xét tính đơn điệu của hàm số ;
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
0;3
.
-------------------------------- HẾT -----------------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm !
Họ và tên thí sinh: …………………………Số báo danh…………………….
Chữ ký cán bộ coi thi số 1……………….Chữ ký cán bộ coi thi số 2……………………
NGƯỜI RA ĐỀ TỔ TRƯỞNG CHUYÊN MÔN BAN GIÁM HIỆU
| 1/8
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT ĐIỆN BIÊN ĐỀ KIỂM TRA 1 TIẾT TRƯỜNG THPT CHÀ CANG
Môn: Giải tích 12 – THPT Năm học 2019 - 2020 Đề chính thức
Thời gian làm bài: 45 phút
(Đề kiểm tra gồm 04 trang)
(Không kể thời gian giao đề)
I. TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm). MÃ ĐỀ 100 Câu 1.
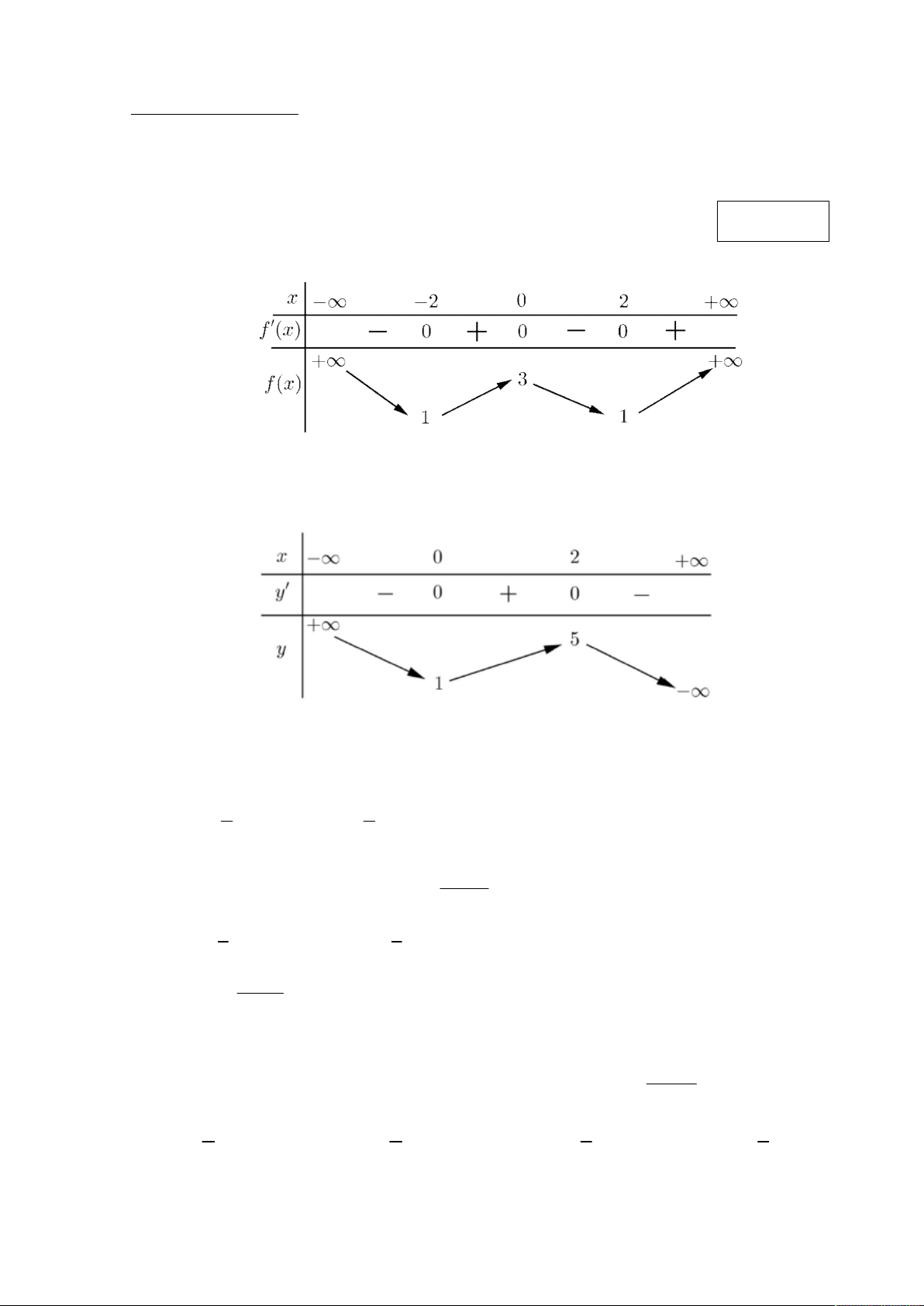
Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  2  ;0 . B. ( ;1  ) . C. 0; 2 . D. (3;1) . Câu 2.
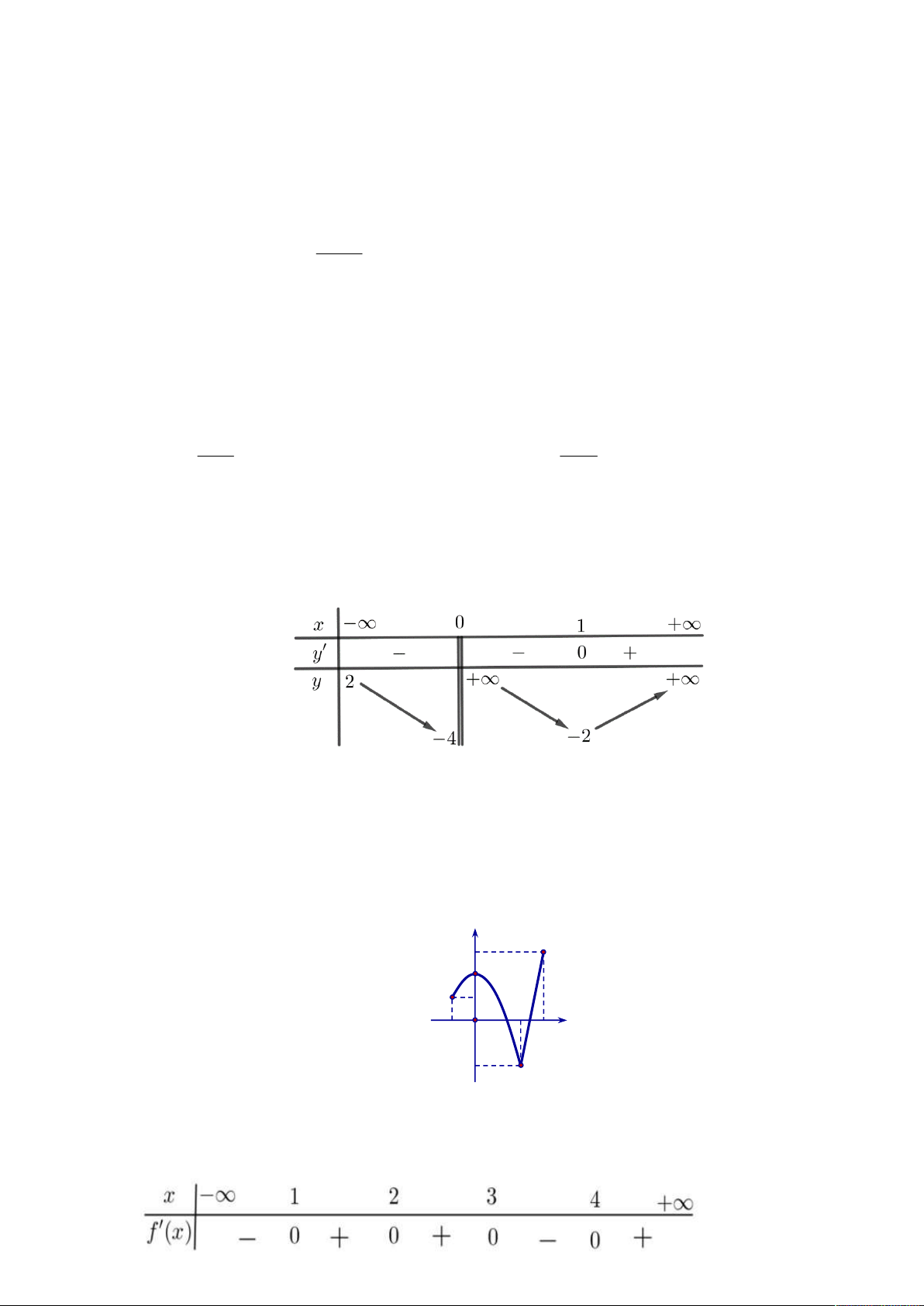
Cho hàm số y f x có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 1. B. 2 . C. 0 . D. 5 . Câu 3. Hàm số 4
y  2x 1 đồng biến trên khoảng nào?  1   1  A.  ;     . B. ;    . C. 0;  . D. ( ;  0) .  2   2  3x 1 Câu 4.
Tìm giá trị lớn nhất M của hàm số y  trên đoạn 0; 2 x 3 1 1 A. M   . B. M  . C. M  5 . D. M  5  . 3 3 2x  3 Câu 5. Hàm số y
có bao nhiêu điểm cực trị? x 1 A. 3 . B. 0 . C. 2 . D. 1. 2x 1 Câu 6.
Tìm phương trình các đường tiệm cận đứng của đồ thị hàm số y  3x 1 2 2 1 1 A. x  . B. y  . C. x   . D. y   . 3 3 3 3 Câu 7.
Giá trị lớn nhất của hàm số 3
f (x)  x  3x  2 trên đoạn [  3;3] bằng A. 16 . B. 20 . C. 0 . D. 4 . Trang 1/4 Mã đề 100 Câu 8.
Cho hàm số y f (x) , có đạo hàm 2
f '(x)  x 1, x
  R . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (1;) .
B. Hàm số nghịch biến trên khoảng ( ;   )  .
C. Hàm số đồng biến trên khoảng ( ;   )  .
D. Hàm số nghịch biến trên các khoảng 1;  1 . 2x  3 Câu 9.
Cho đồ thị hàm số y
. Mệnh đề nào sau đây đúng? x 1
A. Đồ thị hàm số có đường tiệm cận đứng là x  1 .
B. Đồ thị hàm số có đường tiệm cận ngang là x  2  .
C. Đồ thị hàm số có đường tiệm cận đứng là y  1.
D. Đồ thị hàm số có đường tiệm cận ngang là y  2 .
Câu 10. Hàm số nào dưới đây đồng biến trên khoảng  ;   ? x 1 x 1 A. y  . B. 3
y x x . C. y  . D. 3
y  x  3x . x  3 x  2
Câu 11. Tìm giá trị cực tiểu của đồ thị hàm số 3 2
y  2x  3x  2 . A. y  3 . B. y  2 . C. y  0 . D. y 1. CT CT CT CT
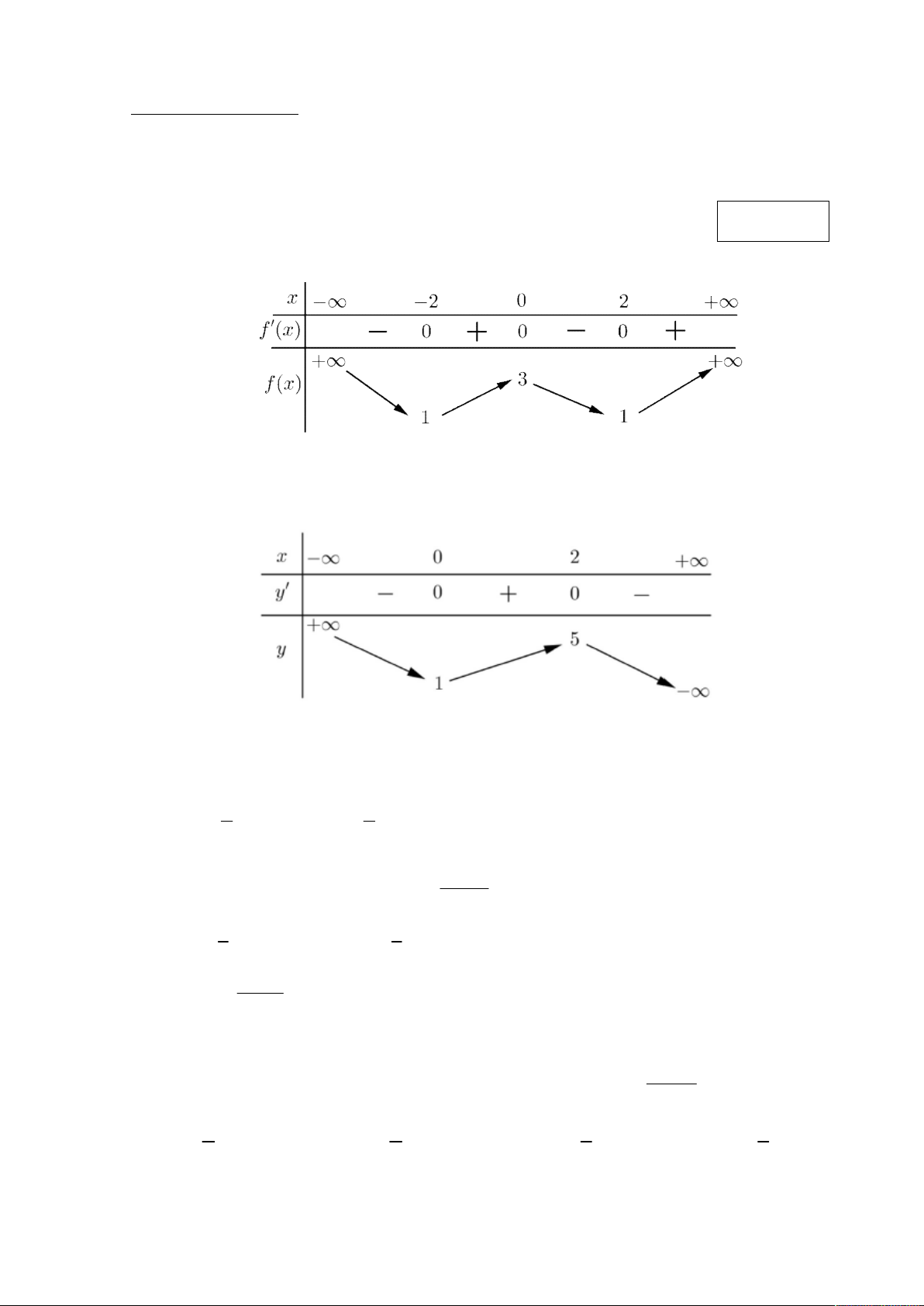
Câu 12. Cho hàm số y f x có bảng biến thiên như sau:
Số tiệm cận ngang của đồ thị hàm số đã cho là A. 4. . B. 1. . C. 3. . D. 2. .
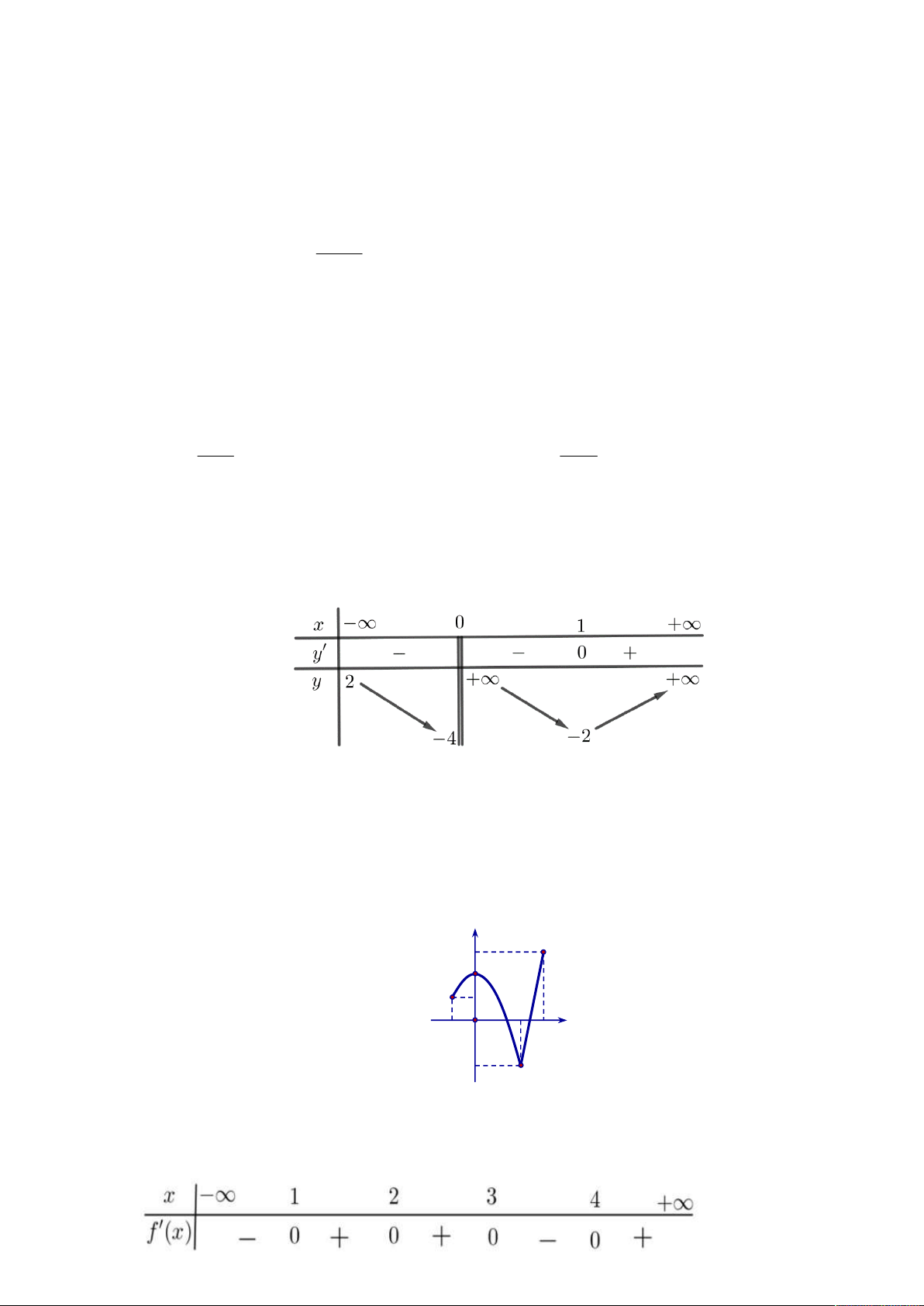
Câu 13. Cho hàm số y f x liên tục trên đoạn  1  ; 
3 và có đồ thị như hình bên. Gọi M và m lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1  ; 
3 . Giá trị của M m bằng y 3 2 1 2 x 1  O 3 2  A. 0 . B. 1. C. 4 . D. 5 .
Câu 14. Cho hàm số f (x) có bảng xét của đạo hàm như sau: Trang 2/4 Mã đề 100
Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 4 . D. 1.
Câu 15. Cho hàm số y f (x) có lim f (x)  1 và lim f (x)  1. Khẳng định nào sau đây là x x khẳng định đúng?
A. Đồ thị hàm số đã cho không có đường tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một đường tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng y  1 và y  1.
D. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng x  1 và x  1.
Câu 16. Tính tổng giá trị cực đại và giá trị cực tiểu của hàm số 3 2
y x  3x  2 . A. 3. B. 2. C. 1. D. 0. 2 x  5
Câu 17. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên 2;  1 . x  2
Tính T M  2m . 21 13 A. T  14 . B. T  10 . C. T   . D. T   . 2 2 2x 1
Câu 18. Đường tiệm cận ngang của đồ thị hàm số y  2 4x  3 A. y  1.
B. y  2; y  2 . C. y  2 . D. y  1  ; y 1.
Câu 19. Cho hàm số f x có đạo hàm 2 3
f '(x)  (x 1)(x  2) (x  3) , x
   . Số điểm cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D. 1. x  2
Câu 20. Đồ thị hàm số y
có bao nhiêu đường tiệm cận. 2 x  4 A. 0 . B. 3 . C. 1. D. 2 .
Câu 21. Tìm tham số m để đồ thị của hàm số y  4 x m  2 2(
1)x  1 có ba điểm cực trị? 1 A. m  1  B. m  1. C. m  1  . D. m   . . 2 1 Câu 22. Hàm số 3 y
x  m   2
1 x  m  
1 x  2 đồng biến trên tập xác định của nó khi 3 A. m  4 . B. 2   m  1  . C. m  2 . D. m  4 . x  2
Câu 23. Có bao nhiêu giá trị nguyên của tham số m để hàm số y
đồng biến trên khoảng x  3m  ;   6 ? A. 2 . B. 6 . C. Vô số. D. 1. 2x m
Câu 24. Hàm số y
đạt giá trị lớn nhất trên đoạn 0  ;1 bằng 1 khi: x 1 A. m  2 . B. m  0 . C. m  1. D. m  2 . Trang 3/4 Mã đề 100
Câu 25. Cho hàm số f x , bảng xét dấu của f  x như sau: x  3  1 1  f  x  0  0  0 
Hàm số y f 3  2x nghịch biến trên khoảng nào dưới đây? A. 4;   . B.  2   ;1 . C. 2; 4 . D. 1; 2 .
II. TỰ LUẬN (2,0 điểm). Cho hàm số 3
y x 12x 1
a) Xét tính đơn điệu của hàm số ;
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0;  3 .
-------------------------------- HẾT -----------------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm !
Họ và tên thí sinh: …………………………Số báo danh…………………….
Chữ ký cán bộ coi thi số 1……………….Chữ ký cán bộ coi thi số 2…………………… NGƯỜI RA ĐỀ TỔ TRƯỞNG CHUYÊN MÔN BAN GIÁM HIỆU Trang 4/4 Mã đề 100 SỞ GD&ĐT ĐIỆN BIÊN ĐỀ KIỂM TRA 1 TIẾT TRƯỜNG THPT CHÀ CANG
Môn: Giải tích 12 – THPT Năm học 2019 - 2020 Đề chính thức
Thời gian làm bài: 45 phút
(Đề kiểm tra gồm 04 trang)
(Không kể thời gian giao đề)
I. TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm). MÃ ĐỀ 100 Câu 1.
Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  2  ;0 . B. ( ;1  ) . C. 0; 2 . D. (3;1) . Câu 2.
Cho hàm số y f x có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 1. B. 2 . C. 0 . D. 5 . Câu 3. Hàm số 4
y  2x 1 đồng biến trên khoảng nào?  1   1  A.  ;     . B. ;    . C. 0;  . D. ( ;  0) .  2   2  3x 1 Câu 4.
Tìm giá trị lớn nhất M của hàm số y  trên đoạn 0; 2 x 3 1 1 A. M   . B. M  . C. M  5 . D. M  5  . 3 3 2x  3 Câu 5. Hàm số y
có bao nhiêu điểm cực trị? x 1 A. 3 . B. 0 . C. 2 . D. 1. 2x 1 Câu 6.
Tìm phương trình các đường tiệm cận đứng của đồ thị hàm số y  3x 1 2 2 1 1 A. x  . B. y  . C. x   . D. y   . 3 3 3 3 Câu 7.
Giá trị lớn nhất của hàm số 3
f (x)  x  3x  2 trên đoạn [  3;3] bằng A. 16 . B. 20 . C. 0 . D. 4 . Trang 1/4 Mã đề 100 Câu 8.
Cho hàm số y f (x) , có đạo hàm 2
f '(x)  x 1, x
  R . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (1;) .
B. Hàm số nghịch biến trên khoảng ( ;   )  .
C. Hàm số đồng biến trên khoảng ( ;   )  .
D. Hàm số nghịch biến trên các khoảng 1;  1 . 2x  3 Câu 9.
Cho đồ thị hàm số y
. Mệnh đề nào sau đây đúng? x 1
A. Đồ thị hàm số có đường tiệm cận đứng là x  1 .
B. Đồ thị hàm số có đường tiệm cận ngang là x  2  .
C. Đồ thị hàm số có đường tiệm cận đứng là y  1.
D. Đồ thị hàm số có đường tiệm cận ngang là y  2 .
Câu 10. Hàm số nào dưới đây đồng biến trên khoảng  ;   ? x 1 x 1 A. y  . B. 3
y x x . C. y  . D. 3
y  x  3x . x  3 x  2
Câu 11. Tìm giá trị cực tiểu của đồ thị hàm số 3 2
y  2x  3x  2 . A. y  3 . B. y  2 . C. y  0 . D. y 1. CT CT CT CT
Câu 12. Cho hàm số y f x có bảng biến thiên như sau:
Số tiệm cận ngang của đồ thị hàm số đã cho là A. 4. . B. 1. . C. 3. . D. 2. .
Câu 13. Cho hàm số y f x liên tục trên đoạn  1  ; 
3 và có đồ thị như hình bên. Gọi M và m lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1  ; 
3 . Giá trị của M m bằng y 3 2 1 2 x 1  O 3 2  A. 0 . B. 1. C. 4 . D. 5 .
Câu 14. Cho hàm số f (x) có bảng xét của đạo hàm như sau: Trang 2/4 Mã đề 100
Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 4 . D. 1.
Câu 15. Cho hàm số y f (x) có lim f (x)  1 và lim f (x)  1. Khẳng định nào sau đây là x x khẳng định đúng?
A. Đồ thị hàm số đã cho không có đường tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một đường tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng y  1 và y  1.
D. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng x  1 và x  1.
Câu 16. Tính tổng giá trị cực đại và giá trị cực tiểu của hàm số 3 2
y x  3x  2 . A. 3. B. 2. C. 1. D. 0. 2 x  5
Câu 17. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên 2;  1 . x  2
Tính T M  2m . 21 13 A. T  14 . B. T  10 . C. T   . D. T   . 2 2 2x 1
Câu 18. Đường tiệm cận ngang của đồ thị hàm số y  2 4x  3 A. y  1.
B. y  2; y  2 . C. y  2 . D. y  1  ; y 1.
Câu 19. Cho hàm số f x có đạo hàm 2 3
f '(x)  (x 1)(x  2) (x  3) , x
   . Số điểm cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D. 1. x  2
Câu 20. Đồ thị hàm số y
có bao nhiêu đường tiệm cận. 2 x  4 A. 0 . B. 3 . C. 1. D. 2 .
Câu 21. Tìm tham số m để đồ thị của hàm số y  4 x m  2 2(
1)x  1 có ba điểm cực trị? 1 A. m  1  B. m  1. C. m  1  . D. m   . . 2 1 Câu 22. Hàm số 3 y
x  m   2
1 x  m  
1 x  2 đồng biến trên tập xác định của nó khi 3 A. m  4 . B. 2   m  1  . C. m  2 . D. m  4 . x  2
Câu 23. Có bao nhiêu giá trị nguyên của tham số m để hàm số y
đồng biến trên khoảng x  3m  ;   6 ? A. 2 . B. 6 . C. Vô số. D. 1. 2x m
Câu 24. Hàm số y
đạt giá trị lớn nhất trên đoạn 0  ;1 bằng 1 khi: x 1 A. m  2 . B. m  0 . C. m  1. D. m  2 . Trang 3/4 Mã đề 100
Câu 25. Cho hàm số f x , bảng xét dấu của f  x như sau: x  3  1 1  f  x  0  0  0 
Hàm số y f 3  2x nghịch biến trên khoảng nào dưới đây? A. 4;   . B.  2   ;1 . C. 2; 4 . D. 1; 2 .
II. TỰ LUẬN (2,0 điểm). Cho hàm số 3
y x 12x 1
a) Xét tính đơn điệu của hàm số ;
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0;  3 .
-------------------------------- HẾT -----------------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm !
Họ và tên thí sinh: …………………………Số báo danh…………………….
Chữ ký cán bộ coi thi số 1……………….Chữ ký cán bộ coi thi số 2…………………… NGƯỜI RA ĐỀ TỔ TRƯỞNG CHUYÊN MÔN BAN GIÁM HIỆU Trang 4/4 Mã đề 100
Document Outline

  • AADe mot tiet so 1-GT12-HKI
  • De mot tiet so 1-GT12-HKI