Đề kiểm tra chất lượng Toán 10 lần 2 năm 2019 – 2020 trường THPT Lý Thái Tổ – Bắc Ninh

SỞ GD & ĐT BẮC NINH
ĐỀ KIỂM TRA CHẤT LƯỢNG LẦN 2
TRƯỜNG THPT LÝ THÁI TỔ
NĂM HỌC 2019 – 2020 ĐỀ THI CHÍNH THỨC
Môn: Toán – Lớp 10
(Đề thi gồm có 01 trang)
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Ngày thi 30 tháng 06 năm 2020
Câu 1 (1,0 điểm) Cho bất phương trình  2
m  m   2
6 x  2m  2x  2  0   1 . Tìm tất cả các giá
trị của tham số m để bất phương trình  
1 nghiệm đúng với mọi x  . 
Câu 2 (2,0 điểm) Giải các bất phương trình sau:
a. 2 2x  5  x  4. b. 2x  1 2x  1  2  3  0. x  1 x  1
Câu 3 (2,0 điểm) a. Cho 1
sin x   . Tính giá trị của biểu thức P  3 cos x.sin 2x  cos 2x. 3    
b. Chứng minh rằng:       2 4 cos x   .cos x  
    4 sin x  1.  3     3 
Câu 4 (3,0 điểm)
1. Trong mặt phẳng tọa độ Ox ,
y cho hai đường thẳng d : x  y  1  0 và d : 7x  y  13  0. 1 2
a. Tính cosin của góc tạo bởi hai đường thẳng d và d . 1 2
b. Viết phương trình tham số của đường thẳng  đi qua gốc tọa độ O và song song với d . 2
c. Viết phương trình đường tròn C  có tâm I nằm trên đường thẳng d , tiếp xúc với d 1 2
và có bán kính R  3 2.
2. Trong mặt phẳng với hệ trục tọa độ Ox ,
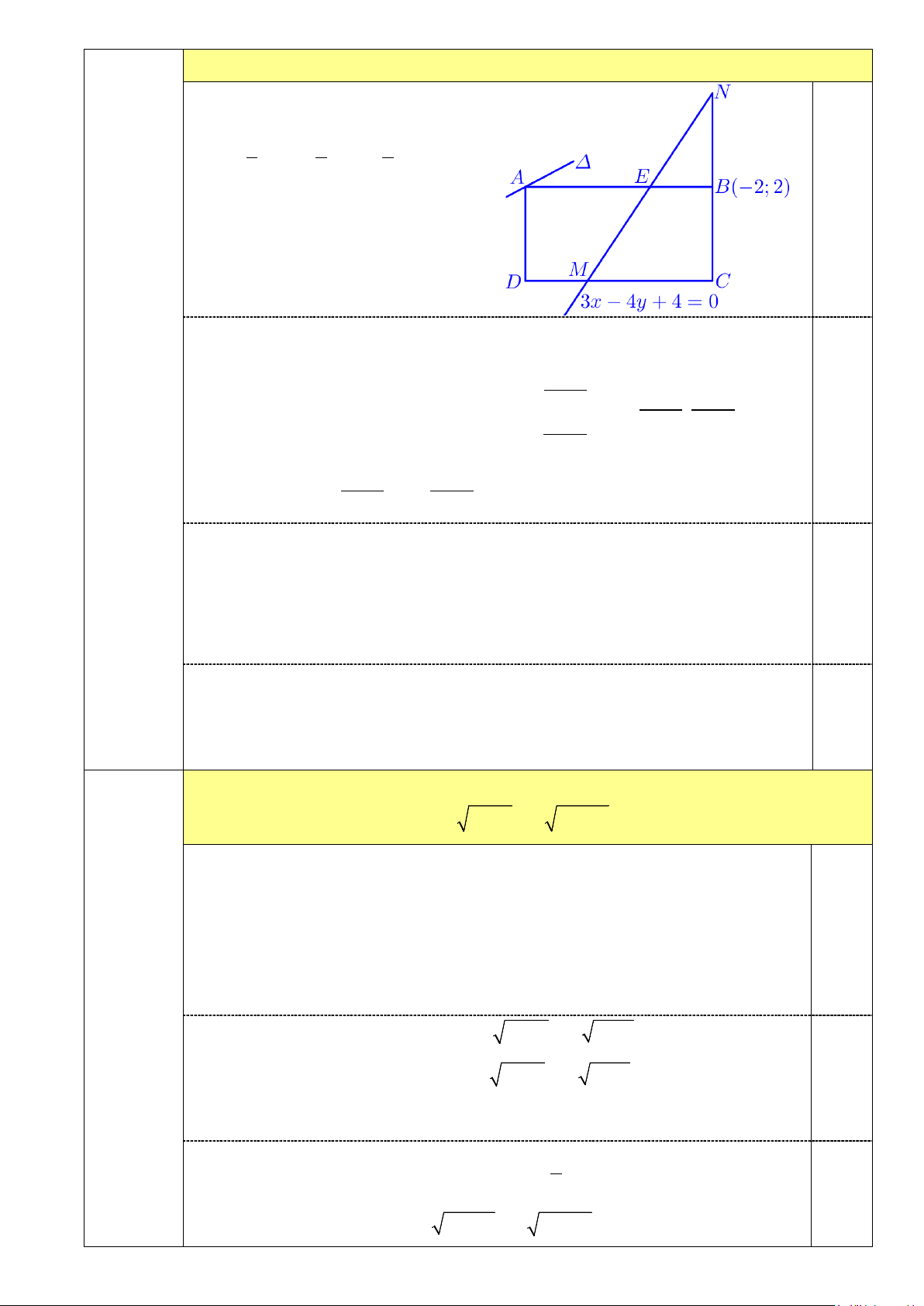
y cho hình chữ nhật ABCD có điểm M nằm trên cạnh
CD sao cho DC  3DM và điểm N đối xứng với điểm C qua điểm B. Biết đỉnh B 2;2,
điểm A nằm trên đường thẳng  : x  y  3  0 và đường thẳng MN có phương trình là
3x  4y  4  0. Xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD. 2 y
  4x  xy  y  12
Câu 5 (1,0 điểm) Giải hệ phương trình:  . 2 2 2
 x  y  x  y  2 4x  y  8x 
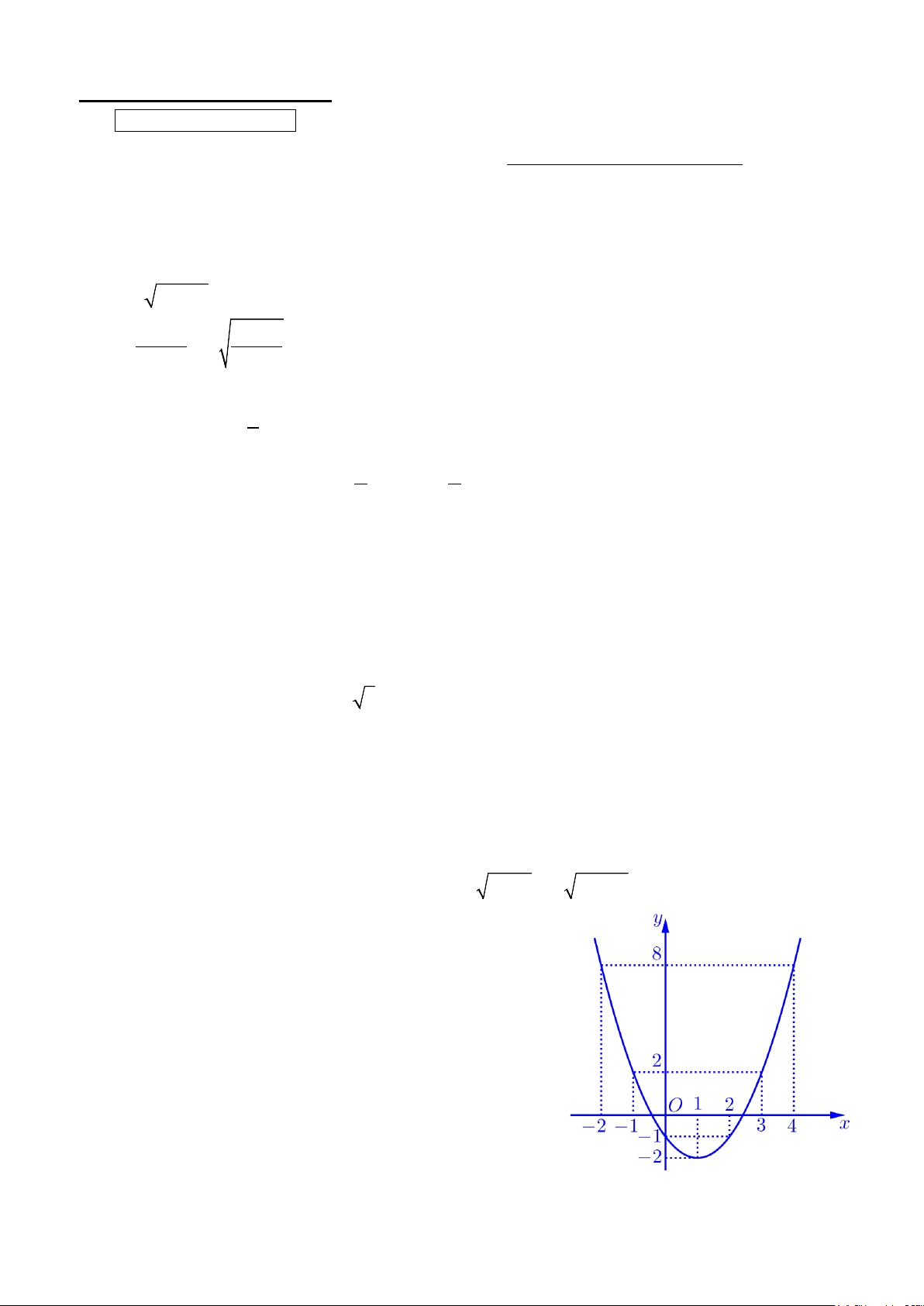
Câu 6 (1,0 điểm) Cho hàm số y  f x có đồ thị như hình vẽ
bên. Hỏi có tất cả bao nhiêu giá trị nguyên dương của tham số
m để bất phương trình f  2 x
  4x  m có nghiệm thuộc khoảng 0;3?
---------------------- HẾT ----------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm. SỞ GD & ĐT BẮC NINH
ĐÁP ÁN KIỂM TRA CHẤT LƯỢNG LẦN 2
TRƯỜNG THPT LÝ THÁI TỔ
NĂM HỌC 2019 – 2020
Môn: Toán – Lớp 10
(Đáp án – thang điểm gồm 04 trang) Câu Đáp án Điểm 1
Cho bất phương trình  2
m  m   2
6 x  2m  2x  2  0  
1 . Tìm tất cả các giá trị
(1,0 điểm) của tham số m để bất phương trình  1 nghiệm đúng với mọi x  . m   2 ▪ TH1: 2 m m 6 0      m   3 
Với m  2   
1  2  0 (luôn đúng)  m  2 thỏa mãn đề bài. 0,25 Với m     1 3
1  10x  2  0  x 
 m  3 không thỏa mãn đề bài. 5 m   2 ▪ TH2: 2 m m 6 0       m   3  0,25 2 m   m  6  0 Khi đó,   1 nghiệm đúng x       . 2   m   6m  16  0   m   3 
m  2 m  8       0,25 m   8 m   2      m   2  
Vậy giá trị m thỏa mãn đề bài là m  ; 2      8;   .  0,25 2
a. (1,0 điểm) 2 2x  5  x  4 . (2,0 điểm)  x   4 x   4  0      BPT   5 2  x 5 0 x           0,25 2   4
 2x  5  x  42 2 8
 x  20  x  8x 16    5  5 x     5      x   2   x  2   2      2 x 2  0,5 2       x 4 0 x       2  x  2     
Vậy tập nghiệm của bất phương trình là 5 S   ;2    2;   . 0,25 2  
b. (1,0 điểm) 2x  1 2x  1  2  3  0 . x  1 x  1 Đặt 2x  1 t  t  0. x  1 t  1 0,5
Khi đó, bất phương trình trở thành: 2 t 2t 3 0      t  3 
 t  1 thỏa mãn điều kiện Trang 1/4 2x  1 2x  1 x  2 x   1 Với t 1 1 1 0           0,25 x  1 x  1 x  1 x  2 
Vậy tập nghiệm của bất phương trình là S  ; 2     1;    . 0,25 3
(2,0 điểm) a. (1,0 điểm) Cho 1
sin x   . Tính giá trị của biểu thức P  3 cos x.sin 2x  cos 2x . 3
Ta có P  3 cosx.2 sinx.cosx  cos2x 0,25 2 2
 6 cos x.sin x  1  2 sin x 0,25   2  x 2 6 1 sin
.sin x  1  2 sin x 0,25     1   1   1  6 1   .       1  2.  1  0,25  9    3 9    
b. (1,0 điểm) Chứng minh rằng:       2 4 cos x   .cos x  
    4 sin x  1.  3     3   2     2 1
VT  2cos2x  cos  4 sin x  2    cos 2x     2  0,5     1 cos2x 3   2
 2 cos2x 1  2  2 cos2x  1 VP (đpcm) 0,5 4
1a. (0,5 điểm) Tính cosin của góc tạo bởi hai đường thẳng d và d . 1 2 (3,0 điểm)  
Ta có: n  1;1 là một VTPT của d và n  7;1 là một VTPT của d . 0,25 2   1   1 2 1.7    1 .  1 Do đó,  4 cos d ,d   . 0,25 1 2  2 2 2 2 5 1  1 . 7  1
1b. (0,5 điểm) Viết phương trình tham số của  đi qua O và song song với d . 2  
 //d   nhận n  7;1 là một VTPT  u  1;7 là một VTCP của . 0,25 2   2 x   t
Mà O 0;0    phương trình tham số của  là:  . 0,25 y   7t 
1c. (1,0 điểm) Viết phương trình đường tròn C  có tâm I nằm trên đường thẳng d , 1
tiếp xúc với d và có bán kính R  3 2 . 2
Giả sử I a;a   1  d . 1 0,25
C tiếp xúc với d  d I;d  R 2  2
7a  a   1  13 a   7  I  7;6   3 2   0,25 2 2 a 
  3  I 3;4 7 1   Với 2 2
I 7;6  phương trình C  là x  7  y  6  18 . 0,25 Với 2 2
I 3;4  phương trình C  là x  3  y  4  18 . 0,25 Trang 2/4
2. (1,0 điểm) Tìm tọa độ các đỉnh còn lại của hình chữ nhật ABCD .
Gọi E  AB  MN.
Vì B là trung điểm CN nên 1 1 1
BE  CM  CD  AB. 2 3 3  
Suy ra AB  3EB   * 0,25  
Giả sử Aa;3 a    AB  2 a;1 a, EB  2  x ;2 y . E E  a  4 2   6  3 x a x     Do đó   E     E a 4 7 a *   3     E  ; .
1  a  6  3y  7 a   0,25    3 3  E y   E  3     Mà a  4   7 a
E  MN  3   4    
  4  0  a  4  A     4; 1. 3   3  
Đường thẳng BC đi qua B 2;2 và nhận AB  6;3 là một VTPT.
 phương trình đường thẳng BC là 2x  y  6  0. 0,25
Vì N  MN  BC  N 4;2.
Mặt khác B là trung điểm CN  C 0;6.   6  0  x x   6 Ta có  D  D
AB  DC      D 6;3. 3   6  y y   3  A   D  0,25 Vậy A4; 
1 , C 0;6, D 6;3. 5  2 y
  4x  xy  y  12   1
(1,0 điểm) Giải hệ phương trình:  . 2 2 2
 x  y  x  y  2 4x  y  8x  2  x   y  0 Điều kiện:   * 4
 x  y  0  PT   2
1  y  y  12  4x  xy  0  y  3y  4 x y  4  0 0,25 y   y y x  4 4 3 0        y   x  3 
▪ Với y     2 4
2  2x  8x  16  x  4  4 x  1  0  x  2 2
2  8  x  4  4 x  1  0 3 0,25 Ta có  
*  x  1 VT  0  3 vô nghiệm. 3      x  
▪ Với y  x     2 3 0  3 3 *    x  . 3  x  3  0 2  Khi đó   2
2  3x  14x  9  2x  3  2 3x  3  0 Trang 3/4 2
 3x  12x  12  2x  3  x  
1  2 3x  3  x  4  0       x  x   2 2 2 x 4x 4 x 4x 4 3 4 4    0
2x  3  x  1
2 3x  3  x  4 0,25  3
x  4x  4  0  x  2  y  1  tm   1 1  3    0  4 
2x  3  x  1
2 3x  3  x  4 Vì 3 1 1 x 
 2x  3  x  1    2 . 2 2
2x  3  x  1 1 1
2 3x  3  x  4  4   .
2 3x  3  x  4 4 0,25 Suy ra 1 1 1 
 2   3  4 vô nghiệm.
2x  3  x  1
2 3x  3  x  4 4
Vậy nghiệm của hệ phương trình là x;y  2;  1 . 6
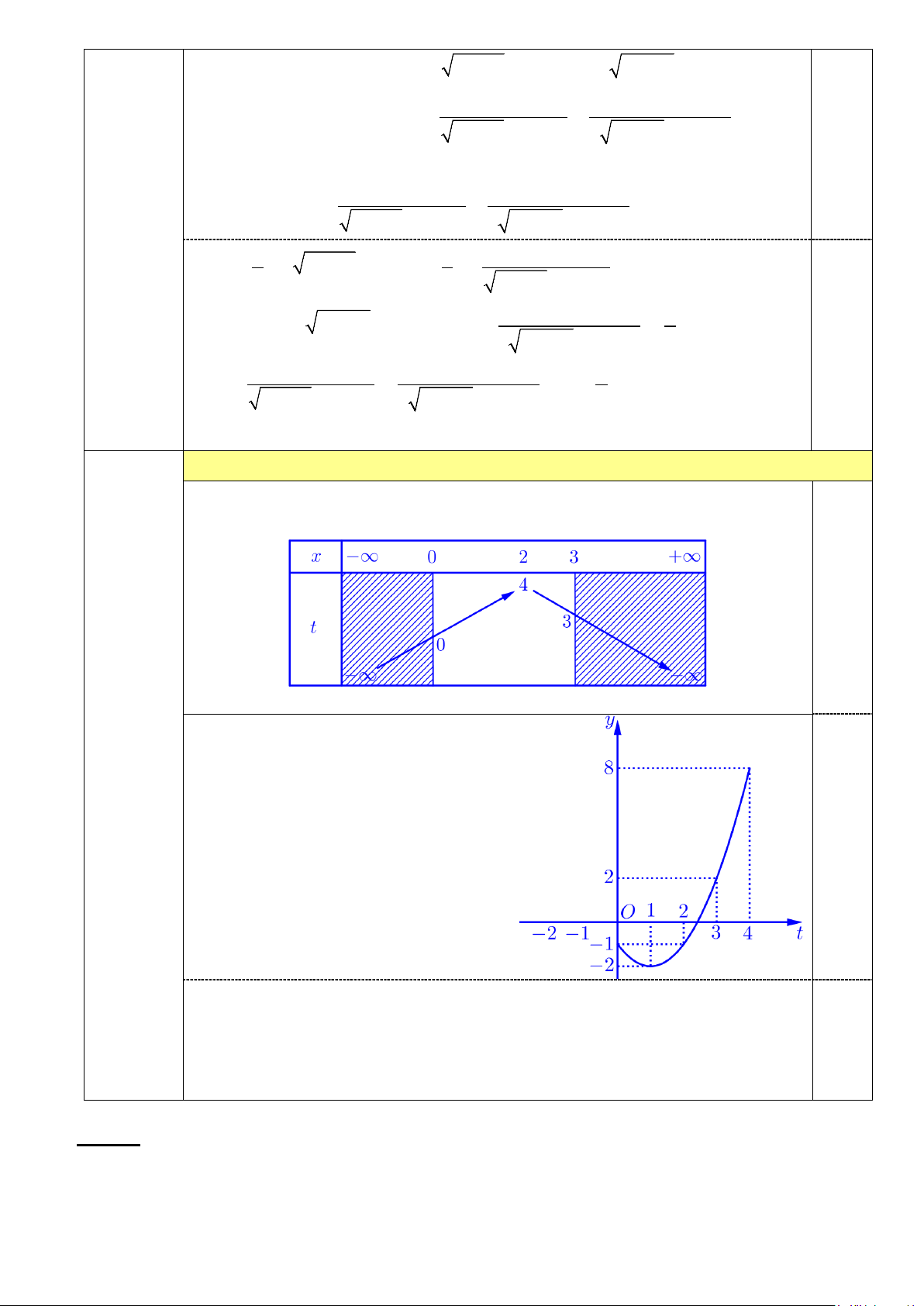
Hỏi có tất cả bao nhiêu giá trị nguyên dương của tham số m … (1,0 điểm) Đặt 2 t  x
  4x với x  0;3 Bảng biến thiên: 0,5 Suy ra 0  t  4.
Khi đó, bất phương trình trở thành:
f t  m   1
Vẽ đồ thị C  của hàm số y  f t ứng với t 0;4   . 0,25
Bất phương trình đã cho có nghiệm thuộc khoảng 0;3    1 có nghiệm thuộc nửa khoảng 0;4 
  có phần đồ thị của hàm số y  f t với t  0;4 nằm phía 0,25
trên đường thẳng d : y  m  m  8.
Vậy số các giá trị nguyên dương của tham số m là 7. }}
▪ Chú ý: Các cách giải khác đáp án và đúng đều cho điểm tối đa. Trang 4/4
Document Outline

• DE THI KHAO SAT K10 KY 2 NAM 2020 (DA SUA)