Đề kiểm tra cuối kỳ 1 Toán 12 năm 2021 – 2022 trường THPT Bảo Thắng 3 – Lào Cai

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra cuối học kỳ 1 môn Giới Toán 12 năm học 2021 – 2022 .Mời bạn đọc đón xem.

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

18 trang 8 tháng trước

Tác giả:

Profile Lan Tường
1/5 - Mã đề 101
THPT SỐ 3 BẢO THẮNG
TỔ: TOÁN – TIN - CN
(Đề thi có 05 trang)
KIỂM TRA CUỐI KỲ 1 NĂM HỌC 2021 - 2022
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(không kể thời gian phát đề)
PHẦN I. TRẮC NGHIỆM (7 điểm)
Câu 1. Thể tích khối hộp chữ nhật có độ dài ba kích thước lần lượt là
3, 4, 6
bằng
A.
24
. B.
12
. C.
72
. D.
18
.
Câu 2. Cho hàm số
(
)
y fx=
có bảng biến thiên như hình vẽ.
Giá trị nhỏ nhất của hàm số
( )
y fx=
trên đoạn
bằng
A.
3−
B.
2
. C.
3
. D.
1−
.
Câu 3. Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào dưới đây?
A.
42
22yx x=−+ +
. B.
32
32yx x=−+ +
. C.
32
32yx x=−+
. D.
42
22
yx x=−+
.
Câu 4. Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
2;3−
B.
( )
3; +∞
C.
( )
2;− +∞
D.
( )
;2−∞ −
Câu 5. Nghiệm của phương trình
4
log ( 1) 2x −=
là
A.
17x = −
B.
17x =
C.
16x =
D.
15x =
Câu 6. Cho
x
là một số thực dương, biểu thức
1
3
6
Px x= ⋅
viết dưới dạng lũy thừa với số mũ hữu tỷ là
A.
2
9
Px=
B.
2
Px=
C.
1
8
Px=
D.
1
2
Px=
Câu 7. Với
a
là số thực dương tùy ý,
3
5
log a
bằng
A.
5
1
log
3
a+
. B.
5
3 log a+
. C.
5
1
log
3
a
. D.
5
3log a
.
Mã đề 101
2/5 - Mã đề 101
Câu 8. Số nghiệm nguyên của bất phương trình
2
log 3x
<
là.
A.
7
. B.
9
. C. Vô số. D.
8
.
Câu 9. Cho hình nón có bán kính đáy bằng
7r
=
và độ dài đường sinh
9l =
. Diện tích xung quanh của
hình nón đã cho là
A.
97
xq
S
π
=
. B.
37
xq
S
π
=
. C.
18 7
xq
S
π
=
. D.
27 7
xq
S
π
=
.
Câu 10. Khối cầu có thể tích
4
V
π
=
. Bán kính
r
của khối cầu đó là
A.
3
r =
. B.
3r =
. C.
3
3r
=
. D.
3
33r =
.
Câu 11. Diện tích xung quanh hình trụ có độ dài đường sinh bằng
l
và bán kính đáy bằng
r
là
A.
1
3
xq
S rl
π
=
. B.
2
xq
S rl
π
=
. C.
4
xq
S rl
π
=
. D.
xq
S rl
π
=
.
Câu 12. Tập xác định của hàm số
(
)
6
log 4yx= −
là
A.
( )
;−∞ +∞
. B.
( )
;4−∞
. C.
[
)
4; +∞
. D.
(
)
4; +∞
.
Câu 13. Cho hình nón có đường sinh bằng
5a
và bán kính đáy bằng
3a
. Tính chiều cao của hình nón theo
a
A.
4a
. B.
8a
. C.
3
a
. D.
6a
cm.
Câu 14. Khối đa diện trong hình vẽ bên có bao nhiêu cạnh?
A.
4
B.
10
C.
12
D.
9
Câu 15. Hàm số
( )
2
4
2
x
fx
+
=
có đạo hàm là
A.
( )
2
4
2 ln 2
x
fx
+
′
=
. B.
( )
2
4
2 .2 ln 2
x
fx x
+
′
=
.
C.
( )
(
)
2
24
4 2 ln 2
x
fx x
+
′
= +
. D.
( )
( )
2
23
42
x
fx x
+
′
= +
.
Câu 16. Hàm số nào dưới đây có đồ thị như hình vẽ bên?
A.
42
22yx x=+−
. B.
42
22yx x=−+ −
. C.
3
22yx x=−−
.
D.
3
22
yx x=−+ −
.
Câu 17. Nghiệm của phương trình
2
39
x−
=
là.
A.
4x 
B.
3x 
C.
3x
D.
4x
Câu 18. Với
a
là số thực dương bất kỳ, mệnh đề nào sau đây đúng?
A.
( )
ln 3 ln 3 lnaa= +
. B.
( )
ln 3 ln 3 lnaa+= +
.
3/5 - Mã đề 101
C.
(
)
ln 5 5.lnaa
=
. D.
1
ln ln
33
a
a=
.
Câu 19. Cho hàm số
( )
fx
có bảng biến thiên như sau:
Điểm cực tiểu của hàm số đã cho là
A.
2x =
. B.
1
x
= −
. C.
3x = −
. D.
1x =
.
Câu 20. Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
+
=
−
là:
A.
1y = −
. B.
2y =
. C.
1y =
. D.
1
2
y =
.
Câu 21. Một khối đồ chơi gồm hai khối trụ
( )
( )
12
,HH
xếp chồng lên nhau, lần lượt có bán kính đáy và
chiều cao tương ứng là
1 12 2
,,,rhrh
thỏa mãn
2 12 1
1
,2
2
r rh h= =
. Biết rằng thể tích của toàn bộ khối đồ chơi
bằng
3
36
cm
, thể tích của khối trụ
( )
1
H
bằng
A.
3
2 0 c m
. B.
3
2 2 c m
. C.
3
1 0 c m
. D.
3
2 4 c m
.
Câu 22. Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác đều cạnh bằng
2, AB
′
tạo với mặt phẳng
đáy góc
0
60
. Thể tích khối lăng trụ
.
ABC A B C
′′′
'bằng:
A.
3
. B.
2
. C.
12
. D.
6
.
Câu 23. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
34
x
y
xx
+
=
−−
là
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 24. Một hình chóp có
18
cạnh. Hỏi hình chóp đó có bao nhiêu mặt ?
A.
11
. B.
10
. C.
13
D.
12
.
Câu 25. Hàm số
2
3
2
xx
y
−
=
có đạo hàm là
4/5 - Mã đề 101
A.
2
3
2 .ln 2
xx−
. B.
2
3
(2 3).2
xx
x
−
−
. C.
2
3
(2 3).2 .ln 2
xx
x
−
−
. D.
2
2 31
( 3 ).2
xx
xx
−−
−
.
Câu 26. Hàm số
(
)
( )
2
2
log 2fx x x
= +
có đạo hàm là
A.
( )
2
ln 2
2
fx
xx
′
=
+
. B.
( )
( )
2
2 2 ln 2
2
x
fx
xx
+
′
=
+
.
C.
(
)
( )
2
22
2 ln 2
x
fx
xx
+
′
=
+
. D.
(
)
( )
2
1
2 ln 2
fx
xx
′
=
+
.
Câu 27. Với mọi
,ab
thỏa mãn
3
22
log log 5ab+=
, khẳng định nào dưới đây là đúng?
A.
3
25ab=
. B.
3
32
ab=
. C.
3
25
ab
+=
. D.
3
32
ab
+=
.
Câu 28. Tìm tập xác định của hàm số
(
)
3
2
2
32yx x
= −+
.
A.
( ) ( )
;1 2;−∞ ∪ + ∞
. B.
{ }
\ 1; 2
. C.
(
] [
)
;1 2;−∞ ∪ + ∞
. D.
( )
1; 2
.
Câu 29. Trong các hàm số sau, hàm số nào nghịch biến trên
?
A.
42
3y xx=−−+
. B.
32
31yx x=−+ +
. C.
5
2
x
y
x
+
=
−
. D.
3
31yx x=−− +
Câu 30. Giá trị nhỏ nhất của hàm số
( )
42
10 2fx x x=−+
trên đoạn
[
]
2;1
−
bằng
A.
2
. B.
22−
. C.
23−
. D.
7−
.
Câu 31. Phương trình
9 3.3 2 0
xx
− +=
có hai nghiệm
1
x
,
2
x
với
12
xx<
. Giá trị của biểu thức
12
23xx+
bằng
A.
3
2log 2
B.
3
3log 2
C.
8
D.
7
Câu 32. Cho hình nón có bán kính đáy bằng
2
và góc ở đỉnh bằng
60°
. Diện tích xung quanh của hình nón
đã cho bằng
A.
83
3
π
. B.
16
π
. C.
8
π
. D.
16 3
3
π
.
Câu 33. Nghiệm của phương trình
( ) ( )
22
log 1 1 log 3 1xx+ += −
là
A.
2x =
. B.
1x =
. C.
3x =
. D.
1x = −
.
Câu 34. Cho hàm số
()fx
liên tục trên
và có bảng xét dấu của
()fx
′
như sau:
Số điểm cực tiểu của hàm số đã cho là
A.
3.
B.
1.
C.
4.
D.
2.
Câu 35. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
5/5 - Mã đề 101
A.
2
32
x
y
x
−
=
−
. B.
2
32
x
y
x
−
=
+
. C.
2
32
x
y
x
+
=
+
. D.
2
32
x
y
x
+
=
−
.
PHẦN II. TỰ LUẬN (3 điểm)
(Lớp 12A2,12A3,12A4,12A5 không làm câu 5, câu 6 phần tự luận)
Câu 1. Ông A gửi tiết kiệm 40 triệu đồng ở ngân hàng X với lãi suất không đổi 5,0% một năm. Bà B gửi tiết
kiệm 70
triệu đồng ở ngân hàng Y với lãi suất không đổi 6,0% một năm. Biết rằng nếu không rút tiền ra khỏi
ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng
số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông
?A
Câu 2. Cho hình lăng trụ tam giác đều
.
ABC A B C
′′′
có
53AA
′
=
, góc giữa đường thẳng
AB
′
và mặt
phẳng
( )
ABC
bằng
60 .
°
Tính thể tích khối lăng trụ
.ABC A B C
′′′
Câu 3. Tìm
m
để đồ thị hàm số
423
2(2 1
4) m
yx m x m+++
= +
có ba điểm cực trị lập thành một tam giác
vuông.
Câu 4. Tìm tất cả các giá trị nguyên của
(
)
0; 20m
∈
để phương trình
( )
2
93 3
log log 3 1 log
xx m− +=−
(
m
là
tham số thực) có đúng hai nghiệm thực phân biệt.
Câu 5. Cho phương trình
(
)
2
2
2
log 4log 02
3
x
xx m− + −=
(
m
là tham số thực). Có tất cả bao nhiêu giá trị
nguyên dương của tham số
m
để phương trình đã cho có đúng hai nghiệm thực phân biệt?
Câu 6. Tìm tất cả các giá trị của tham số
m
để phương trình
( )
2
22
log 2 2log 8 4 2xm x x x m+ − =−− −
có
đúng hai nghiệm thực phân biệt?
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ...................
TRƯỜNG THPT SỐ 3 BẢO THẮNG
TỔ: TOÁN – TIN -CN
HDC ĐỀ THI HỌC KỲ I NĂM 2021-2022
MÔN THI: TOÁN
HƯỚNG DẪN CHẤM
PHẦN I. TRẮC NGHIỆM. (Mỗi đáp án đúng 0.2 điểm)
101 102 103 104
1
C
C
A
A
2
D
C
B
B
3
A
D
B
A
4
A
A
C
C
5
B
D
D
B
6
D
D
A
A
7
D
C
D
A
8
A
B
B
D
9
A
A
B
B
10
C
B
C
D
11
B
C
C
D
12
D
A
B
A
13
A
C
A
C
14
C
B
A
C
15
B
D
B
B
16
C
C
D
B
17
D
B
D
A
18
A
A
A
D
19
B
C
A
D
20
B
D
D
C
21
D
A
D
B
22
D
B
C
A
23
B
C
C
A
24
B
B
A
C
25
C
C
B
C
26
C
A
B
A
27
B
D
D
D
28
A
D
D
A
29
D
A
A
B
30
B
C
A
C
31
B
B
C
D
32
C
D
B
C
33
C
C
C
A
34
D
A
A
B
35
D
B
B
D
II. PHẦN TỰ LUẬN
Câu hỏi MÃ ĐỀ 101 Điểm
Câu 1
Ông A gửi tiết kiệm 40 triệu đồng ở ngân hàng X với lãi suất không đổi 5,0% một năm.
Bà B gửi tiết kiệm 70
triệu đồng ở ngân hàng Y với lãi suất không đổi 6,0% một năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập
vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của bà B
lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông
?A
0,5
Giả sử
(
)
0
nn>∈
là số năm gửi tiền trong ngân hàng của ông A và bà B.
Sau n năm, số tiền cả gốc lẫn lãi của ông A là:
( )
6
1
40.10 1 0,05
n
S = +
(triệu đồng) và của
bà B là:
( )
6
2
70.10 1 0,06
n
S = +
(triệu đồng).
Để tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông
A
thì
12
2.SS<
0,25
Hay
(
) ( )
66
2.40.10 1 0,05 70.10 1 0,06
nn
+< +
1, 05 7
1, 06 8
n

⇔<


1,05
1,06
7
log 15
8
nn

⇔> ⇒≥


Vậy, sau 15 năm thì tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả
vốn lẫn lãi của ông
A
.
0,25
Câu 2
Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có
53AA
′
=
góc giữa đường thẳng
AB
′
và mặt phẳng
( )
ABC
bằng
60 .°
Tính thể tích khối lăng trụ
.
ABC A B C
′′′
0.5
Ta có
AA ABC AB

là hình chiếu vuông góc của
AB
trên mặt phẳng
( )
ABC
. Suy ra góc giữa
AB
′
và mặt phẳng
( )
ABC
là góc
A BA
′
.
0
60A BA
Lại có:
0
0
tan 60 5
tan 60
AA AA
AB
AB
′′
= ⇒= =
0,25
0
1 25 3
. . .sin 60
24
ABC
S AB CB

Thể tích khối lăng trụ
.'' 'ABC A B C
là:
.
25 3 375
. 5 3.
44
ABC
ABC A B C
V A SA


0,25
Tìm
m
để đồ thị hàm số
423
2(2 1 4) myx m x m+++= +
có ba điểm cực trị lập thành một
tam giác vuông.
0,5
Ta có
( )
( )
3
2
2
' 4 42 1 4 2
1
1
0
0
2
y x m x xx
x
y
xm
m
=
′
= ⇔
= + + = ++
=−−
⇒
.
Câu 3
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình
2
21xm=−−
có
2
nghiệm phân biệt khác
1
0 2 10
2
mm⇔− − > ⇔ <−
.
Tính được toạ độ ba điểm cực trị là
( )
3
0; 4Am m+
thuộc Oy; và hai điểm
(
)
( )
( )
( )
22
33
2 1; 2 1 4 ; 2 1; 2 1 4B m m mmC m m mm− −− + + + −− −− + + +
đối xứng
nhau qua Oy. Suy ra, tam giác ABC cân tại A.
0,25
Ta có
( )
( )
2
2 1; 2 1
AB m m= − −− +

;
( )
( )
2
2 1; 2 1AC m m=− −− +

Để tam giác ABC vuông thì
(
) (
)
4
.
21210
0
AB AC AB AC
mm
⊥⇔ =
+
⇔
++ =
 
(
)
3
1
1
211
1
0
2
0
2
m
m
m
m
⇔⇔
= −
+=
−
+=
=
+
(loại giá trị
1
2
m = −
)
Đối chiếu với điều kiện
1
2
m <−
ta tìm được
1m = −
thỏa đề bài.
Câu 4
Tìm tất cả các giá trị nguyên của
(
)
0; 20
m
∈
để phương trình
( )
2
93 3
log log 3 1 logxx m− +=−
(
m
là tham số thực) có đúng hai nghiệm thực phân
biệt.
0,5
Điều kiện:
1
0, 0
3
xm
<≠ >
Phương trình đã cho trở thành
( )
33 3 3 3
1
log log 3 1 log log log
31
x
xx m
xm
− +=− ⇔ =
+
( )
1
31
x
fx
mx
⇔= =
+
. Xét hàm số
( ) ( )
1
, ;0 0;
31 3
x
fx x
x

= ∀ ∈ − ∪ +∞

+

Ta có:
( )
( )
( )
( )
( )
( )
2
2
11
1
, ;0
, ;0
3
31
31 3
31
1
, 0;
, 0;
31
31
x
x
x
x
x
x
fx fx
x
x
x
x
x
x
−

−

∀∈−

∀∈−


+

+

= = ⇒=

+

∀ ∈ +∞
∀ ∈ +∞

+
+
0,25
Bảng biến thiên của hàm số
( )
31
x
fx
x
=
+
Để phương trình có hai khiệm nghiệm thì
11
03
3
m
m
< <⇔ >
.
Do
( )
{ }
0; 20
4;5;6;...;19
m
m
m
∈
⇒∈
∈
.
0,25
Câu 5
Cho phương trình
(
)
2
2
2
log 4log 0
2
3
x
xx m
− + −=
(
m
là tham số thực). Có tất cả bao
nhiêu giá trị nguyên dương của tham số
m
để phương trình đã cho có đúng hai nghiệm
thực phân biệt?
0,5
Điều kiện:
( )
2
0
0
log do 0
02
x
x
x
x mm
m
>
>
⇔

≥>
−≥
.
Ta có
( )
2
2
2
2
2
2
log 4log 3 0
log 4log 230
02
x
x
xx
xx m
m
− +=
− + −=⇔
−=
2
2
2
log 1 2
log 3 8 .
lg
2 o
x
xx
xx
mxm
⇔
= =
=⇔=
=
=
Phương trình
( )
2
2
2
log 4log 023
x
xx m− + −=
có đúng hai nghiệm thực phân biệt
2
2
8
2
log 0
01
2 log 8 2 2
m
m
mm
≤
<≤
⇔⇔
≤ < ≤<
. Do
m
nguyên dương suy ra
{4; 5; 6 55
1
; ;2 }
m
m ∈…
=
.
Vậy có tất cả
1 255 3 253+ −=
giá trị
m
nguyên dương thỏa mãn đề bài.
Câu 6
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
2
22
log 2 2log 8 4 2xm x x x m+ − =−− −
có đúng hai nghiệm thực phân biệt?
0,5
Điều kiện:
0
20
x
xm
>
+>
. Ta có
( )
2
22
log 2 2log 8 4 2xm x x x m+ − =−− −
( ) ( ) ( )
( )
(
)
22 2
22
log 42 42 log 42 ,1
xm xm x x f xm fx⇔ + + + = +⇔ + =
 
 
Xét hàm số
( )
2
logft t t= +
trên khoảng
( )
0; +∞
Ta có
( )
1
1 0, 0
ln 2
ft t
t
′
= + > ∀>
. Suy ra
( )
2
logft t t= +
luôn đồng biến trên khoảng
( )
0; +∞
Do đó
( ) ( ) ( )
22
1 42 4 8x m x m x x hx⇔ + =⇔ =−=
0,25
Xét hàm số
( )
2
8hx x x
= −
trên khoảng
( )
0; +∞
Ta có
( ) ( )
2 8; 0 4hx x gx x
′′
= − =⇔=
Bảng biến thiên của hàm số
( )
2
8hx x x= −
Dựa vào bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệt khi
16 4 0 4 0mm− < < ⇔− < <
0,25
Câu hỏi
MÃ ĐỀ 102
Điểm
Câu 1
Ông A gửi tiết kiệm 40 triệu đồng ở ngân hàng X với lãi suất không đổi 4,5% một năm.
Bà B gửi tiết kiệm 90
triệu đồng ở ngân hàng Y với lãi suất không đổi 5,5% một năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập
vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của bà B
lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông
?A
0,5
Giả sử
( )
0nn>∈
là số năm gửi tiền trong ngân hàng của ông A và bà B.
Sau n năm, số tiền cả gốc lẫn lãi của ông A là:
( )
6
1
45.10 1 0,045
n
S = +
(triệu đồng) và
của bà B là:
( )
6
2
80.10 1 0,055
n
S = +
(triệu đồng).
Để tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông
A
thì
12
2.SS<
0,25
Hay
( ) ( )
66
2.45.10 1 0,045 80.10 1 0,055
nn
+< +
1,045 8
1,055 9
n

⇔<


1,045
1,055
8
log 13
9
nn

⇔> ⇒≥


Vậy, sau 13 năm thì tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả
vốn lẫn lãi của ông
A
.
0,25
Câu 2
Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có
33AA
′
=
góc giữa đường thẳng
AC
′
và mặt phẳng
( )
ABC
bằng
30 .°
Tính thể tích khối lăng trụ
.ABC A B C
′′′
0,5
Ta có
AA ABC AC

là hình chiếu vuông góc của
AC
trên mặt phẳng
( )
ABC
. Suy ra góc giữa
AC
′
và mặt phẳng
( )
ABC
là góc
A CA
′
.
0
03A CA
Lại có:
0
0
tan 30 9
tan 30
AA AA
AC
AC
′′
= ⇒= =
0,25
0
1 81 3
. . .sin 60
24
ABC
S AB CB

Thể tích khối lăng trụ
.ABC A B C

là:
.
81 3 729
. 3 3.
44
ABC
ABC A B C
V A SA


0,25
Tìm
m
để đồ thị hàm số
423
2(3 1 2 3) myx m x m+ + += +
có ba điểm cực trị lập thành
một tam giác vuông.
0,5
Ta có
( )
( )
3
2
2
' 4 43 1 4 3
1
1
0
0
3
y x m x xx
x
y
xm
m
=
′
= ⇔
= + + = ++
=−−
⇒
.
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình
2
31xm=−−
có
2
nghiệm phân biệt khác
1
0 3 10
3
mm⇔− − > ⇔ <−
.
0,25
Câu 3
Tính được toạ độ ba điểm cực trị là
( )
3
0; 2 3Amm+
thuộc Oy; và hai điểm
( )
( )
( )
( )
22
33
3 1; 3 1 2 3 ; 3 1; 3 1 2 3B m m mmC m m mm− −− + + + −− −− + + +
đối xứng
nhau qua Oy. Suy ra, tam giác ABC cân tại A.
Ta có
( )
( )
2
3 1; 3 1AB m m= − −− +

;
( )
( )
2
3 1; 3 1AC m m=− −− +

Để tam giác ABC vuông thì
( ) ( )
4
. 31310 0AB AC AB AC mm⊥⇔ = +⇔ ++ =
 
(
)
3
1
3 10
3
2
3 1 10
3
m
m
m
m
⇔⇔
+=
= −
=
= −
++
Đối chiếu với điều kiện
1
3
m <−
ta tìm được
2
3
m
= −
thỏa đề bài.
0,25
Câu 4
Tìm tất cả các giá trị nguyên của
( )
0; 20
m
∈
để phương trình
( )
2
93 3
log log 6 1 logxx m− +=−
(
m
là tham số thực) có đúng hai nghiệm thực phân
biệt.
0,5
Điều kiện:
1
0, 0
6
xm−<≠ >
Phương trình đã cho trở thành
(
)
33 3 3 3
1
log log 6 1 log log log
61
x
xx m
xm
− +=− ⇔ =
+
( )
1
61
x
fx
mx
⇔= =
+
. Xét hàm số
( )
( )
1
, ;0 0;
61 6
x
fx x
x

= ∀ ∈ − ∪ +∞

+

Ta có:
(
)
( )
( )
( )
( )
( )
2
2
11
1
, ;0
, ;0
6
61
61 6
61
1
, 0;
, 0;
61
61
x
x
x
x
x
x
fx fx
x
x
x
x
x
x
−

−

∀∈−

∀∈−


+

+

= = ⇒=

+

∀ ∈ +∞
∀ ∈ +∞

+
+
0,25
Bảng biến thiên của hàm số
( )
61
x
fx
x
=
+
Để phương trình có hai khiệm nghiệm thì
11
06
6
m
m
< <⇔>
.
Do
( )
{
}
0; 20
7;8;9;...;19
m
m
m
∈
⇒∈
∈
.
0,25
Câu 5
Cho phương trình
( )
2
2
2
log 3log 2 3 0
x
xx m− + −=
(
m
là tham số thực). Có tất cả bao
nhiêu giá trị nguyên dương của tham số
m
để phương trình đã cho có đúng hai nghiệm
thực phân biệt?
0,5
Điều kiện:
(
)
3
0
0
log do 0
30
x
x
x
x mm
m
>
>
⇔

≥>
−≥
.
Ta có
( )
2
22
2
2 2
2log 3log 2 0
log 3log 2 3 0
30
x
x
xx
xx m
m
− −=
− + −=⇔
−=
2
2
3
log 2 4
log 1 2 .
3 log
x
xx
xx
mxm
⇔
= =
=⇔=
=
=
0,25
Phương trình
( )
2
2
2
log 3log 2 3 0
x
xx m− + −=
có đúng hai nghiệm thực phân biệt
3
24
3
log 0
01
2 log 4 3 3
m
m
mm
≤
<≤
⇔⇔
≤ < ≤<
. Do
m
nguyên dương suy ra
{9;10;1 80
1
1; ; }
m
m ∈…
=
.
Vậy có tất cả
1 80 8 73+ −=
giá trị
m
nguyên dương thỏa mãn đề bài.
0,25
Câu 6
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
2
33
log 2 2log 18 9 2xm x x x m+− =− −−
có đúng hai nghiệm thực phân biệt?
0,5
Điều kiện:
0
20
x
xm
>
+>
. Ta có
( )
2
33
log 2 2log 18 9 2xm x x x m
+− =− −−
(
) (
) ( )
( )
(
)
22 2
33
log 92 92 log 92 ,1
xm xm x x f xm fx⇔ + + + = +⇔ + =
 
 
Xét hàm số
( )
3
logft t t= +
trên khoảng
( )
0; +∞
Ta có
( )
1
1 0, 0
ln 3
ft t
t
′
= + > ∀>
. Suy ra
(
)
3
logft t t
= +
luôn đồng biến trên khoảng
( )
0;
+∞
.
Do đó
(
) ( )
( )
22
1 9 2 9 18x m x m x x hx⇔ +=⇔ =− =
0,25
Xét hàm số
( )
2
18hx x x= −
trên khoảng
( )
0; +∞
Ta có
( ) ( )
2 18; 0 9hx x gx x
′′
= − =⇔=
Bảng biến thiên của hàm số
( )
2
18hx x x= −
Dựa vào bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệt khi
81 9 0 9 0mm− < < ⇔− < <
0,25
Câu hỏi
MÃ ĐỀ 103
Điểm
Câu 1
Ông A gửi tiết kiệm 60 triệu đồng ở ngân hàng X với lãi suất không đổi 6,0% một năm.
Bà B gửi tiết kiệm 35
triệu đồng ở ngân hàng Y với lãi suất không đổi 4,5% một năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập
0,5
vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của của
ông
A
lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của bà
?B
Giả sử
( )
0nn>∈
là số năm gửi tiền trong ngân hàng của ông A và bà B.
Sau n năm, số tiền cả gốc lẫn lãi của ông A là:
( )
6
1
60.10 1 0,06
n
S = +
(triệu đồng) và của
bà B là:
( )
6
2
35.10 1 0,045
n
S = +
(triệu đồng).
Để tổng số tiền cả vốn lẫn lãi của Ông A lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của
Bà
B
thì
12
2SS>
0,25
Hay
( ) ( )
66
60.10 1 0,06 2.35.10 1 0,045
nn
+> +
1,045 6
1, 06 7
n

⇔<


1,045
1,06
6
log 11
7
nn

⇔> ⇒≥


Vậy, sau 11 năm thì tổng số tiền cả vốn lẫn lãi của ông
A
lớn hơn hai lần tổng số tiền cả
vốn lẫn lãi của Bà B
0,25
Câu 2
Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có
43AA
′
=
góc giữa đường thẳng
AC
′
và mặt phẳng
( )
ABC
′′′
bằng
30 .°
Tính thể tích khối lăng trụ
.ABC A B C
′′′
0,5
Ta có
( )
CC ABC AC
′ ′′′ ′′
⊥⇒
là hình chiếu vuông góc của
CA
′
trên mặt phẳng
( )
ABC
′′′
. Suy ra góc giữa
CA
′
và mặt phẳng
( )
ABC
′′′
là góc
CA C
′′
.
0
30CA C

Lại có:
0
0
tan 30 12
tan 30
CC CC
AC
CA
′′
′′
=
⇒= =
′′
0,25
0
1
. . .sin 60 36 3
2
ABC
S AB CB

Thể tích khối lăng trụ
.ABC A B C

là:
.
. 4 3.36 3 432
ABC
ABC A B C
VSAA


0,25
Tìm
m
để đồ thị hàm số
423
2(4 1 3 2) myx m x m+ + += +
có ba điểm cực trị lập thành
một tam giác vuông.
0,5
Ta có
( )
( )
3
2
2
' 4 44 1 4 4
1
1
0
0
4
y x m x xx
x
y
xm
m
=
′
= ⇔
= + + = ++
=−−
⇒
.
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình
2
41xm=−−
có
2
nghiệm phân biệt khác
1
0 4 10
4
mm⇔− − > ⇔ <−
.
Tính được toạ độ ba điểm cực trị là
( )
3
0;3 2Amm+
thuộc Oy; và hai điểm
0,25
Câu 3
( )
( )
( )
( )
22
33
4 1; 4 1 3 2 ; 4 1; 4 1 3 2B m m mmC m m mm− −− + + + −− −− + + +
đối xứng
nhau qua Oy. Suy ra, tam giác ABC cân tại A.
Ta có
( )
( )
2
4 1; 4 1
AB m m= − −− +

;
( )
( )
2
4 1; 4 1AC m m=− −− +

Để tam giác ABC vuông thì
(
) (
)
4
.
4141
0
0AB AC AB AC
mm⊥⇔ =
+
⇔
++ =
 
(
)
3
1
4 10
4
1
4 1 10
2
m
m
m
m
⇔⇔
+=
= −
=
= −
++
Đối chiếu với điều kiện
1
4
m
<−
ta tìm được
1
2
m
= −
thỏa đề bài.
0,25
Câu 4
Tìm tất cả các giá trị nguyên của
( )
0; 20m∈
để phương trình
( )
2
93 3
log log 5 1 logxx m− +=−
(
m
là tham số thực) có đúng hai nghiệm thực phân
biệt.
0,5
Điều kiện:
1
0, 0
5
xm
−<≠ >
Phương trình đã cho trở thành
( )
33 3 3 3
1
log log 5 1 log log log
51
x
xx m
xm
− +=− ⇔ =
+
( )
1
51
x
fx
mx
⇔= =
+
. Xét hàm số
( )
( )
1
, ;0 0;
51 5
x
fx x
x

= ∀ ∈ − ∪ +∞

+

Ta có:
( )
( )
( )
( )
( )
( )
2
2
11
1
, ;0
, ;0
5
51
51 5
51
1
, 0;
, 0;
51
51
x
x
x
x
x
x
fx f x
x
x
x
x
x
x
−

−

∀∈−

∀∈−


+

+

′
== ⇒=

+

∀ ∈ +∞
∀ ∈ +∞

+
+
0,25
Bảng biến thiên của hàm số
( )
51
x
fx
x
=
+
Để phương trình có hai khiệm nghiệm thì
11
05
5
m
m
< <⇔ >
.
Do
( )
{
}
0; 20
6;7;8;...;19
m
m
m
∈
⇒∈
∈
.
0,25
Câu 5
Cho phương trình
( )
2
2
2
log 5log 046
x
xx m− + −=
(
m
là tham số thực). Có tất cả bao
nhiêu giá trị nguyên dương của tham số
m
để phương trình đã cho có đúng ba nghiệm
thực phân biệt?
0,5
Điều kiện:
( )
4
0
0
log do 0
04
x
x
x
x mm
m
>
>
⇔

≥>
−≥
.
Ta có
( )
2
2
22
2
2
log 5log 6 0
log 5log 460
04
x
x
xx
xx m
m
− +=
− + −=⇔
−=
2
4
2
log 2 4
log 3 8 .
lg
4 o
x
xx
xx
mxm
⇔
= =
=⇔=
=
=
0,25
Phương trình
(
)
2
2
2
log 5log 046
x
xx m− + −=
có đúng ba nghiệm thực phân biệt
4
0 log 4 1 256mm
⇔ < < ⇔< <
. Do
m
nguyên dương suy ra
{ }
2;3;4; ; 255m ∈…
.
Vậy có tất cả
255 1 254−=
giá trị
m
nguyên dương thỏa mãn đề bài.
0,25
Câu 6
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
2
22
log 4 2log 4 16 4xm x x x m+− = − −
có đúng hai nghiệm thực phân biệt?
0,5
Điều kiện:
0
40
x
xm
>
+>
. Ta có
( )
2
22
log 4 2log 4 16 4xm x x x m+− = − −
( ) ( ) ( )
( )
( )
22 2
22
log 4 4 4 log 4 4 , 1xm xm x x f xm fx⇔ ++ += + ⇔ +=
Xét hàm số
( )
2
log 4ft t t
= +
trên khoảng
( )
0; +∞
Ta có
( )
1
4 0, 0
ln 2
ft t
t
′
= + > ∀>
. Suy ra
( )
2
log 4ft t t= +
luôn đồng biến trên khoảng
( )
0; +∞
.
Do đó
( ) (
)
22
14 4
xmx mx xhx⇔ += ⇔= − =
0,25
Xét hàm số
(
)
2
4
hx x x= −
trên khoảng
(
)
0;
+∞
Ta có
( )
( )
2 4; 0 2hx x hx x
′′
= − =⇔=
Bảng biến thiên của hàm số
( )
2
4hx x x= −
Dựa vào bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệt khi
40m⇔− < <
0,25
Câu hỏi
MÃ ĐỀ 104
Điểm
Câu 1
Ông A gửi tiết kiệm 65 triệu đồng ở ngân hàng X với lãi suất không đổi 6,5% một năm.
Bà B gửi tiết kiệm 37
triệu đồng ở ngân hàng Y với lãi suất không đổi 5,5% một năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập
0,5
vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của ông
A
lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của bà
?B
Giả sử
(
)
0
nn
>∈
là số năm gửi tiền trong ngân hàng của ông A và bà B.
Sau n năm, số tiền cả gốc lẫn lãi của ông A là:
(
)
6
1
65.10 1 0,06
n
S = +
(triệu đồng) và của
bà B là:
( )
6
2
37.10 1 0,055
n
S = +
(triệu đồng).
Để tổng số tiền cả vốn lẫn lãi của Ông
A
lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của
Bà
B
thì
12
2SS
>
0,25
Hay
( ) ( )
66
65.10 1 0,065 2.37.10 1 0,055
nn
+> +
1,055 65
1,065 74
n

⇔<


1,055
1,065
65
log 14
74
nn

⇔> ⇒≥


Vậy, sau 14 năm năm thì tổng số tiền cả vốn lẫn lãi của ông
A
lớn hơn hai lần tổng số
tiền cả vốn lẫn lãi của Bà B
0,25
Câu 2
Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có
23AA
′
=
, góc giữa đường thẳng
BC
′
và mặt phẳng
( )
ABC
′′′
bằng
60 .°
Tính thể tích khối lăng trụ
.ABC A B C
′′′
0,5
Ta có
( )
BB ABC BC
′ ′′′ ′′
⊥⇒
là hình chiếu vuông góc của
BC
′
lên
( )
ABC
′′′
. Suy ra
góc giữa
BC
′
và mặt phẳng
( )
ABC
′′′
là góc
BC B
′′
.
0
60BC B

. Lạ
i có:
0
0
tan 60 2
tan 60
BB BB
BC
BC
′′
′′
=⇒= =
′′
0,25
0
1
. . .sin 60 3
2
ABC
S AB CB

Thể tích khối lăng trụ
.ABC A B C

là:
.
. 2 3. 3 6
ABC
ABC A B C
AAVS


0,25
Câu 3
Tìm
m
để đồ thị hàm số
2 34
2(5 1) 4 myx m x m+= + ++
có ba điểm cực trị lập thành một
tam giác vuông.
0,5
Ta có
( )
( )
2
32
0
0
51
4 451 4 51y x m x xx m
x
y
xm
′
+
=
′
=
−
=++ ⇒
= −
= ⇔
+
.
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình
2
51xm=−−
có
2
nghiệm phân biệt khác
1
0 5 10
5
mm⇔− − > ⇔ <−
.
Tính được toạ độ ba điểm cực trị là
( )
3
0; 4A mm+
thuộc Oy; và hai điểm
( )
( )
( )
( )
22
33
5 1; 5 1 4 ; 5 1; 5 1 4B m m mmC m m mm− −− + + + −− −− + + +
đối xứng
nhau qua Oy. Suy ra, tam giác ABC cân tại A.
0,25
Ta có
( )
( )
2
5 1; 5 1AB m m= − −− +

;
( )
( )
2
5 1; 5 1AC m m
=− −− +

Để tam giác ABC vuông thì
( ) ( )
4
. 51510 0
AB AC AB AC mm⊥⇔ = +⇔ ++ =
 
( )
3
1
5 10
5
2
5 1 10
5
m
m
m
m
⇔⇔
+=
= −
=
= −
++
Đối chiếu với điều kiện
1
5
m
<−
ta tìm được
2
5
m = −
thỏa đề bài.
0,25
Câu 4
Tìm tất cả các giá trị nguyên của
( )
0; 20m ∈
để phương trình
( )
2
93 3
log log 4 1 logxx m− +=−
(
m
là tham số thực) có đúng hai nghiệm thực phân biệt.
0,5
Điều kiện:
1
0, 0
4
xm−<≠ >
Phương trình đã cho trở thành
( )
33 3 3 3
1
log log 4 1 log log log
41
x
xx m
xm
− +=− ⇔ =
+
( )
1
41
x
fx
mx
⇔= =
+
. Xét hàm số
( )
( )
1
, ; 0 0;
41 4
x
fx x
x

= ∀ ∈ − ∪ +∞

+

Ta có:
(
)
( )
(
)
(
)
(
)
( )
2
2
11
1
, ;0
, ;0
4
41
41 4
41
1
, 0;
, 0;
41
41
x
x
x
x
x
x
fx f x
x
x
x
x
x
x
−

−

∀∈−

∀∈−


+

+

′
== ⇒=

+

∀ ∈ +∞
∀ ∈ +∞

+
+
0,25
Bảng biến thiên của hàm số
( )
41
x
fx
x
=
+
Để phương trình có hai khiệm nghiệm thì
11
04
4
m
m
< <⇔>
.
Do
( )
{ }
0; 20
5;6;7;...;19
m
m
m
∈
⇒∈
∈
.
0,25
Câu 5
Cho phương trình
( )
2
2
2
log 6log 058
x
xx m− + −=
(
m
là tham số thực). Có tất cả bao
nhiêu giá trị nguyên dương của tham số
m
để phương trình đã cho có đúng ba nghiệm
thực phân biệt?
0,5
Điều kiện:
( )
5
0
0
log do 0
05
x
x
x
x mm
m
>
>
⇔

≥>
−≥
.
0,25
Ta có
( )
2
2
2
2
2
2
log 6 log 8 0
log 6 log 580
05
x
x
xx
xx m
m
− +=
− + −=⇔
−=
5
2
2
log 2 4
log 4 16 .
g5
lo
x
xx
xx
mx
m
⇔
= =
=⇔=
=
=
Phương trình
( )
2
2
2
log 6log 058
x
xx m− + −=
có đúng ba nghiệm thực phân biệt
5
0 log 4 1 625mm⇔ < < ⇔< <
. Do
m
nguyên dương suy ra
{ }
2;3;4; ;624m ∈…
.
Vậy có tất cả
624 1 623
−=
giá trị
m
nguyên dương thỏa mãn đề bài.
0,25
Câu 6
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
2
33
log 6 2log 9 54 9xm x x x m+− = − −
có đúng hai nghiệm thực phân biệt?
0,5
Điều kiện:
0
60
x
xm
>
+>
. Ta có
( )
2
33
log 6 2log 9 54 9xm x x x m+− = − −
(
)
( ) ( )
( )
( )
22 2
33
log 6 9 6 log 9 6 , 1xm xm x x f xm fx⇔ ++ += + ⇔ +=
Xét hàm số
( )
3
log 9ft t t= +
trên khoảng
( )
0;
+∞
Ta có
( )
1
9 0, 0
ln 3
ft t
t
′
= + > ∀>
. Suy ra
( )
3
log 9ft t t= +
luôn đồng biến trên khoảng
( )
0; +∞
. Do đó
( ) ( )
22
16 6xmx mx xhx⇔ += ⇔= − =
0,25
Xét hàm số
(
)
2
6
hx x x= −
trên khoảng
( )
0; +∞
Ta có
( )
( )
2 6; 0 3hx x hx x
′′
= − =⇔=
Bảng biến thiên của hàm số
( )
2
6hx x x= −
Dựa vào bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệ
t khi
90
m⇔− < <
0,25
--------------------HẾT--------------------
Xem thêm: ĐỀ THI HK1 TOÁN 12
https://toanmath.com/de-thi-hk1-toan-12
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

THPT SỐ 3 BẢO THẮNG
KIỂM TRA CUỐI KỲ 1 NĂM HỌC 2021 - 2022 TỔ: TOÁN – TIN - CN
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(Đề thi có 05 trang)
(không kể thời gian phát đề) Mã đề 101
PHẦN I. TRẮC NGHIỆM (7 điểm)
Câu 1. Thể tích khối hộp chữ nhật có độ dài ba kích thước lần lượt là 3,4,6 bằng A. 24 . B. 12. C. 72 . D. 18.
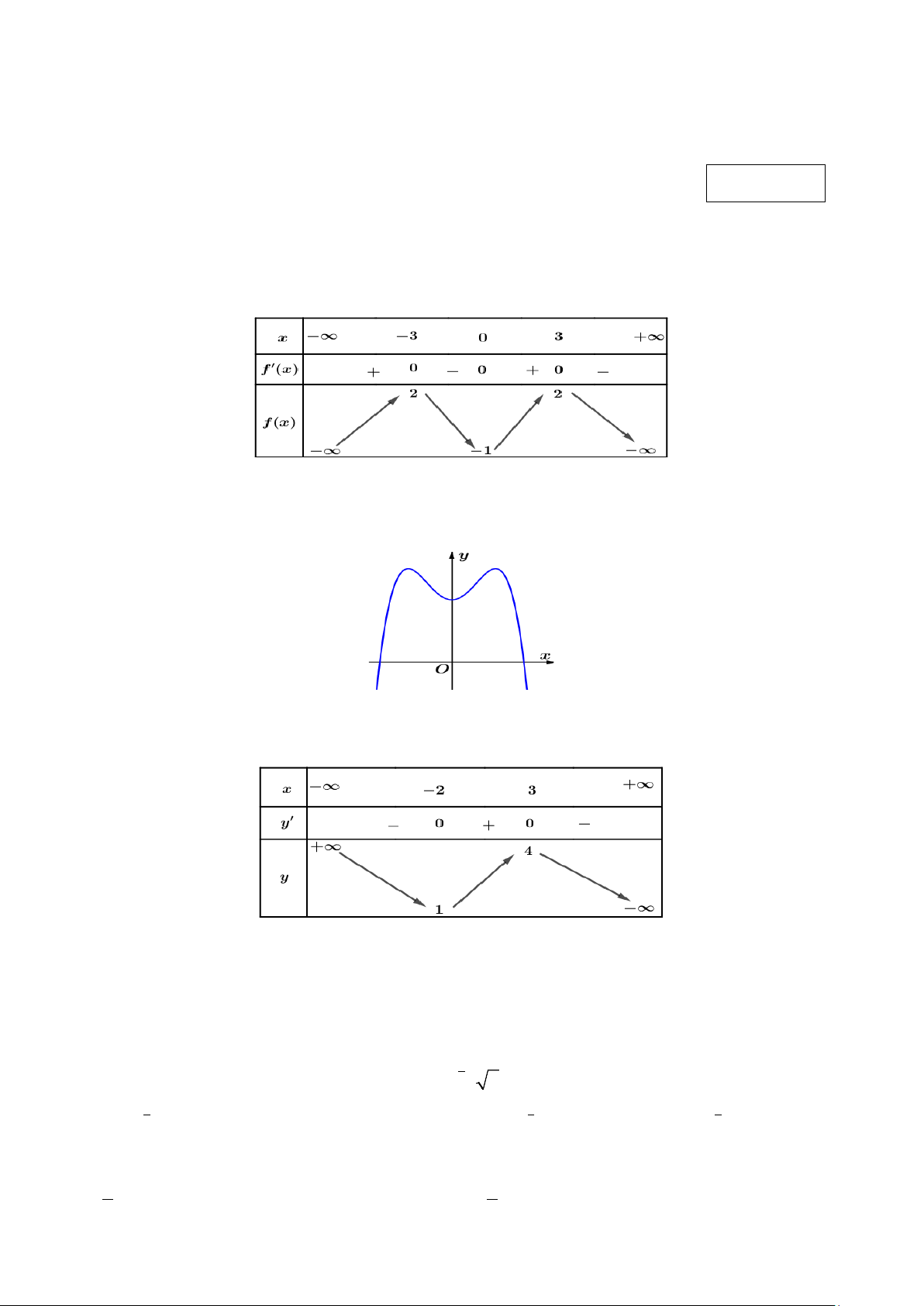
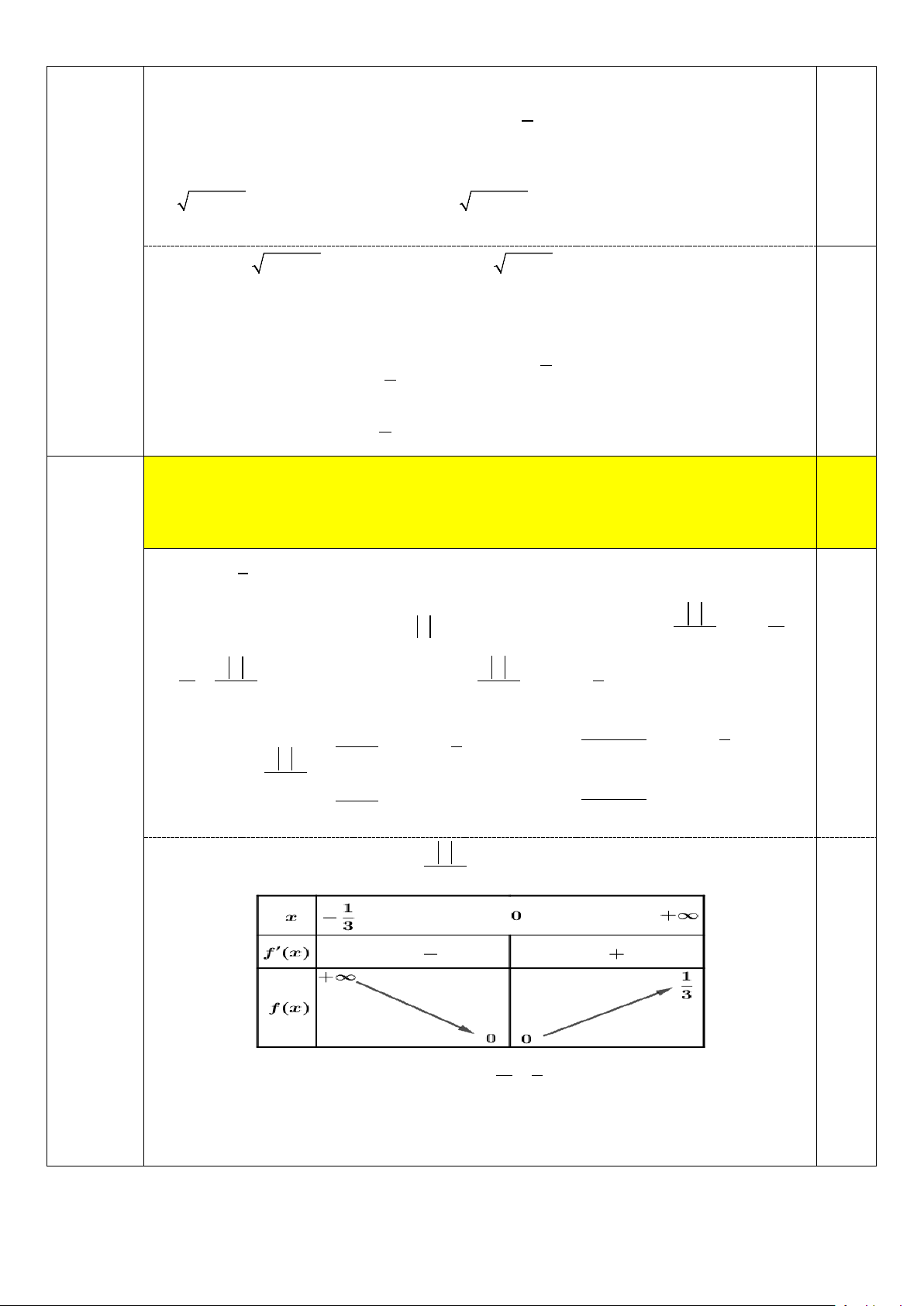
Câu 2. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ.
Giá trị nhỏ nhất của hàm số y = f (x) trên đoạn [ 3; − ]3 bằng A. 3 − B. 2 . C. 3. D. 1 − .
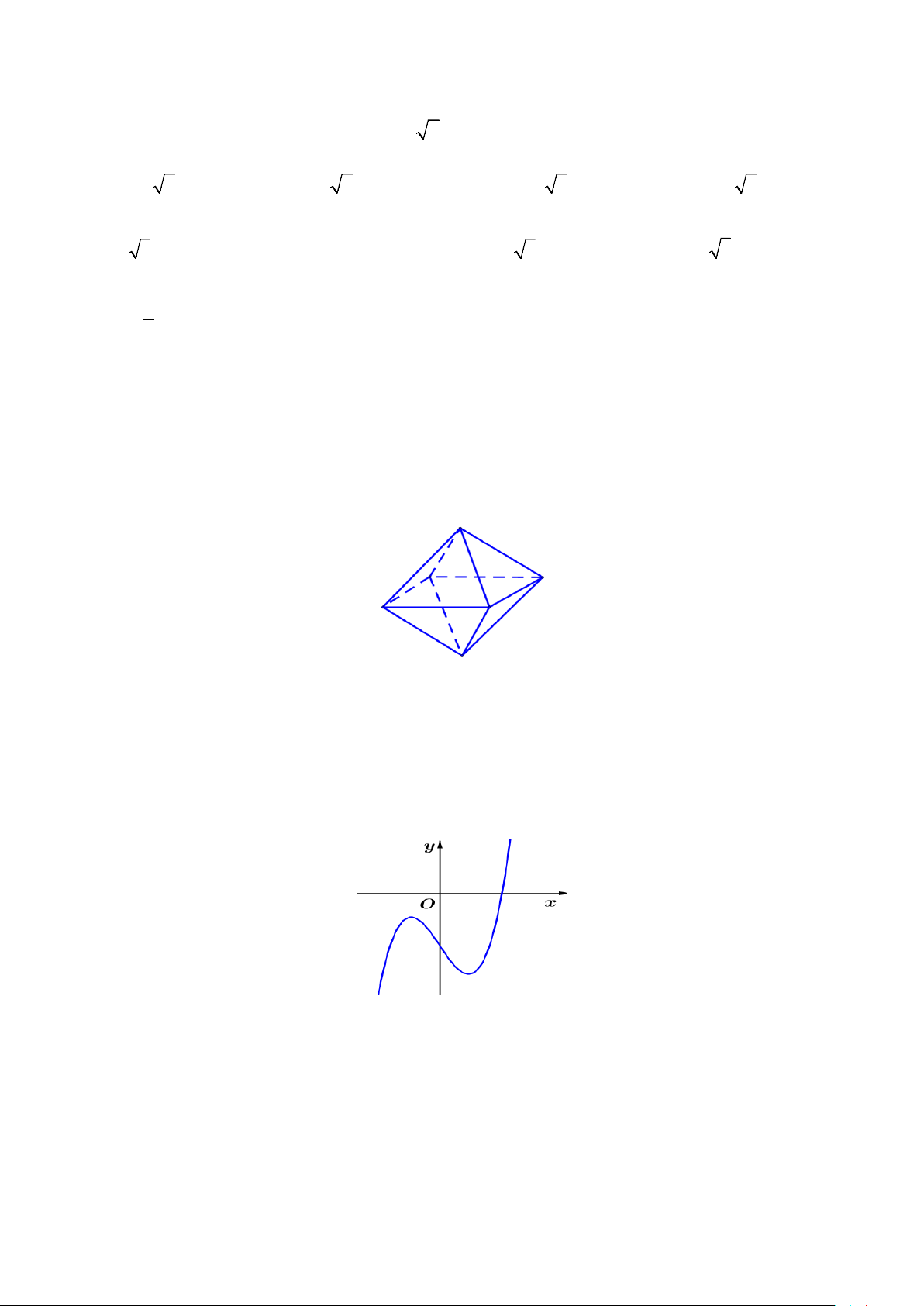
Câu 3. Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào dưới đây? A. 4 2
y = −x + 2x + 2 . B. 3 2
y = −x + 3x + 2 . C. 3 2
y = x − 3x + 2. D. 4 2
y = x − 2x + 2 .
Câu 4. Cho hàm số y = f (x) có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( 2; − 3) B. (3;+ ∞) C. ( 2; − + ∞) D. ( ; −∞ − 2)
Câu 5. Nghiệm của phương trình log (x −1) = 2 là 4 A. x = 17 −
B. x =17
C. x =16 D. x =15 1
Câu 6. Cho x là một số thực dương, biểu thức 6 3
P = x ⋅ x viết dưới dạng lũy thừa với số mũ hữu tỷ là 2 1 1 A. 9 P = x B. 2 P = x C. 8 P = x D. 2 P = x
Câu 7. Với a là số thực dương tùy ý, 3 log a bằng 5
A. 1 + log a .
B. 3+ log a .
C. 1 log a . D. 3log a . 5 3 5 5 3 5 1/5 - Mã đề 101
Câu 8. Số nghiệm nguyên của bất phương trình log x < 3 là. 2 A. 7 . B. 9. C. Vô số. D. 8 .
Câu 9. Cho hình nón có bán kính đáy bằng r = 7 và độ dài đường sinh l = 9 . Diện tích xung quanh của hình nón đã cho là A. S = π . B. S = π . C. S = π . D. S = π . xq 27 7 xq 18 7 xq 3 7 xq 9 7
Câu 10. Khối cầu có thể tích V = 4π . Bán kính r của khối cầu đó là
A. r = 3 .
B. r = 3. C. 3 r = 3 . D. 3 r = 3 3 .
Câu 11. Diện tích xung quanh hình trụ có độ dài đường sinh bằng l và bán kính đáy bằng r là A. 1 S = π rl
S = π rl .
C. S = π rl
S = π rl . xq . B. xq 2 xq 4 . D. 3 xq
Câu 12. Tập xác định của hàm số y = log x − 4 là 6 ( ) A. ( ; −∞ +∞) . B. ( ;4 −∞ ) . C. [4;+∞) . D. (4;+∞) .
Câu 13. Cho hình nón có đường sinh bằng 5a và bán kính đáy bằng 3a . Tính chiều cao của hình nón theo a A. 4a . B. 8a . C. 3a . D. 6a cm.
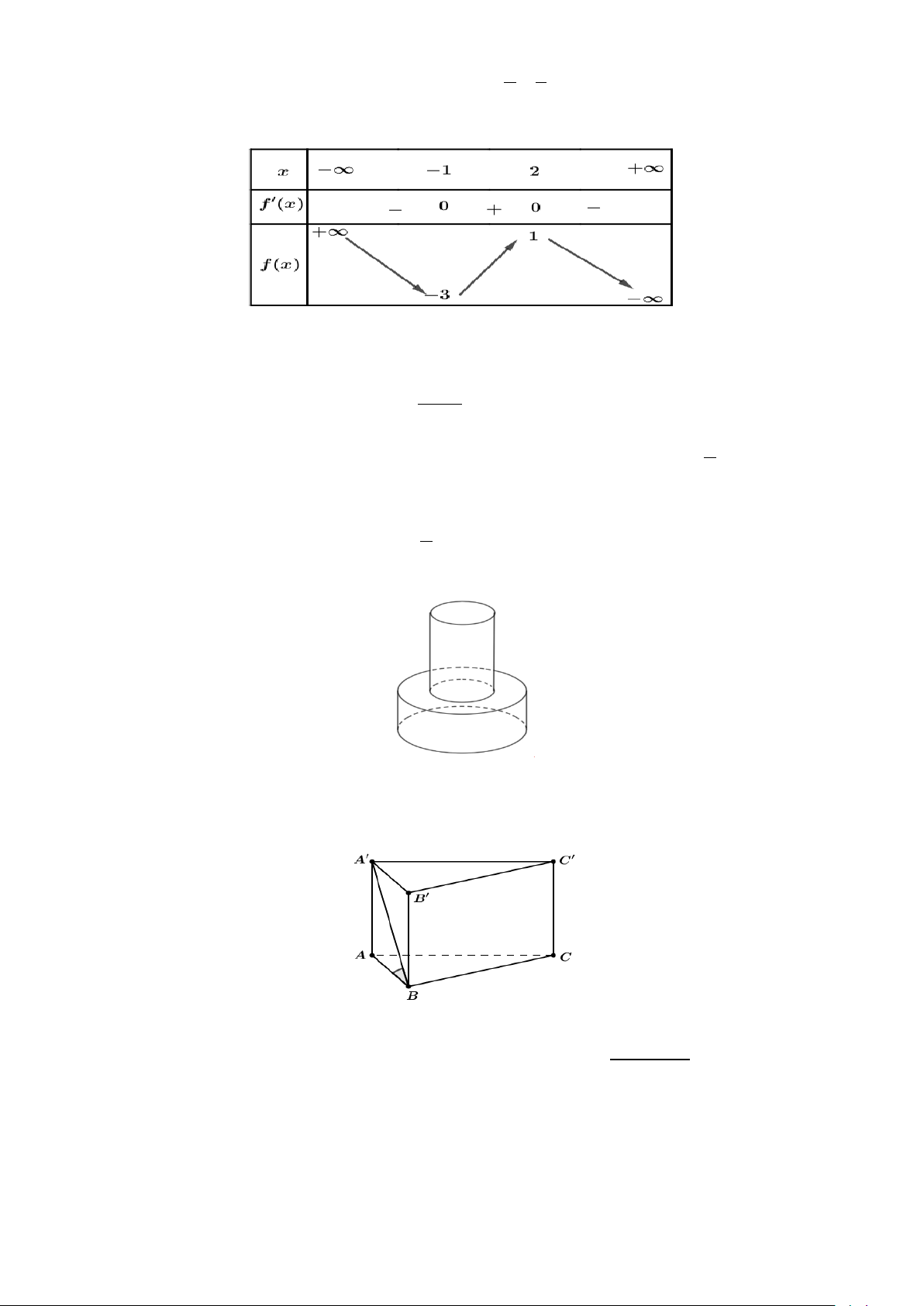
Câu 14. Khối đa diện trong hình vẽ bên có bao nhiêu cạnh? A. 4 B. 10 C. 12 D. 9 Câu 15. Hàm số ( ) 2 4 2x f x + = có đạo hàm là
A. f ′(x) 2 x +4 = 2 ln 2 .
B. f ′(x) 2 x +4 = 2 . x 2 ln 2 .
C. f ′(x) = (x + ) 2 2 x +4 4 2 ln 2 . D. ( ) ( ) 2 2 3 4 2x f x x + ′ = + .
Câu 16. Hàm số nào dưới đây có đồ thị như hình vẽ bên? A. 4 2
y = x + 2x − 2 . B. 4 2
y = −x + 2x − 2 . C. 3
y = x − 2x − 2 . D. 3
y = −x + 2x − 2 .
Câu 17. Nghiệm của phương trình x−2 3 = 9 là.
A. x  4
B. x  3
C. x  3 D. x  4
Câu 18. Với a là số thực dương bất kỳ, mệnh đề nào sau đây đúng?
A. ln (3a) = ln 3+ ln a .
B. ln (3+ a) = ln 3+ ln a . 2/5 - Mã đề 101 C. a
ln (5a) = 5.ln a . D. 1 ln = ln a . 3 3
Câu 19. Cho hàm số f (x) có bảng biến thiên như sau:
Điểm cực tiểu của hàm số đã cho là
A. x = 2 . B. x = 1 − . C. x = 3 − . D. x =1. + Câu 20. 2x 1
Tiệm cận ngang của đồ thị hàm số y = là: x −1 A. 1 y = 1 − .
B. y = 2 . C. y =1. D. y = . 2
Câu 21. Một khối đồ chơi gồm hai khối trụ (H , H xếp chồng lên nhau, lần lượt có bán kính đáy và 1 ) ( 2 )
chiều cao tương ứng là r 1
,h ,r ,h thỏa mãn r = r ,h = 2h . Biết rằng thể tích của toàn bộ khối đồ chơi 1 1 2 2 2 1 2 1 2 bằng 3
36cm , thể tích của khối trụ (H bằng 1 ) A. 3 20 cm . B. 3 22 cm . C. 3 10 cm . D. 3 24 cm .
Câu 22. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác đều cạnh bằng 2, A′B tạo với mặt phẳng đáy góc 0
60 . Thể tích khối lăng trụ ABC.A′B C ′ ′ 'bằng: A. 3. B. 2 . C. 12. D. 6 .
Câu 23. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số x +1 y = là 2 x − 3x − 4 A. 0 . B. 2 . C. 3. D. 1.
Câu 24. Một hình chóp có 18cạnh. Hỏi hình chóp đó có bao nhiêu mặt ? A. 11. B. 10. C. 13 D. 12. Câu 25. Hàm số 2 3 2x x y − = có đạo hàm là 3/5 - Mã đề 101 A. 2x−3 2 x.ln 2. B. 2 3 (2 3).2x x x − − . C. 2 x 3 (2 3).2 x x − − .ln 2 . D. 2 2 3 1 ( 3 ).2x x x x − − − .
Câu 26. Hàm số f (x) = log ( 2
2 x + 2x) có đạo hàm là ln 2 2x + 2 ln 2
A. f ′(x) = .
B. f ′(x) ( ) = . 2 x + 2x 2 x + 2x
C. f ′(x) 2x + 2 = 1 ( .
D. f ′(x) = . 2 x + 2x)ln 2 ( 2x +2x)ln2
Câu 27. Với mọi a,b thỏa mãn 3
log a + log b = 5 , khẳng định nào dưới đây là đúng? 2 2 A. 3 a b = 25 . B. 3 a b = 32. C. 3
a + b = 25. D. 3 a + b = 32 .
Câu 28. Tìm tập xác định của hàm số y = (x − x + )3 2 2 3 2 . A. ( ; −∞ )
1 ∪(2;+ ∞) . B.  \{1; } 2 . C. ( ; −∞ ]
1 ∪[2;+ ∞) . D. (1;2) .
Câu 29. Trong các hàm số sau, hàm số nào nghịch biến trên  ? + A. x 4 2
y = −x − x + 3 . B. 3 2
y = −x + 3x +1. C. 5 y = . D. 3
y = −x − 3x +1 x − 2
Câu 30. Giá trị nhỏ nhất của hàm số f (x) 4 2
= x −10x + 2 trên đoạn [ 2; − ] 1 bằng A. 2 . B. 22 − . C. 23 − . D. 7 − .
Câu 31. Phương trình 9x 3.3x −
+ 2 = 0 có hai nghiệm x , x với x < x . Giá trị của biểu thức 2x + 3x 1 2 1 2 1 2 bằng A. 2log 2 B. 3log 2 C. 3 3 8 D. 7
Câu 32. Cho hình nón có bán kính đáy bằng 2 và góc ở đỉnh bằng 60°. Diện tích xung quanh của hình nón đã cho bằng A. 8 3π . B. 16π . C. 8π . D. 16 3π . 3 3
Câu 33. Nghiệm của phương trình log x +1 +1 = log 3x −1 là 2 ( ) 2 ( )
A. x = 2 . B. x =1.
C. x = 3. D. x = 1 − .
Câu 34. Cho hàm số f (x) liên tục trên  và có bảng xét dấu của f (′x) như sau:
Số điểm cực tiểu của hàm số đã cho là A. 3. B. 1. C. 4. D. 2.
Câu 35. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? 4/5 - Mã đề 101 + + A. x x x − 2 y − = . B. x 2 y = . C. 2 y = . D. 2 y = . 3x − 2 3x + 2 3x + 2 3x − 2
PHẦN II. TỰ LUẬN (3 điểm)
(Lớp 12A2,12A3,12A4,12A5 không làm câu 5, câu 6 phần tự luận)
Câu 1. Ông A gửi tiết kiệm 40 triệu đồng ở ngân hàng X với lãi suất không đổi 5,0% một năm. Bà B gửi tiết
kiệm 70 triệu đồng ở ngân hàng Y với lãi suất không đổi 6,0% một năm. Biết rằng nếu không rút tiền ra khỏi
ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng
số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông A?
Câu 2. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có AA′ = 5 3 , góc giữa đường thẳng A′B và mặt
phẳng ( ABC) bằng 60 .° Tính thể tích khối lăng trụ ABC.A′B C ′ ′
Câu 3. Tìm m để đồ thị hàm số 4 2 3
y = x + 2(2m +1)x + m + 4m có ba điểm cực trị lập thành một tam giác vuông.
Câu 4. Tìm tất cả các giá trị nguyên của m∈(0;20) để phương trình 2
log x − log 3x +1 = −log m ( m là 9 3 ( ) 3
tham số thực) có đúng hai nghiệm thực phân biệt.
Câu 5. Cho phương trình ( 2 log − 4log + 3 2x x x
− m = 0 ( m là tham số thực). Có tất cả bao nhiêu giá trị 2 2 )
nguyên dương của tham số m để phương trình đã cho có đúng hai nghiệm thực phân biệt?
Câu 6. Tìm tất cả các giá trị của tham số m để phương trình log (2x + m) 2
− 2log x = x −8x − 4m − 2 có 2 2
đúng hai nghiệm thực phân biệt?
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ................... 5/5 - Mã đề 101
TRƯỜNG THPT SỐ 3 BẢO THẮNG
HDC ĐỀ THI HỌC KỲ I NĂM 2021-2022
TỔ: TOÁN – TIN -CN MÔN THI: TOÁN HƯỚNG DẪN CHẤM
PHẦN I. TRẮC NGHIỆM. (Mỗi đáp án đúng 0.2 điểm) 101 102 103 104 1 C C A A 2 D C B B 3 A D B A 4 A A C C 5 B D D B 6 D D A A 7 D C D A 8 A B B D 9 A A B B 10 C B C D 11 B C C D 12 D A B A 13 A C A C 14 C B A C 15 B D B B 16 C C D B 17 D B D A 18 A A A D 19 B C A D 20 B D D C 21 D A D B 22 D B C A 23 B C C A 24 B B A C 25 C C B C 26 C A B A 27 B D D D 28 A D D A 29 D A A B 30 B C A C 31 B B C D 32 C D B C 33 C C C A 34 D A A B 35 D B B D II. PHẦN TỰ LUẬN Câu hỏi MÃ ĐỀ 101 Điểm
Ông A gửi tiết kiệm 40 triệu đồng ở ngân hàng X với lãi suất không đổi 5,0% một năm.
Bà B gửi tiết kiệm 70 triệu đồng ở ngân hàng Y với lãi suất không đổi 6,0% một năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập 0,5
vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của bà B
lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông A?
Giả sử n > 0 (n∈) là số năm gửi tiền trong ngân hàng của ông A và bà B. 6
Sau n năm, số tiền cả gốc lẫn lãi của ông A là: 40.10 1 0,05 n S = + (triệu đồng) và của 1 ( ) bà B là: 6 70.10 1 0,06 n S = + (triệu đồng). 2 ( ) 0,25 Câu 1
Để tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông
A thì 2S < S . 1 2 n   Hay 6 ( )n 6 1,05 7 2.40.10 1 0,05 70.10 (1 0,06)n + < + ⇔ <  1,06    8  7 0,25 n log  ⇔ > ⇒ n ≥   15 1,05  8 1,06 
Vậy, sau 15 năm thì tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả
vốn lẫn lãi của ông A .
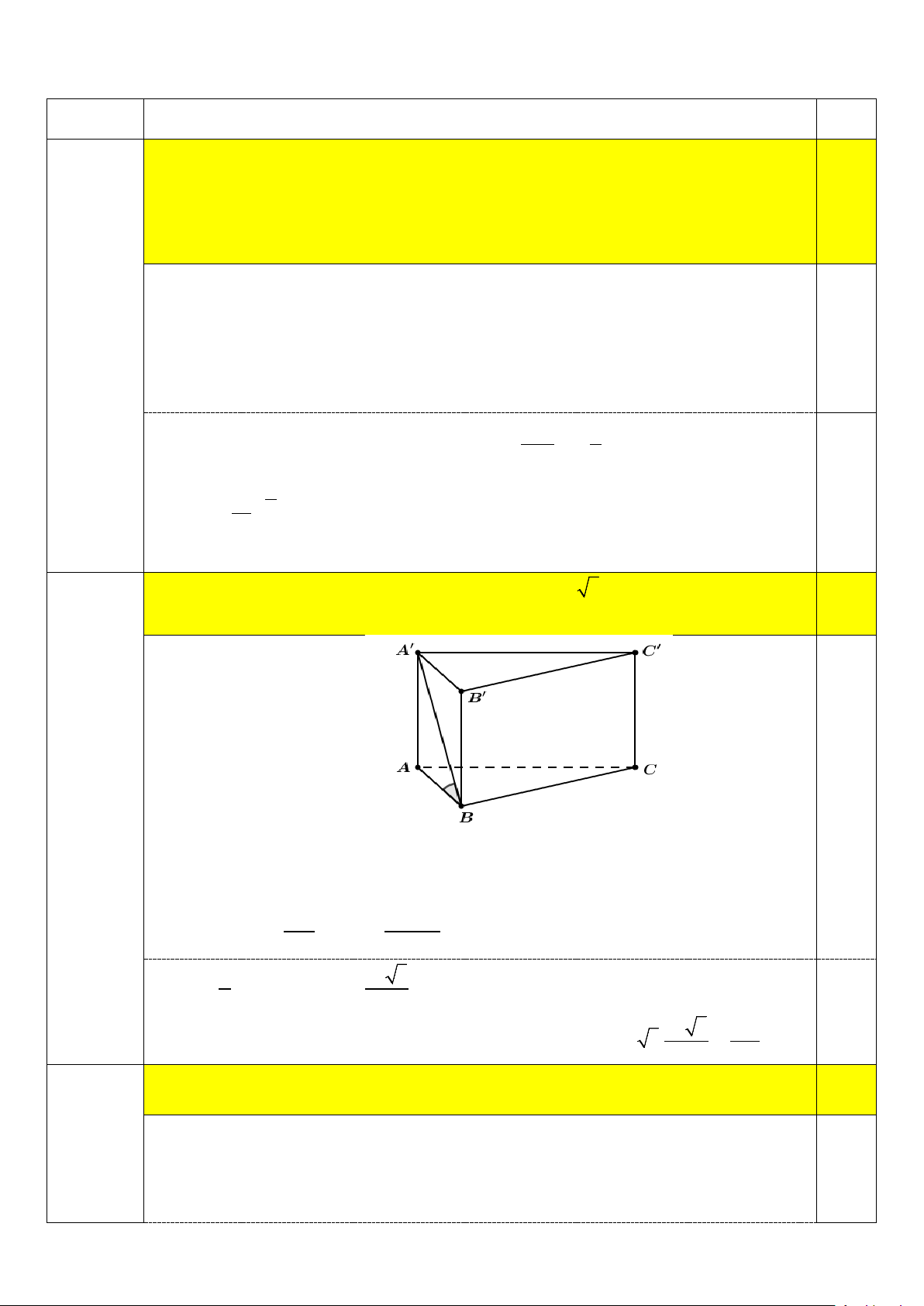
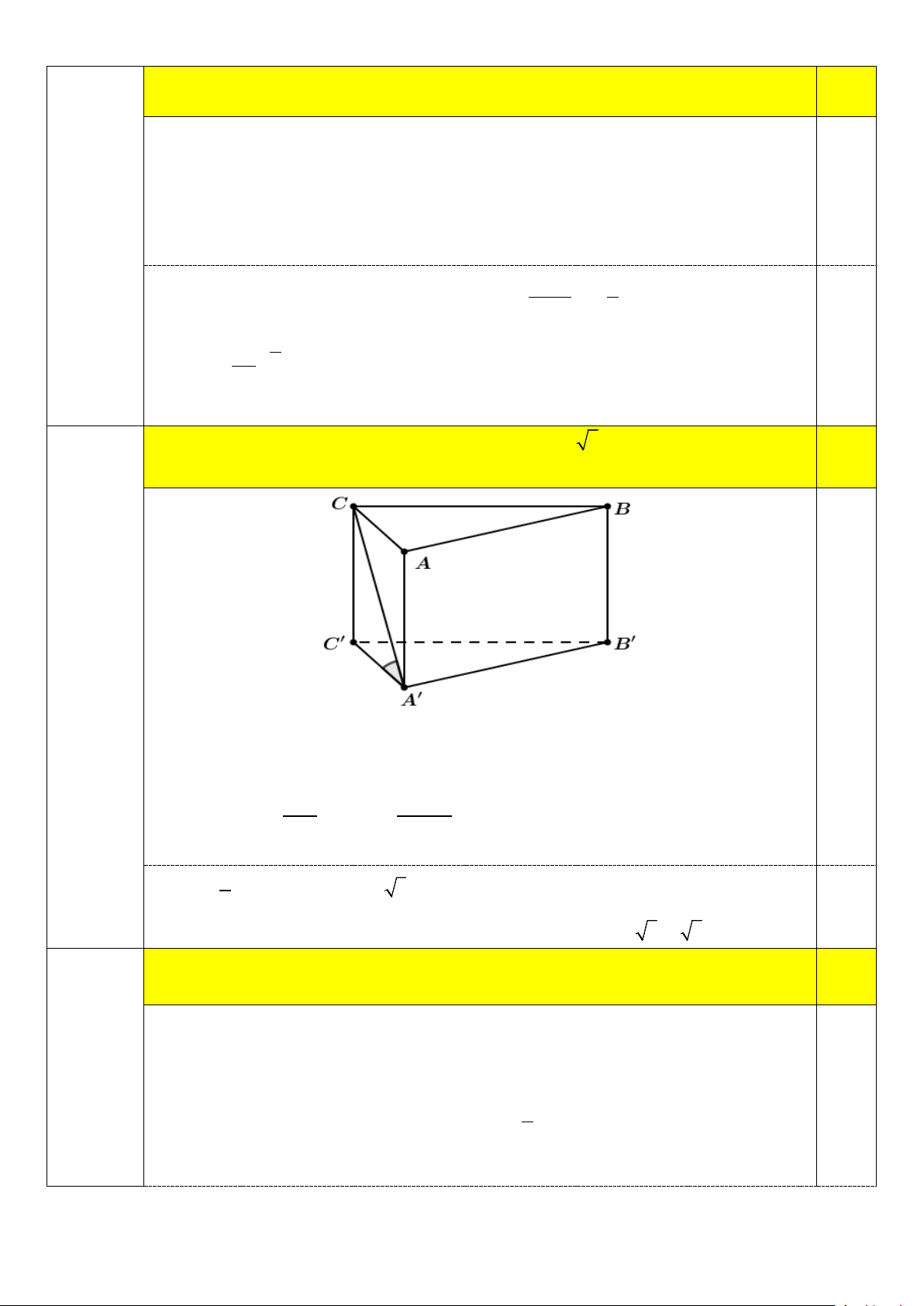
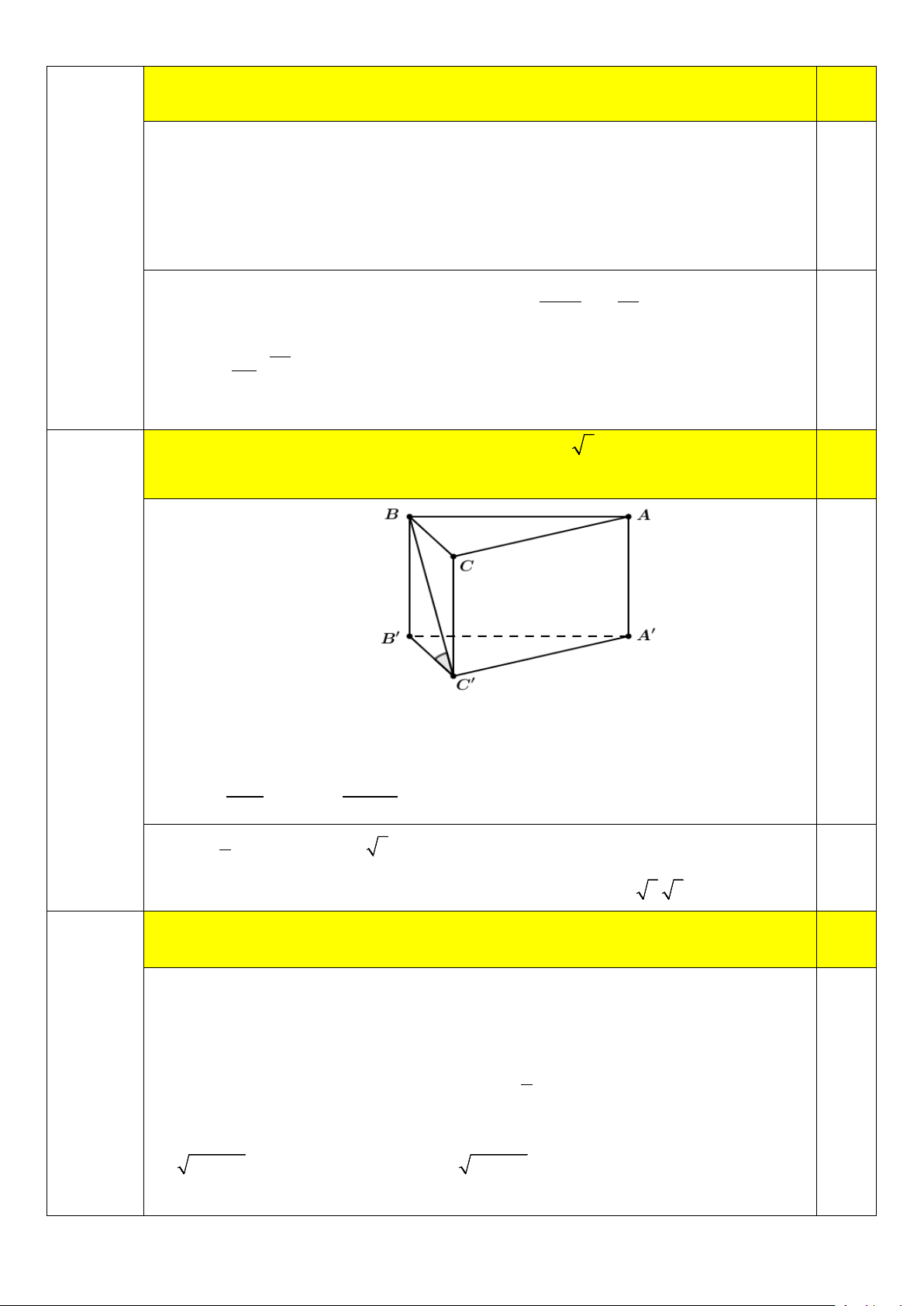
Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có AA′ = 5 3 góc giữa đường thẳng A′B 0.5
và mặt phẳng ( ABC) bằng 60 .° Tính thể tích khối lăng trụ ABC.A′B C ′ ′ 0,25 Câu 2
Ta có AA ABC AB là hình chiếu vuông góc của AB trên mặt phẳng ( ABC)
. Suy ra góc giữa A′B và mặt phẳng ( ABC) là góc  A′BA .  0
ABA  60 AA′ AA′ Lại có: 0 tan 60 = ⇒ AB = = 5 0 AB tan 60 1 0 25 3 S    AB CB ABC . . .sin 60 2 4 0,25
Thể tích khối lăng trụ ABC.A'B 'C 'là: 25 3 375 V        AA .S ABC A B C ABC  5 3. . 4 4
Tìm m để đồ thị hàm số 4 2 3
y = x + 2(2m +1)x + m + 4m có ba điểm cực trị lập thành một 0,5 tam giác vuông. x = 0 Ta có 3
y = x + ( m + ) x = x( 2 ' 4 4 2 1 4 x + 2m + ) 1 ⇒ y′ = 0 ⇔  . 2 x = 2 − m −1
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình 2 x = 2 − m −1 có 2 Câu 3 nghiệm phân biệt khác 1 0 ⇔ 2
− m −1 > 0 ⇔ m < − . 2 0,25
Tính được toạ độ ba điểm cực trị là A( 3
0;m + 4m) thuộc Oy; và hai điểm
B( − m − −( m + )2 3
+ m + m) C(− − m − −( m + )2 3 2 1; 2 1 4 ; 2 1; 2
1 + m + 4m) đối xứng
nhau qua Oy. Suy ra, tam giác ABC cân tại A.  
Ta có AB = ( − m − −( m + )2 2 1; 2
1 ); AC = (− m − −( m + )2 2 1; 2 1 )  
Để tam giác ABC vuông thì AB ⊥ AC ⇔ AB AC = 0 ⇔ ( m + ) + ( m + )4 . 2 1 2 1 = 0 ( = − m + )3 m 1 2 1 +1 = 0  ⇔  ⇔ 1 (loại giá trị 1 m = − ) 2m +1 = 0 m = − 2  2
Đối chiếu với điều kiện 1
m < − ta tìm được m = 1 − thỏa đề bài. 2
Tìm tất cả các giá trị nguyên của m∈(0;20) để phương trình 2
log x − log 3x +1 = −log m ( m là tham số thực) có đúng hai nghiệm thực phân 0,5 9 3 ( ) 3 biệt.
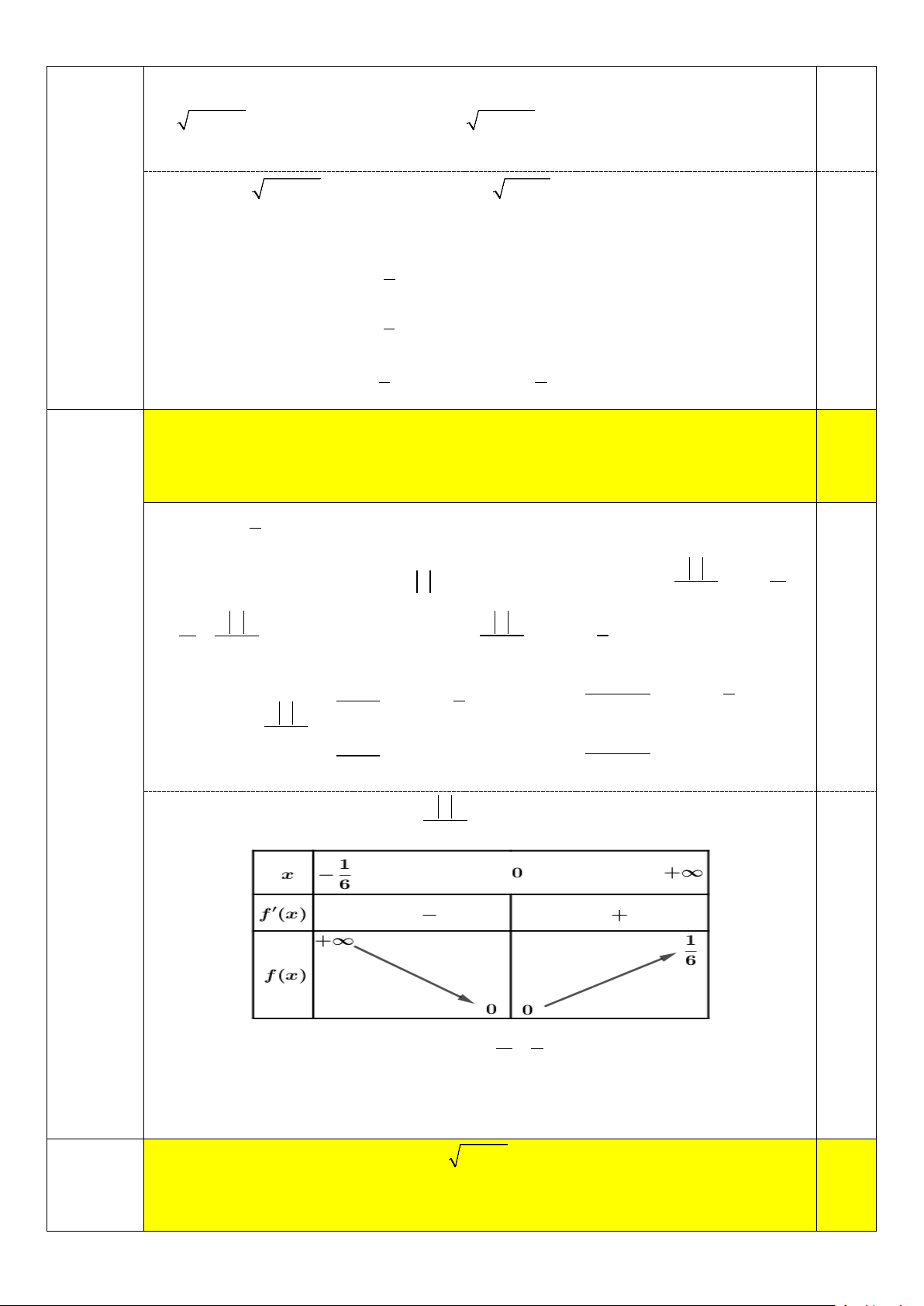
Điều kiện: 1 < x ≠ 0,m > 0 3 x
Phương trình đã cho trở thành 1
log x − log 3x +1 = −log m ⇔ log = log 3 3 ( ) 3 3 3 3x +1 m 1 x x ⇔ =
= f (x) . Xét hàm số f (x)  1 , x ;0 = ∀ ∈ − ∪(0;+∞   ) m 3x +1 3x +1  3  0,25  1 −  1 x  1  ∀ ∈ −  , x ∀ ∈ −  ;0  −  , x  ;0 2  x 3x +1  3   3x +1  3  Ta có: f (x) = =  ⇒ f (x) ( ) = 3x 1  +  x , x ∀ ∈(0;+∞)  1 , x ∀ ∈ 0;+∞ 2 ( ) Câu 4 3x +1 (3x +  )1 x
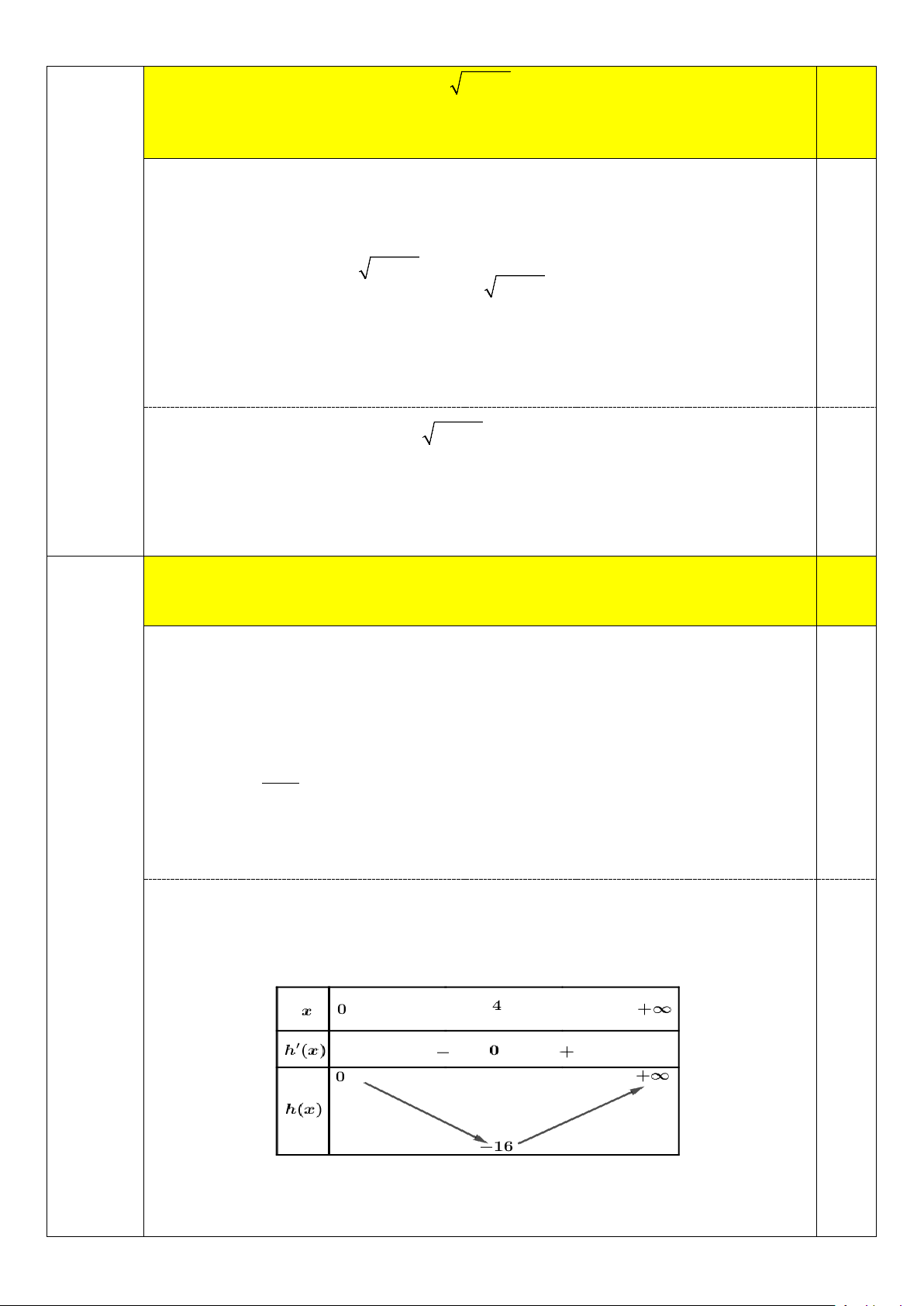
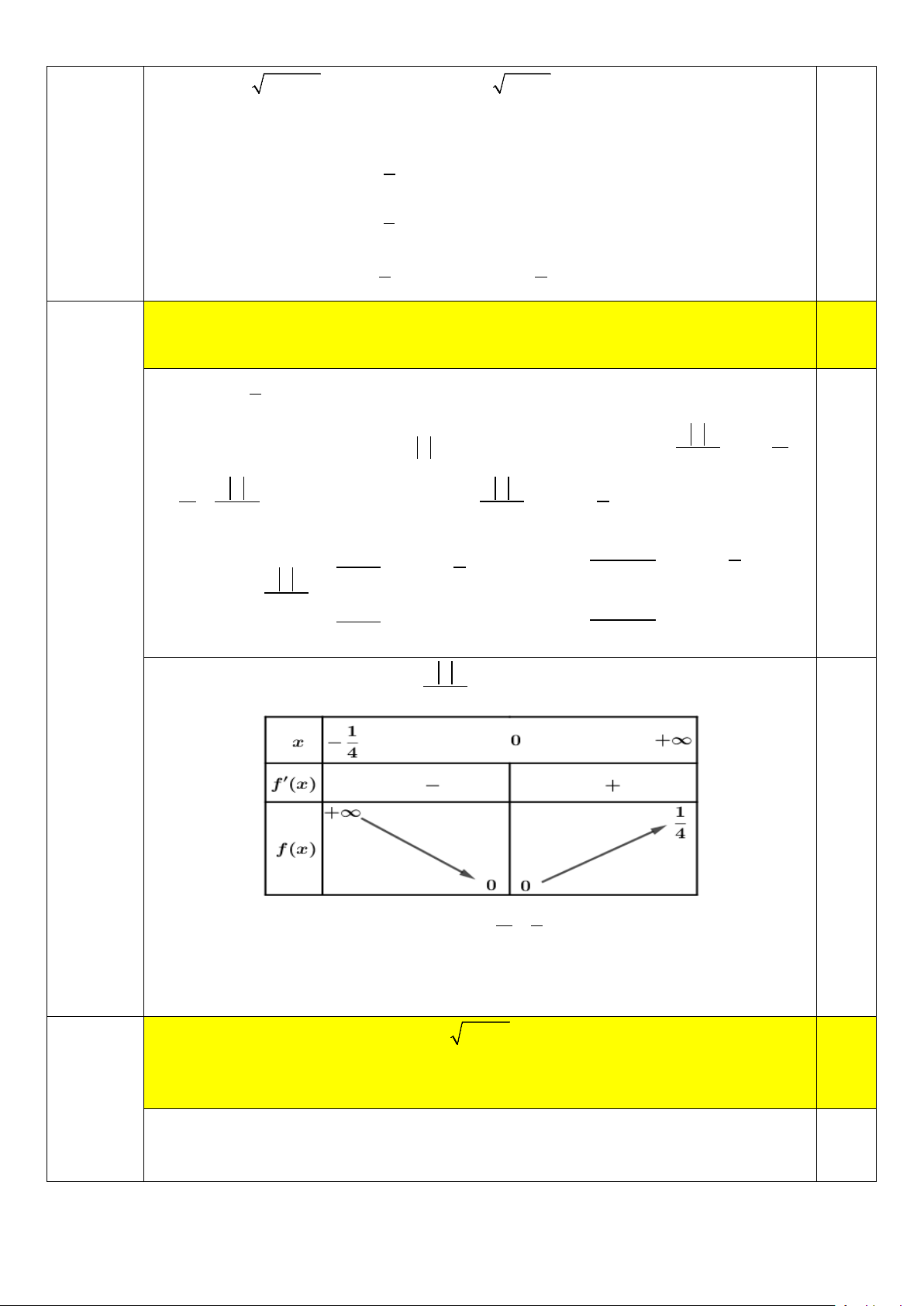
Bảng biến thiên của hàm số f (x) = 3x +1 0,25
Để phương trình có hai khiệm nghiệm thì 1 1 0 < < ⇔ m > 3. m 3 m∈(0;20) Do  ⇒ m∈{4;5;6;...; } 19 . m∈ Cho phương trình ( 2 log − 4log + 3 2x x x
− m = 0 ( m là tham số thực). Có tất cả bao 2 2 )
nhiêu giá trị nguyên dương của tham số m để phương trình đã cho có đúng hai nghiệm 0,5 thực phân biệt? x > 0 x > 0 Điều kiện:  ⇔ .
2x − m ≥ 0
x ≥ log m do m > 0  2 ( ) 2
log x − 4log x + 3 = 0 Ta có ( 2 x 2 2
log x − 4log x + 3 2 − m = 0 ⇔ 2 2 ) 
 2x − m = 0 Câu 5 log x = 1 x = 2 2  ⇔ log x 3  = ⇔ x = 8 . 2   2x =  mx =  log m 2 Phương trình ( 2 log − 4log + 3 2x x x
− m = 0 có đúng hai nghiệm thực phân biệt 2 2 ) log m ≤ 0 0 < m ≤1 m =1 2 ⇔ ⇔   . Do m . 2 8 nguyên dương suy ra  2 ≤ log m < 8 2 ≤ m < 2 m∈{4;5;6;… 5 ;2 5} 2
Vậy có tất cả 1+ 255 − 3 = 253 giá trị m nguyên dương thỏa mãn đề bài.
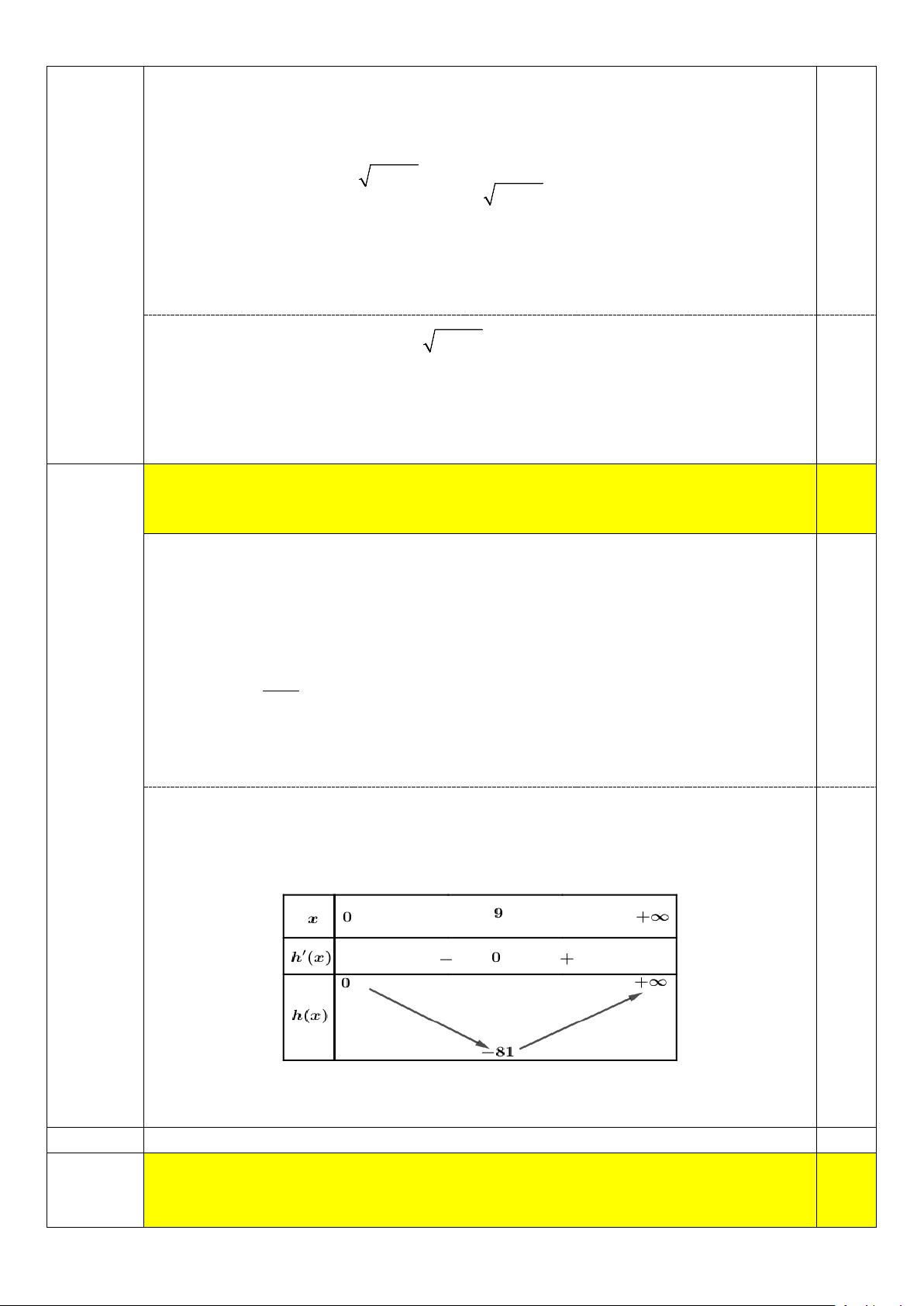
Tìm tất cả các giá trị của tham số
m để phương trình 0,5 log (2x + m) 2
− 2log x = x −8x − 4m − 2 có đúng hai nghiệm thực phân biệt? 2 2 x > 0 Điều kiện: 
. Ta có log 2x + m − 2log x = x −8x − 4m − 2 2 ( ) 2 2x + m > 0 2 ⇔ log 4
 (2x + m) + 4  (2x + m) 2 2
= log x + x ⇔ f 4
 (2x + m) = f  ( 2x , 1 2 2 ) ( )
Xét hàm số f (t) = log t + t trên khoảng (0;+∞) 2 0,25 Ta có f ′(t) 1 = +1 > 0, t
∀ > 0 . Suy ra f (t) = log t + t luôn đồng biến trên khoảng t ln 2 2 (0;+∞)
Do đó ( ) ⇔ ( x + m) 2 2 1 4 2
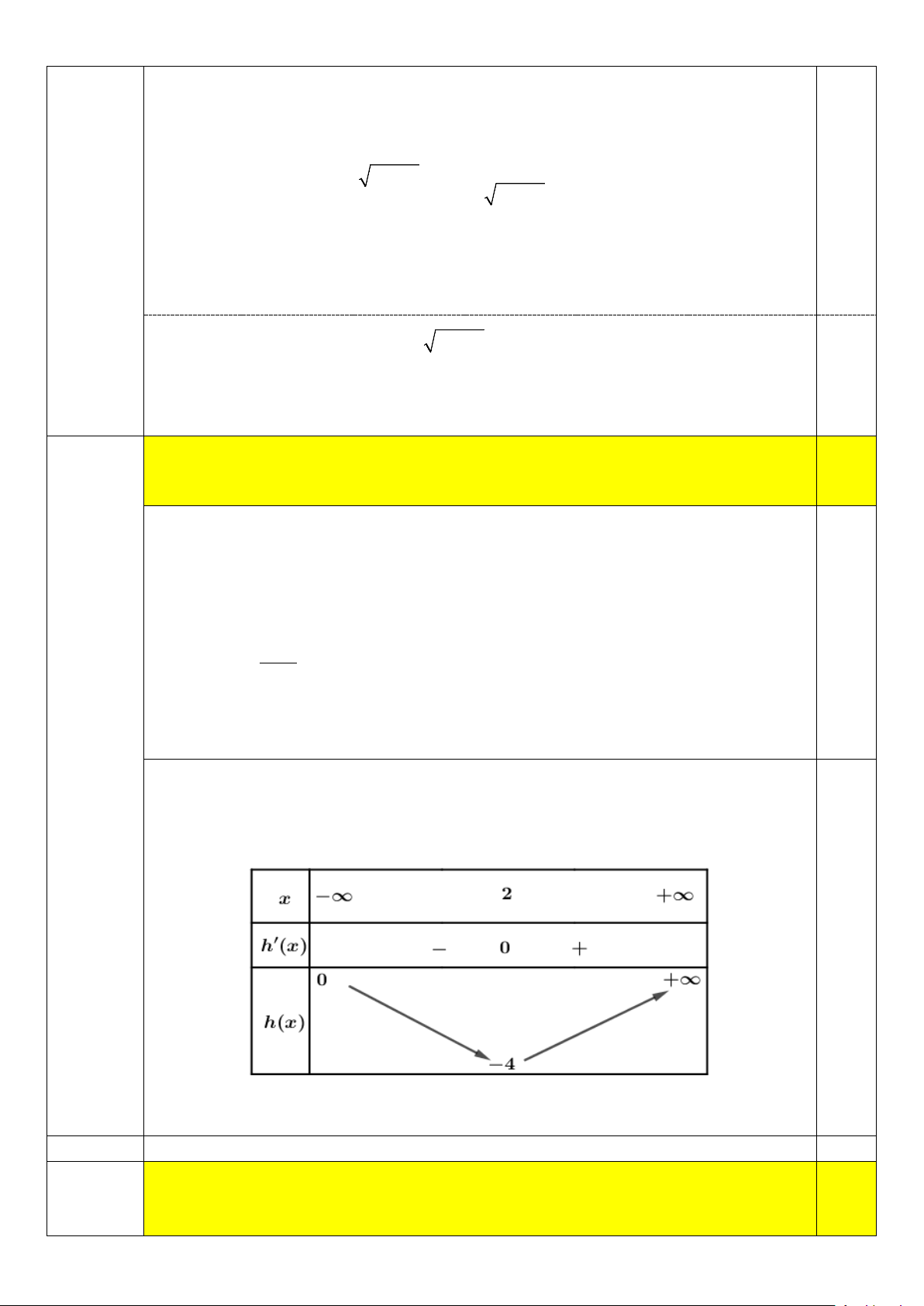
= x ⇔ 4m = x −8x = h(x) Câu 6
Xét hàm số h(x) 2
= x −8x trên khoảng (0;+∞)
Ta có h′(x) = 2x −8; g′(x) = 0 ⇔ x = 4
Bảng biến thiên của hàm số h(x) 2
= x −8x 0,25
Dựa vào bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệt khi 16
− < 4m < 0 ⇔ 4 − < m < 0 Câu hỏi MÃ ĐỀ 102 Điểm
Ông A gửi tiết kiệm 40 triệu đồng ở ngân hàng X với lãi suất không đổi 4,5% một năm.
Bà B gửi tiết kiệm 90 triệu đồng ở ngân hàng Y với lãi suất không đổi 5,5% một năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập 0,5
vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của bà B
lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông A?
Giả sử n > 0 (n∈) là số năm gửi tiền trong ngân hàng của ông A và bà B.
Sau n năm, số tiền cả gốc lẫn lãi của ông A là: 6 45.10 1 0,045 n S = + (triệu đồng) và 1 ( ) 6 0,25 Câu 1 của bà B là: 80.10 1 0,055 n S = + (triệu đồng). 2 ( )
Để tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của ông
A thì 2S < S . 1 2 n   Hay 6 ( )n 6 1,045 8 2.45.10 1 0,045 80.10 (1 0,055)n + < + ⇔ <  1,055    9 0,25  8 n log  ⇔ > ⇒ n ≥   13 1,045  9 1,055 
Vậy, sau 13 năm thì tổng số tiền cả vốn lẫn lãi của bà B lớn hơn hai lần tổng số tiền cả
vốn lẫn lãi của ông A .
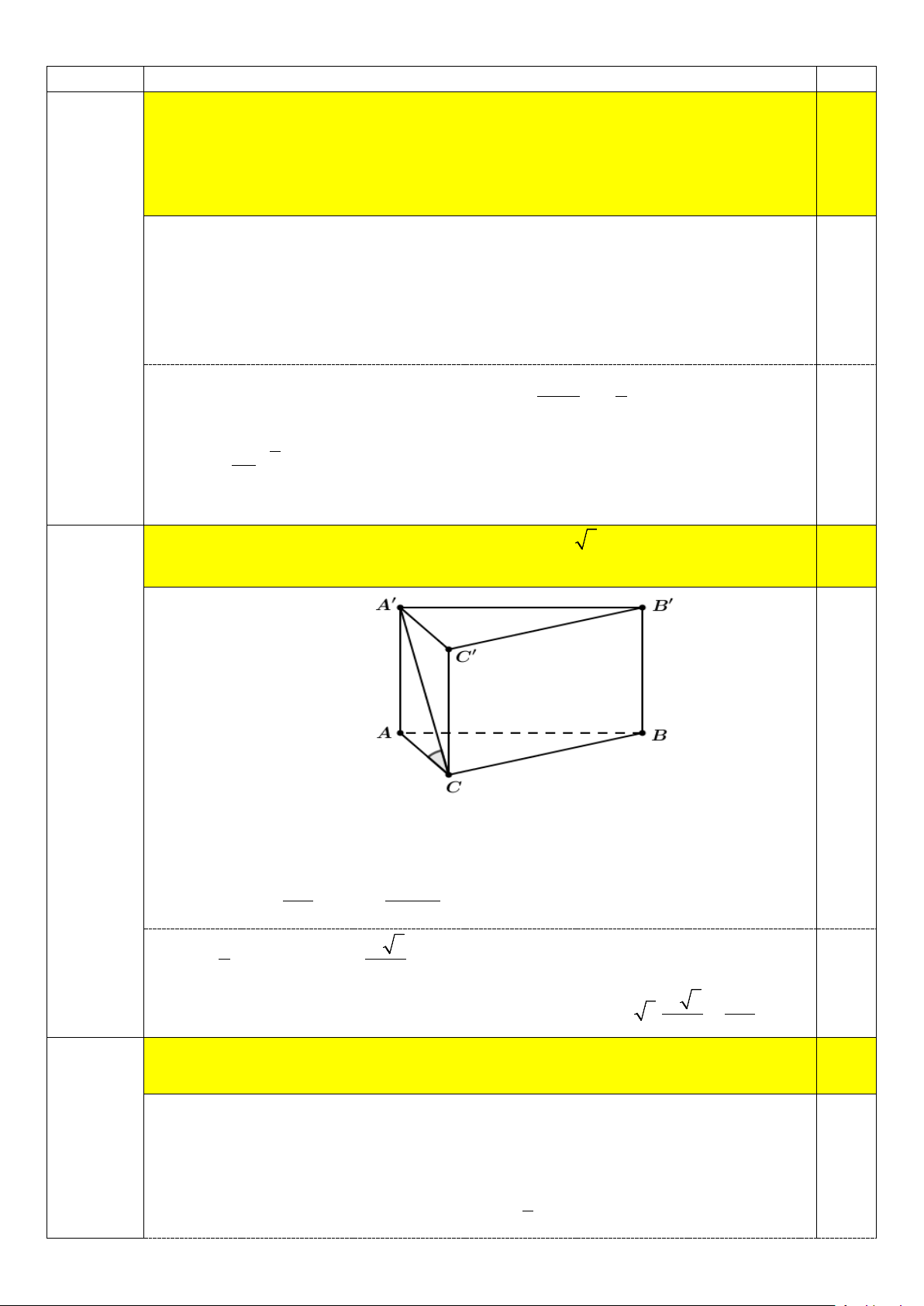
Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có AA′ = 3 3 góc giữa đường thẳng A′C 0,5
và mặt phẳng ( ABC) bằng30 .° Tính thể tích khối lăng trụ ABC.A′B C ′ ′ 0,25 Câu 2
Ta có AA ABC AC là hình chiếu vuông góc của AC trên mặt phẳng ( ABC)
. Suy ra góc giữa A′C và mặt phẳng ( ABC) là góc  A′CA .  0  ACA  0 3 AA′ AA′ Lại có: 0 tan 30 = ⇒ AC = = 9 0 AC tan 30 1 0 81 3 S    AB CB ABC . . .sin 60 2 4 0,25
Thể tích khối lăng trụ ABC.AB C   là: 81 3 729 V        AA .S ABC A B C ABC  3 3. . 4 4
Tìm m để đồ thị hàm số 4 2 3
y = x + 2(3m +1)x + 2m + 3m có ba điểm cực trị lập thành 0,5 một tam giác vuông. x = 0 Ta có 3
y = x + ( m + ) x = x( 2 ' 4 4 3 1 4 x + 3m + ) 1 ⇒ y′ = 0 ⇔ .  2 x = 3 − m −1
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình 2 x = 3 − m −1 có 2 nghiệm phân biệt khác 1 0 ⇔ 3
− m −1 > 0 ⇔ m < − . 3 0,25
Tính được toạ độ ba điểm cực trị là A( 3
0;2m + 3m) thuộc Oy; và hai điểm Câu 3
B( − m − −( m + )2 3
+ m + m) C (− − m − −( m + )2 3 3 1; 3 1 2 3 ; 3 1; 3
1 + 2m + 3m) đối xứng
nhau qua Oy. Suy ra, tam giác ABC cân tại A.  
Ta có AB = ( − m − −( m + )2 3 1; 3
1 ) ; AC = (− m − −( m + )2 3 1; 3 1 )  
Để tam giác ABC vuông thì AB ⊥ AC ⇔ AB AC = 0 ⇔ ( m + ) + ( m + )4 . 3 1 3 1 = 0  2 ( = − 3m + )3 1 +1 = 0 m  3 ⇔ 0,25  ⇔  3m +1 = 0  1 m = −  3
Đối chiếu với điều kiện 1
m < − ta tìm được 2
m = − thỏa đề bài. 3 3
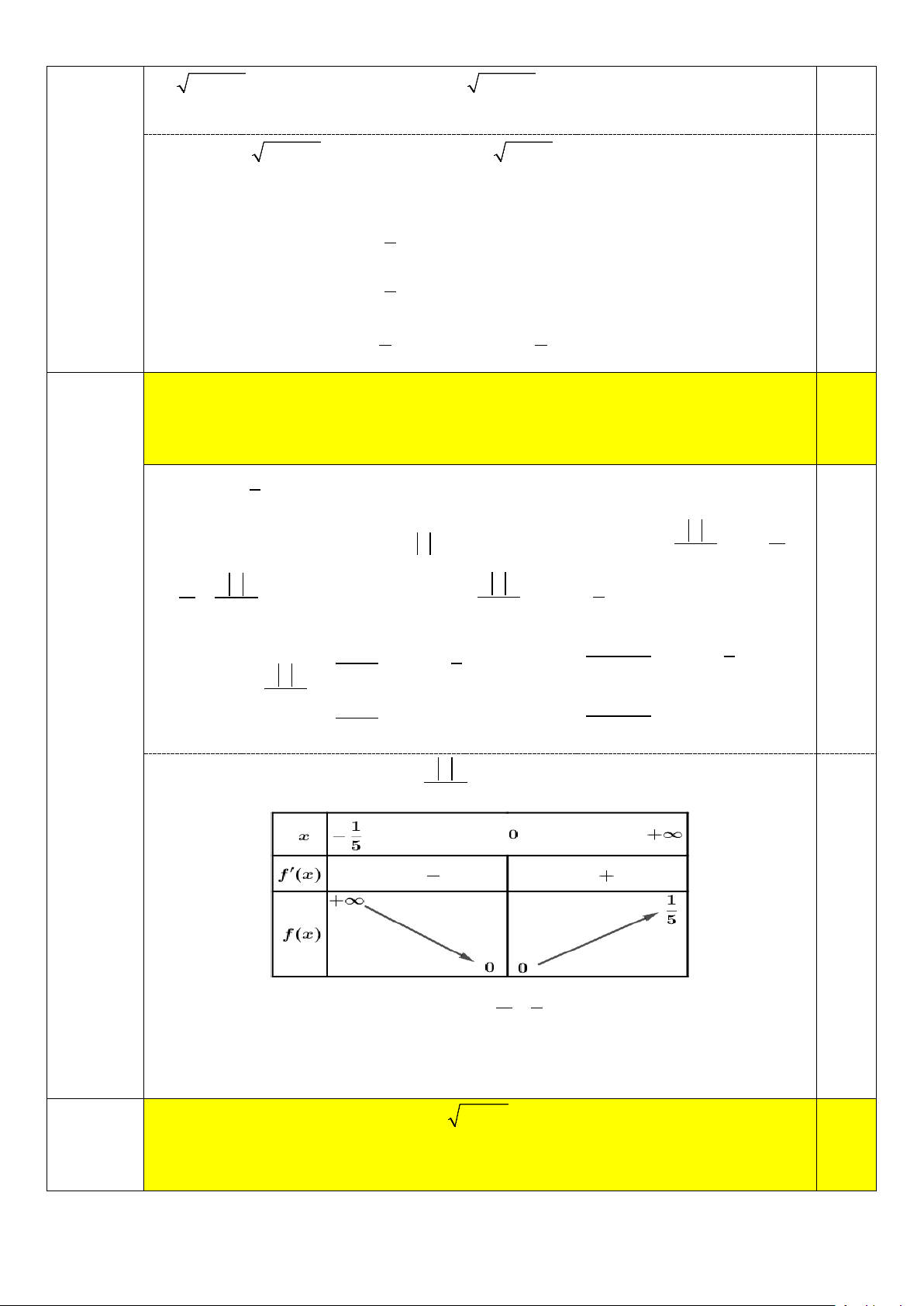
Tìm tất cả các giá trị nguyên của m∈(0;20) để phương trình 2
log x − log 6x +1 = −log m ( 0,5 9 3 ( ) 3
m là tham số thực) có đúng hai nghiệm thực phân biệt. Điều kiện: 1
− < x ≠ 0,m > 0 6 x
Phương trình đã cho trở thành 1
log x − log 6x +1 = −log m ⇔ log = log 3 3 ( ) 3 3 3 6x +1 m 1 x x ⇔ =
= f (x) . Xét hàm số f (x)  1 , x ;0 = ∀ ∈ − ∪(0;+∞   ) m 6x +1 6x +1  6  0,25  1 −  1 x  1  ∀ ∈ −  , x ∀ ∈ −  ;0  −  , x  ;0 2  x 6x +1  6   6x +1  6  Ta có: f (x) = =  ⇒ f (x) ( ) = 6x 1  +  x , x ∀ ∈(0;+∞)  1 , x ∀ ∈ 0;+∞ 2 ( ) Câu 4 6x +1 (6x +  )1 x
Bảng biến thiên của hàm số f (x) = 6x +1 0,25
Để phương trình có hai khiệm nghiệm thì 1 1 0 < < ⇔ m > 6. m 6 m∈(0;20) Do  ⇒ m∈{7;8;9;...; } 19 . m∈ Cho phương trình ( 2 log − 3log + 2 3x x x
− m = 0 ( m là tham số thực). Có tất cả bao 2 2 ) Câu 5
nhiêu giá trị nguyên dương của tham số m để phương trình đã cho có đúng hai nghiệm 0,5 thực phân biệt? x > 0 x > 0 Điều kiện:  ⇔ . 3x  − m ≥ 0
x ≥ log m do m > 0  3 ( ) 2
2log x − 3log x − 2 = 0 Ta có ( 2
log x − 3log x + 2 3x − m = 0 ⇔ 2 2 ) 2 2 
 3x − m = 0 0,25 log x = 2 x = 4 2  ⇔ log x 1  = ⇔ x = 2 . 2   3x =  mx =  log m 3 Phương trình ( 2 log − 3log + 2 3x x x
− m = 0 có đúng hai nghiệm thực phân biệt 2 2 ) log m ≤ 0  < m ≤ m =1 3 0 1 ⇔ ⇔   . Do m . 0,25 2 4 nguyên dương suy ra  2 ≤ log m < 4 3 ≤ m < 3 m∈{9;10;11;…;80} 3
Vậy có tất cả 1+ 80 −8 = 73 giá trị m nguyên dương thỏa mãn đề bài.
Tìm tất cả các giá trị của tham số
m để phương trình 0,5 log (2x + m) 2
− 2log x = x −18x − 9m − 2 có đúng hai nghiệm thực phân biệt? 3 3 x > 0 Điều kiện: 
. Ta có log 2x + m − 2log x = x −18x − 9m − 2 3 ( ) 2 2x + m > 0 3 ⇔ log 9
 (2x + m) + 9  (2x + m) 2 2
= log x + x ⇔ f 9
 (2x + m) = f  ( 2x , 1 3 3 ) ( )
Xét hàm số f (t) = log t + t trên khoảng (0;+∞) 3 0,25 Ta có f ′(t) 1 = +1 > 0, t
∀ > 0 . Suy ra f (t) = log t + t luôn đồng biến trên khoảng t ln 3 3 (0;+∞).
Do đó ( ) ⇔ ( x + m) 2 2 1 9 2
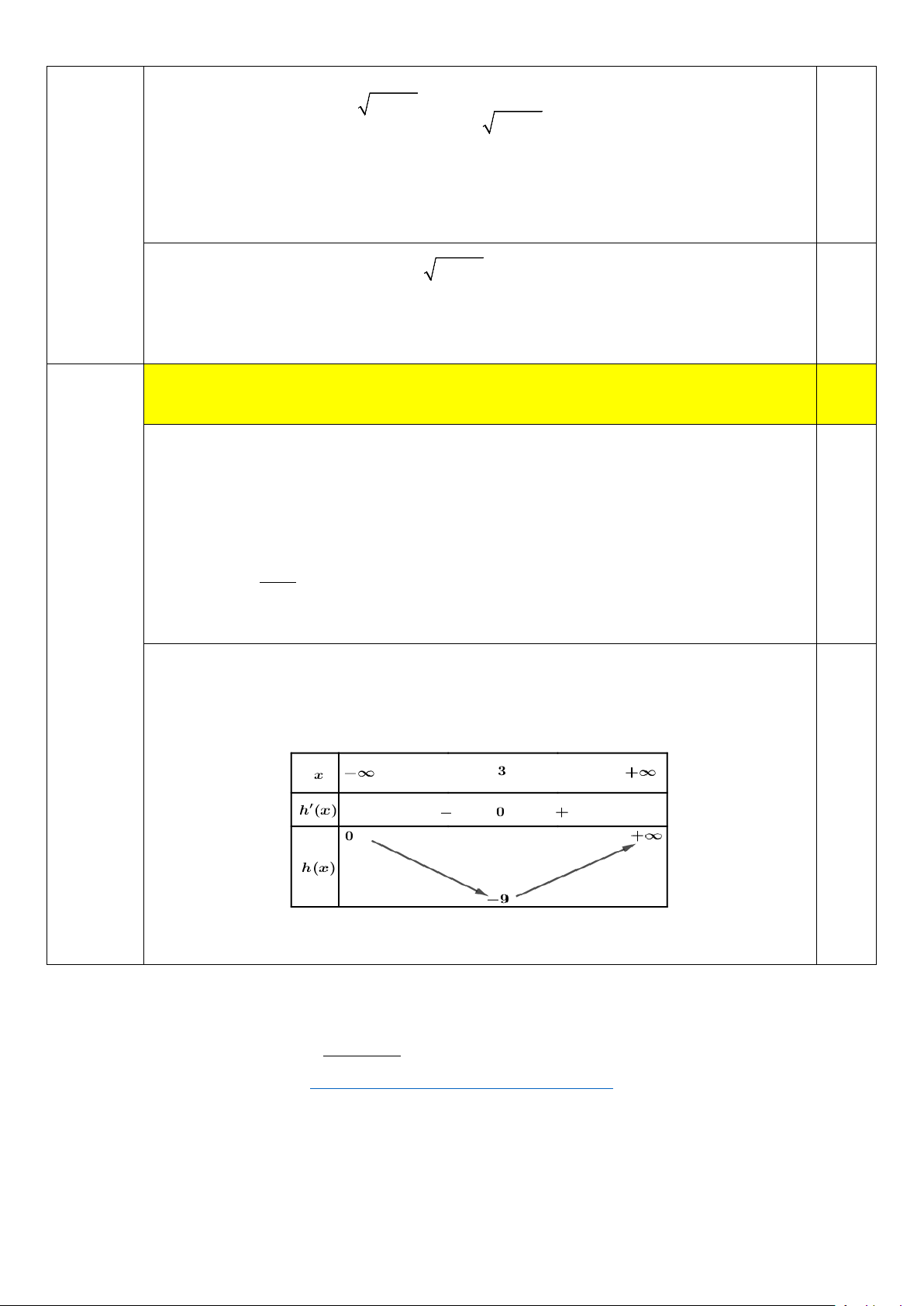
= x ⇔ 9m = x −18x = h(x) Câu 6
Xét hàm số h(x) 2
= x −18x trên khoảng (0;+∞)
Ta có h′(x) = 2x −18; g′(x) = 0 ⇔ x = 9
Bảng biến thiên của hàm số h(x) 2
= x −18x 0,25
Dựa vào bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệt khi 81
− < 9m < 0 ⇔ 9 − < m < 0 Câu hỏi MÃ ĐỀ 103 Điểm
Ông A gửi tiết kiệm 60 triệu đồng ở ngân hàng X với lãi suất không đổi 6,0% một năm. Câu 1
Bà B gửi tiết kiệm 35 triệu đồng ở ngân hàng Y với lãi suất không đổi 4,5% một năm. 0,5
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập
vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của của
ông A lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của bà B?
Giả sử n > 0 (n∈) là số năm gửi tiền trong ngân hàng của ông A và bà B.
Sau n năm, số tiền cả gốc lẫn lãi của ông A là: 6 60.10 1 0,06 n S = + (triệu đồng) và của 1 ( ) bà B là: 6 35.10 1 0,045 n S = + (triệu đồng). 0,25 2 ( )
Để tổng số tiền cả vốn lẫn lãi của Ông A lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của
Bà B thì S > 2S 1 2 n   Hay 6 ( )n 6 1,045 6 60.10 1 0,06 2.35.10 (1 0,045)n + > + ⇔ <  1,06    7 0,25  6 n log  ⇔ > ⇒ n ≥   11 1,045  7 1,06 
Vậy, sau 11 năm thì tổng số tiền cả vốn lẫn lãi của ông A lớn hơn hai lần tổng số tiền cả
vốn lẫn lãi của Bà B
Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có AA′ = 4 3 góc giữa đường thẳng A′C 0,5
và mặt phẳng ( A′B C
′ ′) bằng30 .° Tính thể tích khối lăng trụ ABC.A′B C ′ ′ Câu 2 0,25
Ta có CC′ ⊥ ( A′B C
′ ′) ⇒ A′C′ là hình chiếu vuông góc của CA′ trên mặt phẳng ( A′B C ′ ′)
. Suy ra góc giữa CA′ và mặt phẳng ( A′B C ′ ′) là góc  CA′C′ .  0
CAC  30 CC′ CC′ Lại có: 0 tan 30 = ⇒ A′C′ = =12 0 C A ′ ′ tan 30 1 0 S    AB CB ABC . . .sin 60 36 3 2 0,25
Thể tích khối lăng trụ ABC.AB C   là:V        AA .S ABC A B C ABC  4 3.36 3 432 .
Tìm m để đồ thị hàm số 4 2 3
y = x + 2(4m +1)x + 3m + 2m có ba điểm cực trị lập thành 0,5 một tam giác vuông. x = 0 3 2
y ' = 4x + 4 4m +1 x = 4x x + 4m +1 ⇒ y′ = 0 ⇔ Ta có ( ) ( )  . 2 x = 4 − m −1
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình 2 x = 4 − m −1 có 2 nghiệm phân biệt khác 1 0 ⇔ 4
− m −1 > 0 ⇔ m < − . 4 0,25 3
Tính được toạ độ ba điểm cực trị là A(0;3m + 2m) thuộc Oy; và hai điểm
B( − m − −( m + )2 3
+ m + m) C(− − m − −( m + )2 3 4 1; 4 1 3 2 ; 4 1; 4
1 + 3m + 2m) đối xứng Câu 3
nhau qua Oy. Suy ra, tam giác ABC cân tại A.  
Ta có AB = ( − m − −( m + )2 4 1; 4
1 ); AC = (− m − −( m + )2 4 1; 4 1 )  
Để tam giác ABC vuông thì AB ⊥ AC ⇔ AB AC = 0 ⇔ ( m + ) + ( m + )4 . 4 1 4 1 = 0  1 ( = − 4m + )3 1 +1 = 0 m  2 ⇔ 0,25  ⇔  4m +1 = 0  1 m = −  4
Đối chiếu với điều kiện 1
m < − ta tìm được 1
m = − thỏa đề bài. 4 2
Tìm tất cả các giá trị nguyên của m∈(0;20) để phương trình 2
log x − log 5x +1 = −log m ( m là tham số thực) có đúng hai nghiệm thực phân 0,5 9 3 ( ) 3 biệt. Điều kiện: 1
− < x ≠ 0,m > 0 5 x
Phương trình đã cho trở thành 1
log x − log 5x +1 = −log m ⇔ log = log 3 3 ( ) 3 3 3 5x +1 m 1 x x ⇔ =
= f (x). Xét hàm số f (x)  1 , x ;0 = ∀ ∈ − ∪(0;+∞   ) m 5x +1 5x +1  5  0,25  1 −  1 x  1  ∀ ∈ −  , x ∀ ∈ −  ;0  −  , x  ;0 2  x 5x +1  5   5x +1  5  Ta có: f (x) = =  ⇒ f ′(x) ( ) = 5x 1  +  x , x ∀ ∈(0;+∞)  1 , x ∀ ∈ 0;+∞ 2 ( ) Câu 4 5x +1 (5x +  )1 x
Bảng biến thiên của hàm số f (x) = 5x +1 0,25
Để phương trình có hai khiệm nghiệm thì 1 1 0 < < ⇔ m > 5 . m 5 m∈(0;20) Do  ⇒ m∈{6;7;8;...; } 19 . m∈ Cho phương trình ( 2 log − 5log + 6 4x x x
− m = 0 ( m là tham số thực). Có tất cả bao 2 2 ) Câu 5
nhiêu giá trị nguyên dương của tham số m để phương trình đã cho có đúng ba nghiệm 0,5 thực phân biệt? x > 0 x > 0 Điều kiện:  ⇔ .
4x − m ≥ 0
x ≥ log m do m > 0  4 ( ) 2
log x − 5log x + 6 = 0 Ta có ( 2 x 2 2
log x − 5log x + 6 4 − m = 0 ⇔ 2 2 ) 
 4x − m = 0 0,25 log x = 2 x = 4 2  ⇔ log x 3  = ⇔ x = 8 . 2   4x =  mx =  log m 4 Phương trình ( 2 log − 5log + 6 4x x x
− m = 0 có đúng ba nghiệm thực phân biệt 2 2 )
⇔ 0 < log m < 4 ⇔ 1< m < 256 . Do m m∈ 2;3;4;…;255 . 0,25 4 nguyên dương suy ra { }
Vậy có tất cả 255 −1 = 254 giá trị m nguyên dương thỏa mãn đề bài.
Tìm tất cả các giá trị của tham số
m để phương trình 0,5 log (4x + m) 2
− 2log x = 4x −16x − 4m có đúng hai nghiệm thực phân biệt? 2 2 x > 0 Điều kiện: 
. Ta có log 4x + m − 2log x = 4x −16x − 4m 2 ( ) 2 4x + m > 0 2
⇔ log (4x + m) + 4(4x + m) 2 2
= log x + 4x ⇔ f (4x + m) = f ( 2 x , 1 2 2 ) ( )
Xét hàm số f (t) = log t + 4t trên khoảng (0;+∞) 2 0,25 Ta có f ′(t) 1 = + 4 > 0, t
∀ > 0 . Suy ra f (t) = log t + 4t luôn đồng biến trên khoảng t ln 2 2 (0;+∞). Do đó ( ) 2 2
1 ⇔ 4x + m = x ⇔ m = x − 4x = h(x) = − Câu 6
Xét hàm số h(x) 2
x 4x trên khoảng (0;+∞)
Ta có h′(x) = 2x − 4;h′(x) = 0 ⇔ x = 2
Bảng biến thiên của hàm số h(x) 2
= x − 4x 0,25
Dựa vào bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệt khi ⇔ 4 − < m < 0 Câu hỏi MÃ ĐỀ 104 Điểm
Ông A gửi tiết kiệm 65 triệu đồng ở ngân hàng X với lãi suất không đổi 6,5% một năm. Câu 1
Bà B gửi tiết kiệm 37 triệu đồng ở ngân hàng Y với lãi suất không đổi 5,5% một năm. 0,5
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm,số tiền lãi được nhập
vào vốn ban đầu. Hỏi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của ông A
lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của bà B ?
Giả sử n > 0 (n∈) là số năm gửi tiền trong ngân hàng của ông A và bà B.
Sau n năm, số tiền cả gốc lẫn lãi của ông A là: 6 65.10 1 0,06 n S = + (triệu đồng) và của 1 ( ) bà B là: 6 37.10 1 0,055 n S = + (triệu đồng). 0,25 2 ( )
Để tổng số tiền cả vốn lẫn lãi của Ông A lớn hơn hai lần tổng số tiền cả vốn lẫn lãi của
Bà B thì S > 2S 1 2 n   Hay 6 ( )n 6 1,055 65 65.10 1 0,065 2.37.10 (1 0,055)n + > + ⇔ <  1,065    74 0,25  65 n log  ⇔ > ⇒ n ≥   14 1,055  74 1,065 
Vậy, sau 14 năm năm thì tổng số tiền cả vốn lẫn lãi của ông A lớn hơn hai lần tổng số
tiền cả vốn lẫn lãi của Bà B
Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có AA′ = 2 3 , góc giữa đường thẳng 0,5
BC′ và mặt phẳng ( A′B C
′ ′) bằng60 .° Tính thể tích khối lăng trụ ABC.A′B C ′ ′ Câu 2 0,25
Ta có BB′ ⊥ ( A′B C ′ ′) ⇒ B C
′ ′ là hình chiếu vuông góc của BC′ lên ( A′B C ′ ′). Suy ra
góc giữa BC′ và mặt phẳng ( A′B C ′ ′) là góc  BC B ′ ′.  0  BC B    60 . Lại có: ′ ′ 0 tan 60 BB BB = ⇒ B C ′ ′ = = 2 0 B C ′ ′ tan 60 1 0 S   0,25  AB CB ABC . . .sin 60 3 2
Thể tích khối lăng trụ ABC.AB C   là:V        AA .S ABC A B C ABC  2 3. 3 6 .
Tìm m để đồ thị hàm số 4 2 3
y = x + 2(5m +1)x + 4m + m có ba điểm cực trị lập thành một 0,5 tam giác vuông. x = 0 Ta có 3
y′ = 4x + 4(5m + ) 1 x = 4x( 2 x + 5m + ) 1 ⇒ y′ = 0 ⇔  . 2 x = 5 − m −1
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình 2 x = 5 − m −1 có 2 nghiệm phân biệt khác 1 0 ⇔ 5
− m −1 > 0 ⇔ m < − . 5
Tính được toạ độ ba điểm cực trị là A( 3
0;4m + m) thuộc Oy; và hai điểm 2 3 2
Câu 3 B( − m − −( m + ) + m + m) C (− − m − −( m + ) 3 5 1; 5 1 4 ; 5 1; 5
1 + 4m + m) đối xứng 0,25
nhau qua Oy. Suy ra, tam giác ABC cân tại A.  
Ta có AB = ( − m − −( m + )2 5 1; 5
1 ); AC = (− m − −( m + )2 5 1; 5 1 )  
Để tam giác ABC vuông thì AB ⊥ AC ⇔ AB AC = 0 ⇔ ( m + ) + ( m + )4 . 5 1 5 1 = 0  2 ( = − 5m + )3 1 +1 = 0 m  5 0,25 ⇔  ⇔  5m +1 = 0  1 m = −  5
Đối chiếu với điều kiện 1
m < − ta tìm được 2
m = − thỏa đề bài. 5 5
Tìm tất cả các giá trị nguyên của m∈(0;20) để phương trình 0,5 2
log x − log 4x +1 = −log m ( m là tham số thực) có đúng hai nghiệm thực phân biệt. 9 3 ( ) 3 Điều kiện: 1
− < x ≠ 0,m > 0 4 x
Phương trình đã cho trở thành 1
log x − log 4x +1 = −log m ⇔ log = log 3 3 ( ) 3 3 3 4x +1 m 1 x x ⇔ =
= f (x) . Xét hàm số f (x)  1 , x ;0 = ∀ ∈ − ∪(0;+∞   ) m 4x +1 4x +1  4  0,25  1 −  1 x  1  ∀ ∈ −  , x ∀ ∈ −  ;0  −  , x  ;0 2  x 4x +1  4   4x +1  4  Ta có: f (x) = =  ⇒ f ′(x) ( ) = 4x 1  +  x , x ∀ ∈(0;+∞)  1 , x ∀ ∈ 0;+∞ 2 ( )  +  Câu 4 4x 1 (4x +  )1 x
Bảng biến thiên của hàm số f (x) = 4x +1 0,25
Để phương trình có hai khiệm nghiệm thì 1 1 0 < < ⇔ m > 4 . m 4 m∈(0;20) Do  ⇒ m∈{5;6;7;...; } 19 . m∈ Cho phương trình ( 2 log − 6log + 8 5x x x
− m = 0 ( m là tham số thực). Có tất cả bao 2 2 )
nhiêu giá trị nguyên dương của tham số m để phương trình đã cho có đúng ba nghiệm 0,5 thực phân biệt? x > 0 x > 0 Câu 5 Điều kiện:  ⇔ . 0,25 5x  − m ≥ 0
x ≥ log m do m > 0  5 ( ) 2
log x − 6log x + 8 = 0 Ta có ( 2 x 2 2
log x − 6log x + 8 5 − m = 0 ⇔ 2 2 ) 
 5x − m = 0 log x = 2 x = 4 2  ⇔ log x 4  = ⇔ x =16 . 2   5x = mx =   g lo m 5 Phương trình ( 2 log − 6log + 8 5x x x
− m = 0 có đúng ba nghiệm thực phân biệt 2 2 )
⇔ 0 < log m < 4 ⇔ 1< m < 625. Do m m∈ 2;3;4;…;624 . 0,25 5 nguyên dương suy ra { }
Vậy có tất cả 624 −1 = 623 giá trị m nguyên dương thỏa mãn đề bài.
Tìm tất cả các giá trị của tham số m để phương trình log (6x + m) 2
− 2log x = 9x − 54x − 9m có đúng hai nghiệm thực phân biệt? 0,5 3 3 x > 0 Điều kiện: 
. Ta có log 6x + m − 2log x = 9x − 54x − 9m 3 ( ) 2 6x + m > 0 3
⇔ log (6x + m) + 9(6x + m) 2 2
= log x + 9x ⇔ f (6x + m) = f ( 2 x , 1 3 3 ) ( )
Xét hàm số f (t) = log t + 9t trên khoảng (0;+∞) 0,25 3 Ta có f ′(t) 1 = + 9 > 0, t
∀ > 0 . Suy ra f (t) = log t + 9t luôn đồng biến trên khoảng t ln 3 3 (0;+∞). Do đó ( ) 2 2
1 ⇔ 6x + m = x ⇔ m = x − 6x = h(x) Câu 6
Xét hàm số h(x) 2
= x − 6x trên khoảng (0;+∞)
Ta có h′(x) = 2x − 6;h′(x) = 0 ⇔ x = 3
Bảng biến thiên của hàm số h(x) 2 = x − 6x 0,25
Dựa vào bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệt khi ⇔ 9 − < m < 0
--------------------HẾT--------------------
Xem thêm: ĐỀ THI HK1 TOÁN 12
https://toanmath.com/de-thi-hk1-toan-12
Document Outline

  • de 101
  • HDC12A1