Đề Kiểm Tra Giữa HK1 Toán 12 Chân Trời Sáng Tạo Giải Chi Tiết-Đề 2

ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC 2024-2025 MÔN: TOÁN 12
Thời gian làm bài: 90 phút
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án. Câu 1: [Mức độ: Biết- Năng lực toán học: TD 1.1.]
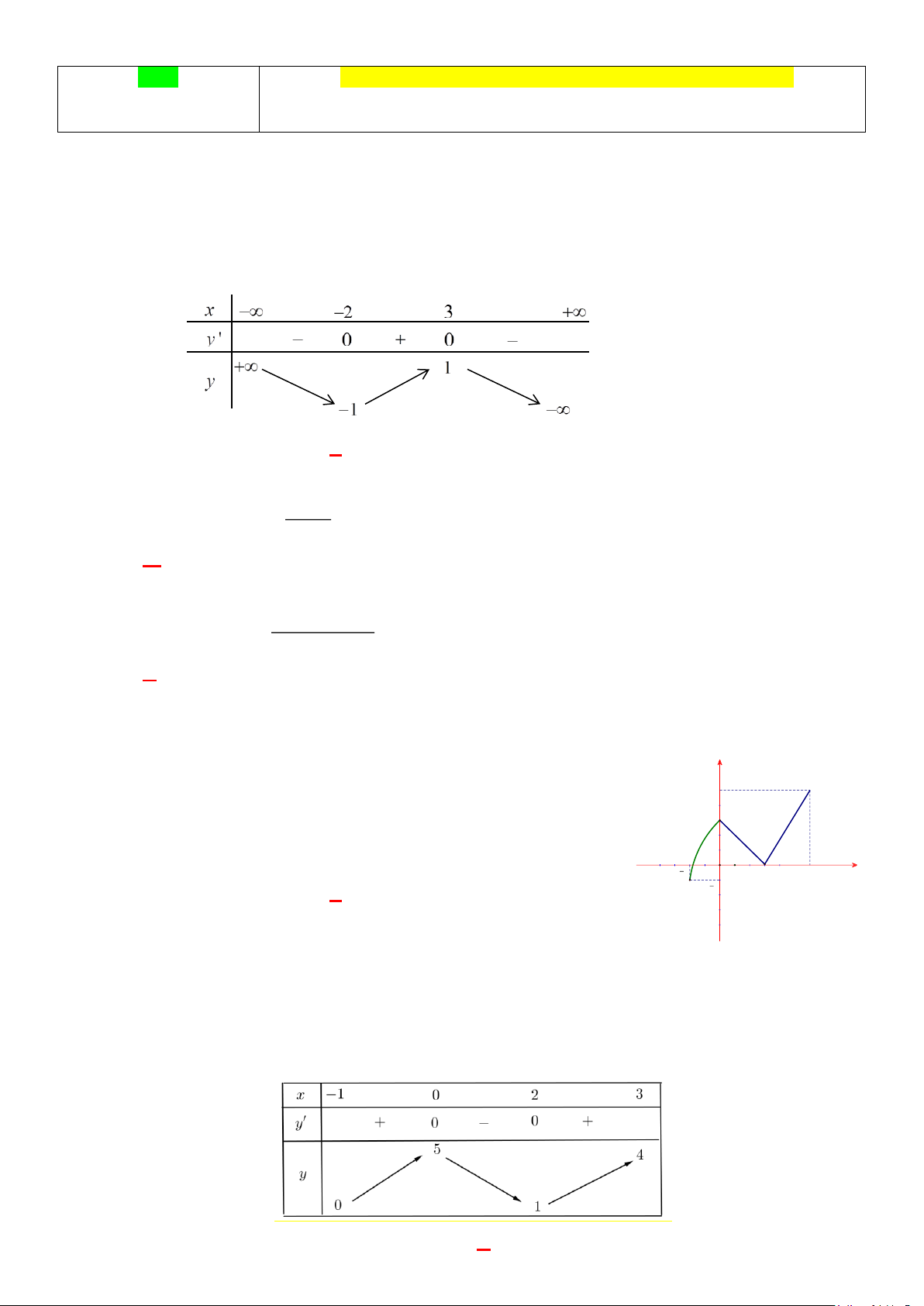
Cho hàm số y = f (x) có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm nào sau đây? A. x = 2 − B. x = 3 C. x = 1 − D. x =1
Câu 2: [ Mức độ: Biết – Năng lực toán học: TD1.1] x +1
Đồ thị hàm số y =
có bao nhiêu điểm cực trị? 2x − 3 A. 0. B. 1. C. 2. D. 3.
Câu 3: [ Mức độ: Hiểu – Năng lực toán học: TD1.2] 2 2x − 8x +11 Cho hàm số y =
có đồ thị (C). Mệnh đề nào sau đây là đúng? 2 x − 4x + 5
A. Đồ thị (C) có tiệm cận ngang là đường thẳng y = 2 và không có tiệm cận đứng.
B. Đồ thị (C) có tiệm cận ngang là đường thẳng y = 2 có tiệm cận đứng là đường thẳng x = 2.
C. Đồ thị (C) có tiệm cận đứng là đường thẳng x = 2 và không có tiệm cận ngang.
D. Đồ thị (C) có tiệm cận ngang là đường thẳng y = -2 và tiệm cận đứng là đường thẳng x = -2. A
Câu 4: [ Mức độ: Biết- Năng lực toán học: MH1.1.] y 5
Cho hàm số y = f ( x) xác định và liên tục trên  2 − ; 6 có đồ 3
thị như hình bên. Giá trị lớn nhất của hàm số trên đoạn  2 − ; 6 là 2 O 1 3 6 x A. 6. B. 5. 1 C. 3. D. -1 B
Câu 5: [ Mức độ: Biết– Năng lực toán học: TD 1.3]
Cho hàm số y = f (x) liên tục và có bảng biến thiên như hình bên dưới. Tìm m là giá trị nhỏ nhất của
hàm số y = f (x) trên đoạn  1 − ;  3 .
A. m = f (0) .
B. m = f (2).
C. m = f (− ) 1 .
D. m = f ( ) 3 . Trang 1 Câu 6: [Mức độ: Biết- Năng lực toán học: TD 1.1.] 2x +1
Đồ thị hàm số y =
có tiệm cận đứng và tiệm cận ngang lần lượt là 2 − x
A. x = 2 ; y = 2
B. x = 2 ; y = −2
C. x = −2 ; y = −2 D. x = 2 − ; y = 2 Câu 7: [Mức độ: Biết- Năng lực toán học: TD1.2.] lim f (x) =
Cho hàm số y = f (x) thoả mãn lim f ( x) =1; lim f (x) =1; lim f (x) = 3 và 3 . x→− x→+ x 2+ x 2− → →
Khẳng định nào sau đây là đúng?
A. Đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.
B. Đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.
C. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
D. Đường thẳng x = 3 là tiệm cận ngang của đồ thị hàm số.
Câu 8: [ Mức độ: Hiểu – Năng lực toán học: TD2.1]
Đồ thị của hàm số nào dưới đây nhận đường thẳng y = 1
− là đường tiện cận ngang? x − 2 x +1 A. y = . B. y = . C. 4 2
y = x − x + 2 . D. 3
y = −x + 3x −1. 1− x 2 + x
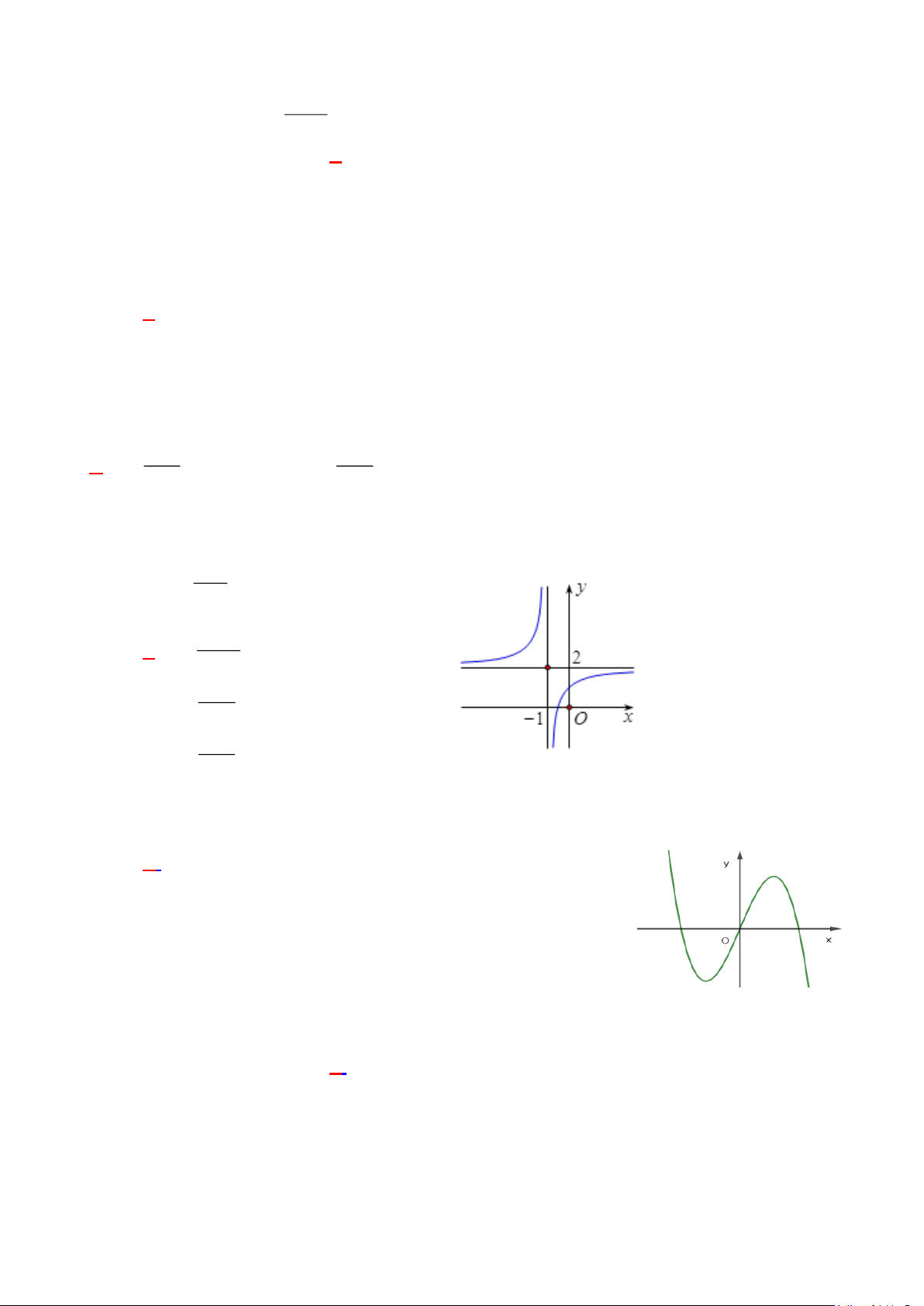
Câu 9: [ Mức độ: Biết – Năng lực toán học: TD1.3]
Đồ thị của hàm số nào dưới đây có dạng như đường cong ở hình bên? x −1 A. y = . x +1 2x +1 B. y = . x +1 x + 2 C. y = . x +1 x + 3 D. y = . 1− x
Câu 10: [ Mức độ: Biết – Năng lực toán học: TD1.3]
Đồ thị của hàm số nào dưới đây có dạng như đường cong ở hình bên? A. 3
y = − x + 3x . B. 3 2
y = x − x +1. C. 3
y = − x + 3x −1. D. 3
y = x − 3x .
Câu 11: [ Mức độ: Biết – Năng lực toán học: TD1.3] Đồ thị hàm số 3 2
y = x +10x − x −10 cắt trục tung tại điểm có tọa độ là A. ( 1 − 0;0). B. (0; 1 − 0) . C. ( 1 − ;0) . D. (1;0) .
Câu 12: [ Mức độ: Hiểu– Năng lực toán học: TD 2.1]
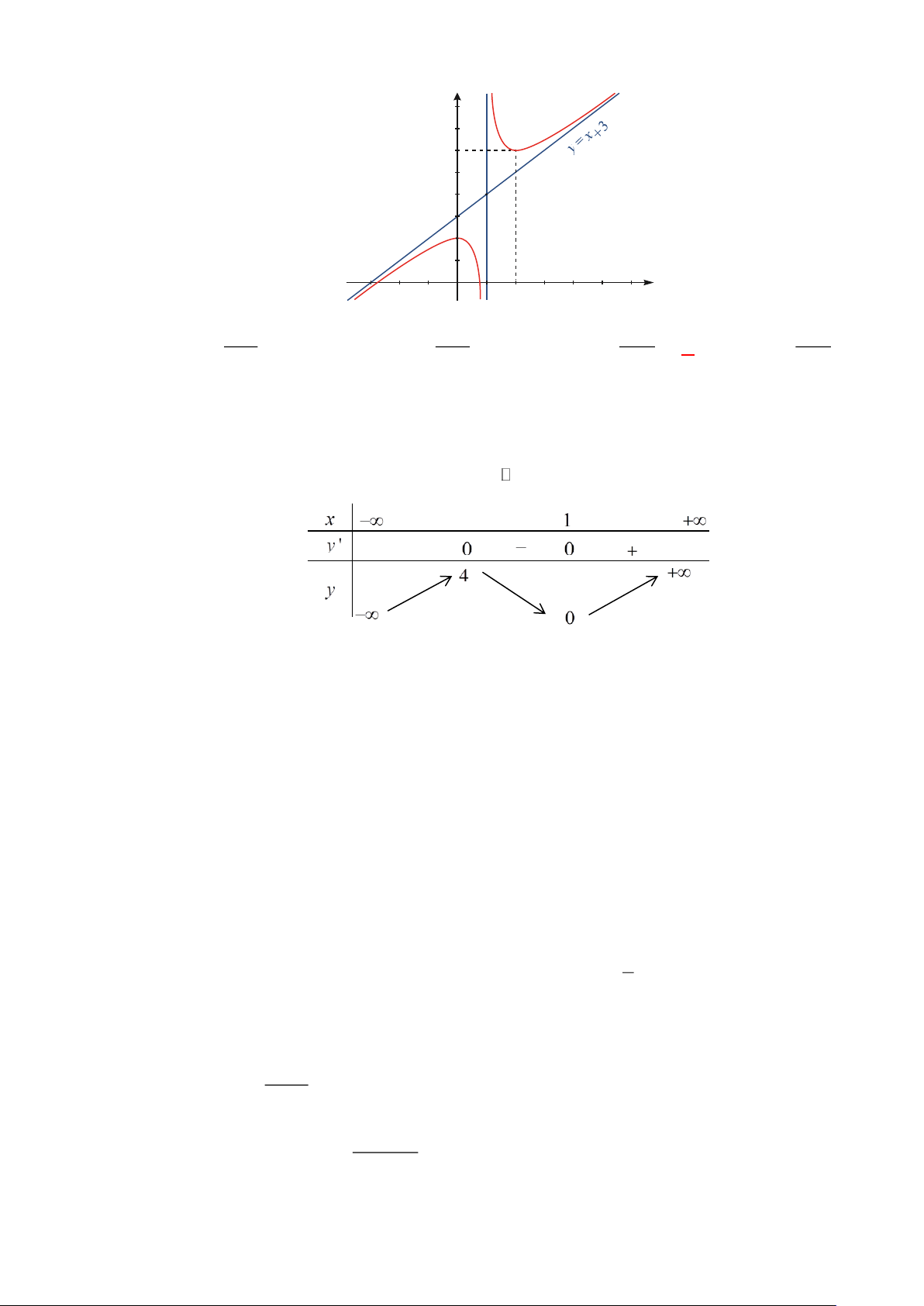
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào? Trang 2 y 6 I 3 2 x = 1 1 –3 O 1 2 x 3 3 1 1
A. y = x + .
B. y = x + 3 + .
C. y = 3- x +
. D. y = x + 3+ . x +1 x +1 x - 1 x - 1
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng (Đ) hoặc sai (S) Câu 1: [Mức độ: Biết- Năng lực toán học: MH 2.1]
Cho hàm số y = f (x) xác định và liên tục trên  có bảng biến thiên như sau - 1 +
a) Hàm số nghịch biến trên khoảng ( 1 − ; ) 1 .
b) f (x)  0 với x  (− ;  − ) 1 (1;+) .
c) Giá trị cực đại của hàm số bằng 0.
d) Hàm số y = f (x) đạt cực tiểu tại x =1. Câu 2: [Mức độ: Hiểu- Năng lực toán học: TD2.3]
Cho hàm số y = f (x) 3 2 = x − 2x + 2.
a) Đạo hàm của hàm số trên là 2
f '(x) = 3x − 4 . x
b) Phương trình f '(x) = 0 có 2 nghiệm phân biệt.  4 
c) Hàm số y = f (x) 3 2
= x − 2x + 2 đồng biến trên khoảng −;  .  3 
d) Hàm số y = f (x) 3 2
= x − 2x + 2 có cực trị. Câu 3: [Mức độ: Hiểu- Năng lực toán học: GQ 2.1] x −1 Xét hàm số y = trên 0;  1 . 2x +1 3
a) Hàm số có đạo hàm y ' = ( . 2x + )2 1 b) y(0) =1. Trang 3 c) y (0) = 1 − . d) min y = 1 − . 0; 1 Câu 4: [ Mức độ: Hiểu- Năng lực toán học: GQ3.1] 1− 4x Cho hàm số y = . Khi đó: 2x −1 1− 4x 1 a) lim y = lim = . x→+ x→+ 2x −1 2 1− 4x 1
b) Đồ thị hàm số y =
có tiệm cận đứng là y = . 2x −1 2  1 
c) Giao điểm hai đường tiệm cận của đồ thị hàm số là ; −2   .  2 
d) Hình chữ nhật giới hạn bởi 2 tiệm cận của đồ thị và hai trục tọa độ có diện tích bằng 1.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: [Mức độ: Vận dụng - Năng lực toán học: MH1.1.]
Chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h) theo công thức: 16000 5 C(v) = +
v (0 < v £ 120) . Vận hành xe với tốc độ trung bình v (km/h) bằng bao nhiêu v 2
để tiết kiệm tiền xăng nhất? Câu 2: [Mức độ: Vận dụng - Năng lực toán học: MH3.1.]
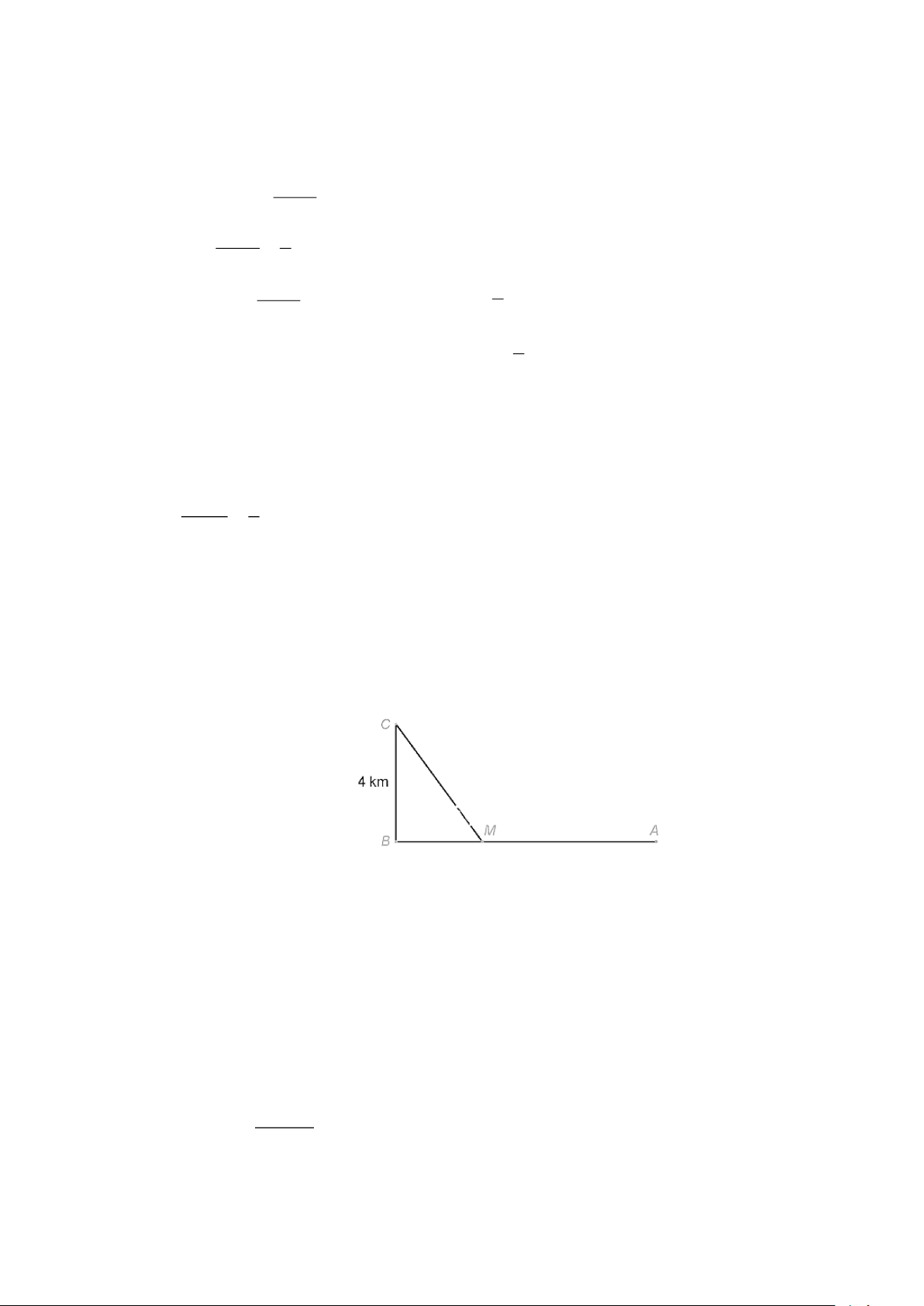
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như hình vẽ. Khoảng
cách từ C đến B là 4km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10km. Tổng chi phí
lắp đặt cho 1km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Điểm M
cách B trên đoạn AB (điểm nối dây từ đất liền ra đảo) một khoảng bằng a (đơn vị: km) để tổng chi
phí lắp đặt là nhỏ nhất. Hỏi a bằng bao nhiêu? Câu 3: [Mức độ: Vận dụng- Năng lực toán học: GQ3.1]
Một tên lửa bay vào không trung với quãng đường đi được s(t) (đơn vị: km) là hàm phụ thuộc
theo biến t ( đơn vị: giây) tuân theo biểu thức sau: s(t) 2 t +3 3t 1 e 2te + = + (km). Vận tốc của tên
lửa sau 1 giây là . n
m e (km/s). Tính tổng T = m + n (Biết hàm biểu thị vận tốc là đạo hàm cấp
một của hàm biểu thị quãng đường theo thời gian). Câu 4: [Mức độ: Vận dụng- Năng lực toán học: GQ 3.2]
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng
thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: ( ) 100t N t = 1000 +
(con), trong đó t (t  0) là thời gian tính bằng giây. Tính số lượng vi 2 100 + t
khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng. Câu 5: [Mức độ: Vận dụng- Năng lực toán học: MH 1.1]
Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng Trang 4
nhanh càng tốt, trên một bờ sông thẳng rộng 3 km (như
hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua
sông để đến C và sau đó chạy đến B , hay có thể chèo trực
tiếp đến B , hoặc anh ta có thể chèo thuyền đến một điểm
D giữa C và B rồi sau đó chạy đến B . Biết anh ấy có thể
chèo thuyền 6 km/ h , chạy 8 km/ h và quãng đường
BC = 8 km . Biết tốc độ của dòng nước là không đáng kể so
với tốc độ chèo thuyền của người đàn ông. Gọi t là khoảng thời gian ngắn nhất (làm tròn đến
đơn vị: phút) để người đàn ông đến B . Tính t. Câu 6: [Mức độ: Vận dụng- Năng lực toán học: GQ 3.1]
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C(x) = 5x + 50 C(x)
(triệu đồng). Khi đó f (x) =
là hàm số thể hiện chi phí sản xuất trung bình cho mỗi sản x
phẩm. Hãy cho biết khi sản xuất càng nhiều sản phẩm thì chi phí cho mỗi sản phẩm không vượt
quá n triệu đồng. Hỏi n bằng bao nhiêu? HẾT
ĐÁP ÁN + HƯỚNG DẪN GIẢI Câu hỏi Đáp án 1 B 2 A 3 A 4 B 5 C 6 B 7 B 8 A 9 B 10 A 11 B 12 D 1 DDSD 2 DDSD 3 DSSD 4 SSDD 1. 80 2. 3 3. 14 4. 1005 5. 80 6. 5 Trang 5 HƯỚNG DẪN GIẢI Câu 1:
[Mức độ: Vận dụng - Năng lực toán học: MH1.1.]
Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h) theo công thức: 16000 5 C(v) = + v
(0 < v £ 120) . Tài xế xe tải lái xe với tốc độ trung bình v là bao nhiêu để tiết v 2 kiệm tiền xăng nhất? HD Giải
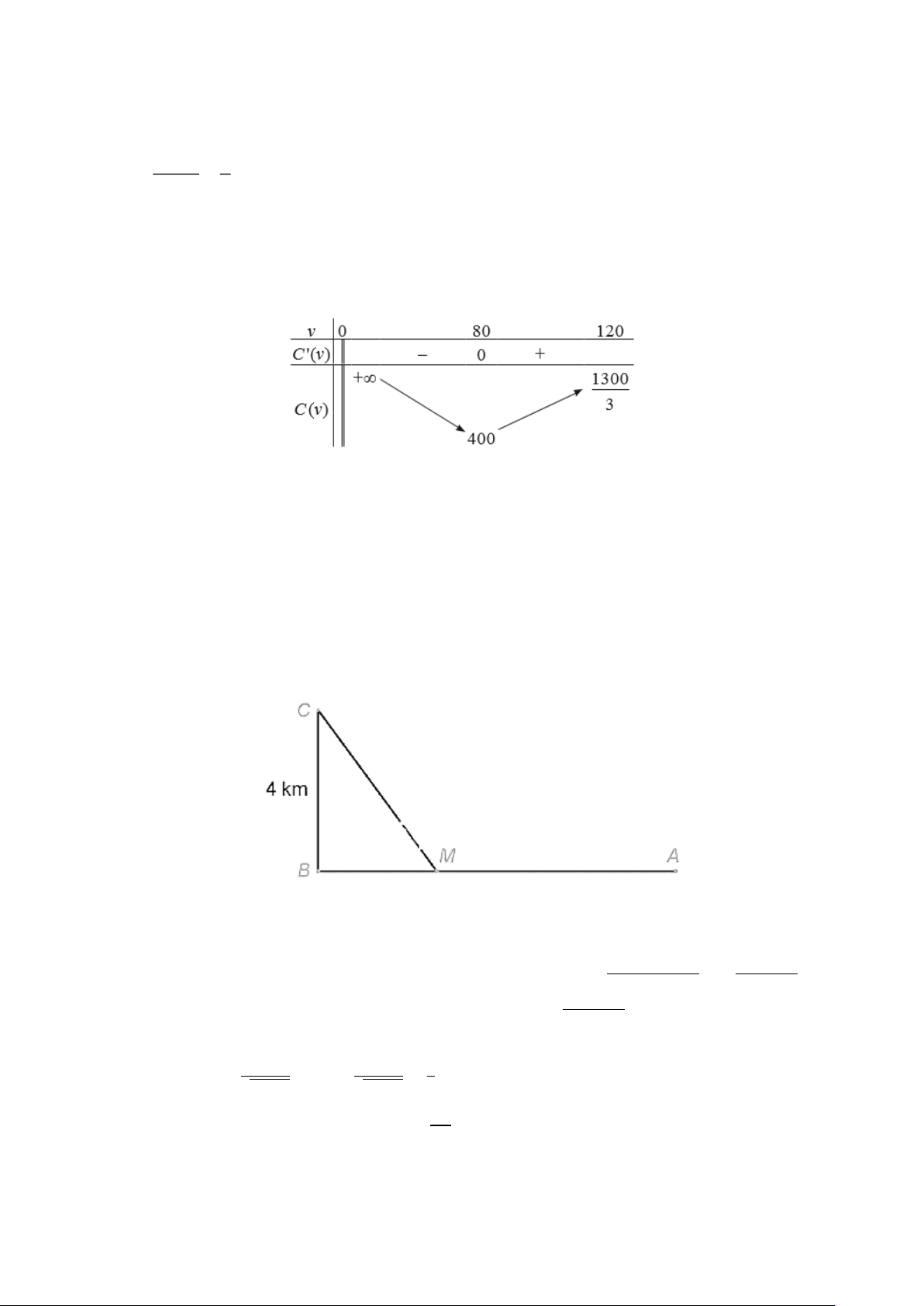
Tập xác định: D = (0; 120]. + Bảng biến thiên:
Quan sát BBT của hàm số, ta nhận thấy hàm số đạt GTNN khi v = 80 và GTNN là 400. Như vậy, để tiết
kiệm tiền xăng nhất, tài xế nên chạy xe với tốc độ trung bình là 80 km/h. Câu 2: [Mức độ: Vận dụng - Năng lực toán học: MH3.1.]
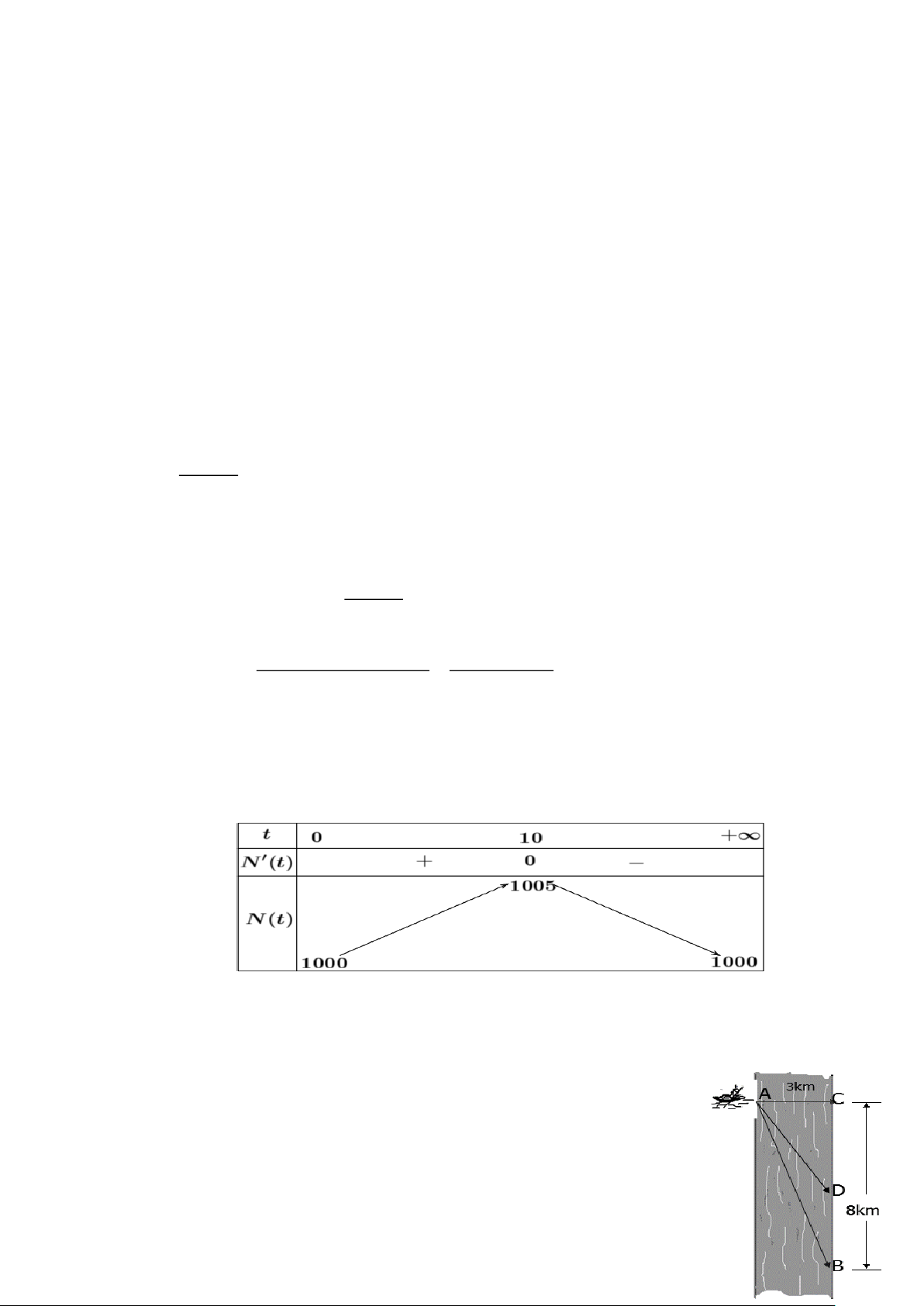
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình vẽ. Khoảng cách
từ C đến B là 4km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10km. Tổng chi phí lắp đặt cho
1km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Điểm M cách B trên đoạn AB
(điểm nối dây từ đất liền ra đảo) một khoảng bao nhiêu km để tổng chi phí lắp đặt là nhỏ nhất. HD Giải
Đặt 𝑀𝐵 = 𝑥(𝑘𝑚, 0 ≤ 𝑥 ≤ 10), khi đó, 𝐴𝑀 = 10 − 𝑥( km) và 𝑀𝐶 = √𝑀𝐵2 + 𝐶𝐵2 = √𝑥2 + 16( km)
Khi đó, chi phí nối điện từ A đến C là: 𝑓(𝑥) = 30(10 − 𝑥) + 50√𝑥2 + 16 (triệu đồng)
Ta có: 𝑓′(𝑥) = −30 + 50𝑥 = 0 ⇔ 𝑥
= 3 ⇔ 25𝑥2 = 9𝑥2 + 144 ⇔ 𝑥 = 3 (do 0 ≤ 𝑥 ≤ 10 ) √𝑥2+16 √𝑥2+16 5
Ta có: 𝑓(0) = 500; 𝑓(3) = 460, 𝑓(10) = 100√29 nên chi phí nhỏ nhất là 460 triệu đồng khi 𝑥 = 3
Vậy 𝑀 cách 𝐵 một khoảng a = 3 (km) trên đoạn 𝐴𝐵 (điểm nối dây từ đất liền ra đảo) thì tổng chi phí lắp đặt là nhỏ nhất. Trang 6 Câu 3: [Mức độ: Vận dụng- Năng lực toán học: GQ3.1]
Một tên lửa bay vào không trung với quãng đường đi được là s(t) (km) là hàm phụ thuộc theo biến t
(giây) tuân theo biểu thức sau: s(t) 2 t +3 3t 1 e 2te + = +
(km). Vận tốc của tên lửa sau 1 giây là . n m e (km/s).
Tính T = m + n (Biết hàm biểu thị vận tốc là đạo hàm cấp một của hàm biểu thị quãng đường theo thời gian)? HD Giải
Ta có: v(t) = s (t) 2 t +3 3t 1 + 3t 1 = te + e + te +   v( ) 4 4 4 4 2 2 6
1 = 2e + 2e + 6e = 10e (km/s) m = 10 Vậy 
 T = m + n = 10 + 4 = 14 n = 4 Câu 4: [Mức độ: Vận dụng- Năng lực toán học: GQ 3.2]
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm,
người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: ( ) 100t N t = 1000 +
(con), trong đó t là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ 2 100 + t
khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng. HD Giải 100t
Xét hàm số N (t) = 1000 + t  0 . 2 ( ) 100 + t 100.( 2
100 + t ) −100t.2t 100.( 2 100 − t )
Ta có: N(t) = ( = . 100 + t )2 (100+t )2 2 2 Khi đó, với t  N(t) 2 2 0,
= 0 100 − t = 0  t =100  t =10 .
Bảng biến thiên của hàm số N (t) như sau:
Căn cứ bảng biến thiên, ta thấy:
Trên khoảng (0;+) hàm số N (t) đạt giá trị lớn nhất bằng 1005 tại t =10.
Vậy số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi
trường dinh dưỡng là 1005 con. Câu 5:
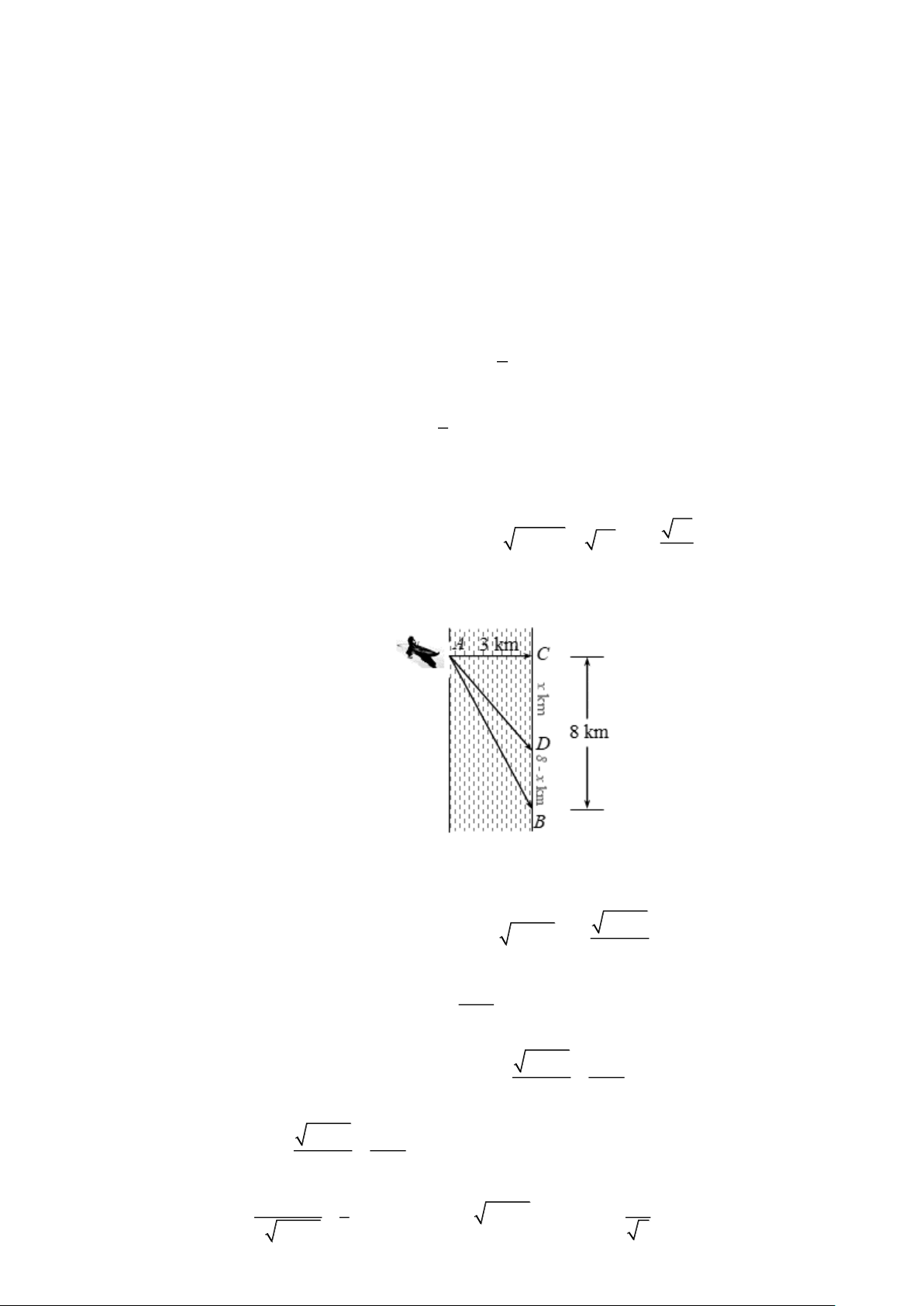
[Mức độ: Vận dụng- Năng lực toán học: MH 1.1]
Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối
diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3 km (như hình vẽ). Anh có Trang 7
thể chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp đến B
, hoặc anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết anh ấy có thể
chèo thuyền 6 km/ h , chạy 8 km/ h và quãng đường BC = 8 km . Biết tốc độ của dòng nước là không đáng kể
so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất (làm tròn đến đơn vị: phút) để
người đàn ông đến B . HD Giải
 TH 1: Anh chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B 3
Thời gian chèo thuyền trên quãng đường AC : = 0,5 (giờ) 6 8
Thời gian chạy trên quãng đường CB : = 1 (giờ) 8
Tổng thời gian di chuyển từ A đến B là 1,5 (giờ) = 90 phút 73
 TH 2: chèo trực tiếp trên quãng đường 2 2 AB = 3 +8 = 73 mất h 1 26 = 86 phút 6  TH 3:
Gọi x (km) là độ dài quãng đường DC ; 8− x (km) là độ dài quãng đường BD . 2 x + 9
Thời gian chèo thuyền trên quãng đường 2 AD = x + 9 là: (giờ) 6 8 − x
Thời gian chạy trên quãng đường DB là: (giờ) 8 2 x + 9 8 − x
Tổng thời gian di chuyển từ A đến B là f ( x) = + 6 8 2 x + 9 8 − x
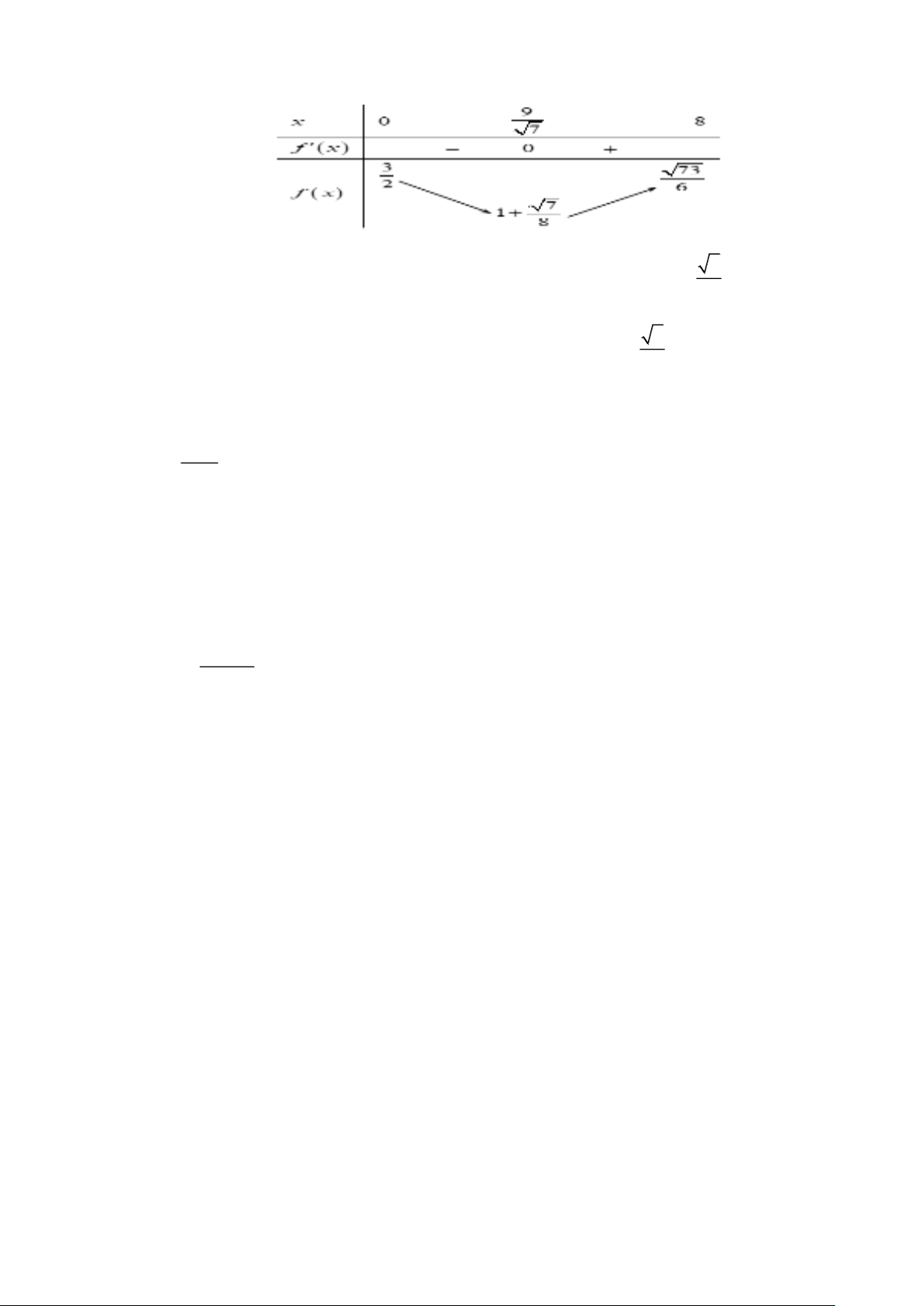
Xét hàm số f ( x) = + trên khoảng (0; 8) 6 8 x 1 9
Ta có f ( x) = − ; f (x) 2
= 0  3 x + 9 = 4x  x = 2 6 x + 9 8 7 Trang 8 Bảng biến thiên 7
Dựa vào BBT ta thấy thời gian ngắn nhất để di chuyển từ A đến B là h 1+ 1 20 = 80 phút 8 7
Vậy khoảng thời gian ngắn nhất để người đàn ông đến B là t = h 1+ 1 20 = 80 phút 8 Câu 6: [Mức độ: Vận dụng- Năng lực toán học: GQ 3.1]
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C(x)=5x+50 (triệu đồng). C(x) Khi đó f (x) =
là hàm số thể hiện chi phí sản xuất trung bình cho mỗi sản phẩm. Hãy cho biết khi x
sản xuất càng nhiều sản phẩm thì chi phí cho mỗi sản phẩm không vượt quá n triệu đồng? Hỏi n bằng bao nhiêu? Đáp số: n=5 HD Giải  5x + 50  lim f (x) = lim = 5   x→+ x→+  x  Vậy : n=5.
---------HẾT---------- Trang 9