Đề kiểm tra giữa học kì 1 Toán 9 năm 2021 – 2022 trường THCS Tô Hoàng – Hà Nội

Đề kiểm tra giữa học kì 1 Toán 9 năm 2021 – 2022 trường THCS Tô Hoàng – Hà Nội gồm 05 câu tự luận, thời gian làm bài 90 phút (không kể thời gian phát đề), kỳ thi được diễn ra vào thứ Tư ngày 03 tháng 11 năm 2021, đề thi có lời giải chi tiết và thang chấm điểm. Mời bạn đọc đón xem.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

5 trang 7 tháng trước

Tác giả:

Profile Hà Việt Anh
ĐỀ KIỂM TRA GIỮA KỲ I – NĂM HỌC 2021-2022
MÔN TOÁN 9
Ngày kiểm tra: 03/11/2021
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Bài 1 (2,0 điểm) Thực hiện phép tính.
a/
5 48 4 27 2 75 108− − +
b/
1
3 8 18 5 50 .3 2
2

− + +



c/
( ) ( )
( )
2
2
2 3 3 2 3+ − − −
d/
1 6 2
5 2 6
2 3 3 1
−
− − −
−−
Bài 2 (2,0 điểm) Giải phương trình
a/
5 2 5 3x− + =
b/
1
4 8 16 32 9 18 21
2
x x x− + − + − =
c/
2
3 6 9 1x x x+ − + =
d/
( )( )
2 3 2 3 1x x x x− − + − = − +
Bài 3(2,0 điểm)
Cho biểu thức
và
x2
Q
x2
+
=
−
với
0; 4xx
a/ Tính giá trị biểu thức Q khi
9x =
b/ Rút gọn P
c/ Cho
P
M
Q
=
. Tìm tất cả các giá trị nguyên của x để
1
M
2
Bài 4 (3,5 điểm)
1/ Để đo chiều rộng AB của một khúc sông mà
không đo trực tiếp được, một người đi từ A đến C đo
được AC = 50m và từ C nhìn thấy B với một góc
nghiệng 62
o
với bờ sông (như hình vẽ). Tính chiều rộng
AB của khúc sông (làm tròn đến mét)
2/ Cho tam giác ABC vuông tại A ( AB > AC) có
đường cao AH. Gọi AD là tia phân giác của
HAB
a/Tính các cạnh AH, AC biết HB = 18cm, HC = 8cm
b/ Chứng minh
ADC
cân tại C và
DH AH AC
BD AB BC
==
c/ Gọi E, F lần lượt là hình chiếu của H trên AB và AC.
Chứng minh
( )
22
AEF ABC
S S 1 cos B .sin C=−
Bài 5 (0,5 điểm)
Cho 3 số dương a, b, c. Chứng minh rằng:
3 3 3
abc
a ac b ba c cb
b c a
+ + + +
----- Chúc các em làm bài thi tốt -----
TRƯỜNG THCS TÔ HOÀNG
HƯỚNG DẪN CHẤM
ĐỀ KIỂM TRA GIỮA KỲ I – NĂM HỌC 2021-2022
MÔN TOÁN 9
Ngày kiểm tra: 03/11/2021
Bài 1: (2,0 điểm)
Thực hiện phép tính
2,0
a/
5 48 4 27 2 75 108 20 3 12 3 10 3 6 3 4 3− − + = − − + =
0,5
b/
1
3 8 18 5 50 .3 2 9 16 3 36 15 3 100 36 8 15 30 63
2

− + + = − + + = − + + =



0,5
c/
( ) ( )
( )
( )
2
2
2 3 3 2 3 2 3 3 2 3 4 3 3 2+ − − − = + − − = − − = −
0,5
d/
1 6 2
5 2 6
2 3 3 1
−
− − −
−−
( )
( )
2
2 3 1
23
3 2 2 3 2 3 2
43
31
2 3 2 3 2 2
−
+
= − − − = + − − −
−
−
= + − − + =
0.5
Bài 2 (2,0 điểm) Giải phương trình
a/
5 2 5 3x− + =
ĐK:
5
2
x
−
0,5
2,0
1
2 5 2 2 5 4 ( d )
2
x x x tm k
−
+ = + = =
KL:
b/
1
4 8 16 32 9 18 21 XD: 2
2
x x x DK x− + − + − =
2 2 2 2 3 2 21
7 2 21 2 3 2 9 11( / )
x x x
x x x x t mdk
− + − + − =
− = − = − = =
KL….
0,5
c/
( )
2
2
3 6 9 1 3 3 1 0x x x x x+ − + = − + − =
ĐKXĐ:
xR
3 3 1 0xx − + − =
(1)
+ Nếu
3x
ta có
(1) 3 3 1 0 4 4 1( )x x x x khtm loai − + − = = =
+ Nếu
3x
ta có
(1) 3 3 1 0 2 2 1 ( / )x x x x t mdk − + + − = = − = −
Vậy nhiệm của PT là x = -1
0,5
d/
( )( )
2 3 2 3 1x x x x− − + − = − +
ĐKXĐ:
3x
0.5
( )( )
( ) ( )
( )( )
2 3 2 3 1
2 3 1 3 1 0
3 1 2 1 0 2 1 ( 3 1 0)
3( / )
x x x x
x x x
x x x vi x
x t mdk
− − + − = − +
− − + − − + =
− + − − = − = − +
=
KL:…..
Bài 3: (2,0 điểm)
a. Tính giá trị của biểu thức
2
2
x
Q
x
+
=
−
khi x = 9
0; 4xx
0,5
0,5
Thay x = 9(t/m đkxđ) vào Q ta được
9 2 3 2 5
5
3 2 1
92
Q
++
= = = =
−
−
KL:…..
b. Rút gọn biểu thức
2
4
22
x x x x
P
x
xx
−
= + −
−
−+
1,0
( )( )
22
4
2 2 2 2
22
x x x x x x x x
P
x
x x x x
xx
−−
= + − = + −
−
− + − +
−+
ĐK
0; 4xx
0,25
( )
( )( )
( )
( )( ) ( )( )
22
2
2 2 2 2 2 2
x x x x
xx
x x x x x x
+−
−
= + −
− + − + − +
0,25
( )( ) ( )( )
( )
( )( )
2
2 2 2 2
2
2 2 2 2 2 2
xx
x x x x x x x x x
x
x x x x x x
+
+ + − − + +
= = = =
−
− + − + − +
0, 5
c/ Cho
P
M
Q
=
. Tìm tất cả các giá trị nguyên của x để
1
M
2
0,5
:M P Q=
=
2
x
x −
:
2
2
x
x
+
−
=
2
x
x +
0,25
( )
1 1 2 2 2
0 0 0 2( 2 0) 4
22
2 2( 2)
22
x x x x
M x Vi x x
xx
x
− − −
− +
++
+
Kết hợp với đkxđ
04x
vì x nguyên nên
0;1;2;3x
0,25
Bài 4 (3,5 điểm)
1/Xét ABC vuông tại B, có:
0
.tan 50.tan62 94( )AB AC C m= =
Vậy khoảng cách AB là 94m
0,5
Vẽ hình đúng đến câu a: 0,25
điểm
1,25
a/Tính AH, AC
Tính được HA = 12 cm 0,5
Tính được
208 4 13AC cm==
0,5
b/Chứng minh
ADC
cân tại C và
DH AH AC
BD AB BC
==
0,5
1,25
+ Chứng minh:
ADC
cân.
00
ˆ ˆ ˆ ˆ
ˆˆ
90 ; 90CAD BAD ADC DAH DAC ADC+ = + = =
Chứng minh:
DH AH AC
BD AB BC
==
0,25
0,25
0,25
Áp dụng tính chất tia phân giác của tam giác BAH , ta có:
DH AH
BD AB
=
Chứng minh:
(g.g)
AH AC
AHC BAC
AB BC
=
Suy ra
DH AH AC
BD AB BC
==
c/Chứng minh:
( )
22
1 cos .sin
AEF ABC
S S B C=−
0,5
Chứng minh AE.AB = AF. AC
(c.g.c)AEF ACB
2
22
22
EF EF
AEF
ACB
S
AH
S BC BC BC

= = =


Xét tam giác ABC vuông tại A có
( )
2 2 2 2 2
2 2 2 2
2 2 4 2
sin ;sin
.
1 os sin .sin .
AC AB
BC
BC BC
AC AB AH BC AH
c B C Sin B C
BC BC BC BC
==
− = = = =
Mà
( )
2
2 2 2 2
2
sin .sin 1 os sin
AEF AEF
AEF ACB
ACB ACB
SS
AH
B C S S c B C
S BC S
= = = −
0,5
Bài 5: (0,5 điểm)
Cho 3 số dương a, b, c. Chứng minh rằng:
3 3 3
abc
a ac b ba c cb
b c a
+ + + +
0,5
Áp dụng bất đẳng thức cosi cho 3 số dương ta có
3 3 3 3
2 2 2
3
3 . . 3
a a a a
b b a
b b b b
+ + =
Tương tự
33
22
3
bb
cb
cc
+ + =
;
33
22
3
cc
ac
aa
+ +
3 3 3
2 2 2
abc
abc
b c a
+ + + +
Dễ chứng minh được:
2 2 2
a b c ab bc ca+ + + +
( ) ( ) ( )
2 2 2
2 2 2
22
a a b b b c c c a
a b c ab bc ca
abc
+ + + + +
+ + + + +
+ + =
(2)
Lại áp dụng bđt cosi ta có
( ) ( ) ( )
2
a a b b b c c c a
a ac b ba c cb
+ + + + +
+ +
(3)
Từ (1), (2), (3) suy ra điều phải chứng minh
Dấu bằng sảy ra khi a = b = c
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THCS TÔ HOÀNG
ĐỀ KIỂM TRA GIỮA KỲ I – NĂM HỌC 2021-2022 MÔN TOÁN 9 Ngày kiểm tra: 03/11/2021
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Bài 1 (2,0 điểm) Thực hiện phép tính.  1 
a/ 5 48 − 4 27 − 2 75 + 108 b/ 3 8 − 18 + 5 + 50 .3 2   2   2 1 6 − 2 c/ ( + ) ( − ) − (− )2 2 3 3 2 3 d/ − − 5 − 2 6 2 − 3 3 −1
Bài 2 (2,0 điểm) Giải phương trình 1 a/ 5 − 2x + 5 = 3 b/ 4x −8 +
16x − 32 + 9x −18 = 21 2 c/ 2
3x + x − 6x + 9 = 1
d/ (x − 2)(x − ) 3 + x − 2 = x − 3 +1
Bài 3(2,0 điểm) x x x − 2 x x + 2 Cho biểu thức P = + − và Q =
với x  0; x  4 x − 2 x + 2 x − 4 x − 2
a/ Tính giá trị biểu thức Q khi x = 9 b/ Rút gọn P P 1 c/ Cho M =
. Tìm tất cả các giá trị nguyên của x để M  Q 2
Bài 4 (3,5 điểm)
1/ Để đo chiều rộng AB của một khúc sông mà
không đo trực tiếp được, một người đi từ A đến C đo
được AC = 50m và từ C nhìn thấy B với một góc
nghiệng 62o với bờ sông (như hình vẽ). Tính chiều rộng
AB của khúc sông (làm tròn đến mét)
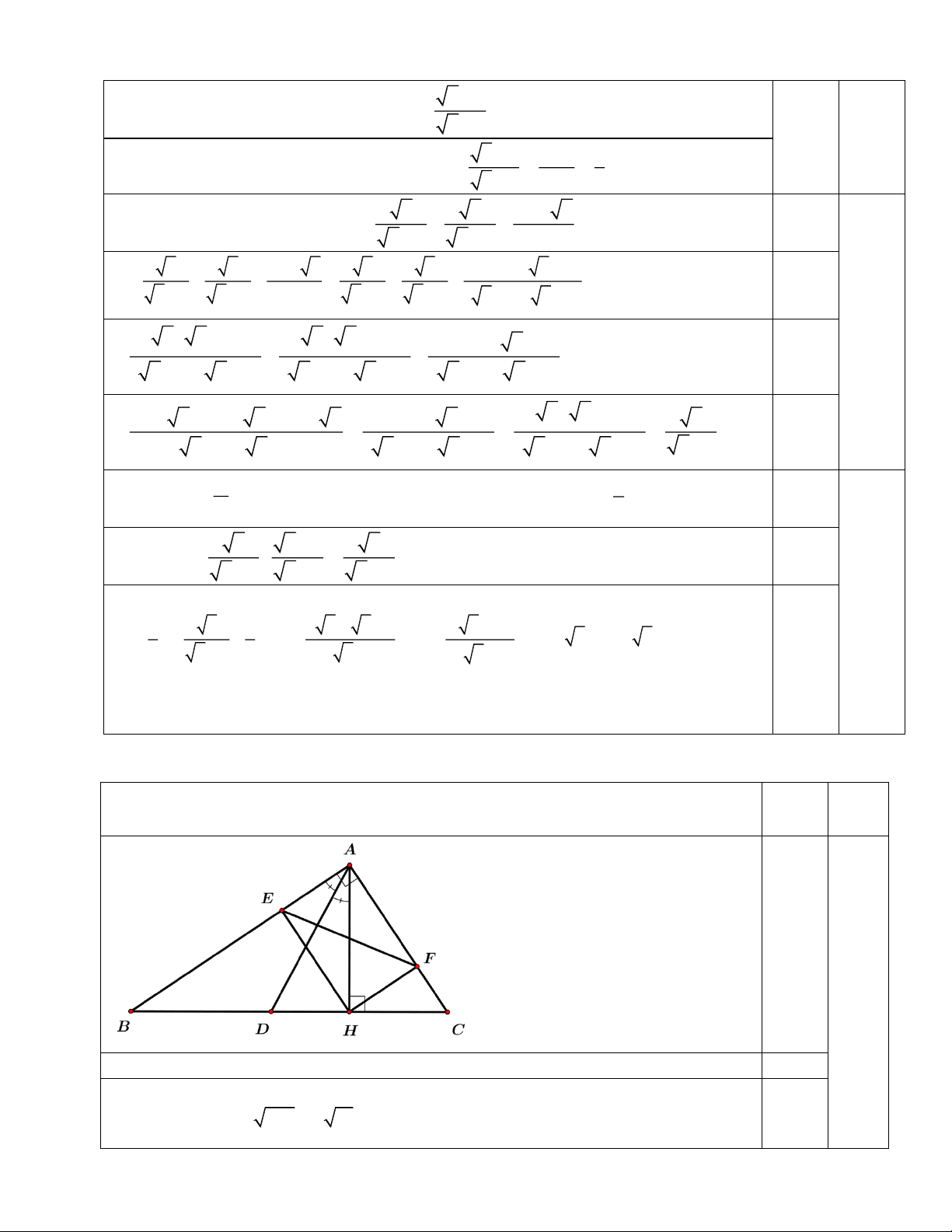
2/ Cho tam giác ABC vuông tại A ( AB > AC) có
đường cao AH. Gọi AD là tia phân giác của HAB
a/Tính các cạnh AH, AC biết HB = 18cm, HC = 8cm DH AH AC b/ Chứng minh A
DC cân tại C và = = BD AB BC
c/ Gọi E, F lần lượt là hình chiếu của H trên AB và AC. Chứng minhS = S ( 2 1− cos B) 2 .sin C AEF ABC
Bài 5 (0,5 điểm) 3 3 3 a b c
Cho 3 số dương a, b, c. Chứng minh rằng: + +
a ac + b ba + c cb b c a
----- Chúc các em làm bài thi tốt ----- HƯỚNG DẪN CHẤM
ĐỀ KIỂM TRA GIỮA KỲ I – NĂM HỌC 2021-2022 MÔN TOÁN 9 Ngày kiểm tra: 03/11/2021
Bài 1: (2,0 điểm)
Thực hiện phép tính
a/ 5 48 − 4 27 − 2 75 + 108 = 20 3 −12 3 −10 3 + 6 3 = 4 3 0,5  1  0,5 b/ 3 8 − 18 + 5
+ 50 .3 2 = 9 16 −3 36 +15 + 3 100 = 36 −8 +15 + 30= 63   2   2 2 c/ (2 + 3) ( 3 − 2) − ( 3
− ) = (2 + 3) 3 − 2 −3 = 4 −3−3 = 2 − 0,5 1 6 − 2 2,0 d/ − − 5 − 2 6 2 − 3 3 −1 2 ( 3 − + )1 2 3 0.5 = −
− ( 3 − 2)2 = 2+ 3 − 2 − 3 − 2 4 − 3 3 −1 = 2 + 3 − 2 − 3 + 2 = 2
Bài 2 (2,0 điểm) Giải phương trình −
a/ 5 − 2x + 5 = 3 ĐK: 5 x  2 0,5 1 −
 2x + 5 = 2  2x + 5 = 4  x = (t d m k) KL: 2 1 b/ 4x −8 +
16x − 32 + 9x −18 = 21 D X K D : x  2 2
 2 x − 2 + 2 x − 2 + 3 x − 2 = 21 0,5
 7 x − 2 = 21  x − 2 = 3  x − 2 = 9  x = 11(t / mdk) KL….
c/ x + x − x + =  ( x − )2 2 3 6 9 1 3
+ 3x −1 = 0 ĐKXĐ: xR
x −3 + 3x −1= 0(1) 0,5
+ Nếu x  3 ta có (1)  x − 3 + 3x −1 = 0  4x = 4  x = 1(khtm loai) 2,0
+ Nếu x  3 ta có (1)  −x + 3 + 3x −1 = 0  2x = 2 −  x = 1 − (t / mdk)
Vậy nhiệm của PT là x = -1
d/ (x − 2)(x − ) 3 + x − 2 =
x − 3 +1 ĐKXĐ: x  3
(x − 2)(x −3) + x − 2 = x −3 +1
x − 2 ( x −3 + ) 1 − ( x − 3 + ) 1 = 0 0.5  ( x −3 + ) 1 ( x − 2 − ) 1 = 0 
x − 2 = 1 (vi x − 3 +1  0)
x = 3(t / mdk) KL:…..
Bài 3: (2,0 điểm) x + 2
a. Tính giá trị của biểu thức Q =
khi x = 9 x  0; x  4 x − 2 0,5 0,5 9 + 2 3 + 2 5
Thay x = 9(t/m đkxđ) vào Q ta được Q = = = = 5 KL:….. 9 − 2 3 − 2 1 x x x − 2 x
b. Rút gọn biểu thức P = + − x − 2 x + 2 x − 4 x x x − 2 x x x x − 2 x P = + − = + −
ĐK x  0; x  4 0,25 x − 2 x + 2 x − 4 x − 2 x + 2 ( x −2)( x +2) + − 1,0 x ( x 2) x ( x 2) x − 2 x = ( + − 0,25
x − 2)( x + 2) ( x − 2)( x + 2) ( x − 2)( x + 2) x + x + x + x − x − x + x x + x ( x 2 2 2 2 2 ) x = ( = = = 0, 5 x − 2)( x + 2)
( x −2)( x +2) ( x −2)( x +2) x −2 P 1 c/ Cho M =
. Tìm tất cả các giá trị nguyên của x để M  Q 2 x x + 2 x
M = P : Q = : = 0,25 x − 2 x − 2 x + 2 0,5 1 x 1 2 x − x − 2 x − 2 M   −  0   0 
  x Vi x +   x x + 2 2( x + 2) 2( x + 2) 0 2( 2 0) 4 2 2 0,25
Kết hợp với đkxđ  0  x  4 vì x nguyên nên x 0;1;2;  3
Bài 4 (3,5 điểm)
1/Xét ABC vuông tại B, có: 0
AB = AC. tan C = 50. tan 62  94(m) 0,5
Vậy khoảng cách AB là 94m
Vẽ hình đúng đến câu a: 0,25 điểm 1,25 a/Tính AH, AC Tính được HA = 12 cm 0,5
Tính được AC = 208 = 4 13cm 0,5 DH AH AC b/Chứng minh A
DC cân tại C và = = BD AB BC
+ Chứng minh: ADC cân. 0,5 0 0 ˆ ˆ ˆ ˆ ˆ ˆ
CAD + BAD = 90 ; ADC + DAH = 90  DAC = ADC DH AH AC Chứng minh: = = BD AB BC 1,25 DH AH 0,25
Áp dụng tính chất tia phân giác của tam giác BAH , ta có: = BD AB AH AC 0,25 Chứng minh: AHC BAC (g.g)  = AB BC DH AH AC 0,25 Suy ra = = BD AB BC
c/Chứng minh: S = S ( 2 − B) 2 1 cos .sin C AEF ABC
Chứng minh AE.AB = AF. AC  AEF ACB(c.g.c) 2 2 2 S  EF  EF AH AEF  = = =   2 2 SBC BC BC ACB
Xét tam giác ABC vuông tại A có AC AB = = 0,5 sin B ;sin C BC BC 0,5  ( AC AB AH BC AH 1− o c s B) 2 2 2 2 2 . 2 2 2 2 sin C = Sin . B sin C = . = = 2 2 4 2 BC BC BC BC 2 S AH S Mà AEF AEF 2 2 =  = sin .
B sin C S = S − c B C AEF ACB ( 2 1 os ) 2 sin 2 S BC S ACB ACB
Bài 5: (0,5 điểm)
Cho 3 số dương a, b, c. Chứng minh rằng: 3 3 3 a b c + + 
a ac + b ba + c cb b c a
Áp dụng bất đẳng thức cosi cho 3 số dương ta có 3 3 3 3 a a a a 2 2 2 3 + + b  3 . .b = 3a b b b b 3 3 3 3 Tương tự b b c c 2 2 + + c = 3b ; 2 2 + + a  3c c c a a 3 3 3 a b c 0,5 2 2 2 + +
a + b + c b c a Dễ chứng minh được: 2 2 2
a + b + c ab + bc + ca 2 2 2
a + b + c + ab + bc + ca
a a + b + b b + c + c c + a 2 2 2 ( ) ( ) ( )
a + b + c  = (2) 2 2
Lại áp dụng bđt cosi ta có
a (a + b) + b(b + c) + c (c + a)  a ac +b ba +c cb (3) 2
Từ (1), (2), (3) suy ra điều phải chứng minh
Dấu bằng sảy ra khi a = b = c