Đề kiểm tra giữa học kỳ 1 Toán 10 năm 2021 – 2022 sở GD&ĐT Bắc Ninh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 BẮC NINH
NĂM HỌC 2021 – 2022
Môn: TOÁN – Lớp 10
Thời gian làm bài: 90 phút (không kể thời gian giao đề) (Đề có 02 trang)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu 1. Cho mệnh đề P : " x   : 3x  5  0". Mệnh đề phủ định của mệnh đề P là
A. P : " x   : 3x  5  0".
B. P : " x   : 3x  5  0" .
C. P : " x   : 3x  5  0" .
D. P : " x   : 3x  5  0".
Câu 2. Tập hợp A  4;4 có tất cả bao nhiêu tập hợp con? A. 4 . B. 3 . C. 2 . D. 1.
Câu 3. Cho tập hợp B  1;2;3;4; 
5 và C  2;4;6;8. Khẳng định nào dưới đây là sai?
A. B C  2;4.
B. B \C  6;8.
C. B C  1;2;3;4;5;6;8.
D. C \ B  6;8.
Câu 4. Tập 3;12  0;    bằng A. 12;    .
B. 1;2;3;4;5;6;7;8;9;10;1  1 . C. 3;    . D. 0;12.
Câu 5. Tập xác định 2x  3
D của hàm số y  là 2 x  3x  2
A. D  1;2. B. D   ;   1  2;.  
C. D   \ 1;  2 . D. 3 D  \  ;1;2     .  2   
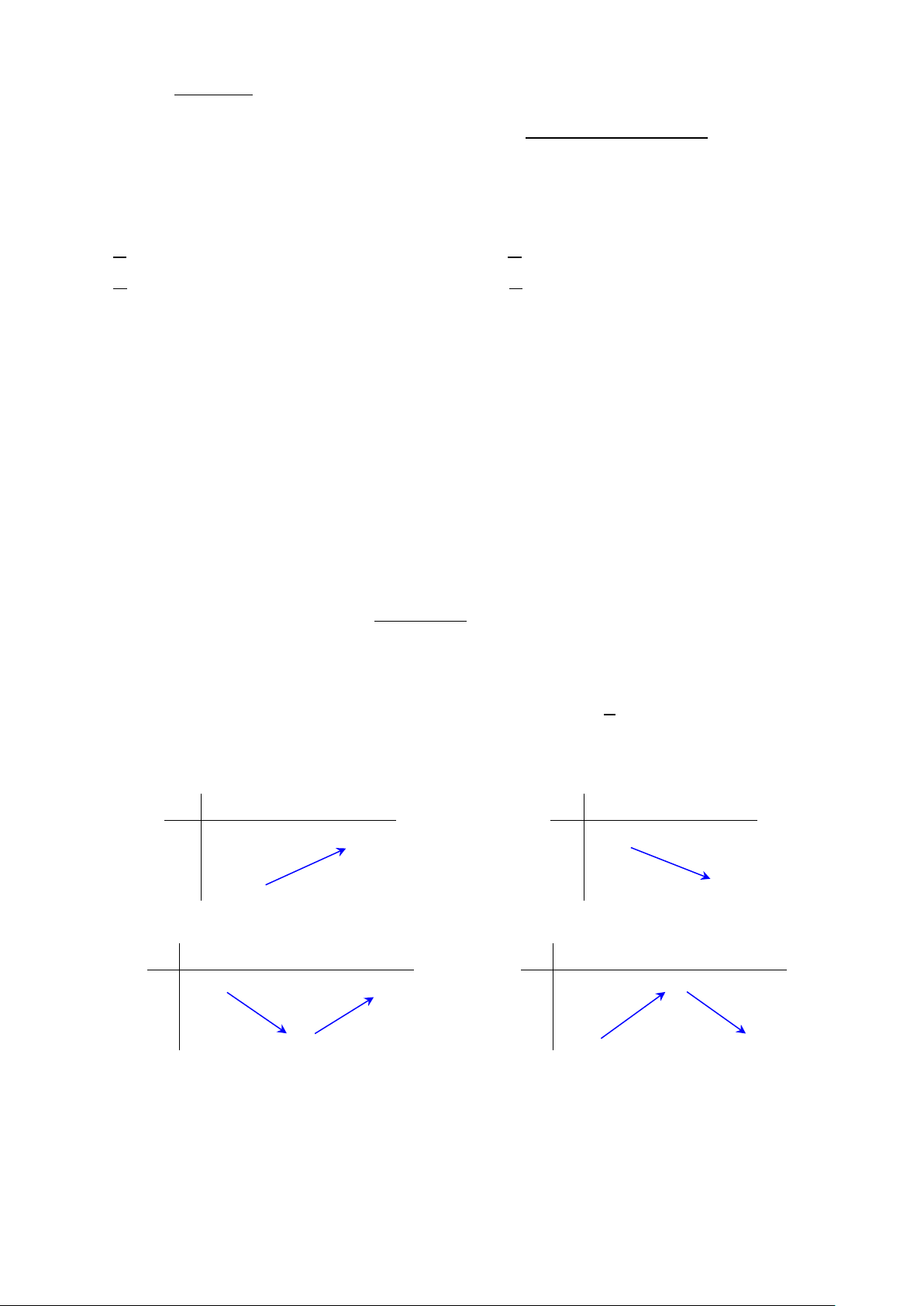
Câu 6. Hàm số y  3x  5 có bảng biến thiên là hình nào dưới đây? x   x     y y   Hình 1 Hình 2 x  0  x  0    0 y y   0 Hình 3 Hình 4 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. 
Câu 7. Vectơ đối của vectơ AB là   A. BA. B. BA  . C. AB  . D. BA  .
Câu 8. Cho ba điểm bất kỳ A , B , C . Khẳng định nào dưới đây là sai?           
A. AB  AC  CB .
B. BC  AC  AB .
C. AB  BC  AC .
D. AB  BA  .
Câu 9. Cho hình vuông ABCD có tâm là điểm O . Khẳng định nào dưới đây là đúng? A D O B C           
A. AB  AD  AO .
B. AB  DC  0 .
C. OA  OC .
D. DA  DC  DB .
Câu 10. Cho tam giác ABC có điểm M là trung điểm của BC . Khẳng định nào dưới đây là sai?    
A. AB  BC  AC .
B. AB  AC  2AM .    
C. AB  AC  AB  AC .
D. AB  AC  CB . 2
Câu 11. Để hàm số 3x  5 y 
có tập xác định là  thì giá trị của tham số m bằng mx  1 A. 1. B. 0 . C. 1. D. 3 .
Câu 12. Có bao nhiêu giá trị của m để đồ thị hai hàm số 4
y  m x  m và y  x  1 song song với nhau? A. 1. B. 2 . C. 0 . D. 4 .
PHẦN II. TỰ LUẬN (7,0 điểm) Câu 13. (2,0 điểm)
a) Xét tính chẵn, lẻ của hàm số y  f x 4  x  2 .
b) Tìm tập xác định của hàm số y  2x  7 . Câu 14. (2,0 điểm) Cho hàm số y    m 2 2021 2
x  m  2   1 (m là tham số).
a) Tìm tất cả các giá trị của tham số m để đồ thị hàm số  
1 đi qua điểm M 1;2026.
b) Tìm tập S gồm tất cả các giá trị nguyên dương của tham số m để hàm số   1 đồng biến trên . 
Tính tổng tất cả các phần tử của S . Câu 15. (2,5 điểm)
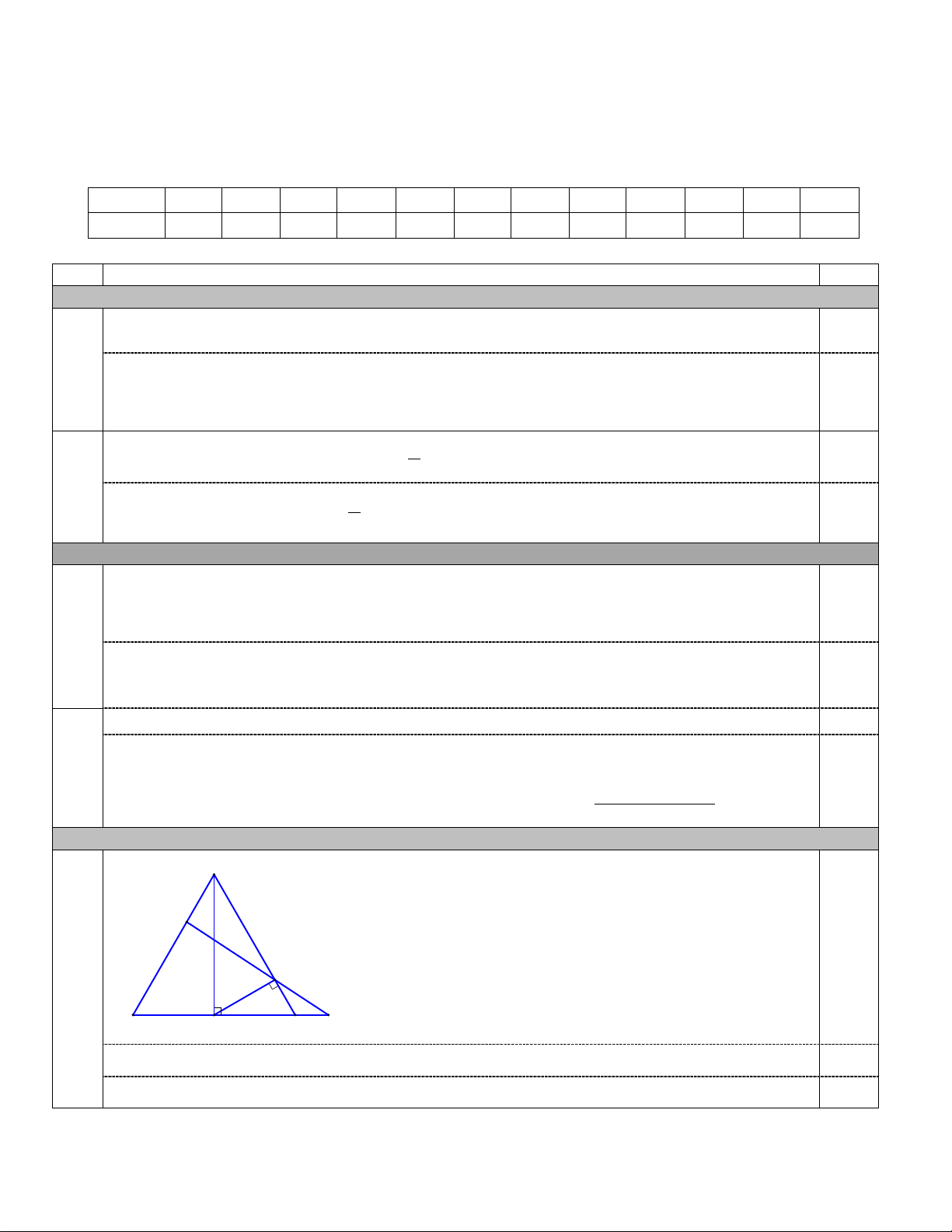
Cho tam giác ABC đều có cạnh bằng 6. Gọi H là trung điểm của đoạn thẳng BC , K là chân  
đường vuông góc kẻ từ điểm H lên AC . Điểm M thỏa mãn BM  2MA .    
a) Chứng minh BH CM  CH  BM .   
b) Tính BA  AC và AM .  
c) Gọi điểm F thỏa mãn BC  5FC . Chứng minh ba điểm M , K , F thẳng hàng. Câu 16. (0,5 điểm)
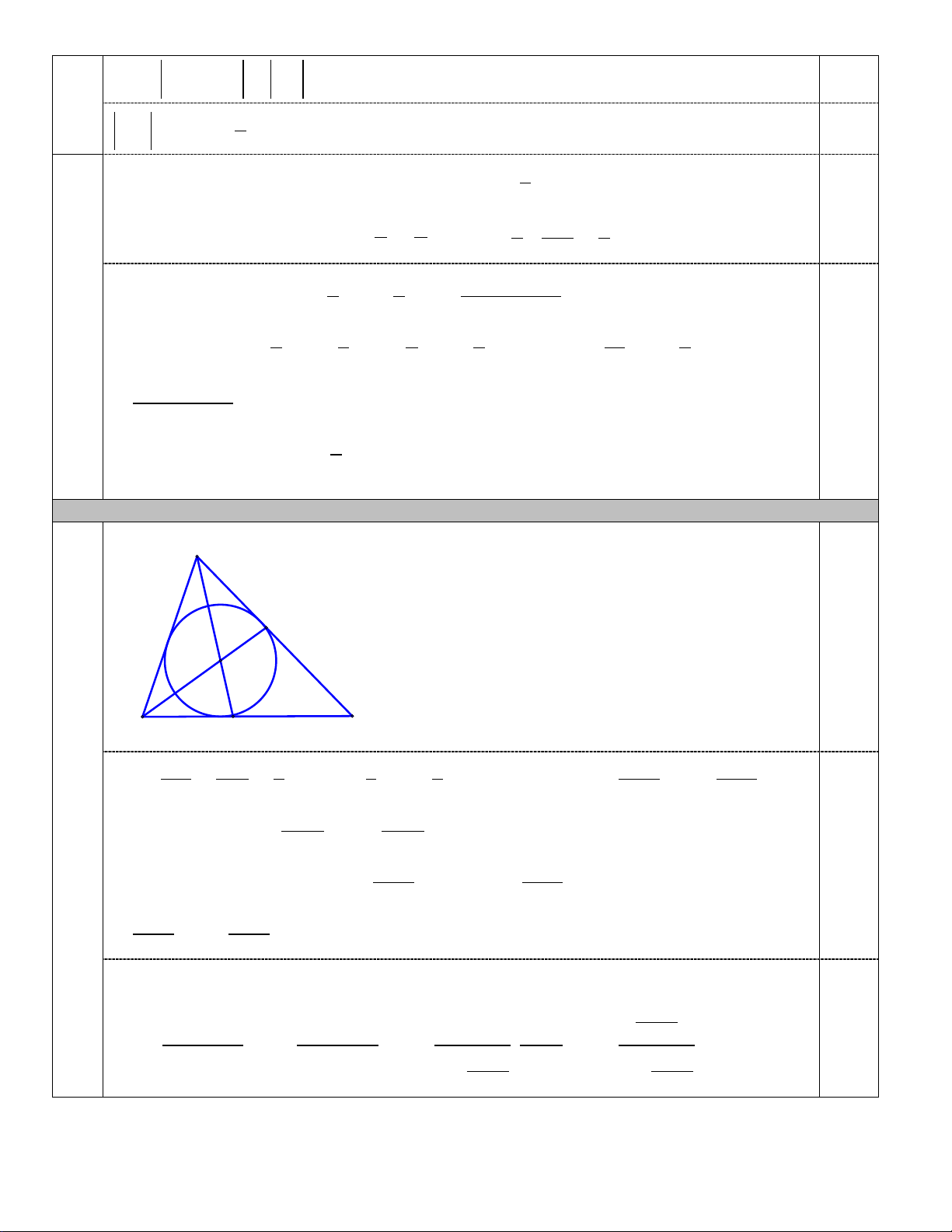
Cho tam giác ABC có BC  a , AC  b , AB  c . Gọi I là tâm đường tròn nội tiếp tam giác    
ABC . Chứng minh aIA  bIB  cIC  0 . -------- Hết --------
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
KIỂM TRA GIỮA HỌC KỲ 1 ¯¯¯¯¯¯¯¯¯¯
NĂM HỌC 2021 – 2022
Môn: Toán – Lớp 10
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B A B D C B A B D C B A
PHẦN II. TỰ LUẬN (7,0 điểm) Câu
Lời giải sơ lược Điểm 13. (2,0 điểm)
a) Tập xác định: D   .
* x  D  x   D . 0,5 * f  x     x  4 4
 2  x  2  f x. 0,5
Vậy hàm số f x là hàm số chẵn.
b) Điều kiện xác định 7
2x  7  0  x  0,5 2  
Tập xác định của hàm số 7 D  ;      . 0,5 2   14. (2,0 điểm)
a) Vì đồ thị hàm số  1 đi qua điểm M 1;2026 nên ta có phương trình  0,5  m 2 2 2021 2
.1  m  2  2026  m  2m  3  0 m   1  
. Vậy có hai giá trị của m thỏa mãn điều kiện đầu bài là m  1, m  3 . 0,5 m   3 
b) * Để hàm số đồng biến trên   2021  2m  0  m  1010,5 . 0,5
Do m nguyên dương nên tập hợp các giá trị m thỏa mãn là 1;2;3;...;  1010 . 10101  1010 0,5
Tổng tất cả các phần tử của tập hợp trên là 1  2  ...  1010   50550 . 2 15. (2,5 điểm) a) A M K B H C F        
BH CM  CH  BM  BH CH  BM CM 0,5  
 BC  BC (luôn đúng). Suy ra điều phải chứng minh. 0,5 b)   
Ta có BA  AC  BC  BC  6. 0,5  1
AM  AM  AB  2 . 0,5 3
c) Xét tam giác ABH vuông tại H có AB  6, 1
CH  BC  3 . 2 0,25 Ta có 2 9 3
CK.CA  CH  CK   9 AK  AK  , 3  . 6 2 2 AC 4        Ta có 3 1 9AC  4AB
MK  AK  AM  AC  AB   1, 4 3 12    1  1  1  1    
KF  KC CF  AC  BC  AC  AC AB 9 1  AC  AB 4 5 4 5 20 5   9AC  4AB 0,25  2. 20   Từ   1 và 2 suy ra 5
MK  KF . Vậy ba điểm M , K , F thẳng hàng. 3
(Nếu học sinh sử dụng định lý Menelaus để chứng minh mà đúng vẫn cho điểm tối đa) 16. (0,5 điểm) A
Gọi AE , BF lần lượt là đường phân F
giác trong góc A và góc B . Suy ra
AE  BF  I . I B E C Ta có BE AB c c c         c ac BE EC BC BE  BE  BC  . EC AC b b b b  c b  c Tương tự ta có c bc AF  AC  . a  c a  c         0,25 Suy ra c c
AE  AB  BE  AB  BC  AB  AC AB b  c b  c b  c   AB  AC   * . b  c b  c Từ   * suy ra bc  AB  AF  c c   0,25    . a  c AI AF AB AC  AB AB  AF AB  AF bc a  c bc c  c  a  c a  c  c  b   AI  AC  AB
a  b  c
a  b  c         
 a b cAI  cAC bAB  cAC AIbAB AIaAI  0    
 cIC  bIB  aIA  0 .
Suy ra điều phải chứng minh.
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 10
https://toanmath.com/de-thi-giua-hk1-toan-10
Document Outline

• Toan 10.KTGK.21.22.De
• Toan 10.KTGK.21.22.Da