

Preview text:
PHÒNG GD & ĐT QUẬN BA ĐÌNH
KIỂM TRA HỌC KÌ I MÔN TOÁN 7
TRƯỜNG THCS THÀNH CÔNG Năm học 2021 - 2022
Thời gian làm bài : 90 phút
Lưu ý: Học sinh làm bài ra giấy thi và không sử dụng máy tính
Bài 1. (2,5 điểm) Thực hiện phép tính 2 5 4 3 1 4 −2 4 4 − 3 1 36 3 3 a) − . b) + : c) − − + : 4 3 5 3 15 5 5 10 25 10 10
Bài 2. (2,0 điểm) Tìm x, biết: 2 7 − 1 5 3 4 1 a) x − = b) ( − ) 1 3x 4 . 5x + = 0 c) x − = : 2 3 2 2 5 3 3
Bài 3. (1,5 điểm)
Trong đợt tổng kết cuối năm, lớp 7A có số học sinh giỏi, khá, trung bình lần lượt tỉ lệ
với 6; 5; 2. Biết rằng tổng số học sinh giỏi và khá hơn số học sinh trung bình là 36 bạn. Tính
số học sinh mỗi loại của lớp 7A.
Bài 4. (3,5 điểm)
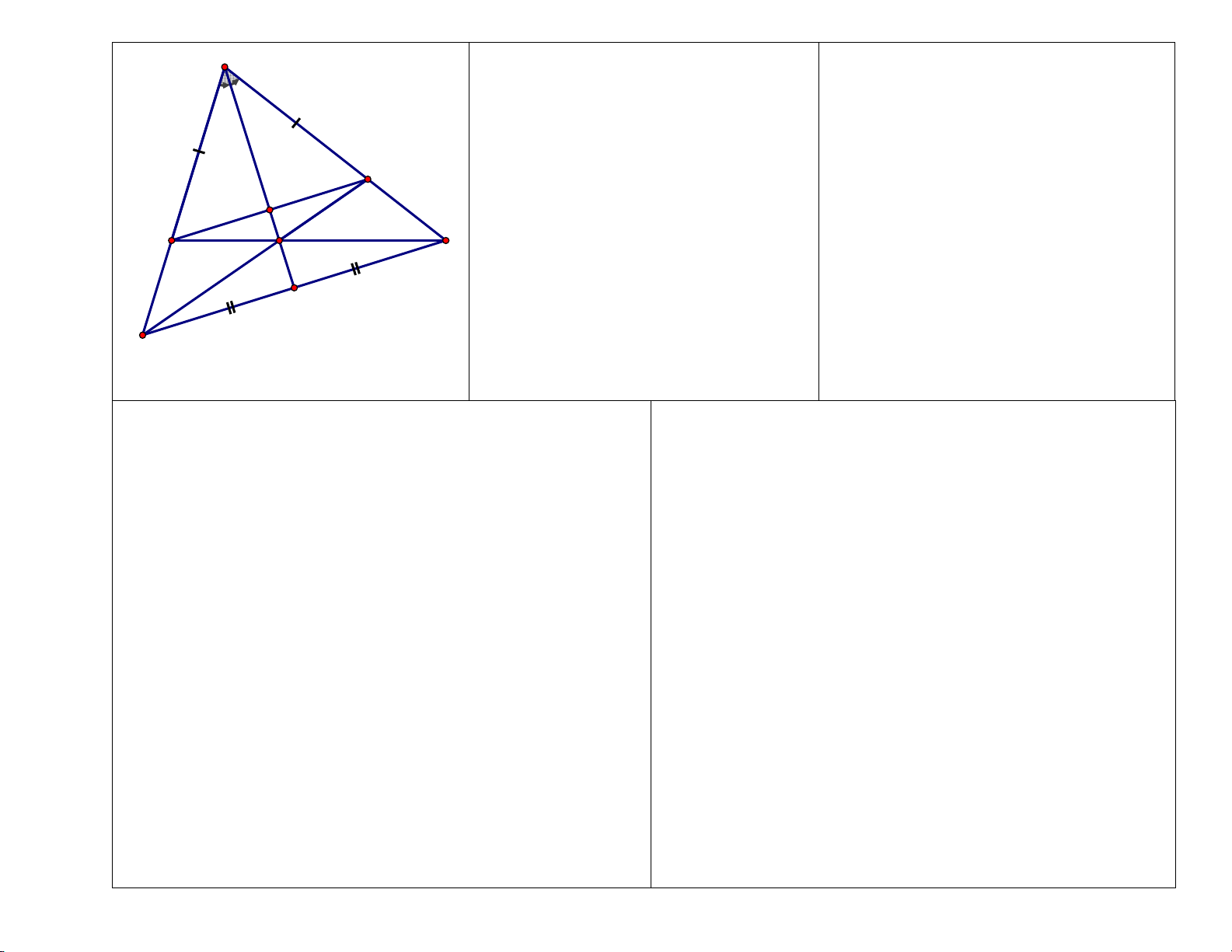
Cho tam giác ABC (AB < AC). Kẻ AM là tia phân giác của góc A (M thuộc BC). Trên
AC lấy điểm D sao cho AB = AD.
a) Chứng minh: ∆ABM = ∆ADM
b) Gọi I là giao điểm của AM và BD. Chứng minh: AI ⊥ BD.
c) Kéo dài DM cắt AB tại H. Chứng minh: ∆MBH = ∆MDC
d) Gọi P là trung điểm của đoạn HC. Chứng minh: ba điểm A, M, P thẳng hàng.
Bài 5. (0,5 điểm)
Tìm các cặp số nguyên (x; y) sao cho: xy – x + 2(y – 1) = 2 -------Hết------
ĐÁP ÁN KIỂM TRA HỌC KÌ 1 – MÔN TOÁN 7 Năm học 2021 - 2022
Bài 1. (2,5 điểm) Thực hiện phép tính 3 1 4 Điểm 2 − − Điểm 5 4 Điểm a) − 2 4 4 3 1 36 3 3 . + − − + b) : c) : 4 3 5 3 15 5 5 10 25 10 10 9 4 4 0,25 − 0,25 0,25 = 4 4 5 6 1 6 3 − . = + . = − − + 12 12 5 9 15 4 10 10 5 10 5 4 4 1 − = 0,25 0,25 1 6 3 0,25 . = + = − + 12 5 9 3 2 5 10 1 4 3 − = 5 12 3 0,25 = + = − + 0,25 3 9 9 10 10 10 0,25 1 = − 2 = 9 0,25 5
Bài 2. (2,0 điểm) Tìm x, biết: 7 − 1 5 Điểm Điểm 2 Điểm a) x − = b) ( − ) 1 3 4 1 3x 4 . 5x + = 0 c) x − = : 2 3 2 2 5 3 3 7 − 5 1 0,25 TH1: 3x – 4 = 0 2 x = + 3 2 2 3 3x = 4 x − = 4 0,25 5 7 − 17 4 x = 0,25 x = 0,25 2 2 6 3 3 2 2 x − = 2 = ( 2 − ) 17 7 − 1 x = : TH2: 5x + = 0 5 6 2 2 3 1 − 7 0,25 1 − TH1: x − = 2 = x = 5x 5 21 2 3 1 − x = 2 + x = 5 10 0,25 13 x = 0,25 5 4 1 − 3 Vậy x ∈ ; TH2: x − = 2 − 3 10 5 3 x = 2 − + 5 7 − x = 0,25 5 1 3 −7 Vậy x ∈ ; 5 5
Bài 3. (1,5 điểm)
- Gọi số học sinh giỏi, khá, trung bình của lớp 7A lần lượt là: x, y, z (ĐK: x, y, z ∈ N*; học sinh) 0,25
- Vì số học sinh giỏi, khá, trung bình lần lượt tỉ lệ với 6; 5; 2 x y z = = (1) 0,25 6 5 2
- Vì tổng số học sinh giỏi và khá hơn số học sinh trung bình là 36 bạn
x + y − z = 36 (2) 0,25
- Từ (1) và (2), áp dụng tính chất dãy tỉ số bằng nhau, ta có: x y z
x + y − z 36 = = = = = 4 6 5 2 6 + 5 − 0,25 2 9 x = 4 6 x = 24 y
= 4 y = 20 (TMĐK) 0,25 5 z = 8 z = 4 2
Vậy số học sinh giỏi, khá, trung bình của lớp 7A lần lượt là 24, 20, 8 học sinh. 0,25
Bài 4. (3,5 điểm) A
a) Xét ∆ABM và ∆ADM có:
b) Xét ∆ABI và ∆ADI có: AB = AD (gt) 0,25 AB = AD (gt)
BAM = DAM (AM là phân giác) 0,25 BAI = DAI (cmt) AM: cạnh chung 0,25 AI: cạnh chung D
=> ∆ABM = ∆ADM (c.g.c) 0,25
=> ∆ABI = ∆ADI (c.g.c) 0,5 I
=> BIA = DIA (hai góc tương ứng) B C M Mà 0
BIA + DIA = 180 (hai góc kề bù) 0,25 P => 0
BIA = DIA = 90 => AI ⊥ BD 0,25 H 0,25 c) Vì ∆ABM = ∆ADM (cm a)
d) Vì ∆HBM = ∆CDM (cmt) => BH = DC (2 cạnh t/ứng)
=> BM = DM (2 cạnh t/ứng); ABM = ADM (hai góc t/ứng) 0,25
Mà AB = AD (gt) => AH = AC Mà 0 ABM + HBM = 180 ; 0 ADM + CDM = 180 (kề bù) Xét ∆AHP và ∆ACP có:
=> HBM = CDM 0,25 AH = AC (cmt) Xét ∆HBM và ∆CDM có: AP cạnh chung HBM = CDM (cmt)
HP = CP (vì P là trung điểm của HC) BM = DM (cmt) => ∆AHP = ∆ACP (c.c.c) BMH = DMH (đối đỉnh)
=> HAP = CAP (2 góc t/ứng)
=> ∆HBM = ∆CDM (g.c.g) 0,25 => AP là phân giác của HAC 0,25
=> AP là phân giác của BAC
Mà AM là phân giác của BAC => AM trùng AP
=> A, M, P thẳng hàng. 0,25
Bài 5. (0,5 điểm)
Ta có: xy – x + 2(y – 1) = 2 x ( y − ) 1 + 2 ( y − )
1 = 2 ( x + 2)( y − ) 1 = 2
x ∈ Z (x + 2)∈ Z Vì
mà ( x + 2)( y − )
1 = 2 ( x + 2) ; ( y − ) 1 ∈U (2) 0,25 y
∈ Z ( y − ) 1 ∈ Z Mà Ư(2) = { ± 1; ± 2} Ta lập bảng giá trị: x + 2 1 – 1 2 – 2 x – 1 – 3 0 – 4 y – 1 2 – 2 1 – 1 y 3 – 1 2 0 Vậy x = – 1; y = 3 x = – 3; y = – 1 0,25 x = 0; y = 2 x = – 4; y = 0




