


















Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH
ĐỀ KIỂM TRA NĂNG LỰC GIÁO VIÊN
TRƯỜNG THPT LÝ THÁI TỔ NĂM HỌC 2018 - 2019
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ Môn thi: Toán
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(Đề thi có 50 câu trắc nghiệm) Mã đề thi 132 2x - 1
Câu 1: Phương trình các đường tiệm cận của đồ thị hàm số y = ? 3 - x
A. y = 3;x = 2 - . B. y = 2; - x = 3.
C. y = 2;x = 3 - .
D. y = 2;x = 3.
Câu 2: Số nghiệm nguyên thuộc é 20;20ù - 2x 1 + x 2 êë
úû của bất phương trình (2
- 9.2 + 4) x + 2x - 3 ³ 0 là: A. 38.. B. 36. C. 37.. D. 19. . y
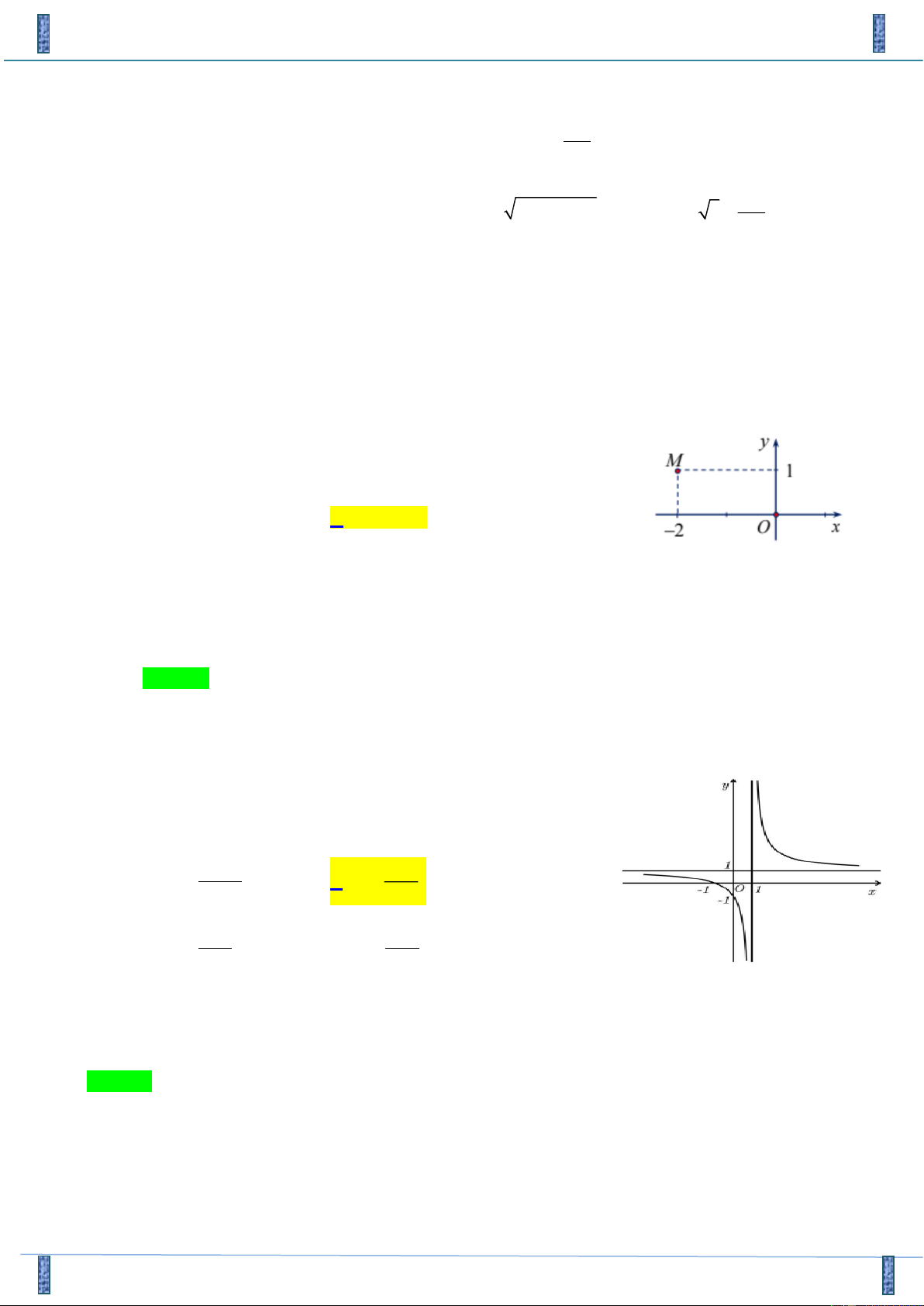
Câu 3: Điểm M trong hình vẽ bên là điểm biểu diễn số phức M 1
A. z = 1 - 2i..
B. z = 2 + i. . C. z = 1 + 2 . i . D. z = 2 - + i. .
Câu 4:Đường cong trong hình bên là đồ thị của một hàm số trong 2 O x
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi đó là hàm số nào? 2x - 1 x + 1 A. y = . B. y = . x - 1 x - 1 x - 1 x + 1 C. y = . D. y = . x + 1 1 - x e x + 1 Câu 5: Biết
dx = ln ae + b ò
với a,b là các số 2 ( )
x + x ln x 1
nguyên dương. Tính giá trị của biểu thức 2 2
T = a - ab + b ? A. 3. . B. 1. . C. 0.. D. 8.
Câu 6: Biết rằng m = m là giá trị của tham số m sao cho 0
phương trình 9x - 2(2 + ) 1 3x m + 3(4m - ) 1 = 0 có hai
nghiệm thực x ,x thỏa mãn(x + 2 x + 2 = 12 . Khi đó m thuộc khoảng nào sau đây ? 1 )( 2 ) 1 2 0 A. (3;9) B. (9;+¥) (1;3) -2; 0 C. D. ( )
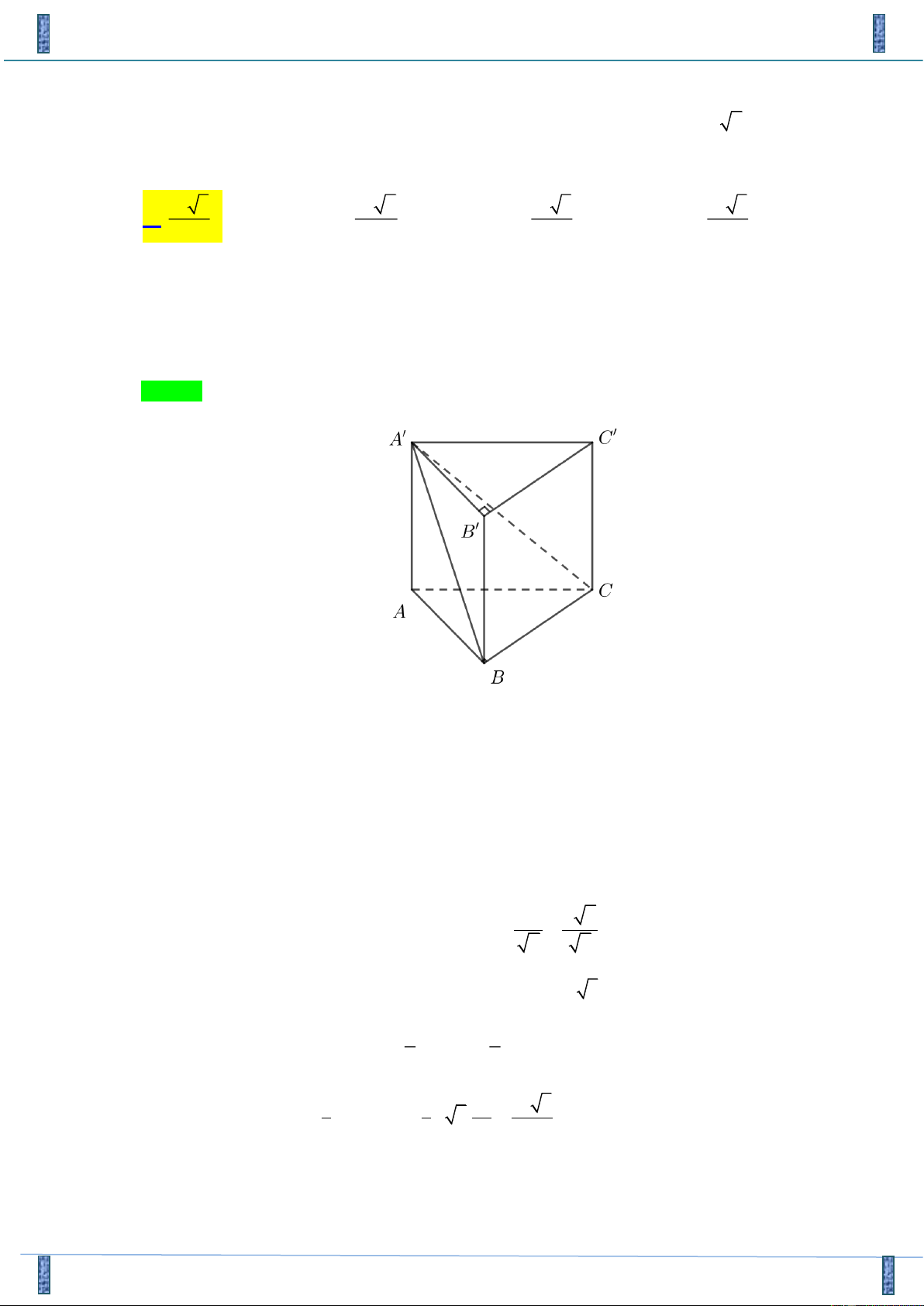
Câu 7: Cho lăng trụ đứng ' ' '
ABC .A B C đáy là tam giác vuông cân tại B , AC = a 2 , biết góc giữa
( 'ABC) và đáy bằng 0
60 . Tính thể tích V của khối lăng trụ. 3 a 3 3 a 6 3 a 3 3 a 3 A. V = .. B. V = . . C. V = .. D. V = .. 6 6 3 2
Câu 8: Tính đạo hàm của hàm số x
y = e sin 2x. A. x
e (sin 2x - cos 2x). B. x e cos 2x C. x
e (sin 2x + cos 2x) D. x
e (sin 2x + 2 cos 2x)
Câu 9: Từ các chữ số 0;1;2; 3; 4;5;6 lập được bao nhiêu số tự nhiên gồm hai chữ số? A. 13 . B. 49 C. 36 . D. 42
Trang 1/6 - Mã đề thi 132 Câu 10: Cho , a ,
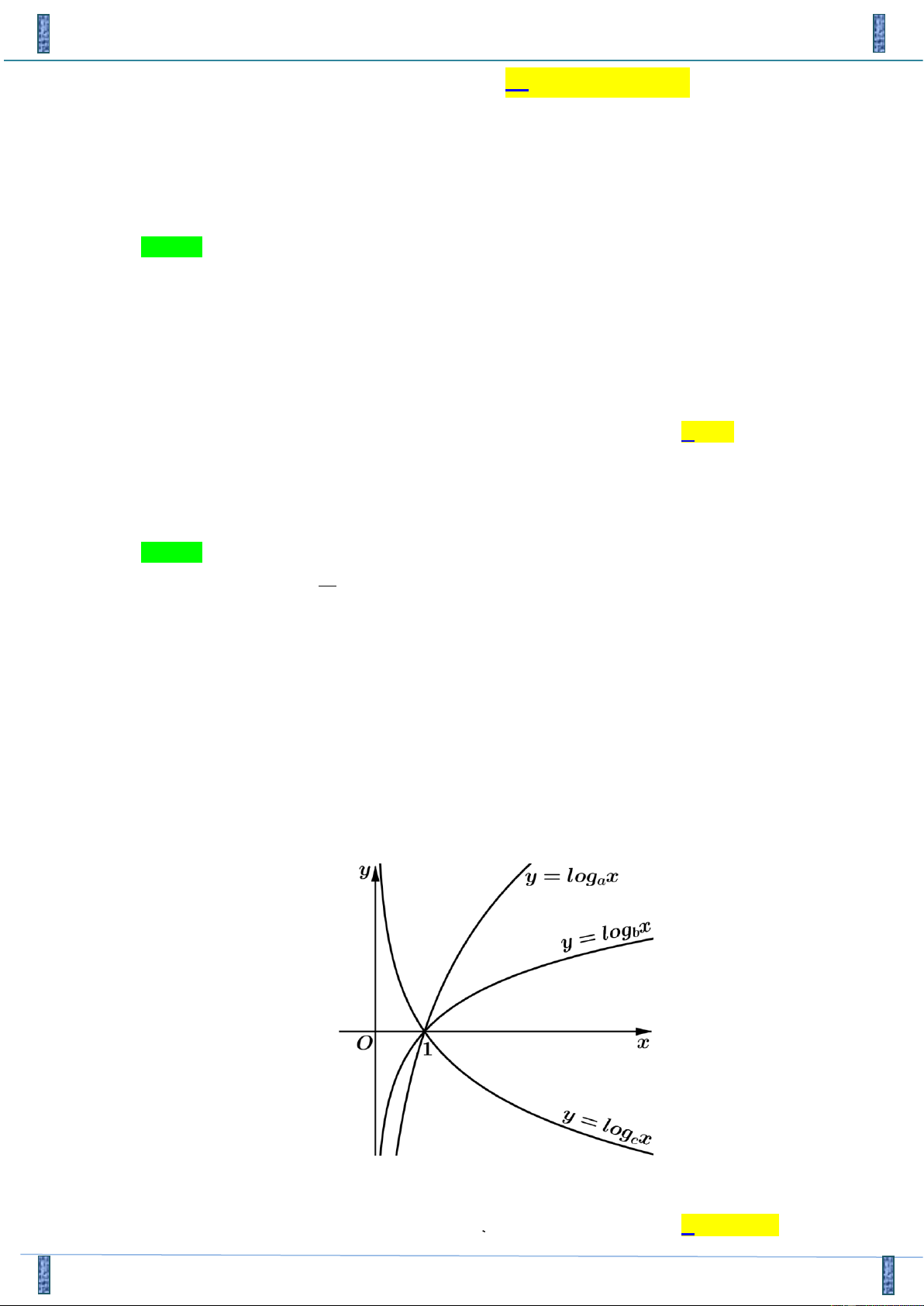
b c là các số thực dương và khác 1. Hình vẽ bên là đồ thị y y=log
của ba hàm số y = log x,y = log x,y = log x. Khẳng định nào sau đây là ax a b c đúng?
A. a < c < b.
B. a < b < c. y=logbx
C. c < b < a.
c < a < b. D. 1 x O
Câu 11: Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng x - 1 y + 2 z - 3 d : = =
. Hỏi d đi qua điểm nào trong các điểm sau: y=log 3 4 - 5 - cx A. C(-3; 4;5) B. D(3;-4;-5) C. B(-1;2;-3) D. (1 A ;-2; 3) ì 2 ïx -16 ïï khi x > 4
Câu 12: Tìm m để hàm số f (x) = í x - 4
liên tục tại điểm x = 4. mx ïï +1 khi x £ 4 ïïî 7 -7 A. m = . B. m = 8 . C. m = . D. m = -8 . 4 4
Câu 13: Tập hợp nghiệm của bất phương trình log x + 1 < 3 là: 2 ( ) A. S = (-1;8). B. S = (- ;7 ¥ ). C. S = (- ; ¥ 8). D. S = (-1;7). Câu 14: Cho , a ,
b c là các đường thẳng trong không gian. Xét các mệnh đề sau
(I ) Nếu a ^ b và b ^ c thì a c .
(II) Nếu a ^ (a)và b (a) thì a ^b .
(III ) Nếu a b và b ^ c thì c ^a .
(IV ) Nếu a ^b , b ^ c và a cắt c thì b ^ ( ,ac) .
Có bao nhiêu mệnh đề đúng ? A. 3 B. 4 C. 2 . D. 1 . 2
Câu 15: Cho số phức z = (1 - i) (1 + 2i). Số phức z có phần ảo là A. 2 . B. -2 . C. 4 . D. -2i .
Câu 16: Trong mặt phẳng với hệ trục tọa độ Ox , y cho (2
A ;-3),B(1; 0). Phép tịnh tiến theo
u = (4;-3)biến điểm ,AB tương ứng thành ' '
A ,B .Khi đó, độ dài đoạn thẳng ' ' AB bằng: A. ' ' AB = 10. B. ' ' A B = 5. C. ' ' A B = 13. D. ' ' A B = 10 3
Câu 17: Tìm tập xác định của hàm số y ( 2x 7x 1 )- = - + 0 A. \ {2; } 5 B. ( ; -¥ 2) È (5;+ ) ¥ C. D. (2;5)
Câu 18: Tìm tất cả giá trị của tham số m để phương trình 2
2 sin x + m sin 2x = 2m vô nghiệm? m é £ 0 é ê m < 0 ê A. ê 4 . B. 4 4 . D. ê 4 . m ê ³ ê ê 0 £ m £ 0 < m < m > ë 3 3 ê C. 3 ë 3
Câu 19: Cho mặt phẳng (a) : 2x - 3y - 4z + 1 = 0 . Khi đó, một véc- tơ pháp tuyến của (a) A. n = (2;3; 4 - ) B. n = (2; 3 - ;4) C. n = ( 2 - ;3;4) D. n = ( 2 - ;3;1)
Trang 2/6 - Mã đề thi 132 2x - 1
Câu 20: Phương trình tiếp tuyến của đồ thị hàm số y =
tại điểm có hoành độ bằng -2 ? x + 1 A. y = 3 - x + 1.
B. y = 3x + 11.
C. y = 3x + 5. D. y = 3 - x -1.
Câu 21: Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số 3 2
y = 2x + 3x -12x +1trên đoạn é 1;3ù - êë
úû . Khi đó tổng M +m có giá trị là một số thuộc khoảng dưới đây: A. (0;2) . B. (39; 42) . C. (3;5) . D. (59; 61) .
Câu 22: Cho hai mặt phẳng (a) : 3x -2y + 2z + 7 = 0,(b) : 5x - 4y + 3z + 1 = 0 . Phương trình mặt
phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả(a) và (b) là:
A. 2x - y - 2z = 0.
B. 2x - y + 2z = 0.
C. 2x + y - 2z = 0.
D. 2x + y - 2z + 1 = 0. p 2
Câu 23: Giá trị của sinxdx ò bằng 0 p A. 0 . B. 1. . C. -1.. D. .. 2
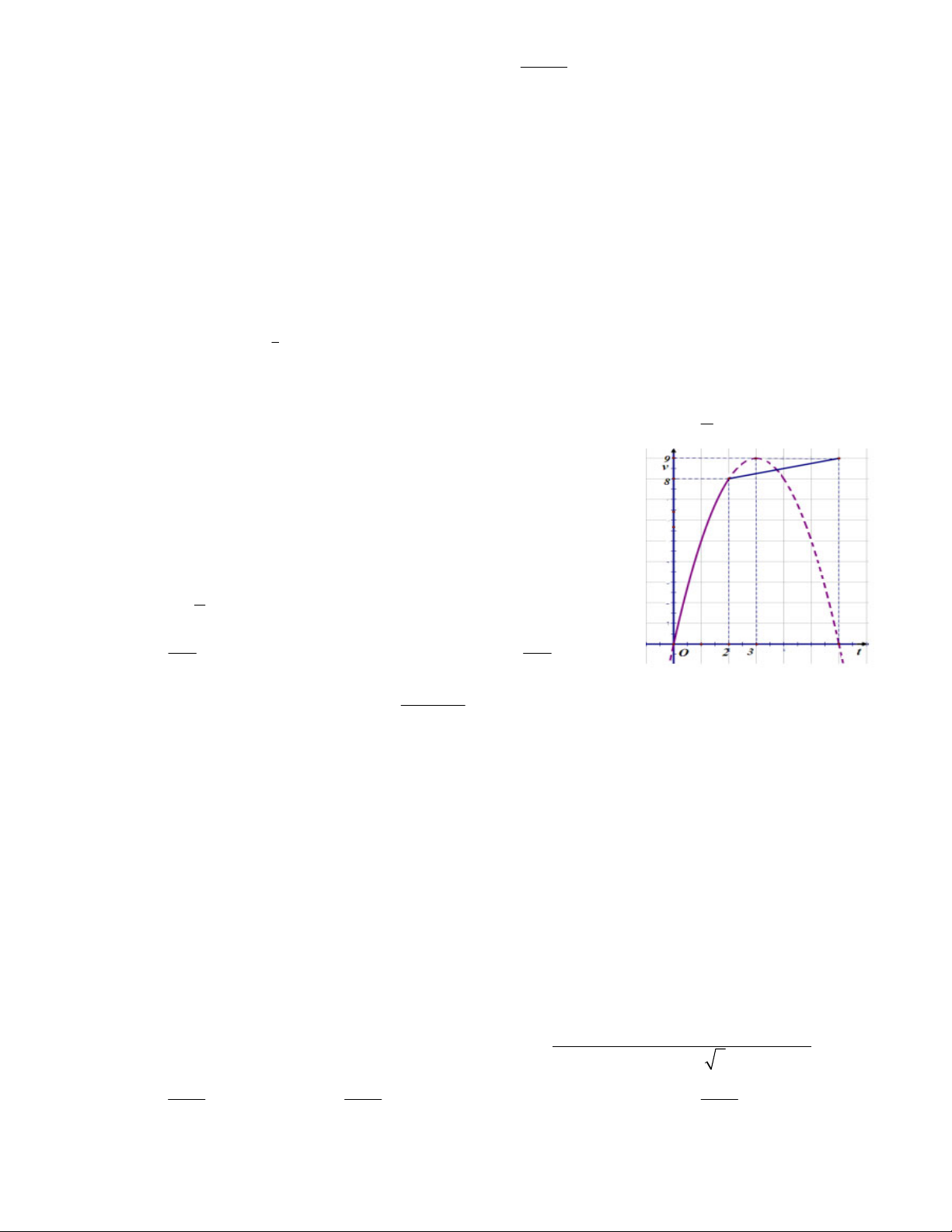
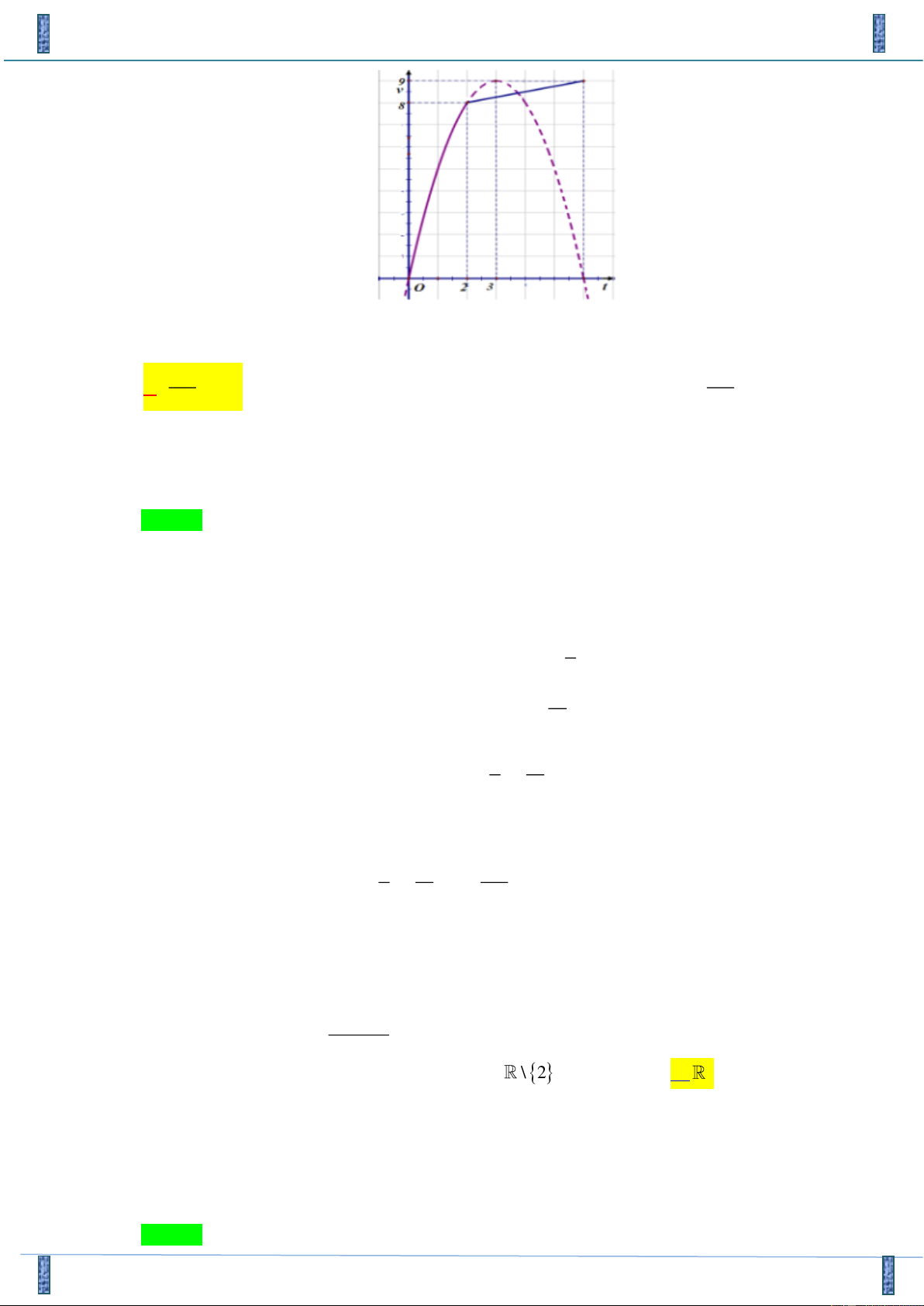
Câu 24: Một vật chuyển động trong 6 giờ với vận tốc v (km / h)phụ
thuộc vào thời gian t(h) có đồ thị vận tốc như hình bên. Trong khoảng
thời gian 2 giờ từ khi bắt đầu chuyển động, đồ thị là một phần đường
parabol có đỉnh I (3;9)và có trục đối xứng song song với trục tung.
Khoảng thời gian còn lại, đồ thị vận tốc là một đường thẳng có hệ số 1
góc bằng .Tính quãng đường s mà vật di chuyển được trong 6giờ ? 4 130 134 A.
(m). B. 9(m).. C. 40(m). D. (m) 3 3 sin x + 1
Câu 25: Tập xác định của hàm số y = là sin x - 2 A. (-2;+¥) B. (2;+¥) C. \ { } 2 . D.
Câu 26: Diện tích toàn phần của hình trụ có bán kính đáy ,
R chiều cao h và độ dài đường sinh l là? A. 2 S = 2 R p + R p l . B. 2 S = R p + R p l . tp tp C. 2 S = 2 R p + 2 R p l . D. 2 S = R p + 2 R p l . tp tp
Câu 27: Mệnh đề nào sau đây sai? A. kf
ò (x)dx = k f
ò (x)dx với mọi hằng số k và với mọi hàm số f (x) liên tục trên . B. f ¢
ò (x)dx = f (x)+C với mọi hàm số f (x) có đạo hàm trên . C. éf
ò ê (x) g(x)ù + dx = f f x , g x ë ú
ò (x)dx + g ò (x)dx û
, với mọi hàm số ( ) ( )liên tục trên . D. éf
ò ê (x) g(x)ù - dx = f f x , g x ë ú
ò (x)dx - g ò (x)dx û
, với mọi hàm số ( ) ( ) liên tục trên .
3 - cos 2x + sin 2x - 5 sin x - cos x
Câu 28: Tổng các nghiệm thuộc é0;100pù êë úû của phương trình = 0 2 cos x - 3 7475 7375 7573 A. p.. B. p.. C. 4950p. . D. . p 3 3 3
Trang 3/6 - Mã đề thi 132
Câu 29: Hàm số nào trong các hàm số sau có bảng biến thiên như hình vẽ? A. 3 2 y = x - - 3x + 1 . B. 3 2
y = 2x + 6x - 1. C. 3 2
y = x + 3x - 1 . D. 3 2
y = -2x + 6x - 1.
Câu 30: Gọi S là tổng tất cả các nghiệm của phương trình
1 log( 2x -2x + )1+ log(x + 9) = 2- log4. Tính S ? 2 A. S = -8.
B. S = -8 - 5 2. S = -8 + 5 2. S = - C. D. 12. (m - 1)sin x - 2
Câu 31: Cho hàm số y =
. Tìm tất cả giá trị của tham số m để hàm số nghịch biến trên sin x - m p khoảng (0; ) 2 m é < 1 - m é £ 1 - m é £ 0 A. 1 - < m < 2. B. ê . C. ê . D. ê . m ê > 2 ê ê ê ³ ³ ë m 2 êë m 1 êë
Câu 32: Trong mặt phẳng tọa độ Oxy , ở các góc phần tư I , thứ II , thứ III , thứ IV cho lần lượt
1;2; 3; 4 điểm phân biệt. Biết rằng các điểm không nằm trên trục tọa độ và không có bất kỳ 3 điểm nào
thẳng hàng. Chọn ngẫu nhiên 3 điểm bất kì trong 10 điểm trên. Tính xác suất để 3 điểm tạo thành một
tam giác có đúng 2 cạnh cắt trục tọa độ ? 11 1 5 13 A. . B. . C. .. D. . 24 24 12 24 Câu 33: Cho hàm số 4 2
y = mx - (2m + 1)x + 1. Tìm tất cả các giá trị của m để hàm số có một điểm cực đại? 1 1 1 1
A. - £ m < 0. B. m £ - . m ³ - . - £ m £ 0. 2 2 C. 2 D. 2
Câu 34: Cho M là tập hợp các số phức z thỏa mãn 2z - i = 2 + iz . Gọi z ,z là hai số phức thuộc 1 2
tập hợp M sao cho z - z = 1. Tính giá trị của biểu thức P = z + z 1 2 1 2 3 A. P = .. B. P = 3. . C. P = 2. D. P = 2 . 2
(1 + i)8 (-1- 2i)
Câu 35: Tính modun của số phức w = b + ci ( ,
b c Î ), biết số phức là nghiệm của (1-i)7 phương trình 2
z + bz + c = 0. A. 2 43. B. 26.. C. 62.. D. 2 34..
Câu 36: Hình chop S.ABC có đáy là tam giác vuông tại B có AB = a,AC = 2a. SA vuông góc với
mặt phẳng đáy, SA = 2a. Gọi j là góc tạo bởi hai mặt phẳng (SAC ),(SBC ). Tính cosj = ? 3 1 15 3 A. . B. . C. . D. . 5 2 5 2
Trang 4/6 - Mã đề thi 132 Câu 37: Cho hàm số 3 2
y = f (x) = ax + bx + cx + d có đồ thị như hình bên. Có y
bao nhiêu giá trị nguyên của tham số m để phương trình 2
f ( x )-(m - 3)f (x ) + m - 4 = 0 có 7 nghiệm phân biệt? A. 3.. B. 1. 1 C. 2. . D. 4.. 1 2 x O
Câu 38: Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng x y + 1 2 - z d : = =
. Gọi P là mặt phẳng chứa d và tạo với mặt -3 1 -2 1
phẳng(Q) : 2x - y - 2z - 2 = 0 một góc có số đo nhỏ nhất. Điểm A(1;2;3) cách
mặt phẳng P một khoảng bằng: 5 3 7 11 4 3 A. 3. B. . C. . . 3 11 D. 3
Câu 39: Biết n là số nguyên dương thỏa mãn2( 2 2 2 2
C +C +C + ... +C
= A .Tìm hệ số của số n ) 2 3 2 3 4 n 1 + n æ 1 ö hạng chứa 26
x trong khai triển ç 7 ç + x ÷÷ ç ( vớix ¹ 0) 4 ÷ çèx ÷ø A. 356. B. 210. . C. 792.. D. 924. . Câu 40: Cho hàm số 3 2
f (x) = mx - 2mx + (m + 1)x - 2 (m là tham số). Số các giá trị nguyên của
tham số m để hàm số y = f (x) có 1 điểm cực trị? A. 4. B. 2. C. 3. D. Vô số.
Câu 41: Cho hàm số f (x)liên tục và dương trên (0; ) +¥ thỏa mãn '
f (x) + ( x + ) 2 2 4 f (x) = 0 và a f ( ) 1 0 = a
. Tính tổng S = f (0) + f (1) + f (2) + ... + f (2018) = với a Î , b Î , tối giản. Khi đó, 3 b b b -a = ? A. -1. . B. 1011. . C. 1. D. 2018.
Câu 42: Gọi z = a +bi (a,b Î ) là số phức thỏa mãn điều kiện z -1 - 2i + z + 2 - 3i = 10 và
có mô đun nhỏ nhất. Tính S = 7a + b ? A. 7.. B. 0. C. 5.. D. -12..
Câu 43: Cho hàm số y = f (x) có đồ thị (P) như hình vẽ. Biết ìïf
ï (1 + 4v) = f (5 - 8u)
(u ;v là một nghiệm của hệ phương trình ïí 0 0 )
ï 2u + 3v = 2u + v ïïî a a và *
u + v = ,a Î ,
b Î , tối giản. Giá trị của biểu thức 0 0 b b
P a b? A. 3. B. 4. C. 1. . D. 2.
Câu 44: Cho x,y,z là các số thực dương thỏa mãn: ( 2 2 2
5 x + y + z ) = 9(xy + 2yz + zx).Giá trị lớn x 1
nhất của biểu thức T = - 2 2 y + z
(x + y + z)3 31 25 A. 16. . B. . . C. 12. . D. . 2 2
Trang 5/6 - Mã đề thi 132 æ4 5ö
Câu 45: Trong mặt phẳng với hệ trục tọa độ Oxy , cho DABC .có tâm đường tròn ngoại tiếp I çç ; ÷÷ ç , çè3 3÷÷ø æ1 8ö
trực tâm H çç ; ÷÷ ç
và trung điểm của cạnh BC là M (1; )
1 .Tính độ dài cạnhBC çè3 3÷÷ø A. 5 2. . B. 2. C. 2 5. . D. 5..
Câu 46: Trong không gian với hệ trục tọa độ Oxyz ,cho hai mặt phẳng song song
(a : 2x -y + 2z -1 = 0.(a : 2x -y + 2z + 5 = 0và một điểm A(-1;1; ) 1 nằm trong khoảng giữa 2 ) 1 )
của hai mặt phẳng đó. Gọi (S) là mặt cầu qua A và tiếp xúc với (a , a . Biết rằng khi (S)thay đổi thì 1 ) ( 2 )
tâm I của nó nằm trên một đường tròn cố định ( )
w . Tính diện tích hình tròn giới hạn bởi ( ) w ? 2 4 8 16 A. . p B. p. . C. p. . D. . p . 3 9 9 9
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, các cạnh bên của hình chóp bằng
nhau và bằng 6 (cm), AB = 4(cm). Khi thể tích khối chóp S.ABCD đạt giá trị lớn nhất, tính diện tích
mặt cầu ngoại tiếp S.ABCD ? A. 2 12 ( p cm ) B. 2 4 ( p cm ) . C. 2 9 ( p cm ) D. 2 36 ( p cm ).
Câu 48: Trong không gian với hệ trục tọa độ Oxyz ,cho ba điểm ( A 1;4;5), ( B 3;4;0),C(2; 1 - ;0) và mặt
phẳng (a) : 3x - 3y - 2z -12 = 0 . Gọi M (a; ;
b c) Î (a) sao cho 2 2 2
MA + MB + 3MC đạt giá trị nhỏ
nhất. Tính tổng S = a + b + c . A. 3. B. 2. C. -2. D. 2.
Câu 49: Cho hình tứ diện ABCD có AD ^ (ABC ), ABC là tam giác vuông tại B . Biết BC = 2(cm)
,AB = 2 3(cm),AD = 6(cm). Quay các tam giác ABC và ABD ( bao gồm cả điểm bên trong 2 tam
giác) xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng 5 3 3 3 64 3 A. 3 3 ( p cm ) B. 3 ( p cm ) C. 3 ( p cm ). D. 3 ( p cm ). 2 2 3
Câu 50: Cho điểm M nằm trên cạnh SA , điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC SM 1 SN sao cho = ,
= 2. Mặt phẳng (a) qua MN và song song với SC chia khối chóp thành 2 MA 2 NB V
phần. Gọi V là thể tích của khối đa diện chứa A, V là thể tích của khối đa diện còn lại. Tính tỉ số 1 = ? 1 2 V2 V 5 V 6 V 5 V 4 A. 1 = . B. 1 = . C. 1 = . D. 1 = . V 6 V 5 V 4 V 5 2 2 2 2
----------- HẾT ----------
Trang 6/6 - Mã đề thi 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019
LỜI GIẢI CHI TIẾT
thantaithanh@gmail.com 2x − 1 Câu 1.
Phương trình các đường tiệm cận của đồ thị hàm số y = là: 3 − x
A. y = 3; x = 2 − . B. y = 2 − ; x = 3.
C. y = 2; x = 3 − .
D. y = 2; x = 3 . Lời giải
Tác giả: Nguyễn Trung Thành, FB: https://www.facebook.com/thantaithanh Chọn B. 2x − 1 Ta có: lim y = lim = 2
− nên y = −2 là đường tiệm cận ngang của đồ thị hàm số và x→
x→ 3 − x 2x − 1 2x − 1 lim y = lim = − ; lim y = lim
= + nên x = 3 là đường tiệm cận đứng của đồ + − x→3 x→3+ − x→3 x→3 3 x − 3 − x thị hàm số.
thantaithanh@gmail.com Câu 2. +
Số nghiệm nguyên thuộc đoạn 2 − 0; 2
0 của bất phương trình: 2x 1 x 2 2
− 9.2 + 4 x + 2x − 3 0 là A. 38 . B. 36 . C. 37 . D. 19 . Lời giải
Tác giả: Nguyễn Trung Thành, FB: https://www.facebook.com/thantaithanh Chọn B. Điều kiện: 2
x + 2x − 3 0 x −3 hoặc x 1 (*) .
Vì x là số nguyên thuộc đoạn 2 − 0; 2
0 nên ta xét các trường hợp sau: Trường hợp 1. + +
3 x 20 , khi đó dễ thấy 2x 1 x x − = ( x 1 2 9.2 2 2 − 9) 0 nên 2 x 1 + x 2 2
− 9.2 + 4 x + 2x − 3 0 , do đó trên 3; 2
0 bất phương trình có 18 nghiệm nguyên.
Trường hợp 2. x = 2 thay trực tiếp vào bất phương trình ta có: 4 5 − 4 0 (đúng).
Do đó x = 2 thỏa mãn yêu cầu bài toán.
Trường hợp 3. x = 1 thay trực tiếp vào bất phương trình ta có: 1 − 0 0 (sai).
Do đó x = 1 không thỏa mãn yêu cầu bài toán. Trường hợp 4. 2 − 0 x 4
− . Khi đó, xét hàm số: f (x) 2
= x + 2x − 3, dễ thấy
min f ( x) = f ( 4 − ) = 5 nên 2
4 x + 2x − 3 4 5, x 2 − 0; 4 − (a) . 20 − ; 4 − + − − Mặt khác, đặt 2x t = , khi đó 2x 1 x 2 2
− 9.2 = 2t − 9t , 20 4 20 − x 4 − 2 t 2 .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 9 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Khi đó xét hàm số − − g (t) 2
= 2t − 9t với 20 4 2
t 2 , dễ thấy min g (t) − 71 4 = g 2 = − (b) 20 − −4 ( ) 2 ; 2 128 x+ x 71
Từ (a) , (b) suy ra min = − + + − = − = − . Do đó − − h ( x ) 2 1 2 2 9.2 4 x 2x 3 h 4 4 5 0 20; 4 ( ) 128
bất phương trình đã cho nghiệm đúng với mọi 2 − 0 x 4 − , nên trên đoạn 2 − 0; 4 − bất
phương trình có 17 nghiệm nguyên. Trường hợp x = 3
− thay trực tiếp vào bất phương trình ta thấy không thỏa mãn.
Vậy số nghiệm nguyên của bất phương trình là: 36.
Phamvantuan190593@gmail.com Câu 3.
Điểm M trong hình vẽ bên là điểm biểu diễn số phức?
A. z = 1− 2i .
B. z = 2 + i .
C. z = 1+ 2i . D. z = 2 − + i Lời giải
Tác giả: Phạm Văn Tuấn – FB: Phạm Tuấn Chọn D.
Dựa vào hình vẽ ta thấy điểm M biểu diễn số phức z có phần thực bằng 2 − và phần ảo bằng
1. Vậy số phức z = 2 − + i . Câu 4.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? 2x −1 x +1 A. y = . B. y = . x −1 x −1 x −1 x +1 C. y = . D. y = x +1 1− x Lời giải
Tác giả: Phạm Văn Tuấn – FB: Phạm Tuấn Chọn B.
- Đồ thị hàm số có đường TCĐ x = 1 nên loại C
- Đồ thị hàm số có đường TCN y = 1 nên loại A và D
- Nhận xét thêm, tại x = 0 thì y = 1 − ta chọn B
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 10 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019
chipbong07@gmail.com e x +1 Câu 5. Biết
dx = ln ae + b
với a, b là các số nguyên dương. Tính giá trị của biểu thức 2 ( )
x + x ln x 1 2 2
T = a − ab + b . A. 3. B. 1. C. 0. D. 8. Lời giải
Tác giả : Đặng Hoài Ân, FB: Đặng Ân Chọn B 1 + e e 1 x +1
e d ( x + ln x) e x dx = dx = =ln
(x + ln x) = ln(e+ ) 1 2 1
x + x ln x x + ln x x + ln x 1 1 1
Vậy a = 1, b = 1 nên 2 2
T = a − ab + b = 1. Câu 6. Biết rằng m = m là giá trị của tham số m sao cho phương trình 0 9x − 2 (2 + ) 1 3x m + 3(4m − )
1 = 0 có hai nghiệm thực x , x thỏa mãn ( x + 2 x + 2 = 12 . Khi 1 )( 2 ) 1 2
đó m thuộc khoảng nào sau đây 0 A. (3;9) . B. (9; +) . C. (1;3) . D. (-2; 0) . Lời giải
Tác giả : Đặng Hoài Ân, FB: Đặng Ân Chọn C 9x − 2 (2 + ) 1 3x m + 3(4m − ) 1 = 0 (1) t = Đặt = 3x t
, t 0 . Pt(1) trở thành: 2 t − 2(2m + ) 1 t + 3(4m − ) 1 = 3 0 . t = 4m −1 Để 1
pt(1) có 2 nghiệm thì điều kiện cần và đủ là 4m −1 0 m . 4
Khi đó pt (1) có hai nghiệm x = 1 và x = log (4m − ) 1 . 1 2 3
Từ giả thiết ( x + 2 x + 2 = 12 3(log (4m - )
1 + 2 = 12 log (4m − ) 1 = 2 3 ) 1 )( 2 ) 3 1 m = .( 5 2 3 + ) 1 = . Vậy m (1;3). 4 2
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 11 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019
Lephuonganh510@gmail.com Câu 7.
Cho lăng trụ đứng AB .
C A' B 'C ' đáy là tam giác vuông cân tại B, AC = a 2, biết góc giữa
( A'BC) và đáy bằng 0
60 . Tính thể tích V của khối lăng trụ? 3 a 3 3 a 6 3 a 3 3 a 3 A. . B. . C. . D. . 6 6 3 2 Lời giải
Tác giả : Lê Phương Anh, FB: Phuonganh510 Chọn A BC ⊥ BB '
BC ⊥ ( ABB' A') BC ⊥ A'B BC ⊥ BA (
A'BC) ( ABC) = BC
Ta có A' B ( A'BC), A' B ⊥ BC (( A' BC ),( ABC )) 0 = A' BA = 60 AB
( ABC), AB ⊥ BC AC a 2
Tam giác ABC vuông cân tại B nên AB = BC = = = a . 2 2
Xét tam giác A' AB vuông tại A có 0 AA' = A .
B tan 60 = a 3 . 1 1
Diện tích tam giác ABC là 2 S
= BC.BA = a ABC 2 2 2 3 1 1 a a 3
Thể tích lăng trụ là V = AA'.S = a 3. = . 3 ABC 3 2 6 Câu 8. Tính đạo hàm hàm số x
y = e .sin 2x A. x
e (sin 2x − cos 2x) . B. x e .cos 2x .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 12 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 C. x
e (sin 2x + cos 2x) . D. x
e (sin 2x + 2 cos 2x) . Lời giải
Tác giả : Lê Phương Anh, FB: Phuonganh510 Chọn D
' = ( x.sin 2 ) = ( x ) .sin 2 x + .(sin 2 ) x = .sin 2 + 2 x.cos 2 x y e x e x e x e x e
x = e (sin 2x + 2cos 2x)
Duanquy@gmail.com Câu 9.
Từ các chữ số 0;1; 2;3; 4;5; 6 lập được bao nhiêu số tự nhiên gồm hai chữ số? A. 13 . B. 49 . C. 36 . D. 42 . Lời giải
Tác giả : Nguyễn Đức Duẩn, FB: Duan Nguyen Duc Chọn D
Gọi số cần lập có dạng ab . Để lập được số có 2 chữ số ta cần thực hiện liên tiếp hai hành động.
Chọn một chữ số khác 0 vào vị trí a có 6 cách.
Ứng với mỗi cách chọn một số vào vị trí a có 7 cách chọn một số vào vị trí b .
Theo quy tắc nhân ta có số các số có 2 chữ số lập được là 6.7 = 42 số.
Duanquy@gmail.com
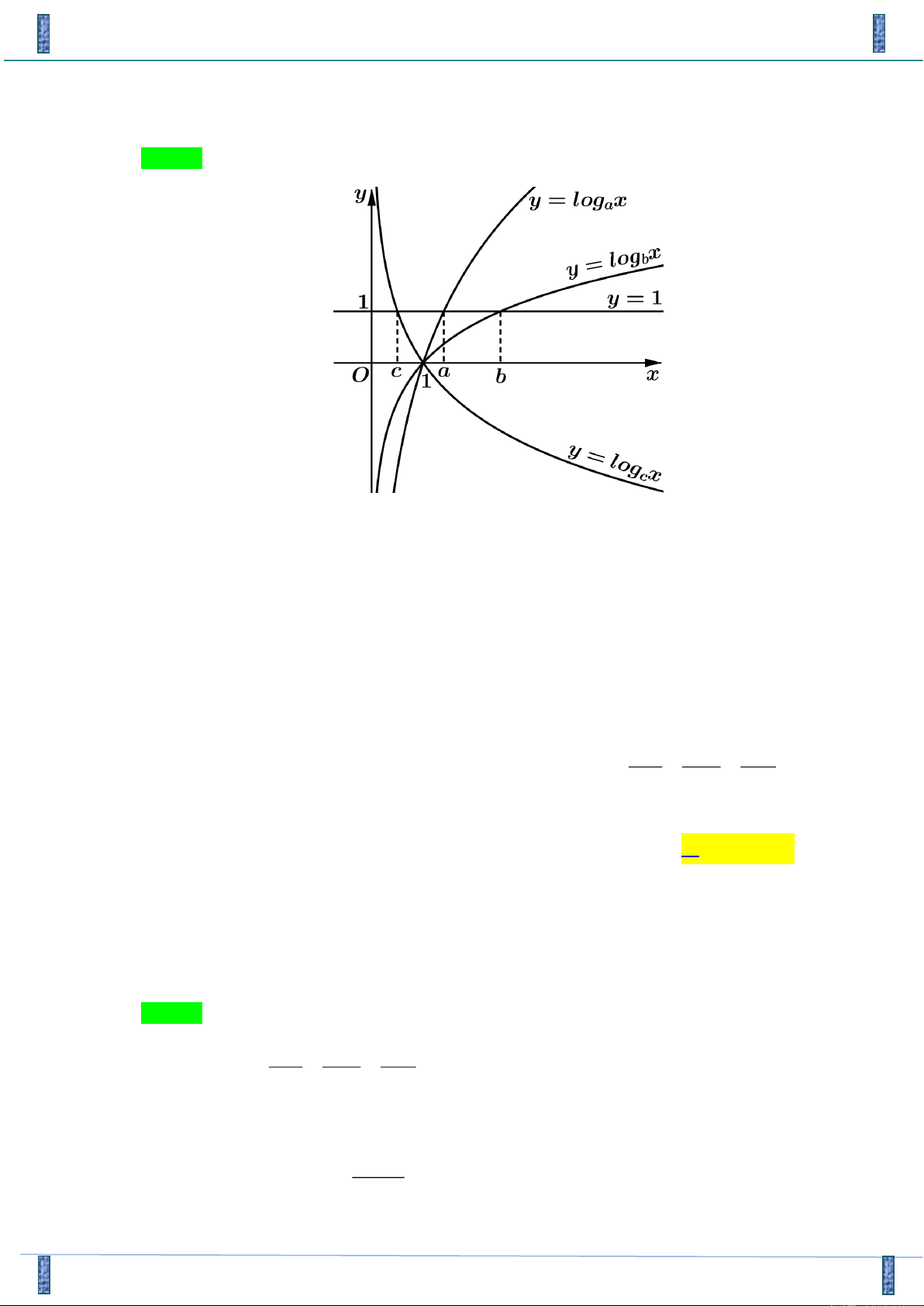
Câu 10. Cho a, ,
b c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số y = log , x y = log ,
x y = log x . a b c
Khẳng định nào sau đây là đúng?
A. a c b .
B. a b c .
C. c b a .
D. c a b .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 13 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Lời giải
Tác giả : Nguyễn Đức Duẩn, FB: Duan Nguyen Duc Chọn D a,b 1
Theo hình dạng của đồ thị ta có . 0 c 1
Vẽ đường thẳng y = 1 cắt đồ thị hai hàm số y = log ,
x y = log x lần lượt tại 2 điểm a b M ( ;1 a ), N ( ;1
b ) . Ta thấy điểm N bên phải điểm M nên b a .
Vậy c a b .
pandahoa@gmail.com x −1 y + 2 z − 3
Câu 11. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d : = = . Hỏi d đi 3 4 − 5 −
qua điểm nào trong các điểm sau:
A. C (−3; 4;5) .
B. D (3; − 4; − 5) .
C. B (−1; 2; − 3) .
D. A(1; − 2;3) . Lời giải
Tác giả : Nguyễn Phú Hòa, FB: Nguyễn Phú Hòa Chọn D x − y + z − Đườ 1 2 3 ng thẳng d : = =
đi qua điểm A(1;− 2;3) . 3 4 − 5 −
pandahoa@gmail.com 2 x −16 khi x 4
Câu 12. Tìm m để hàm số f ( x) = x − 4
liên tục tại điểm x = 4 .
mx +1 khi x 4
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 14 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 7 7 A. m = . B. m = 8 . C. m = − . D. m = 8 − . 4 4 Lời giải
Tác giả : Nguyễn Phú Hòa, FB: Nguyễn Phú Hòa Chọn A x −16
Ta có lim f ( x) = f (4) = 4m +1 ; lim f ( x) 2 = lim = lim (x + 4) = 8. − + + + x→4 x→4 x→4 x − 4 x→4
Hàm số liên tục tại điểm x = 4 lim f ( x) = lim f ( x) = f (4) 4m +1 = 7 8 m = . − + x→4 x→4 4
Nguyenhoach95@gmail.com
Câu 13. Tập hợp nghiệm của bất phương trình log x +1 3 là: 2 ( ) A. S = ( 1 − ; 8) . B. S = (− ; 7) . C. S = (− ; 8). D. S = ( 1 − ; 7) . Lời giải
Tác giả : Nguyễn Đức Hoạch, FB: Hoạch Nguyễn Chọn D x +1 0 x 1 − Ta có: log2 ( x + ) 1 3 3 −1 x 7 x +1 2 x 7
Vậy tập nghiệm của bất phương trình là S = ( 1 − ; 7) .
Câu 14. Cho a, ,
b c là các đường thẳng trong không gian. Xét các mệnh đề sau:
(I ) Nếu a ⊥ b và b ⊥ c thì a / /c .
(II ) Nếu a ⊥ ( ) và b / /( ) thì a ⊥ b.
(III ) Nếu a / /b và b ⊥ c thì c ⊥ a .
(IV ) Nếu a ⊥ ,b b ⊥ c và a cắt c thì b ⊥ (a, c).
Có bao nhiêu mệnh đề đúng? A. 3. B. 4. C. 2. D. 1. Lời giải
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 15 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019
Tác giả : Nguyễn Đức Hoạch, FB: Hoạch Nguyễn Chọn A
Mệnh đề ( I ) sai vì a và c có thể cắt nhau hoặc chéo nhau hoặc song song.
Mệnh đề ( II ) , ( III ) và ( IV ) đúng.
nguyentuanblog1010@gmail.com 2
Câu 15. Cho số phức z = (1− i) (1+ 2i) . Số phức z có phần ảo là: A. 2 . B. 2 − . C. 4 . D. 2 − i . Lời giải
Tác giả:Phạm Chí Tuân, FB: Tuân Chí Phạm Chọn B 2
Ta có: z = ( − i) ( + i) = ( 2
− i + i )( + i) = − i( + i) 2 1 1 2 1 2 1 2 2 1 2 = 2
− i − 4i = 4 − 2i .
Suy ra số phức z có phần ảo là: 2 − .
Câu 16. Trong mặt phẳng với hệ trục tọa độ Oxy , cho A(2; 3
− ), B(1;0) . Phép tịnh tiến theo u = (4; 3 − ) biến điểm ,
A B tương ứng thành A ', B ' . Khi đó, độ dài đoạn thẳng A' B ' là:
A. A' B ' = 10 .
B. A' B ' = 5 .
C. A' B ' = 13 .
D. A' B ' = 10 . Lời giải
Tác giả:Phạm Chí Tuân, FB: Tuân Chí Phạm Chọn D
Theo tính chất của phép tịnh tiến
Nếu T ( M ) = M ' , T ( N ) = N ' thì MN = M ' N ' suy ra MN = M ' N ' . u u 2 2
Áp dụng vào bài toán ta có A' B ' = AB = (1− 2) + (0 + 3) = 10 .
vungoctan131@gmail.com −
Câu 17. Tìm tập xác định của hàm số y = ( x − x + ) 3 2 7 10
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 16 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 A. \ 2; 5 .
B. (−; 2) (5; +) . C. . D. (2;5) . Lời giải
Tác giả : Vũ Ngọc Tân, FB: Vũ Ngọc Tân . Chọn A x 2 ĐKXĐ: 2
x − 7x +10 0 . x 5 Vậy TXĐ: D = \ 2; 5 .
Câu 18. Tìm tất cả các giá trị của tham số m để phương trình 2
2sin x + msin2x = 2m vô nghiệm? m 0 4 4 A. 4 . B. 0 m . C. 0 m . m 3 3 3 m 0 D. 4 . m 3 Lời giải
Tác giả : Vũ Ngọc Tân, FB: Vũ Ngọc Tân . Chọn D Ta có: 2
2sin x + msin2x = 2m msin2x - cos2x = 2m - 1 ( ) 1 m 0 Điề u kiện phương trình ( )
1 vô nghiệm là: m +1 (2m − )2 2 2 1
3m − 4m 0 4 . m 3 m 0 Vậy với 4
thì phương trình trên vô nghiệm. m 3
kimoanh0102@gmail.com
Câu 19: Cho mặt phẳng ( ) : 2x − 3y − 4z +1 = 0 . Khi đó, một véc tơ pháp tuyến của ( ) A. n = (2;3; 4 − ). B. n = (2; 3 − ;4) . C. n = ( 2 − ;3;4). D. n = ( 2 − ;3; ) 1 .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 17 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn C
Mặt phẳng ( ) : 2x − 3y − 4z +1 = 0 có một véc tơ pháp tuyến n = 2; 3 − ; 4 − 0 ( ). Nhận thấy n = ( 2 − ;3;4) = −n n
0 , hay n cùng phương với 0 .
Do đó véc tơ n = ( 2
− ;3;4)cũng là một véc tơ pháp tuyến của mặt phẳng( ) 2x −1
Câu 20: Phương trình tiếp tuyến của đồ thị hàm số y = x
tại điểm có hoành độ bằng 2? − + 1 A. y = 3 − x +1.
B. y = 3x + 11.
C. y = 3x + 5 . D. y = 3 − x −1. Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn B Tập xác định: D = \ − 1 . 2x −1 3 y = y ' = x . + 1 (x + )2 1 y( 2 − ) = 5; y'( 2 − ) = 3 .
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 2 − là:
y − y = y ' x x − x
y − 5 = 3 x + 2 y = 3x +11. 0 ( 0 )( 0 ) ( )
maisonltt@gmail.com
Câu 21. Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số 3 2
y = 2x + 3x −12x +1trên đoạn 1;3 . Khi đó tổng M
m có giá trị là một số thuộc khoảng dưới đây: A. (0;2) . B. (39; 42) . C. (3; 5) . D. (59;61) . Lời giải
Họ và tên tác giả : Nguyễn Thị Mai . Tên FB: Mai Nguyễn Chọn B 2 y ' 6x 6x 12
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 18 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 x 1 y ' 0 x 2 Ta có: y(1) 6 ;y( 2) 21 ;y( 1) 14 ;y(3) 46 Nên M 46;m 6 M m 40 .
maisonltt@gmail.com
Câu 22. Cho hai mặt phẳng : 3x 2y 2z 7 0, : 5x 4y 3z 1 0 . Phương trình mặt
phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả và là: A. 2x y 2z 0. B. 2x y 2z 0. C. 2x y 2z 0. D. 2x y 2z 1 0. Lời giải
Họ và tên tác giả : Nguyễn Thị Mai . Tên FB: Mai Nguyễn Chọn C
Véc tơ pháp tuyến của hai mặt phẳng lần lượt là n 3; 2;2 ,n 5; 4; 3 . n ;n 2;1; 2
Phương trình mặt phẳng đi qua gốc tọa độ O ,VTPT n 2;1; 2 : 2x y 2z 0. 2
Câu 23. Giá trị của sin xdx bằng 0 A.0. B.1. C.-1. D. . 2 Lời giải
Tác giả :Nguyễn Văn Nghĩa, FB: Nghĩa Văn Nguyễn Chọn B 2
+ Tính được sin xdx = − cos x 2 = 1 . 0 0 Câu 24.
Một vật chuyển động trong 6 giờ với vận tốc v (km / h) phụ thuộc vào thời gian t (h) có đồ thị như
hình bên dưới. Trong khoảng thời gian 2 giờ từ khi bắt đầu chuyển động, đồ thị là một phần đường
Parabol có đỉnh I (3;9) và có trục đối xứng song song với trục tung. Khoảng thời gian còn lại, đồ thị 1
vận tốc là một đường thẳng có hệ số góc bằng
. Tính quảng đường s mà vật di chuyển được trong 6 4 giờ?
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 19 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 130 134 A. (km) . B. 9 (km) . C. 40 (km) . D. (km) . 3 3 Lời giải
Tác giả :Nguyễn Văn Nghĩa, FB: Nghĩa Văn Nguyễn Chọn A
+ Vì Parabol đi qua O(0; 0) và có tọa độ đỉnh I (3;9) nên thiết lập được phương trình Parabol là
(P) y = v(t) 2 : = t − + 6t; t 0;2 1
+ Sau 2 giờ đầu thì hàm vận tốc có dạng là hàm bậc nhất y =
t + m , dựa trên đồ thị ta thấy đi qua 4 15
điểm có tọa độ (6;9) nên thế vào hàm số và tìm được m = . 2 1 15
Nên hàm vận tốc từ giờ thứ 2 đến giờ thứ 6 là y = t + ; t [2;6] 4 2
+ Quảng đường vật đi được bằng tổng đoạn đường 2 giờ đầu và đoạn đường 4 giờ sau. 2
S = S + S = ( t − + 6t) 6 1 15 130 2 dt + t + dt = km 1 2 ( ) 4 2 3 0 2
huynhthanhtinhspt@gmail.com s inx +1
Câu 25: Tập xác định của hàm số y = là s inx − 2 A. ( 2; − + ) B. (2; + ) C. \ 2 . D. . Lời giải
Tác giả : Huỳnh Thanh Tịnh , FB: huynhthanhtinh Chọn D
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 20 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Ta có 1 − sinx 1, x
. Do đó sinx − 2 0, x
. Vậy tập xác định D =
Câu 26: Diện tích toàn phần của hình trụ có bán kính đáy R, chiều cao h và độ dài đường sinh l là ? A. 2
S = 2 R + Rl B. 2
S = R + Rl tp tp C. 2
S = 2 R + 2 Rl D. 2
S = R + 2 Rl tp tp Lời giải
Tác giả : Huỳnh Thanh Tịnh , FB: huynhthanhtinh Chọn C 2
Ta có S = 2S + S = 2 R + 2 Rl tp ñ xq
Capuchino135@gmail.com
Câu 27: Mệnh đề nào sau đây sai? A.
kf (x)dx = k f (x)dx
với mọi hằng số k và với mọi hàm số f (x) liên tục trên . B. f (
x)dx = f (x) + C
với mọi hàm số f (x) có đạo hàm trên .
C. f (x) + g(x)dx = f (x)dx + g(x)dx
với mọi hàm số f (x), g(x) liên tục trên .
D. f (x) − g(x)dx = f (x)dx − g(x)dx
với mọi hàm số f (x), g(x) liên tục trên . Lời giải
Tác giả : Trần Thơm, FB: Kem LY Chọn A
Do kf (x)dx = k f (x)dx
với mọi hằng số k 0 và với mọi hàm số f (x) liên tục trên nên A là mệnh đề sai. − x + x − x − x
Câu 28. Tính tổng các nghiệm thuộc 0;100 của phương trình 3 cos 2 sin 2 5sin cos = 0 . 2 cos x − 3 7475 7375 7573 A. . B. . C. 4950 . D. . 3 3 3 Lời giải
Tác giả : Trần Thơm, FB: Kem LY
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 21 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Chọn A Điề 3
u kiện xác định: 2 cos x − 3 0 cos x
x + l2 (l ) . 2 6 − x + x − x − x Với x
+ l2 (l ) phương trình 3 cos2 sin 2 5sin cos = 0 6 2 cos x − 3
3− cos 2x + sin 2x − 5sin x − cos x = 0 2
3−1+ 2sin x + 2sin x cos x − 5sin x − cos x = 0 2
(2sin x cos x − cos x) + 2sin x − 5sin x + 2 = 0 2
cos x(2sin x −1) + (2sin x − sin x) − (4sin x − 2) = 0
(2sin x −1)(cos x + sin x − 2) = 0
2sin x −1 = 0 (vì cos x + sin x − 2 = 2 sin x + − 2 2 − 2 0 ) 4 x = + k2 1 6 sin x = (k ) 2 5 x = + k2 6 5
Kết hợp điều kiện, phương trình có nghiệm x =
+ k2 (k ) . 6 Mà x 5 5 595 0;100 0
+ k2 100 − k 6 12 12 k k = 0;1;2;3;...;49. 49 5 7475
Vậy tổng các nghiệm thuộc 0;100 của phương trình bằng + k2 = . k = 6 3 0 49 5
Chú ý: Tính tổng + k2
bằng cách sử dụng máy tính cầm tay: Nhập tổng như sau k = 6 0
rồi ấn phím = được kết quả.
nguyenthithutrang215@gmail.com 2 3
Câu 29 . Cho hàm số có đạo hàm 5
y ' = x (2x − ) 1 ( x + )
1 (3x − 2) . Hàm số có bao nhiêu điểm cực trị? A. 4. B. 3. C. 11. D. 2. Lời giải
Tác giả : Nguyễn Thị Thu Trang, FB: Trang Nguyễn
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 22 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Chọn B x = 0 1 x = 2
y ' = 0 x = 1 − 2 x = 3
Vì y ' không đổi dấu khi qua các nghiệm bội chẵn nên số điềm cực trị của hàm số là 3 2x +1
Câu 30 . Cho hàm số y =
(C) . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M (−2;3) . x +1
A. y = x + 5 .
B. y = 2x + 7 .
C. y = 3x + 9 .
D. y = −x +1 . Lời giải
Tác giả : Nguyễn Thị Thu Trang, FB: Trang Nguyễn Chọn A TXĐ: \ − 1 1 y ' = y ' 2 − =1 2 ( ) (x + ) 1
Phương trình tiếp tuyến của đồ thị (C ) tại điểm M (−2;3) là: y = x + 5
hungnguyen24061984@gmail.com m
Câu 31. Cho biểu thức 5 3 8 2 2 2 n =
, trong đó m là phân số tối giản. Gọi 2 2
P = m + n . Khẳng định n nào sau đây đúng?
A. P (330;340) .
B. P (350;360) .
C. P (260;370) .
D. P (340;350) . Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng Chọn D 3 1 1 3 1 1 11 + + Ta có 5 3 5 3 3 5 10 30 5 10 30 15 8 2 2 = 2 2 2 = 2 .2 .2 = 2 = 2 m 11 m =11 2 2 2 2 =
P = m + n =11 +15 = 346 . n 15 n =15
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 23 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Câu 32. Cho hàm số 3
y = x − 3x + 4 (C) . Tiếp tuyến của đồ thị (C) tại điểm M ( 2 − ;2) có hệ số góc bằng bao nhiêu? A. 9 . B. 0 . C. 24 . D. 45 . Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng Chọn A Ta có 2 y = 3x − 3
Tiếp tuyến của đồ thị (C) tại điểm M ( 2
− ;2) có hệ số góc là: k = y( 2 − ) = 9 . Câu 33: Cho hàm số 4
y = mx − ( m + ) 2 2
1 x +1. Tìm tất cả các giá trị của m để hàm số có một điểm cực đại. 1 1 1 1 A. − m 0 . B. m − . C. m − . D. − m 0 . 2 2 2 2 Lời giải
Tác giả: Nguyễn Thị Dung, FB: dungbt nguyen Chọn C
Có 3 trường hợp sau thỏa mãn yêu cầu:
TH1: Hàm số là đa thức bậc 2 có hệ số của 2
x âm (đồ thị là parabol hướng bề lõm xuống dưới) m = 0 . − ( = m + ) m 0 2 1 0
TH2: Hàm số là đa thức bậc 4 có đồ thị dạng a 0 m 0 1 − m 0 . . a b 0 2m +1 0 2
TH3: Hàm số là đa thức bậc 4 có đồ thị dạng
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 24 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019
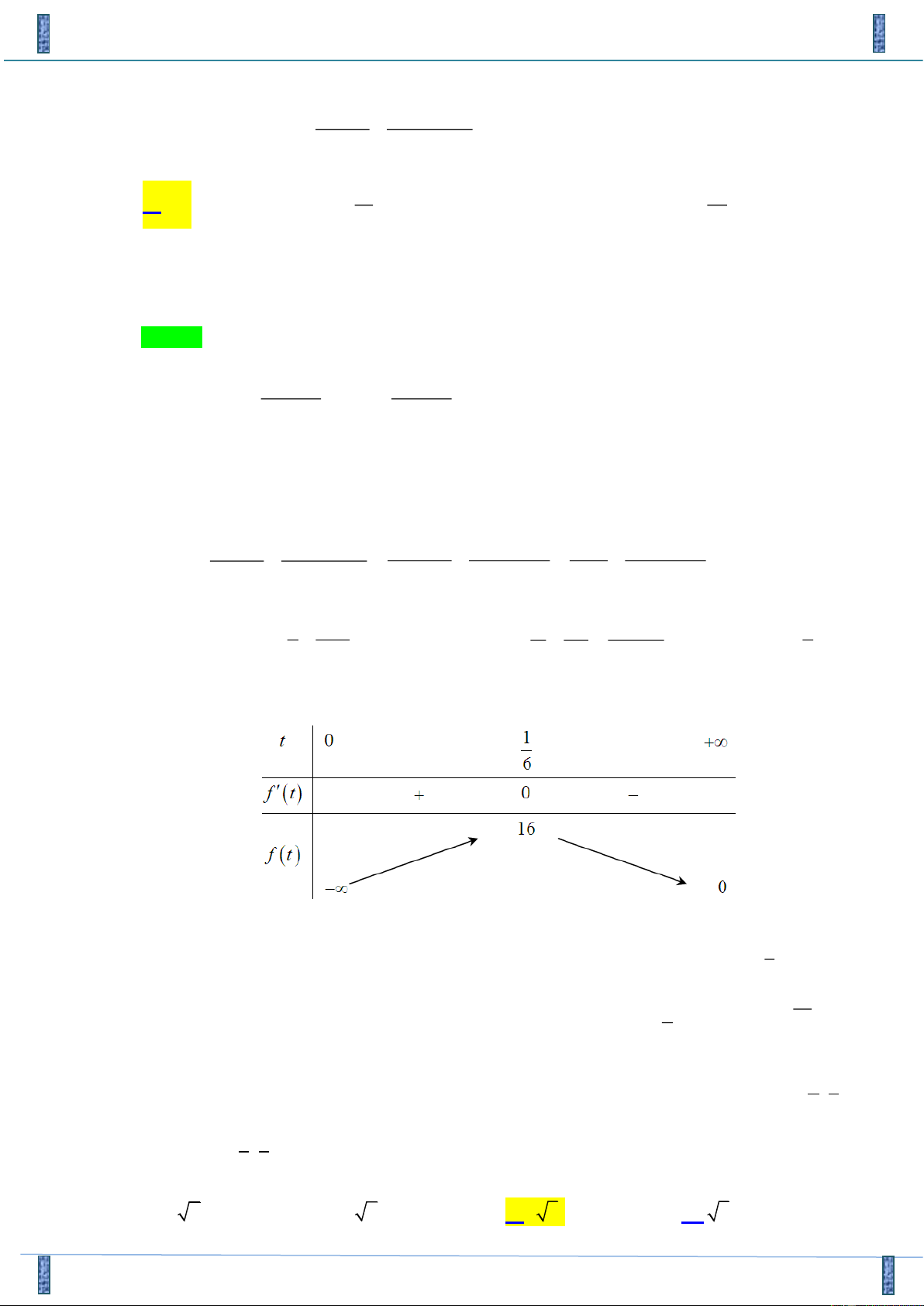
Câu 44. Cho x , y , z là các số thực dương thỏa mãn ( 2 2 2
5 x + y + z ) = 9( xy + 2yz + zx) . Giá trị lớn x 1
nhất của biểu thức T = − . 2 2 y + z
(x + y + z)3 31 25 A. 16 . B. . C. 12 . D. . 2 2 Lời giải Chọn A y + z ( y + z)2 2 2 ( )2 Ta có y + z và yz . 2 4 2 Và theo giả thiết ( 2 2 2
5 x + y + z ) = 9( xy + 2yz + zx) 2
5x + 5( y + z) −9x( y + z) = 28yz
x + ( y + z)2 − x( y + z) ( y + z)2 2 5 5 9 7
(5x + y + z)(x − 2y − 2z) 0 x 2( y + z). x 1 4 ( y + z) 1 4 1 Vậy T = − − = − . 2 2 y + z ( 2 3 3
x + y + z )3
( y + z) 27( y + z) y + z 27 ( y + z ) 4 1 4 1 1− 36t
Xét hàm số f (t ) = −
với t 0 , có f (t ) 2 = − + = , f (t ) = 1 0 t = . 3 t 27t 2 4 4 t 9t 9t 6 Bảng biến thiên:
x = 2( y + z) 1 x = 3
Dựa vào BBT suy ra giá trị lớn nhất của T = 16 đạt được tại y = z . 1 1 = = y z y + z = 12 6 4 5
Câu 45 . Trong mặt phẳng với hệ trục tọa độ Oxy , cho ABC
có tâm đường tròn ngoại tiếp I ; , 3 3 1 8 trực tâm H ;
và trung điểm của cạnh BC là M (1; )
1 . Tính độ dài cạnh BC . 3 3 A. 5 2 . B. 2 . C. 2 5 . D. 5 .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 34 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Lời giải Chọn C 1 2 2 4 Ta có MI = ;
và HA = 2MI nên HA = ; A (1;4) 3 3 3 3 5 2 5 IB = IA = ; IM = 3 3 2 5 2 5 2 2 BM = BI − IM = − = 5 BC = 2 5 3 3
Câu 46 . Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng song song
( : 2x − y + 2z −1= 0 , ( : 2x − y + 2z +5 = 0 và một điểm A(−1;1; ) 1 nằm trong khoảng 2 ) 1 )
giữa của hai mặt phẳng đó. Gọi (S ) là mặt cầu đi qua A và tiếp xúc với ( , . Biết rằng 1 ) ( 2 )
khi (S ) thay đổi thì tâm I của nó nằm trên một đường tròn cố định ( ) . Tính diện tích hình
tròn giới hạn bởi ( ) . 2 4 8 16 A. . B. . C. . D. . 3 9 9 9 Lời giải Chọn C Nhận thấy: ( / / và M (1;1;0) ( nên 1 ) 1 ) ( 2 ) − + + d (( 2.1 1 2.0 5 , = d M , = = 2 . 1 ) ( 2 )) ( ( 2)) 2 2 2 2 +1 + 2
Vì (S ) tiếp xúc với ( ,
nên tâm I của (S ) luôn thuộc mặt phẳng ( P) song song với 1 ) ( 2 )
( , và cách ( , một khoảng bằng 1. (1) 1 ) ( 2 ) 1 ) ( 2 )
Khi đó (S ) có bán kính R = 1 và (P) : 2x − y + 2z + 2 = 0
Mặt khác, (S ) đi qua A(−1;1; )
1 nên IA = R = 1. Vậy, I luôn thuộc mặt cầu (S ') tâm A và có
bán kính R ' = 1 . (2)
Từ (1) và (2) ta thấy, khi (S ) thay đổi thì tâm I của nó nằm trên một đường tròn cố định
() = (P)(S ') . 2.( 1 − ) −1+ 2.1+ 2 1 Ta có: d ( , A ( P)) = = 2 2 2 + + 3 2 1 2 1 8
Bán kính của đường tròn ( ) là r. Ta có r = R ' − d ( , A ( P)) 2 2 2 2 =1− = . 3 9
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 35 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 8
Diện tích hình tròn giới hạn bởi ( ) bằng . 9
luuhuephuongtailieu@gmail.com
Câu 47. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, các cạnh bên của hình chóp bằng
6 cm , AB = 4 cm . Khi thể tích khối chóp S.ABCD đạt giá trị lớn nhất, tính diện tích mặt cầu
ngoại tiếp S.ABCD . A. 2 12 cm . B. 2 4 cm . C. 2 9 cm . D. 2 36 cm . Lời giải
Tác giả : Lưu Huệ Phương, FB: Lưu Huệ Phương Chọn D S M I A D O B C
Gọi O là giao điểm của AC và BD .
Ta có SAC cân tại S nên SO ⊥ AC và SBD cân tại S nên SO ⊥ BD .
Khi đó SO ⊥ ( ABCD).
Ta có: SAO = SBO = SCO = SDO OA = OB = OC = OD
Vậy hình bình hành ABCD là hình chữ nhật. 2 AC + Đặ 16 x t 2 2
BC = x AC = 4 + x AO = = . 2 2 2 2 16 + x 8 − x
Xét SAO vuông tại O , ta có: 2 2 SO =
SA − AO = 6 − = 4 2 2 1 1 8 − x 2
Thể tích khối chóp S.ABCD là: 2 V = S . O S = . .4x = . 8 − x .x S . ABCD 3 ABCD 3 2 3 2 2 + 2 2 2 2 8 − x + x 8
Áp dụng bất đẳng thức : a b ab ta có: 2 V = . 8 − x .x . = . 2 3 3 2 3 Dấu " = " xảy ra 2
8 − x = x x = 2. Do đó: BC = 2, SO = 1.
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 36 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019
Gọi M là trung điểm của SA , trong (SAO) kẻ đường trung trực của SA cắt SO tại I .
Khi đó mặt cầu ngoại tiếp khối chóp S.ABCD có tâm I và bán kính R = IS. 2 SI SM SA 6 Vì SM I ∽ SO ( A g.g) nên = SI = =
= 3 R = 3(c ) m . SA SO 2.SO 2.1
Diện tích mặt cầu ngoại tiếp khối chóp S.ABCD là: 2 2 2
4 R = 4.3 = 36 (cm ) .
luuhuephuongtailieu@gmail.com
Câu 48. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A(1; 4;5), B (3; 4;0),C (2; 1 − ;0) và mặt
phẳng ( ) : 3x − 3y − 2z −12 = 0. Gọi M (a; ;
b c) thuộc ( ) sao cho 2 2 2
MA + MB + 3MC đạt
giá trị nhỏ nhất. Tính tổng S = a + b + . c A. 3 . B. 2 . C. 2 − . D. 1. Lời giải
Tác giả : Lưu Huệ Phương, FB: Lưu Huệ Phương Chọn A Gọi điểm I ( ;
x y; z ) thỏa mãn IA + IB + 3IC = 0.
IA = (1− ;x4− y;5− z)
IA = (1− ;x4− y;5− z) Mà IB = (3 − ;
x 4 − y; −z ) IB = (3 − ;
x 4 − y; −z ) IC ( = 2 − ; x 1 − − y;−z) 3IC = (6 − 3 ; x 3 − − 3 ; y 3 − z )
IA + IB + 3IC = (10 − 5 ;
x 5 − 5 y;5 − 5z ) x = 2
Do đó: IA + IB + 3IC = 0 y =1 I (2;1; ) 1 . z =1 2 2 2 Mặt khác: 2 2 2
MA + MB + 3MC = (MI + IA) + (MI + IB) + 3(MI + IC) 2 2 2 2
= 5MI + 2.MI. IA + IB + 3IC + IA + IB + 3 IC 0 Vì I , ,
A B,C cố định nên 2 2 2
IA + IB + 3IC không đổi Do đó: 2 2 2
MA + MB + 3MC 2
nhỏ nhất MI nhỏ nhất MI nhỏ nhất ( )
M là hình chiếu của I trên mặt phẳng . ( )
Phương trình đường thẳng d qua I và vuông góc với mặt phẳng là:
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 37 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 x − 2 y −1 z −1 = = . 3 3 − 2 −
M = d ( ). Gọi
Tọa độ của M là nghiệm của hệ phương trình: 7 x = 2 x − 2 y −1 z −1 3
− x + 6 = 3y − 3 = = 1 7 1 3 3 − 2 − 2
− x + 4 = 3z − 3
y = − M ; − ; 0 . 2
x − y − z − = 2 2 3 3 2 12 0
3x − 3y − 2z −12 = 0 z = 0 7 1 a = ,b = −
, c = 0 S = a + b + c = 3. Vậy 2 2 AD ABC BC 2(cm)
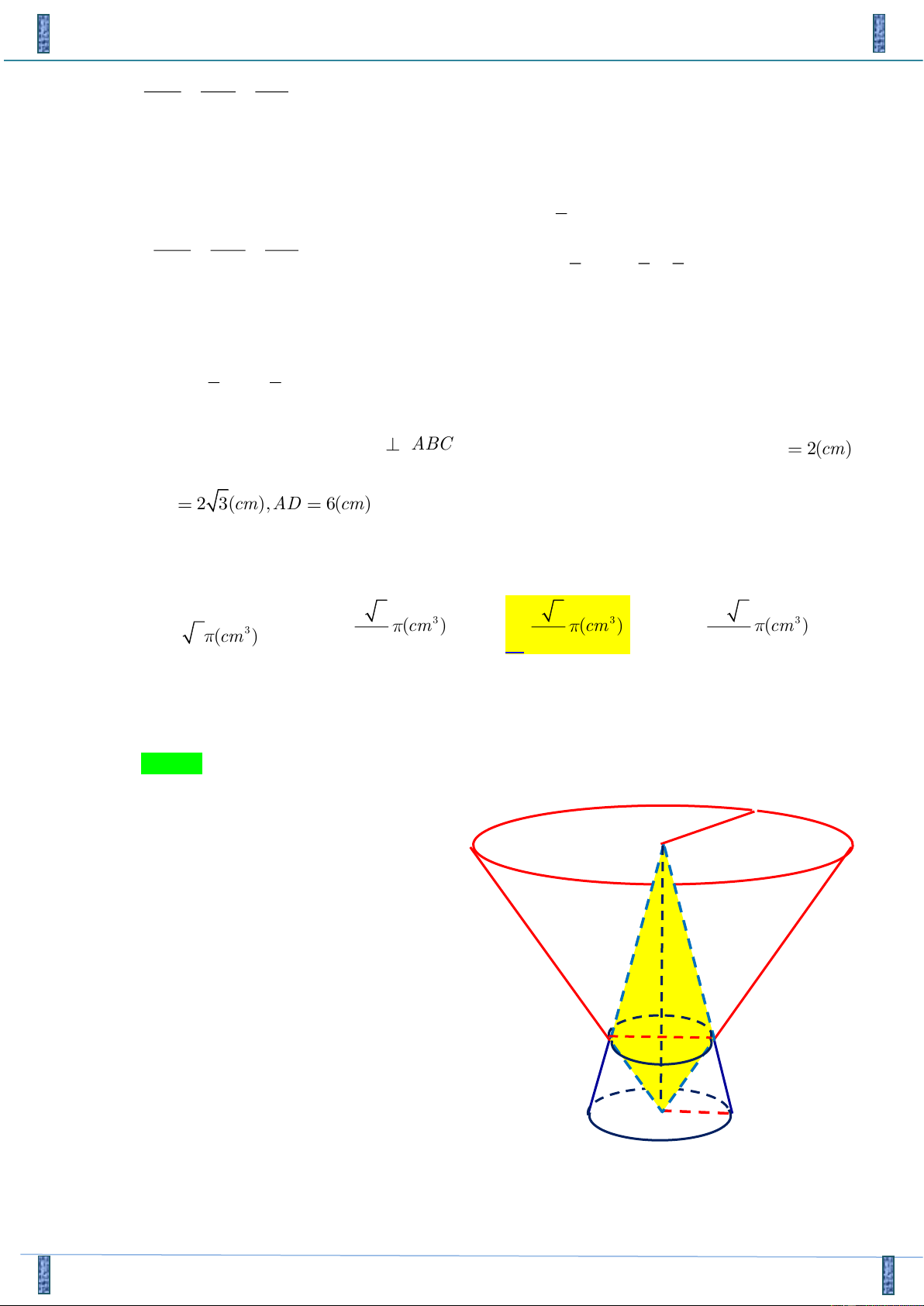
Câu 49. Cho hình tứ diện ABCD có
, ABC là tam giác vuông tại B . Biết ,AB 2 3(cm),AD
6(cm) . Quay các tam giác ABC và ABD ( bao gồm cả điểm bên
trong 2 tam giác) xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung
của 2 khối tròn xoay đó bằng 5 3 3 3 64 3 3 3 3 3 (cm ) (cm ) (cm ) 3 (cm ) A. B. 2 C. 2 . D. 3 . Lời giải Chọn C D A E N M B
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 38 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 Dễ thấy AD ABC AD R1
Gọi M = BD AC và N là hình chiếu của M trên AB. Dễ dàng chứng minh được tỉ lệ: MN AN = MN BN (1) AD AN AN 3 BN 1 (1) ; và = (2) = = = 3 = ; = BC AB AD AB (2) BC BN AB 4 AB 4 3 3 3 3 AN = ; BN = ; MN = 2 2 2
Phần thể tích chung của 2 khối tròn xoay là phần thể tích khi quay tam giác AMB xung quanh
trục AB. Gọi V là thể tích khối tròn xoay khi quay tam giác BMN xung quanh AB 1
Và V là thể tích khối tròn xoay khi quay tam giác AMN xung quanh AB 2 3 3 9 3 3 3
Dễ tính được: V = (dvtt) và V =
(dvtt) V + V =
(dvtt) . Chọn C. 1 8 2 1 2 8 2
Câu 50. Cho điểm M nằm trên cạnh SA , điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC SM 1 SN sao cho , 2. Mặt phẳng
qua MN và song song với SC chia khối chóp MA 2 NB
thành 2 phần. Gọi V là thể tích của khối đa diện chứa A, V là thể tích của khối đa diện còn lại. 1 2 V Tính tỉ số 1 ? V2 V 5 V 6 V 5 V 4 1 . 1 . 1 . 1 . V 6 V 5 V 4 V 5 A. 2 B. 2 C. 2 D. 2 Lời giải Chọn C
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 39 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Kiểm Tra Năng Lực GV Lý Thái Tổ BN 2018-2019 SM 1 SN CE 1 CF Vì SC / / ( ) nên , 2 , 2. MA 2 NB EA 2 FB
MN; EF; AB SAB Mặt khác dễ thấy:
đồng quy tại P. Áp dụng Menelaus trong tam giác : MS PA NB PA . . =1 = 4 MA PB NS PB V AM AE AP 2 2 4 16 AMEP . . . . V AS AC AB 3 3 3 27 ASCB V BN BF BP 1 1 1 1 BNFP . . . . V BS BC BA 3 3 3 27 BSCA V V −V 16 1 15 V 15 5 AMNBFE AMEP BNFP = = − = 1 = = . Chọn C. V V 27 27 27 V 12 4 SABC SABC 2
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 40 Mã đề 132
Document Outline
- GVG_132.pdf
- [STRONG TEAM TOÁN VD-VDC]-Kiểm Tra Năng Lực GV Lý Thái Tổ BN 18-19.pdf




