Đề kiểm tra theo bài học chủ đề hệ thức lượng trong tam giác
Tài liệu gồm 77 trang, được biên soạn bởi thầy giáo Huỳnh Văn Ánh, tuyển tập bộ đề kiểm tra theo bài học chủ đề hệ thức lượng trong tam giác môn Toán 10, có đáp án và lời giải chi tiết.
Cấu trúc đề kiểm tra:
+ Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (12 câu).
+ Phần 2. Câu trắc nghiệm đúng sai (04 câu).
+ Phần 3. Câu trắc nghiệm trả lời ngắn (06 câu).
Chủ đề: Đề thi Toán 10 257 tài liệu
Môn: Toán 10 3.1 K tài liệu
Tác giả:
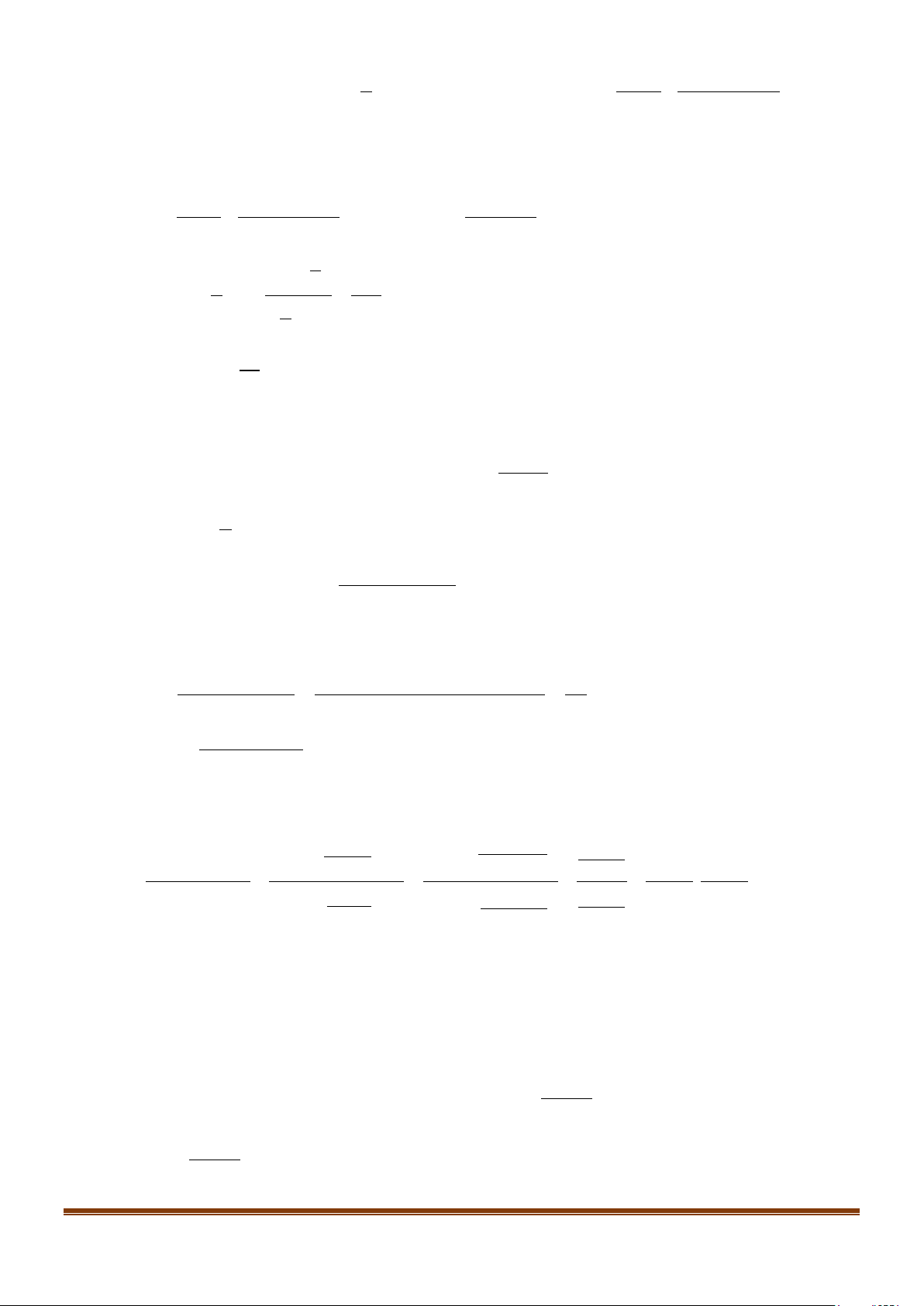
Preview text:
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC NG ƯƠ III HỆ THỨC LƯỢNG TRONG TAM GIÁC CH
BÀI. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180° ĐỀ TEST SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
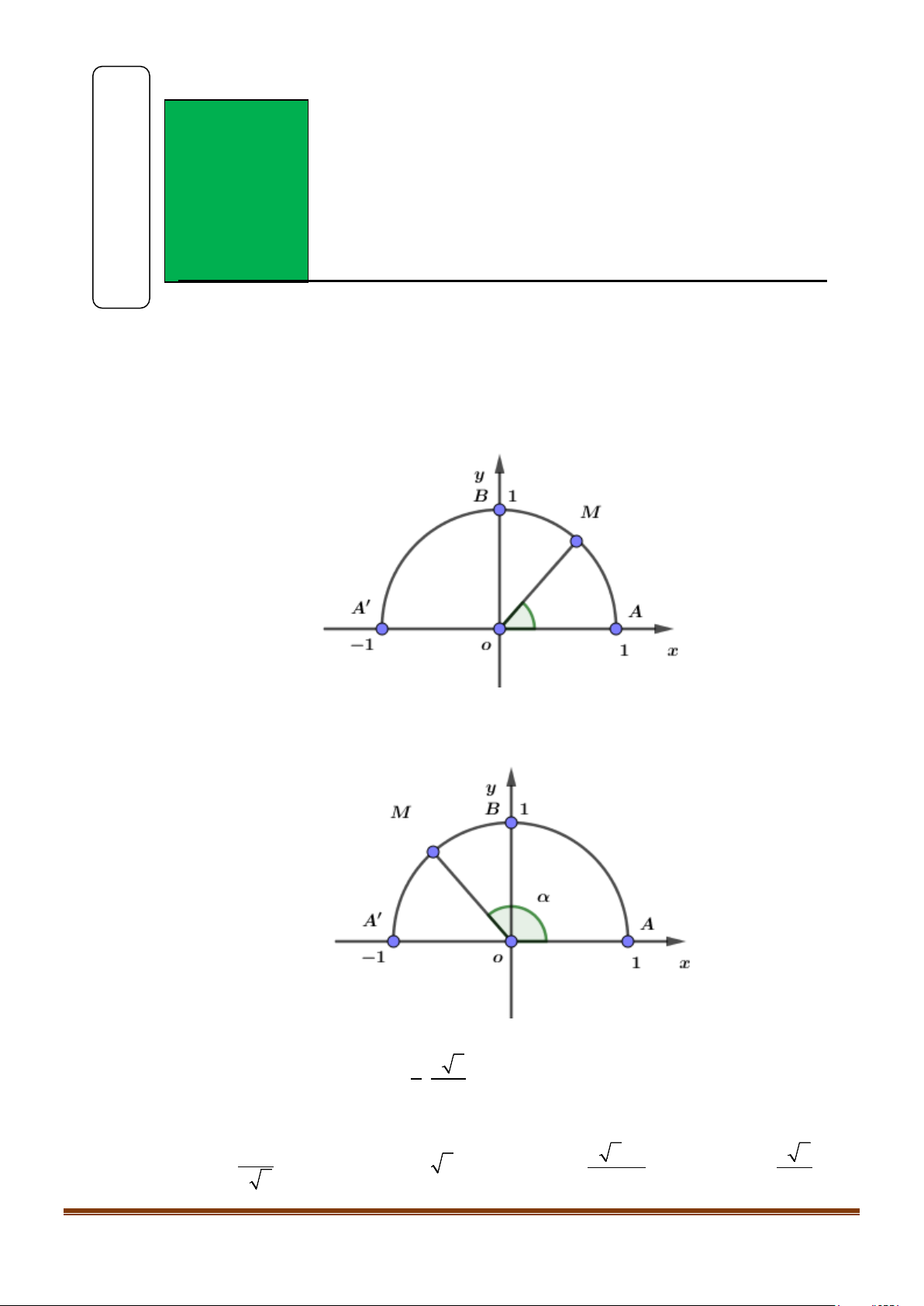
Câu 1: Trên nửa đường tròn đơn vị cho điểm M sao cho
xoM = α như hình bên. Tìm mệnh đề đúng. A. sinα > 0. B. sinα < 0 . C. sinα = 0. D. sinα =1.
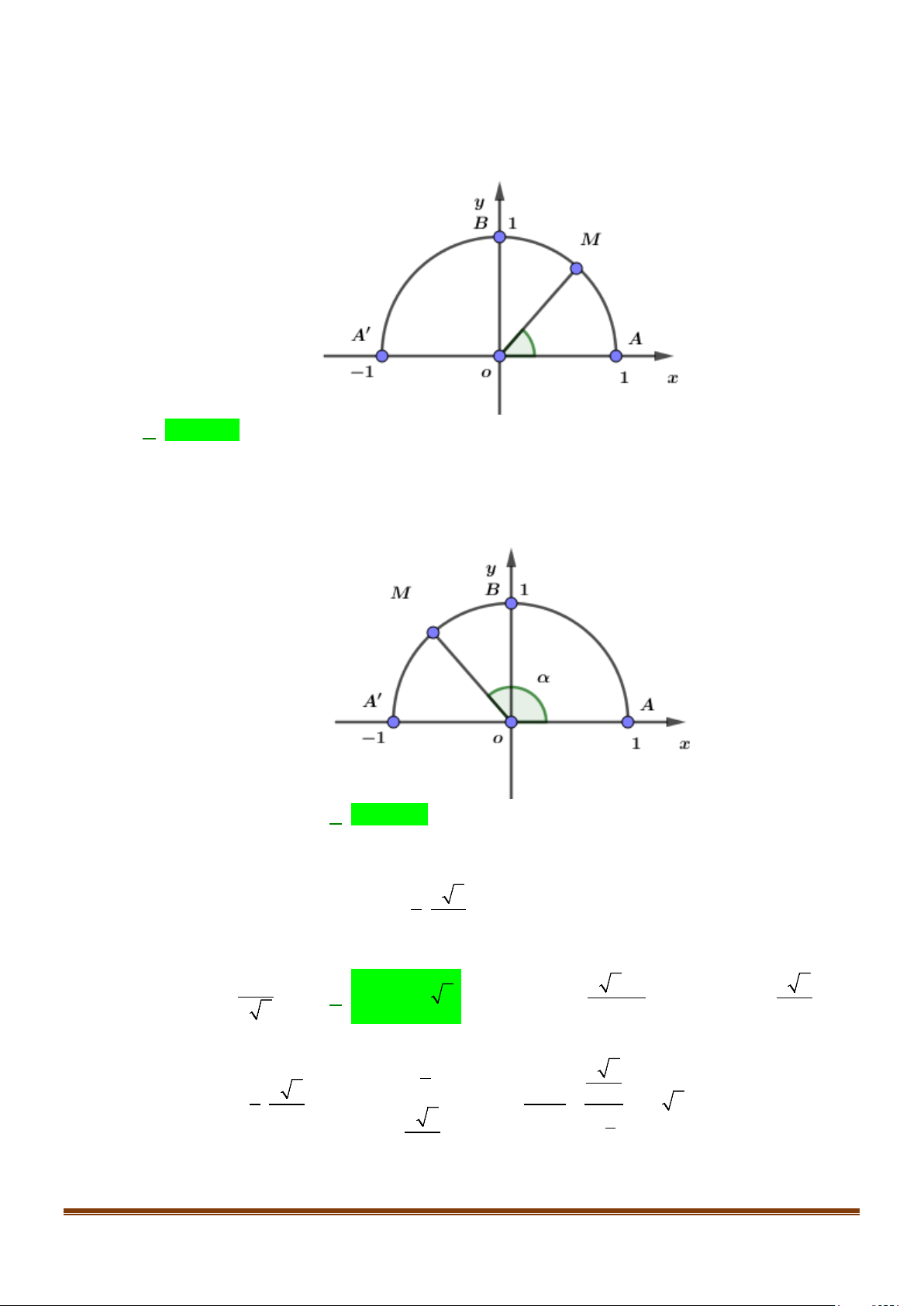
Câu 2: Trên nửa đường tròn đơn vị cho điểm M sao cho
xoM = α như hình bên. Tìm mệnh đề đúng. A. os c α > 0 . B. os c α < 0 . C. os c α = 0 . D. os c α = 1 − .
Câu 3: Cho góc α = xOM với điểm 1 2 2 M − ;
trên nửa đường tròn đơn vị. Giá trị lượng giác của 3 3 tanα là A. 1 tanα = − . B. tanα = 2 − 2 . C. 2 2 1 tanα − = . D. 2 2 tanα = − . 2 2 3 9 Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 4: Cho góc α = xOM với điểm 1 2 2 M ;
trên nửa đường tròn đơn vị. Giá trị lượng giác của 3 3 cotα là A. 1 cotα = . B. cotα = 2 2 . C. 2 2 1 cotα − = . D. 2 2 cotα = . 2 2 3 9
Câu 5: Biểu thức E = sin(180° − x) − 2cos(90° − x) + cos .xtan x (x ≠ 90°) sau khi thu gọn bằng với
biểu thức nào trong 4 biểu thức dưới đây: A. A = 0 . B. B = 2 − sin x .
C. C = sin x . D. D = 2 − cos x .
Câu 6: Cho tam giác ABC , tính giá trị biểu thức P = sin .
A cos(B + C) + cos .
A sin (B + C) A. 0 . B. 1. C. 1 − . D. 2 .
Câu 7: Rút gọn biểu thức A = −sin(180° − x) + cos(180° − x) + cos x ta được
A. A = −sin x .
B. A = sin x .
C. A = 2sin x .
D. A = cos x . Câu 8: Cho 4 cosα = với 0 α 90° < < . Tính sinα . 5 A. 1 sinα = . B. 1 sinα = − . C. 3 sinα = . D. 3 sinα = ± . 5 5 5 5 α Câu 9: Cho cotα = 3
− 2 với 90° < α <180° . Khi đó giá trị cos sinα + bằng: 2 A. 2 19 − − . B. 2 19 . C. 19 . D. 19 . 19 19 19 19 Câu 10: Cho 3 sinα ,(90° α 180° = < < ). Tính P cot(180° = −α ) 5 3 3 4 4 A. P = . B. P = − . C. P = − . D. P = . 4 4 3 3
Câu 11: Cho góc α thỏa mãn 0° α 180° < < , 1 2 cosα = − ,sinα =
. Khẳng định nào sau đây sai? 3 3 A. tanα = − 2 . B. 2 cotα = − . 2 C. ( ° −α) 2 sin 180 = − . D. ( ° −α) 1 cos 180 = . 3 3 2
sin a + tan a
Câu 12: Kết quả rút gọn của biểu thức + 1 bằng cos a +1 1 1 A. 2 . B. 1+ tanα . C. . D. . 2 cos α 2 sin α
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho 0° < α < 90°. a) sinα > 0 b) cot(90° −α) > 0. c) sin(135° −α)<0. α d) sin 90 + ° < 0. 2 Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 2: Cho góc α =
xOM với điểm M (x ; y trên nửa đường tròn đơn vị. 0 0 )
a) sinα = x ;cosα = y 0 0 .
b) Nếu x < 0 < α < 0 thì 0 0 0 90 . c) Nếu 1 2 2 x = ; y = thì giá trị 1 cotα = . 0 0 3 3 2 2 d) Nếu 1 2 2 α − α x = − ; y = thì giá trị tan cot 7 = . 0 0 3 3 tanα + cotα 9 Câu 3: Cho 1
cosα = và 0° < α < 90° . 3 a) tanα > 0. b) ( 0 +α) 2 sin 90 = 3
c) Giá trị tanα = 2 2. 2 + α d) 1 sin 2 =1+ 2 tan α 2 1− sin α Câu 4: Cho 5 sin x =
và 90° < x <180°. 13
a) cos x > 0.
b) Giá trị của biểu thức 2 2 94
P 2sin x cos x − = − = . 169 c) Giá trị 5 tan x = . 12 2
d) Giá trị của biểu thức sin x 25 A = = 2 1+ cos x 313
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1: − Cho góc 3 sin x 2cos x x thỏa mãn 4
cot x = . Tính giá trị của biểu thức: B = − 3 2
sin x cos x + 4sin x Câu 2: Biết 1 cosα − =
. Giá trị đúng của biểu thức 2 2
P = 4sin α + 8tan α là: 2 sin a + 5cos Câu 3: a
Tính giá trị biểu thức C =
khi tan a = 2 . (kết quả làm tròn đến hàng phần trăm) 3 3 sin a − 2cos a 2 2
Câu 4: Giả sử tan x −sin x = tann x . Khi đó n có giá trị là 2 2 cot x − os c x
Câu 5: Tính giá trị của biểu thức 2 2 2 2 2 sin .
a tan a + 4sin a − tan a + 3cos a Câu 6: Cho ,
A B,C là ba góc trong tam giác ABC . Tính giá trị của biểu thức sau: ° + + 2 ° B 2 180 = cos 180 − − cos A C
+ tan B .tan A + C P 2 2 2 2
---------- HẾT --------- Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
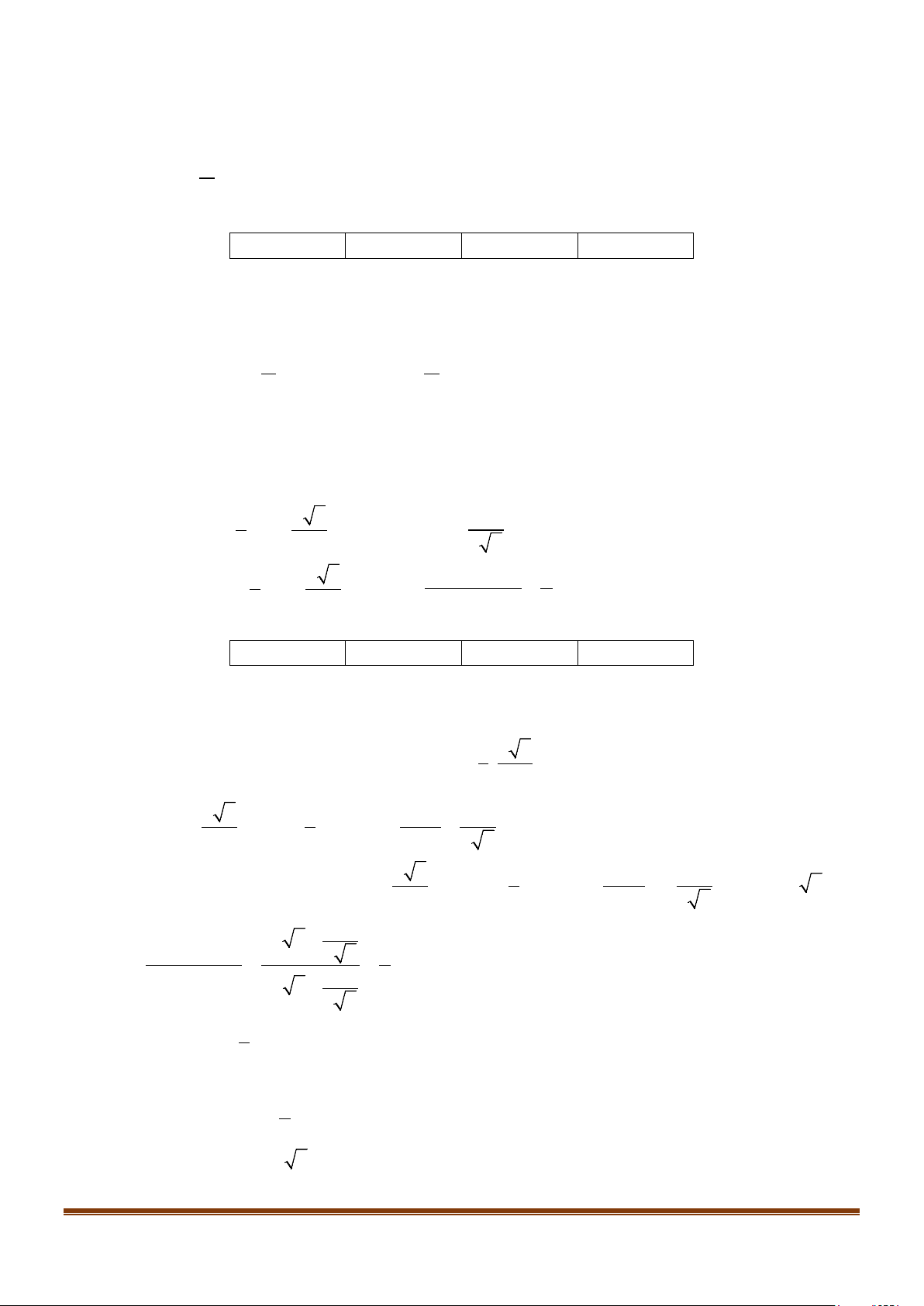
Câu 1: Trên nửa đường tròn đơn vị cho điểm M sao cho
xoM = α như hình bên. Tìm mệnh đề đúng. A. sinα > 0. B. sinα < 0 . C. sinα = 0. D. sinα =1. Lời giải
+) Chiếu điểm M lên trục oy sin 0 .
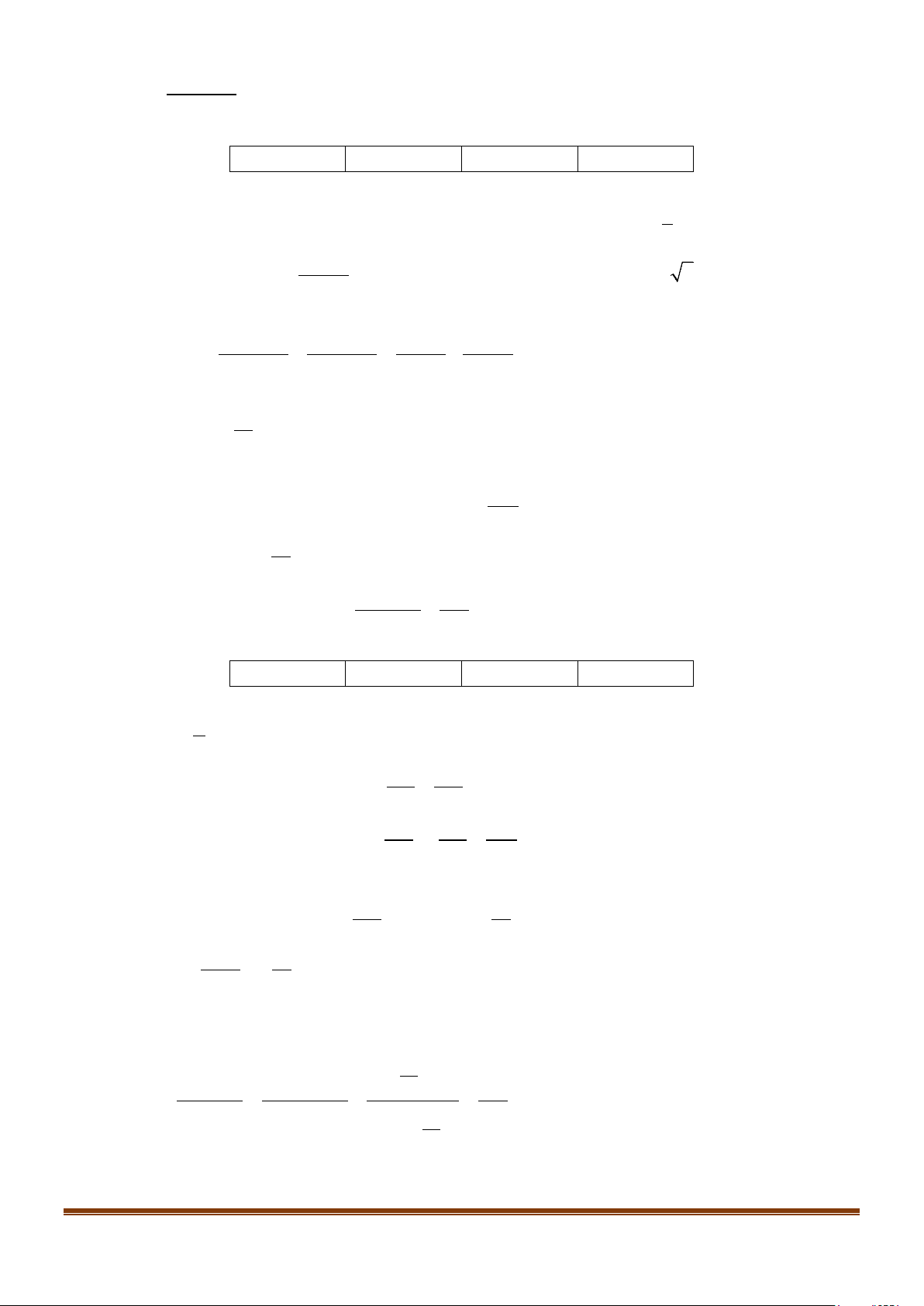
Câu 2: Trên nửa đường tròn đơn vị cho điểm M sao cho
xoM = α như hình bên. Tìm mệnh đề đúng. A. os c α > 0 . B. os c α < 0 . C. os c α = 0 . D. os c α = 1 − . Lời giải
+) Chiếu điểm M lên trục ox cos 0.
Câu 3: Cho góc α = xOM với điểm 1 2 2 M − ;
trên nửa đường tròn đơn vị. Giá trị lượng giác của 3 3 tanα là A. 1 tanα = − . B. tanα = 2 − 2 . C. 2 2 1 tanα − = . D. 2 2 tanα = − . 2 2 3 9 Lời giải 1 2 2 cosα = − Ta thấy 1 2 2 3 sinα 3 M − ; ⇒ ⇒ tanα = = = 2 − 2 . 3 3 2 2 cosα 1 sinα − = 3 3 Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 4: Cho góc α = xOM với điểm 1 2 2 M ;
trên nửa đường tròn đơn vị. Giá trị lượng giác của 3 3 cotα là A. 1 cotα = . B. cotα = 2 2 . C. 2 2 1 cotα − = . D. 2 2 cotα = . 2 2 3 9 Lời giải 1 1 cosα = Ta thấy 1 2 2 3 cosα 3 1 M ; ⇒ ⇒ cotα = = = . 3 3 2 2 sinα 2 2 2 2 sinα = 3 3
Câu 5: Biểu thức E = sin(180° − x) − 2cos(90° − x) + cos .xtan x (x ≠ 90°) sau khi thu gọn bằng với
biểu thức nào trong 4 biểu thức dưới đây: A. A = 0 . B. B = 2 − sin x .
C. C = sin x . D. D = 2 − cos x . Lời giải
Ta có: sin (180° − x) = sin x ; cos(90° − x) = sin x ; sin cos .tan = cos . x x x x = sin x . cos x
Vậy E = sin (180° − x) − 2cos(90° − x) + cos .xtan x (x ≠ 90°)
= sin x − 2sin x + sin x = 0.
Câu 6: Cho tam giác ABC , tính giá trị biểu thức P = sin .
A cos(B + C) + cos .
A sin (B + C) A. 0 . B. 1. C. 1 − . D. 2 . Lời giải
Trong tam giác ABC , có + = ° − B C 180 A .
Suy ra sin (B + C) = sin A ; cos(B + C) = −cos A. Vậy P = sin .
A cos(B + C) + cos .
A sin (B + C) = −sin . A cos A + cos . A sin A = 0 .
Câu 7: Rút gọn biểu thức A = −sin(180° − x) + cos(180° − x) + cos x ta được
A. A = −sin x .
B. A = sin x .
C. A = 2sin x .
D. A = cos x . Lời giải
Ta có A = −sin (180° − x) + cos(180° − x) + cos x
= −sin x − cos x + cos x = −sin x Câu 8: Cho 4 cosα = với 0 α 90° < < . Tính sinα . 5 1 1 3 3 A. sinα = . B. sinα = − . C. sinα = . D. sinα = ± . 5 5 5 5 Lời giải 2 3 Ta có: 2 2 4 9 sin α =1− cos α =1− = ⇒ sinα = ± . 5 25 5 3
Do 0 < α < 90° nên sinα > 0. Suy ra, sinα = . 5 α Câu 9: Cho cotα = 3
− 2 với 90° < α <180° . Khi đó giá trị cos sinα + bằng: 2 Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 2 19 − − . B. 2 19 . C. 19 . D. 19 . 19 19 19 19 Lời giải 1 Ta có 2 =1+ cot α =1+18 =19 2 1 ⇒ sin α = 1 ⇒ sinα = ± 2 sin α 19 19
Vì 90° < α <180° ⇒ sinα > 0 1 3 2 ⇒ sinα = ⇒ cosα = sinα.cotα = − 19 19 cosα 1 3 2 19 Suy ra sinα + = − = − . 2 19 19 19 Câu 10: Cho 3 sinα ,(90° α 180° = < < ). Tính P cot(180° = −α ) 5 3 3 4 4 A. P = . B. P = − . C. P = − . D. P = . 4 4 3 3 Lời giải Do ° ° 1 25 4
90 < α <180 ⇒ cotα < 0 ⇒ cotα = − −1 = − −1 = − . 2 sin α 9 3 P ( ° = −α ) 4 cot 180 = −cotα = 3
Câu 11: Cho góc α thỏa mãn 0° α 180° < < , 1 2 cosα = − ,sinα =
. Khẳng định nào sau đây sai? 3 3 A. tanα = − 2 . B. 2 cotα = − . 2 C. ( ° −α) 2 sin 180 = − . D. ( ° −α) 1 cos 180 = . 3 3 Lời giải α Ta có: sin tanα = = − 2 ; cosα 2 cotα = = − ; ( ° −α) 1 cos 180 = −cosα = . cosα sinα 2 3 ( ° −α) 2 sin 180 = sinα = . 3 2
sin a + tan a
Câu 12: Kết quả rút gọn của biểu thức + 1 bằng cos a +1 1 1 A. 2 . B. 1+ tanα . C. . D. . 2 cos α 2 sin α Lời giải
sin a(cosa + ) 2 1 2 2 sin a tan a cosa + sin a 1 Ta có 2 + 1 = +1 = + 1 = tan a +1 = . 2 cos a +1 cosa +1 cos a cos a
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho 0° < α < 90°. Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC a) sinα > 0 b) cot(90° −α) > 0. c) sin(135° −α)<0. α d) sin 90 + ° < 0. 2 Lời giải a) Đúng b) Đúng c) Sai d) Sai
a) Ta có: 0° < α < 90°⇒ sinα > 0. Đúng. b) Ta có: 0
cot(90 −α) = tanα > 0 . Đúng.
c) Ta có: 45° <135° −α <135° ⇒ sin(135° −α) > 0 Sai. α α
d) Ta có: 90° < + 90° <135° ⇒ sin( + 90 ) ° > 0 . Sai. 2 2
Câu 2: Cho góc α =
xOM với điểm M (x ; y trên nửa đường tròn đơn vị. 0 0 )
a) sinα = x ;cosα = y 0 0 .
b) Nếu x < 0 < α < 0 thì 0 0 0 90 . c) Nếu 1 2 2 x = ; y = thì giá trị 1 cotα = . 0 0 3 3 2 2 d) Nếu 1 2 2 α − α x = − ; y = thì giá trị tan cot 7 = . 0 0 3 3 tanα + cotα 9 Lời giải a) Sai b) Sai c) Đúng d) Đúng
a) Khẳng định SAI vì điểm M (x ; y trên nửa đường tròn đơn vị thì sinα = y ;cosα = x 0 0 ) 0 0
b) Khẳng định SAI vì x < 0 ° < α 0 thì 90 < 180° .
c) Khẳng định ĐÚNG vì điểm 1 2 2 M ;
trên nửa đường tròn đơn vị thì 3 3 2 2 1 cosα 1 sinα = ,cosα = ⇒ cotα = = . 3 3 sinα 2 2 d α
) Khẳng định ĐÚNG vì 2 2 1 cos 1 sinα = ,cosα = − ⇒ cotα = = − , tanα = 2 − 2 nên 3 3 sinα 2 2 1 2 − 2 + tanα − cotα 2 2 7 = = . tanα + cotα 1 9 2 − 2 − 2 2 Câu 3: Cho 1
cosα = và 0° < α < 90° . 3 a) tanα > 0. b) ( 0 +α) 2 sin 90 = 3
c) Giá trị tanα = 2 2. Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 + α d) 1 sin 2 =1+ 2 tan α 2 1− sin α Lời giải a) Đúng b) Sai c) Đúng d) Đúng a) Vì 0 0
0 < α < 90 nên tanα > 0. Vậy mệnh đề Đúng. b) Ta có: ( 0 +α) = ( 0 0 − −α ) = ( 0 −α) 1 sin 90 sin 180 90 sin 90
= cosα = . Vậy mệnh đề Sai 3 c) Ta có 2 1 2 2 tan α +1 =
⇔ tan α +1 = 9 ⇔ tan α = 8 ⇔ tanα = 2 2 2 cos α
Vậy mệnh đề Đúng. 2 2 2 + α + α α d) Ta có: 1 sin 1 sin 1 sin 2 2 2 = = +
= tan α +1+ tan α = 2 tan α +1 2 2 2 2 1− sin α cos α cos α cos α
Vậy mệnh đề đúng. Câu 4: Cho 5 sin x =
và 90° < x <180°. 13
a) cos x > 0.
b) Giá trị của biểu thức 2 2 94
P 2sin x cos x − = − = . 169 c) Giá trị 5 tan x = . 12 2
d) Giá trị của biểu thức sin x 25 A = = 2
1+ cos x 313Lời giải a) Sai b) Đúng c) Sai d) Đúng
a) Do π < x < π nên cos x < 0. Vậy mệnh đề sai. 2 b) Ta có: 2 2 25 144
cos x =1− sin x =1− = . 169 169 − Do đó 2 2 25 144 94
P = 2sin x − cos x = 2. − = . 169 169 169 Vậy mệnh đề đúng.
c) Do cos x < 0 và 2 144 cos x = nên 12 cos x = − . 169 13 sin x 5 tan x = = − . cos x 12
Vậy mệnh đề sai. d) Ta có: 2 5 2 2 sin x sin x 13 25 A = = = = 2 2 2
1+ cos x 1+1− sin x 5 313 1+1− 13
Vậy mệnh đề đúng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Page 8
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 1: − Cho góc 3 sin x 2cos x x thỏa mãn 4
cot x = . Tính giá trị của biểu thức: B = − 3 2
sin x cos x + 4sin x Lời giải Trả lời: 8,65 Ta có: 3 sin x − 2cos x = − = ( 2 1− 2cot 3 1+ cot x B x − 2 )
sin x cos x + 4sin x cot x + 4 4 2 1− 2 4 3 415 = 31+ − = 3 4 48 + 4 3 Câu 2: Biết 1 cosα − =
. Giá trị đúng của biểu thức 2 2
P = 4sin α + 8tan α là: 2 Lời giải Trả lời: 27 Ta có 2 2 2 1
P 4sin α 8tan α 4(1 cos α) 8 1 = + = − + − 2 cos α 1 P 4 1 = − + 8(4 − ) 1 = 3+ 24 = 27 4 sin a + 5cos Câu 3: a
Tính giá trị biểu thức C =
khi tan a = 2 . (kết quả làm tròn đến hàng phần trăm) 3 3
sin a − 2cos a Lời giải Trả lời: 5,83 sin a + 5cos a tan a( 2 1+ tan a) + 5( 2 1+ tan a) C = 35 = = . 3 3 sin a − 2cos a 3 tan a − 2 6 2 2
Câu 4: Giả sử tan x −sin x = tann x . Khi đó n có giá trị là 2 2 cot x − os c x Lời giải Trả lời: 6 2 − 4 1 1 cos x 2 2 sin sin x − 1 sin x x 2 2 2 2 4 2 2 tan x − sin x cos x cos x
cos x sin x sin x 6 = = = = . = tan x 2 2 2 4 2 4 cot x − os c x 2 1
1− sin x cos x 2 cos x cos cos x − 1 x 2 cos x 2 2 sin x sin x sin x Vậy n = 6 .
Câu 5: Tính giá trị của biểu thức 2 2 2 2 2 sin .
a tan a + 4sin a − tan a + 3cos a Lời giải Trả lời: 3 Ta có 2 2 2 2 2 2 1 2 2 2 sin .
a tan a + 4sin a − tan a + 3cos a = sin a
−1 + 4sin a − tan a + 3cos a 2 cos a 2 sin a 2 2 2 2 2 2 =
− sin a + 4sin a − tan a + 3cos a = 3sin a + 3cos a = 3. 2 cos a Page 9
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 6: Cho ,
A B,C là ba góc trong tam giác ABC . Tính giá trị của biểu thức sau: ° + + 2 ° B 2 180 = cos 180 − − cos A C
+ tan B .tan A + C P 2 2 2 2 Lời giải Trả lời: 1 Ta có: + + + − ° ° 180° A C 180° 180° 180 180 cos cos B cos180° B A B C A C B + + = ⇔ + = − ⇒ = = − 2 2 2
A + B + C 90° A+C 90° B tan A+C tan90° B = ⇒ = − ⇒ = − = cot B . 2 2 2 2 2 2 ° + + Khi đó: 2 ° B 2 180 = cos 180 − − cos A C
+ tan B .tan A + C P 2 2 2 2 2 ° B 2 cos 180 cos 180° B = − − − + tan B .cot B = 1. 2 2 2 2
---------- HẾT ---------- Page 10
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC NG ƯƠ III HỆ THỨC LƯỢNG TRONG TAM GIÁC CH
BÀI. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180° ĐỀ TEST SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
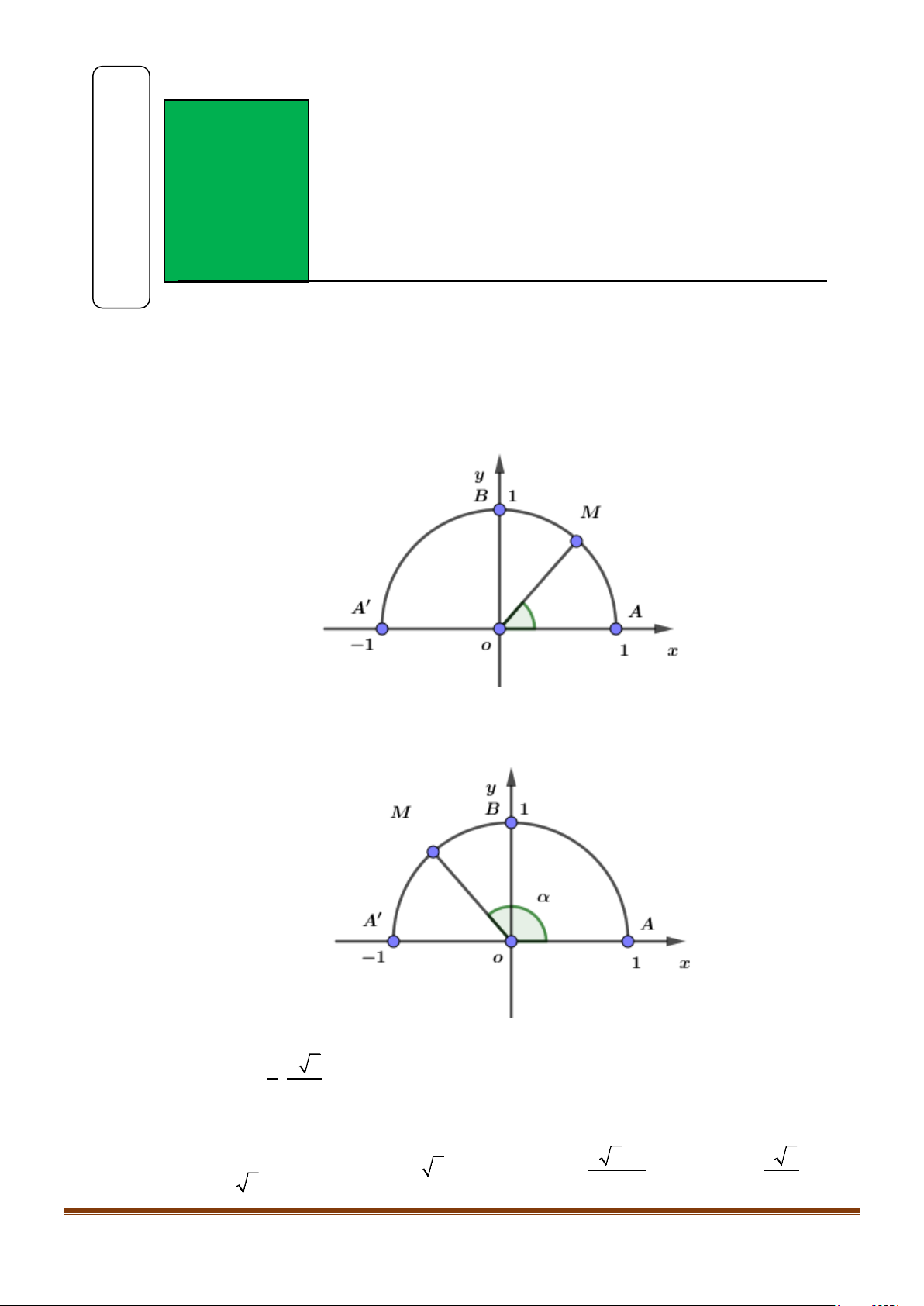
Câu 1: Trên nửa đường tròn đơn vị cho điểm M sao cho
xoM = α như hình bên. Tìm mệnh đề đúng. A. os c α > 0 . B. os c α < 0 . C. os c α = 0 . D. os c α = 1 − .
Câu 2: Trên nửa đường tròn đơn vị cho điểm M sao cho
xoM = α như hình bên. Tìm mệnh đề đúng. A. sinα > 0. B. sinα < 0 . C. sinα = 0. D. sinα =1. Câu 3: Cho điểm 1 2 2 M − ;
trên nửa đường tròn đơn vị. Gọi góc α =
xOM ′ với M ′ là điểm đối 3 3
xứng với M qua trục Oy . Giá trị lượng giác của tanα là A. 1 tanα = . B. tanα = 2 2 . C. 2 2 1 tanα − = . D. 2 2 tanα = . 2 2 3 9 Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 4: Cho điểm 2 2 M − ;
trên nửa đường tròn đơn vị. Gọi góc α =
xOM ′ với M ′ là điểm đối 2 2
xứng với M qua trục Oy . Khẳng định nào sau đây đúng? A. cosα < 0 . B. cosα > 0 . C. cotα < 0 . D. tanα < 0.
Câu 5: Rút gọn biểu thức S = cos(90° − x)sin(180° − x) −sin(90° − x)cos(180° − x) ta được
A. S = 0. B. 2 2
S = sin x − cos .x C. S = 2sin xcos .x D. S =1.
Câu 6: Tính A = sin(180° − x) + sin(90° − x) + cos(180° − x) − cos(90° − x) . A. 0. B. 1. C. 2 . D. 1 − .
Câu 7: Tính M = tan1°.tan 2°.tan3°...tan89° . A. 1. B. 2 . C. 1 − . D. 1 . 2
Câu 8: Tính A = cos10° + cos30° + cos50° +...+ cos150° + cos170° . A. 0 . B. 2 . C. 1 − . D. 1. Câu 9: Tính 2 2 2 2
A = cos 15° + cos 75° + cos 105° + cos 165° . A. 0. B. 1. C. 2. D. 1 − . 2 2 4
sin x − cos x + cos x Câu 10: Cho 0 A =
0 ≤ x ≤180 . Chọn mệnh đề đúng trong các mệnh đề sau. 2 2 4 ( 0 )
cos x −sin x + sin x + A. 4 A = tan x . B. sin x cos x A = . C. 4 A = cot x . D. 2 A = cot x . sin x Câu 11: 3
Cho sin x + cos x = ( 0 0
0 ≤ x ≤180 ) . Biểu thức B = sin x − cos x bằng 4 9 A. 3 . B. 23 . C. 23 . D. 4 16 4 16 . Câu 12: Cho 2 0 2 0 2 0 2 0
D = cos 10 + cos 20 + cos 30 +...+ cos 180 . Chọn mệnh đề đúng trong các mệnh đề sau. A. D = 0 . B. D = 8. C. D = 2022 . D. D =18 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. Câu 1: Cho 1
sinα = với 90° < α <180° . 3
a) Điểm M trên nửa đường tròn đơn vị phía trên trục Ox sao cho
xOM = α thì M có tung độ bằng 1 . 3 b) Giá trị 2 2 cosα = . 3 c) Giá trị cotα = 2 − 2 .
d) Giá trị tanα + 3cotα 25 = . tanα + cotα 9 Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 2: 1
Cho tanα = với 0° < α < 90° . 2 a) ( 0
sin 180 −α ) < 0. b) Giá trị ( 0 −α) 2 cos 180 = . 5 c) Giá trị 2 cot α = 2.
d) Giá trị sinα + 3cosα = 7. sinα − cosα Câu 3: Cho 1
sinα = với 90° < α <180° . 3
a) cos(180° −α ) < 0 . b) 2 2 cosα = − . 3 c) 2 cot α = 8 .
d) 5tanα + cotα = 4 . tanα + cotα
Câu 4: Cho tan a − cot a = 3 . a) 2 2
A = tan a + cot a =11.
b) B = tan a + cot a = 13 . c) 4 4
C = tan a − cot a = ± 33 13 . d) 6 6
D = tan a − cot a =36.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hai góc α và β với α + β =180°, tìm giá trị của biểu thức: P =1−sinα sin β + cosα cos β Câu 2: Cho 1
sinα = − . Tính giá trị biểu thức 2 2
P = 2cos α − 4sin α . (kết quả làm tròn đến hàng phần trăm) 4
Câu 3: Cho α là góc tù và 4
sinα = . Giá trị của biểu thức A = sinα − 2cosα là 5 2 2
Câu 4: Cho góc x thỏa mãn + + 0 sin x 2cos x 1
° < x <180°và tan x = 3, giá trị của biểu thức A = là 2 2
3sin x + cos x −1
(kết quả làm tròn đến hàng phần trăm) Câu 5: +
Tính giá trị biểu thức sin a 5cos a C =
khi tan a = 2 . (kết quả làm tròn đến hàng phần trăm) 3 3 sin a − 2cos a
Câu 6: Cho tam giác ABC . Tính giá trị biểu thức P = sin .
A cos(B + C) + cos .
A sin (B + C)
---------- HẾT ---------- Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
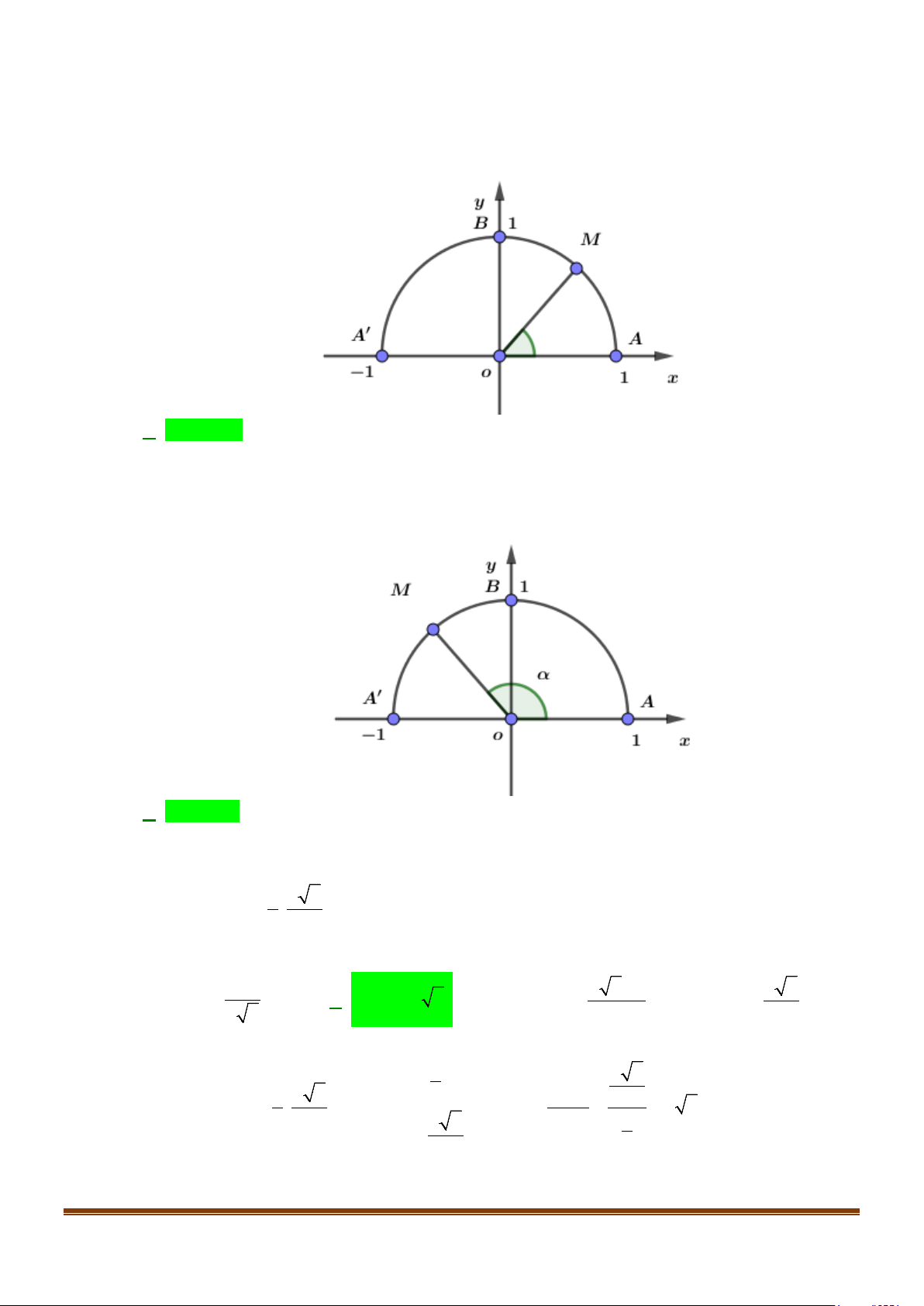
Câu 1: Trên nửa đường tròn đơn vị cho điểm M sao cho
xoM = α như hình bên. Tìm mệnh đề đúng. A. os c α > 0 . B. os c α < 0 . C. os c α = 0 . D. os c α = 1 − . Lời giải
+) Chiếu điểm M lên trục ox cos 0.
Câu 2: Trên nửa đường tròn đơn vị cho điểm M sao cho
xoM = α như hình bên. Tìm mệnh đề đúng. A. sinα > 0. B. sinα < 0 . C. sinα = 0. D. sinα =1. Lời giải
+) Chiếu điểm M lên trục oy sin 0 . Câu 3: Cho điểm 1 2 2 M − ;
trên nửa đường tròn đơn vị. Gọi góc α =
xOM ′ với M ′ là điểm đối 3 3
xứng với M qua trục Oy . Giá trị lượng giác của tanα là A. 1 tanα = . B. tanα = 2 2 . C. 2 2 1 tanα − = . D. 2 2 tanα = . 2 2 3 9 Lời giải 1 2 2 cosα = Theo bài 1 2 2 3 sinα 3 ⇒ M ′ ; ⇒ ⇒ tanα = = = 2 2 . 3 3 2 2 cosα 1 sinα = 3 3 Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 4: Cho điểm 2 2 M − ;
trên nửa đường tròn đơn vị. Gọi góc α =
xOM ′ với M ′ là điểm đối 2 2
xứng với M qua trục Oy . Khẳng định nào sau đây đúng? A. cosα < 0 . B. cosα > 0 . C. cotα < 0 . D. tanα < 0. Lời giải 2 cosα = > 0 Theo bài 2 2 2 ⇒ M ′ ; ⇒ ⇒ tanα > 0, cotα > 0 . 2 2 2 sinα = > 0 2
Câu 5: Rút gọn biểu thức S = cos(90° − x)sin(180° − x) −sin(90° − x)cos(180° − x) ta được
A. S = 0. B. 2 2
S = sin x − cos .x C. S = 2sin xcos .x D. S =1. Lời giải
S = cos(90° − x)sin(180° − x) −sin(90° − x)cos(180° − x) = x x − x(− x) 2 2 sin .sin cos
cos = sin x + cos x =1.
Câu 6: Tính A = sin(180° − x) + sin(90° − x) + cos(180° − x) − cos(90° − x) . A. 0. B. 1. C. 2 . D. 1 − . Lời giải
A = sin (180° − x) + sin(90° − x) + cos(180° − x) − cos(90° − x)
= sin x + cos x − cos x − sin x = 0 .
Câu 7: Tính M = tan1°.tan 2°.tan3°...tan89° . A. 1. B. 2 . C. 1 − . D. 1 . 2 Lời giải
Ta có: tan (90° −α ) = cotα và tanα.cotα =1. Suy ra:
M = tan1°.tan 2°.tan 3°...tan89°
= tan1°.tan 2°.tan 3°...tan (90° − 2°).tan (90° −1°)
= (tan1°.cot1°).(tan 2°.cot 2°)...(tan 44°.cot 44°).tan 45° =1.1.1...1 =1.
Câu 8: Tính A = cos10° + cos30° + cos50° +...+ cos150° + cos170° . A. 0 . B. 2 . C. 1 − . D. 1. Lời giải
Do cos(180° −α ) = −cosα ⇒ cos(180° −α ) + cosα = 0. Suy ra:
A = (cos10° + cos170°) + (cos30° + cos150°) +...+ cos90° = cos90° = 0 . Câu 9: Tính 2 2 2 2
A = cos 15° + cos 75° + cos 105° + cos 165° . A. 0. B. 1. C. 2. D. 1 − . Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC Lời giải
Ta có: cos165° = cos(180° −15°) = −cos15°; cos105° = cos(180° − 75°) = −cos75° . Suy ra: 2 2 2 2
A = cos 15° + cos 75° + cos 105° + cos 165° 2 2
= cos 15° + cos 75° + (−cos75°)2 + (−cos15°)2 = ( 2 2 2 cos 15° + cos 75°) = ( 2 2
2 cos 15° + cos (90° −15°)) = ( 2 2 2 cos 15° + sin 15°) = 2 . 2 2 4
sin x − cos x + cos x Câu 10: Cho 0 A =
0 ≤ x ≤180 . Chọn mệnh đề đúng trong các mệnh đề sau. 2 2 4 ( 0 )
cos x −sin x + sin x + A. 4 A = tan x x x . B. sin cos A = . C. 4 A = cot x . D. 2 A = cot x .
sin x Lời giải 2 2 4
sin x − cos x + cos x Ta có: A = 2 2 4
cos x −sin x + sin x 2 2 2 2 2 2 2 2 4
sin x − cos x(1− cos x) sin x − cos .xsin x sin x(1− cos x) sin x 4 = = = = = tan x 2 2 2 2 2 2 2 2 4
cos x − sin x(1− sin x) cos x − sin .xcos x cos x(1− sin x) cos x 3
Câu 11: Cho sin x + cos x = ( 0 0
0 ≤ x ≤180 ) . Biểu thức B = sin x −cos x bằng 4 9 A. 3 . B. 23 . C. 23 . D. 4 16 4 16 . Lời giải 3 9
*sin x + cos x = ⇔ ( sin x + cos x)2 = 4 16 2 2 9 9 7
⇔ sin x + cos x + 2sin .xcos x =
⇔ 1+ 2sin .xcos x =
⇔ 2sin .xcos x = − 16 16 16 * 2 B = ( x − x)2 2 2 7 23 23 sin cos
= sin x + cos x − 2sin .xcos x =1+ = ⇒ B = 16 16 4 Câu 12: Cho 2 0 2 0 2 0 2 0
D = cos 10 + cos 20 + cos 30 +...+ cos 180 . Chọn mệnh đề đúng trong các mệnh đề sau. A. D = 0 . B. D = 8. C. D = 2022 . D. D =18 . Lời giải Công thức áp dụng: 2 2 sin α + cos α =1 ( 0 −α) 0 0 0 0 0 0 0 0 cos 90
= sinα ⇒ cos80 = sin10 ,cos70 = sin 20 , cos60 = sin 30 , cos50 = sin 40 0 0 0 0 0 0 0
cos(180 −α) = −cosα ⇒ cos170 = −cos10 , cos160 = −cos 20 ,..., cos100 = −cos80 Ta có: 2 0 2 0 2 0 2 0
D = cos 10 + cos 20 + cos 30 +...+ cos 180 2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0
= cos 10 + cos 20 +...+ cos 80 + cos 90 + cos 100 +...+ cos 160 + cos 170 + cos 180 2 0 2 0 2 0 2 0 2 0 2 0 2 0
= cos 10 + cos 20 +...+ cos 80 + cos 90 + cos 80 +...+ cos 20 + cos 10 +1 Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC = ( 2 0 2 0 2 0 + + + ) 2 0
2 cos 10 cos 20 ... cos 80 + cos 90 +1 = ( 2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0
2 cos 10 + cos 20 + cos 30 + cos 40 + cos 50 + cos 60 + cos 70 + cos 80 )+ 0 +1 = ( 2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0
2 cos 10 + cos 20 + cos 30 + cos 40 + sin 40 + sin 30 + sin 20 + sin 10 )+1 = ( 2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0
2 sin 10 + cos 10 + sin 20 + cos 20 + sin 30 + cos 30 + sin 40 + cos 40 )+1 = 2(1+1+1+ ) 1 +1= 9
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. Câu 1: Cho 1
sinα = với 90° < α <180° . 3
a) Điểm M trên nửa đường tròn đơn vị phía trên trục Ox sao cho
xOM = α thì M có tung độ bằng 1 . 3 b) Giá trị 2 2 cosα = . 3 c) Giá trị cotα = 2 − 2 .
d) Giá trị tanα + 3cotα 25 = . tanα + cotα 9 Lời giải a) Đúng b) Sai c) Đúng d) Đúng
a.) Khẳng định đúng vì điểm M trên nửa đường tròn đơn vị phía trên trục Ox sao cho xOM = α có 1 y = α ⇔ y = . M sin M 3
b.) Vì 90° < α <180° nên cosα < 0 mặt khác 2 2 sin α + cos α =1 suy ra 2 1 2 2
cosα = − 1− sin α = − 1− = − 9 3
c.) Vì 90° < α <180° nên cotα < 0 . Ta có 1 2 1 = 1+ cot α ⇒ cotα = − −1 = 2 − 2 . 2 2 sin α sin α
d.) Vì 90° < α <180° nên tanα <;cotα < 0 . Ta có 1 2 1 = 1+ cot α ⇒ cotα = − −1 = 2 − 2 . 2 2 sin α sin α 1 tanα.cotα =1 ⇔ tanα = − . 2 2 Vậy tanα + 3cotα 25 = . tanα + cotα 9 Câu 2: 1
Cho tanα = với 0° < α < 90° . 2 a) ( 0
sin 180 −α ) < 0. Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC b) Giá trị ( 0 −α) 2 cos 180 = . 5 c) Giá trị 2 cot α = 2.
d) Giá trị sinα + 3cosα = 7. sinα − cosα Lời giải a) Sai b) Sai c) Sai d) Sai π
a) Mệnh đề sai vì 0 < α < thì sinα > 0, ta có ( 0
sin 180 −α ) = sinα > 0. 2 b) Mệnh đề sai Vì vì π
0 < α < thì cosα > 0 2 Giá trị ( 0 −α) 1 2 cos 180 = − cosα = − = − . 2 1+ tan α 5 c) Mệnh đề sai 1 cotα = = 2 nên 2 cot α = 4. tanα d) Mệnh đề sai sinα +3 α α + Do cosα cos tan 3 ≠ 0 nên = = 7 sinα − . tanα −1 −1 cosα Câu 3: Cho 1
sinα = với 90° < α <180° . 3
a) cos(180° −α ) < 0 . b) 2 2 cosα = − . 3 c) 2 cot α = 8 .
d) 5tanα + cotα = 4 . tanα + cotα Lời giải a) Sai b) Đúng c) Đúng d) Đúng
a) Mệnh đề sai vì 90° < α <180° ⇒ cosα < 0 mà cos(180° −α ) = −cosα > 0
b) Mệnh đề đúng vì 90° < α <180° nên cosα < 0 . 2 Do đó: 2 1 2 2 cosα = − 1− sin α = 1− = − . 3 3
c) Mệnh đề đúng vì 2 1 1 cot α = −1 = −1 = 8. 2 2 sin α 1 3 d) Mệnh đề sai Page 8
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC 5 1 + cotα 2 4 + 2 5tanα + cotα cotα 5 + cot α sin α 9 + 4 13 = = = = = . 2 tanα + cotα 1 1+ cot α 1 9 9 + cotα 2 cotα sin α
Câu 4: Cho tan a − cot a = 3 . a) 2 2
A = tan a + cot a =11.
b) B = tan a + cot a = 13 . c) 4 4
C = tan a − cot a = ± 33 13 . d) 6 6
D = tan a − cot a =36. Lời giải a) Đúng b) Sai c) Đúng d) Đúng a) Ta có: 2 2 2
tan a − cot a = 3⇔ (tan a − cot a) = 9⇔ tan a + cot a − 2 = 9 2 2
⇒ tan a + cot a =11 Do đó, A đúng. b)Theo câu a), ta có: 2 2 2 2
A = tan a + cot a =11 ⇔ tan a + cot a + 2.tan . a cot a =13 2
⇔ (tan a + cot a) =13⇒ tan a + cot a = ± 13 . Do đó, B sai. c)Ta có: 4 4 2 2 2 2
C = tan a − cot a =(tan a − cot a)(tan a + cot a) 2 2
= (tan a − cot a)(tan a + cot a)(tan a + cot a) = 3 ± 3 13 . Do đó, C đúng. d) Ta có: 6 6 2 3 2 3
D = tan a − cot a = (tan a) − (cot a) 2 2
= (tan a − cot a)(tan a + cot a + tan . a cot a)= 36 Do đó, D đúng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hai góc α và β với α + β =180°, tìm giá trị của biểu thức: P =1−sinα sin β + cosα cos β Lời giải Trả lời: 0 si n β = sinα
Vì 2 góc α và β bù nhau nên ta có: cos β = −cosα
Do đó: P =1− sinα sinα − cosα cosα P = − ( 2 2 1 sin α + cos α ) P =1−1 = 0 Câu 2: Cho 1
sinα = − . Tính giá trị biểu thức 2 2
P = 2cos α − 4sin α . (kết quả làm tròn đến hàng phần trăm) 4 Lời giải Trả lời: 1,63 2 1 sin α = Do 1 sinα = − 16 ⇒ 4 2 2 1 15 cos α =1− sin α =1− = 16 16 Page 9
Sưu tầm và biên soạn
CHUYÊN ĐỀ III – TOÁN 10 – CHƯƠNG III – HỆ THỨC LƯỢNG TRONG TAM GIÁC Vậy 15 1 13 P = 2. − 4. = . 16 16 8
Câu 3: Cho α là góc tù và 4
sinα = . Giá trị của biểu thức A = sinα − 2cosα là 5 Lời giải Trả lời: 2 2 Vì 4 sinα = 2 2 4 9 ⇒ cos α =1− sin α =1− = 5 5 25 3 cosα − ⇒ = . 5 Vậy 4 3 A 2. = − − = 2. 5 5 2 2
Câu 4: Cho góc x thỏa mãn + + 0 sin x 2cos x 1
° < x <180°và tan x = 3, giá trị của biểu thức A = là 2 2
3sin x + cos x −1
(kết quả làm tròn đến hàng phần trăm) Lời giải Trả lời: 1,17 2 2 2 2 Ta có
sin x + 2cos x +1 tan x + 2 + (1+ tan x) 9 + 2 + (1+ 9) 7 A = = = = . 2 2 2 2
3sin x + cos x −1 3tan x +1− (1+ tan x) 3.9 +1− (1+ 9) 6 Câu 5: +
Tính giá trị biểu thức sin a 5cos a C =
khi tan a = 2 . (kết quả làm tròn đến hàng phần trăm) 3 3
sin a − 2cos a Lời giải Trả lời: 5,83 sin a + 5cos a tan a( 2 1+ tan a) + 5( 2 1+ tan a) C = 35 = = . 3 3 sin a − 2cos a 3 tan a − 2 6
Câu 6: Cho tam giác ABC . Tính giá trị biểu thức P = sin .
A cos(B + C) + cos .
A sin (B + C) Lời giải Trả lời: 0 Ta có + + 0 = ⇒ + 0 = − A B C 180 B C 180 A Do đó: (B +C) = ( 0 cos
cos 180 − A) = −cos A và (B + C) = ( 0 sin
sin 180 − A) = sin A Vậy: P = sin .
A cos(B + C) + cos .
A sin (B + C) = −sin . A cos A + cos . A sin A = 0 .
---------- HẾT ---------- Page 10
Sưu tầm và biên soạn