157 trang 3 lượt tải

Đề kiểm tra theo bài học chủ đề phương pháp tọa độ trong không gian

5

Tài liệu gồm 157 trang, được biên soạn bởi thầy giáo Huỳnh Văn Ánh, tuyển tập bộ đề kiểm tra theo bài học chủ đề phương pháp tọa độ trong không gian môn Toán 12, có đáp án và lời giải chi tiết.

Chủ đề: Đề thi Toán 12 501 tài liệu

Môn: Toán 12 4.1 K tài liệu

Tác giả:

Profile

Linh Đan

1 ngày trước
Danh sách Quiz
/157
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 1
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
BÀI: PHƯƠNG TRÌNH MẶT PHẲNG
ĐỀ TEST SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:2 3 2 0P x yz+ ++=
. Véctơ nào dưới
đây là một véctơ pháp tuyến của
( )
P
?
A.
( )
2
2; 3;1n
. B.
(
)
3
2; 3; 2n
. C.
( )
1
2; 3; 0n
. D.
( )
4
2; 0;3n
.
Câu 2: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
Điểm nào dưới đây
thuộc
( )
P
?
A.
( )
0; 0; 5P −
. B.
( )
1;1; 6M
. C.
( )
2; 1; 5Q −
. D.
(
)
5;0;0N
−
.
Câu 3: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(
)
1; 2; 0
A −
và
( )
3; 0; 2B
. Mặt phẳng trung
trực của đoạn thẳng
AB
có phương trình là
A.
30xyz
++−=
. B.
2 20
xyz
−++=
. C.
2 40xyz++−=
. D.
2 20xyz−+−=
.
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, phương trình nào dưới đây là phương trình mặt phẳng đi
qua điểm
( )
1; 2; 3M −
và có một vectơ pháp tuyến
( )
1; 2; 3
n = −
.
A.
2 3 12 0xyz−++=
. B.
2 3 60xyz− − −=
. C.
2 3 12 0xyz−+−=
. D.
2 3 60xyz− − +=
.
Câu 5: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
1;1; 1A −
,
( )
2; 1; 0B
( )
1; 1; 2C −
. Mặt phẳng
đi qua
A
và vuông góc với đường thẳng
BC
có phương trình là
A.
3 2 10xz+ +=
. B.
2 2 10xyz+ − +=
. C.
2 2 10xyz+ − −=
. D.
3 2 10xz+ −=
.
Câu 6: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
2; 1;4M −
và mặt phẳng
(
)
:3 2 1 0
P x yz− ++=
. Phương trình của mặt phẳng đi qua
M
và song song với mặt phẳng
( )
P
là
A.
2 2 4 21 0xyz−+−=
. B.
3 2 12 0x yz− +− =
. C.
2 2 4 21 0
xyz−++=
.D.
3 2 12 0
x yz− ++ =
Câu 7: Trong không gian với hệ tọa độ
Oxyz
. Mặt phẳng
( )
α
đi qua điểm
( )
1; 5; 2
M −
đồng thời có
cặp vetơ chỉ phương
(
)
0;1;1u =
và
( )
3; 5;1v =−−
có phương trình là
A.
70yz+−=
. B.
2 50
xyz−++=
.
C.
5 2 50xyz−+ + + =
. D.
2 50xyz++−=
.
CHƯƠNG
V
PHƯƠNG PHÁP TỌA ĐỘ
TRONG KHÔNG GIAN
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
Câu 8: Trong không gian với hệ tọa độ
( )
Oxyz
,cho ba điểm
( )
0; 2;1A
,
(
)
3; 0;1
B
,
( )
1;0;0C
. Phương
trình mặt phẳng
(
)
ABC
là
A.
2 3 4 20xyz− − +=
. B.
4 6 8 20xyz+ − +=
.
C.
2 3 4 20xyz+ − −=
. D.
23420xyz− − −=
.
Câu 9: Trong không gian với hệ tọa độ
Oxyz
, tính khoảng cách từ
( )
1; 2; 3M −
đến mặt phẳng
( )
: 2 2 10 0Px y z+ +−=
.
A.
11
3
. B.
3
. C.
7
3
. D.
4
3
.
Câu 10: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
: 90P ax by cz+ + −=
chứa hai
điểm
( )
3; 2;1A
,
(
)
3; 5; 2B −
và vuông góc với mặt phẳng
( )
:3 4 0Q xyz+++=
. Tính tổng
S abc=++
.
A.
12S = −
. B.
2S =
. C.
4S = −
. D.
2S = −
.
Câu 11: Trong không gian với hệ tọa độ
Oxyz
, điểm
M
thuộc trục
Oy
và cách đều hai mặt phẳng:
( )
: 10Pxyz+ −+=
và
( )
: 50Qxyz−+−=
có tọa độ là
A.
( )
0; 3; 0M −
. B.
(
)
0; 3; 0
M
. C.
( )
0; 2; 0M −
. D.
( )
0; 1; 0M
.
Câu 12: Trong không gian hệ toạ độ
Oxyz
, lập phương trình các mặt phẳng song song với mặt phẳng
( )
: 30xyz
β
+−+=
và cách
( )
β
một khoảng bằng
3
.
A.
60xyz+−+=
;
0xyz+−=
. B.
60xyz+−+=
.
C.
60xyz
−−+=
;
0
xyz−−=
. D.
60xyz
+++=
;
0xyz++=
.
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Trong không gian
Oxyz
, cho ba điểm
( ) (
) ( )
1;1; 1 ; 1; 2; 3 ; 2; 1; 2AB C−−
.
a) Ba điểm
,,ABC
đã cho thẳng hàng.
b) Có vô số mặt phẳng đi qua ba điểm
,,ABC
đã cho.
c) Mặt phẳng
( )
ABC
có một vectơ pháp tuyến
( )
1; 2; 3 .n =
d) Mặt phẳng
( )
ABC
có phương trình là
2 3 60xyz
+ + −=
.
Câu 2: Trong không gian
Oxyz
, cho hai mặt phẳng
(
) (
)
,
PQ
lần lượt có phương trình là
( )
: 2 3 10Px y z− + +=
và
( )
:2 4 6 1 0Qxyz− + +=
.
a) Các vectơ pháp tuyến của hai mặt phẳng trên cùng phương.
b) Hai mặt phẳng
( )
P
và
( )
Q
đều đi qua điểm
( )
1;1; 2M
.
c) Khoảng cách giữa hai mặt phẳng
( )
P
và
( )
Q
bằng
14
.
14
d) Phương trình mặt phẳng
(
)
R
cách đều hai mặt phẳng
( )
P
và
( )
Q
là:
4 8 12 5 0xy z+ + −=
.
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 3
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
Câu 3: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
1; 2; 0A
,
( )
1; 0; 2
B
,
( )
2; 1; 3
C
, và mặt
phẳng
(
)
: 2 70Pxy z−+ +=
.
a) Mặt phẳng
( )
ABC
có một véctơ pháp tuyến là
( )
2;1;1
.
b) Mặt phẳng
( )
ABC
đi qua điểm
(
)
3; 1; 5
M
.
c) Mặt phẳng
(
)
ABC
vuông góc với mặt phẳng
( )
P
.
d) Khoảng cách từ điểm
A
đến mặt phẳng
( )
P
bằng
6.
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
( )
;0;0Aa
,
( )
0; ; 0
Bb
,
( )
0; 0;
Cc
với
,,abc
đều dương.
a) Mặt phẳng
( )
ABC
có phương trình
1
xyz
abc
++=
b) Mặt phẳng
( )
ABC
đi qua điểm
( )
1; 2; 3G
sao cho
G
là trọng tâm
ABC∆
là
6 3 2 18 0xyz+++=
c) Mặt phẳng
(
)
ABC
đi qua điểm
( )
1;1; 1H
sao cho
H
là trực tâm
ABC∆
là
30
xyz++−=
d) Mặt phẳng
(
)
ABC
đi qua điểm
( )
2; 2; 3
M −
sao cho độ dài
,,OA OB OC
theo thứ tự tạo thành
cấp số cộng có công sai bằng
2
. Khoảng cách từ gốc tọa độ
O
tới mặt phẳng
( )
α
bằng
m
n
với
m
n
là phân số tối giản, khi đó
19T mn= +=
.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(1; 4; 5)A
,
(3; 4;0), (2; 1;0)BC−
và mặt phẳng
( ) :3 3 2 29 0Pxyz+−−=
. Gọi
(;;)M abc
là điểm thuộc
()
P
sao cho biểu thức
22 2
3T MA MB MC=++
đạt GTNN. Tính tổng
abc++
.
Câu 2: Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
(
) (
)
(
) (
)
2; 0; 0 , 0; 4; 0 , 0; 0; 6 , 2; 4; 6
ABCD
.
Gọi
(
)
P
là mặt phẳng song song với mặt phẳng
(
)
ABC
,
( )
P
cách đều
D
và mặt phẳng
( )
ABC
. Phương trình của mặt phẳng
( )
P
là
20ax by z d+ + +=
với
,,abd
∈
. Giá trị của
d
bằng bao
nhiêu?
Câu 3: Trong không gian với hệ tọa độ
Oxyz
, Cho hai điểm
(
)
3; 1; 2
A −
,
( )
2; 3; 3B
−
,
( )
2; 1; 2C
−−
. Gọi
(;;)M abc
là điểm thuộc mặt phẳng
( )
Oyz
sao
.. .MA MB MB MC MC MA
++
     
có giá trị min. Tính
tổng
2a bc−+
.
Câu 4: Biết góc quan sát ngang của một camera là
116°
.
Trong không gian
Oxyz
, camera được đặt tại điểm
( )
2; 1; 5A
và chiếu thẳng về phía mặt phẳng
( )
: 2 2 13 0P xy z−− + =
. Hỏi vùng quan sát được
trên mặt phẳng
( )
P
của camera là hình tròn có đường
kính bằng bao nhiêu? (làm tròn kết quả đến chữ số
hàng chục)
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 4
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
Câu 5: Một phần sân trường được định vị bởi các điểm
,,,ABC D
, như hình vẽ.
Bước đầu chúng được lấy “thăng bằng” để có cùng độ cao, biết
ABCD
là hình thang vuông ở
A
và
B
với độ dài
25m
AB
=
,
15m
AD
=
,
18mBC =
. Do yêu cầu kĩ thuật, khi lát phẳng phàn
sân trường phải thoát nước về góc sân ở
C
nên người ta lấy độ cao ở các điểm
B
,
C
,
D
xuống
thấp hơn so với độ cao ở
A
là
10 cm
,
cma
,
6 cm
tương ứng. Giá trị của
a
là
Câu 6: Trong tiết thể dục học về kĩ thuật chuyền bóng hơi, Nam và An đang tập chuyền bóng cho nhau,
Nam ném bóng cho An đỡ, quả bóng bay lên cao nhưng lại lệch sang phải của Nam và rơi xuống
vị trí cách An
0,5m
và cách Nam
4,5m
được mô tả bằng hình vẽ bên dưới
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng
( )
1
:0
2
ax ycxd
α
+ + +=
và vuông góc
với mặt đất. Khi đó giá trị của
acd++
bằng (kết quả làm tròn đến hàng phần chục).
---------- HẾT ----------
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 5
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:2 3 2 0P x yz+ ++=
. Véctơ nào dưới
đây là một véctơ pháp tuyến của
( )
P
?
A.
(
)
2
2; 3;1
n
. B.
(
)
3
2; 3; 2n
. C.
( )
1
2; 3; 0n
. D.
(
)
4
2; 0;3
n
.
Lời giải
Véctơ pháp tuyến của
(
)
P
là
( )
2
2; 3;1
n
.
Câu 2: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
Điểm nào dưới đây
thuộc
(
)
P
?
A.
(
)
0; 0; 5P −
. B.
( )
1;1; 6M
. C.
( )
2; 1; 5Q −
. D.
( )
5;0;0N
−
.
Lời giải
Ta có
1 2.1 6 5 0− +−=
nên
( )
1;1; 6M
thuộc mặt phẳng
( )
P
.
Câu 3: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1; 2; 0A
−
và
( )
3; 0; 2B
. Mặt phẳng trung
trực của đoạn thẳng
AB
có phương trình là
A.
30xyz++−=
. B.
2 20xyz
−++=
. C.
2 40xyz++−=
. D.
2 20xyz−+−=
.
Lời giải
Gọi
I
là trung điểm của đoạn thẳng
AB
. Suy ra
( )
1;1; 1I
.
Ta có
(
)
4; 2; 2AB
= −

.
Phương trình mặt phẳng trung trực của đoạn thẳng
AB
đi qua trung điểm
I
của
AB
và nhận
AB

làm vtpt, nên có phương trình là
( )
:2 2 0xyz
α
−+−=
.
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, phương trình nào dưới đây là phương trình mặt phẳng đi
qua điểm
( )
1; 2; 3M −
và có một vectơ pháp tuyến
(
)
1; 2; 3n = −
.
A.
2 3 12 0xyz
−++=
. B.
2 3 60xyz− − −=
. C.
2 3 12 0xyz− +−=
. D.
2 3 60xyz− − +=
.
Lời giải
Phương trình mặt phẳng đi qua điểm
( )
1; 2; 3M −
và có một vectơ pháp tuyến
( )
1; 2; 3
n = −
là
( ) ( ) ( )
1 12 23 3 0xyz−− − + + =
2 3 12 0xyz⇔− + + =
.
Câu 5: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
1;1; 1A −
,
( )
2; 1; 0B
( )
1; 1; 2C −
. Mặt phẳng
đi qua
A
và vuông góc với đường thẳng
BC
có phương trình là
A.
3 2 10xz+ +=
. B.
2 2 10xyz+ − +=
. C.
2 2 10xyz+ − −=
. D.
3 2 10xz
+ −=
.
Lời giải
Ta có
( )
1; 2; 2BC =−−

là một véctơ pháp tuyến của mặt phẳng
( )
P
cần tìm.
( )
1; 2; 2n BC=−= −

cũng là một véctơ pháp tuyến của mặt phẳng
(
)
P
.
Vậy phương trình mặt phẳng
( )
P
là
2 2 10
xyz+ − +=
.
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 6
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
Câu 6: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
2; 1;4M −
và mặt phẳng
( )
:3 2 1 0P x yz− ++=
. Phương trình của mặt phẳng đi qua
M
và song song với mặt phẳng
( )
P
là
A.
2 2 4 21 0xyz
−+−=
. B.
3 2 12 0x yz− +− =
. C.
2 2 4 21 0xyz−++=
.D.
3 2 12 0x yz
− ++ =
Lời giải
Phương trình của mặt phẳng đi qua
M
và song song với mặt phẳng
( )
P
là
( )
(
) ( )
3221 40x yz−− ++−=
3 2 12 0
x yz⇔ − +− =
.
Câu 7: Trong không gian với hệ tọa độ
Oxyz
. Mặt phẳng
( )
α
đi qua điểm
(
)
1; 5; 2
M
−
đồng thời có
cặp vetơ chỉ phương
( )
0;1;1
u =
và
( )
3; 5;1v =−−
có phương trình là
A.
70yz+−=
. B.
2 50xyz−++=
.
C.
5 2 50xyz−+ + + =
. D.
2 50xyz++−=
.
Lời giải
Ta có
( ) ( )
, 6; 3; 3 3 2 ; 1;1uv

=−= −


. Chọn
( )
2; 1; 1n = −
là 1 véc tơ pháp tuyến của
( )
α
.
Phương trình mặt phẳng qua
( )
1; 5; 2M −
nhận
( )
2; 1; 1n
= −
làm 1 véc tơ pháp tuyến là:
( ) ( )
( )
2 1 5 2 0 2 50x y z xyz+ − − + − =⇔ −++=
.
Câu 8: Trong không gian với hệ tọa độ
( )
Oxyz
,cho ba điểm
( )
0; 2;1A
,
( )
3; 0;1B
,
(
)
1;0;0C
. Phương
trình mặt phẳng
( )
ABC
là
A.
2 3 4 20xyz− − +=
. B.
4 6 8 20xyz+ − +=
.
C.
2 3 4 20xyz
+ − −=
. D.
23420xyz
− − −=
.
Lời giải
Ta có
( )
( )
3;2;0, 1;2;1AB AC= − −−
 
Vì mặt phẳng
( )
ABC
đi qua ba điểm
,,ABC
nên
( )
VTPT , 2; 3; 4n AB AC

= = −

 
Phương trình mặt phẳng
( )
ABC
:
( ) ( ) ( )
2 0 3 2 4 1 0 2 3 4 20x y z xyz− + − − − =⇔ + − −=
.
Câu 9: Trong không gian với hệ tọa độ
Oxyz
, tính khoảng cách từ
(
)
1; 2; 3M −
đến mặt phẳng
( )
: 2 2 10 0Px y z++−=
.
A.
11
3
. B.
3
. C.
7
3
. D.
4
3
.
Lời giải
Ta có
( )
( )
( )
222
1 2 2 2 3 10
11
11
;
33
122
..
dM P
+ + −−
−
= = =
++
.
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 7
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
Câu 10: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
: 90P ax by cz+ + −=
chứa hai
điểm
( )
3; 2;1A
,
( )
3; 5; 2B −
và vuông góc với mặt phẳng
( )
:3 4 0Q xyz+++=
. Tính tổng
S abc=++
.
A.
12
S = −
. B.
2S =
. C.
4S = −
. D.
2
S = −
.
Lời giải
Ta có
(
)
6; 3;1AB = −

.
(
)
(
)
3;1;1
Q
n
=

là VTPT của mp
( )
Q
.
Mp
( )
P
chứa hai điểm
(
)
3; 2;1A
,
( )
3; 5; 2B −
và vuông góc với mặt phẳng
(
)
Q
.
( ) ( )
( )
, 2;9; 15
pQ
n AB n

⇒= = −

  
là VTPT của mp
( )
P
Vì
( ) ( )
3; 2;1AP∈
(
)
: 2 9 15 9 0
Pxy z
⇒ + − −=
hoặc
( )
:291590P xy z− − + +=
Mặt khác
( )
: 90
P ax by cz
+ + −=
2; 9; 15abc⇒= = =−
.
Vậy
(
)
2 9 15 4S abc= + + = + +− =−
.
Câu 11: Trong không gian với hệ tọa độ
Oxyz
, điểm
M
thuộc trục
Oy
và cách đều hai mặt phẳng:
( )
: 10Pxyz+ −+=
và
( )
: 50Qxyz−+−=
có tọa độ là
A.
( )
0; 3; 0M −
. B.
( )
0; 3; 0M
. C.
( )
0; 2; 0M −
. D.
( )
0; 1; 0M
.
Lời giải
Ta có
( )
0; ; 0M Oy M y∈⇒
.
Theo giả thiết:
(
)
( )
( )
( )
15
3
33
yy
dMP dMQ y
+ −−
= ⇔ = ⇔=−
.
Vậy
( )
0; 3; 0M −
.
Câu 12: Trong không gian hệ toạ độ
Oxyz
, lập phương trình các mặt phẳng song song với mặt phẳng
( )
: 30xyz
β
+−+=
và cách
( )
β
một khoảng bằng
3
.
A.
60xyz+−+=
;
0xyz+−=
. B.
60
xyz+−+=
.
C.
60
xyz−−+=
;
0xyz−−=
. D.
60xyz+++=
;
0xyz++=
.
Lời giải
Gọi mặt phẳng
( )
α
cần tìm.
Vì
( ) ( )
αβ
//
nên phương trình
( )
α
có dạng :
0xyzc+−+=
với
{ }
\3c ∈
.
Lấy điểm
(
) ( )
1; 1;1I
β
−− ∈
.
Vì khoảng cách từ
( )
α
đến
( )
β
bằng
3
nên ta có :
( )
( )
111
,3 3
3
c
dI
α
−−−+
=⇔=
3
3
3
c −
⇔=
0
6
c
c
=
⇔
=
. (thỏa điều kiện
{ }
\3c ∈
).
Vậy phương trình
( )
α
là:
60xyz+−+=
;
0xyz+−=
.
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 8
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Trong không gian
Oxyz
, cho ba điểm
(
) (
)
( )
1;1; 1 ; 1; 2; 3 ; 2; 1; 2
AB C
−−
.
a) Ba điểm
,,ABC
đã cho thẳng hàng.
b) Có vô số mặt phẳng đi qua ba điểm
,,ABC
đã cho.
c) Mặt phẳng
( )
ABC
có một vectơ pháp tuyến
( )
1; 2; 3 .n =
d) Mặt phẳng
(
)
ABC
có phương trình là
2 3 60
xyz+ + −=
.
Lời giải
a) Sai
b) Sai
c) Đúng
d) Đúng
a) Ta có:
( ) ( )
0; 3; 2 ; 1; 2;1AB AC=−=−
 
và
03
;
12
AB AC
−
≠⇒
−
 
không cùng phương. Do đó ba
điểm
,,ABC
không thẳng hàng. Vậy a) Sai.
b) Ta có ba điểm
,,ABC
không thẳng hàng nên tồn tại một mặt duy nhất qua ba điểm này. Vậy
b) Sai.
c) Ta có: VTPT
( )
, 1; 2; 3 .
n AB AC

= =

 
Vậy c) Đúng.
d) Mặt phẳng
( )
ABC
đi qua điểm
( )
1;1; 1A
và nhận vectơ
(
)
1; 2; 3
n =
làm một vectơ pháp tuyến
là:
(
) ( )
( )
1 12 13 1 0xyz
−+ −+ −=
hay
( )
: 6 0.ABC x y z++−=
Vậy d) Đúng.
Câu 2: Trong không gian
Oxyz
, cho hai mặt phẳng
( )
( )
,
PQ
lần lượt có phương trình là
( )
: 2 3 10Px y z
− + +=
và
(
)
:2 4 6 1 0
Qxyz− + +=
.
a) Các vectơ pháp tuyến của hai mặt phẳng trên cùng phương.
b) Hai mặt phẳng
( )
P
và
( )
Q
đều đi qua điểm
( )
1;1; 2M
.
c) Khoảng cách giữa hai mặt phẳng
( )
P
và
( )
Q
bằng
14
.
14
d) Phương trình mặt phẳng
( )
R
cách đều hai mặt phẳng
( )
P
và
( )
Q
là:
4 8 12 5 0xy z+ + −=
.
Lời giải
a) Đúng
b) Sai
c) Sai
d) Đúng
a) Ta có: một VTPT
( )
1; 2; 3
P
n = −

, một VTPT
( )
2; 4; 6
Q
n = −

và
2;
Q P PQ
n n nn= ⇒
   
cùng
phương. Vậy a) Đúng.
b) Ta có
( ) ( )
1 231
//
2 461
PQ
−
= = ≠⇒
−
. Do đó hai mặt phẳng
( )
P
và
( )
Q
không có điểm chung.
Vậy b) Sai.
c) Ta có
( ) ( )
//PQ
.
Lấy điểm
( ) ( ) ( ) ( )
( )
( )
( )
( )
2
22
2.1 4.1 6.0 1
14
1;1; 0 , , .
28
2 46
N P d P Q dN Q
−++
∈⇒ = = =
+− +
Vậy c) Sai.
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 9
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
d) Ta có
( ) (
)
//
PQ
. Lấy
(
)
( )
(
)
1
1;1; 0 ; 1; 0;
2
N PP Q

∈ −∈


. Gọi
I
là trung điểm
11
1; ;
24
MN I

⇒−


. Ycbt
( )
R⇒
qua
I
và nhận vectơ
( )
1; 2; 3n
làm một vectơ pháp tuyến là:
( )
11
1 12 3 0
24
xy z

−+ − + + =


hay
( )
: 4 8 12 5 0Rxy z+ + −=
.
Vậy d) Đúng.
Câu 3: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(
)
1; 2; 0A
,
(
)
1; 0; 2B
,
( )
2; 1; 3C
, và mặt
phẳng
( )
: 2 70Pxy z−+ +=
.
a) Mặt phẳng
( )
ABC
có một véctơ pháp tuyến là
( )
2;1;1
.
b) Mặt phẳng
( )
ABC
đi qua điểm
( )
3; 1; 5M
.
c) Mặt phẳng
( )
ABC
vuông góc với mặt phẳng
( )
P
.
d) Khoảng cách từ điểm
A
đến mặt phẳng
( )
P
bằng
6.
Lời giải
a) Sai
b) Đúng
c) Sai
d) Sai
a) Sai.
Ta có:
( ) ( ) ( ) ( )
0; 2; 2 , 1;1;1 , 4; 2; 2 2 2;1;1 2.AB BC AB BC n

− ⇒ =− =−=

   
Mặt phẳng
( )
ABC
có một véctơ pháp tuyến:
( )
2;1;1 .n −
b) Đúng
Phương trình mặt phẳng
( )
ABC
:
( ) ( ) ( )
2 11 21 0 0 2 0x y z xyz− − + − + − = ⇔− + + =
.
Thay toạ độ điểm
( )
3; 1; 5
M
vào phương trình mặt phẳng
(
)
ABC
:
2.3 1 5 0− ++ =
: thoả
mãn.
c) Sai.
Ta có vecto pháp tuyến của mặt phẳng
( )
P
:
( )
1; 1; 2
P
n = −

.
. 2.1 1.1 1.2 1 0
P
nn=− − + =−≠ ⇒

Mặt phẳng
( )
ABC
không vuông góc với mặt phẳng
( )
P
.
d) Sai.
( )
( )
1 2 2.0 7
; 6.
114
dAP
−+ +
= =
++
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
( )
;0;0Aa
,
( )
0; ; 0Bb
,
( )
0; 0;Cc
với
,,abc
đều dương.
a) Mặt phẳng
( )
ABC
có phương trình
1
xyz
abc
++=
b) Mặt phẳng
( )
ABC
đi qua điểm
( )
1; 2; 3G
sao cho
G
là trọng tâm
ABC∆
là
6 3 2 18 0xyz+++=
c) Mặt phẳng
( )
ABC
đi qua điểm
( )
1;1; 1H
sao cho
H
là trực tâm
ABC∆
là
30xyz++−=
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 10
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
d) Mặt phẳng
( )
ABC
đi qua điểm
(
)
2; 2; 3
M −
sao cho độ dài
,,OA OB OC
theo thứ tự tạo thành
cấp số cộng có công sai bằng
2
. Khoảng cách từ gốc tọa độ
O
tới mặt phẳng
( )
α
bằng
m
n
với
m
n
là phân số tối giản, khi đó
19T mn= +=
.
Lời giải
a) Đúng
b) Sai
c) Đúng
d) Đúng
a) Đúng
Theo phương trình mặt phẳng theo đoạn chắn ta có mặt phẳng
( )
ABC
có phương trình
1
xyz
abc
++=
b) Sai
Vì
G
là trọng tâm
ABC∆
ta có
1
3
3
26
3
9
3
3
a
a
b
b
c
c
=
=

=⇔=


=
=
Mặt phẳng
( )
ABC
có phương trình
1
369
xyz
++=⇔
6 3 2 18 0xyz++−=
c) Đúng
Vì
( )
1;1; 1H
là trực tâm
ABC∆
ta có
(
)
111
1
3
.0 0 3
03
.0
H ABC
a
abc
HA BC b c b
ac c
HB AC
++=
∈
=
= ⇔ −+ = ⇔ =


−= =
=
 
 
Phương trình
( )
ABC
là:
30xyz++−=
d) Đúng
Giả sử mặt phẳng
( )
α
cắt tia
Ox
tại điểm có hoành độ bằng
a
( )
0a >
khi đó phương trình mặt
phẳng
( )
α
có dạng
1
24
xy z
aa a
++=
++
.
Do
( )
α
đi qua điểm
( )
2; 2; 3M −
nên ta có
22 3
1
24aa a
−
++=
++
2a⇔=
.
Vậy
( )
α
cắt
,,Ox Oy Oz
lần lượt tại
( )
2; 0; 0A
,
( )
0; 4; 0B
,
( )
0; 0; 6C
.
Gọi
( )
(
)
,d d O ABC=
.
Áp dụng công thức tính nhanh ta có
2 2 2 2 222
1 1 1 1 1 1 1 49
2 4 6 144d OA OB OC
= + + =++=
2
144 12
49 7
dd⇒ = ⇒=
.
Vậy:
19T mn= +=
.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 11
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
Câu 1: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(1; 4; 5)
A
,
(3; 4;0), (2; 1;0)BC−
và mặt phẳng
( ) :3 3 2 29 0Pxyz+−−=
. Gọi
(;;)M abc
là điểm thuộc
()
P
sao cho biểu thức
22 2
3T MA MB MC=++
đạt GTNN. Tính tổng
abc
++
.
Lời giải
Chọn điểm
I
thỏa mãn
( )
3 0 2;1;1IA IB IC I++ =⇒
  
Ta có:
( ) ( ) ( )
( )
22 2
22 2
2 22 2
22
22
22
2
3
3
5 2.
5
3
MA MB MC
MI IA MI IB MI IC
MI MI
T MA
IA IB IC IA IB IC
MI IA IB C
BC
I
MM
=++
=+++ + +
= + ++ + + +
= +++
=++
  
     
   
min min
T MI⇔
Suy ra,
M
là hình chiếu của
I
trên mặt phẳng
( )
P
Gọi
∆
là đường thẳng đi qua
I
và vuông góc với
( )
P
( )
3; 3; 2
P
un
∆
⇒== −
 
23
: 13
12
xt
yt
zt
= +
∆=+
= −
( )
2 3 ;1 3 ;1 2M M ttt∈∆⇒ ++−
( ) ( ) ( ) ( )
( )
3 2 3 3 1 3 2 1 2 29 0
1 5; 4; 1
MP t t t
tM
∈ ⇔ +++− −−=
⇔=⇒ −
Vậy
5418abc+ + = + −=
.
Câu 2: Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
( ) ( ) (
) ( )
2; 0; 0 , 0; 4; 0 , 0; 0; 6 , 2; 4; 6ABCD
.
Gọi
( )
P
là mặt phẳng song song với mặt phẳng
(
)
ABC
,
( )
P
cách đều
D
và mặt phẳng
(
)
ABC
. Phương trình của mặt phẳng
( )
P
là
20ax by z d
+ + +=
với
,,abd∈
. Giá trị của
d
bằng bao
nhiêu?
Lời giải
Phương trình mặt phẳng
( )
ABC
là:
1 6 3 2 12 0
246
xyz
xyz++=⇔ + + − =
Mặt phẳng
( )
P
song song với mặt phẳng
( )
ABC
nên
( )
P
có dạng:
( )
6 3 2 0 12x y zd d+ + + = ≠−
Vì
( )
P
cách đều
D
và mặt phẳng
( )
ABC
nên ta có:
( )
( )
( ) ( )
( )
( )
( )
( )
( )
; ; ;;d D P d ABC P d D P d A P= ⇔=
36 12 24d dd⇔ += +⇔=−
.
Vậy phương trình mặt phẳng
( )
P
là:
6 3 2 24 0xyz++−=
.
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 12
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
Câu 3: Trong không gian với hệ tọa độ
Oxyz
, Cho hai điểm
( )
3; 1; 2A −
,
( )
2; 3; 3B −
,
(
)
2; 1; 2C −−
. Gọi
(;;)M abc
là điểm thuộc mặt phẳng
( )
Oyz
sao
.. .
MA MB MB MC MC MA
++
     
có giá trị min. Tính
tổng
2a bc−+
.
Lời giải
Gọi
( )
;;I abc
, sao cho
0IA IB IC++ =
  
I⇒
là trong tâm
ABC∆
⇒
( )
1;1; 1I −
.
Ta có:
.. .MA MB MB MC MC MA++
     
( ) ( ) ( ) ( ) ( ) ( )
.. .MI IA MI IB MI IB MI IC MI IC MI IA=+ +++ +++ +
           
( ) ( )
2
32 . . .MI MI IA IB IC IA IB IB IC IC IA
= + ++ + + +
         
, (mà
0
IA IB IC++ =
  
)
(
)
2
3 .. .
MI IA IB IB IC IC IA=+ ++
     
Vì điểm
,,,I ABC
cố định nên
.. .IA IB IB IC IC IA++
     
có giá trị không đổi.
Để
.. .MA MB MB MC MC MA++
     
có giá trị min
MI⇔
min.
Mà
I
cố định nên
M
là hình chiếu của
I
lên
( )
Oyz
, suy ra
( )
0; 1; 1
M −
.
Vậy
2 0 2.1 1 3
a bc
− + = − −=−
.
Câu 4: Biết góc quan sát ngang của một camera là
116°
. Trong không gian
Oxyz
, camera được đặt tại
điểm
( )
2; 1; 5A
và chiếu thẳng về phía mặt phẳng
( )
: 2 2 13 0P xy z−− + =
. Hỏi vùng quan sát
được trên mặt phẳng
( )
P
của camera là hình tròn có đường kính bằng bao nhiêu? (làm tròn kết
quả đến chữ số hàng chục)
Lời giải
Gọi
,,ABC
là các điểm như hình vẽ bên dưới và
H
là hình chiếu vuông góc của
A
lên mặt
phẳng
( )
P
.
Hình vẽ
Theo đề
116 58BAC BAH= °⇒ = °
.
Khi đó
( )
( )
2212513
d, 2
414
AH A P
⋅−− ⋅+
= = =
++
(đvđd).
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 13
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
Xét tam giác
ABH
vuông tại
H
, ta có:
tan tan 58 2 2 tan 58
BH
BAH BH
AH
= ⇒ = °⋅ = °
(đvđd).
Suy ra
2 2 2tan58 6,4
BC BH= = ⋅ °≈
(đvđd)
Vậy vùng quan sát của camera trên mặt phẳng
(
)
P
là hình tròn có đường kính khoảng
6, 4
(đvđd).
Câu 5: Một phần sân trường được định vị bởi các điểm
,,,ABC D
, như hình vẽ.
Bước đầu chúng được lấy “thăng bằng” để có cùng độ cao, biết
ABCD
là hình thang vuông ở
A
và
B
với độ dài
25mAB =
,
15mAD =
,
18mBC =
. Do yêu cầu kĩ thuật, khi lát phẳng phàn
sân trường phải thoát nước về góc sân ở
C
nên người ta lấy độ cao ở các điểm
B
,
C
,
D
xuống
thấp hơn so với độ cao ở
A
là
10 cm
,
cma
,
6 cm
tương ứng. Giá trị của
a
là
Lời giải
Chọn hệ trục tọa độ
Oxyz
sao cho:
OA
≡
, tia
Ox AD≡
; tia
Oy AB≡
.
Khi đó,
( )
0; 0; 0A
;
( )
0; 2500;0B
;
( )
1800; 2500;0C
;
( )
1500;0;0D
.
Khi hạ độ cao các điểm ở các điểm
B
,
C
,
D
xuống thấp hơn so với độ cao ở
A
là
10 cm
,
cma
,
6 cm
tương ứng ta có các điểm mới
( )
0; 2500; 10B
′
−
;
( )
1800; 2500;Ca
′
−
;
( )
1500;0; 6D
′
−
.
Theo bài ra có bốn điểm
A
;
B
′
;
C
′
;
D
′
đồng phẳng.
Phương trình mặt phẳng
( )
: 250 0AB D x y z
′′
++ =
.
Do
( ) ( )
1800; 2500;C a AB D
′ ′′
−∈
nên có:
1800 2500 250 0 17, 2aa+ − =⇔=
.
Vậy
17, 2cma =
.
Câu 6: Trong tiết thể dục học về kĩ thuật chuyền bóng hơi, Nam và An đang tập chuyền bóng cho nhau,
Nam ném bóng cho An đỡ, quả bóng bay lên cao nhưng lại lệch sang phải của Nam và rơi xuống
vị trí cách An
0,5m
và cách Nam
4,5m
được mô tả bằng hình vẽ bên dưới
z
y
x
B'
C'
D'
D
C
B
A
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 14
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng
(
)
1
:0
2
ax ycxd
α
+ + +=
và vuông góc với mặt đất.
Khi đó giá trị của
acd++
bằng (kết quả làm tròn đến hàng phần chục).
Lời giải
Chọn hệ trục như hình vẽ. Gọi
M
là điểm mà quả bóng chạm đất.
Khi đó
0,5
M
x =
,
22
4,5 0,5 2 5
M
y = −=
Vì
( ) ( )
Oxy
α
⊥
nên
( )
α
có véc tơ chỉ phương
( )
0; 0;1k =
.
Mà
( )
α
có véc tơ chỉ phương
( )
0, 5; 2 5; 0OM =

Khi đó véc tơ pháp tuyến của
( )
α
là
( )
, 2 5;0,5;0n k OM
α

= = −

 
.
Vậy
( )
: 2 5 0,5 0xy
α
−+=
nên
2 5; 0,5; 0; 0 4,5a b c d abcd=− = = = ⇒ + + + ≈−
.
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 1
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
BÀI: PHƯƠNG TRÌNH MẶT PHẲNG
ĐỀ TEST SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian
Oxyz
, một vectơ pháp tuyến của mặt phẳng
1
2 13
x yz
+ +=
−−
là
A.
(3; 6; 2)
n
= −
. B.
(2; 1; 3)n = −
. C.
(3;6;2)
n =−−−
. D.
( 2; 1; 3)n =−−
.
Câu 2: Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
đi qua 3 điểm
( )
2;0;0M −
,
( )
0; 1;0N −
,
(
)
0;0;3
P
là
A.
3 6 2 60xyz+ − −=
. B.
2 3 10xy z
+ − −=
.
C.
362 0xyz
+−=
. D.
36260
xyz+ − +=
.
Câu 3: Trong không gian
Oxyz
, cho điểm
( )
1; 2; 3A
. Mặt phẳng chứa điểm
A
và trục
Oz
có phương
trình là
A.
20xy−=
. B.
0xyz+−=
. C.
320yz−=
. D.
30xz
−=
vô số.
Câu 4: Trong không gian
Oxyz
, cho điểm
( )
2;1;3A −−
và mặt phẳng
( )
:3 2 4 5 0Pxyz− + −=
. Gọi
(
)
Q
là mặt phẳng đi qua
A
và song song với mặt phẳng
(
)
P
. Mặt phẳng
( )
Q
có phương trình
là:
A.
32440xyz− + −=
B.
3 2 4 40xyz− + +=
. C.
3 2 4 50xyz− + +=
.D.
3 2 4 80xyz+ + +=
.
Câu 5: Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
đi qua hai điểm
( )
2; 1;0A −
,
( )
1;1; 2B
và vuông góc với mặt phẳng
( )
: 2 30Q xy z++ −=
là.
A.
2 4 3 80x yz+ − −=
. B.
2430x yz+−=
.
C.
2 4 3 80x yz+ − +=
. D.
2430xyz−−=
.
Câu 6: Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
đi qua điểm
(
)
2;1; 2M −
và vuông góc
với hai mặt phẳng
( )
: 2 30Q xy z++ −=
và
( )
: 40R xyz
−−+=
là.
A.
3 2 90xyz
+ − +=
. B.
2 2 90xy z+− −=
. C.
3 2 90xyz+ − −=
. D.
2 2 90xy z+− +=
.
Câu 7: Trong không gian
,Oxyz
cho các điểm
( ) ( ) ( ) ( )
5;1;3 , 1; 6; 2 , 5; 0; 4 , 4; 0; 6ABC D
. Viết phương
trình mặt phẳng
( )
P
đi qua hai điểm
,AB
và song song với
.CD
A.
4 5 24 0x yz− ++ =
. B.
2 10xz− +=
C.
10 9 5 74 0xyz++−=
. D.
10 9 5 74 0xyz+++=
.
CHƯƠNG
V
PHƯƠNG PHÁP TỌA ĐỘ
TRONG KHÔNG GIAN
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
Câu 8: Trong không gian
,Oxyz
mặt phẳng
( ):2 2 0P xyz++−=
song song với mặt phẳng nào dưới
đây?
A.
11
10
22
xyz+ − −=
. B.
20xyz−−−=
.C.
4 2 2 40xyz+ + +=
. D.
2 20xyz++−=
.
Câu 9: Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 3 0xy
α
−+=
. Mặt phẳng nào sau đây vuông góc
với mặt phẳng
( )
α
?
A.
( )
1
:2 3 0xy z
α
− +− =
. B.
( )
2
: 5 20x yz
α
+ +−=
.
C.
( )
3
:4 2 7 0xy
α
− +=
. D.
(
)
4
: 2 10
x yz
α
+ −+=
.
Câu 10: Trong không gian
Oxyz
, điểm
M
thuộc trục
Oy
và cách đều hai mặt phẳng:
( )
: 10Pxyz
+ −+=
và
( )
: 50Qxyz−+−=
có tọa độ là
A.
( )
0; 3; 0M −
. B.
( )
0; 3; 0M
. C.
( )
0; 2; 0M −
. D.
( )
0; 1; 0M
.
Câu 11: Trong không gian
Oxyz
khoảng cách giữa hai mặt phẳng
( )
: 2 3 10Px y z+ + −=
và
( )
: 2 3 60Qx y z+ + +=
là
A.
7
14
. B.
8
14
. C.
14
. D.
5
14
.
Câu 12: Trong không gian
,Oxyz
cho
( ) ( )
2; 0; 0 , 0; 4; 0 ,AB
( )
0; 0; 6
C
. Gọi
(
)
P
là mặt phẳng không
chứa gốc tọa độ và song song với
(
)
mp ABC
, biết khoảng cách giữa mặt phẳng
( )
P
và mặt
phẳng
( )
ABC
bằng
12
7
. Phương trình của
(
)
P
là
A.
6 3 2 12 0
xyz++−=
. B.
6320xyz++=
.
C.
6 3 2 24 0xyz++−=
. D.
6 3 2 36 0xyz++−=
.
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Trong không gian
Oxyz
, cho ba điểm
( ) ( ) ( )
1;1;0 , 1; 1; 2 , 1; 2;1ABC− −−
.
a) Một vecto pháp tuyến của mặt phẳng
( )
ABC
là
,AB AC


 
.
b) Vecto
( )
1;2;3
n =
là một vecto pháp tuyến của mặt phẳng
( )
ABC
.
c) Vecto
( )
1;1;0u =
là một vecto pháp tuyến của mặt phẳng đi qua
O
và chứa đưởng thẳng
AB
.
d) Vecto
(
)
1;2;3v =
là một vecto pháp tuyến của mặt phẳng song song với hai đưởng thẳng
AB
và
OC
.
Câu 2: Cho các điểm
( ) ( )
( )
1; 2; 0 ; 2; 1;1 ; 1; 1; 2ABC−−
.
a) Phương trình mặt phẳng
( )
ABC
là
2 3 30x yz
+ − −=
.
b) Phương trình mặt phẳng
( )
α
qua
A
và vuông góc với
BC
là
2 50x yz
− −−=
.
c) Phương trình mặt phẳng trung trực
( )
β
của đoạn
AC
là
6 4 10yz+ −=
.
d) Phương trình mặt phẳng
( )
γ
chứa trục
Ox
và điểm
C
là
20yz+=
.
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 3
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
Câu 3: Trong không gian với hệ trục toạ độ
Oxyz
, cho điểm
(
)
1; 2; 5A
và mặt phẳng
( )
: 2 2 60xyz
α
+ + −=
.
a) Véc tơ
( )
1;2;2n =
là một vectơ pháp tuyến của
(
)
α
.
b) Phương trình mặt phẳng
(
)
β
đi qua điểm
A
và song song với mặt phẳng
( )
α
có phương trình
2 2 15 0xyz+ ++=
c) Phương trình mặt phẳng
(
)
γ
đi qua hai điểm
O
và
A
đồng thời vuông góc với mặt phẳng
(
)
α
có phương trình
20
xy
−=
.
d) Điểm
(
)
M
α
∈
sao cho
,,AOM
thẳng hàng thì tọa độ
24
; ;2
55
M



.
Câu 4: Trong không gian với hệ trục toạ độ
Oxyz
, cho ba điểm
( ) ( ) ( )
1; 2; 2 ; 2;1; 2 ; 3; 2;1A BC−−
.
a) Phương trình mặt phẳng
( )
P
đi qua ba điểm
,,ABC
có một véc tơ pháp tuyến là
,n AB AC

=

 
.
b) Phương trình mặt phẳng
(
)
P
là
13 5 2 27 0xyz+−+=
.
c) Phương trình mặt phẳng đi qua điểm
( )
1; 2; 2A −
và nhận
BC

làm véc tơ pháp tuyến có dạng:
( )
( ) (
)
113 2120
xx y z+ − +− −=
.
d) Phương trình mặt phẳng đi qua ba điểm
;;EFK
lần lượt là hình chiếu vuông góc của
A
lên
trục
;;Ox Oy Oz
có phương trình
1
122
xyz
+−=
.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong hệ tục toạ độ không gian
Oxyz
, cho
( )
1;0;0A
,
( )
0; ; 0Bb
,
( )
0; 0;
Cc
, biết
,0bc>
,
phương trình mặt phẳng
( )
: 10Pyz−+=
. Tính
M cb= +
biết
( ) ( )
ABC P⊥
,
( )
1
;
3
d O ABC =


.
Câu 2: Trong không gian
Oxyz
cho hai điểm
( ) ( )
1; 2; 0 , 1; 1; 3AB−
và mặt phẳng
( )
: 2 3 5 0.Px y z− + −=
Phương trình của mặt phẳng đi qua hai điểm
,AB
, đồng thời vuông góc
( )
P
là
2 0.x ay bz c 
Giá trị của biểu thức
23abc++
bằng
Câu 3: Trong không gian
Oxyz
, mặt phẳng
( )
α
qua hai điểm
( )
1;2; 0A
,
( )
4;1; 2B
và cách đều hai
điểm
( )
2;1; 1C −−
,
( )
0; 3;1D −
có dạng
1 0 ( 0)ax by cz a+ + += <
. Tính
P abc=++
.
Câu 4: Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 3 1 0x yz
α
+ ++=
. Gọi
( )
P
là mặt phẳng song
song với
( )
α
, cắt các tia
O ,O ,Oxyz
lần lượt tại các điểm
A
,
B
,
C
sao cho thể tích khối tứ diện
OABC
bằng
6
. Tính khoảng cách từ gốc tọa độ
O
đến mặt phẳng
( )
P
(kết quả làm tròn đến
hàng phần trăm).
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 4
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
Câu 5: Một sân vận động được xây dựng theo mô hình là hình chóp cụt
.OAGD BCFE
có hai đáy song
song với nhau. Mặt sân OAGD là hình chữ nhật và được gắn hệ trục
Oxyz
như hình vẽ (đơn vị
trên mỗi trục tọa độ là mét). Mặt sân
OAGD
có chiều dài
100OA m=
, chiều rộng
60OD m=
và
tọa độ điểm
( )
10;10;8B
. Giả sử phương trình tổng quát của mặt phẳng
( )
OACB
có dạng
0
ax y cz d
++ +=
. Tính giá trị biểu thức
acd
++
.
Câu 6: Manhattanhenge (Hình 1) là một sự kiện diễn ra khi Mặt Trời mọc hoặc khi Mặt Trời lặn nằm
thẳng hàng với các tuyến phố Đông - Tây thuộc mạng lưới đường phố chính tại quận Manhattan
của thành phố New York. Khi mặt trời lặn, tia sáng song song mặt đất lệch một góc khoảng
0
38
so với hướng tây (Hình 2).
Giả sử mặt tiền các tòa nhà hai bên đường nằm trong 2 mặt phẳng song song cách nhau
30m
và
vuông góc với mặt đất. Biết rằng mặt phẳng phía bắc đi qua gốc
O
của hệ trục
Oxyz
, với tia
Oz
vuông góc với mặt đất và hướng lên trên. Phương trình mặt phẳng thứ hai có dạng
( ): 0Q x ay bz c
+ + +=
, với
0
sin
m
c
n
=
. Tính
mn+
.
---------- HẾT ----------
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 5
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
HƯỚNG DẪN GIAIT CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian
Oxyz
, một vectơ pháp tuyến của mặt phẳng
1
2 13
x yz
+ +=
−−
là
A.
(3; 6; 2)n
= −
. B.
(2; 1; 3)n = −
. C.
(3;6;2)n =−−−
. D.
( 2; 1; 3)n =−−
.
Lời giải
Phương trình
136260.
2 13
x yz
xyz+ + =⇔ + − +=
−−
Một vectơ pháp tuyến của mặt phẳng đã cho là
(3; 6; 2)n = −
.
Câu 2: Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
đi qua 3 điểm
( )
2;0;0
M
−
,
( )
0; 1;0N −
,
( )
0;0;3P
là
A.
3 6 2 60xyz
+ − −=
. B.
2 3 10
xy z+ − −=
.
C.
362 0xyz+−=
. D.
36260xyz+ − +=
.
Lời giải
Áp dụng phương trình mặt phẳn theo đoạn chắn, ta có phương trình mặt
( )
MNP
là
136260
2 13
x yz
xyz+ + =⇔ + − +=
−−
.
Câu 3: Trong không gian
Oxyz
, cho điểm
( )
1; 2; 3
A
. Mặt phẳng chứa điểm
A
và trục
Oz
có phương
trình là
A.
20xy−=
. B.
0xyz+−=
. C.
320yz−=
. D.
30xz−=
vô số.
Lời giải
Gọi
( )
P
là mặt phẳng chứa điểm
A
và trục
Oz
.
Oz
đi qua điểm
( )
0; 0; 0O
và có vectơ chỉ phương
( )
0; 0;1
u =
.
Mặt phẳng
(
)
P
có vectơ pháp tuyến
( )
, 2; 1; 0n u OA

= = −



và đi qua điểm
( )
0; 0; 0O
nên có
phương trình
20xy−=
.
Câu 4: Trong không gian
Oxyz
, cho điểm
( )
2;1;3A −−
và mặt phẳng
( )
:3 2 4 5 0Pxyz− + −=
. Gọi
(
)
Q
là mặt phẳng đi qua
A
và song song với mặt phẳng
( )
P
. Mặt phẳng
( )
Q
có phương trình
là:
A.
32440xyz− + −=
B.
3 2 4 40xyz− + +=
. C.
3 2 4 50xyz− + +=
.D.
3 2 4 80xyz+ + +=
.
Lời giải
Mặt phẳng
(
)
:3 2 4 5 0Pxyz
− + −=
có một vectơ pháp tuyến là
(
)
3; 2; 4n = −
.
Do
( )
Q
song song với
( )
P
nên
( )
Q
có vectơ pháp tuyến là
(
)
3; 2; 4n = −
.
Phương trình mặt phẳng
( )
Q
:
( ) (
) ( )
3221430x yz− − ++ + =
3 2 4 40xyz⇔ − + +=
.
Câu 5: Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
đi qua hai điểm
( )
2; 1;0A −
,
( )
1;1; 2B
và vuông góc với mặt phẳng
( )
: 2 30Q xy z++ −=
là.
A.
2 4 3 80x yz+ − −=
. B.
2430xyz+−=
.
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 6
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
C.
2 4 3 80x yz
+ − +=
. D.
2430
xyz
−−=
.
Lời giải
Mặt phẳng
(
)
Q
có một vectơ pháp tuyến
( )
( )
1;1; 2
Q
n =
.
Mặt phẳng
( )
P
đi qua hai điểm
( )
2; 1;0A −
,
( )
1;1; 2B
và vuông góc với mặt phẳng
( )
Q
nên
có cặp vectơ chỉ phương là
(
)
1;2;2
AB = −

và
( )
(
)
1;1; 2
Q
n =
. Do đó
( )
P
có vectơ pháp tuyến
là:
( ) ( )
( )
; 2;4; 3
PQ
n AB n

= = −


.
Mặt phẳng
( )
P
đi qua điểm
( )
2; 1;0A −
và nhận
( )
( )
2;4; 3
P
n
= −
làm một vectơ pháp tuyến
nên có phương trình:
( ) ( ) ( )
2 2 4 13 0 0 2 4 3 0x y z xyz− + +− − =⇔ + − =
.
Câu 6: Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
đi qua điểm
( )
2;1; 2M −
và vuông góc
với hai mặt phẳng
( )
: 2 30Q xy z++ −=
và
( )
: 40R xyz−−+=
là.
A.
3 2 90
xyz+ − +=
. B.
2 2 90xy z+− −=
.
C.
3 2 90xyz+ − −=
. D.
2 2 90
xy z
+− +=
.
Lời giải
Mặt phẳng
( )
Q
,
( )
R
có một vectơ pháp tuyến lần lượt là
( )
( )
1;1; 2
Q
n =
và
( )
( )
1; 1; 1
R
n = −−
.
Mặt phẳng
( )
P
đi qua điểm
( )
2;1; 2M −
và vuông góc với hai mặt phẳng
( )
Q
và
( )
R
nên có
cặp vectơ chỉ phương là
( )
(
)
1;1; 2
Q
n =
và
( )
( )
1; 1; 1
R
n = −−
. Do đó
(
)
P
có vectơ pháp tuyến là
(
)
(
) (
)
(
)
; 1;3; 2
P QR
n nn

= = −


.
Mặt phẳng
( )
P
đi qua điểm
( )
2;1; 2M −
và nhận
(
)
(
)
1;3; 2
P
n = −
làm một vectơ pháp tuyến
nên có phương trình:
( ) ( ) ( )
1231220 3290x y z xyz− + − − + =⇔+ − −=
.
Câu 7: Trong không gian
,Oxyz
cho các điểm
(
) ( ) ( ) ( )
5;1;3 , 1; 6; 2 , 5; 0; 4 , 4; 0; 6
ABC D
. Viết phương
trình mặt phẳng
( )
P
đi qua hai điểm
,AB
và song song với
.CD
A.
4 5 24 0x yz
− ++ =
. B.
2 10xz− +=
C.
10 9 5 74 0xyz
++−=
. D.
10 9 5 74 0xyz+++=
.
Lời giải
Ta có
(
) ( ) (
)
4;5; 1 , 1; 0; 2 ; 10; 9; 5AB CD n AB CD

=− − =− ⇒= =

   
Ta có mp
( )
P
đi qua
( )
5; 1; 3A
và nhận
( )
10; 9;5n =
làm vectơ pháp tuyến nên có phương trình
(
) ( ) ( )
10 5 9 1 5 3 0 10 9 5 74 0.x y z xyz−+ −+ − =⇔ + + − =
Câu 8: Trong không gian
,Oxyz
mặt phẳng
( ):2 2 0P xyz++−=
song song với mặt phẳng nào dưới
đây?
A.
11
10
22
xyz+ − −=
. B.
20xyz−−−=
.C.
4 2 2 40xyz+ + +=
. D.
2 20xyz++−=
.
Lời giải
Xét
( ):2 2 0P xyz++−=
và
( )
1
11
: 10
22
Q xyz+ − −=
có
( )
21 1
11
1
22
P=≠⇒
−
không song

Tài liệu khác của Toán 12

Preview text:

ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN NG ƯƠ
V PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN CH
BÀI: PHƯƠNG TRÌNH MẶT PHẲNG ĐỀ TEST SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x + 3y + z + 2 = 0. Véctơ nào dưới
đây là một véctơ pháp tuyến của (P) ?
A. n 2;3;1 .
B. n 2;3;2 . C. n 2;3;0 . D. n 2;0;3 . 4 ( ) 1 ( ) 3 ( ) 2 ( )
Câu 2: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P): x − 2y + z −5 = 0. Điểm nào dưới đây thuộc (P) ? A. P(0;0; 5 − ) .
B. M (1;1;6) . C. Q(2; 1; − 5) . D. N ( 5 − ;0;0) .
Câu 3: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A( 1;
− 2;0) và B(3;0;2) . Mặt phẳng trung
trực của đoạn thẳng AB có phương trình là
A. x + y + z − 3 = 0 .
B. 2x − y + z + 2 = 0 . C. 2x + y + z − 4 = 0 . D. 2x − y + z − 2 = 0.
Câu 4: Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt phẳng đi  qua điểm M (1;2; 3
− ) và có một vectơ pháp tuyến n = (1; 2 − ;3).
A. x − 2y + 3z +12 = 0 . B. x − 2y − 3z − 6 = 0. C. x − 2y + 3z −12 = 0. D. x − 2y − 3z + 6 = 0 .
Câu 5: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A( 1; − 1; )
1 , B(2;1;0) C (1; 1; − 2) . Mặt phẳng
đi qua A và vuông góc với đường thẳng BC có phương trình là
A. 3x + 2z +1 = 0.
B. x + 2y − 2z +1 = 0. C. x + 2y − 2z −1 = 0. D. 3x + 2z −1 = 0 .
Câu 6: Trong không gian với hệ tọa độ Oxyz , cho điểm M (2;−1;4) và mặt phẳng
(P):3x − 2y + z +1= 0 . Phương trình của mặt phẳng đi qua M và song song với mặt phẳng (P) là
A. 2x − 2y + 4z − 21 = 0 . B. 3x − 2y + z −12 = 0. C. 2x − 2y + 4z + 21= 0 .D. 3x − 2y + z +12 = 0
Câu 7: Trong không gian với hệ tọa độ Oxyz . Mặt phẳng (α ) đi qua điểm M ( 1; − 5;2) đồng thời có  
cặp vetơ chỉ phương u = (0;1 ) ;1 và v = ( 3 − ; 5 − ; ) 1 có phương trình là
A. y + z − 7 = 0.
B. 2x − y + z + 5 = 0 .
C. −x + 5y + 2z + 5 = 0 .
D. 2x + y + z − 5 = 0 .
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 1
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 8: Trong không gian với hệ tọa độ (Oxyz) ,cho ba điểm A(0;2; ) 1 , B(3;0; )
1 , C (1;0;0) . Phương
trình mặt phẳng ( ABC)là
A. 2x −3y − 4z + 2 = 0 .
B. 4x + 6y −8z + 2 = 0 .
C. 2x + 3y − 4z − 2 = 0 .
D. 2x −3y − 4z − 2 = 0 .
Câu 9: Trong không gian với hệ tọa độ Oxyz , tính khoảng cách từ M (1;2; 3 − ) đến mặt phẳng
(P):x + 2y + 2z −10 = 0. A. 11. B. 3. C. 7 . D. 4 . 3 3 3
Câu 10: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng (P) : ax + by + cz −9 = 0 chứa hai điểm A(3;2; ) 1 , B( 3
− ;5;2) và vuông góc với mặt phẳng (Q) :3x + y + z + 4 = 0 . Tính tổng
S = a + b + c . A. S = 12 − .
B. S = 2 . C. S = 4 − . D. S = 2 − .
Câu 11: Trong không gian với hệ tọa độ Oxyz , điểm M thuộc trục Oy và cách đều hai mặt phẳng:
(P): x + y − z +1= 0 và (Q): x − y + z −5 = 0 có tọa độ là A. M (0; 3 − ;0) .
B. M (0;3;0) . C. M (0; 2; − 0).
D. M (0;1;0) .
Câu 12: Trong không gian hệ toạ độ Oxyz , lập phương trình các mặt phẳng song song với mặt phẳng
(β ): x + y − z +3 = 0 và cách (β ) một khoảng bằng 3 .
A. x + y − z + 6 = 0 ; x + y − z = 0 .
B. x + y − z + 6 = 0 .
C. x − y − z + 6 = 0 ; x − y − z = 0.
D. x + y + z + 6 = 0; x + y + z = 0 .
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Trong không gian Oxyz , cho ba điểm A(1;1; ) 1 ; B(1; 2 − ;3);C (2; 1; − 2) . a) Ba điểm ,
A B,C đã cho thẳng hàng.
b) Có vô số mặt phẳng đi qua ba điểm ,
A B,C đã cho. 
c) Mặt phẳng ( ABC) có một vectơ pháp tuyến n = (1;2;3).
d) Mặt phẳng ( ABC) có phương trình là x + 2y + 3z − 6 = 0 .
Câu 2: Trong không gian Oxyz , cho hai mặt phẳng (P),(Q) lần lượt có phương trình là
(P): x − 2y +3z +1= 0 và (Q):2x − 4y + 6z +1= 0.
a) Các vectơ pháp tuyến của hai mặt phẳng trên cùng phương.
b) Hai mặt phẳng (P) và (Q) đều đi qua điểm M (1;1;2) .
c) Khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 14 . 14
d) Phương trình mặt phẳng (R) cách đều hai mặt phẳng (P) và (Q) là:
4x + 8y +12z − 5 = 0.
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 3: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;2;0) , B(1;0;2) , C (2;1;3), và mặt
phẳng (P) : x − y + 2z + 7 = 0 .
a) Mặt phẳng ( ABC) có một véctơ pháp tuyến là (2;1 ) ;1 .
b) Mặt phẳng ( ABC) đi qua điểm M (3;1;5) .
c) Mặt phẳng ( ABC) vuông góc với mặt phẳng (P) .
d) Khoảng cách từ điểm A đến mặt phẳng (P) bằng 6.
Câu 4: Trong không gian với hệ tọa độOxyz , cho 3 điểm A( ;0 a ;0) , B(0; ;
b 0) , C (0;0;c) với a, , b c đều dương.
a) Mặt phẳng ( ABC) có phương trình x y z + + = 1 a b c
b) Mặt phẳng ( ABC) đi qua điểm G(1;2;3) sao cho G là trọng tâm A ∆ BC là
6x + 3y + 2z +18 = 0
c) Mặt phẳng ( ABC) đi qua điểm H (1;1; )
1 sao cho H là trực tâm A
∆ BC là x + y + z − 3 = 0
d) Mặt phẳng ( ABC) đi qua điểm M (2; 2; − )3 sao cho độ dài ,
OA OB,OC theo thứ tự tạo thành
cấp số cộng có công sai bằng 2 . Khoảng cách từ gốc tọa độ O tới mặt phẳng (α) bằng m với n
m là phân số tối giản, khi đó T = m+n =19. n
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho ba điểm (
A 1;4;5) , B(3;4;0),C(2; 1 − ;0) và mặt phẳng
(P) :3x + 3y − 2z − 29 = 0. Gọi M ( ; a ;
b c) là điểm thuộc (P) sao cho biểu thức 2 2 2
T = MA + MB + 3MC đạt GTNN. Tính tổng a + b + c .
Câu 2: Trong không gian với hệ tọa độ Oxyz , cho các điểm A(2;0;0), B(0;4;0),C (0;0;6), D(2;4;6).
Gọi (P) là mặt phẳng song song với mặt phẳng ( ABC),(P) cách đều D và mặt phẳng ( ABC)
. Phương trình của mặt phẳng (P) là ax + by + 2z + d = 0 với a,b,d ∈ . Giá trị của d bằng bao nhiêu?
Câu 3: Trong không gian với hệ tọa độ Oxyz , Cho hai điểm A(3; 1; − 2) , B(2;3; 3 − ) , C ( 2 − ;1; 2 − ). Gọi
      M ( ; a ;
b c) là điểm thuộc mặt phẳng (Oyz) sao . MA MB + .
MB MC + MC.MA có giá trị min. Tính
tổng a − 2b + c .
Câu 4: Biết góc quan sát ngang của một camera là 116° .
Trong không gian Oxyz , camera được đặt tại điểm
A(2;1;5) và chiếu thẳng về phía mặt phẳng
(P):2x − y − 2z +13 = 0. Hỏi vùng quan sát được
trên mặt phẳng (P) của camera là hình tròn có đường
kính bằng bao nhiêu? (làm tròn kết quả đến chữ số hàng chục)
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 3
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
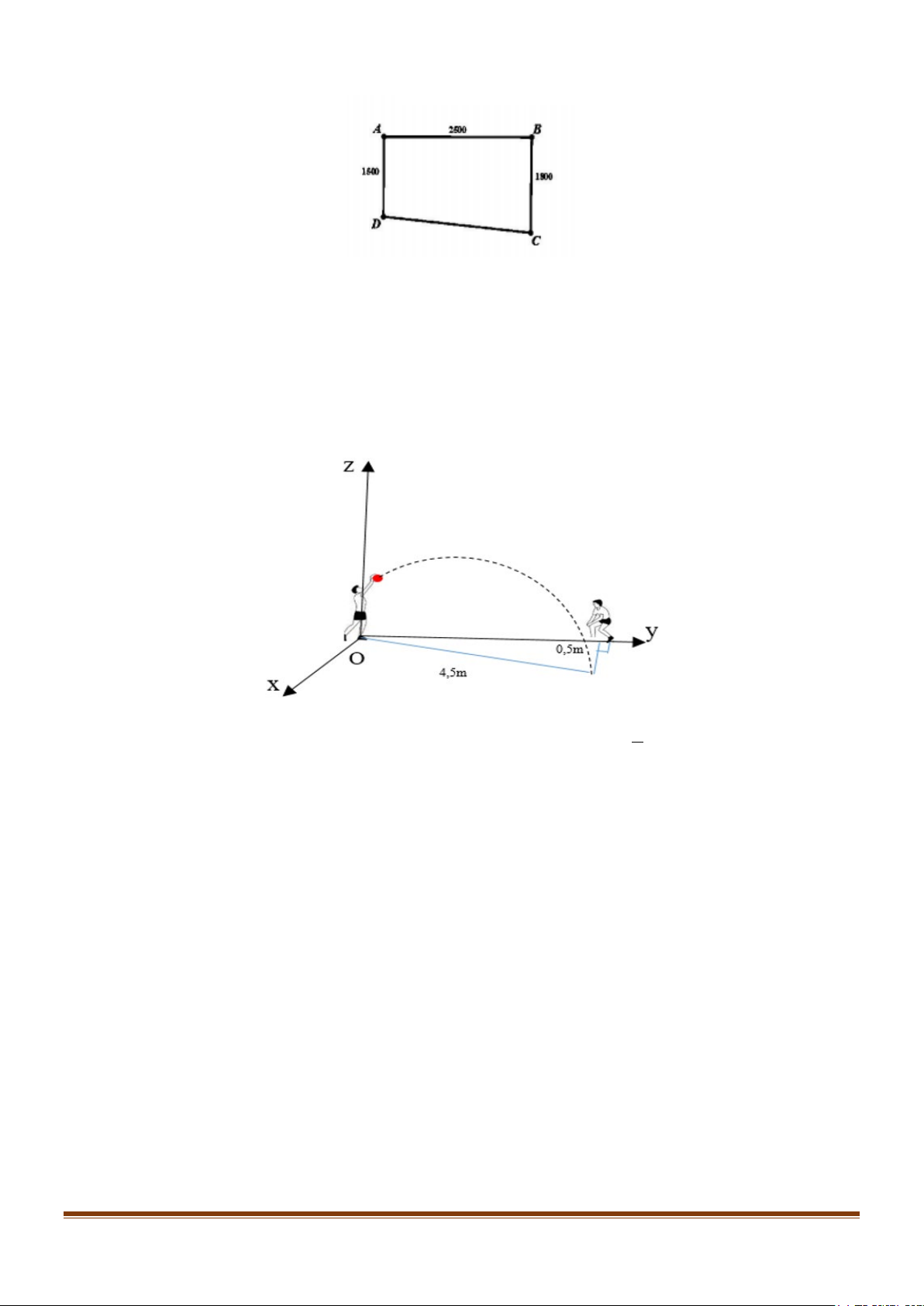
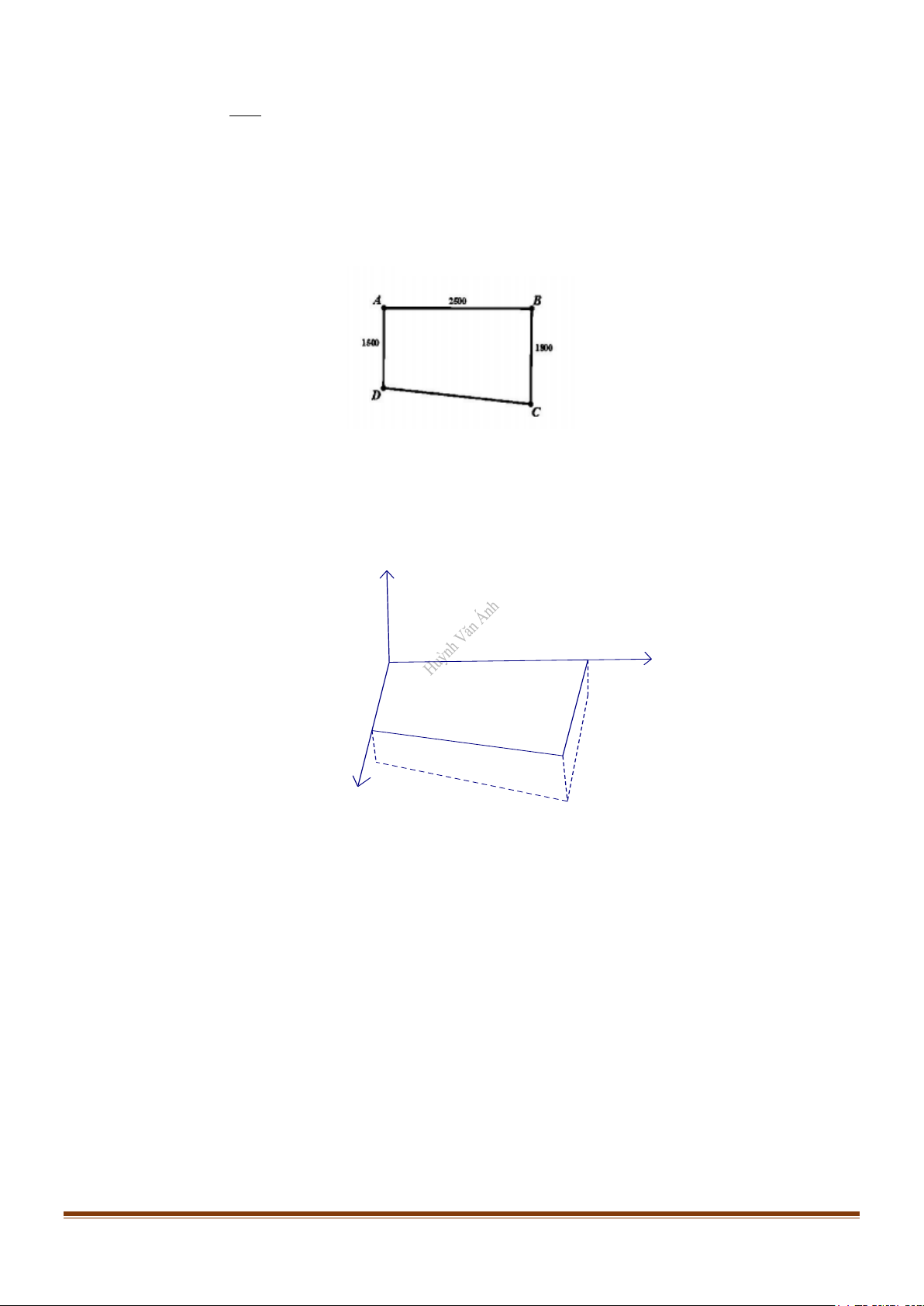
Câu 5: Một phần sân trường được định vị bởi các điểm ,
A B,C, D , như hình vẽ.
Bước đầu chúng được lấy “thăng bằng” để có cùng độ cao, biết ABCD là hình thang vuông ở
A và B với độ dài AB = 25m , AD =15m , BC =18m . Do yêu cầu kĩ thuật, khi lát phẳng phàn
sân trường phải thoát nước về góc sân ở C nên người ta lấy độ cao ở các điểm B , C , D xuống
thấp hơn so với độ cao ở A là 10cm , a cm , 6cm tương ứng. Giá trị của a là
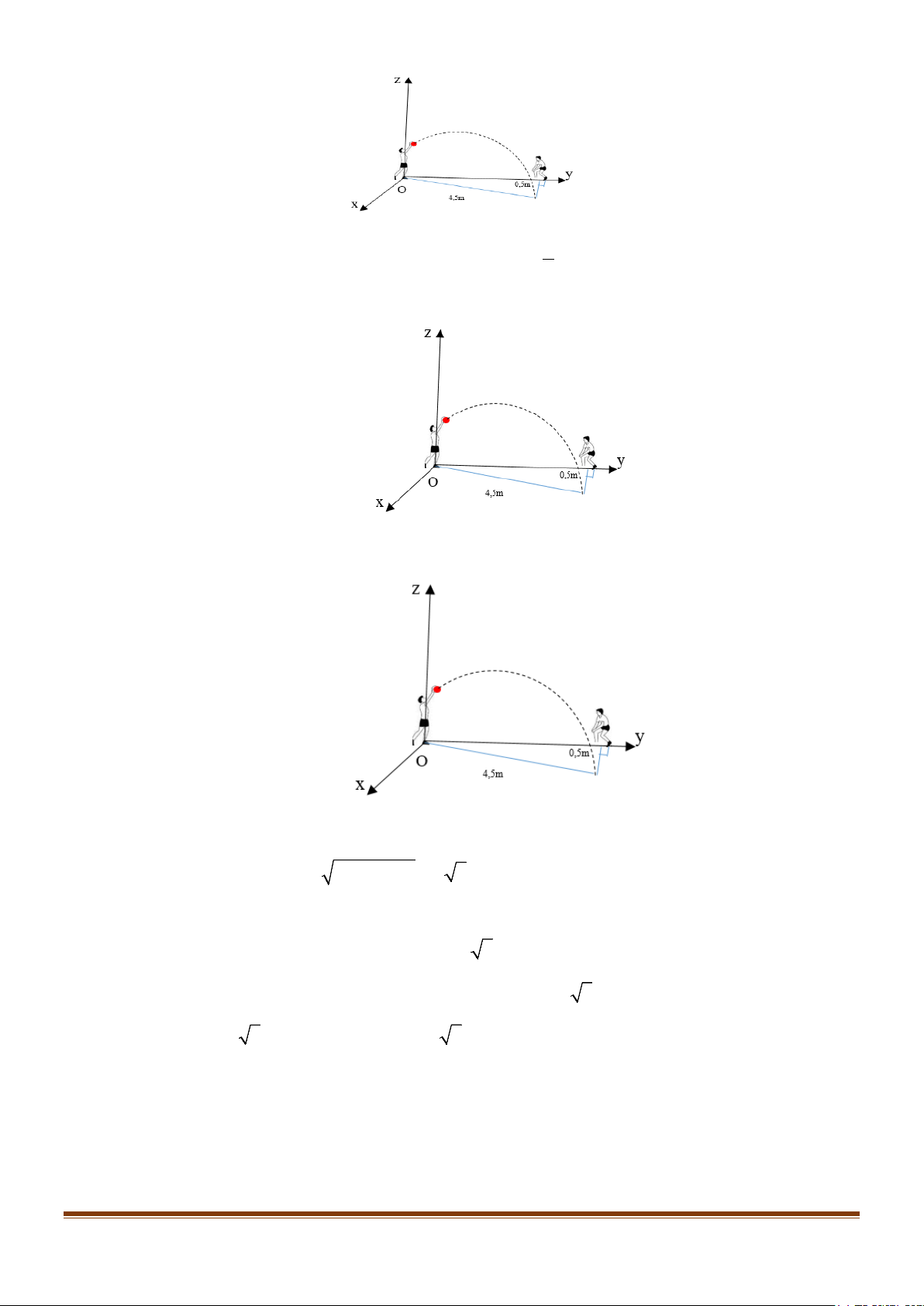
Câu 6: Trong tiết thể dục học về kĩ thuật chuyền bóng hơi, Nam và An đang tập chuyền bóng cho nhau,
Nam ném bóng cho An đỡ, quả bóng bay lên cao nhưng lại lệch sang phải của Nam và rơi xuống
vị trí cách An 0,5m và cách Nam 4,5m được mô tả bằng hình vẽ bên dưới
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng (α ) 1
: ax + y + cx + d = 0 và vuông góc 2
với mặt đất. Khi đó giá trị của a + c + d bằng (kết quả làm tròn đến hàng phần chục).
---------- HẾT ----------
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 4
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x + 3y + z + 2 = 0. Véctơ nào dưới
đây là một véctơ pháp tuyến của (P) ?
A. n 2;3;1 .
B. n 2;3;2 . C. n 2;3;0 . D. n 2;0;3 . 4 ( ) 1 ( ) 3 ( ) 2 ( ) Lời giải
Véctơ pháp tuyến của (P) là n 2;3;1 . 2 ( )
Câu 2: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P): x − 2y + z −5 = 0. Điểm nào dưới đây thuộc (P) ? A. P(0;0; 5 − ) .
B. M (1;1;6) . C. Q(2; 1; − 5) . D. N ( 5 − ;0;0) . Lời giải
Ta có 1− 2.1+ 6 − 5 = 0 nên M (1;1;6) thuộc mặt phẳng (P) .
Câu 3: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A( 1;
− 2;0) và B(3;0;2) . Mặt phẳng trung
trực của đoạn thẳng AB có phương trình là
A. x + y + z − 3 = 0 .
B. 2x − y + z + 2 = 0 . C. 2x + y + z − 4 = 0 . D. 2x − y + z − 2 = 0. Lời giải
Gọi I là trung điểm của đoạn thẳng AB . Suy ra I (1;1; ) 1 .  Ta có AB = (4; 2; − 2) .
Phương trình mặt phẳng trung trực của đoạn thẳng AB đi qua trung điểm I của AB và nhận 
AB làm vtpt, nên có phương trình là (α ): 2x − y + z − 2 = 0 .
Câu 4: Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt phẳng đi  qua điểm M (1;2; 3
− ) và có một vectơ pháp tuyến n = (1; 2 − ;3).
A. x − 2y + 3z +12 = 0 . B. x − 2y − 3z − 6 = 0. C. x − 2y + 3z −12 = 0. D. x − 2y − 3z + 6 = 0 . Lời giải
Phương trình mặt phẳng đi qua điểm M (1;2; 3
− ) và có một vectơ pháp tuyến n = (1; 2 − ;3) là ( 1 x − )
1 − 2( y − 2) + 3(z + 3) = 0 ⇔ x − 2y + 3z +12 = 0.
Câu 5: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A( 1; − 1; )
1 , B(2;1;0) C (1; 1; − 2) . Mặt phẳng
đi qua A và vuông góc với đường thẳng BC có phương trình là
A. 3x + 2z +1 = 0.
B. x + 2y − 2z +1 = 0. C. x + 2y − 2z −1 = 0. D. 3x + 2z −1 = 0 . Lời giải  Ta có BC = ( 1; − 2
− ;2) là một véctơ pháp tuyến của mặt phẳng (P) cần tìm.  
n = −BC = (1;2; 2
− ) cũng là một véctơ pháp tuyến của mặt phẳng (P) .
Vậy phương trình mặt phẳng (P) là x + 2y − 2z +1 = 0.
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 5
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 6: Trong không gian với hệ tọa độ Oxyz , cho điểm M (2;−1;4) và mặt phẳng
(P):3x − 2y + z +1= 0 . Phương trình của mặt phẳng đi qua M và song song với mặt phẳng (P) là
A. 2x − 2y + 4z − 21 = 0 . B. 3x − 2y + z −12 = 0. C.
2x − 2y + 4z + 21 = 0 .D.
3x − 2y + z +12 = 0 Lời giải
Phương trình của mặt phẳng đi qua M và song song với mặt phẳng (P) là
3(x − 2) − 2( y + )
1 + (z − 4) = 0 ⇔ 3x − 2y + z −12 = 0 .
Câu 7: Trong không gian với hệ tọa độ Oxyz . Mặt phẳng (α ) đi qua điểm M ( 1; − 5;2) đồng thời có  
cặp vetơ chỉ phương u = (0;1 ) ;1 và v = ( 3 − ; 5 − ; ) 1 có phương trình là
A. y + z − 7 = 0.
B. 2x − y + z + 5 = 0 .
C. −x + 5y + 2z + 5 = 0 . D. 2x + y + z − 5 = 0 . Lời giải   
Ta có u,v = (6; 3 − ;3) = 3(2;−1; ) 1   . Chọn n = (2; 1; − )
1 là 1 véc tơ pháp tuyến của (α ) . 
Phương trình mặt phẳng qua M ( 1;
− 5;2) nhận n = (2; 1; − )
1 làm 1 véc tơ pháp tuyến là: 2(x + )
1 − ( y −5) + (z − 2) = 0 ⇔ 2x − y + z + 5 = 0 .
Câu 8: Trong không gian với hệ tọa độ (Oxyz) ,cho ba điểm A(0;2; ) 1 , B(3;0; )
1 , C (1;0;0) . Phương
trình mặt phẳng ( ABC)là
A. 2x −3y − 4z + 2 = 0 . B. 4x + 6y −8z + 2 = 0 .
C. 2x + 3y − 4z − 2 = 0 . D. 2x −3y − 4z − 2 = 0 . Lời giải   Ta có AB = (3; 2 − ;0), AC (1; 2 − ;− ) 1   
Vì mặt phẳng ( ABC)đi qua ba điểm ,
A B,C nên VTPT n = AB, AC = (2;3; 4 − )  
Phương trình mặt phẳng ( ABC): 2(x − 0) + 3( y − 2) − 4(z − )
1 = 0 ⇔ 2x + 3y − 4z − 2 = 0.
Câu 9: Trong không gian với hệ tọa độ Oxyz , tính khoảng cách từ M (1;2; 3 − ) đến mặt phẳng
(P):x + 2y + 2z −10 = 0. A. 11. B. 3. C. 7 . D. 4 . 3 3 3 Lời giải 1+ 2.2 + 2. 3 − −10 11 −
Ta có d (M (P)) ( ) 11 ; = = = . 2 2 2 1 + 2 + 2 3 3
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 6
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 10: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng (P) : ax + by + cz −9 = 0 chứa hai điểm A(3;2; ) 1 , B( 3
− ;5;2) và vuông góc với mặt phẳng (Q) :3x + y + z + 4 = 0 . Tính tổng
S = a + b + c . A. S = 12 − .
B. S = 2 . C. S = 4 − . D. S = 2 − . Lời giải  Ta có AB = ( 6 − ;3; ) 1 .  n = (3;1 ) ( )
;1 là VTPT của mp(Q) . Q
Mp(P) chứa hai điểm A(3;2; ) 1 , B( 3
− ;5;2) và vuông góc với mặt phẳng (Q) .   
⇒ n = AB,n  = (2;9; 1
− 5 là VTPT của mp (P) pQ ) ( ) ( )  Vì A(3;2; )
1 ∈(P) ⇒ (P) : 2x + 9y −15z −9 = 0 hoặc (P) : 2
− x − 9y +15z + 9 = 0
Mặt khác (P) : ax + by + cz −9 = 0 ⇒ a = 2;b = 9;c = 1 − 5.
Vậy S = a + b + c = 2 + 9 + ( 15 − ) = 4 − .
Câu 11: Trong không gian với hệ tọa độ Oxyz , điểm M thuộc trục Oy và cách đều hai mặt phẳng:
(P): x + y − z +1= 0 và (Q): x − y + z −5 = 0 có tọa độ là A. M (0; 3 − ;0) .
B. M (0;3;0) . C. M (0; 2; − 0).
D. M (0;1;0) . Lời giải
Ta có M ∈Oy ⇒ M (0; y;0) . y + −y −
Theo giả thiết: d (M (P)) = d (M (Q)) 1 5 ⇔ = ⇔ y = 3 − . 3 3 Vậy M (0;−3;0) .
Câu 12: Trong không gian hệ toạ độ Oxyz , lập phương trình các mặt phẳng song song với mặt phẳng
(β ): x + y − z +3 = 0 và cách (β ) một khoảng bằng 3 .
A. x + y − z + 6 = 0 ; x + y − z = 0 .
B. x + y − z + 6 = 0 .
C. x − y − z + 6 = 0 ; x − y − z = 0.
D. x + y + z + 6 = 0; x + y + z = 0 . Lời giải
Gọi mặt phẳng (α ) cần tìm.
Vì (α )// (β ) nên phương trình (α ) có dạng : x + y − z + c = 0 với c∈ \{ } 3 . Lấy điểm I ( 1; − 1; − ) 1 ∈(β ) .
Vì khoảng cách từ (α ) đến (β ) bằng 3 nên ta có : ( ( − − − + c − 3 c = 0 α )) 1 1 1 c d I, = 3 ⇔ = 3 ⇔ = 3 ⇔
. (thỏa điều kiện c∈ \{ } 3 ). 3 3  c = 6
Vậy phương trình (α ) là: x + y − z + 6 = 0 ; x + y − z = 0 .
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 7
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Trong không gian Oxyz , cho ba điểm A(1;1; ) 1 ; B(1; 2 − ;3);C (2; 1; − 2) . a) Ba điểm ,
A B,C đã cho thẳng hàng.
b) Có vô số mặt phẳng đi qua ba điểm ,
A B,C đã cho. 
c) Mặt phẳng ( ABC) có một vectơ pháp tuyến n = (1;2;3).
d) Mặt phẳng ( ABC) có phương trình là x + 2y + 3z − 6 = 0 . Lời giải a) Sai b) Sai c) Đúng d) Đúng     a) Ta có: AB = (0; 3 − ;2); AC = (1; 2; − ) 1 và 0 3 − ≠ ⇒ A ;
B AC không cùng phương. Do đó ba 1 2 − điểm ,
A B,C không thẳng hàng. Vậy a) Sai. b) Ta có ba điểm ,
A B,C không thẳng hàng nên tồn tại một mặt duy nhất qua ba điểm này. Vậy b) Sai.   
c) Ta có: VTPT n = AB, AC = (1;2;3).   Vậy c) Đúng. 
d) Mặt phẳng ( ABC) đi qua điểm A(1;1; )
1 và nhận vectơ n = (1;2;3) làm một vectơ pháp tuyến là: 1(x − ) 1 + 2( y − ) 1 + 3(z − )
1 = 0 hay ( ABC): x + y + z − 6 = 0. Vậy d) Đúng.
Câu 2: Trong không gian Oxyz , cho hai mặt phẳng (P),(Q) lần lượt có phương trình là
(P): x − 2y +3z +1= 0 và (Q):2x − 4y + 6z +1= 0.
a) Các vectơ pháp tuyến của hai mặt phẳng trên cùng phương.
b) Hai mặt phẳng (P) và (Q) đều đi qua điểm M (1;1;2) .
c) Khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 14 . 14
d) Phương trình mặt phẳng (R) cách đều hai mặt phẳng (P) và (Q) là:
4x + 8y +12z − 5 = 0. Lời giải a) Đúng b) Sai c) Sai d) Đúng      
a) Ta có: một VTPT n = − , một VTPT n = −
và n = n ⇒ n n cùng Q 2 P P ; Q (2; 4;6) P (1; 2;3) Q
phương. Vậy a) Đúng. − b) Ta có 1 2 3 1 =
= ≠ ⇒ (P) / / (Q) . Do đó hai mặt phẳng (P) và (Q) không có điểm chung. 2 4 − 6 1 Vậy b) Sai.
c) Ta có (P) / / (Q). 2.1− 4.1+ 6.0 +1 Lấy điểm N (
)∈(P) ⇒ d ((P) (Q)) = d (N (Q)) 14 1;1;0 , , = = . 2 + (− )2 2 28 2 4 + 6 Vậy c) Sai.
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 8
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
d) Ta có (P) / / (Q). Lấy N ( ) (P)  1 1;1;0 ; P 1;0;  ∈ − ∈ 
 (Q). Gọi I là trung điểm  2  1 1  MN I 1; ;  ⇒ − 
. Ycbt ⇒ (R) qua I và nhận vectơ n(1;2;3) làm một vectơ pháp tuyến là: 2 4    (x )  1   1 1 1 2 y 3 z  − + − + + =   
 0 hay (R) : 4x + 8y +12z − 5 = 0.  2   4  Vậy d) Đúng.
Câu 3: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;2;0) , B(1;0;2) , C (2;1;3), và mặt
phẳng (P) : x − y + 2z + 7 = 0 .
a) Mặt phẳng ( ABC) có một véctơ pháp tuyến là (2;1 ) ;1 .
b) Mặt phẳng ( ABC) đi qua điểm M (3;1;5) .
c) Mặt phẳng ( ABC) vuông góc với mặt phẳng (P) .
d) Khoảng cách từ điểm A đến mặt phẳng (P) bằng 6. Lời giải a) Sai b) Đúng c) Sai d) Sai a) Sai.      Ta có: AB(0; 2; − 2), BC (1;1; )
1 ⇒ AB, BC = ( 4; − 2;2) = 2( 2; − 1; ) 1 = 2.n  
Mặt phẳng ( ABC) có một véctơ pháp tuyến: n( 2 − ;1 ) ;1 . b) Đúng
Phương trình mặt phẳng ( ABC): 2 − (x − )
1 +1( y − 2) +1(z − 0) = 0 ⇔ 2
− x + y + z = 0 .
Thay toạ độ điểm M (3;1;5) vào phương trình mặt phẳng ( ABC): 2.3 − +1+ 5 = 0 : thoả mãn. c) Sai. 
Ta có vecto pháp tuyến của mặt phẳng (P) : n = − . P (1; 1;2)   n n = − − +
= − ≠ ⇒ Mặt phẳng ( ABC) không vuông góc với mặt phẳng P . 2.1 1.1 1.2 1 0 (P) . d) Sai. − + +
d ( A (P)) 1 2 2.0 7 ; = = 6. 1+1+ 4
Câu 4: Trong không gian với hệ tọa độOxyz , cho 3 điểm A( ;0 a ;0) , B(0; ;
b 0) , C (0;0;c) với a, , b c đều dương.
a) Mặt phẳng ( ABC) có phương trình x y z + + = 1 a b c
b) Mặt phẳng ( ABC) đi qua điểm G(1;2;3) sao cho G là trọng tâm A ∆ BC là
6x + 3y + 2z +18 = 0
c) Mặt phẳng ( ABC) đi qua điểm H (1;1; )
1 sao cho H là trực tâm A
∆ BC là x + y + z − 3 = 0
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 9
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
d) Mặt phẳng ( ABC) đi qua điểm M (2; 2; − )3 sao cho độ dài ,
OA OB,OC theo thứ tự tạo thành
cấp số cộng có công sai bằng 2 . Khoảng cách từ gốc tọa độ O tới mặt phẳng (α) bằng m với n
m là phân số tối giản, khi đó T = m+n =19. n Lời giải a) Đúng b) Sai c) Đúng d) Đúng a) Đúng
Theo phương trình mặt phẳng theo đoạn chắn ta có mặt phẳng ( ABC) có phương trình x y z + + = 1 a b c b) Sai a =1  3  a = 3
Vì G là trọng tâm Ab ∆ BC ta có  2 b  = ⇔  = 6 3  c =  9  c = 3 3
Mặt phẳng ( ABC) có phương trình x y z
+ + = 1 ⇔ 6x + 3y + 2z −18 = 0 3 6 9 c) Đúng 1 1 1 H ∈( ABC) + + = 1 a b ca = 3     Vì H (1;1; ) 1 là trực tâm A ∆ BC ta có  . HA BC 0  b c 0  = ⇔ − + = ⇔ b = 3    . HB AC = 0  a c 0  − = c = 3   
Phương trình ( ABC)là: x + y + z −3 = 0 d) Đúng
Giả sử mặt phẳng (α) cắt tia Ox tại điểm có hoành độ bằng a (a > 0) khi đó phương trình mặt
phẳng (α) có dạng x y z + + = 1. a a + 2 a + 4 Do (α) −
đi qua điểm M (2; 2; − )3 nên ta có 2 2 3 + + = 1 ⇔ a = 2. a a + 2 a + 4
Vậy (α) cắt Ox,Oy,Oz lần lượt tại A(2;0;0) , B(0;4;0) ,C(0;0;6) .
Gọi d = d (O,( ABC) .
Áp dụng công thức tính nhanh ta có 1 1 1 1 1 1 1 49 = + + = + + = 2 2 2 2 2 2 2 d OA OB OC 2 4 6 144 2 144 12 ⇒ d = ⇒ d = . 49 7
Vậy: T = m + n =19 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 10
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho ba điểm (
A 1;4;5) , B(3;4;0),C(2; 1 − ;0) và mặt phẳng
(P) :3x + 3y − 2z − 29 = 0. Gọi M ( ; a ;
b c) là điểm thuộc (P) sao cho biểu thức 2 2 2
T = MA + MB + 3MC đạt GTNN. Tính tổng a + b + c . Lời giải    
Chọn điểm I thỏa mãn IA + IB + 3IC = 0 ⇒ I (2;1 ) ;1 Ta có: 2 2 2
T = MA + B M + 3 C M 2 2 2
= MA + MB + 3MC      
= (MI + IA)2 +(MI + IB)2 +3(MI + IC)2
    2
= 5MI + 2MI.(IA+ IB + IC) 2 2 2
+ IA + IB + IC 2 2 2 2
= 5MI + IA + IB + C I T ⇔ MI min min
Suy ra, M là hình chiếu của I trên mặt phẳng (P)
Gọi ∆ là đường thẳng đi qua I và vuông góc với (P)   ⇒ u = = − ∆ nP (3;3; 2) x = 2 + 3t : 
∆ y =1+ 3t z =1−  2t
M ∈∆ ⇒ M (2 + 3t;1+ 3t;1− 2t)
M ∈(P) ⇔ 3(2 + 3t) + 3(1+ 3t) − 2(1− 2t) − 29 = 0
⇔ t =1⇒ M (5;4;− ) 1
Vậy a + b + c = 5 + 4 −1 = 8.
Câu 2: Trong không gian với hệ tọa độ Oxyz , cho các điểm A(2;0;0), B(0;4;0),C (0;0;6), D(2;4;6).
Gọi (P) là mặt phẳng song song với mặt phẳng ( ABC),(P) cách đều D và mặt phẳng ( ABC)
. Phương trình của mặt phẳng (P) là ax + by + 2z + d = 0 với a,b,d ∈ . Giá trị của d bằng bao nhiêu? Lời giải
Phương trình mặt phẳng ( ABC) là: x y z
+ + =1 ⇔ 6x + 3y + 2z −12 = 0 2 4 6
Mặt phẳng (P) song song với mặt phẳng ( ABC) nên (P) có dạng:
6x + 3y + 2z + d = 0 (d ≠ 12 − ) Vì (P) cách đều D và mặt phẳng ( ABC) nên ta có: d ( ;
D (P)) = d (( ABC);(P)) ⇔ d ( ;
D (P)) = d ( ;
A (P)) ⇔ 36 + d = 12 + d ⇔ d = 24 − .
Vậy phương trình mặt phẳng (P) là: 6x + 3y + 2z − 24 = 0 .
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 11
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 3: Trong không gian với hệ tọa độ Oxyz , Cho hai điểm A(3; 1; − 2) , B(2;3; 3 − ) , C ( 2 − ;1; 2 − ). Gọi
      M ( ; a ;
b c) là điểm thuộc mặt phẳng (Oyz) sao . MA MB + .
MB MC + MC.MA có giá trị min. Tính
tổng a − 2b + c . Lời giải
    Gọi I ( ; a ;
b c), sao cho IA+ IB + IC = 0 ⇒ I là trong tâm A
∆ BC ⇒ I (1;1;− ) 1 .
      Ta có: . MA MB + .
MB MC + MC.MA
   
   
   
= (MI + IA).(MI + IB)+(MI + IB).(MI + IC)+(MI + IC).(MI + IA)
   
     
    2
= 3MI + 2MI (IA+ IB + IC) +( . IA IB + .
IB IC + IC.IA) , (mà IA+ IB + IC = 0)
      2 = 3MI + ( . IA IB + .
IB IC + IC.IA)
      Vì điểm I, ,
A B,C cố định nên . IA IB + .
IB IC + IC.IA có giá trị không đổi.
      Để . MA MB + .
MB MC + MC.MA có giá trị min ⇔ MI min.
Mà I cố định nên M là hình chiếu của I lên(Oyz) , suy ra M (0;1;− ) 1 .
Vậy a − 2b + c = 0 − 2.1−1 = 3 − .
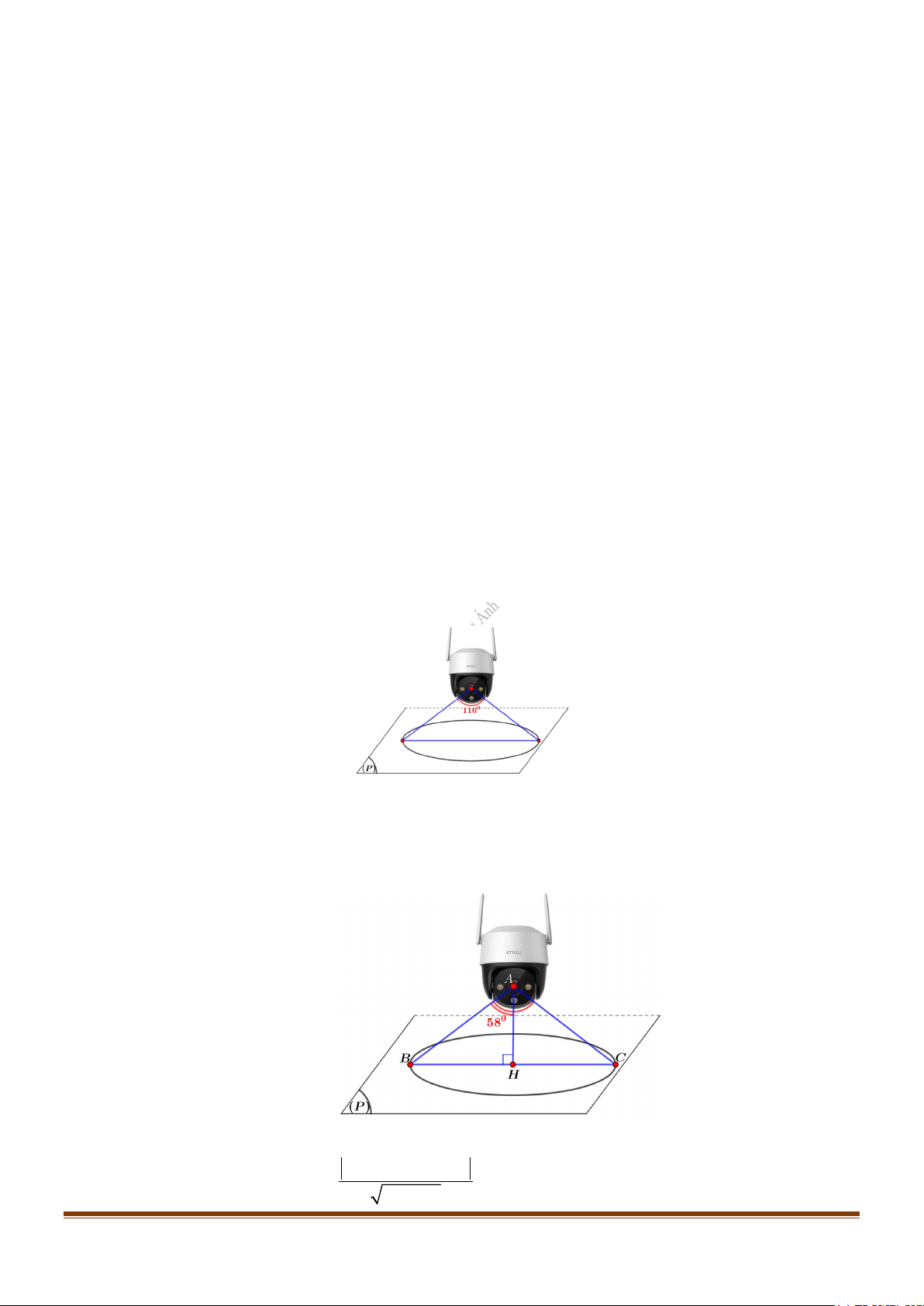
Câu 4: Biết góc quan sát ngang của một camera là 116°. Trong không gian Oxyz , camera được đặt tại
điểm A(2;1;5) và chiếu thẳng về phía mặt phẳng (P) : 2x − y − 2z +13 = 0 . Hỏi vùng quan sát
được trên mặt phẳng (P) của camera là hình tròn có đường kính bằng bao nhiêu? (làm tròn kết
quả đến chữ số hàng chục) Lời giải Gọi ,
A B,C là các điểm như hình vẽ bên dưới và H là hình chiếu vuông góc của A lên mặt phẳng (P) . Hình vẽ Theo đề  = ° ⇒  BAC 116 BAH = 58°. ⋅ − − ⋅ +
Khi đó AH = ( A (P)) 2 2 1 2 5 13 d , = = 2 (đvđd). 4 +1+ 4
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 12
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Xét tam giác ABH vuông tại H , ta có:  tan BH BAH =
⇒ BH = tan 58°⋅2 = 2 tan 58° (đvđd). AH
Suy ra BC = 2BH = 2⋅2 tan 58° ≈ 6,4 (đvđd)
Vậy vùng quan sát của camera trên mặt phẳng (P) là hình tròn có đường kính khoảng 6,4 (đvđd).
Câu 5: Một phần sân trường được định vị bởi các điểm ,
A B,C, D , như hình vẽ.
Bước đầu chúng được lấy “thăng bằng” để có cùng độ cao, biết ABCD là hình thang vuông ở
A và B với độ dài AB = 25m , AD =15m , BC =18m . Do yêu cầu kĩ thuật, khi lát phẳng phàn
sân trường phải thoát nước về góc sân ở C nên người ta lấy độ cao ở các điểm B , C , D xuống
thấp hơn so với độ cao ở A là 10cm , a cm , 6cm tương ứng. Giá trị của a là Lời giải z B A y B' D C x D' C'
Chọn hệ trục tọa độ Oxyz sao cho: O ≡ A, tia Ox ≡ AD ; tia Oy ≡ AB .
Khi đó, A(0;0;0) ; B(0;2500;0) ; C (1800;2500;0) ; D(1500;0;0) .
Khi hạ độ cao các điểm ở các điểm B , C , D xuống thấp hơn so với độ cao ở A là 10cm ,
a cm , 6cm tương ứng ta có các điểm mới B′(0;2500;−10); C′(1800;2500;− a); D′(1500;0;− 6) .
Theo bài ra có bốn điểm A ; B′; C′ ; D′ đồng phẳng.
Phương trình mặt phẳng ( AB D
′ ′) : x + y + 250z = 0 .
Do C′(1800; 2500;− a)∈( AB D
′ ′) nên có: 1800 + 2500 − 250a = 0 ⇔ a =17,2 . Vậy a =17,2cm .
Câu 6: Trong tiết thể dục học về kĩ thuật chuyền bóng hơi, Nam và An đang tập chuyền bóng cho nhau,
Nam ném bóng cho An đỡ, quả bóng bay lên cao nhưng lại lệch sang phải của Nam và rơi xuống
vị trí cách An 0,5m và cách Nam 4,5m được mô tả bằng hình vẽ bên dưới
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 13
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng (α ) 1
: ax + y + cx + d = 0 và vuông góc với mặt đất. 2
Khi đó giá trị của a + c + d bằng (kết quả làm tròn đến hàng phần chục). Lời giải
Chọn hệ trục như hình vẽ. Gọi M là điểm mà quả bóng chạm đất. Khi đó x = M 0,5, 2 2 y = − = M 4,5 0,5 2 5 
Vì (α ) ⊥ (Oxy) nên (α ) có véc tơ chỉ phương k = (0;0; ) 1 . 
Mà (α ) có véc tơ chỉ phương OM = (0,5;2 5;0)   
Khi đó véc tơ pháp tuyến của (α ) là n =   = − . α k,OM   ( 2 5;0,5;0) Vậy (α ) : 2
− 5x + 0,5y = 0 nên a = 2
− 5;b = 0,5;c = 0;d = 0 ⇒ a + b + c + d ≈ 4, − 5.
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 14
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN NG ƯƠ
V PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN CH
BÀI: PHƯƠNG TRÌNH MẶT PHẲNG ĐỀ TEST SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian Oxyz , một vectơ pháp tuyến của mặt phẳng x y z + + =1 là 2 − 1 − 3     A. n = (3;6; 2 − ). B. n = (2; 1 − ;3) . C. n = ( 3 − ; 6 − ; 2 − ) . D. n = ( 2; − 1 − ;3) .
Câu 2: Trong không gian Oxyz , phương trình mặt phẳng (P) đi qua 3 điểm M ( 2; − 0;0) , N (0;−1;0) , P(0;0;3) là
A. 3x + 6y − 2z − 6 = 0 . B. 2x + y − 3z −1 = 0 .
C. 3x + 6y − 2z = 0.
D. 3x + 6y − 2z + 6 = 0 .
Câu 3: Trong không gian Oxyz , cho điểm A(1;2;3) . Mặt phẳng chứa điểm A và trục Oz có phương trình là
A. 2x − y = 0.
B. x + y − z = 0 .
C. 3y − 2z = 0.
D. 3x − z = 0vô số.
Câu 4: Trong không gian Oxyz , cho điểm A(2; 1 − ; 3
− ) và mặt phẳng (P) :3x − 2y + 4z − 5 = 0 . Gọi
(Q) là mặt phẳng đi qua A và song song với mặt phẳng (P) . Mặt phẳng (Q) có phương trình là:
A. 3x − 2y + 4z − 4 = 0 B. 3x − 2y + 4z + 4 = 0 . C. 3x − 2y + 4z + 5 = 0 .D.3x + 2y + 4z + 8 = 0 .
Câu 5: Trong không gian Oxyz , phương trình mặt phẳng (P) đi qua hai điểm A(2;−1;0) , B(1;1;2)
và vuông góc với mặt phẳng (Q) : x + y + 2z −3 = 0 là.
A. 2x + 4y − 3z −8 = 0 . B. 2x + 4y −3z = 0.
C. 2x + 4y − 3z + 8 = 0. D. 2x − 4y −3z = 0.
Câu 6: Trong không gian Oxyz , phương trình mặt phẳng (P) đi qua điểm M (2;1;− 2) và vuông góc
với hai mặt phẳng (Q) : x + y + 2z −3 = 0 và (R) : x − y − z + 4 = 0 là.
A. x + 3y − 2z + 9 = 0 . B. 2x + y − 2z − 9 = 0 . C. x + 3y − 2z − 9 = 0. D. 2x + y − 2z + 9 = 0.
Câu 7: Trong không gian Oxyz, cho các điểm A(5;1;3), B(1;6;2),C (5;0;4), D(4;0;6) . Viết phương
trình mặt phẳng (P) đi qua hai điểm ,
A B và song song với . CD
A. 4x − 5y + z + 24 = 0 .
B. x − 2z +1 = 0
C. 10x + 9y + 5z − 74 = 0.
D. 10x + 9y + 5z + 74 = 0 .
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 1
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 8: Trong không gian Oxyz, mặt phẳng (P) : 2x + y + z − 2 = 0 song song với mặt phẳng nào dưới đây? A. 1 1
x + y − z −1 = 0 . B. x − y − z − 2 = 0 .C. 4x + 2y + 2z + 4 = 0 . D. 2x + y + z − 2 = 0 . 2 2
Câu 9: Trong không gian Oxyz , cho mặt phẳng (α ) : 2x − y + 3 = 0. Mặt phẳng nào sau đây vuông góc với mặt phẳng (α ) ? A. (α : 2
− x + y − 3z = 0 .
B. (α : x + 5y + z − 2 = 0. 2 ) 1 )
C. (α : 4x − 2y + 7 = 0 .
D. (α : x + 2y − z +1= 0 . 4 ) 3 )
Câu 10: Trong không gian Oxyz , điểm M thuộc trục Oy và cách đều hai mặt phẳng:
(P): x + y − z +1= 0 và (Q): x − y + z −5 = 0 có tọa độ là A. M (0; 3 − ;0) . B. M (0;3;0) . C. M (0; 2; − 0).
D. M (0;1;0) .
Câu 11: Trong không gian Oxyz khoảng cách giữa hai mặt phẳng (P): x + 2y + 3z −1= 0 và
(Q): x + 2y +3z + 6 = 0 là A. 7 . B. 8 . C. 14. D. 5 . 14 14 14
Câu 12: Trong không gian Oxyz, cho A(2;0;0),B(0;4;0), C(0;0;6). Gọi (P) là mặt phẳng không
chứa gốc tọa độ và song song với mp( ABC) , biết khoảng cách giữa mặt phẳng (P) và mặt
phẳng ( ABC) bằng 12 . Phương trình của (P) là 7
A. 6x + 3y + 2z −12 = 0 . B. 6x + 3y + 2z = 0.
C. 6x + 3y + 2z − 24 = 0 . D. 6x + 3y + 2z − 36 = 0 .
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Trong không gian Oxyz , cho ba điểm A( 1;
− 1;0), B(1;−1;2), C (1;− 2; ) 1 .  
a) Một vecto pháp tuyến của mặt phẳng ( ABC) là AB, AC   . 
b) Vecto n = (1;2;3) là một vecto pháp tuyến của mặt phẳng ( ABC). 
c) Vecto u = (1;1;0) là một vecto pháp tuyến của mặt phẳng đi qua O và chứa đưởng thẳng AB . 
d) Vecto v = (1;2;3) là một vecto pháp tuyến của mặt phẳng song song với hai đưởng thẳng AB và OC .
Câu 2: Cho các điểm A(1; 2 − ;0); B(2; 1; − ) 1 ;C (1;1;2).
a) Phương trình mặt phẳng ( ABC) là x + 2y −3z −3 = 0 .
b) Phương trình mặt phẳng (α ) qua A và vuông góc với BC là x − 2y − z −5 = 0 .
c) Phương trình mặt phẳng trung trực (β ) của đoạn AC là 6y + 4z −1 = 0.
d) Phương trình mặt phẳng (γ ) chứa trục Ox và điểm C là 2y + z = 0 .
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 3: Trong không gian với hệ trục toạ độ Oxyz , cho điểm A(1;2;5) và mặt phẳng
(α ): x + 2y + 2z −6 = 0 . 
a) Véc tơ n = (1;2;2) là một vectơ pháp tuyến của (α ) .
b) Phương trình mặt phẳng (β ) đi qua điểm A và song song với mặt phẳng (α ) có phương trình
x + 2y + 2z +15 = 0
c) Phương trình mặt phẳng (γ ) đi qua hai điểm O và A đồng thời vuông góc với mặt phẳng
(α ) có phương trình 2x − y = 0. 2 4 d) Điểm  M ∈(α ) sao cho ,
A O, M thẳng hàng thì tọa độ M  ; ;2 . 5 5   
Câu 4: Trong không gian với hệ trục toạ độ Oxyz , cho ba điểm A(1;2;− 2); B(2;1;2);C (3; 2; − ) 1 .   
a) Phương trình mặt phẳng (P) đi qua ba điểm ,
A B,C có một véc tơ pháp tuyến là n = AB, AC   .
b) Phương trình mặt phẳng (P) là 13x + 5y − 2z + 27 = 0 . 
c) Phương trình mặt phẳng đi qua điểm A(1;2;− 2) và nhận BC làm véc tơ pháp tuyến có dạng: 1(x + )
1 x − 3( y + 2) −1(z − 2) = 0 .
d) Phương trình mặt phẳng đi qua ba điểm E; F; K lần lượt là hình chiếu vuông góc của A lên trục ;
Ox Oy;Oz có phương trình x y z + − = 1. 1 2 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong hệ tục toạ độ không gian Oxyz , cho A(1;0;0), B(0; ;
b 0) , C (0;0;c) , biết b,c > 0 ,
phương trình mặt phẳng (P) : y − z +1 = 0. Tính M = c + b biết ( ABC) ⊥ (P) , d O  ( ABC) 1 ;  =  . 3
Câu 2: Trong không gian Oxyz cho hai điểm A( 1;
− 2; 0), B(1;1; 3) và mặt phẳng
(P): x − 2y +3z −5 = 0. Phương trình của mặt phẳng đi qua hai điểm ,A B, đồng thời vuông góc
(P) là 2xaybz c  0. Giá trị của biểu thức a + 2b +3c bằng
Câu 3: Trong không gian Oxyz , mặt phẳng (α ) qua hai điểm A(1;2;0), B(4;1;2) và cách đều hai điểm C ( 2 − ;1;− ) 1 , D(0;−3; )
1 có dạng ax + by + cz +1 = 0 (a < 0) . Tính P = a + b + c .
Câu 4: Trong không gian Oxyz , cho mặt phẳng (α ): 2x + 3y + z +1= 0 . Gọi (P) là mặt phẳng song
song với (α ) , cắt các tia Ox,Oy,Oz lần lượt tại các điểm A , B ,C sao cho thể tích khối tứ diện
OABC bằng 6 . Tính khoảng cách từ gốc tọa độ O đến mặt phẳng (P) (kết quả làm tròn đến hàng phần trăm).
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 3
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 5: Một sân vận động được xây dựng theo mô hình là hình chóp cụt OAG .
D BCFE có hai đáy song
song với nhau. Mặt sân OAGD là hình chữ nhật và được gắn hệ trục Oxyz như hình vẽ (đơn vị
trên mỗi trục tọa độ là mét). Mặt sân OAGD có chiều dài OA =100m , chiều rộng OD = 60m và
tọa độ điểm B(10;10;8) . Giả sử phương trình tổng quát của mặt phẳng (OACB) có dạng
ax + y + cz + d = 0 . Tính giá trị biểu thức a + c + d .
Câu 6: Manhattanhenge (Hình 1) là một sự kiện diễn ra khi Mặt Trời mọc hoặc khi Mặt Trời lặn nằm
thẳng hàng với các tuyến phố Đông - Tây thuộc mạng lưới đường phố chính tại quận Manhattan
của thành phố New York. Khi mặt trời lặn, tia sáng song song mặt đất lệch một góc khoảng 0 38
so với hướng tây (Hình 2).
Giả sử mặt tiền các tòa nhà hai bên đường nằm trong 2 mặt phẳng song song cách nhau 30m và
vuông góc với mặt đất. Biết rằng mặt phẳng phía bắc đi qua gốc O của hệ trục Oxyz , với tia Oz
vuông góc với mặt đất và hướng lên trên. Phương trình mặt phẳng thứ hai có dạng
(Q) : x + ay + bz + c = 0 m , với c = . Tính m + n . 0 sin n
---------- HẾT ----------
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 4
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn
ĐỀ TEST THEO BÀI – CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
HƯỚNG DẪN GIAIT CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian Oxyz , một vectơ pháp tuyến của mặt phẳng x y z + + =1 là 2 − 1 − 3     A. n = (3;6; 2 − ). B. n = (2; 1 − ;3) . C. n = ( 3 − ; 6 − ; 2 − ) . D. n = ( 2; − 1 − ;3) . Lời giải Phương trình x y z +
+ = 1 ⇔ 3x + 6y − 2z + 6 = 0. 2 − 1 − 3 
Một vectơ pháp tuyến của mặt phẳng đã cho là n = (3;6; 2 − ) .
Câu 2: Trong không gian Oxyz , phương trình mặt phẳng (P) đi qua 3 điểm M ( 2; − 0;0) , N (0;−1;0) , P(0;0;3) là
A. 3x + 6y − 2z − 6 = 0 . B. 2x + y − 3z −1 = 0 .
C. 3x + 6y − 2z = 0.
D. 3x + 6y − 2z + 6 = 0 . Lời giải
Áp dụng phương trình mặt phẳn theo đoạn chắn, ta có phương trình mặt (MNP) là x y z +
+ = 1 ⇔ 3x + 6y − 2z + 6 = 0 . 2 − 1 − 3
Câu 3: Trong không gian Oxyz , cho điểm A(1;2;3) . Mặt phẳng chứa điểm A và trục Oz có phương trình là
A. 2x − y = 0.
B. x + y − z = 0 .
C. 3y − 2z = 0.
D. 3x − z = 0vô số. Lời giải
Gọi (P) là mặt phẳng chứa điểm A và trục Oz .
Oz đi qua điểm O(0;0;0) và có vectơ chỉ phương u = (0;0; ) 1 .   
Mặt phẳng (P) có vectơ pháp tuyến n = u,OA = ( 2 − ;1;0)  
và đi qua điểm O(0;0;0) nên có
phương trình 2x − y = 0.
Câu 4: Trong không gian Oxyz , cho điểm A(2; 1 − ; 3
− ) và mặt phẳng (P) :3x − 2y + 4z − 5 = 0 . Gọi
(Q) là mặt phẳng đi qua A và song song với mặt phẳng (P) . Mặt phẳng (Q) có phương trình là:
A. 3x − 2y + 4z − 4 = 0 B. 3x − 2y + 4z + 4 = 0 . C. 3x − 2y + 4z + 5 = 0 .D.3x + 2y + 4z + 8 = 0 . Lời giải
Mặt phẳng (P) :3x − 2y + 4z −5 = 0 có một vectơ pháp tuyến là n = (3; 2 − ;4) . 
Do (Q) song song với (P) nên (Q) có vectơ pháp tuyến là n = (3; 2 − ;4) .
Phương trình mặt phẳng (Q) : 3(x − 2) − 2( y + )
1 + 4(z + 3) = 0 ⇔ 3x − 2y + 4z + 4 = 0 .
Câu 5: Trong không gian Oxyz , phương trình mặt phẳng (P) đi qua hai điểm A(2;−1;0) , B(1;1;2)
và vuông góc với mặt phẳng (Q) : x + y + 2z −3 = 0 là.
A. 2x + 4y − 3z −8 = 0 . B. 2x + 4y −3z = 0.
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 5
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
C. 2x + 4y − 3z + 8 = 0. D. 2x − 4y −3z = 0. Lời giải
Mặt phẳng (Q) có một vectơ pháp tuyến n(Q) = (1;1;2) .
Mặt phẳng (P) đi qua hai điểm A(2;−1;0) , B(1;1;2) và vuông góc với mặt phẳng (Q) nên  
có cặp vectơ chỉ phương là AB = ( 1
− ;2;2) và n(Q) = (1;1;2) . Do đó (P) có vectơ pháp tuyến   
là: n(P) = AB;n(Q)  = (2;4;−3)   . 
Mặt phẳng (P) đi qua điểm A(2;−1;0) và nhận n(P) = (2;4;−3) làm một vectơ pháp tuyến
nên có phương trình: 2(x − 2) + 4( y + )
1 − 3(z − 0) = 0 ⇔ 2x + 4y −3z = 0 .
Câu 6: Trong không gian Oxyz , phương trình mặt phẳng (P) đi qua điểm M (2;1;− 2) và vuông góc
với hai mặt phẳng (Q) : x + y + 2z −3 = 0 và (R) : x − y − z + 4 = 0 là.
A. x + 3y − 2z + 9 = 0 . B. 2x + y − 2z − 9 = 0 .
C. x + 3y − 2z − 9 = 0. D. 2x + y − 2z + 9 = 0. Lời giải  
Mặt phẳng (Q) , (R) có một vectơ pháp tuyến lần lượt là n(Q) = (1;1;2) và n(R) = (1;−1;− ) 1 .
Mặt phẳng (P) đi qua điểm M (2;1;− 2) và vuông góc với hai mặt phẳng (Q) và (R) nên có  
cặp vectơ chỉ phương là n(Q) = (1;1;2) và n(R) = (1;−1;− )
1 . Do đó (P) có vectơ pháp tuyến là   
n(P) = n(Q) ;n(R)  = (1;3;− 2)   . 
Mặt phẳng (P) đi qua điểm M (2;1;− 2) và nhận n(P) = (1;3;− 2) làm một vectơ pháp tuyến
nên có phương trình: 1(x − 2) + 3( y − )
1 − 2(z + 2) = 0 ⇔ x + 3y − 2z −9 = 0 .
Câu 7: Trong không gian Oxyz, cho các điểm A(5;1;3), B(1;6;2),C (5;0;4), D(4;0;6) . Viết phương
trình mặt phẳng (P) đi qua hai điểm ,
A B và song song với . CD
A. 4x − 5y + z + 24 = 0 .
B. x − 2z +1 = 0
C. 10x + 9y + 5z − 74 = 0.
D. 10x + 9y + 5z + 74 = 0 . Lời giải      Ta có AB = ( 4; − 5;− ) 1 ,CD = ( 1
− ;0;2) ⇒ n = A ; B CD = (10;9;5)  
Ta có mp (P) đi qua A(5;1;3) và nhận n = (10;9;5)làm vectơ pháp tuyến nên có phương trình
10(x − 5) + 9( y − )
1 + 5(z − 3) = 0 ⇔ 10x + 9y + 5z − 74 = 0.
Câu 8: Trong không gian Oxyz, mặt phẳng (P) : 2x + y + z − 2 = 0 song song với mặt phẳng nào dưới đây? A. 1 1
x + y − z −1 = 0 . B. x − y − z − 2 = 0 .C. 4x + 2y + 2z + 4 = 0 . D. 2x + y + z − 2 = 0 . 2 2 Lời giải Xét ( 2 1 1
P) : 2x + y + z − 2 = 0 và ( 1 1
Q : x + y − z −1 = 0 có = ≠ ⇒ (P) không song 1 ) 2 2 1 1 1 − 2 2
Giáo viên: Huỳnh Văn Ánh – 42 Nguyễn Cư Trinh – Thuận Hòa – TP Huế – ĐT: 0984164935 Page 6
Chuyên luyện thi: Tuyển sinh vào lớp 10 – Tốt Nghiệp THPT – BDKT Toán 10; 11; 12
Sưu tầm và biện soạn

Tài liệu liên quan: