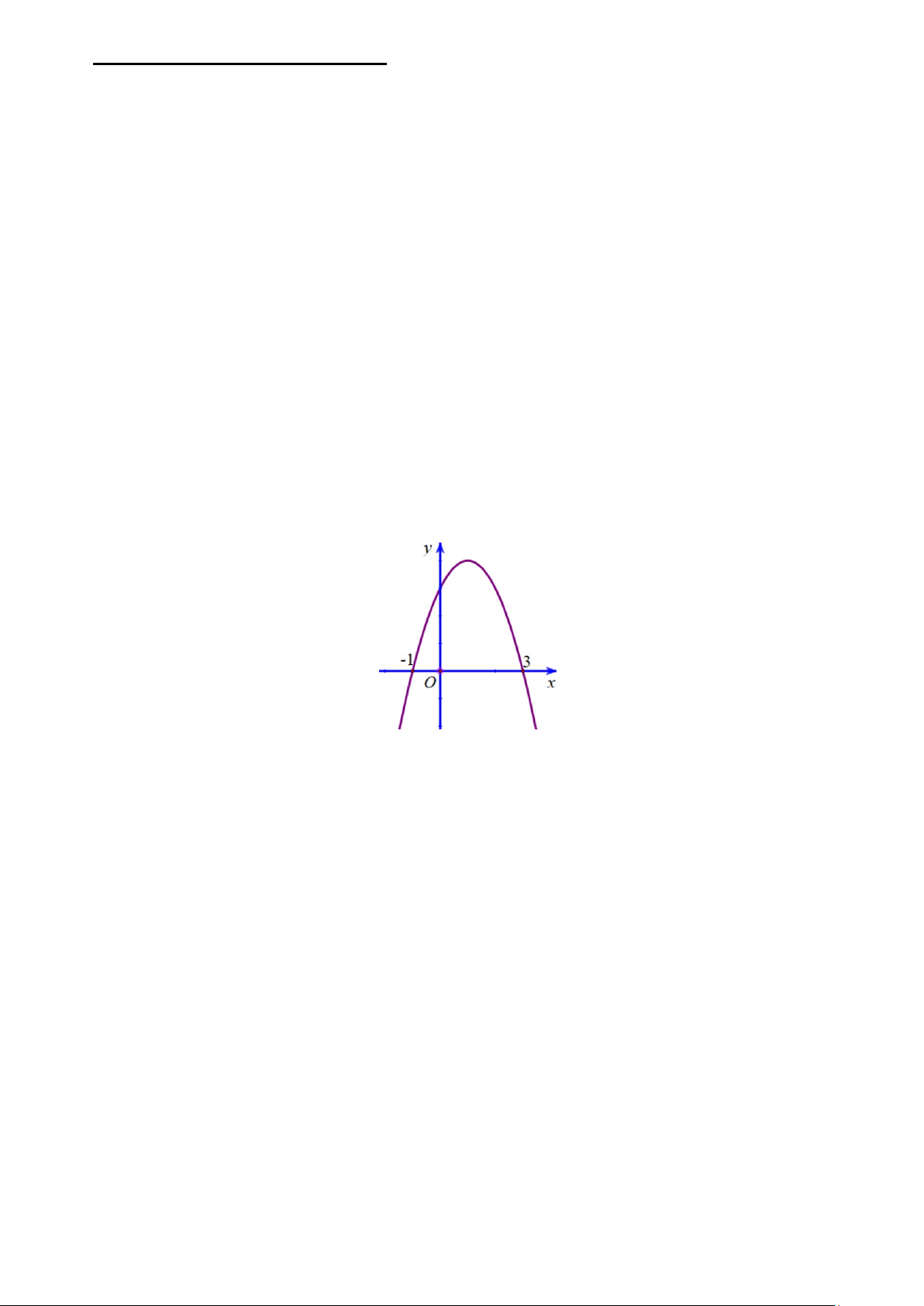















Preview text:
SỞ GIÁO DỤC & ĐÀO TẠO BẮC NINH
ĐỀ KIỂM TRA CHẤT LƯỢNG LẦN 3
TRƯỜNG THPT LƯƠNG TÀI SỐ 2 Môn: TOÁN 10
Năm học: 2022 - 2023 Mã đề thi: 301
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(50 câu trắc nghiệm)
Ngày kiểm tra: 12 tháng 03 năm 2023
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
Câu 1: Tìm tất cả các giá trị của tham số m sao cho ( ; m +∞) ⊂ (1;+∞) ? A. m <1. B. m ≤1. C. m ≥1. D. m >1.
Câu 2: Cho tập hợp A = {2;3;4;5; }
6 . Số phần tử của tập hợp A là A. 6. B. 4. C. 5. D. 3.
Câu 3: Trên hệ tọa độ Oxy, cho hai véc tơ a = (2;− ) 1 ,b = (3; 2
− ) . Tọa độ của véc tơ b − a là A. (1; 3 − ) . B. ( 1; − 3 − ) . C. (1; ) 1 − . D. ( 1; − ) 1 .
Câu 4: Số hạng thứ 4 trong khai triển Newton của đa thức P(x) = ( + x)18 1 là A. 4 C . C x . C . C x . 18 B. 4 4 18 C. 318 D. 3 3 18
Câu 5: Cho hàm số bậc hai y = f (x) có đồ thị như hình vẽ. Tập nghiệm của bất phương trình f (x) > 0 là A. ( ; −∞ − ) 1 ∪(3;+∞) . B. ( 1; − 3) . C. (0;3). D. [ 1; − ] 3 .
Câu 6: Trên mặt phẳng tọa độ Oxy, phương trình của đường thẳng d đi qua điểm A(2;− ) 1 có véc tơ pháp tuyến n = (3;2) là
A. 3x + 2y − 4 = 0.
B. 3x + 2y + 4 = 0 .
C. 2x − 3y − 7 = 0.
D. 3x − 2y −8 = 0 .
Câu 7: Một ban cán sự lớp có 3 người gồm 1 lớp trưởng, 1 bí thư và 1 ủy viên. Tính số cách tạo một ban cán
sự lớp từ một nhóm 10 học sinh. A. 120. B. 720. C. 1000. D. 30.
Câu 8: Trong khai triển Newton của f (x) = ( x − )8
2 1 thành đa thức, biến x có số mũ cao nhất bằng bao nhiêu? A. 7. B. 9. C. 16. D. 8.
Câu 9: Cho tập hợp X = {1;2;3;4; }
5 . Một tổ hợp chập hai của 5 phần tử trong X là A. {2; } 5 . B. 2 C . A . 5 C. 10. D. 25
Câu 10: Bạn A có 4 chiếc áo sơ mi khác nhau và 6 chiếc quần âu khác nhau. Từ số áo và quần đã có, bạn A
có thể tạo ra được bao nhiêu bộ lễ phục gồm 1 quần âu và 1 áo sơ mi. A. 24. B. 10. C. 15. D. 360.
Câu 11: Số chỉnh hợp chập 3 của 6 phần tử là A. 3!. B. 3 C . A . 6 C. 36 D. 6!.
Câu 12: Tính số cách xếp 6 quyển sách Toán khác nhau thành hàng ngang trên một giá sách.
Trang 1/4 - Mã đề thi 301 A. 6. B. 36. C. 720. D. 120.
Câu 13: Tập nghiệm của bất phương trình 2
x − 5x + 6 ≥ 0 là A. T = ( ; −∞ 2]∪[3;+∞). B. T = ( ; −∞ ] 1 ∪[6;+∞) . C. T = [2; ] 3 . D. T = [1;6].
Câu 14: Từ 15 quả cầu được đánh số từ 1 đến 15, chọn ra 4 quả cầu. Tính số cách chọn ra 4 quả cầu được đánh số lẻ. A. 2. B. 35. C. 1680. D. 70.
Câu 15: Trên mặt phẳng tọa độ Oxy, tọa độ giao điểm của hai đường thẳng ∆ : 2x + y −3 = 0 và 1
∆ : x − y − 3 = 0 là 1 A. (2; ) 1 . B. (2; ) 1 − . C. ( 2; − ) 1 . D. ( 2; − − ) 1 .
Câu 16: Nghiệm của phương trình 2x −1 = x là A. x = 1 − . B. x = 2 . C. x =1. D. x = 0 .
Câu 17: Phương trình 2 2
2x − 2x − 2 = x + x − 2 có tất cả bao nhiêu nghiệm? A. 0. B. 2. C. 1. D. 3.
Câu 18: Trên mặt phẳng tọa độ Oxy, cho đường thẳng d : 2x − y + 3 = 0 . Điểm nào sau đây thuộc đường thẳng d? A. P(1;− ) 1 . B. Q( 1; − ) 1 . C. M ( 2; − ) 1 . D. N (0; 3 − ) .
Câu 19: Cho khai triển đa thức P(x) = (2 − x)12 2 11 12
= a + a x + a x +...+ a x + a x . Tìm 0 1 2 11 12 a . 8 A. 7920 − . B. 7920. C. 8 7920x . D. 8 7920 − x .
Câu 20: Từ tập hợp E = {1;2;3;4;5; }
6 có thể tạo được bao nhiêu số tự nhiên có 4 chữ số (các chữ số đôi một khác nhau). A. 360. B. 15. C. 24. D. 4096.
Câu 21: Trên mặt phẳng tọa độ Oxy, phương trình tham số của đường thẳng đi qua hai điểm A(3;− ) 1 , B(1;3) là x = 2 − + 3t x =1+ 2t x =1− 2t x = 1− 2t A. . B. . C. . D. . y = 4 − t y = 3 + t y = 3 + 4t y = 3 + 2t
Câu 22: Một nhóm học sinh có 4 nam và 5 nữ. Tính số cách chọn 1 học sinh trong nhóm. A. 9. B. 120. C. 20. D. 24.
Câu 23: Trong các biểu thức được cho bởi các phương án A, B, C, D dưới đây, biểu thức nào là một tam thức bậc hai?
A. f (x) = x −3 x + 2 . B. f (x) 2
= x − 3x + 2 .
C. f (x) = 3x + 2. D. f (x) 3 2
= x − 3x + 2 .
Câu 24: Tìm tập xác định của hàm số y = x + 2 .
A. D = [2;+∞). B. D = ( 2; − +∞) .
C. D = (2;+∞) . D. D = [ 2; − +∞) .
Câu 25: Cho bất phương trình 2x − y + 3 > 0. Một nghiệm của bất phương trình đã cho là A. ( 1; − ) 1 . B. ( 2; − 0) . C. (1; ) 1 − . D. (0;4) .
Câu 26: Khai triển Newton của P(x) = ( x + )15 3
2 có tất cả bao nhiêu số hạng? A. 15. B. 17. C. 14. D. 16.
Câu 27: Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n . Mệnh đề nào dưới đây là đúng? A. k k! C = . B. k k! C = . C. k n! C = . D. k n! C = . n
(n − k)!n! n (n − k)! n (n − k)! n
(n − k)!k!
Trang 2/4 - Mã đề thi 301
Câu 28: Trên mặt phẳng tọa độ Oxy, cho hai véc tơ u = (3;4) và v = ( 1; − 2). Tích vô hướng . u v bằng A. 11 − . B. 11. C. 5 − . D. 5.
Câu 29: Trên mặt phẳng tọa độ Oxy, góc giữa hai véc tơ a = (1;− ) 1 và b = ( 2; − 0) có số đo bằng A. 60°. B. 45°. C. 90°. D. 135° .
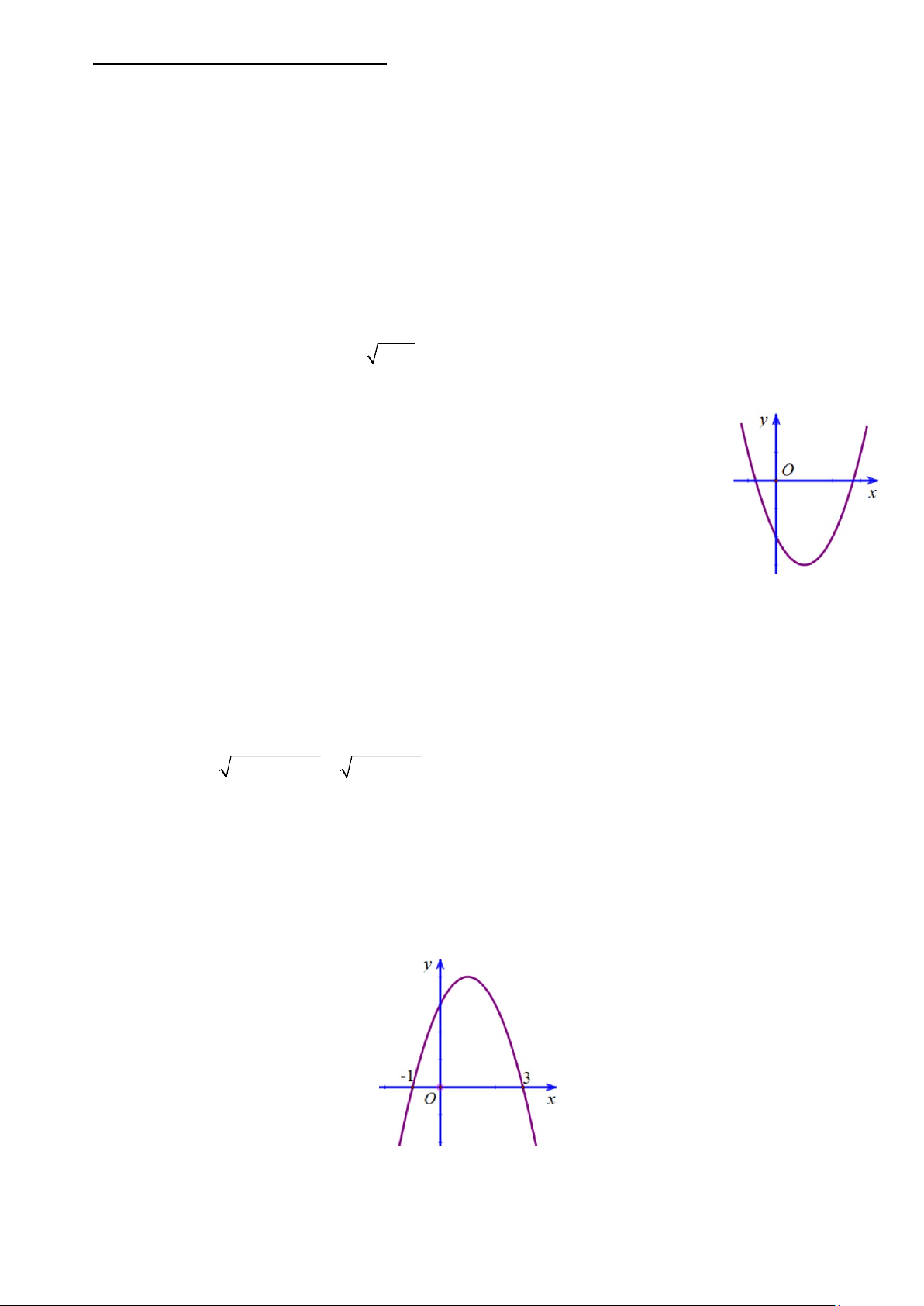
Câu 30: Đường parabol trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau A. 2
y = −x + 2x − 2. B. 2
y = x − 2x − 2. C. 2
y = x + 2x − 2 . D. 2
y = −x − 2x − 2.
Câu 31: Số giao điểm của parabol 2
y = x + x − 2 và đường thẳng y = −x +1 là A. 0. B. 2. C. 1. D. 3.
Câu 32: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :3x + 4y − 5 = 0 và điểm M (3;4) . Khoảng cách từ
M tới đường thẳng ∆ bằng
A. d (M ,∆) = 4 .
B. d (M ,∆) = 5.
C. d (M ,∆) = 20 .
D. d (M ,∆) = 6 .
x + y + z = 0
Câu 33: Nghiệm của hệ phương trình x − 2y − z = 4 là
2x + y − 2z = 2 − A. ( 1; − 2;− ) 1 . B. (1;1; 2 − ) . C. (1;2; ) 1 . D. (1; 2 − ; ) 1 . x = 2 + t
Câu 34: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :
(t là tham số). Một véc tơ chỉ phương y = 1+ 3t của ∆ là A. u = (1;3). B. u = (1;2) . C. u = (3; ) 1 . D. u = (2; ) 1 .
Câu 35: Trên mặt phẳng tọa độ Oxy, cho hai đường thẳng d : x − 2y + 3 = 0 và 1
d : m +1 x + m −1 y + 2 = 0 . Tìm m để hai đường thẳng vuông góc với nhau. 2 ( ) ( ) A. m = 3 . B. m = 3 − . C. m = 1 − . D. m =1.
Câu 36: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ : x − 2y +1 = 0. Phương trình đường thẳng d đi qua
M (2;0) và song song với ∆ là
A. 2x − y − 4 = 0 .
B. x − 2y + 2 = 0 .
C. 2x + y − 4 = 0 .
D. x − 2y − 2 = 0 .
Câu 37: Một bộ câu hỏi có 8 câu hỏi lí thuyết và 6 câu hỏi bài tập. Tính số cách tạo một đề kiểm tra gồm 3
câu hỏi lí thuyết và 2 câu hỏi bài tập từ bộ câu hỏi ban đầu. A. 71. B. 10080. C. 840. D. 36.
Câu 38: Số hoán vị của 3 phần tử là A. 6. B. 3. C. 9. D. 27.
Câu 39: Cho n là số tự nhiên thỏa mãn 0 1 2 n 1 − n 2007
C + C + C + + C + C = . Trong khai triển n n n ... n n 2 P(x) = ( n
3 2.x − 3) thành đa thức có tất cả bao nhiêu số hạng với hệ số nguyên dương? A. 335. B. 334. C. 670. D. 1004.
Trang 3/4 - Mã đề thi 301
Câu 40: Cho tam giác nhọn ABC có diện tích bằng 6 3 (đvdt) và độ dài các cạnh AB = 4, AC = 6 . Tính
khoảng cách giữa hai điểm B và C? A. BC = 2 7 . B. BC = 2 10 . C. BC = 2 19 . D. BC = 4 7 .
Câu 41: Cho đa giác đều 2n cạnh (n ≥ 2) . Biết số tam giác có đỉnh trùng với đỉnh của đa giác gấp 68 lần số
hình chữ nhật có đỉnh trùng với các đỉnh của đa giác. Tìm n? A. 24. B. 23. C. 26. D. 25.
Câu 42: Trên hệ trục tọa độ Oxy, cho hai đường thẳng d : 2x + 4y −1 = 0 và d : x − 2y + 3 = 0 . Viết phương 1 2
trình đường phân giác của góc nhọn tạo bởi hai đường thẳng d và d . 1 2
A. 8y − 7 = 0. B. 4x + 5 = 0 .
C. 8y −5 = 0 .
D. 4x −5 = 0 .
Câu 43: Trên hệ trục tọa độ Oxy, xét các điểm A(3; ) 1 , B( 1; − 5 − ) và M ( ;4
m − 2m) với m là tham số nguyên.
Khi tam giác MAB vuông tại M, hãy tính độ dài đoạn thẳng OM. A. OM = 2 2 . B. OM = 4 10 . C. OM = 4 . D. OM = 4 2 .
Câu 44: Tìm m để hàm số 2
y = x + 2mx + 4m + 5 xác định với mọi x ∈ . A. 1 − < m < 5. B. 1 − ≤ m ≤ 5. C. 5 − ≤ m ≤1. D. m ≤ 1 − hoặc m ≥ 5 .
Câu 45: Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số 2
y = x − 2 m + 2 x + m + 4 đồng
biến trên khoảng (6;+∞)? A. 8. B. 9. C. 13. D. 11.
Câu 46: Có tất cả bao nhiêu số tự nhiên m sao cho phương trình 2
x − 4x + m −1 = 2x + 2 có đúng hai nghiệm cùng dương? A. 8. B. 10. C. 9. D. Vô số.
Câu 47: Bạn Ninh có 12 viên kẹo giống nhau, mỗi ngày Ninh chỉ được sử dụng đúng một hoặc hai viên kẹo.
Bạn Ninh có tất cả bao nhiêu cách sử dụng hết số kẹo đã có? A. 4807. B. 5526. C. 7. D. 233.
Câu 48: Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và không có hai chữ số 2 và 3 đứng
cạnh nhau, được tạo từ tập A = {0;1;2;3;4; }
5 . Số phần tử của tập S là A. 180. B. 240. C. 66. D. 192.
Câu 49: Trên hệ trục tọa độ Oxy, cho hai điểm A(3 ) ;1 , B(0 )
;1 và các đường thẳng ∆ : 2x − y − 2 = 0, 1 x = 3 − + t ∆ :
(t là tham số). Gọi M và N lần lượt là các điểm thay đổi trên ∆ và ∆ . Tìm giá trị nhỏ nhất 2 y = 1− t 1 2
T của biểu thức = + + . min T AM BN MN A. T = 9 . B. T = 3 5 . C. T = 6 . D. T = 3+ 3 2 . min min min min
Câu 50: Cho tam giác đều ABC có cạnh bằng 12, M là điểm thay đổi tùy ý. Tìm giá trị nhỏ nhất của 2 2 2
T = 2MA + MB + MC . A. T =180 . B. T = 288. C. T =192 . D. T =153 . min min min min
----------------------------------------------- ----------- HẾT ----------
Trang 4/4 - Mã đề thi 301
SỞ GIÁO DỤC & ĐÀO TẠO BẮC NINH
ĐỀ KIỂM TRA CHẤT LƯỢNG LẦN 3
TRƯỜNG THPT LƯƠNG TÀI SỐ 2 Môn: TOÁN 10
Năm học: 2022 - 2023 Mã đề thi: 302
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(50 câu trắc nghiệm)
Ngày kiểm tra: 12 tháng 03 năm 2023
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
Câu 1: Cho tập hợp X = {1;2;3;4; }
5 . Một tổ hợp chập hai của 5 phần tử trong X là A. {2; } 5 . B. 2 A . C . 5 C. 25 D. 10.
Câu 2: Trên hệ tọa độ Oxy, cho hai véc tơ a = (2;− ) 1 ,b = (3; 2
− ) . Tọa độ của véc tơ b − a là A. (1; ) 1 − . B. (1; 3 − ) . C. ( 1; − ) 1 . D. ( 1; − 3 − ) .
Câu 3: Số hạng thứ 4 trong khai triển Newton của đa thức P(x) = ( + x)18 1 là A. 4 C . C x . C . C x . 18 B. 4 4 18 C. 318 D. 3 3 18
Câu 4: Trên mặt phẳng tọa độ Oxy, phương trình của đường thẳng d đi qua điểm A(2;− ) 1 có véc tơ pháp tuyến n = (3;2) là
A. 2x − 3y − 7 = 0.
B. 3x + 2y − 4 = 0.
C. 3x − 2y −8 = 0 .
D. 3x + 2y + 4 = 0 .
Câu 5: Cho hàm số bậc hai y = f (x) có đồ thị như hình vẽ. Tập nghiệm của bất phương trình f (x) > 0 là A. ( ; −∞ − ) 1 ∪(3;+∞) . B. [ 1; − ] 3 . C. (0;3). D. ( 1; − 3) .
Câu 6: Trên mặt phẳng tọa độ Oxy, phương trình tham số của đường thẳng đi qua hai điểm A(3;− ) 1 , B(1;3) là x = 2 − + 3t x =1− 2t x =1+ 2t x =1− 2t A. . B. . C. . D. . y = 4 − t y = 3 + 2t y = 3 + t y = 3 + 4t
Câu 7: Khai triển Newton của P(x) = ( x + )15 3
2 có tất cả bao nhiêu số hạng? A. 15. B. 17. C. 14. D. 16.
Câu 8: Trong khai triển Newton của f (x) = ( x − )8
2 1 thành đa thức, biến x có số mũ cao nhất bằng bao nhiêu? A. 8. B. 9. C. 16. D. 7.
Câu 9: Một nhóm học sinh có 4 nam và 5 nữ. Tính số cách chọn 1 học sinh trong nhóm. A. 120. B. 9. C. 24. D. 20.
Trang 1/4 - Mã đề thi 302
Câu 10: Đường parabol trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau A. 2
y = −x + 2x − 2. B. 2
y = x − 2x − 2. C. 2
y = −x − 2x − 2. D. 2
y = x + 2x − 2 .
Câu 11: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :3x + 4y − 5 = 0 và điểm M (3;4) . Khoảng cách từ
M tới đường thẳng ∆ bằng
A. d (M ,∆) = 20 .
B. d (M ,∆) = 5.
C. d (M ,∆) = 4 .
D. d (M ,∆) = 6 .
Câu 12: Từ 15 quả cầu được đánh số từ 1 đến 15, chọn ra 4 quả cầu. Tính số cách chọn ra 4 quả cầu được đánh số lẻ. A. 2. B. 70. C. 1680. D. 35.
Câu 13: Từ tập hợp E = {1;2;3;4;5; }
6 có thể tạo được bao nhiêu số tự nhiên có 4 chữ số (các chữ số đôi một khác nhau). A. 360. B. 15. C. 24. D. 4096.
x + y + z = 0
Câu 14: Nghiệm của hệ phương trình x − 2y − z = 4 là
2x + y − 2z = 2 − A. (1; 2 − ; ) 1 . B. (1;2; ) 1 . C. (1;1; 2 − ) . D. ( 1; − 2;− ) 1 .
Câu 15: Cho tập hợp A = {2;3;4;5; }
6 . Số phần tử của tập hợp A là A. 4. B. 3. C. 6. D. 5.
Câu 16: Phương trình 2 2
2x − 2x − 2 = x + x − 2 có tất cả bao nhiêu nghiệm? A. 2. B. 0. C. 1. D. 3.
Câu 17: Trên mặt phẳng tọa độ Oxy, cho đường thẳng d : 2x − y + 3 = 0 . Điểm nào sau đây thuộc đường thẳng d? A. P(1;− ) 1 . B. Q( 1; − ) 1 . C. M ( 2; − ) 1 . D. N (0; 3 − ) .
Câu 18: Trong các biểu thức được cho bởi các phương án A, B, C, D dưới đây, biểu thức nào là một tam thức bậc hai?
A. f (x) = 3x + 2.
B. f (x) = x −3 x + 2 . C. f (x) 3 2
= x − 3x + 2 . D. f (x) 2
= x − 3x + 2 .
Câu 19: Tập nghiệm của bất phương trình 2
x − 5x + 6 ≥ 0 là A. T = [2; ] 3 . B. T = [1;6]. C. T = ( ; −∞ 2]∪[3;+∞). D. T = ( ; −∞ ] 1 ∪[6;+∞) .
Câu 20: Tìm tập xác định của hàm số y = x + 2 .
A. D = [2;+∞). B. D = ( 2; − +∞) .
C. D = (2;+∞) . D. D = [ 2; − +∞) .
Câu 21: Một bộ câu hỏi có 8 câu hỏi lí thuyết và 6 câu hỏi bài tập. Tính số cách tạo một đề kiểm tra gồm 3
câu hỏi lí thuyết và 2 câu hỏi bài tập từ bộ câu hỏi ban đầu. A. 71. B. 10080. C. 840. D. 36.
Câu 22: Cho bất phương trình 2x − y + 3 > 0. Một nghiệm của bất phương trình đã cho là A. ( 1; − ) 1 . B. ( 2; − 0) . C. (1; ) 1 − . D. (0;4) .
Câu 23: Cho khai triển đa thức P(x) = (2 − x)12 2 11 12
= a + a x + a x +...+ a x + a x . Tìm 0 1 2 11 12 a . 8 A. 7920 − . B. 8 7920 − x . C. 8 7920x . D. 7920.
Trang 2/4 - Mã đề thi 302
Câu 24: Trên mặt phẳng tọa độ Oxy, góc giữa hai véc tơ a = (1;− ) 1 và b = ( 2; − 0) có số đo bằng A. 60°. B. 45°. C. 90°. D. 135° .
Câu 25: Trên mặt phẳng tọa độ Oxy, tọa độ giao điểm của hai đường thẳng ∆ : 2x + y −3 = 0 và 1
∆ : x − y − 3 = 0 là 1 A. (2; ) 1 − . B. ( 2; − − ) 1 . C. (2; ) 1 . D. ( 2; − ) 1 .
Câu 26: Một ban cán sự lớp có 3 người gồm 1 lớp trưởng, 1 bí thư và 1 ủy viên. Tính số cách tạo một ban cán
sự lớp từ một nhóm 10 học sinh. A. 1000. B. 30. C. 120. D. 720.
Câu 27: Tìm tất cả các giá trị của tham số m sao cho ( ; m +∞) ⊂ (1;+∞) ? A. m <1. B. m >1. C. m ≥1. D. m ≤1.
Câu 28: Số giao điểm của parabol 2
y = x + x − 2 và đường thẳng y = −x +1 là A. 0. B. 1. C. 3. D. 2.
Câu 29: Trên mặt phẳng tọa độ Oxy, cho hai véc tơ u = (3;4) và v = ( 1; − 2). Tích vô hướng . u v bằng A. 5. B. 11 − . C. 5 − . D. 11. x = 2 + t
Câu 30: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :
(t là tham số). Một véc tơ chỉ phương y = 1+ 3t của ∆ là A. u = (1;3). B. u = (3; ) 1 . C. u = (2; ) 1 . D. u = (1;2) .
Câu 31: Số chỉnh hợp chập 3 của 6 phần tử là A. 3 C . A . 6 B. 3!. C. 36 D. 6!.
Câu 32: Nghiệm của phương trình 2x −1 = x là A. x = 2 . B. x = 0 . C. x = 1 − . D. x =1.
Câu 33: Trên mặt phẳng tọa độ Oxy, cho hai đường thẳng d : x − 2y + 3 = 0 và 1
d : m +1 x + m −1 y + 2 = 0 . Tìm m để hai đường thẳng vuông góc với nhau. 2 ( ) ( ) A. m = 3 . B. m = 3 − . C. m = 1 − . D. m =1.
Câu 34: Tính số cách xếp 6 quyển sách Toán khác nhau thành hàng ngang trên một giá sách. A. 6. B. 120. C. 720. D. 36.
Câu 35: Bạn A có 4 chiếc áo sơ mi khác nhau và 6 chiếc quần âu khác nhau. Từ số áo và quần đã có, bạn A
có thể tạo ra được bao nhiêu bộ lễ phục gồm 1 quần âu và 1 áo sơ mi. A. 24. B. 360. C. 15. D. 10.
Câu 36: Số hoán vị của 3 phần tử là A. 9. B. 3. C. 6. D. 27.
Câu 37: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ : x − 2y +1 = 0. Phương trình đường thẳng d đi qua
M (2;0) và song song với ∆ là
A. 2x − y − 4 = 0 .
B. x − 2y + 2 = 0 .
C. 2x + y − 4 = 0 .
D. x − 2y − 2 = 0 .
Câu 38: Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n . Mệnh đề nào dưới đây là đúng? A. k k! C = . B. k k! C = . C. k n! C = . D. k n! C = . n
(n − k)!n! n (n − k)! n
(n − k)!k! n (n − k)!
Câu 39: Cho n là số tự nhiên thỏa mãn 0 1 2 n 1 − n 2007
C + C + C + + C + C = . Trong khai triển n n n ... n n 2 P(x) = ( n
3 2.x − 3) thành đa thức có tất cả bao nhiêu số hạng với hệ số nguyên dương? A. 670. B. 335. C. 334. D. 1004.
Trang 3/4 - Mã đề thi 302
Câu 40: Trên hệ trục tọa độ Oxy, cho hai đường thẳng d : 2x + 4y −1 = 0 và d : x − 2y + 3 = 0 . Viết phương 1 2
trình đường phân giác của góc nhọn tạo bởi hai đường thẳng d và d . 1 2
A. 4x + 5 = 0 .
B. 8y − 7 = 0.
C. 8y −5 = 0 .
D. 4x −5 = 0 .
Câu 41: Cho tam giác nhọn ABC có diện tích bằng 6 3 (đvdt) và độ dài các cạnh AB = 4, AC = 6 . Tính
khoảng cách giữa hai điểm B và C? A. BC = 2 7 . B. BC = 4 7 . C. BC = 2 19 . D. BC = 2 10 .
Câu 42: Trên hệ trục tọa độ Oxy, xét các điểm A(3; ) 1 , B( 1; − 5 − ) và M ( ;4
m − 2m) với m là tham số nguyên.
Khi tam giác MAB vuông tại M, hãy tính độ dài đoạn thẳng OM. A. OM = 2 2 . B. OM = 4 10 . C. OM = 4 . D. OM = 4 2 .
Câu 43: Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số 2
y = x − 2 m + 2 x + m + 4 đồng
biến trên khoảng (6;+∞)? A. 8. B. 9. C. 13. D. 11.
Câu 44: Tìm m để hàm số 2
y = x + 2mx + 4m + 5 xác định với mọi x ∈ . A. 1 − < m < 5. B. 1 − ≤ m ≤ 5. C. 5 − ≤ m ≤1. D. m ≤ 1 − hoặc m ≥ 5 .
Câu 45: Cho đa giác đều 2n cạnh (n ≥ 2) . Biết số tam giác có đỉnh trùng với đỉnh của đa giác gấp 68 lần số
hình chữ nhật có đỉnh trùng với các đỉnh của đa giác. Tìm n? A. 26. B. 23. C. 25. D. 24.
Câu 46: Cho tam giác đều ABC có cạnh bằng 12, M là điểm thay đổi tùy ý. Tìm giá trị nhỏ nhất của 2 2 2
T = 2MA + MB + MC . A. T =192 . B. T = 288. C. T =180 . D. T =153 . min min min min
Câu 47: Trên hệ trục tọa độ Oxy, cho hai điểm A(3 ) ;1 , B(0 )
;1 và các đường thẳng ∆ : 2x − y − 2 = 0, 1 x = 3 − + t ∆ :
(t là tham số). Gọi M và N lần lượt là các điểm thay đổi trên ∆ và ∆ . Tìm giá trị nhỏ nhất 2 y = 1− t 1 2
T của biểu thức = + + . min T AM BN MN A. T = 9 . B. T = 3 5 . C. T = 6 . D. T = 3+ 3 2 . min min min min
Câu 48: Bạn Ninh có 12 viên kẹo giống nhau, mỗi ngày Ninh chỉ được sử dụng đúng một hoặc hai viên kẹo.
Bạn Ninh có tất cả bao nhiêu cách sử dụng hết số kẹo đã có? A. 4807. B. 233. C. 5526. D. 7.
Câu 49: Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và không có hai chữ số 2 và 3 đứng
cạnh nhau, được tạo từ tập A = {0;1;2;3;4; }
5 . Số phần tử của tập S là A. 192. B. 66. C. 240. D. 180.
Câu 50: Có tất cả bao nhiêu số tự nhiên m sao cho phương trình 2
x − 4x + m −1 = 2x + 2 có đúng hai nghiệm cùng dương? A. 8. B. 9. C. 10. D. Vô số.
----------------------------------------------- ----------- HẾT ----------
Trang 4/4 - Mã đề thi 302
SỞ GIÁO DỤC & ĐÀO TẠO BẮC NINH
ĐỀ KIỂM TRA CHẤT LƯỢNG LẦN 3
TRƯỜNG THPT LƯƠNG TÀI SỐ 2 Môn: TOÁN 10
Năm học: 2022 - 2023 Mã đề thi: 303
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(50 câu trắc nghiệm)
Ngày kiểm tra: 12 tháng 03 năm 2023
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
Câu 1: Tập nghiệm của bất phương trình 2
x −5x + 6 ≥ 0 là A. T = [2; ] 3 . B. T = [1;6]. C. T = ( ; −∞ ] 1 ∪[6;+∞) . D. T = ( ; −∞ 2]∪[3;+∞).
Câu 2: Tìm tập xác định của hàm số y = x + 2 . A. D = ( 2; − +∞) . B. D = [ 2; − +∞) .
C. D = [2;+∞).
D. D = (2;+∞) .
Câu 3: Đường parabol trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau A. 2
y = −x + 2x − 2. B. 2
y = x − 2x − 2. C. 2
y = −x − 2x − 2. D. 2
y = x + 2x − 2 .
Câu 4: Từ tập hợp E = {1;2;3;4;5; }
6 có thể tạo được bao nhiêu số tự nhiên có 4 chữ số (các chữ số đôi một khác nhau). A. 24. B. 15. C. 4096. D. 360.
Câu 5: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ : x − 2y +1 = 0. Phương trình đường thẳng d đi qua
M (2;0) và song song với ∆ là
A. 2x + y − 4 = 0 .
B. x − 2y + 2 = 0 .
C. x − 2y − 2 = 0 .
D. 2x − y − 4 = 0 .
Câu 6: Phương trình 2 2
2x − 2x − 2 = x + x − 2 có tất cả bao nhiêu nghiệm? A. 2. B. 1. C. 0. D. 3.
Câu 7: Trên mặt phẳng tọa độ Oxy, phương trình tham số của đường thẳng đi qua hai điểm A(3;− ) 1 , B(1;3) là x =1− 2t x =1+ 2t x =1− 2t x = 2 − + 3t A. . B. . C. . D. . y = 3 + 4t y = 3 + t y = 3 + 2t y = 4 − t
Câu 8: Cho hàm số bậc hai y = f (x) có đồ thị như hình vẽ. Tập nghiệm của bất phương trình f (x) > 0 là A. (0;3). B. ( ; −∞ − ) 1 ∪(3;+∞) . C. ( 1; − 3) . D. [ 1; − ] 3 .
Câu 9: Số giao điểm của parabol 2
y = x + x − 2 và đường thẳng y = −x +1 là
Trang 1/4 - Mã đề thi 303 A. 0. B. 1. C. 3. D. 2.
Câu 10: Một ban cán sự lớp có 3 người gồm 1 lớp trưởng, 1 bí thư và 1 ủy viên. Tính số cách tạo một ban cán
sự lớp từ một nhóm 10 học sinh. A. 1000. B. 30. C. 720. D. 120.
Câu 11: Tính số cách xếp 6 quyển sách Toán khác nhau thành hàng ngang trên một giá sách. A. 720. B. 6. C. 120. D. 36.
Câu 12: Số chỉnh hợp chập 3 của 6 phần tử là A. 3 C . A . 6 B. 3!. C. 36 D. 6!.
Câu 13: Từ 15 quả cầu được đánh số từ 1 đến 15, chọn ra 4 quả cầu. Tính số cách chọn ra 4 quả cầu được đánh số lẻ. A. 2. B. 70. C. 35. D. 1680.
Câu 14: Cho tập hợp A = {2;3;4;5; }
6 . Số phần tử của tập hợp A là A. 4. B. 3. C. 6. D. 5.
Câu 15: Một nhóm học sinh có 4 nam và 5 nữ. Tính số cách chọn 1 học sinh trong nhóm. A. 24. B. 120. C. 9. D. 20.
Câu 16: Bạn A có 4 chiếc áo sơ mi khác nhau và 6 chiếc quần âu khác nhau. Từ số áo và quần đã có, bạn A
có thể tạo ra được bao nhiêu bộ lễ phục gồm 1 quần âu và 1 áo sơ mi. A. 24. B. 360. C. 15. D. 10.
Câu 17: Trong các biểu thức được cho bởi các phương án A, B, C, D dưới đây, biểu thức nào là một tam thức bậc hai?
A. f (x) = 3x + 2.
B. f (x) = x −3 x + 2 . C. f (x) 3 2
= x − 3x + 2 . D. f (x) 2
= x − 3x + 2 .
Câu 18: Một bộ câu hỏi có 8 câu hỏi lí thuyết và 6 câu hỏi bài tập. Tính số cách tạo một đề kiểm tra gồm 3
câu hỏi lí thuyết và 2 câu hỏi bài tập từ bộ câu hỏi ban đầu. A. 840. B. 71. C. 10080. D. 36.
Câu 19: Cho khai triển đa thức P(x) = (2 − x)12 2 11 12
= a + a x + a x +...+ a x + a x . Tìm 0 1 2 11 12 a . 8 A. 7920 − . B. 8 7920 − x . C. 8 7920x . D. 7920.
Câu 20: Trên hệ tọa độ Oxy, cho hai véc tơ a = (2;− ) 1 ,b = (3; 2
− ) . Tọa độ của véc tơ b − a là A. (1; ) 1 − . B. ( 1; − 3 − ) . C. ( 1; − ) 1 . D. (1; 3 − ) .
Câu 21: Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n . Mệnh đề nào dưới đây là đúng? A. k k! C = . B. k k! C = . C. k n! C = . D. k n! C = . n
(n − k)!n! n (n − k)! n
(n − k)!k! n (n − k)!
Câu 22: Trên mặt phẳng tọa độ Oxy, tọa độ giao điểm của hai đường thẳng ∆ : 2x + y −3 = 0 và 1
∆ : x − y − 3 = 0 là 1 A. (2; ) 1 − . B. ( 2; − − ) 1 . C. (2; ) 1 . D. ( 2; − ) 1 .
Câu 23: Số hạng thứ 4 trong khai triển Newton của đa thức P(x) = ( + x)18 1 là A. 4 C . C . C x . C x . 18 B. 318 C. 4 4 18 D. 3 3 18 x = 2 + t
Câu 24: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :
(t là tham số). Một véc tơ chỉ phương y = 1+ 3t của ∆ là A. u = (1;3). B. u = (3; ) 1 . C. u = (2; ) 1 . D. u = (1;2) .
Câu 25: Trên mặt phẳng tọa độ Oxy, phương trình của đường thẳng d đi qua điểm A(2;− ) 1 có véc tơ pháp tuyến n = (3;2) là
Trang 2/4 - Mã đề thi 303
A. 3x − 2y −8 = 0 .
B. 2x − 3y − 7 = 0.
C. 3x + 2y + 4 = 0 .
D. 3x + 2y − 4 = 0.
Câu 26: Tìm tất cả các giá trị của tham số m sao cho ( ; m +∞) ⊂ (1;+∞) ? A. m <1. B. m ≥1. C. m >1. D. m ≤1.
Câu 27: Trên mặt phẳng tọa độ Oxy, cho đường thẳng d : 2x − y + 3 = 0 . Điểm nào sau đây thuộc đường thẳng d? A. N (0; 3 − ) . B. M ( 2; − ) 1 . C. Q( 1; − ) 1 . D. P(1;− ) 1 .
Câu 28: Trên mặt phẳng tọa độ Oxy, cho hai véc tơ u = (3;4) và v = ( 1; − 2). Tích vô hướng . u v bằng A. 5. B. 11 − . C. 5 − . D. 11.
Câu 29: Cho bất phương trình 2x − y + 3 > 0. Một nghiệm của bất phương trình đã cho là A. ( 1; − ) 1 . B. (1; ) 1 − . C. (0;4) . D. ( 2; − 0) .
Câu 30: Trên mặt phẳng tọa độ Oxy, góc giữa hai véc tơ a = (1;− ) 1 và b = ( 2; − 0) có số đo bằng A. 90° . B. 45°. C. 135° . D. 60°.
Câu 31: Nghiệm của phương trình 2x −1 = x là A. x = 2 . B. x = 0 . C. x = 1 − . D. x =1.
Câu 32: Trên mặt phẳng tọa độ Oxy, cho hai đường thẳng d : x − 2y + 3 = 0 và 1
d : m +1 x + m −1 y + 2 = 0 . Tìm m để hai đường thẳng vuông góc với nhau. 2 ( ) ( ) A. m = 3 . B. m = 3 − . C. m = 1 − . D. m =1.
Câu 33: Số hoán vị của 3 phần tử là A. 9. B. 3. C. 6. D. 27.
Câu 34: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :3x + 4y − 5 = 0 và điểm M (3;4) . Khoảng cách từ
M tới đường thẳng ∆ bằng
A. d (M ,∆) = 5.
B. d (M ,∆) = 20 .
C. d (M ,∆) = 4 .
D. d (M ,∆) = 6 .
Câu 35: Cho tập hợp X = {1;2;3;4; }
5 . Một tổ hợp chập hai của 5 phần tử trong X là A. 10. B. {2; } 5 . C. 2 C . A . 5 D. 25
Câu 36: Khai triển Newton của P(x) = ( x + )15 3
2 có tất cả bao nhiêu số hạng? A. 15. B. 14. C. 16. D. 17.
x + y + z = 0
Câu 37: Nghiệm của hệ phương trình x − 2y − z = 4 là
2x + y − 2z = 2 − A. (1;1; 2 − ) . B. (1; 2 − ; ) 1 . C. ( 1; − 2;− ) 1 . D. (1;2; ) 1 .
Câu 38: Trong khai triển Newton của f (x) = ( x − )8
2 1 thành đa thức, biến x có số mũ cao nhất bằng bao nhiêu? A. 8. B. 9. C. 16. D. 7.
Câu 39: Trên hệ trục tọa độ Oxy, xét các điểm A(3; ) 1 , B( 1; − 5 − ) và M ( ;4
m − 2m) với m là tham số nguyên.
Khi tam giác MAB vuông tại M, hãy tính độ dài đoạn thẳng OM. A. OM = 4 . B. OM = 2 2 . C. OM = 4 2 . D. OM = 4 10 .
Câu 40: Trên hệ trục tọa độ Oxy, cho hai đường thẳng d : 2x + 4y −1 = 0 và d : x − 2y + 3 = 0 . Viết phương 1 2
trình đường phân giác của góc nhọn tạo bởi hai đường thẳng d và d . 1 2
A. 8y − 7 = 0.
B. 8y −5 = 0 . C. 4x + 5 = 0 .
D. 4x −5 = 0 .
Trang 3/4 - Mã đề thi 303
Câu 41: Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số 2
y = x − 2 m + 2 x + m + 4 đồng
biến trên khoảng (6;+∞)? A. 8. B. 9. C. 13. D. 11.
Câu 42: Cho đa giác đều 2n cạnh (n ≥ 2) . Biết số tam giác có đỉnh trùng với đỉnh của đa giác gấp 68 lần số
hình chữ nhật có đỉnh trùng với các đỉnh của đa giác. Tìm n? A. 26. B. 24. C. 23. D. 25.
Câu 43: Tìm m để hàm số 2
y = x + 2mx + 4m + 5 xác định với mọi x ∈ . A. 1 − < m < 5. B. 1 − ≤ m ≤ 5. C. 5 − ≤ m ≤1. D. m ≤ 1 − hoặc m ≥ 5 .
Câu 44: Cho tam giác nhọn ABC có diện tích bằng 6 3 (đvdt) và độ dài các cạnh AB = 4, AC = 6 . Tính
khoảng cách giữa hai điểm B và C? A. BC = 4 7 . B. BC = 2 10 . C. BC = 2 19 . D. BC = 2 7 .
Câu 45: Cho n là số tự nhiên thỏa mãn 0 1 2 n 1 − n 2007
C + C + C + + C + C = . Trong khai triển n n n ... n n 2 P(x) = ( n
3 2.x − 3) thành đa thức có tất cả bao nhiêu số hạng với hệ số nguyên dương? A. 1004. B. 334. C. 670. D. 335.
Câu 46: Bạn Ninh có 12 viên kẹo giống nhau, mỗi ngày Ninh chỉ được sử dụng đúng một hoặc hai viên kẹo.
Bạn Ninh có tất cả bao nhiêu cách sử dụng hết số kẹo đã có? A. 4807. B. 233. C. 5526. D. 7.
Câu 47: Có tất cả bao nhiêu số tự nhiên m sao cho phương trình 2
x − 4x + m −1 = 2x + 2 có đúng hai nghiệm cùng dương? A. 8. B. 9. C. 10. D. Vô số.
Câu 48: Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và không có hai chữ số 2 và 3 đứng
cạnh nhau, được tạo từ tập A = {0;1;2;3;4; }
5 . Số phần tử của tập S là A. 192. B. 66. C. 240. D. 180.
Câu 49: Cho tam giác đều ABC có cạnh bằng 12, M là điểm thay đổi tùy ý. Tìm giá trị nhỏ nhất của 2 2 2
T = 2MA + MB + MC . A. T = 288. B. T =192 . C. T =153 . D. T =180 . min min min min
Câu 50: Trên hệ trục tọa độ Oxy, cho hai điểm A(3 ) ;1 , B(0 )
;1 và các đường thẳng ∆ : 2x − y − 2 = 0, 1 x = 3 − + t ∆ :
(t là tham số). Gọi M và N lần lượt là các điểm thay đổi trên ∆ và ∆ . Tìm giá trị nhỏ nhất 2 y = 1− t 1 2
T của biểu thức = + + . min T AM BN MN A. T = 9 . B. T = 6 . C. T = 3 5 . D. T = 3+ 3 2 . min min min min
----------------------------------------------- ----------- HẾT ----------
Trang 4/4 - Mã đề thi 303
SỞ GIÁO DỤC & ĐÀO TẠO BẮC NINH
ĐỀ KIỂM TRA CHẤT LƯỢNG LẦN 3
TRƯỜNG THPT LƯƠNG TÀI SỐ 2 Môn: TOÁN 10
Năm học: 2022 - 2023 Mã đề thi: 304
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(50 câu trắc nghiệm)
Ngày kiểm tra: 12 tháng 03 năm 2023
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
Câu 1: Tập nghiệm của bất phương trình 2
x −5x + 6 ≥ 0 là A. T = ( ; −∞ 2]∪[3;+∞). B. T = [1;6]. C. T = [2; ] 3 . D. T = ( ; −∞ ] 1 ∪[6;+∞) . x = 2 + t
Câu 2: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :
(t là tham số). Một véc tơ chỉ phương của y = 1+ 3t ∆ là A. u = (1;3). B. u = (3; ) 1 . C. u = (2; ) 1 . D. u = (1;2) .
Câu 3: Tính số cách xếp 6 quyển sách Toán khác nhau thành hàng ngang trên một giá sách. A. 720. B. 6. C. 120. D. 36.
Câu 4: Khai triển Newton của P(x) = ( x + )15 3
2 có tất cả bao nhiêu số hạng? A. 15. B. 14. C. 16. D. 17.
Câu 5: Một ban cán sự lớp có 3 người gồm 1 lớp trưởng, 1 bí thư và 1 ủy viên. Tính số cách tạo một ban cán
sự lớp từ một nhóm 10 học sinh. A. 30. B. 720. C. 1000. D. 120.
Câu 6: Trên mặt phẳng tọa độ Oxy, cho hai véc tơ u = (3;4) và v = ( 1; − 2). Tích vô hướng . u v bằng A. 5. B. 11 − . C. 5 − . D. 11.
Câu 7: Trên mặt phẳng tọa độ Oxy, góc giữa hai véc tơ a = (1;− ) 1 và b = ( 2; − 0) có số đo bằng A. 60°. B. 135° . C. 90°. D. 45°.
Câu 8: Trên mặt phẳng tọa độ Oxy, tọa độ giao điểm của hai đường thẳng ∆ : 2x + y −3 = 0 và 1
∆ : x − y − 3 = 0 là 1 A. ( 2; − ) 1 . B. ( 2; − − ) 1 . C. (2; ) 1 . D. (2; ) 1 − .
Câu 9: Trong các biểu thức được cho bởi các phương án A, B, C, D dưới đây, biểu thức nào là một tam thức bậc hai?
A. f (x) = 3x + 2. B. f (x) = x −3 x + 2 . C. f (x) 3 2
= x − 3x + 2 . D. f (x) 2
= x − 3x + 2 .
Câu 10: Một bộ câu hỏi có 8 câu hỏi lí thuyết và 6 câu hỏi bài tập. Tính số cách tạo một đề kiểm tra gồm 3
câu hỏi lí thuyết và 2 câu hỏi bài tập từ bộ câu hỏi ban đầu. A. 71. B. 36. C. 10080. D. 840.
Câu 11: Cho hàm số bậc hai y = f (x) có đồ thị như hình vẽ. Tập nghiệm của bất
phương trình f (x) > 0 là A. (0;3). B. [ 1; − ] 3 . C. ( 1; − 3) . D. ( ; −∞ − ) 1 ∪(3;+∞) .
Câu 12: Phương trình 2 2
2x − 2x − 2 = x + x − 2 có tất cả bao nhiêu nghiệm?
Trang 1/4 - Mã đề thi 304 A. 1. B. 0. C. 2. D. 3.
Câu 13: Số hạng thứ 4 trong khai triển Newton của đa thức P(x) = ( + x)18 1 là A. 3 C . C x . C . C x . 18 B. 4 4 18 C. 418 D. 3 3 18
Câu 14: Một nhóm học sinh có 4 nam và 5 nữ. Tính số cách chọn 1 học sinh trong nhóm. A. 24. B. 120. C. 9. D. 20.
Câu 15: Tìm tập xác định của hàm số y = x + 2 .
A. D = [2;+∞). B. D = [ 2; − +∞) .
C. D = (2;+∞) . D. D = ( 2; − +∞) .
Câu 16: Cho bất phương trình 2x − y + 3 > 0. Một nghiệm của bất phương trình đã cho là A. ( 1; − ) 1 . B. (0;4) . C. (1; ) 1 − . D. ( 2; − 0) .
Câu 17: Trên hệ tọa độ Oxy, cho hai véc tơ a = (2;− ) 1 ,b = (3; 2
− ) . Tọa độ của véc tơ b − a là A. (1; ) 1 − . B. ( 1; − 3 − ) . C. ( 1; − ) 1 . D. (1; 3 − ) .
Câu 18: Bạn A có 4 chiếc áo sơ mi khác nhau và 6 chiếc quần âu khác nhau. Từ số áo và quần đã có, bạn A
có thể tạo ra được bao nhiêu bộ lễ phục gồm 1 quần âu và 1 áo sơ mi. A. 15. B. 10. C. 24. D. 360.
Câu 19: Cho tập hợp A = {2;3;4;5; }
6 . Số phần tử của tập hợp A là A. 4. B. 5. C. 6. D. 3.
Câu 20: Số chỉnh hợp chập 3 của 6 phần tử là A. 3 C . A . 6 B. 6!. C. 3!. D. 36
Câu 21: Trên mặt phẳng tọa độ Oxy, cho đường thẳng d : 2x − y + 3 = 0 . Điểm nào sau đây thuộc đường thẳng d? A. M ( 2; − ) 1 . B. N (0; 3 − ) . C. Q( 1; − ) 1 . D. P(1;− ) 1 .
Câu 22: Trên mặt phẳng tọa độ Oxy, cho hai đường thẳng d : x − 2y + 3 = 0 và 1
d : m +1 x + m −1 y + 2 = 0 . Tìm m để hai đường thẳng vuông góc với nhau. 2 ( ) ( ) A. m = 3 . B. m =1. C. m = 1 − . D. m = 3 − .
Câu 23: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ : x − 2y +1 = 0. Phương trình đường thẳng d đi qua
M (2;0) và song song với ∆ là
A. 2x − y − 4 = 0 .
B. x − 2y + 2 = 0 .
C. 2x + y − 4 = 0 .
D. x − 2y − 2 = 0 .
Câu 24: Trên mặt phẳng tọa độ Oxy, phương trình của đường thẳng d đi qua điểm A(2;− ) 1 có véc tơ pháp tuyến n = (3;2) là
A. 3x − 2y −8 = 0 .
B. 2x − 3y − 7 = 0.
C. 3x + 2y + 4 = 0 .
D. 3x + 2y − 4 = 0.
Câu 25: Đường parabol trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau A. 2
y = x − 2x − 2. B. 2
y = x + 2x − 2 . C. 2
y = −x − 2x − 2. D. 2
y = −x + 2x − 2.
Trang 2/4 - Mã đề thi 304
Câu 26: Trên mặt phẳng tọa độ Oxy, phương trình tham số của đường thẳng đi qua hai điểm A(3;− ) 1 , B(1;3) là x =1− 2t x =1− 2t x =1+ 2t x = 2 − + 3t A. . B. . C. . D. . y = 3 + 2t y = 3 + 4t y = 3 + t y = 4 − t
x + y + z = 0
Câu 27: Nghiệm của hệ phương trình x − 2y − z = 4 là
2x + y − 2z = 2 − A. (1;1; 2 − ) . B. (1; 2 − ; ) 1 . C. ( 1; − 2;− ) 1 . D. (1;2; ) 1 .
Câu 28: Số giao điểm của parabol 2
y = x + x − 2 và đường thẳng y = −x +1 là A. 0. B. 2. C. 3. D. 1.
Câu 29: Từ 15 quả cầu được đánh số từ 1 đến 15, chọn ra 4 quả cầu. Tính số cách chọn ra 4 quả cầu được đánh số lẻ. A. 35. B. 2. C. 1680. D. 70.
Câu 30: Nghiệm của phương trình 2x −1 = x là A. x = 2 . B. x = 0 . C. x = 1 − . D. x =1.
Câu 31: Cho khai triển đa thức P(x) = (2 − x)12 2 11 12
= a + a x + a x +...+ a x + a x . Tìm 0 1 2 11 12 a . 8 A. 7920 − . B. 8 7920 − x . C. 7920. D. 8 7920x .
Câu 32: Số hoán vị của 3 phần tử là A. 9. B. 3. C. 6. D. 27.
Câu 33: Trên mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :3x + 4y − 5 = 0 và điểm M (3;4) . Khoảng cách từ
M tới đường thẳng ∆ bằng
A. d (M ,∆) = 5.
B. d (M ,∆) = 20 .
C. d (M ,∆) = 4 .
D. d (M ,∆) = 6 .
Câu 34: Cho tập hợp X = {1;2;3;4; }
5 . Một tổ hợp chập hai của 5 phần tử trong X là A. 10. B. {2; } 5 . C. 2 C . A . 5 D. 25
Câu 35: Từ tập hợp E = {1;2;3;4;5; }
6 có thể tạo được bao nhiêu số tự nhiên có 4 chữ số (các chữ số đôi một khác nhau). A. 360. B. 4096. C. 24. D. 15.
Câu 36: Trong khai triển Newton của f (x) = ( x − )8
2 1 thành đa thức, biến x có số mũ cao nhất bằng bao nhiêu? A. 8. B. 9. C. 16. D. 7.
Câu 37: Tìm tất cả các giá trị của tham số m sao cho ( ; m +∞) ⊂ (1;+∞) ? A. m <1. B. m ≥1. C. m >1. D. m ≤1.
Câu 38: Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n . Mệnh đề nào dưới đây là đúng? A. k k! C = . B. k k! C = . C. k n! C = . D. k n! C = . n
(n − k)!n! n (n − k)! n
(n − k)!k! n (n − k)!
Câu 39: Cho tam giác nhọn ABC có diện tích bằng 6 3 (đvdt) và độ dài các cạnh AB = 4, AC = 6 . Tính
khoảng cách giữa hai điểm B và C? A. BC = 4 7 . B. BC = 2 10 . C. BC = 2 19 . D. BC = 2 7 .
Câu 40: Tìm m để hàm số 2
y = x + 2mx + 4m + 5 xác định với mọi x ∈ . A. 1 − < m < 5. B. 1 − ≤ m ≤ 5. C. 5 − ≤ m ≤1. D. m ≤ 1 − hoặc m ≥ 5 .
Trang 3/4 - Mã đề thi 304
Câu 41: Trên hệ trục tọa độ Oxy, xét các điểm A(3; ) 1 , B( 1; − 5 − ) và M ( ;4
m − 2m) với m là tham số nguyên.
Khi tam giác MAB vuông tại M, hãy tính độ dài đoạn thẳng OM. A. OM = 4 2 . B. OM = 4 . C. OM = 2 2 . D. OM = 4 10 .
Câu 42: Trên hệ trục tọa độ Oxy, cho hai đường thẳng d : 2x + 4y −1 = 0 và d : x − 2y + 3 = 0 . Viết phương 1 2
trình đường phân giác của góc nhọn tạo bởi hai đường thẳng d và d . 1 2
A. 8y − 7 = 0. B. 4x + 5 = 0 .
C. 8y −5 = 0 .
D. 4x −5 = 0 .
Câu 43: Cho đa giác đều 2n cạnh (n ≥ 2) . Biết số tam giác có đỉnh trùng với đỉnh của đa giác gấp 68 lần số
hình chữ nhật có đỉnh trùng với các đỉnh của đa giác. Tìm n? A. 24. B. 23. C. 25. D. 26.
Câu 44: Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số 2
y = x − 2 m + 2 x + m + 4 đồng
biến trên khoảng (6;+∞)? A. 13. B. 11. C. 8. D. 9.
Câu 45: Cho n là số tự nhiên thỏa mãn 0 1 2 n 1 − n 2007
C + C + C + + C + C = . Trong khai triển n n n ... n n 2 P(x) = ( n
3 2.x − 3) thành đa thức có tất cả bao nhiêu số hạng với hệ số nguyên dương? A. 334. B. 1004. C. 670. D. 335.
Câu 46: Có tất cả bao nhiêu số tự nhiên m sao cho phương trình 2
x − 4x + m −1 = 2x + 2 có đúng hai nghiệm cùng dương? A. 10. B. 9. C. Vô số. D. 8.
Câu 47: Trên hệ trục tọa độ Oxy, cho hai điểm A(3 ) ;1 , B(0 )
;1 và các đường thẳng ∆ : 2x − y − 2 = 0, 1 x = 3 − + t ∆ :
(t là tham số). Gọi M và N lần lượt là các điểm thay đổi trên ∆ và ∆ . Tìm giá trị nhỏ nhất 2 y = 1− t 1 2
T của biểu thức = + + . min T AM BN MN A. T = 9 . B. T = 6 . C. T = 3 5 . D. T = 3+ 3 2 . min min min min
Câu 48: Cho tam giác đều ABC có cạnh bằng 12, M là điểm thay đổi tùy ý. Tìm giá trị nhỏ nhất của 2 2 2
T = 2MA + MB + MC . A. T = 288. B. T =192 . C. T =153 . D. T =180 . min min min min
Câu 49: Bạn Ninh có 12 viên kẹo giống nhau, mỗi ngày Ninh chỉ được sử dụng đúng một hoặc hai viên kẹo.
Bạn Ninh có tất cả bao nhiêu cách sử dụng hết số kẹo đã có? A. 5526. B. 4807. C. 233. D. 7.
Câu 50: Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và không có hai chữ số 2 và 3 đứng
cạnh nhau, được tạo từ tập A = {0;1;2;3;4; }
5 . Số phần tử của tập S là A. 192. B. 240. C. 180. D. 66.
----------------------------------------------- ----------- HẾT ----------
Trang 4/4 - Mã đề thi 304
ĐÁP ÁN ĐỀ CLC LẦN 3 - TOÁN 10 Mã đề
Câu Đáp án Mã đề
Câu Đáp án Mã đề
Câu Đáp án Mã đề Câu Đáp án 301 1 C 302 1 A 303 1 D 304 1 A 301 2 C 302 2 A 303 2 B 304 2 A 301 3 C 302 3 D 303 3 B 304 3 A 301 4 D 302 4 B 303 4 D 304 4 C 301 5 B 302 5 D 303 5 C 304 5 B 301 6 A 302 6 D 303 6 B 304 6 A 301 7 B 302 7 D 303 7 A 304 7 B 301 8 D 302 8 A 303 8 C 304 8 D 301 9 A 302 9 B 303 9 D 304 9 D 301 10 A 302 10 B 303 10 C 304 10 D 301 11 C 302 11 C 303 11 A 304 11 C 301 12 C 302 12 B 303 12 C 304 12 A 301 13 A 302 13 A 303 13 B 304 13 D 301 14 D 302 14 A 303 14 D 304 14 C 301 15 B 302 15 D 303 15 C 304 15 B 301 16 C 302 16 C 303 16 A 304 16 C 301 17 C 302 17 B 303 17 D 304 17 A 301 18 B 302 18 D 303 18 A 304 18 C 301 19 B 302 19 C 303 19 D 304 19 B 301 20 A 302 20 D 303 20 A 304 20 D 301 21 C 302 21 C 303 21 C 304 21 C 301 22 A 302 22 C 303 22 A 304 22 A 301 23 B 302 23 D 303 23 D 304 23 D 301 24 D 302 24 D 303 24 A 304 24 D 301 25 C 302 25 A 303 25 D 304 25 A 301 26 D 302 26 D 303 26 B 304 26 B 301 27 D 302 27 C 303 27 C 304 27 B 301 28 D 302 28 D 303 28 A 304 28 B 301 29 D 302 29 A 303 29 B 304 29 D 301 30 B 302 30 A 303 30 C 304 30 D 301 31 B 302 31 C 303 31 D 304 31 C 301 32 A 302 32 D 303 32 A 304 32 C 301 33 D 302 33 A 303 33 C 304 33 C 301 34 A 302 34 C 303 34 C 304 34 B 301 35 A 302 35 A 303 35 B 304 35 A 301 36 D 302 36 C 303 36 C 304 36 A 301 37 C 302 37 D 303 37 B 304 37 B 301 38 A 302 38 C 303 38 A 304 38 C 301 39 A 302 39 B 303 39 C 304 39 D 301 40 A 302 40 B 303 40 A 304 40 B 301 41 C 302 41 A 303 41 B 304 41 A 301 42 A 302 42 D 303 42 A 304 42 A 301 43 D 302 43 B 303 43 B 304 43 D 301 44 B 302 44 B 303 44 D 304 44 D 301 45 B 302 45 A 303 45 D 304 45 D 301 46 C 302 46 C 303 46 B 304 46 B 301 47 D 302 47 B 303 47 B 304 47 C 301 48 B 302 48 B 303 48 C 304 48 D 301 49 B 302 49 C 303 49 D 304 49 C 301 50 A 302 50 B 303 50 C 304 50 B
Document Outline
- 3_TOÁN10L3_301
- 3_TOÁN10L3_302
- 3_TOÁN10L3_303
- 3_TOÁN10L3_304
- 3_TOÁN10L3_ĐÁP ÁN
- Table1




