Đề KSCL Toán 9 cuối năm 2022 – 2023 phòng GD&ĐT thành phố Vinh – Nghệ An
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2022 – 2023 phòng GD&ĐT thành phố Vinh – Nghệ An giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
trường
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT CHẤT LƯỢNG CUỐI NĂM THÀNH PHỐ VINH NĂM HỌC 2022- 2023 ĐỀ THI CHÍNH Môn: Toán 9 (Đề thi gồm TH có
ỨC 01 trang)
Thời gian: 90 phút ( không kể thời gian giao đề)
Bài 1: (2,5 điểm )
a) Giải hệ phương trình : x 2y 3
4x 5y 6 b) Giải phương trình : 2
4x 7x 2 0
Bài 2: (1,5 điểm ) Cho hai hàm số 1 2 y
x và y x 4 2 1
a) Trong các điểm A 2 2 2;2 , B ;
điểm nào thuộc đồ thị hàm số 2 y x ? Vì 3 9 2 sao?
b) Tìm tọa độ giao điểm của đồ thị hai hàm số trên.
Bài 3: (1,5 điểm)
Trong một cuộc họp, ban đầu người ta bố trí 360 ghế theo các dãy và số ghế trong
mỗi dãy bằng nhau. Tuy nhiên sau đó để khu vực sân khấu rộng hơn người ta thêm 4 ghế
vào mỗi dãy thì bớt được 3 dãy và số ghế trong phòng không thay đổi. Hỏi theo sự sắp
xếp ban đầu thì trong phòng họp bố trí bao nhiêu dãy ghế?
Bài 4:(4 điểm )
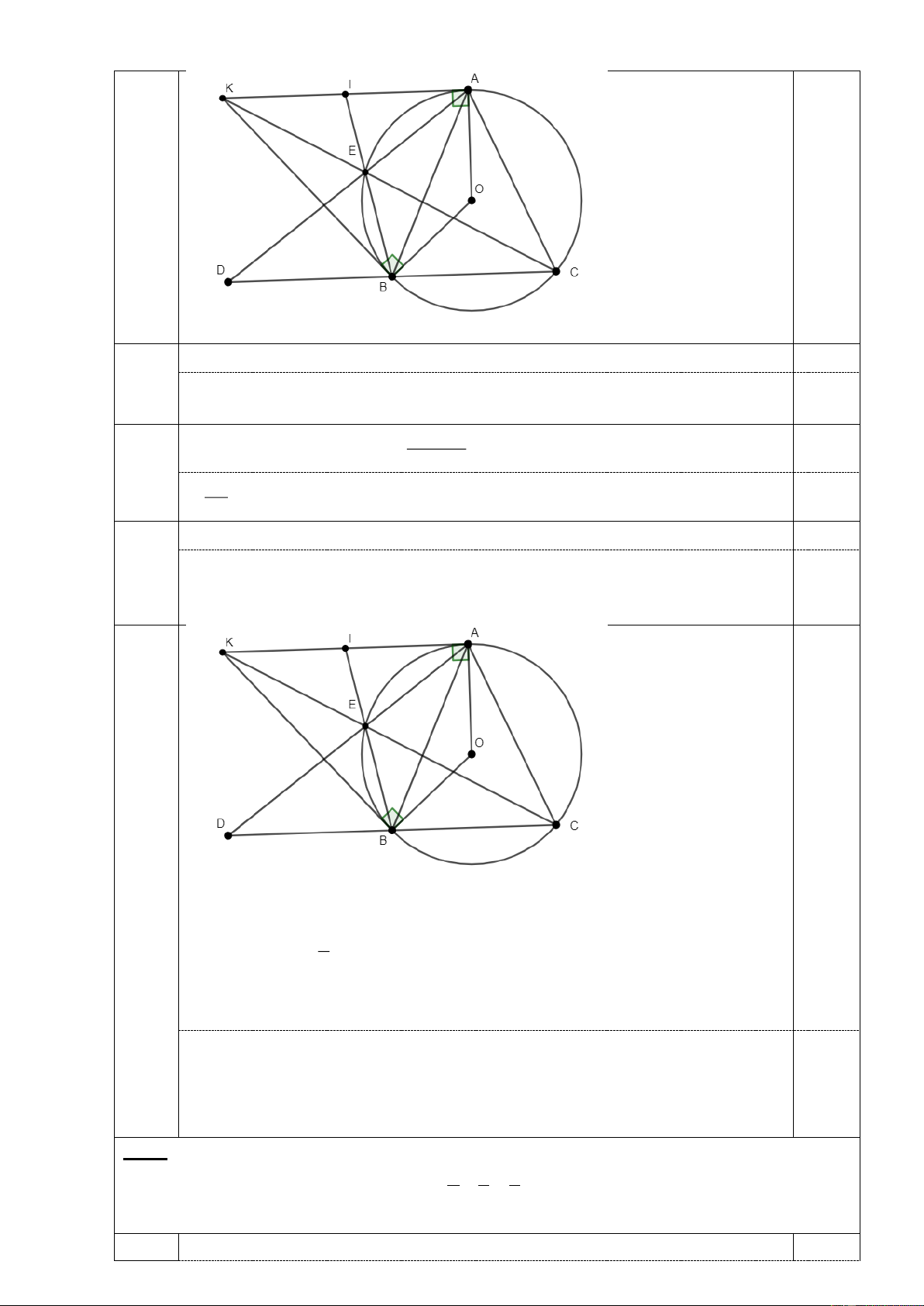
Cho tam giác ABC cân tại A BC B
A , nội tiếp đường tròn O . Tiếp tuyến tại A
và B của đường tròn O cắt nhau tại điểm K .
a) Chứng minh tứ giác AKBO nội tiếp b) Biết · 3 ; 100o OB cm BOC
. Tính độ dài cung nhỏ BC của đường tròn O c) Chứng minh · · AKB BAC
d) Gọi D là điểm đối xứng với C qua B ; tia AD cắt đường tròn Otại điểm thứ
hai là E khác A . Chứng minh ba điểm K , E,C thẳng hàng.
Bài 5: (0,5 điểm )
Cho hai số a,b thỏa mãn 1 1 1
. Chứng minh rằng ít nhất một trong hai a b 2 phương trình 2
x ax b 0 và 2
x bx a 0 có nghiệm.
………………Hết……………..
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT CHẤT LƯỢNG CUỐI NĂM THÀNH PHỐ VINH NĂM HỌC 2022-2023 HƯỚNG DẪN CHẤM Môn: Toán 9 Câu Nội dung Điểm
Bài 1: (2,5 điểm )
a) Giải hệ phương trình : x 2y 3
4x 5y 6
b) Giải phương trình : 2
4x 7x 2 0
x 2y 3
4x 8y 12 0,25
4x 5y 6
4x 5y 6 3 y 6 0,25
x 2y 3 a y 2 0,25
x 2y 3 y 2 . x 1 0,25
Vậy hệ phương trình có nghiệm 1 ;2 2 7 4.4. 2 81 0 0,5
Suy ra phương trình có hai nghiệm phân biệt 7 9 1 x 0,5 1 b 2.4 4 7 9 x 2 2 2.4 0,5 Vậy 1 S 2; 4
Bài 2: (1,5 điểm ) Cho hai hàm số 1 2 y
x và y x 4 2 1
a) Trong các điểm A 2 2 2;2 , B ;
điểm nào thuộc đồ thị hàm số 2 y x ? 3 9 2 Vì sao?
b) Tìm tọa độ hai giao điểm của đồ thị hai hàm số trên. 1 Ta có: . 2 2 2 0,25 2
Do đó điểm A thuộc đồ thị hàm số 1 2 y x 0,25 2 a 2 1 2 2 2 Ta có: . 0,25 2 3 9 9
Do đó điểm B không thuộc đồ thị hàm số 1 2 y x 0,25 2 b 1
Gọi A (x ; y ) là giao điểm của 2 y
x và y x 4 0,25 0 0 2
y x 4 0 0 Khi đó: 1 2 y x 0 0 2 Suy ra: 1 2 x x 4 0 0 2 Hay 1
x là nghiệm của pt: 2
x x 4 0 2 x 4 2
x 2x 8 0 x 2
Với x 2 thì y 2 . Với x 4 thì y 8 . 0,25 Vậy đồ thị hàm số 1 2 y
x và y x 4 cắt nhau tại hai điểm phân biệt 2 A( 2; 2 ); B( 4 ; 8 ).
Bài 3: (1,5 điểm)
Trong một cuộc họp, ban đầu người ta bố trí 360 ghế theo các dãy và số ghế trong
mỗi dãy bằng nhau. Tuy nhiên sau đó để khu vực sân khấu rộng hơn người ta thêm 4 ghế
vào mỗi dãy thì bớt được 3 dãy và số ghế trong phòng không thay đổi. Hỏi theo sự sắp
xếp ban đầu thì trong phòng họp bố trí bao nhiêu dãy ghế?
Gọi số dãy ghế trong phòng họp ban đầu là x (dãy). ĐK: *
x ¥ , x 3. 0,25 360
Số ghế trong mỗi dãy ban đầu là: (ghế) 0,25 x
Khi mở rộng khu vực sân khấu, số dãy ghế còn lại là: x 3 (dãy) 0,25
Số ghế trong mỗi dãy lúc đó là: 360 (ghế) x 3
Theo đề bài, ta có phương trình: 360 360 4 0,25 x 3 x 2
x 3x 270 0 0,25 Giải pt ta được:
x 18 (TM); x 15 (loại) 1 2
Vậy theo sự sắp xếp ban đầu thì trong phòng họp bố trí 18 dãy ghế. 0,25
Bài 4:(4 điểm )
Cho tam giác ABC cân tại A BC B
A , nội tiếp đường tròn O . Tiếp tuyến tại
A và B của đường tròn O cắt nhau tại điểm K .
a) Chứng minh tứ giác AKBO nội tiếp b) Biết · 3 ; 100o OB cm BOC
. Tính độ dài cung nhỏ BC của đường tròn O c) Chứng minh · · AKB BAC
d) Gọi D là điểm đối xứng với C qua B ; tia AD cắt đường tròn Otại điểm thứ
hai là E khác A . Chứng minh ba điểm K , E,C thẳng hàng. 0,5 Vẽ hình xong câu a)
KA, KB là các tiếp tuyến suy ra · · 90o KAO KBO 0,5 a Xét tứ giác KAOB: · ·
90o 90o 180o KAO KBO 0,5
Suy ra tứ giác KAOB nội tiếp. Độ dài cung tròn BC là .3.100 l 0,5 b 180 5 (cm). 0,5 3 · ·
AK //BC KAB ABC (so le trong) 0,5
Xét hai tam giác cân KAB và ABC có góc ở đáy bằng nhau suy ra góc ở c đỉnh cũng bằng nhau. 0,5 Từ đó · · AKB BAC . 0,25 d BE cắt AK ở I. Ta có · ·
AKB BAC (câu b)) 2 A
BC ∽ K
AB AB BC.AK . 1 + · · » IAB ACB sđ AB (1) 2 + · · ·
ADC IAE IBA (2) Từ (1) và (2) suy ra 2 A
DC ∽ I
BA DC.IA AC.AB AB . Khi đó B . C AK I . ACD B . C AK 2B .
C IA AK 2IA hay I là trung điểm của AK. 0,25 2 2 · · · ·
IK IA I . E IB I
EK ∽ I
KB IEK IKB BAC BEC · · · · 180o BEC BEK IEK BEK
K,E,C thẳng hàng.
Bài 5: (0,5 điểm )
Cho các số hai số a,b thỏa mãn 1 1 1
. Chứng minh rằng ít nhất một trong hai a b 2 phương trình 2
x ax b 0 và 2
x bx a 0 có nghiệm. 0,25 Xét phương trình: 2
x ax b 0 có 2
a 4b . 1 Xét phương trình: 2
x bx a 0 có 2
b 4a . 2
Giả sử cả hai pt đều vô nghiệm.
Suy ra 0 và 0 . 1 2 Suy ra 0 1 2 Hay 2 2
a b 4a b 0 (1) Theo giả thiết: 1 1 1 a b 2 Suy ra: a b 1 hay ab a b (2). ab 2 2 Từ (1) và (2) suy ra: 0,25 2 2
a b 2ab 0
Hay a b2 0 (vô lý).
Vậy ít nhất một trong hai phương trình 2
x ax b 0 và 2
x bx a 0 có nghiệm.
Lưu ý: Học sinh giải cách khác đúng vẫn cho điểm tối đa