Đề KSCL Toán thi vào 10 năm 2023 – 2024 trường THPT Quảng Xương 4 – Thanh Hoá

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề khảo sát chất lượng môn Toán thi tuyển sinh vào lớp 10 THPT năm học 2023 – 2024 trường THPT Quảng Xương 4, tỉnh Thanh Hoá; đề thi có đáp án và hướng dẫn chấm điểm. Mời các bạn đón xem!

461 231 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
SỞ GD&ĐT THANH HÓA
TRƯỜNG THPT QUẢNG XƯƠNG 4
ĐỀ KSCL CÁC MÔN THI VÀO LỚP 10 THPT
NĂM HỌC 2023-2024
MÔN: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Câu I. (2.0 điểm) Cho biểu thức:
1 22
12
a
P
a aa a

=+⋅

−− +

với
0a >
và
1a ≠
.
1) Rút gọn biểu thức
P
.
2) Tính giá trị của
P
khi
3 22a = +
.
Câu II. (2.0 điểm)
1) Giải hệ phương trình:
38
46
xy
xy
+=
−=
.
2) Trong hệ toạ độ
cho điểm
( )
2; 2
A
, đường thẳng
:4dy x=−+
và parabol
( )
2
:P y ax=
. Tìm
a
để parabol
( )
2
:P y ax
=
đi qua điểm
A
. Với giá trị
a
tìm được,
hãy xác định tọa độ điểm
B
là giao điểm thứ hai của
( )
d
và
( )
P
.
Câu III. (2.0 điểm) Cho phương trình bậc hai
2
25 0x xm−− =
(
m
là tham số)
1) Giải phương trình khi
3m =
.
2) Tìm giá trị của tham số
m
phương trình có
2
nghiệm
12
,xx
phân biệt và thỏa mãn
( )
2
12 1 2
. 5 3 10115xx x m x
− +=
.
Câu IV. (3.0 điểm) Từ một điểm
M
nằm ngoài đường tròn
( )
;OR
. Vẽ hai tiếp tuyến
,MA MB
(
,AB
là tiếp điểm) và một cát tuyến qua
M
cắt đường tròn tại
C
,
D
(
C
nằm giữa
M
và
)D
. Gọi
E
là giao điểm của
AB
và
OM
.
1) Chứng minh tứ giác
OAMB
nội tiếp.
2) Chứng minh
..MC MD ME MO=
.
3) Giả sử
3
OM R=
. Tìm diện tích lớn nhất của tứ giác
MADB
.
Câu V. (1.0 điểm) Cho các số thực
,, 1
abc>−
. Chứng minh rằng:
2 2 22 22
222
1.
111
bc a ca b ab c
bc ca ab
+− +− +−
++≤
++ ++ ++
===========HẾT===========
Thí sinh không được sử dụng tài liệu; cán bộ coi thi không giải thích gì thêm.
SỞ GD&ĐT THANH HÓA
TRƯỜNG THPT QUẢNG XƯƠNG 4
HƯỚNG DẪN CHẤM
ĐỀ KSCL CÁC MÔN THI VÀO LỚP 10 THPT
NĂM HỌC 2023-2024
MÔN: TOÁN
Câu/ý
Lời giải – Đáp án
Điểm
I.1)
Cho biểu thức:
1 22
12
a
P
a aa a

=+⋅

−− +

với
0a >
và
1a ≠
.
1) Rút gọn biểu thức
P
Với
0a >
và
1a
≠
, ta có:
1 22
12
a
P
a aa a

=+⋅

−− +

(
)
1 22
12
1
a
aa
aa


=+⋅

−+
−

( )
22
2
1
aa
a
aa
+
= ⋅
+
−
2
.
1a
=
−
0,5
0,5
I.2)
2) Tính giá trị của
P
khi
3 22a = +
Khi
3 22
a = +
(thỏa mãn điều kiện xác định), ta có:
(
)
2
322 22.2.11 21 21 21
a = + = + += + = += +
;
Suy ra:
2 22
2
12112
P
a
= = = =
− +−
.
Vậy
2P =
khi
3 22a
= +
.
0,5
0,5
II.1)
Giải hệ phương trình:
38
46
xy
xy
+=
−=
.
Ta có:
3 8 7 14
4 63 8
xy x
xy xy
+= =

⇔

−= +=

22
3.2 8 2
xx
yy
= =

⇔⇔

+= =

.
Vậy hệ phương trình đã cho có nghiệm
( ) ( )
; 2; 2
xy =
.
0,5
0,5
II.2)
Trong hệ toạ độ
cho điểm
( )
2; 2A
, đường thẳng
:4dy x=−+
và parabol
( )
2
:
P y ax=
.Tìm
a
để parabol
( )
2
:P y ax=
đi qua điểm
A
. Với giá trị
a
tìm
được, hãy xác định tọa độ điểm
B
là giao điểm thứ hai của
( )
d
và
( )
P
.
Thay
2, 2xy= =
vào pt
( )
1
:4 2
2
Pa a=⇔=
suy ra
( )
2
1
:
2
Py x=
.
Phương trình hoành độ giao điểm
( )
P
và
( )
d
:
22
22
1
4 2 80
48
2
xy
x x xx
xy
=⇒=
=−+ ⇔ + −= ⇔
=−⇒ =
.
Vậy giao điểm còn lại là
( )
4;8B −
.
0,5
0,5
III.1)
Cho phương trình bậc hai
2
25 0x xm−− =
(
m
là tham số)
1) Giải phương trình khi
3m =
Với
3m
=
phương trình trở thành
2
2 15 0xx−−=
.
Ta có
1 15 16
′
∆= + =
Phương trình có hai nghiệm phân biệt
1
1 16 3x
=−=−
;
2
1 16 5x =+=
0,5
0,5
III.2)
Tìm giá trị của tham số
m
phương trình có
2
nghiệm
12
,xx
phân biệt và thỏa
mãn
(
)
2
12 1 2
. 5 3 10115xx x m x− +=
.
Để phương trình có hai nghiệm phân biệt thì
2
1
0 15 0
5
mm
′
∆>⇔ + >⇔ >−
.
Khi đó, theo Vi-et ta có:
12
12
2
2 (1)
1
5
5 (2)
1
xx
m
xx m
−
+=− =
−
= = −
.
Theo đề bài ta có:
( )
2
12 1 2
. 5 3 10115xx x m x
− +=
(3).
Từ
( )
12
12xx⇒=−
. Thay vào (2) và (3), ta có:
( )
( ) ( )( )
22
2
22 2 2
25
2 . 2 5 3 10115
xx m
xx x m x
− =−
− −− + =
( )
( )
( )
2
22
22
22 2 2 2 2
52
2 . 2 2 3 10115
mx x
xx x x x x
= −
⇔
− −− − + =
( ) ( )
( )
2
22
22
22 2 2 2
52
2 . 2 10115
mx x
xx x x x
= −
⇔
− −− + =
2
22
23 2 32
22 2 222
52
2 2 2 10115
mx x
xx x xxx
= −
⇔
−− − ++=
2
22
2
22
52
2 10115
mx x
xx
= −
⇔
−=
.
5 10115 2023
mm⇒ = ⇔=
(thỏa mãn).
Vậy
2023
m =
.
0,25
0,25
0,25
0,25
IV.1)
Từ một điểm
M
nằm ngoài đường tròn
( )
;OR
. Vẽ hai tiếp tuyến
,MA MB
(
,AB
là tiếp điểm) và một cát tuyến qua
M
cắt đường tròn tại
C
,
D
(
C
nằm giữa
M
và
)D
. Gọi
E
là giao điểm của
AB
và
OM
.
1) Chứng minh tứ giác
OAMB
nội tiếp.
E
D
O
B
C
A
M
Vì
,MA MB
là tiếp tuyến của
(
)
O
nên ta có
90MAO MBO= = °
( tính chất
tiếp tuyến).
Do đó
180MAO MBO+=°
⇒
tứ giác
MAOB
là tứ giác nội tiếp.
0,5
0,5
IV.2)
Chứng minh
..MC MD ME MO=
.
Xét
MAC
và
MDA
có:
M
chung và
MAC MDA=
nên
(.)MAC MDA g g

∽
Do đó:
MA MC
MD MA
=
2
.MA MC MD⇒=
(1)
Vì
,MA MB
là tiếp tuyến của
( )
O
nên ta có
MO
là trung trực của
AB
.
Xét tam giác
MAO
vuông tại
A
có
AE MO⊥
nên
2
.MA ME MO=
(2)
Từ (1) và (2), ta có
..MC MD ME MO=
0,5
0,5
IV.3)
Giả sử
3
OM R=
. Tìm diện tích lớn nhất của tứ giác
MADB
.
Xét tam giác
MAO
vuông tại
A
có
AE MO
⊥
nên
2
.OA OE OM
=
3
R
OE⇒=
8
3
33
RR
ME R⇒ = −=
2
2
8 22
.
93
RR
AE ME MO AE
⇒ = = ⇒=
42
3
R
AB⇒=
.
Hạ:
DH AB⊥
thì ta có
4
33
RR
DH DE DO OE R≤ ≤ + =+=
Do đó:
11
..
22
MADB MAB DAB
S S S ME AB DH AB=+= +
2
1842144282
.. ..
23 3 23 3 3
RR RR R
≤+=
.
Vậy
MADB
S
đạt GTLN là
2
82
3
R
khi
,,,MCOD
thẳng hàng.
0,25
0,25
0,25
0,25
V.
Cho các số thực
,, 1abc>−
. Chứng minh rằng:
2 2 22 22
222
1
111
bc a ca b ab c
bc ca ab
+− +− +−
++≤
++ ++ ++
.
Bất đẳng thức đã cho tương đương với:
222
222
111
2
111
abc
bc ca ab
+++
++≥
++ ++ ++
Sử dụng bất đẳng thức AM – GM ta có
2
22 2
1
1 0,1 1
2
b
bc bc c
+
++ > ++ ≤+ +
.
Suy ra
( )
(
)
2
2
2
22
21
1
1
1 21
a
a
bc
bc
+
+
≥
++
++ +
.
Tương tự ta có
( )
( )
( )
( )
2
2
2
22
2
2
2
22
21
1
1
1 21
21
1
1
1 21
b
b
ca
ca
c
c
ab
ab
+
+
≥
++
++ +
+
+
≥
++
++ +
.
Cộng theo vế 3 bất đẳng thức trên và đặt
2 22
1, 1, 1xa yb zc=+=+=+
ta
được
0,25
0,25
222
222
1 1 1 222
222
111
a b c xyz
y zz xx y
bc ca ab
+++
+ + ≥++
+++
++ ++ ++
2
222
xyz
y zz xx y

= ++

+++

Sử dụng bất đẳng thức C – S (Cô-si cộng mẫu) ta có
( )
(
)
( )
( )
(
)
( )
(
)
( )
2
2
222 2 2 2
3
1
33
xyz
xyz
yzzxxyxyzyzxzxy
x y z xy yz zx
xy yz zx xy yz zx
++
++≥
+ + + ++ +++
++ + +
=≥=
++ ++
.
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1
abc= = =
.
0.25
0,25
==========Hết==========
(Học sinh giải đúng theo cách khác vẫn cho điểm tối đa)
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT THANH HÓA
ĐỀ KSCL CÁC MÔN THI VÀO LỚP 10 THPT
TRƯỜNG THPT QUẢNG XƯƠNG 4 NĂM HỌC 2023-2024 MÔN: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian phát đề) Câu I. (  
2.0 điểm) Cho biểu thức: 1 2 2 a P = + ⋅ 
với a > 0 và a ≠1. a 1 a a  − −  a + 2
1) Rút gọn biểu thức P .
2) Tính giá trị của P khi a = 3 + 2 2 .
Câu II. (2.0 điểm) 3  x + y = 8
1) Giải hệ phương trình:  . 4x − y = 6
2) Trong hệ toạ độ Oxy cho điểm A(2;2) , đường thẳng d : y = −x + 4 và parabol (P) 2
: y = ax . Tìm a để parabol (P) 2
: y = ax đi qua điểm A. Với giá trị a tìm được,
hãy xác định tọa độ điểm B là giao điểm thứ hai của (d ) và (P).
Câu III. (2.0 điểm) Cho phương trình bậc hai 2
x − 2x − 5m = 0 ( m là tham số)
1) Giải phương trình khi m = 3 .
2) Tìm giá trị của tham số m phương trình có 2 nghiệm x , x phân biệt và thỏa mãn 1 2 2
x .x − x 5m + 3x =10115. 1 2 1 ( 2 )
Câu IV. (3.0 điểm) Từ một điểm M nằm ngoài đường tròn ( ;
O R). Vẽ hai tiếp tuyến , MA MB ( ,
A B là tiếp điểm) và một cát tuyến qua M cắt đường tròn tại C , D (C nằm giữa M
và D). Gọi E là giao điểm của AB và OM .
1) Chứng minh tứ giác OAMB nội tiếp.
2) Chứng minh MC.MD = ME.MO .
3) Giả sử OM = 3R . Tìm diện tích lớn nhất của tứ giác MADB .
Câu V. (1.0 điểm) Cho các số thực
a,b,c > 1 − . Chứng minh rằng: 2 2 2 2 2 2
b + c − a
c + a − b
a + b − c + + ≤1. 2 2 2 1+ b + c 1+ c + a 1+ a + b
===========HẾT===========
Thí sinh không được sử dụng tài liệu; cán bộ coi thi không giải thích gì thêm. SỞ GD&ĐT THANH HÓA HƯỚNG DẪN CHẤM
TRƯỜNG THPT QUẢNG XƯƠNG 4
ĐỀ KSCL CÁC MÔN THI VÀO LỚP 10 THPT NĂM HỌC 2023-2024 MÔN: TOÁN Câu/ý
Lời giải – Đáp án Điểm Cho biểu thức:  1 2  2 a P = + ⋅ 
với a > 0 và a ≠1. a 1 a a  − −  a + 2
1) Rút gọn biểu thức P
Với a > 0 và a ≠1, ta có: I.1)    1 2  2 a P = + ⋅ 1 2 2 a    = + ⋅  a 1 a a  − −  a + 2  a −1 a ( a − 0,5  )1 a +2  a + 2 2 a 2 = ⋅ = . 0,5 a ( a − ) 1 a + 2 a −1
2) Tính giá trị của P khi a = 3+ 2 2
Khi a = 3 + 2 2 (thỏa mãn điều kiện xác định), ta có:
a = 3 + 2 2 = 2 + 2. 2.1+1 = ( 2 + )2 = + = + 0,5 I.2) 1 2 1 2 1; Suy ra: 2 2 2 P = = = = 2 . a −1 2 +1−1 2
Vậy P = 2 khi a = 3 + 2 2 . 0,5 3  x + y = 8
Giải hệ phương trình: . 4x − y = 6 3  x + y = 8 7x =14 Ta có:  ⇔  II.1) 0,5 4x − y = 6 3  x + y = 8 x = 2 x = 2 ⇔  ⇔ . 3.2  y 8  + = y = 2
Vậy hệ phương trình đã cho có nghiệm ( ; x y) = (2;2) . 0,5
Trong hệ toạ độ Oxy cho điểm A(2;2) , đường thẳng d : y = −x + 4 và parabol (P) 2
: y = ax .Tìm a để parabol (P) 2
: y = ax đi qua điểm A. Với giá trị a tìm
được, hãy xác định tọa độ điểm B là giao điểm thứ hai của (d ) và (P).
Thay x = 2, y = 2 vào pt (P) 1
: 4a = 2 ⇔ a = suy ra (P) 1 2 : y = x . 0,5 II.2) 2 2
Phương trình hoành độ giao điểm (P) và(d ): 1
x = 2 ⇒ y = 2 2 2
x = −x + 4 ⇔ x + 2x − 8 = 0 ⇔ . 2  x = 4 − ⇒ y = 8
Vậy giao điểm còn lại là B( 4; − 8) . 0,5
Cho phương trình bậc hai 2
x − 2x − 5m = 0 ( m là tham số)
1) Giải phương trình khi m = 3
III.1) Với m = 3 phương trình trở thành 2
x − 2x −15 = 0. Ta có ∆′ =1+15 =16 0,5
Phương trình có hai nghiệm phân biệt x =1− 16 = 3 − ; x =1+ 16 = 5 0,5 1 2
Tìm giá trị của tham số m phương trình có 2 nghiệm x , x phân biệt và thỏa 1 2 mãn 2
x .x − x 5m + 3x =10115. 1 2 1 ( 2 )
Để phương trình có hai nghiệm phân biệt thì 2 1
∆′ > 0 ⇔ 1 + 5m > 0 ⇔ m > − . 5 0,25  2 − x + x = − = 2 (1)  1 2
Khi đó, theo Vi-et ta có:  1  . 5 − mx x = = 5 − m (2) 1 2  1 Theo đề bài ta có: 2
x .x − x 5m + 3x =10115 (3). 1 2 1 ( 2 ) Từ ( )
1 ⇒ x = 2 − x . Thay vào (2) và (3), ta có: 0,25 1 2 III.2) (  2 − x x = 5 −  m 2 ) 2 (   2 − x  ) 2
.x − 2 − x 5m + 3x =10115 2 2 ( 2 ) ( 2 ) 2 5  m = x −  2x 2 2
⇔ (2− x ) 2.x −(2− x ) 
( 2x −2x +3x =  10115 2 2 2 2 2 2 ) 2 5  m = x −  2x 2 2 ⇔ ( 0,25 2 − x ) 2
.x − (2 − x )  ( 2x + x =  10115 2 2 2 2 2 ) 2 5
 m = x − 2x 2 5
 m = x − 2x 2 2 ⇔  2 2 ⇔  . 2 3 2 3 2
2x − x − 2x − 2x + x + x =10115 2
x − 2x =10115 2 2 2 2 2 2 2 2
⇒ 5m =10115 ⇔ m = 2023 (thỏa mãn). Vậy m = 2023 . 0,25
Từ một điểm M nằm ngoài đường tròn ( ;
O R). Vẽ hai tiếp tuyến , MA MB ( , A B
là tiếp điểm) và một cát tuyến qua M cắt đường tròn tại C , D (C nằm giữa M
và D). Gọi E là giao điểm của AB và OM .
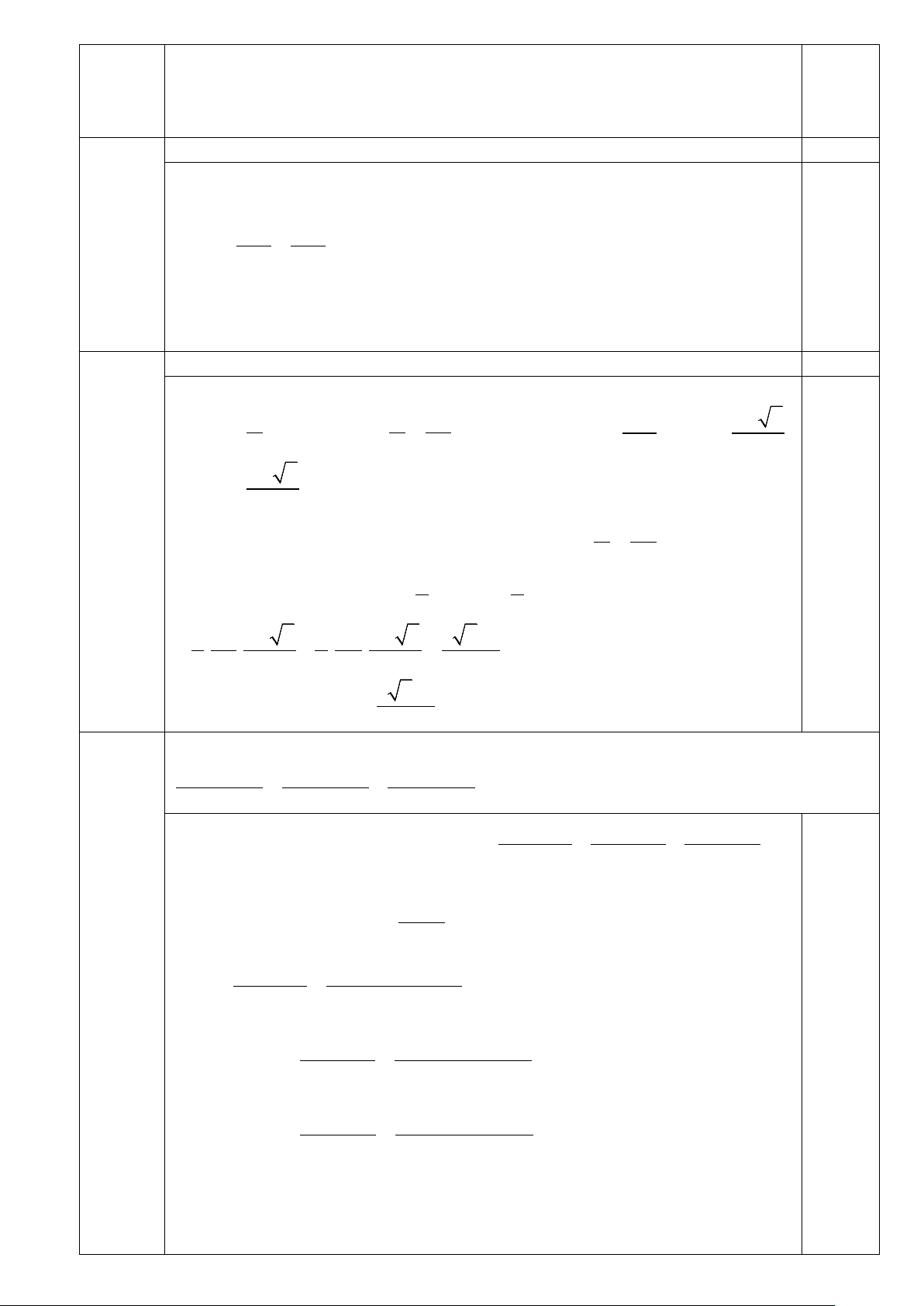
1) Chứng minh tứ giác OAMB nội tiếp. A D IV.1) C M E O B Vì ,
MA MB là tiếp tuyến của (O) nên ta có  = 
MAO MBO = 90° ( tính chất 0,5 tiếp tuyến). Do đó  + 
MAO MBO =180° ⇒ tứ giác MAOB là tứ giác nội tiếp. 0,5
Chứng minh MC.MD = ME.MO .
Xét MAC và MDA có:  M chung và  =  MAC MDA nên MAC  ∽ MD ( A g.g)
IV.2) Do đó: MA MC = 2
⇒ MA = MC.MD (1) 0,5 MD MA Vì ,
MA MB là tiếp tuyến của (O) nên ta có MO là trung trực của AB .
Xét tam giác MAO vuông tại A có AE ⊥ MO nên 2
MA = ME.MO (2)
Từ (1) và (2), ta có MC.MD = ME.MO 0,5
Giả sử OM = 3R . Tìm diện tích lớn nhất của tứ giác MADB .
Xét tam giác MAO vuông tại A có AE ⊥ MO nên 2
OA = OE.OM R 2 ⇒ OE = R 8 ⇒ = 3 R ME R − = 2 8R 2R 2
⇒ AE = ME.MO = ⇒ AE = 3 3 3 9 3 4R 2 ⇒ AB = . 0,25 3 R R 0,25
IV.3) Hạ: DH ⊥ AB thì ta có 4
DH ≤ DE ≤ DO + OE = R + = 3 3 Do đó: 1 1 S = S + S = ME AB + DH AB MADB MAB DAB . . 2 2 0,25 2
1 8R 4R 2 1 4R 4R 2 8 2 . . . . R ≤ + = . 2 3 3 2 3 3 3 2 Vậy S
đạt GTLN là 8 2R khi M ,C,O, D thẳng hàng. MADB 3 0,25 Cho các số thực
a,b,c > 1 − . Chứng minh rằng: 2 2 2 2 2 2
b + c − a
c + a − b
a + b − c + + ≤1. 2 2 2 1+ b + c 1+ c + a 1+ a + b 2 2 2
Bất đẳng thức đã cho tương đương với: 1+ a 1+ b 1+ c + + ≥ 2 2 2 2 1+ b + c 1+ c + a 1+ a + b 0,25
Sử dụng bất đẳng thức AM – GM ta có 2 2 2 1+ b 2
1+ b + c > 0,1+ b + c ≤1+ + c . 2 1+ a 2( 2 2 1+ a ) V. Suy ra ≥ . 2 2 1+ b + c 1+ b + 2( 2 1+ c ) 1+ b 2( 2 2 1+ b ) Tương tự ta có ≥ . 2 2 1+ c + a 1+ c + 2( 2 1+ a ) 1+ c 2( 2 2 1+ c ) ≥ 0,25 2 2 1+ a + b 1+ a + 2( 2 1+ b )
Cộng theo vế 3 bất đẳng thức trên và đặt 2 2 2
x = a +1, y = b +1, z = c +1ta được 2 2 2 1+ a 1+ b 1+ c 2x 2y 2z + + ≥ + + 2 2 2 1+ b + c 1+ c + a 1+ a + b
y + 2z z + 2x x + 2y   = 2 x y z + + 0.25 
y 2z z 2x x 2y  + + + 
Sử dụng bất đẳng thức C – S (Cô-si cộng mẫu) ta có x y z
(x + y + z)2 + + ≥
y + 2z z + 2x x + 2y x( y + 2z) + y (z + 2x) + z (x + 2y) . (
x + y + z)2
3(xy + yz + zx) = ( ≥ =
xy + yz + zx)
(xy + yz + zx) 1 3 3
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
a = b = c =1. 0,25
==========Hết==========
(Học sinh giải đúng theo cách khác vẫn cho điểm tối đa)