Đề KSCL Toán vào lớp 10 năm 2022 – 2023 phòng GD&ĐT Thọ Xuân – Thanh Hoá
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề khảo sát chất lượng môn Toán ôn thi tuyển sinh vào lớp 10 THPT năm học 2022 – 2023 phòng Giáo dục và Đào tạo huyện Thọ Xuân, tỉnh Thanh Hoá; kỳ thi được diễn ra vào ngày 02 tháng 06 năm 2022; đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm. Mời các bạn đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG VÀO LỚP 10 THPT THỌ XUÂN NĂM HỌC 2022 - 2023 Môn: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Ngày kiểm tra: 02/6/2022
(Đề gồm 01 trang, 05 câu)
Câu 1 (2,0 điểm) Giải phương trình và hệ phương trình sau: 2x − y = 5 a) x2 - 3x - 4 = 0 b) x + 3y = 1 −
Câu 2 (2,0 điểm) Cho biểu thức: x 2 x 3x + 2 x +1 P = + + : với x ≥ 0, x ≠ 4. x - 2 x + 2 4 - x x + 2 a) Rút gọn P. 5 b) Tìm x để P = x + 1
Câu 3 (2,0 điểm) Trong hệ trục tọa độ Oxy, cho parabol (P): y = 2x2 và đường thẳng (d):
y = (m + 1)x – m + 3 (m là tham số )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm A và B phân biệt
với mọi giá trị của m
b) Gọi tọa độ điểm A và điểm B là A (x1; y1) và B(x2; y2). Tìm m để 2y1 + 2y2 = (m + 1)x2 + 2 + 8
Câu 4 (3,0 điểm) Cho nửa đường tròn tâm O, bán kính R, đường kính AB, I là điểm cố định thuộc
đoạn thẳng OB. Vẽ đường thẳng d vuông góc với AB tại I, d cắt nửa đường tròn (O) tại K. Lấy
điểm M bất kỳ thuộc cung nhỏ BK, tia BM cắt đường thẳng d tại điểm C, đoạn thẳng AM cắt
đường thẳng d tại điểm N, AC cắt nửa đường tròn (O) tại D.
a) Chứng minh tứ giác BMNI là tứ giác nội tiếp
b) Chứng minh ba điểm B, N, D thẳng hàng và tính AD.AC + BM.BC theo R
c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác ANC. Chứng minh O’ luôn nằm trên một
đường thẳng cố định khi M di chuyển trên cung nhỏ KB 1 1 1
Câu 5 (1,0 điểm): Cho 3 số thực dương x, y, z thỏa mãn: + +
= 1. Tìm giá trị nhỏ nhất 2 2 2 x y z 2 2 2 2 2 2 y z z x x y
của biểu thức: P = + + x ( . 2 2 y + z ) y ( 2 2
z + x ) z ( 2 2 x + y )
---------------- HẾT ---------------
Họ và tên thí sinh: .............................................. SBD…………………....
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT CHẤT THỌ XUÂN
LƯỢNG VÁO LỚP 10 THPT
NĂM HỌC 2022 – 2023 Môn thi: TOÁN
(Hướng dẫn chấm gồm có 06 trang) Câu Nội dung Biểu điểm
Câu a, Phương trình x2 - 3x - 4 = 0 là phương trình bậc hai có − 0,25 1 c
a - b + c = 0 nên phương trình có hai nghiệm là: x1 = -1; x2 = = 4. a 0,5
Vậy tập nghiệm của phương trình là: S = 1 − ; 4 0,25 2x − y = 5 ,
b x +3y = 1 − 0,25 6x − 3y =15 x + 3y =−1 0,25 7x =14 0,25 x + 3y =−1 x = 2 y = 1 −
Vậy hệ phương trình có nghiệm duy nhất là: (x; y) = (2; -1) 0,25 Câu
a) Với x ≥ 0, x ≠ 4 ta có : 2 x 2 x 3x + 2 x +1 P = + + : x - 2 x + 2 4 - x x + 2
x ( x +2) + 2 x ( x - 2) - (3x + 2) x + 2 P = . 0,25 ( x - 2) ( x + 2) x +1 x + 2 x + 2x - 4 x - 3x - 2 x + 2 = . 0,25 ( x +2) ( x - 2) x +1 -2 x - 2 x + 2 = . 0,25 + ( x + 2) ( x - 2) x 1 2( − x +1) x + 2 = . ( x + 2) ( x - 2) x +1 0,25 2 − = x - 2 Kết luận :…
b) Với x ≥ 0, x ≠ 4 ta có: 5 P = x + 1 2 − 5 = x − 2 x + 1 = 2 − ( x + ) 1 = 5( x − 2) 0,25
− 2 x −2=5 x −10 0,25 2 −
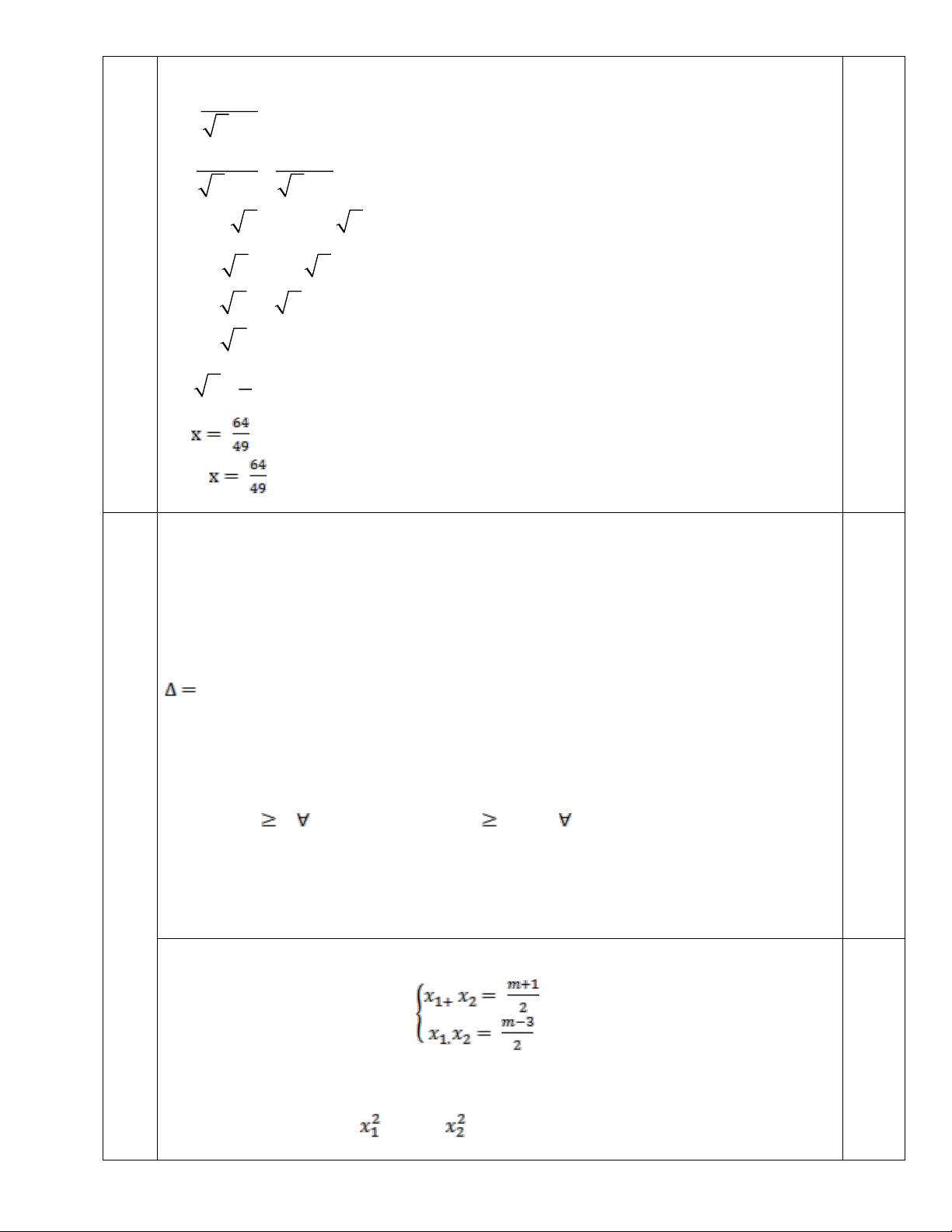
x −5 x = 2 −10 7 − x = −8 8 0,25 x = 7 (thỏa mãn ĐKXĐ) 0,25 Vậy
Câu Phương trình hoành độ giao điểm của (d) và (P) là: 3 2x2 = (m + 1)x – m + 3
2x2 - (m + 1)x + m - 3 = 0 (1) 0,25
Phương trình trên là phương trình bậ c hai có:
(m + 1)2 – 4.2.(m-3) = m2 + 2m + 1 – 8m + 24 0,25 = m2 – 6m + 25 = (m – 3) 2 + 16
Vì (m – 3)2 0 m nên (m – 3)2 + 16 16 > 0 m 0,25
Suy ra phương trình (1) có hai nghiệ m phân biệt với mọi m 0,25
Do đó đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt với mọi giá trị của m
b) Vì x1; x2 là hoành độ giao điểm nên x1; x2 là nghiệm của phương trình (1)
Áp dụng hệ thức Vi-ét ta có: 0,25
Vì A (x1; y1) và B(x2; y2) là tọa độ giao điểm của (d) và (P) nên y1 = 2 ; y2 = 2 Ta có: 2y1 + 2y2 = (m+1)x2 + 2 + 8 4 4 = 2.( )x2 + 2 + 8 0,25 4 4 = 2. + 2 + 2 + 8 2 2 - 2. - 8 = 0
2(x1 + x2)2 – 6x1x2 - 8 = 0 2. – 8 = 0
m2 + 2m + 1 – 6m + 18 – 16 = 0 m2 – 4m + 3 = 0 0,25 0,25 Vậy m Câu 4 0,25
a) Chứng minh tứ giác BMNI là tứ giác nội tiếp Ta có:
= 900 (góc nội tiếp chắn nửa đường tròn) 0,25 = 900 (Gt) 0,25 0,25 Do đó: + = 900 + 900 = 1800
Suy ra tứ giác BMNI là tứ giác nội tiếp.
b) Chứng minh ba điểm B, N, D thẳng hàng và tính AD.AC + BM.BC theo R
- Chứng minh N là trực tâm của tam giác ABC và BD vuông góc với AC suy ra B, 0,25 N, D thẳng hàng. - Chứng minh đồng dạng với , suy ra: 0,25 AD.AC = AI.AB (1) - Chứng minh đồng dạng với , suy ra: 0,25 BM.BC = BI.BA (2) Từ (1) và (2) suy ra: AD.AC + BM.BC = AI.AB + BI.BA 0,25 = AB(AI + BI) = AB.AB = 4R2
c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác ANC. Chứng minh O’ luôn nằm
trên một đường thẳng cố định khi M di chuyển trên cung nhỏ KB
Lấy điểm E đối xứng với điểm B qua điểm I. Vì điểm I và điểm B cố định nên điểm E cố định. 0,25
Tam giác NBE cân tại N (vì có đường cao đồng thời là đường trung tuyến) suy ra: Mà (cùng phụ với ) nên . 0,25
Suy ra tứ giác AENC là tứ giác nội tiếp
Do đó đường tròn ngoại tiếp tứ giác AENC cũng chính là đường tròn ngoại tiếp tam giác ANC .
Tâm O’ của đường tròn ngoại tiếp tam giác ANC cũng chính là tâm của đường
tròn ngoại tiếp tứ giác AENC. 0,25
Suy ra: O’A = O’E hay O’ nằm trên đường trên đường trung trực của đoạn thẳng AE cố định. 0,25
Vậy khi M di chuyển trên cung nhỏ KB thì tâm O’ của đường tròn ngoại tiếp tam
giác ANC luôn nằm trên đường trung trực của đoạn thẳng AE cố định Câu Đặ 1 1 1 t = ; a = ; b = c thì a, , b c 0 và 2 2 2
a + b + c = 1. 5 x y z 2 2 2 a b c a b c P = + + = + + 2 2 2 2 2 2 b + c c + a a + b a ( 2 − a ) b( 2 − b ) c( 2 1 1 1 − c ) 0,25
Áp dụng bất đẳng thức Côsi cho 3 số dương ta có 3 (
a + − a + − a a 1 − a ) 2 2 2 2 1 1 2 1 1 4 2 2 2 2 2
= .2a (1− a )(1− a ) = 2 2 3 27 0,25 2 2 a 3 3 2 2
a(1− a ) a (1) 2 3 3 a(1− a ) 2 2 2 Tương tự b 3 3 c 3 3 : 2 2 b (2); c (3) 2 2 b(1− b ) 2 c(1 − c ) 2 0,25 3 3 3 3
Từ (1); (2); (3) suy ra: P ( 2 2 2
a + b + c ) = . 2 2 Đẳ 1
ng thức xảy ra a = b = c =
hay x = y = z = 3. 3 0,25 3 3
Vậy giá trị nhỏ nhất của P là
. xảy ra khi x = y = z = 3. 2 Chú ý:
- Nếu học sinh làm cách khác mà đúng vẫn cho điểm tối đa
- Bài 2b nếu học sinh không so sánh giá trị tìm được của x với ĐKXĐ thì trừ 0,25 điểm
Document Outline
- Câu 2 (2,0 điểm) Cho biểu thức:
- P = với x ≥ 0, x ≠ 4.