Đề luyện thi tốt nghiệp THPT 2021 môn Toán Trường Mỹ Việt -Đề 3 (có lời giải chi tiết)
Đề luyện thi tốt nghiệp THPT 2021 môn Toán Trường Mỹ Việt -Đề 3 có lời giải chi tiết. Tài liệu được biên soạn dưới dạng file PDF bao gồm 17 trang tổng hợp các kiến thức tổng hợp giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Tài liệu liên quan:
Preview text:
TRƯỜNG THCS & THPT MỸ VIỆT
KỲ THI TỐT NGHIỆP THPT NĂM 2020 – 2021
------------------------------------ ĐỀ THI THỬ Bài thi: TOÁN
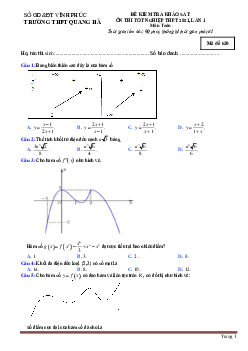
Thời gian làm bài: 90 phút, không kể thời gian phát đề ĐỀ THI SỐ 03 I. NHẬN BIẾT Câu 1. Cho hàm số ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ bên dưới. y f(x)=x^3-3x^2+4 T ?p h?p 1 x -
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại x = 2 .
B. Hàm số đạt cực đại tại x = 4 .
C. Hàm số có hai điểm cực trị.
D. Hàm số đạt cực đại tại x = 0 .
Câu 2. Đường cong trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây? 1 A. 3 2 y =
x − x +1. B. 3 2
y = x − 3x +1. C. 3 2
y = −x + 3x +1. D. 3 2
y = −x − 3x +1. 3
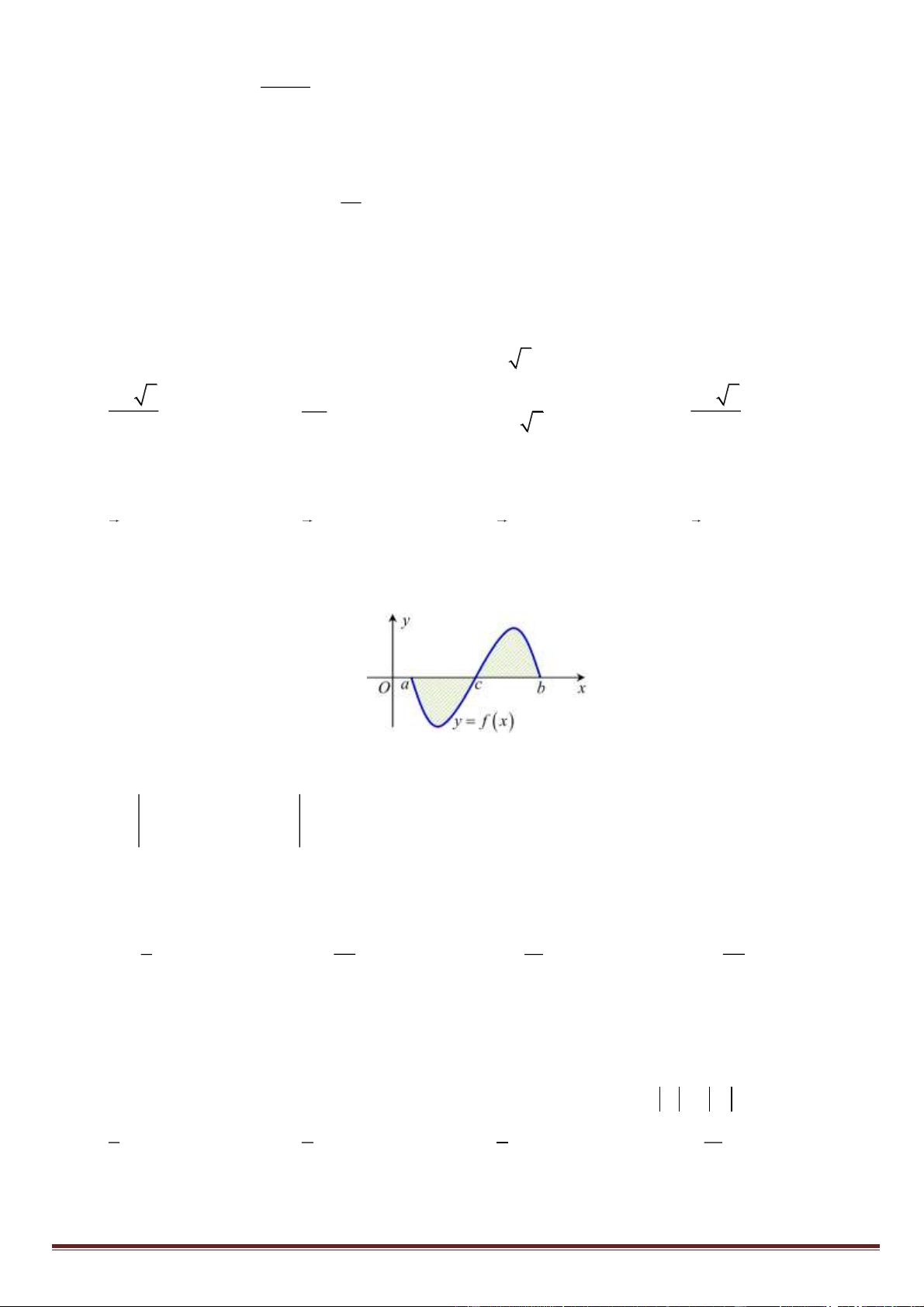
Câu 3. Cho hàm số y = f ( x) xác định và liên tục trên khoảng (− ;
+), có bảng biến thiên như hình sau:
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng ( 1 − ;+)
B. Hàm số nghịch biến trên (1;+) .
C. Hàm số đồng biến trên khoảng (− ; 2 − ).
D. Hàm số nghịch biến trên ( ) ;1 − . Trang 1 2x − 3
Câu 4. Đồ thị hàm số y =
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: x −1
A. x = 1 và y = 3 − . B. x = 1 − và y = 2.
C. x = 1 và y = 2 .
D. x = 2 và y = 1 .
Câu 5. Trong các dãy số sau, dãy số nào là cấp số cộng n n A. u = − n . B. u = .
C. u = 2n . D. 2 u = n . n ( ) 1 n n n 3n
Câu 6. Tìm tập xác định D của hàm số y = log ( 2 x − 2x . 2 ) A. D = (− ; 0 2;+) B. D = (− ; 0) 2;+)
C. D = (0;+) D. D = (− ; 0)(2;+)
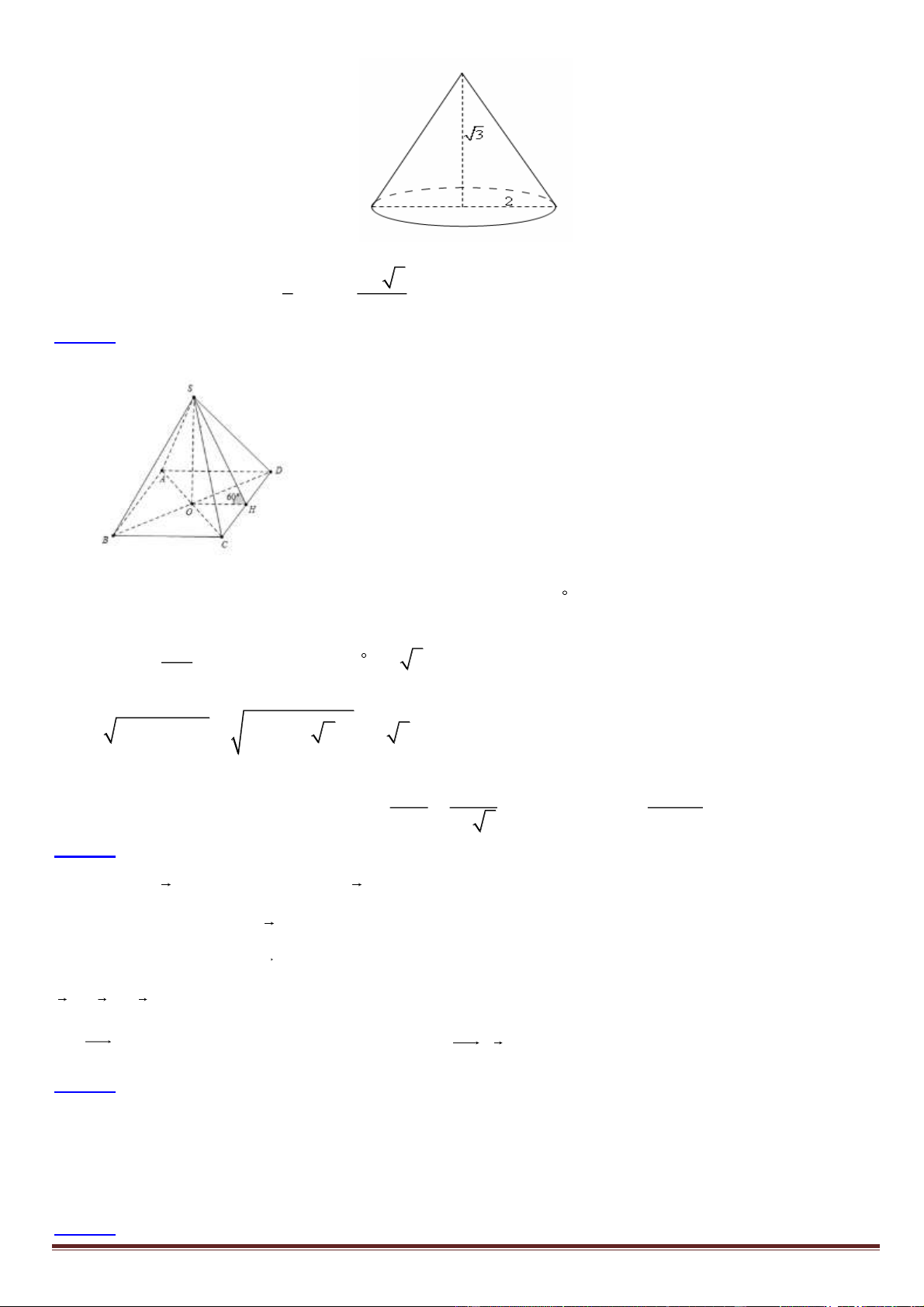
Câu 7. Cho khối nón có bán kính đáy r = 2 , chiều cao h =
3 . Thể tích của khối nón là: 4 3 4 2 3 A. 3 . B. 3 . C. 4 3 . D. 3 .
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2
− x + y −3z +1= 0. Một véctơ pháp
tuyến của mặt phẳng (P) là A. n = (2; 1 − ;− ) 3 B. n = (4; 2 − ;6) C. n = ( 2 − ; 1 − ; ) 3 D. n = ( 2 − ;1; ) 3
Câu 9. Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( x) , trục hoành, đường thẳng
x = a , x = b . Hỏi khẳng định nào dưới đây là khẳng định đúng? c b b
A. S = − f
(x)dx+ f
(x)dx. B. S = f
(x)dx. a c a c b c b C. S = f
(x)dx+ f
(x)dx . D. S = f
(x)dx+ f
(x)dx. a c a c II. THÔNG HỂU
Câu 10. Giải bất phương trình log 3x − 2 log
6 − 5x được tập nghiệm là ( ; a b) Hãy tính tổng 2 ( ) 2 ( )
S = a + b 8 28 11 26 A. S = B. S = C. S = D. S = 5 15 5 5 2 −x 2 −x
Câu 11. Cho hai hàm số F ( x) = ( x + ax + b)e và f ( x) = (−x + 3x + 6)e . Tìm a và b để F ( x)
là một nguyên hàm của hàm số f ( x). A. a = 1 − ,b = 7 .
B. a = 1,b = 7
C. a = 1,b = 7 − . D. a = 1 − ,b = 7 − . 2 2
Câu 12. Gọi z , z z − z + = z + z 1
2 là hai nghiệm phức của phương trình 2 3 2 0. Tính 1 2 8 2 4 11 A. B. C. D. − 3 3 3 9 Trang 2
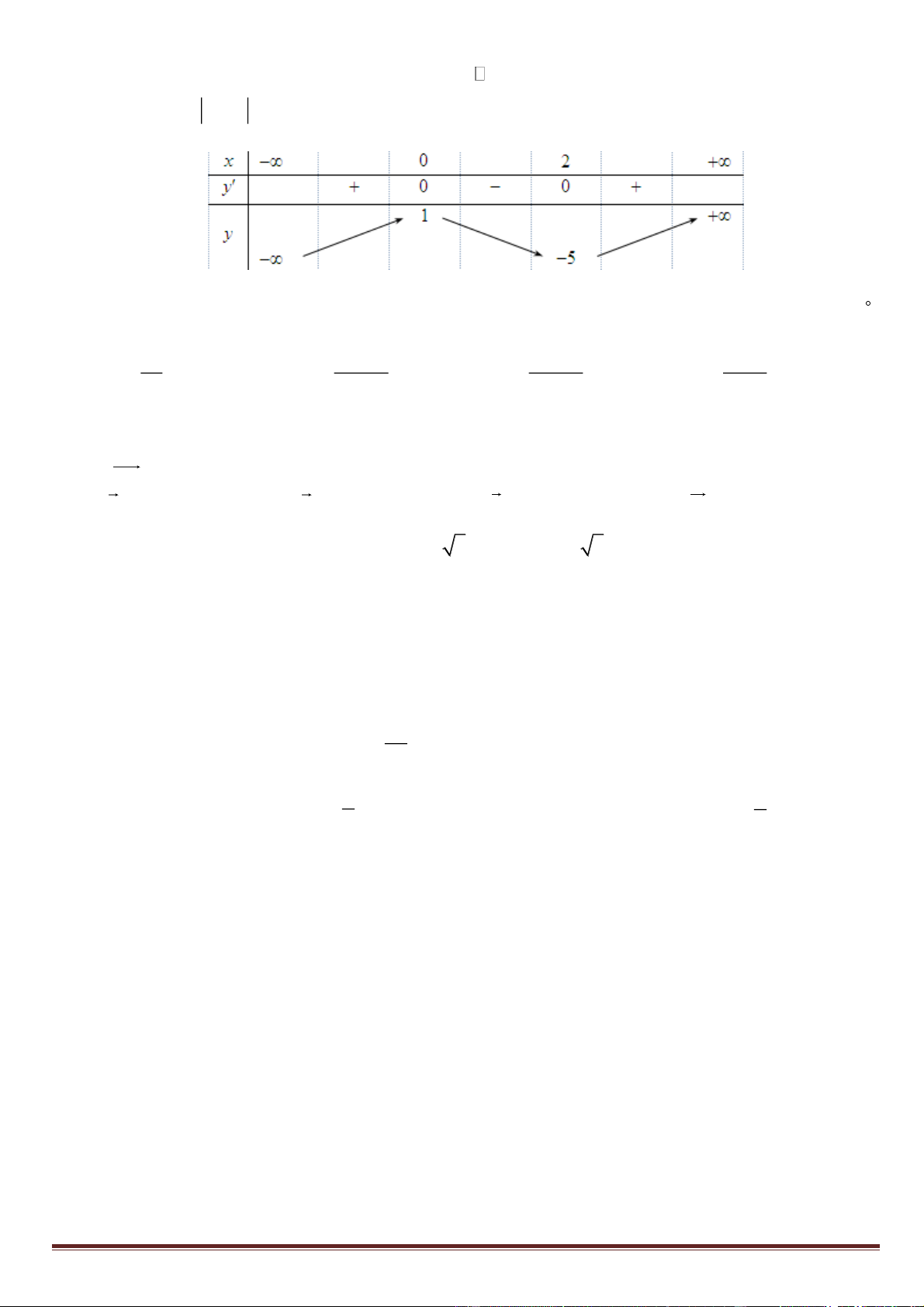
Câu 13. Cho hàm số y = f ( x) xác định, liên tục trên và có bảng biến thên như hình bên. Tìm số nghiệm
của phương trình 3 f ( x) − 7 = 0 . A. 0 . B. 4 . C. 5 . D. 6 .
Câu 14. Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a , các mặt bên tạo với đáy một góc 60 .
Tính diện tích S của mặt cầu ngoại tiếp hình chóp. 2 a 2 25 a 2 32 a 2 8 a A. S = B. S = . C. S = . D. S = . 12 3 3 3
Câu 15. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng (P) : 3x − 2y + 2z − 5 = 0 và
(Q):4x +5y − z +1= 0. Các điểm ,
A B phân biệt cùng thuộc giao tuyến của hai mặt phẳng (P) và (Q) .
Khi đó AB cùng phương với véctơ nào sau đây? A. v = ( 8 − ;11; 2 − 3) B. k = (4;5;− ) 1 C. u = (8; 11 − ; 23 − ) D. w = (3; 2 − ;2) x+
Câu 16. Tìm tập nghiệm S của bất phương trình ( − ) 1 3 1 4 − 2 3
A. S = (− ;1 B. S = (− ) ;1
C. S = 1;+)
D. S = (1;+)
Câu 17. Phần ảo của số phức z = ( − i)2 1 2 +1 A. 4 B. 4 − i C. 3 − D. 4 −
Câu 18. Tìm giá trị lớn nhất của hàm số y = f ( x) 3 2
= x − 2x + x − 2 trên đoạn 0;2. 50 A. max y = 2 − B. max y = −
C. max y = 1
D. max y = 0 0;2 0;2 27 0 ;2 0;2 4 a a
Câu 19. Biết I = x ln
(2x + )1dx = ln3−c, trong đó a, b, c là các số nguyên dương và là phân số tối b b 0
giản. Tính S = a + b + c .
A. S = 72 .
B. S = 68
C. S = 60 .
D. S = 17 .
Câu 20. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x + 2y + z + 6 = 0. Tìm tọa độ điểm
M thuộc tia Oz sao cho khoảng cách từ M đến (P) bằng 3 .
A. M (0;0;3) B. M (0;0; ) 3 , M (0;0; 1 − 5) C. M (0;0; 1 − 5) D. M (0;0;2 ) 1
Câu 21. Trong không gian với hệ trục tọa độ Oxyz , cho điểm I (2; 2
− ;0). Viết phương trình mặt cầu tâm I
bán kính R = 4 2 2 2 2
A. ( x + ) + ( y − ) 2 2 2 + z =16
B. ( x − ) + ( y + ) 2 2 2 + z =16 2 2 2 2
C. ( x − ) + ( y + ) 2 2 2 + z = 4
D. ( x + ) + ( y − ) 2 2 2 + z = 4
Câu 22. Tìm tập nghiệm S của phương trình log x 5 − x = 1 6 ( )
A. S = 2; 3 .
B. S = 2;3;− 1 .
C. S = 2;− 6 .
D. S = 2;3; 4 . Trang 3 9 0 9 Câu 23. Giả sử f
(x)dx = 37 và g
(x)dx =16. Khi đó, I = 2 f
(x)+3g(x)dx bằng: 0 9 0
A. I = 26 .
B. I = 58 .
C. I = 143 .
D. I = 122.
Câu 24. Cho hình bát diện đều cạnh a . Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Tính S . A. 2
S = 4 3a . B. 2
S = 2 3a . C. 2 S = 3a . D. 2 S = 8a .
Câu 25. Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng ( ) : x − y + 2z = l và đường thẳng x y z −1 : = =
. Góc giữa đường thẳng và mặt phẳng ( ) bằng 1 2 1 − A. 120 B. 30 C. 60 D. 150
Câu 26. Tính đạo hàm của hàm số y = log ( 2x + 2 . 5 ) A. . B. . 2x ln 5 2x y ' = ( y ' = 2 x + 2) ( 2x +2)ln5 C. . D. . 1 2x y ' = ( y ' = 2 x + 2)ln 5 ( 2x +2)
Câu 27. Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng 25o . Tìm 2 góc còn lại? A. 75o ; 80o. B. 60o ; 95o. C. 60o ; 90o. D. 65o ; 90o.
Câu 28. Cho cấp số nhân (u với u = 3; q= − 2 . Số 19 là số hạng thứ mấy của (u ? n ) n ) 1
A. Số hạng thứ 7.
B. Không là số hạng của cấp số đã cho.
C. Số hạng thứ 5.
D. Số hạng thứ 6. 45 1
Câu 29. Số hạng không chứa x trong khai triển x − là: 2 x A. 5 C − C C C − 45 . B. 30 45 . C. 15 45 . D. 15 45 . III. VẬN DỤNG
Câu 30. Trong không gian Oxyz, cho bốn điểm ( A 3;0; ) 0 , B(0;2; ) 0 , C(0;0; ) 6 và D(1;1; ) 1 . Gọi D là
đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm , A ,
B C đến D là lớn nhất, hỏi D đi qua
điểm nào trong các điểm dưới đây? A. M (5;7; ) 3 . B. M (3;4; ) 3 . C. M (7;13; ) 5 . D. M (- 1;- 2; ) 1 .
Câu 31. Cho hàm số 3 2
y = x − 3x + 6x + 5. Tiếp tuyến của đồ thị hàm số có hệ số góc nhỏ nhất có phương trình là
A. y = 3x + 9.
B. y = 3x + 3 .
C. y = 3x +12.
D. y = 3x + 6 .
Câu 32. Cho số phức z thoả mãn z − 3 + 4i = 2, w = 2z +1− .
i Khi đó w có giá trị lớn nhất là: A. 4 + 130 B. 2 + 130 C. 4 + 74 D. 16 + 74
Câu 33. Một chất điểm đang cuyển động với vận tốc v = 15m / s 0
thì tăng vận tốc với gia tốc a (t ) 2 = t + t ( 2
4 m / s ) . Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng vận tốc.
A. 68,25 m.
B. 70,25 m.
C. 69,75 m.
D. 67,25 m. Trang 4
Câu 34. Cho hình lăng trụ AB .
C A' B 'C ' có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của A' lên
mặt phẳng ( ABC ) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường thẳng AA' và BC a 3 bằng
. Thể tích V của khối lăng trụ AB .
C A' B 'C ' tính theo a là: 4 3 2a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 24 12 1 1 1 1 465
Câu 35. Tìm n biết + + + ...+ =
luôn đúng với mọi x 0, x 1. log x log x log x log x log x 2 2 3 n 2 2 2 2
A. n .
B. n = 30 . C. n = 31 −
D. n = 31. 1 2
Câu 36. Cho hàm số f ( x) liên tục trên và thỏa mãn f
(x)dx = 9. Tính tích phân f
(1−3x)+9 dx 5 − 0 A. 27. B. 75. C. 15. D. 21. 1 2
Câu 37. Tìm tất cả các giá trị của tham số m để hàm số 3 y = x + (m − ) 2
1 x + (2m − 3) x − đồng biến 3 3 trên (1;+)
A. m 2 .
B. m 2 .
C. m 1.
D. m 1
Câu 38. Cho lăng trụ tam giác đều AB . C A B C
có cạnh đáy bằng a và AB ⊥ BC . Khi đó thể tích của khối
lăng trụ trên sẽ là: 3 6a 3 7a 3 6a A. V = . B. V = . C. 3 V = 6a . D. V = . 8 8 4 x
Câu 39. Số nghiệm thực của phương trình 5 x + − 2017 = 0 2 x − 2 A. 4 B. 5 C. 2 D. 3
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x + y − 2z + 3 = 0 và điểm I (1;1;0) .
Phương trình mặt cầu tâm I và tiếp xúc với (P) là: 2 2 2 2 2 5
A. ( x − ) + ( y − ) 2 25 1 1 + z = . B. ( x − ) 1 + ( y − ) 1 + z = . 6 6 2 2 2 2
C. ( x + ) + ( y + ) 2 25 1 1 + z = .
D. ( x − ) + ( y − ) 2 5 1 1 + z = . 6 6
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho hai điểm M ( 2 − ; 2 − ; ) 1 , A(1;2;− ) 3 và đường thẳng x +1 y − 5 z d : = =
. Tìm một vectơ chỉ phương u của đường thẳng đi qua M , vuông góc với đường 2 2 1 −
thẳng d đồng thời cách điểm A một khoảng bé nhất.
A. u = (2;2;− ) 1 .
B. u = (1;7;− ) 1 .
C. u = (1;0;2) . D. u = (3;4; 4 − ) .
Câu 42. Cho đường tròn 2 2
(C) : x + y + 4x − 6 y + 5 = 0 . Đường thẳng d đi qua (
A 3; 2) và cắt (C) theo một
dây cung ngắn nhất có phương trình là
A. x + y −1 = 0 .
B. x − y −1 = 0.
C. x − y +1 = 0 .
D. 2x − y + 2 = 0 .
Câu 43. Cho hình trụ có diện tích toàn phần là 4 và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông.
Tính thể tích khối trụ. 4 6 4 6 6 A. . B. . C. . D. . 9 9 9 12 Trang 5
Câu 44. Đề thi trắc nghiệm môn Toán gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời trong đó chỉ có một
phương án trả lời đúng. Mỗi câu trả lời đúng được , điểm. Một học sinh không học bài nên mỗi câu trả lời
đều chọn ngẫu nhiên một phương án. Xác suất để học sinh đó được đúng 5 điểm là: 25 25 25 1 3 C . 50 25 25 4 4 1 3 A. . B. 25 C . . 50 50 4 4 4 25 25 3 25 25 . 1 3 4 4 C. . . D. . 4 4 50 4 b 16
Câu 45. Cho a 0, b 0 và a khác 1 thỏa mãn log b = ; log a = . Tính tổng a + . b a 2 4 b A. 12 B. 10 C. 18 D. 16 2 3
Câu 46. Cho hàm số f ( x) có đạo hàm f '( x) = ( x + ) 1 ( x − )
1 (2 − x).. Hàm số f ( x) đồng biến trên
khoảng nào dưới đây? A. (1;2). B. (2;+). C. ( 1 − ; ) 1 . D. (− ; − ) 1 .
Câu 47. Cho hàm số y = f ( x) xác định trên M và có đạo hàm f ( x) = ( x + )( x − )2 ' 2 1 . Khẳng định nào
sau đây là khẳng định đúng?
A. Hàm số y = f ( x) đồng biến trên ( 2
− ;+). B. Hàm số y = f (x) đạt cực đại tại x = 2 − .
C. Hàm số y = f ( x) đạt cực đại tiểu x = 1.
D. Hàm số y = f ( x) nghịch biến trên ( 2 − ; ) 1 .
Câu 48. Cho số phức z thỏa mãn: 2
(3 + 2i)z + (2 − i) = 4 + i . Hiệu phần thực và phần ảo của số phức z là: A. 3 B. 2 C. 1 D. 0 IV. VẬN DỤNG CAO
Câu 49. Cho hàm số y = f (x) có đạo hàm trên R . Đường cong trong hình vẽ bên là đồ thị của hàm số y = f (
x), ( y = f (x) liên tục trên R). Xét hàm số 2
g(x) = f (x − 2) . Mệnh đề nào dưới đây sai?
A. Hàm số g(x) nghịch biến trên (− ; 2 − ).
B. Hàm số g(x) đồng biến trên (2;+) .
C. Hàm số g(x) nghịch biến trên ( 1 − ;0).
D. Hàm số g(x) nghịch biến trên (0;2) .
Câu 50. Bất phương trình 3 2
2x + 3x + 6x +16 − 4 − x 2 3 có tập nghiệm là ;
a b . Hỏi tổng a + b có giá trị là bao nhiêu? A. 3 B. 2 − C. 4 D. 5
------------- HẾT ------------- Trang 6 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B C D C B B A C D A B C D B A D B C C D D C D B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D D A A B B C A A C A B A A D C B C B A B A D A D Câu 1. Lời giải Vì u u 2(n 1) 2n 2 u n 1 + − = + − = n
nên n là CSC với công bội là 2. Câu 2. Lời giải
Nhìn đồ thị ta thấy hàm số đạt cực đại tại x = 0 . Do đó chọn B. Câu 3. Lời giải 2 x 3 3 x − 2 0 6 6 log 3x − 2 log
6 − 5x 6 − 5x 0
x 1 x . 2 ( ) 2 ( ) 5 5
3x − 2 6 − 5x x 1 6 11
a = 1;b = S = . 5 5 Câu 4. Lời giải 2 −x
Ta có F( x) = (−x + (2 − a) x + a − b)e = f ( x) nên 2 − a = 3 và a − b = 6 Vậy a = 1
− và b = −7 . Câu 5. Lời giải 2 1 i 23
3z − z + 2 = 0 z = 6 2 2 2 2 + − 2 2 1 i 23 1 i 23 1 23 4 z + z = + = 2 + = 1 2 6 6 6 6 3 Câu 6. Lời giải Trang 7 f (x) 7 = ( ) 1 7 3
Ta có 3 f ( x) − 7 = 0 f ( x) = 3 f (x) 7 = − ( 2) 3
Dựa vào bảng biến thiên thì có 1 nghiệm; có 3 nghiệm, vậy phương trình ban đầu có 4 nghiệm. Câu 7. Lời giải
Áp dụng công thức tính đạo hàm hàm số logarit ( u = a ) u' log ' . u ln a ( 2x +2)' 2x
Cách giải: Ta có: y ' = ( = 2 x + 2)ln5 ( 2 x + 2)ln5
Chú ý khi giải: HS thường quên tính u ' dẫn đến chọn nhầm đáp án A. Câu 8. Lời giải
Phương trình mặt phẳng ( x y z
ABC ) là + + = 1 2x + 3y + z − 6 = 0 . 3 2 6
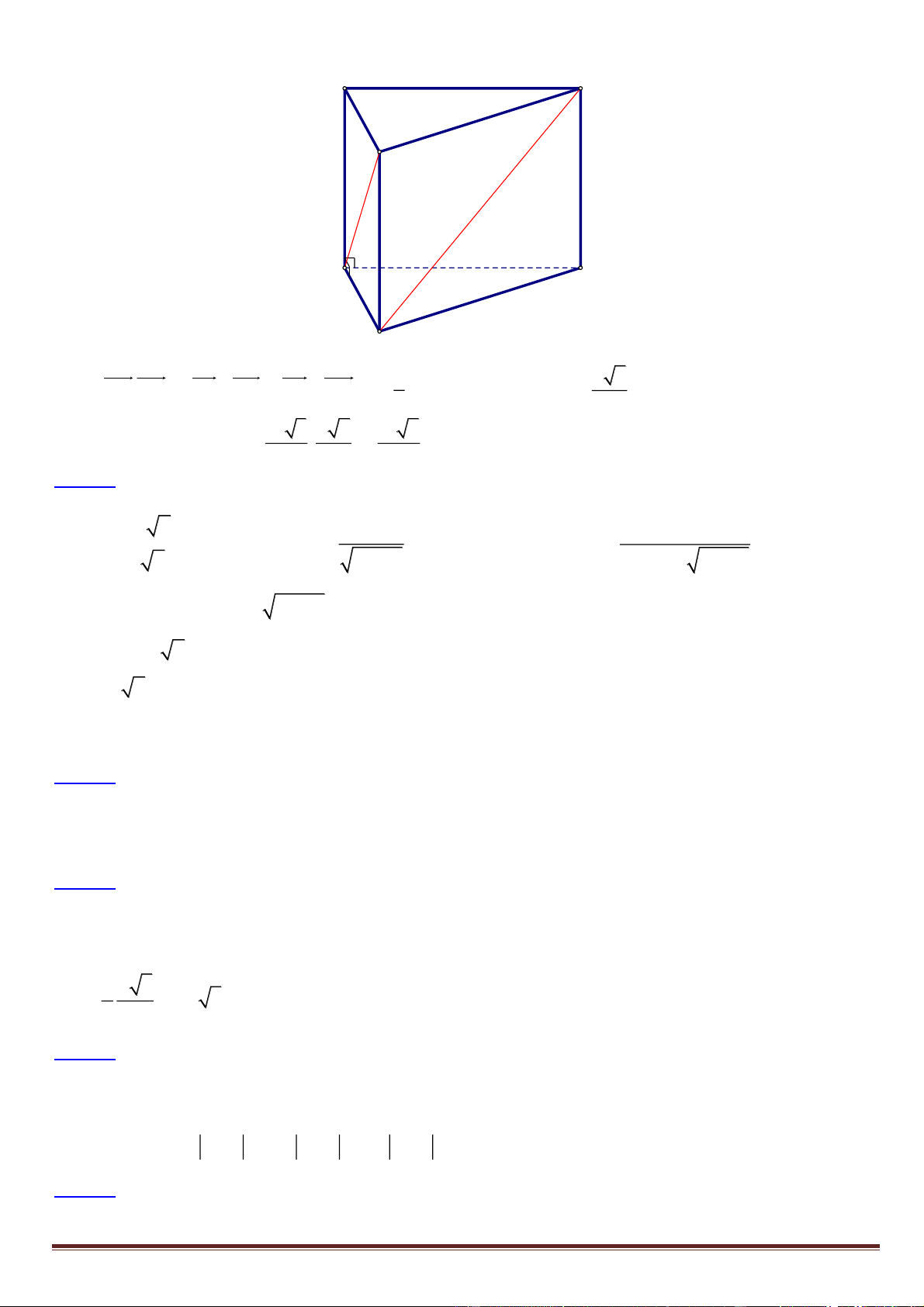
Dễ thấy D ( ABC). Gọi H, K, I lần lượt là hình chiếu của , A , B C trên Δ .
Do Δ là đường thẳng đi qua D nên AH A , D BK B , D CI CD .
Vậy để khoảng cách từ các điểm , A ,
B C đến Δ là lớn nhất thì Δ là đường thẳng đi qua D và vuông góc với x =1+ 2t (
ABC ). Vậy phương trình đường thẳng Δ là y = 1+ 3t (t ) . Kiểm tra ta thấy điểm M (5;7; ) 3 . z =1+t Câu 9. Lời giải
Dựa vào hình dạng đồ thì, ta thấy đây là đồ thị của hàm số bậc 3 với hệ số a 0 . Nên loại A, B.
Đồ thị hàm số đạt cực tiểu tại x = 0 và x 0 . 1 2 + Xét 3 2
y = −x − 3x +1. x = 0 Ta có 2 1 y = 3
− x − 6x = 0 . Loại x = 2 − 2 D. + Xét 3 2
y = −x + 3x +1. x = 0 Ta có 2 1 = − + = y 3x 6x 0 . x = 2 2 Câu 10. Lời giải Hàm số có nghĩa 2
x − 2x 0 x 0 hoặc x 2
Vậy tập xác định D của hàm số là D = (− ; 0)(2;+) Câu 11. Trang 8 Lời giải 1 4 3
Thể tích của khối nón là: 2 V = r h = . 3 3 Câu 12. Lời giải
Dựng OH ⊥ CD lại có CD ⊥ SO CD ⊥ (SHO) SHO = 60 . AD Ta có: OH =
= a SO = a tan 60 = a 3 2 SD = SO + OD = a + (a )2 2 2 2 3 2 = a 5 2 2 2 SA 5a 2 25 a
ÁP dung công thức giải nhanh ta có: ( R = = S = R = C ) (C) 4 . 2SO 2a 3 3 Câu 13. Lời giải
Ta có: ( P) ⊥ n( = − ⊥ = − P)
(3; 2;2), (Q) n(Q) (4;5; ) 1 . AB
(P) AB ⊥ n (P) Do
nên đường thẳng AB có véctơ chỉ phương là: AB
(Q) AB ⊥ n (Q) u = n( = − −
Q) , n( P) (8; 11; 23)
Do AB cũng là một véc tơ chỉ phương của AB nên AB//u = (8; 1 − 1; 2 − 3) . Câu 14. Lời giải Gọi M ( ;
a b) là điểm thuộc đồ thị hàm số có tiếp tuyến thỏa mãn đề bài. 2 2 2
Ta có y = 3x − 6x + 6 y(a) = 3a − 6a + 6 = 3(a − ) 1
+ 3 3 min y(a) = 3 a =1 Suy ra y ( )
1 = 9 PTTT tại M (1;9) là y = 3( x − )
1 + 9y = 3x + 6 Câu 15. Trang 9 Lời giải x 1 + x 1 + 2 Ta có ( 3 − ) 1 4 − 2 3 ( 3 − ) 1 ( 3 − ) 1
x +1 2 x 1
Vậy tập nghiệm s của bất phương trình là S = (− ) ;1 Câu 16. Lời giải w −1 + i x −1+ ( y + ) 1 i
Đặt w = x + yi z = = . 2 2
(x −7) +( y +9)i
z − 3 + 4i = 2
= 2 (x − 7)2 + ( y + 9)2 = 4 (x − 7)2 + ( 9 + )2 =16. 2
=>Tập hợp điểm biểu diễn số phức w là đường tròn tâm I (7; 9
− ) bán kính R = 4.
Khi đó w có giá trị lớn nhất là OI + R = 4 + 130 . Câu 17. Lời giải 2 2
Ta có z = ( − i) + = − i + ( i) 2 1 2 1 2 4 2
= 2 − 4i + 4i = 2 − − 4i Câu 18. Lời giải
Ta có :u + u + u = 180 25 + 25 + d + 25 + 2d = 180 d = 35 1 2 3 .
Vâỵ u = 60; u = 95 2 3 Câu 19. Lời giải
Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng (− ; − )
1 suy ra hàm số cũng đồng biến trên (− ; 2 − ). Câu 20. Lời giải lim y = 2 lim y = − + x→+ x 1 → Ta có
tiệm cận ngang y = 2. ;
tiệm cận đứng x =1. lim y = 2 = + lim y x→− − x 1 → Câu 21. Lời giải f ( x) 2 = 3x − 4x +1 x = 1 f '( x) 2
= 0 3x − 4x +1 = 0 1 x = 3 f ( ) 1 50 0 = 2 − ; f = − ; f ( ) 1 = 2
− ; f (2) = 0 max f (x) = f (2) = 0 3 27 0;2 Câu 22. Lời giải Trang 10 2 du = dx u = ln(2x + ) 2 4 4 2 1 x + x x Đặt 2 1
I = ln(2x + ) 1 − dx 2 dv = xdx x 2 + 0 2x 1 0 v = 2 2 4 x I = ( x + ) 4 2 4 2 4 x 1 1 x x 1 1 ln 2 1 − − + dx = ln 2x +1 −
− x + ln 2x +1 2 + 0 2 4 4 (2x ) ( ) ( ) 1 2 0 4 4 8 0 0 a = 63 63 I = ln 3 − 3 b
= 4 S = a + b + c = 70 4 c = 3 Cách : PP hằng số 2 du = dx + u = ln(2x + ) 2x 1 2 4 4 1 4x −1 2x −1 Đặt I = ln 1 (2x + ) 1 − dx 2 dv = xdx x − ( x + )( x − ) 8 0 4 2 1 2 1 0 4 v = = 2 8 a = − 63 ( 2x ) 63 4 4 63 I = ln 9 = = ln 3 − 3 b
= 4 S = a + b + c = 70. 8 4 0 4 c = 3 Câu 23. Lời giải 3 t
Ta có v (t ) = a
(t)dt = ( 2t + 4t)dt = + 2t +C(m / s) 3 t
Do khi bắt đầu tăng tốc v = 15 v
= 15 C = 15 v t = + 2t +15 0 nên ( t− ) ( ) 3 2 0 3 3 3 3 4 3 t t 2
Khi đó quãng đường đi được S = v (t) 2 3
dt = 15 + + 2t dt = 15 + + t = 69,75m . 3 12 3 0 0 0 Câu 24. Lời giải Trang 11
Gọi D là trung điểm của BC, H là chân đường cao kẻ từ A’ đến , và K là chân đường cao kẻ từ H đến AA’. Dễ 3
thấy khoảng cách từ BC đến AA’ bằng với khoảng cách từ D đến AA’ và bằng d ( H , A A ') . Ta có 2 d ( H ') 2 3 3 , AA = HK = a = a . 3 4 6 Ta có d ( H ') 2 2 3 3 , AA = AD = a =
a . Xét tam giác vuông AHA’ ta có: 3 3 2 3 1 1 1 2 2 = − = 12a − 3a = 1
3a . AH = a . 2 2 A' H HK A' H 3 3 3 V = S A' H = a .
ABC. A' B'C ' A' B'C ' 12 Chọn phương án D. Câu 25. Lời giải 1 1 1 1 Ta có 2 3 + + +...+
= log 2 + log 2 + log 2 +...+ log 2n log log log log x x x x x x x x 2 2 3 2 2 2n = ( 2 3 n = = x ) 465 log 2.2 .2 ...2 465log 2 log 2 x x 2 3 2.2 .2 ...2n n
1+ 2 + 3+...+ n = 465 (n + ) 1 = 465 2 n = 30 2
n + n − 930 = 0 n = 30 n = 31 − Câu 26. Lời giải 2 2 2 2 f
(1−3x)+9 dx = f
(1−3x)dx + 9dx = f
(1−3x)dx +18. 0 0 0 0 2 5 − 1 1 1 1 1 1
Đặt 1− 3x = t f
(1−3x)dx = − f (t)dt = f (t)dt = f
(x)dx = .9 = 3 3 3 3 3 0 1 5 − 5 − 2 f
(1−3x)+9 dx = 21 . 0 Câu 27. Lời giải • Ta có 2
y = x + 2(m − ) 1 x + 2m − 3 −x + x +
• Hàm số đồng biến trên (1;+) khi và chỉ khi y x ( +) 2 2 3 0, 1; 2m . x + 1 2 2 −x + 2x + 3 − x +1
• Đặt g ( x) = g(x) ( ) = = 1 − 0; x (1;+) x +1 (x + )2 1 Trang 12
• Do đó max g ( x) = g ( )
1 = 2 2m 2 m 1. (1;+) Câu 28. Lời giải
Vì M thuộc tia Oz nên M (0;0; z với z 0 . M ) M z + 6 z = 3 M M
Vì khoảng cách từ M đến mặt phẳng (P) bằng 3 nên ta có = 3 . 3 z = 15 − M Vì z 0 M 0;0;3 M nên ( ). Câu 29. Lời giải n 1 − n 1 − Ta có n 1 u u .q − = 192 = 3. 2 − 2 −
= 64 n −1 = 6 n = 7 . n 1 ( ) ( ) Câu 30. Lời giải Véc tơ pháp tuyế 1
n của mặt phẳng (P) là ( n = − − = − − . P) ( 2;1; 3) .(4; 2;6) 2 Câu 31. Lời giải 2 2
Ta có (S ) ( x − ) + ( y + ) 2 2 : 2 2 + z = 4 =16. Câu 32. Lời giải Từ đồ thị ta có 3 f '( )
x = x − 3x − 2 . Do đó 2 2 3 2 g '( )
x = 2xf '(x − 2) = 2 (
x (x − 2) − 3(x − 2) − 2) x = 2 − x = 1 −
g'(x) = 0 x = 0 x =1 x = 2
Ta có g'(x) 0, x ( 1 − ;0).
Vậy g(x) đồng biến trên ( 1 − ;0) Câu 33. Lời giải
Phương pháp: Cách giải phương trình log f (x) = b f (x) b = a
a f x a (0 1; ( ) 0)
Cách giải: Điều kiện: x(5 − x) 0 0 x 5 x = log x
(5 − x) = 1 x (5− x) 2 2
= 6 x − 5x + 6 = 0 tm 6 ( ) x = 3 Vậy S = 2; 3 . Câu 34. Lời giải Trang 13 A' C' B' x A C B 1 a
Ta có AB .BC = ( AB + BB).(BC + CC) 2 2 = − a + x = 2 0 x = A A = . 2 2 2 3
Vậy thể tích lăng trụ là a 3 a 2 a 6 V = . = . 4 2 8 Câu 35. Lời giải x − 2 x 2 ĐK: . Ta xét f ( x) 5 = x +
− 2017 . Có f (x) 4 = 5x − . x 2 2 x − 2
( 2x −2) 2x −2 f ( x) 4 = x ( 2 x − ) 2 0 5 2 x − 2 − 2 = 0
Xét với x − 2 thì f (x) 0 f (x) = 0 không có nghiệm trong khoảng này. Với x 2 thì ( )
* có vế trai là đồng biến nên chỉ có tối đa một nghiệm tức là f ( x) chỉ có tối đa nghệm.
Mà f (1,45) 0; f ( )
3 0; f (10) 0 nên f ( x) có nghiệm thuộc (1,45; )
3 ;(3;10) từ đó f ( x) = 0 có đúng nghiệm. Câu 36. Lời giải 9 9 9 9 0
Ta có: I = 2 f
(x)+3g(x)dx = 2 f
(x)dx+ 3g
(x)dx = 2 f
(x)dx−3 g
(x)dx = 26 . 0 0 0 0 9 Câu 37. Lời giải
Số mặt của bát diện đều là 8; các mặt của bát diện đều cạnh a là các tam giác đều cạnh a . 1 a 3 2 S = 8
a = 2 3a . 2 2 Câu 38. Lời giải
Dựa vào hình vẽ ta thấy: x( ;
a c) f ( x) 0 và x ( ;
c b) f ( x) 0 . b c b c b Do đó, ta có: S = f
(x) dx = f
(x) dx+ f
(x) dx = − f
(x)dx+ f
(x)dx. a a c a c Câu 39. Lời giải Trang 14
Mặt cầu tiếp xúc mặt phẳng nên bán kính mặt cầu là: r = d ( I ( P)) 5 , = . 6 2 2
Vậy phương trình mặt cầu là: ( x − ) + ( y − ) 2 25 1 1 + z = . 6 Câu 40. Lời giải
Tập xác định: D = [−2,4] Xét hàm số f ( x) 3 2
= 2x + 3x + 6x +16 − 4 − x 2 x + x + f '(x) 6 6 6 1 = + 0 3 2
2x + 3x + 6x +16 2 4 − x
Suy ra hàm số f đồng biến trên tập xác định.
Ta nhận thấy phương trình 3 2
2x + 3x + 6x +16 − 4 − x = 2 3 có một nghiệm x = 1.
Suy ra trong đoạn [1,4] thì bất phương trình đã cho luôn đúng . Do đó tổng a + b = 5. Câu 41. Lời giải
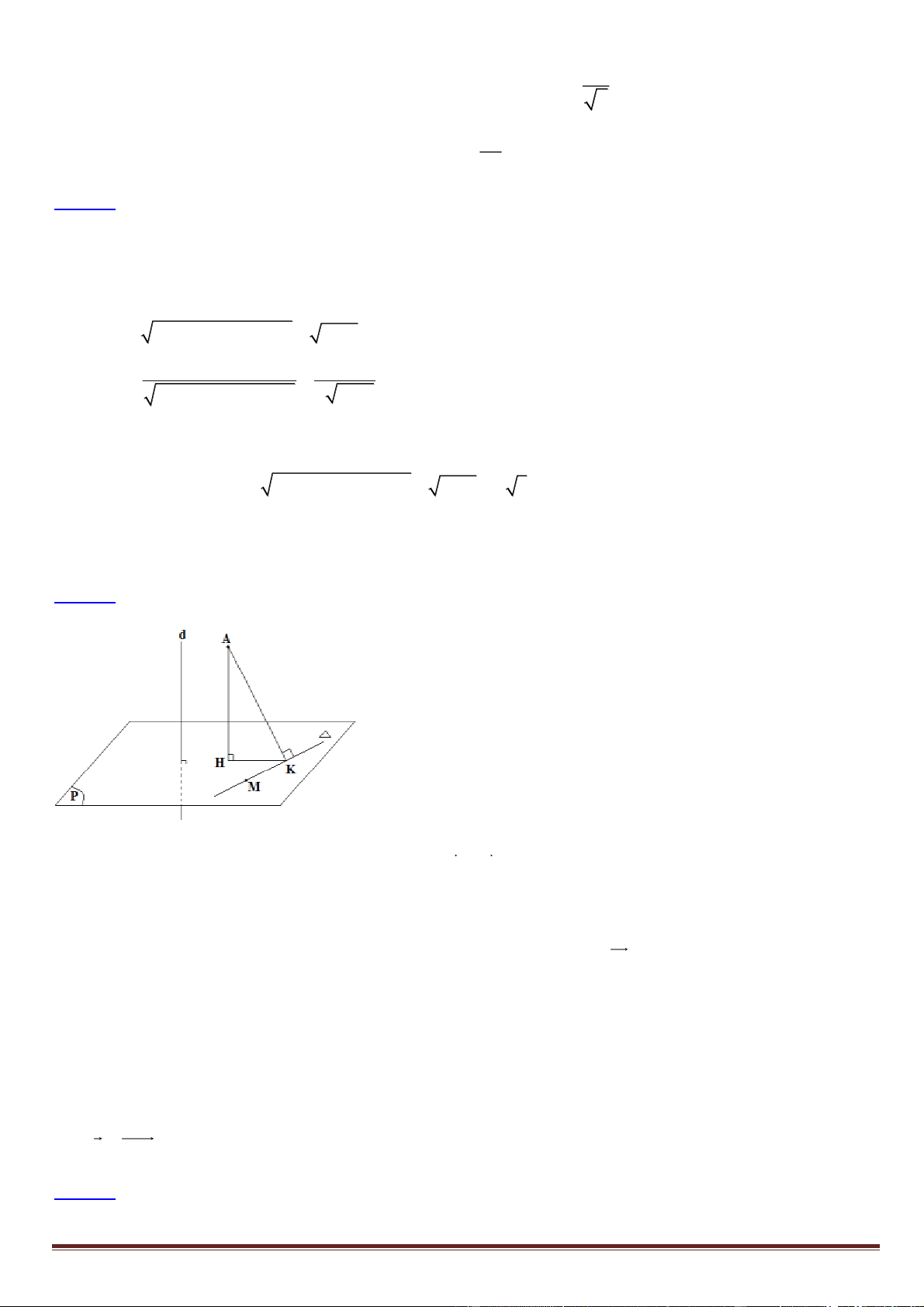
Gọi (P) là mp đi qua M và vuông góc với d , khi đó (P) chứa .
Mp ( P) qua M ( 2 − ; 2 − ; )
1 và có vectơ pháp tuyến n = u = (2; 2; − ) 1 nên có phương trình: P d
(P):2x +2y − z +9 = 0.
Gọi H, K lần lượt là hình chiếu của A lên (P) và . Khi đó: AK AH :const nên AK min
khi K H . Đường thẳng AH đi qua A(1, 2, − )
3 và có vectơ chỉ phương u = (2; 2; − ) 1 nên d x = 1+ 2t
AH có phương trình tham số: y = 2 + 2t . z = −3−t
H AH H (1+ 2t;2 + 2t; 3 − −t) .
H (P) 2(1+ 2t ) + 2(2 + 2t ) − ( 3
− −t)+9 = 0 t = 2 − H ( 3 − ; 2 − ;− ) 1 .
Vậy u = HM = (1;0;2) . Câu 42. Lời giải Trang 15 N H A M I . f ( x y) 2 2 ;
= x + y − 4x − 6y + 5.
f (3; 2) = 9 + 4 −12 −12 + 5 = 6 − 0.
Vậy A(3; 2) ở trong (C).
Dây cung MN ngắn nhất IH lớn nhất H A MN có vectơ pháp tuyến là IA = (1; − ) 1 . Vậy d có
phương trình: 1(x −3) −1(y − 2) = 0 x − y −1= 0 . Câu 43. Lời giải
Gọi bán kính đáy là R độ dài đường sinh là: 2R
Diện tích toàn phần của hình trụ là: 2 2 2
S = 2 R + 2 .2
R R = 6 R = 4 R = tp 6 3 Thể tích khối trụ là: 2 2 4 6 V
R .2R 2 = = = . 6 9 Câu 44. Lời giải
Học sinh đó làm đúng được 5 điểm khi làm được đúng 5 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai. 1 3
Xác suất để học sinh là đúng một câu bất kỳ là , làm sai một câu là
. Do đó xác suất để học sinh đó làm 4 4 25 1
đúng 5 câu bất kỳ trong số 50 câu là 25 C . 50 . 4 25 3
Xác suất để hoạc sinh đó làm sai 5 câu còn lại là . 4 25 25 1 3
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: 25 C . 50 . 4 4 Câu 45. Lời giải 16 16 b • log = = 2 b a a b = a = 2 thay vào log b = ta được: 16 2. b a 4 Câu 46. Lời giải Ta có ( n ) = (1; 1 − ;2),u = (1; 2; − ) 1 1− 2 − 2 1 Suy ra sin (( ), ) =
= (( ),) = 30 6 6 2 Câu 47. Lời giải
Ta có bảng xét dấu của y . Trang 16
Từ bảng trên thì hàm số f ( x) đồng biến trên (1;2). Câu 48. Lời giải 45 45 1 − k k −k − k − k k Ta có: x − = ( 2 x − x
có số hạng tổng quát là: 45 C x ( 2 −x ) 45 3 = C x . 1 − . 45 45 ( ) 2 ) x
Số hạng không chứa x tương ứng với 45 − 3k = 0 k = 15. Vậy số hạng không chứa x là: 15 C − . 45 Câu 49. Lời giải
Ta lập bảng xét dấu của y '
Từ bảng xét dấu trên thì hàm số đồng biến trên ( 2 − ;+). Câu 50. Lời giải + i Ta có 2
(3 + 2i)z + (2 − i) = 4 + i
+ i z = + i − ( −i)2 (3 2 ) 4 2 (3+ 2i)z =1+ 1 5 5i z = z =1+ i 3 + 2i
phần thực của số phức z là a = 1, phần ảo của số phức z là b = 1.
Vậy a − b = 0. Trang 17