Đề mẫu kiểm tra học kỳ 1 môn Toán 12 năm học 2018 – 2019

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề mẫu thi học kỳ 1 môn Giới Toán 12 năm học 2018 – 2019 .Mời bạn đọc đón xem.

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

30 trang 8 tháng trước

Tác giả:

Profile Lan Tường
1
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12
NĂM HỌC: 2018-2019
ĐỀ 1
PHẦN I: TRẮC NGHIỆM (6 điểm)Thời gian 60 phút-30 câu.
Câu 1: Cho hm s
42
21y x x
. Mnh đ no dưi đây đng?
A. Hm s đồng bin trên khong
;1
. B. Hm s đồng bin trên khong
0;1
.
C. Hm s nghch bin trên khong
1;1
. D. Hm s đồng bin trên khong
1;2
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 2: Cho hm s
32
31y x mx x
vi
m
l tham s. Có bao nhiêu giá tr nguyên của
m
để hm s
đồng bin trên khong
; 
?
A. 6. B. Vô s. C. 7. D. 5.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 3: Hm s
có giá tr cực đại bằng bao nhiêu?
A.
0
. B.
2
. C.
5
. D.
1
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 4: Cho hm s
y f x
xác đnh v có đạo hm liên tục trên khong
;ab
. Bit đồ th của hm s
y f x
trên khong
;ab
cắt trục honh tại hai điểm có honh độ lần lượt l
1
x
,
2
x
vtip xc vi
trục honh tại hai điểm có honh độ lần lượt l
3
x
,
4
x
như hình vẽ dưi đây.
Hỏi trong khong
;ab
, hm s
y f x
có bao nhiêu điểm cực tr?
A. 4. B. 7. C. 5. D. 2.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 5: Giá tr nhỏ nhất của hm s
1
2
x
y
x
trên đoạn
1;1
bằng
A.
3
. B.
0
. C.
2
. D. Không tồn tại.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 6: Vi giá tr no của tham s m thì giá tr ln nhất của hm s
2
cos 3cosf x x x m
trên đoạn
0;8
bằng 2?
A.
4m
. B.
4m 
. C.
1
4
m 
. D.
2m 
.
……………………………………………………………………………………………………….…………
()y f x
O
1
x
2
x
3
x
4
x
a
b
y
x
2
Câu 7: Đường thẳng no dưi đây l tim cận ngang của đồ th hm s
13
2
x
y
x
?
A.
3
2
y 
. B.
1y
. C.
3y 
. D.
1
2
y
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 8: Cho hm s
y f x
xác đnh v liên tục trên
\1
thỏa
1
lim 3
x
fx
v
1
lim
x
fx
.
Khẳng đnh no sau đây đng?
A. Đồ th hm s đã cho có tim cận ngang v không có tim cận đứng.
B. Đồ th hm s đã cho có tim cận ngang l đường thẳng
3y
.
C. Đồ th hm s đã cho có tim cận đứng l đường thẳng
1x
.
D. Đồ th hm s đã cho không có tim cận.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 9: Đường cong ở hình bên l đồ th của một trong bn hm s dưi đây.
Hm s đó l hm s no?
A.
3
4y x x
. B.
32
31y x x
. C.
42
32y x x
. D.
3
1yx
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 10: Cho hm s
y f x
có bng bin thiên như hình bên.
Mnh đ no dưi đây đng?
A. Hm s có một điểm cực tr. B. Đồ th hm s không có tim cận đứng.
C. Đồ th hm s không có tim cận ngang. D. Hm s có giá tr nhỏ nhất.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 11: H s góc tip tuyn của đồ th hm s
lnyx
tại điểm có honh độ
1
e
bằng
A.
e
. B.
0
. C.
1
. D.
1
e
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 12: Cho hm s
42
–1y x x m
(
m
l tham s) thỏa mãn đồ th của nó cắt trục honh tại đng 2
điểm
,A
B
sao cho
2AB
. Mnh đ no sau đây đng?
A.
0m
. B.
4m
. C.
02m
. D.
24m
.
+
–
x
y’
y
+
2
–5
+
+
6
5
+
y
x
t
1
x
=
x
3
3
∙
x
2
+ 1
O
3
Câu 13: Hm s no sau đây l đạo hm của hm s
21x
ye
?
A.
2
2.
x
ee
. B.
2
4
x
e
. C.
21
ln 2
x
e
. D.
21
2
ln10
x
e
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 14: Tập xác đnh của hm s
2
2
16 4yx

l
A.
2;2
. B.
; 2 2; 
. C.
; 
. D.
\ 2;2
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 15: Hm s no trong các hm s dưi đây có đồ th l hình vẽ bên?
A.
3
logyx
. B.
1
3
logyx
.
C.
3
x
y
. D.
1
3
x
y



.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 16: Cho
a
v
b
l hai s thực dương. Mnh đ no dưi đây đng?
A.
log log .loga b a b
. B.
log log logab a b
.
C.
log log loga b a b
. D.
log log .logab a b
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 17: Cho
log 2
a
b
, giá tr biểu thức
4
82
log
a
ba
bằng
A.
9
2
. B.
9
. C.
2
. D.
8
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 18: Cho
a
v
b
l hai s thực dương thỏa mãn
22
1
33
33
3
1a b a b ab



. Giá tr ln nhất của
biểu thức
ab
bằng
A.
1
2
. B.
1
. C.
2
. D.
1
4
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
y
1
O
x
4
Câu 19: Cho phương trình
2
22
log 2 log 3 5 0x m x m
. Vi giá tr của tham s thực
m
thì phương trình
có 2 nghim phân bit
1
,x
2
x
thỏa mãn
12
.8xx
?
A.
3
2
m
. B.
3m
. C.
13
3
m
. D.
4m
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 20: Sự tăng trưởng của một loại vi khuẩn tuân theo công thức
.
rt
S A e
, trong đó
A
l s lượng vi
khuẩn ban đầu,
r
l tỉ l tăng trưởng,
t
l thời gian tăng trưởng. Bit rằng s lượng vi khuẩn ban đầu l
100 con v sau 5 giờ có 500 con. Hỏi sau 2 giờ thì s lượng vi khuẩn gần vi kt qu no sau đây nhất?
A. 190 con. B. 200 con. C. 195 con. D. 205 con.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 21: Trong các khi đa din sau đây, khi no có tâm đi xứng?
A. Khi tứ din đu. B. Khi lăng trụ tam giác đu.
C. Khi chóp tứ giác đu. D. Khi hộp.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 22: Cho hình chóp
.S ABC
có
SA
vuông góc vi mặt phẳng
ABC
v
SA a
. Tam giác
ABC
vuông
tại
B
v
AB a
. Khong cách từ
A
đn mặt phẳng
SBC
bằng
A.
3
3
a
. B.
6
3
a
. C.
2a
. D.
2
2
a
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 23: Cho hình chóp
.S ABCD
có đáy
ABCD
l hình chữ nhật,
AB a
,
2AD a
. Cạnh bên
SA
vuông
góc vi mặt đáy v
SA a
. Thể tích của khi chóp
.S ABC
bằng
A.
3
a
. B.
3
1
3
a
. C.
3
2
3
a
. D.
3
2a
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 24: Cho hình chóp
.S ABC
có
ABC
l tam giác đu cạnh
a
, tam giác
SAB
đu v nằm trong mặt
phẳng vuông góc vi mặt phẳng
ABC
. Gọi
I
l trung điểm
SC
. Thể tích của khi chóp
SABI
bằng
A.
3
3
16
a
. B.
3
3
8
a
. C.
3
8
a
. D.
3
16
a
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
5
Câu 25: Mặt phẳng
A BD
chia khi hộp chữ nhật
.ABCD ABCD
thnh hai khi. Gọi
1
V
l thể tích của
khi chứa điểm
A
v
2
V
l thể tích của khi còn lại. Tỉ s
1
2
V
V
bằng
A.
1
5
. B.
1
3
. C.
2
3
. D.
3
5
.
……………………………………………………………………………………………………….…………
Câu 26: Cho lăng trụ đu
. ' ' 'ABC A B C
có cạnh đáy bằng
a
. Góc giữa đường thẳng
'BC
v mặt
ABC
bằng
0
30
. Thể tích của khi lăng trụ đã cho bằng
A.
3
6
a
. B.
3
3
4
a
. C.
3
12
a
. D.
3
4
a
.
……………………………………………………………………………………………………….…………
Câu 27: Cho tam giác
OAB
vuông tại
O
có
2, AB a
OB a
. Quay tam giác
OAB
xung quanh cạnh
OA
tạo thnh khi tròn xoay. Thể tích của khi tròn xoay ny bằng
A.
3
3a
. B.
3
3
3
a
. C.
3
2
3
a
. D.
3
2
a
.
……………………………………………………………………………………………………….…………
Câu 28: Cho hình chữ nhật
ABCD
có
6AB
v
10AD
. Gọi
,M
,N
,P
Q
lần lượt l trung điểm của
,AB
,CD
AD
v
BC
.
Thể tích khi tròn xoay sinh ra khi quay phần gạch sọc trong hình vẽ bên quanh trục
MN
bằng
A.
60
. B.
30
. C.
90
. D.
120
.
……………………………………………………………………………………………………….…………
Câu 29: Cho hình lập phương có cạnh bằng
a
. Din tích của mặt cầu nội tip hình lập phương bằng
A.
2
3
a
. B.
2
a
. C.
2
4 a
. D.
2
4
3
a
.
Câu 30: Cho hình trụ m thit din qua trục l hình chữ nhật có chu vi bằng
36cm
. Khi đó, thể tích của
khi trụ đó có giá tr ln nhất bằng bao nhiêu?
A.
3
216 ( )cm
. B.
3
432 ( )cm
. C.
3
864 ( )cm
. D.
3
464 ( )cm
.
……………………………………………………………………………………………………….…………
PHẦN II: TỰ LUẬN (4.0 điểm) Thời gian 30 phút - 10 câu
Câu 1: Tìm tất c giá tr tham s m để hm s
1
xm
y
x
tăng trên từng khong xác đnh.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
N
M
Q
A
B
C
D
P
6
Câu 2: Tìm tất c các đường tim cận ngang của đồ th hm s
2
1
3
x
y
x
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 3: Tìm m để hm s
3 2 2
1y x mx m x
đạt cực tiểu tại
1x
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 4: Gii phương trình
2
3 9 3 0
x

.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 5: Gii phương trình
3
log 4 2x 
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 6: Gii bất phương trình
31
11
24
x



.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 7: Gii bất phương trình
2
22
log log 2x x x
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 8: Tính diện tích
S
của mặt cầu biết rằng thể tích của khối cầu bằng
36
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 9: Cho khi nón
N
có đường kính đáy bằng 8 v din tích xung quanh bằng
15
. Tính thể tích
V
của khi nón
N
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 10: Cho khi trụ
T
có bán kính đáy bằng
5
v din tích xung quanh bằng
8
. Tính thể tích
V
của
khi trụ
T
.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Hết
1
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12
NĂM HỌC 2018-2019
ĐỀ 2
PHẦN I: TRẮC NGHIỆM (6 điểm) Thời gian 60 phút-30 câu.
Câu 1: Cho hm s
32
31 y x x
. Mnh đ no dưi đây đng ?
A. Hm s nghch bin trên khong
0;1
. B. Hm s đng bin trên khong
1;2
.
C. Hm s nghch bin trên khong
;0
. D. Hm s đng bin trên khong
1; 
.
………………………….…………………………………………………………………………………………
Câu 2: Vi giá tr no của tham s thực của
m
thì hm s
32
1 3 1 y x m x x
đng bin trên khong
; 
?
A.
; 4 2; 
B.
; 4 2; 
C.
4;2
D.
4;2
………………………….…………………………………………………………………………………………
Câu 3: Hm s
42
44 y x x
đạt cực tiểu tại điểm no?
A.
2, 2, 0 x x x
B.
2, 2 xx
C.
2, 0xx
D.
2x
………………………….…………………………………………………………………………………………
Câu 4: Cho s hm s
32
3 3 , y x mx mx m m
. Vi giá tr no của m thì đ th hm s có hai điểm
cực tr v hai điểm đó cách đu đường thẳng
3x
?
A.
1m
B.
3m
C.
2m
D.
0m
………………………….…………………………………………………………………………………………
Câu 5: Giá tr nhỏ nhất của hm s
42
22 f x x x
trên đoạn
0;2
bằng
A.
10
B.
2
C.
1
D.
0
………………………….…………………………………………………………………………………………
Câu 6: Vi giá tr no của m thì giá tr ln nhất của hm s
21
1

xm
fx
x
trên đoạn
1;2
bằng 2?
A.
1m
B.
2m
C.
3m
D. không có
m
………………………….…………………………………………………………………………………………
Câu 7: Đường thẳng no dưi đây l tim cận ngang của đ th hm s
31
2

x
y
x
?
A.
2x
B.
2y
C.
3y
D.
3x
2
Câu 8: Vi giá tr no của tham s m thì tim cận đứng của đ th hm s
3
1

x
y
xm
đi qua điểm
2;3A
?
A.
3m
B.
1m
C.
1m
D.
3m
………………………….…………………………………………………………………………………………
Câu 9: Đường cong trong hình vẽ dưi đây l đ th của một hm s trong bn hm s được lit kê ở bn
phương án A, B, C, D dưi đây.
Hỏi đó l hm s no?
A.
23
1
x
y
x
B.
1
1
x
y
x
C.
22
1
x
y
x
D.
21
1
x
y
x
………………………….…………………………………………………………………………………………
Câu 10: Cho hm s
y f x
có bng bin thiên như hình vẽ dưi đây. Hỏi hm s đã cho có bao nhiêu cực
tr?
A. 4 B. 1 C. 2 D. 3
………………………….…………………………………………………………………………………………
Câu 11: Phương trình no sau đây l phương trình tip tuyn của đ th hm s
3
2 8 2 y x x
tại điểm có
honh độ bằng 0?
A.
82yx
B.
2y
C.
21yx
D.
62yx
………………………….…………………………………………………………………………………………
Câu 12: Cho hm s
21
1
x
y
x
có đ th
C
. Vi các giá tr no của
m
thì đường thẳng
:1 d y x m
cắt
C
tại hai điểm phân bit
, AB
v
23AB
?
A.
4 10m
B.
43m
C.
2 10m
D.
23m
………………………….…………………………………………………………………………………………
Câu 13: Hm no sau đây l đạo hm của hm s
2
1
log
12
y
x



?
–1
y
O
x
1
-
x
y’
y
1
+
+
8
-
0
–4
4
0
-
3
3
A.
2
'
ln4 ln 2
y
x
B.
2
'
ln2 ln4
y
x
C.
2
'
ln2 ln 4
y
x
D.
2
'
ln4 ln2
y
x
………………………….…………………………………………………………………………………………
Câu 14: Tập no sau đây l tập xác đnh của hm s
2
7
log 2y x x
?
A.
; 2 0; 
B.
2;0
C.
;2
D.
2; 
………………………….…………………………………………………………………………………………
Câu 15: Cho ba s thực dương
,a
,b
c
khác 1. Đ th các hm s
log ,
a
yx
log ,
b
yx
log
c
yx
được cho
trong hình vẽ bên.
Mnh đ no dưi đây đng?
A.
a c b
. B.
abc
. C.
c a b
. D.
b c a
.
………………………….…………………………………………………………………………………………
Câu 16: Giá tr nhỏ nhất của hm s
2 40
20 20 1283
x
y x x e
trên tập s thực bằng
A.
1238
B.
280
163.e
C.
320
157.e
D.
300
8.e
………………………….…………………………………………………………………………………………
Câu 17: Cho hai s thực dương
,ab
thỏa mãn
log 2000
a
b
. Giá tr biểu thức
3
log .
a
b
ba
bằng
A.
4006
11997
B.
4006
11997
C.
2669999
4
D.
2669999
4
………………………….…………………………………………………………………………………………
Câu 18: Cho hai s thực dương
a
v
b
thỏa mãn
3 4 7
log log log ( ). a b a b
Tỉ s
a
b
bằng
A.
3
4
B.
4
7
C.
7
4
D.
7
3
………………………….…………………………………………………………………………………………
Câu 19: Bit rằng phương trình
22
2
4 2 6
xx
m
có đng 3 nghim. Mnh đ no sau đây đng?
A.
2m
B.
23m
C.
35m
D.
5 m
………………………….…………………………………………………………………………………………
1
y
x
O
y= log
b
x
y= log
c
x
y= log
a
x
4
Câu 20: Bạn A l sinh viên của một trường Đại học, bạn mun vay tin ngân hng vi lãi suất ưu đãi để trang
tri kinh phí học tập hng năm. Đầu mỗi năm học, bạn ấy vay ngân hng s tin 10 triu đng vi lãi suất mỗi
năm l 4%. S tin m A nợ ngân hng sau 3 năm l bao nhiêu bit rằng trong 3 năm đó, ngân hng không thay
đổi lãi suất (kt qu lm tròn đn nghìn đng)?
A. 32.464640 đng B. 32.216.000 đng C. 30.216.464 đng D. 31.200.000 đng
………………………….…………………………………………………………………………………………
Câu 21: Hình lăng trụ tứ giác đu (không l hình lập phương) có bao nhiêu mặt phẳng đi xứng?
A. 4 B. 5 C. 2 D. 3
………………………….…………………………………………………………………………………………
Câu 22: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
l hình vuông cạnh
a
, cạnh bên
SA
vuông góc vi
mặt phẳng đáy v
2SA a
. Thể tích
V
của khi chóp
.S ABCD
bằng
A.
3
2
6
a
B.
3
2
4
a
C.
3
2a
D.
3
2
3
a
………………………….…………………………………………………………………………………………
Câu 23: Cho khi tứ din đu
ABCD
có cạnh bằng a. Gọi
', 'BC
lần lượt l trung điểm của các cạnh AB v
AC. Thể tích V của khi tứ din
''AB C D
bằng
A.
3
3
48
a
. B.
3
2
48
a
. C.
3
24
a
. D.
3
2
24
a
.
………………………….…………………………………………………………………………………………
Câu 24: Cho hình chóp
.S ABCD
có đáy
ABCD
l hình vuông,
SA
vuông góc vi đáy, mặt bên
SBC
hợp
vi đáy một góc bằng
60 ,
M
l trung điểm của
.CD
Bit thể tích khi chóp
.S ABCD
bằng
3
3
,
3
a
khong
cách từ
M
đn mặt phẳng
SBC
bằng
A.
3
6
a
B.
3
4
a
C.
3
2
a
D.
3a
………………………….…………………………………………………………………………………………
Câu 25: Cho lăng trụ đứng
. ' ' 'ABC A B C
có các cạnh bằng a . Thể tích V khi tứ din
''ABA C
bằng
A.
3
3
4
a
B.
3
3
6
a
C.
3
6
a
D.
3
3
12
a
………………………….…………………………………………………………………………………………
Câu 26: Cho hình lăng trụ đu
. ' 'C'ABC A B
có cạnh đáy bằng
a
, cạnh bên bằng
3a
. Thể tích của khi lăng
trụ bằng
A.
3
3
4
a
B.
3
3
4
a
C.
3
3
7
a
D.
3
7
5
a
5
Câu 27: Trong không gian cho tam giác
ABC
vuông tại
A
,
AB a
v
0
30ACB
. Thể tích của khi nón
nhận được khi quay tam giác
ABC
quanh cạnh
AC
bằng
A.
3
3
3
a
. B.
3
3 a
. C.
3
3
9
a
. D.
3
a
.
………………………….…………………………………………………………………………………………
Câu 28: Một khi nón có thể tích bằng
30
. Nu giữ nguyên chiu cao v tăng bán kính mặt đáy của khi nón
lên hai lần thì thể tích của khi nón mi bằng bao nhiêu?
A.
120
B.
60
C.
40
D.
480
………………………….…………………………………………………………………………………………
Câu 29: Cho hình trụ có bán kính đáy bằng
,a
chu vi của thit din qua trục bằng
10 .a
Thể tích của khi trụ
gii hạn bởi hình trụ đã cho bằng
A.
3
4.a
B.
3
3.a
C.
3
.a
D.
3
5.a
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 30:Một hình trụ có đường kính đáy bằng chiu cao v nội tip trong mặt cầu bán kính R. Din tích xung
quanh của hình trụ bằng
A.
2
2 R
B.
2
2 R
C.
2
22R
D.
2
4 R
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
PHẦN II: TỰ LUẬN (4 điểm)Thời gian 30 phút - 10 câu
Câu 1: Tìm m để hm s
42
24y x m x
có 3 cực tr.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 2: Tìm tất c các đường tim cận đứng của đ th hm s
2
2
1
x
y
x
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 3: Cho hm s
y f x
bit
'y f x
có bng bin thiên như sau
–
x
f’’
f’
+
2
–5
-
+
1
-1
3
3
0
6
Hm s
3y f x x
đng bin trên khong no?
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 4: Gii phương trình
2
2 4 2 0
x

.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 5: Gii phương trình
2
log 4 3x 
.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 6: Gii bất phương trình
31
11
28
x



.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 7: Gii bất phương trình
2
ln ln 2 3x x x
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 8: Tính din tích
S
của mặt cầu bit rằng bán kính của mặt cầu bằng
2
.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 9: Cho khi nón có đường kính đáy bằng 8 v thể tích bằng
15
. Tính din tích xung quanh của hình nón.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 10: Cho khi trụ có thể tích bằng 1
5
v din tích xung quanh bằng
8
. Tính bán kính đường tròn đáy
của hình trụ.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Hết
1
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12
NĂM HỌC 2017-2018
ĐỀ 3
PHẦN I: TRẮC NGHIỆM (6.0 điểm) Thời gian 60 phút-30 câu
Câu 1: Cho hm s
42
21 y x x
. Mnh đ no dưi đây đng ?
A. Hm s nghch bin trên khong
0;1
. B. Hm s đng bin trên khong
1;2
.
C. Hm s nghch bin trên khong
;0
. D. Hm s đng bin trên khong
2; 1
.
………………………….………………………………………………………………………………………
Câu 2: Tập tất c các tham s thực no của
m
thì hm s
32
31 y mx mx x
đng bin trên khong
; 
?
A.
0;9
B.
;0 9; 
C.
0;9
D.
9;
………………………….………………………………………………………………………………………
Câu 3: Hm s
32
44 y x x
có giá tr cực tiểu bằng bao nhiêu?
A.
0
B.
8
3
C.
4
D.
148
27
………………………….………………………………………………………………………………………
Câu 4: Cho s hm s
32
3 y x mx x
có đ th
C
. Bit rằng đường thẳng
3y
cắt
C
tại 3 điểm A,
B, C thỏa mãn
BA BC
. Mnh đ no sau đây đng?
A.
1m
B.
03m
C.
35m
D.
5m
………………………….………………………………………………………………………………………
Câu 5: Giá tr nhỏ nhất của hm s
1
2
x
fx
x
trên đoạn
0;2
bằng
A.
0
B.
1
2
C.
1
4
D. không tn tại.
………………………….………………………………………………………………………………………
………………………….………………………………………………………………………………………
Câu 6: Vi tất c các giá tr no của m thì giá tr ln nhất của hm s
2
cos 4cos f x x x m
trên đoạn
0;8
bằng 2?
A.
1m
B.
3m
C.
4m
D. không có
m
2
Câu 7: Đường thẳng no dưi đây l tim cận ngang của đ th hm s
31
2

x
y
x
?
A.
2x
B.
1
3
x
C.
0y
D. đ th không có tim cận ngang.
………………………….………………………………………………………………………………………
Câu 8: Cho hm s
y f x
có
lim 3

x
fx
v
lim 3


x
fx
. Khẳng đnh no sau đây l khẳng đnh
đng?
A. Đ th hm s đã cho có đng một tim cận ngang.
B. Đ th hm s đã cho có hai tim cận ngang l các đường thẳng
3x
v
3x
.
C. Đ th hm s đã cho có hai tim cận ngang l các đường thẳng
3y
v
3y
D. Đ th hm s đã cho không có tim cận ngang.
………………………….………………………………………………………………………………………
Câu 9: Hm s
()y f x
xác đnh, liên tục trên
\1
v có bng bin thiên như hình dưi đây:
Hm s
()fx
l hm no sau đây?
A.
1
1
x
y
x
B.
1
1
x
y
x
C.
1
1
x
y
x
D.
1
1
x
y
x
………………………….………………………………………………………………………………………
Câu 10: Cho hm s có bng bin thiên như sau:
Mnh đ no dưi đây đng?
A. Hm s có bn điểm cực tr. B. Hm s đạt cực tiểu tại
2x
.
C. Hm s không có giá tr ln nhất. D. Hm s đạt cực tiểu tại
5x
.
Câu 11: H s góc tip tuyn của đ th hm s
ln 1yx
tại điểm có honh độ
1
e
bằng
A.
e
B.
0
C.
1
D.
1
e
3
+
∞
+
y
–5
x
–
1
2
+
0
2
0
–5
0
y’
-
x
A
–
y
y’
1
+
+
+
1
1
–
+
3
………………………….………………………………………………………………………………………
Câu 12: Cho hm s
32
1
1
32
m
f x x x
có đ th
C
. Bit rằng đ th
fx
v trục honh có một
điểm chung. Mnh đ no sau đây đng?
A.
2m
B.
21 m
C.
14m
D.
5m
………………………….………………………………………………………………………………………
Câu 13: Hm no sau đây l đạo hm của hm s
log ln2yx
?
A.
2
ln2 .ln10
y
xx
. B.
1
ln2 .ln10
y
xx
. C.
1
2 ln2 .ln10
y
xx
. D.
1
ln2
y
xx
.
………………………….………………………………………………………………………………………
Câu 14: Cho s thực
x
thỏa
2 8 8 2
log log log logxx
. Giá tr biểu thức
2018
2
log x
bằng
A.
1009
1
3
. B.
1009
27
. C.
2018
27
. D.
2018
1
3
.
Câu 14: Hm s
2
2
16 4
e
yx
có tập xác đnh l:
A.
2;2
. B.
; 2 2;
. C.
; 
. D.
\ 2;2R
………………………….………………………………………………………………………………………
Câu 15: Hm s no trong các hm s dưi đây có đ th l hình vẽ bên?
A.
3
logyx
. B.
1
3
logyx
. C.
3
x
y
. D.
1
3



x
y
.
………………………….………………………………………………………………………………………
Câu 16: Giá tr nhỏ nhất của hm s trên l:
A.
1
B.
2
21e
C.
1e
D.
1
1
e
………………………….………………………………………………………………………………………
Câu 17: Cho
a
l s dương khác 1,
b
l s dương v
m
l s thực bất kì. Mnh đ no dưi đây đng ?
A.
1
log log .
m
aa
bb
m
B.
log log .
m
aa
b m b
C.
1
log log .
m
m
a
bb
a
D.
log log .
m
a
a
b m b
………………………….………………………………………………………………………………………
( ) ln 1y f x x x
2
1; e


y
1
O
x
4
Câu 18: Cho biểu thức
2 2 2
(ln log ) ln log
aa
P a e a e
, vi
a
l s dương khác 1. Mnh đ no dưi đây
đng ?
A.
2
2ln 1Pa
. B.
2
2lnPa
. C.
2
ln 2Pa
. D.
2
2ln 2Pa
.
………………………….………………………………………………………………………………………
Câu 19: Cho phương trình
9 2( 1)3 3 4 0
xx
mm
. Vi giá tr thực no của tham s
m
thì phương
trình có 2 nghim phân bit
12
,xx
sao cho
12
3xx
?
A.
31
3
m
B.
5
2
m
C.
7
3
m
D.
3.m
………………………….………………………………………………………………………………………
Câu 20: Sự tăng trưởng của một loại vi khuẩn tuân theo công thức
.
rt
S Ae
, trong đó
A
l s lượng vi
khuẩn ban đầu,
r
l tỉ l tăng trưởng ( r > 0 ),
t
l thời gian tăng trưởng. Bit rằng s lượng vi khuẩn ban
đầu l 100 con v sau 5 giờ có 300 con. Để s lượng vi khuẩn ban đầu tăng gấp đôi thì thời gian tăng trưởng
t
gần vi kt qu no sau đây nhất?
A. 3 giờ 9 pht. B. 3 giờ 2 pht. C. 3 giờ 16 pht. D. 3 giờ 30 pht.
………………………….………………………………………………………………………………………
Câu 21: Hình lăng trụ có thể có s cạnh l s no sau đây ?
A. 2015 B. 2017 C. 2018 D. 2016
………………………….………………………………………………………………………………………
Câu 22: Cho hình chóp
.S ABC
có SA vuông góc vi mặt phẳng
ABC
v
2SA a
. Tam giác ABC vuông
cân tại B v
2AC a
. Sin góc
hợp bởi đường thẳng SB v mặt phẳng
ABC
bằng
A.
3
2
. B.
2
2
. C.
1
2
. D.
25
5
.
………………………….………………………………………………………………………………………
Câu 23: Cho khi chóp
.S ABC
có
SA
vuông góc vi đáy,
4,SA
6,AB
10BC
v
8CA
. Thể tích
của khi chóp
.S ABC
bằng
A.
40
. B.
192
. C.
32
. D.
24
.
………………………….………………………………………………………………………………………
Câu 24: Cho hình chóp
.S ABC
có đáy
ABC
l tam giác đu, mặt bên
SAB
vuông góc vi mặt phẳng đáy
v tam giác
SAB
vuông tại
S
,
3,SA a
SB a
. Thể tích của khi chóp
.S ABC
bằng
A.
3
1
4
a
.B.
3
1
3
a
. C.
3
1
6
a
. D.
3
1
2
a
.
5
Câu 25: Cho khi lăng trụ
.
ABC A B C
có
5 , 6 AB BC a AC a
. Hình chiu vuông góc của
A
trên mặt
phẳng
ABC
l trung điểm của
AB
v
133
2
a
AC
. Thể tích của khi lăng trụ
.
ABC A B C
bằng
A.
3
12 .a
B.
3
12 133 .a
C.
3
36 .a
D.
3
4 133 .a
………………………….………………………………………………………………………………………
Câu 26: Cho lăng trụ đu
. ' ' 'ABC A B C
có cạnh đáy bằng
2a
. Din tích xung quanh bằng
2
63a
. Thể tích
của khi lăng trụ bằng
A.
3
1
4
a
. B.
3
3
4
a
. C.
3
a
. D.
3
3a
.
………………………….………………………………………………………………………………………
Câu 27: Cho tam giác
OAB
vuông tại
O
có
2 ,AB a
OB a
quay xung quanh cạnh
AB
tạo thnh khi
tròn xoay. Thể tích của khi tròn xoay ny bằng
A.
3
3a
. B.
3
3
3
a
. C.
3
4
3
a
. D.
3
2
a
.
………………………….………………………………………………………………………………………
Câu 28: Cho một hình nón có bán kính đáy bằng
a
v góc ở đỉnh bằng
60
. Din tích xung quanh của hình
nón đó bằng
A.
2
4 a
. B.
2
23
3
a
. C.
2
43
3
a
. D.
2
2 a
.
………………………….………………………………………………………………………………………
Câu 29:
Trong không gian, cho hình chữ nhật
ABCD
có
1AB
v
2AD
. Gọi
,M
N
lần lượt l trung
điểm của
AD
v
BC
. Quay hình chữ nhật đó xung quanh trục
MN
, ta được một hình trụ. Din tích ton
phần của hình trụ đó bằng
A.
4
. B.
2
. C.
6
. D.
10
.
………………………….………………………………………………………………………………………
Câu 30: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
3, 4, ' 5 AB AD AA
. Din tích
S
của mặt cầu
ngoại tip khi chóp
''ACB D
bằng
A .
100 .
B.
60 .
C.
50 .
D.
80 .
………………………….………………………………………………………………………………………
6
PHẦN 2: TỰ LUẬN (4 ĐIỂM)
Thời gian 30 phút - 10 câu
Câu 1: Tìm tim cận đứng của đ th hm s
3
21
x
y
x
.
…………………………………………………………………………………………………
Câu 2: Tìm khong đng bin của hm s
3
2
3y x x
.
…………………………………………………………………………………………………
Câu 3: Gọi
1 2 3
,,x x x
lần lượt l các điểm cực tr của hm s
42
1
21
2
y x x
, trong đó
1 2 3
x x x
. Tính
giá tr biểu thức
333
1 2 3
A x x x
.
………………………………………………………………………………………………
Câu 4: Gii phương trình
1
2 5 0
x

.
…………………………………………………………………………………………………
Câu 5: Gii phương trình
1
2
log 5 3x 
.
…………………………………………………………………………………………………
Câu 6: Gii bất phương trình
2
11
48
x



.
…………………………………………………………………………………………………
Câu 7: Gii bất phương trình
2
log 1 logx x x
.
…………………………………………………………………………………………………
Câu 8: Quay một hình tròn có đường kính bằng 4 xung quanh một đường kính của nó.Tính thể tích khi
tròn xoay thu được.
…………………………………………………………………………………………………
Câu 9: Cho khi nón có bán kính đáy bằng 3 v thể tích bằng
16
. Tính din tích xung quanh của hình nón.
…………………………………………………………………………………………………
Câu 10: Cho khi trụ có thể tích bằng
12
v din tích xung quanh bằng
8
. Tính bán kính đường tròn
đáy của hình trụ.
………………………….………………………………………………………………………………………
………………………….………………………………………………………………………………………
Ht
1
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12
NĂM HỌC 2018-2019
ĐỀ 4
PHẦN I: TRẮC NGHIỆM (6.0điểm)Thời gian 60 phút-30 câu
Câu 1: Hàm số nào sau đây đồng biến trên
(0; )
?
A.
42
.y x x
B.
42
.y x x
C.
42
.y x x
D.
42
.y x x
………………………….………………………………………………………………………………………
Câu 2: Có bao nhiêu giá trị nguyên dương của tham số thực
m
để hàm số
32
1
4
3
y x mx mx m
đồng biến
trên khoảng
; 
?
A.
1.
B.
2.
C.
4.
D.
3.
………………………….………………………………………………………………………………………
Câu 3: Trên đoạn
[ 1;2]
, hàm số
42
2y x x
có giá trị cực đại bằng
A.
1.
B.
8.
C.
1.
D.
0.
………………………….………………………………………………………………………………………
Câu 4: Cho số hàm số
32
2 9 12y x x x m
. Với giá trị thực nào của tham số m thì đồ thị hàm số có hai điểm
cực trị và điểm cực tiểu nằm trên trục hoành?
A.
0.m
B.
1.m
C.
5.m 
D.
4.m 
………………………….………………………………………………………………………………………
Câu 5: Giá trị nhỏ nhất của hàm số
2
3f x x x
bằng
A.
0.
B.
1
.
2
C.
11
.
4
D.
11
.
2
………………………….………………………………………………………………………………………
Câu 6: Với tất cả các giá trị nào của tham số m thì giá trị nhỏ nhất của hàm số
22
ln( 1)f x x m
trên đoạn
1;2
bằng
ln3
?
A.
0;1 .
B.
1;0 .
C.
1;1 .
D. không có
m
.
………………………….………………………………………………………………………………………
Câu 7: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số
21
2
x
y
x
?
A.
0.y
B.
2.y
C.
2.y
D.
1.y
2
Câu 8: Với giá trị nào của tham số m thì đồ thị hàm số
21
1
xm
y
x

không có đường tiệm cận đứng?
A.
1
.
2
m
B.
2.m
C.
0.m
D.
1.m 
………………………….………………………………………………………………………………………
Câu 9: Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây.
Hỏi đó là hàm số nào?
A.
23
.
1
x
y
x
B.
2
.
1
x
y
x
C.
.
1
x
y
x
D.
2
.
1
x
y
x
………………………….………………………………………………………………………………………
Câu 10: Cho hàm số
y f x
có bảng biến thiên như hình vẽ dưới đây. Mệnh đề nào đúng?
A.
0.
CT
y
B.
maxy 5.
C.
miny 4.
D.
5.
CD
y
………………………….………………………………………………………………………………………
Câu 11: Phương trình nào sau đây là phương trình tiếp tuyến của đồ thị hàm số
32
2 3 12 10y x x x
tại điểm
cực đại của đồ thị hàm số?
A.
17 .yx
B.
10.y
C.
10 .yx
D.
17.y 
………………………….………………………………………………………………………………………
Câu 12: Cho hàm số
1
x
y
x
có đồ thị
C
. Với các giá trị nào của
m
thì đường thẳng
:1d y x m
cắt
C
tại hai điểm phân biệt
, AB
và
AB
ngắn nhất?
A.
2.m
B.
10.m
C.
1.m 
D.
0.m
………………………….………………………………………………………………………………………
Câu 13: Hàm số
2
log cosyx
có đạo hàm là
A.
1
2
' log e.tan .yx
B.
' ln2.tan .yx
C.
1
2
' log e.cot .yx
D.
tan
'.
ln 2
x
y
x
y'
y
-
∞
+
∞
-
∞
-
-1
5
-
+
∞
1
||
0
+
4
y
x
g
2
y
=
1
f
2
x
= 2
w
1
x
=
2
∙
x
x
+ 1
2
-1
O
3
Câu 14: Tập nào sau đây là tập xác định của hàm số
2
7
log 2yx
?
A.
; 2 7; . 
B.
2; .
C.
0; .
D.
\ 2 .
………………………….………………………………………………………………………………………
Câu 15: Cho ba hàm số
2
x
y
,
yx
và
()y f x
có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A.
1
2
( ) log .y f x x
B.
( ) ln .y f x x
C.
2
( ) log .y f x x
D.
( ) log .y f x x
………………………….………………………………………………………………………………………
Câu 16: Giá trị nhỏ nhất của hàm số
2
50 1000xx
ye

trên tập số thực bằng
A.
25 5
.e
B.
25
.e
C.
1000
.e
D.
375
.e
………………………….………………………………………………………………………………………
Câu 17: Cho hai số thực dương
,ab
và
1ab
thỏa mãn
1
log
2018
ab
a
. Giá trị biểu thức
log
ab
a
b
bằng
A.
504
.
1009
B.
504
.
1009
C.
1009
.
504
D.
1009
.
504
………………………….………………………………………………………………………………………
Câu 18: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2
log ( 2 4)y x mx
có tập xác định là ?
A.
3.
B.
4.
C.
2.
D.
1.
………………………….………………………………………………………………………………………
Câu 19: Tìm tất cả các giá trị của tham số
m
để phương trình
4
2
21
x
x
m
có 2 ngiệm phân biệt?
A.
2 1.m
B.
1 0.m
C.
3 4.m
D.
3.m
………………………….………………………………………………………………………………………
Câu 20: Sự tăng trưởng dân số được ước tính theo công thức tăng trưởng mũ
.
nr
S Ae
, (
A
dân số ban đầu,
n
thời gian (năm),
r
tỷ lệ tăng trưởng). Biết rằng tỷ lệ tăng trưởng dân số thế giới hằng năm là
1.32%
. Năm 2018,
dân số thế giới vào khoảng
7,5
tỷ người. Với mức tăng trưởng như trên thì dân số năm 2030 là bao nhiêu?
A. 8,78 tỷ người. B. 7,78 tỷ người. C. 9,78 tỷ người. D. 6,78 tỷ người.
………………………….………………………………………………………………………………………
Câu 21: Hình chóp nào sau đây không nội tiếp được trong mặt cầu?
A. Hình chóp
SABCD
có đáy
ABCD
vuông. B. Hình chóp
SABCD
có đáy
ABCD
thoi.
C. Hình chóp
SABCD
có đáy
ABCD
hình chữ nhật. D. Hình chóp
SABCD
có
0
180ABC CDA
.
y
x
y=f(x)
O
y=x
y=2
x
v
1
x
=
x
u
1
x
=
ln
x
ln
2
( )
t
1
x
=
2
x
4
Câu 22: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông, cạnh bên
SA
vuông góc với mặt phẳng
đáy . Gọi
,MN
lần lượt là trung điểm
BC
,
.CD
Biết thể tích của khối chóp
.S ABCD
bằng
0
V
thì khi đó thể
tích khối
.S AMN
bằng
A.
0
3
8
V
. B.
0
1
4
V
. C.
0
2
3
V
. D.
0
5
8
V
.
………………………….………………………………………………………………………………………
Câu 23: Cho khối tứ diện đều
ABCD
có cạnh bằng a. Gọi
, MN
lần lượt là trung điểm của các cạnh AB và
AC,
K
là điểm trên
AD
sao cho
2AK KD
. Thể tích của khối tứ diện
AMNK
A.
3
3
.
72
a
B.
3
2
48
a
C.
3
2
.
72
a
D.
3
2
.
24
a
………………………….………………………………………………………………………………………
Câu 24: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật ,
SA
vuông góc với đáy,
2 , 4 .AB a AD a
M
là trung điểm
SB
,
N
là trung điểm
SD
. Biết khoảng cách từ
S
đền mặt phẳng
()AMN
bằng
8 21
21
a
.
Thể tích khối chóp
.S ABCD
bằng
A.
3
22
.
21
a
B.
3
64
.
3
a
C.
3
8
.
3
a
D.
3
21
.
3
a
5
Câu 25: Cho lăng trụ
. ' ' ' 'ABCD A B C D
có đáy
ABCD
là hình vuông cạnh bằng a, tâm
.O
Hình chiếu vuông
góc của
'B
trên mặt phẳng
()ABCD
là
O
. Góc hợp bởi
'BB
và mặt phẳng
()ABCD
bằng
0
60
. Thể tích V
khối tứ diện
'ABCD
bằng
A.
3
6
.
4
a
B.
3
6
.
12
a
C.
3
6
.
6
a
D.
3
3
.
12
a
………………………….………………………………………………………………………………………
Câu 26: Cho hình lăng trụ đều
. ' 'C'ABC A B
có cạnh đáy bằng
a
, cạnh bên bằng
3a
. Thể tích của khối lăng
trụ bằng
A.
3
.
3
a
B.
3
3
.
4
a
C.
3
.
6
a
D.
3
5
.
3
a
Câu 27: Hình nón tròn xoay có đường cao
40h cm
, bán kính đáy
50r cm
. Một thiết diện qua đỉnh của hình
nón và khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là
24cm
. Diện tích của thiết diện bằng
A.
2
800 .cm
B.
2
1600 .cm
C.
2
2000 .cm
D.
2
2200 .cm
Câu 28: Một khối nón có thể tích bằng
16
3
. Nếu chiều cao của khối nón bằng đường kính thì diện tích xung
quanh
xq
S
của khối nón bằng
A.
45
.
3
xq
S
B.
5.
xq
S
C.
2 5 .
xq
S
D.
4 5 .
xq
S
Câu 29: Mặt phẳng
()P
cắt hình cầu
()S
theo thiết diện là đường tròn có bán kính bằng
3.
Biết khoảng cách từ
tâm mặt cầu đến mặt phẳng
()P
bằng
4.
Thể tích V của khối cầu
()S
bằng
A.
500
.
3
V
B.
400
.
3
V
C.
100
.
3
V
D.
50
.
3
V
Câu 30: Một hình trụ có diện tích một đáy bằng
8
, diện tích xung quanh
32
. Thể tích khối trụ là
A.
50 2 .
B.
32 2 .
C.
72 2 .
D.
64 2 .
PHẦN II: TỰ LUẬN (4 điểm)
Thời gian 30 phút - 10 câu
Câu 1: Tìm m để hàm số
42
24y mx m x
có hai cực đại và một cực tiểu.
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 2: Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số
1
1
x
y
x
?
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
6
Câu 3: Cho hàm số
( ), ( )y f x y g x
liên tục trên
[ 2;2]
, biết đồ thị của hàm số
'( ), '( )f x g x
như hình vẽ
(đường đậm là đồ thị
'( )fx
) . Tìm các khoảng đồng biến của hàm số
( ) ( )?y f x g x
…………………………………………………………………………
……………………………………………………………………….…
Câu 4: Giải phương trình
2
2 2 2 0
x
x
.
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 5: Giải phương trình
22
1
log 1 log 3
4
x
.
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 6: Tìm tập nghiệm của bất phương trình
1
29
34
x



.
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 7: Giải bất phương trình
ln3
ln( 1)xe
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 8: Cho hình chóp
.S ABC
, tam giác
ABC
vuông tại
B
,
SA
vuông góc mặt phẳng
()ABC
. Xác định tâm
của mặt cầu ngoại tiếp hình chóp
.S ABC
.
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 9: Cho khối nón có diện tích đáy bằng
1
2
, khoảng cách từ đỉnh của khối nón đến một điểm bất kỳ trên
đường tròn đáy bằng
10
2
. Thể tích khối nón bằng bao nhiêu?
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 10: Cho khối trụ có diện tích toàn phần bằng
3
, chiều cao của khối trụ là
2
. Tính thể tích khối trụ đó.
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Hết
y
x
2
-1
1
-2
w
1
x
( )
=
x
2
2
v
1
x
( )
=
x
4
4
∙
x
2
+ 2
O
1
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12
NĂM HỌC 2018-2019
ĐỀ 5
PHẦN 1: Hình thức trắc nghiệm (6.0 điểm)
Câu 1: Cho hm s
2
1
y
x
. Mnh đ no dưi đây đng ?
A. Hm s nghch bin trên khong
\{1}.
B. Hm s đng bin trên khong
\{1}.
C. Hm s nghch bin trên khong
;1 .
D. Hm s đng bin trên khong
1; 
.
………………………….………………………………………………………………………………………
Câu 2: Vi giá tr no của tham s thực của
m
thì hm s
3 2 2
39y x mx mx m
nghch bin trên khong
; 
?
A.
0 3.m
B.
3 4.m
C.
1 0.m
D.
4m
.
………………………….………………………………………………………………………………………
Câu 3: Hm s
1
1
yx
x

đạt cực tiểu tại điểm no?
A.
1.x
B.
0.x
C.
2.x
D.
2.x 
………………………….………………………………………………………………………………………
Câu 4: Cho s hm s
3 2 2
2 ( 3 3 27)y x m m x
. Nu tập hợp
T
l tập tất c các giá tr của tham s
m
để
hm s đạt cực tiểu tại
3x 
thì mnh đ no đng?
A.
3;4 .T 
B.
(0;4].T
C.
( 3;0].T 
D.
[ 3;1).T 
………………………….………………………………………………………………………………………
Câu 5: Cho hm s
2
2
1
fx
x
. Vi mọi
x
thuộc đoạn
1;3
, mnh đ no đng?
A.
1
( ) 1
2
fx
. B.
1 ( ) 5fx
. C.
1 ( ) 0fx
. D.
1
( ) 2
5
fx
.
………………………….………………………………………………………………………………………
Câu 6: Vi giá tr no của m thì giá tr ln nhất của hm s
2
2
1
1
x mx
fx
x

bằng 1?
A.
2018.m
B.
0.m
C.
.m
D. Không có
m
.
………………………….………………………………………………………………………………………
………………………….………………………………………………………………………………………
………………………….………………………………………………………………………………………
2
Câu 7: Đ th của hm s no sau đây có tim cận đứng ?
A.
2
3 5 2
.
2
xx
y
x

B.
2
1
.
2
y
x
C.
12
.
3
x
y
x

D.
21
.
x
y
x
………………………….………………………………………………………………………………………
Câu 8: Đường tim cận đứng, tim cận ngang của đ th hm s
2
xm
y
xm

tạo vi hai trục tọa độ thnh một
tứ giác có din tích bằng
2
. Khi đó, phát biểu no sau đây đng?
A.
; 5 .m 
B.
6;10 .m
C.
5; 1 .m
D.
1;5 .m
………………………….………………………………………………………………………………………
Câu 9: Đường cong trong hình vẽ dưi đây l đ th của một hm s trong bn hm s được lit kê ở bn
phương án A, B, C, D dưi đây. Hỏi đó l hm s no?
A.
32
.y x x
B.
2
.y x x
C.
42
.y x x
D.
42
.y x x
Câu 10: Cho hm s
y f x
có bng bin thiên như hình vẽ dưi đây.
Mnh đ no đng?
A. Hm s có đng một cực tr.
B. Hm s có giá tr ln nhất bằng 6.
C. Hm s có giá tr cực tiểu bằng 3.
D. Hm s đạt cực đại tại
1x 
v đạt cực tiểu tại
3.x
………………………….………………………………………………………………………………………
Câu 11: Tip tuyn của đ th hm s
5
51y x x
tại
( 2;23)M
cắt hai trục tọa độ tại
,AB
. Khi đó din tích
S
của tam giác
OAB
( vi
O
l gc tọa độ) bằng
A.
16129
.
150
S
B.
16129
.
75
S
C.
127
.
25
S
D.
16129
.
151
S
………………………….………………………………………………………………………………………
………………………….………………………………………………………………………………………
-1
x
y'
y
-
∞
+
∞
+
∞
+
-1
6
+
-
∞
3
||
0
-
y
x
t
1
x
=
x
4
+
x
2
O
3
Câu 12: Đ th hm s no sau đây cắt trục honh tại bn điểm phân bit?
A.
42
3 2.y x x
B.
32
3 2.y x x
C.
42
3 2.y x x
D.
42
3 2.y x x
………………………….………………………………………………………………………………………
Câu 13: Hm no sau đây l đạo hm của hm s
22x
y xe e
?
A.
2
' (2 1)
x
y x e
B.
2
' (2 1) 2
x
y x e e
. C.
2
' 2 2
x
y xe e
.
D.
2
' ( 1)
x
y x e
.
………………………….………………………………………………………………………………………
Câu 14: Tập xác đnh
D
của hm s
2
3
( ) 2 3f x x x
l
A.
( 3;2).D 
B.
( 3;2].D 
C.
( ;2]\ 3 .D 
D.
;2 \ 0 .D 
………………………….………………………………………………………………………………………
Câu 15: Đ th hm s
ln
()
ln3
x
y f x
được cho trong hình vẽ bên.
Đ th hm s
(3 )y f x
l đ th no trong các đ th sau đây?
A. B. C. D.
………………………….………………………………………………………………………………………
Câu 16: Giá tr ln nhất của hm s
()
ln
x
fx
x
trên
3
[2; ]e
bằng
A.
4
.
8
e
B.
5
.
22
e
C.
3
.
3
e
D.
1339
.
200
………………………….………………………………………………………………………………………
Câu 17: Cho
log 3
a
b
. Giá tr
log
b
a
a
b
bằng
A.
3 1.
B.
31
.
23
C.
3 1.
D.
31
.
32
………………………….………………………………………………………………………………………
Câu 18: Nu
17 15
38
aa
v
log 2 5 log 2 3
bb
thì
A.
1
.
1
a
b
B.
01
.
1
a
b

C.
1
.
01
a
b

D.
01
.
01
a
b


y
x
w
1
x
( )
=
ln
x
( )
ln
3
( )
1
1
v
1
x
( )
=
ln
3
∙
x
( )
ln
3
( )
y
x
-1
1
y
x
O
2
1
v
1
x
( )
=
ln
3
∙
x
( )
ln
3
( )
+ 1
y
x
O
2
1
v
1
x
( )
=
2
x
y
x
1
3
1
v
1
x
( )
=
ln
x
( )
ln
3
( )
O
4
Câu 19: Tổng tất c các nghim của phương trình
22
2
2 2 3
x x x x

l
A.
0.
B.
2.
C.
1.
D.
1.
………………………….………………………………………………………………………………………
Câu 20: Ông A gửi vo ngân hng 20 triu đng vi lãi suất
0.75%
mỗi tháng. Hằng tháng Ông A rt ra 300
nghìn đng vo ngy tính lãi. Hỏi sau hai năm Ông A còn lại bao nhiêu tin ( lm tròn đn 1000 đng) ?
A.
1.607.000
đng. B.
16.071.000
đng. C.
16.072.000
đng. D.
16.073.000
đng.
………………………….………………………………………………………………………………………
Câu 21: Cho hình chóp
.S ABCD
có đáy
ABCD
l hình bình hnh v có thể tích l
0
V
. Gọi
,MN
lần lượt l
trung điểm
,SA SC
. Mặt phẳng
BMN
cắt
SD
tại
K
. Tính thể tích khi
.S BMKN
theo
0
V
?
A.
0
2
V.
3
B.
0
2
V.
19
C.
0
1
V.
6
D.
0
1
V.
4
………………………….………………………………………………………………………………………
Câu 22: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
l chữ nhật,
,AB a
cạnh bên
SA
vuông góc vi mặt
phẳng đáy v
5SA a
, góc giữa mặt phẳng
()SBD
v
()ABCD
bằng
, bit
5
tan
2
. Tính thể tích
V
của
khi chóp
.S ABCD
A.
3
23
.
5
a
V
B.
3
55
.
2
a
V
C.
3
25
.
5
a
V
D.
3
25
.
3
a
V
………………………….………………………………………………………………………………………
Câu 23: Cho khi tứ din đu
.S ABC
. Mặt phẳng
()P
qua trung điểm
M
của
SA
v song song mặt phẳng
()ABC
cắt
,SB SC
lần lượt tại
,NK
. Tỷ s thể tích
SMNK
SABC
V
V
bằng
A.
2
3
. B.
1
.
4
C.
3
.
2
D.
1
.
8
………………………….………………………………………………………………………………………
Câu 24: Cho hình chóp
.S ABC
có đáy
ABC
l l tam giác đu cạnh
a
. Hình chiu vuông góc của
S
trên mặt
phẳng
ABC
l trung điểm của
AB
, góc giữa
SC
v mặt phẳng đáy bằng
0
30
. Tính thể tích
V
của khi chóp
.?S ABC
A.
3
3
4
a
V
. B.
3
2
24
a
V
. C.
3
3
2
a
V
. D.
3
3
.
24
a
V
Câu 25: Cho lăng trụ
. ' ' 'ABC A B C
có
'.A ABC
l tứ din đu cạnh bằng a . Thể tích V khi chóp
' ' 'A BCC B
bằng
A.
3
2
.
6
a
V
B.
3
2
.
4
a
V
C.
3
2
.
12
a
V
D.
3
3
.
6
a
V
5
Câu 26: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
tam giác
ABC
vuông tại
B
,
BC a
,
0
60ACB
,
'AB
tạo vi
mặt phẳng
()ABC
một góc
0
30
. Thể tích của khi lăng trụ
. ' ' 'ABC A B C
bằng
A.
3
3.a
B.
3
3
.
2
a
C.
3
3
.
3
a
D.
3
33
.
3
a
………………………….………………………………………………………………………………………
Câu 27: Trong không gian cho tam giác
ABC
vuông tại
A
,
AB a
v
0
30ACB
. Thể tích của khi nón
nhận được khi quay tam giác
ABC
quanh cạnh
AC
bằng
A.
3
3
3
a
. B.
3
3 a
. C.
3
3
9
a
. D.
3
a
.
………………………….………………………………………………………………………………………
Câu 28: Một khi nón có thể tích bằng
30
. Nu giữ nguyên chiu cao v tăng bán kính mặt đáy của khi nón
lên hai lần thì thể tích V của khi nón mi bằng bao nhiêu?
A.
120
V
. B.
60
V
. C.
40
V
. D.
480
V
.
………………………….………………………………………………………………………………………
Câu 29: Thit din qua trục của hình trụ l một hình vuông cạnh bằng
2a
. Gọi
12
,SS
lần lượt l din tích xung
quanh v din tích ton phần của hình trụ đó. Mnh đ no đng?
A.
12
43SS
. B.
12
32SS
. C.
12
2SS
. D.
12
23SS
.
………………………….………………………………………………………………………………………
Câu 30: Cho tứ din
ABCD
có tam giác
ABC
vuông tại
B
, cạnh
DA
vuông góc mặt phẳng
()ABC
. Bit
3,AB a
4,BC a
5DA a
. Tính bán kính mặt cầu ngoại tip khi tứ din
ABCD
theo
.a
A.
52
.
2
a
B.
52
.
3
a
C.
53
.
2
a
D.
53
.
8
a
………………………….………………………………………………………………………………………
Phần 2: Hình thức tự luận (4.0 điểm). Thời gian 30 phút - 10 câu
Câu 1: Tìm điểm cực đại của đ th hm s
32
31y x x
.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 2: Tìm tất c các đường tim cận đứng của đ th hm s
2
2
6
x
y
xx

.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
6
Câu 3: Cho hm s
y f x
bit
'y f x
có đ th như hình vẽ bên
Hm s
y f x x
có mấy cực tr
Câu 4: Gii phương trình
log log6
6 12
x
x
.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 5: Gii phương trình
2
log log 4 1x 
.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 6: Gii phương trình
84
2 6.2 16 0
xx
.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 7: Tìm tập nghim bất phương trình
2
log log( 2 11)x x x
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 8: Tính thể tích
V
khi cầu bit rằng bán kính của khi cầu cầu bằng
3.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 9: Cho khi nón có đường kính đáy bằng 8 v đường sinh bằng 10. Tính thể tích của khi nón.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 10: Thit din qua trục của khi trụ l hình vuông có chu vi bằng 10. Tính thể tích khi trụ đó ?
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Hết
y
x
1
2
s
1
x
= 2
∙
x
4
4
∙
x
2
+
0,5
∙
x
( )
+ 2
O
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

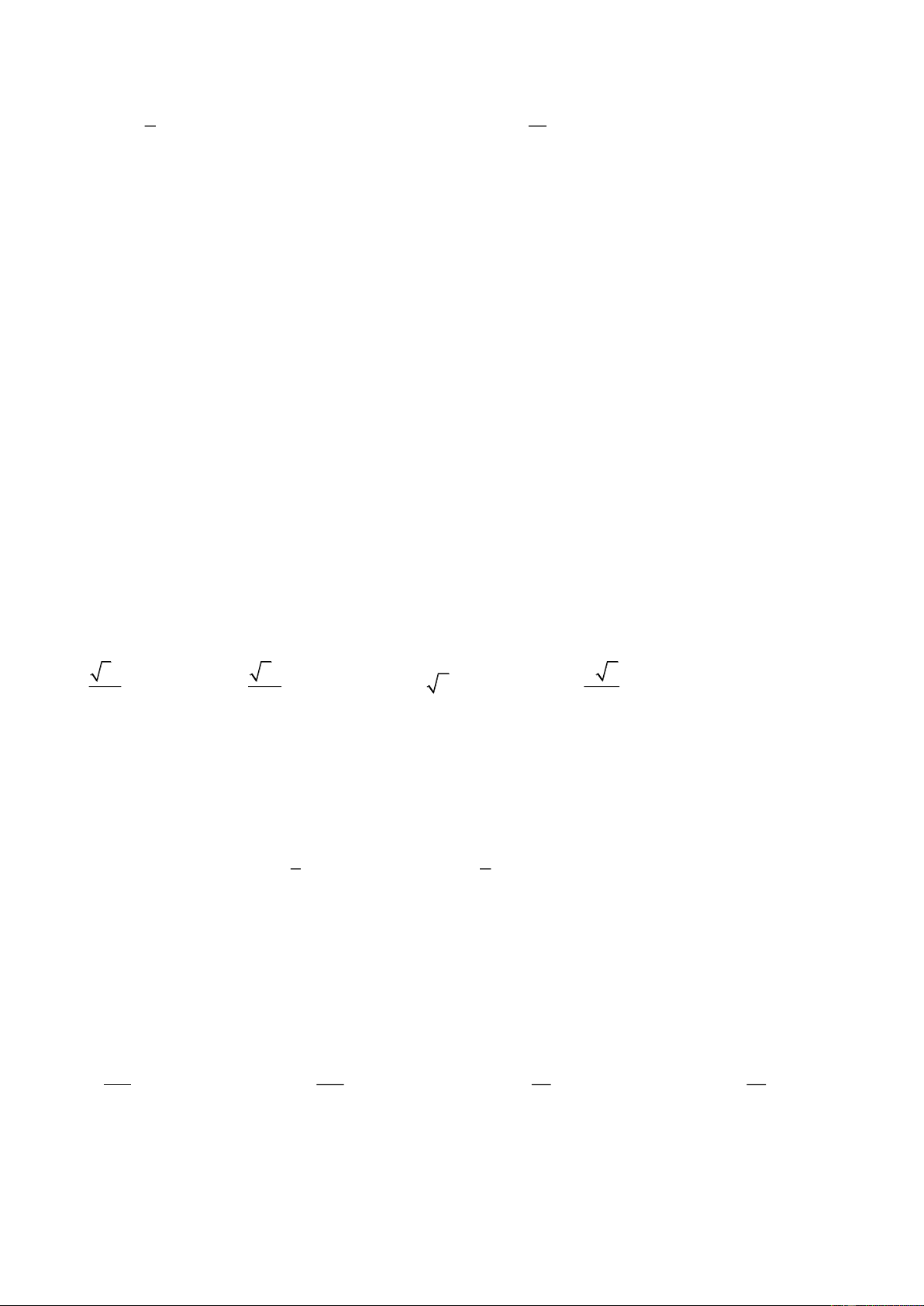
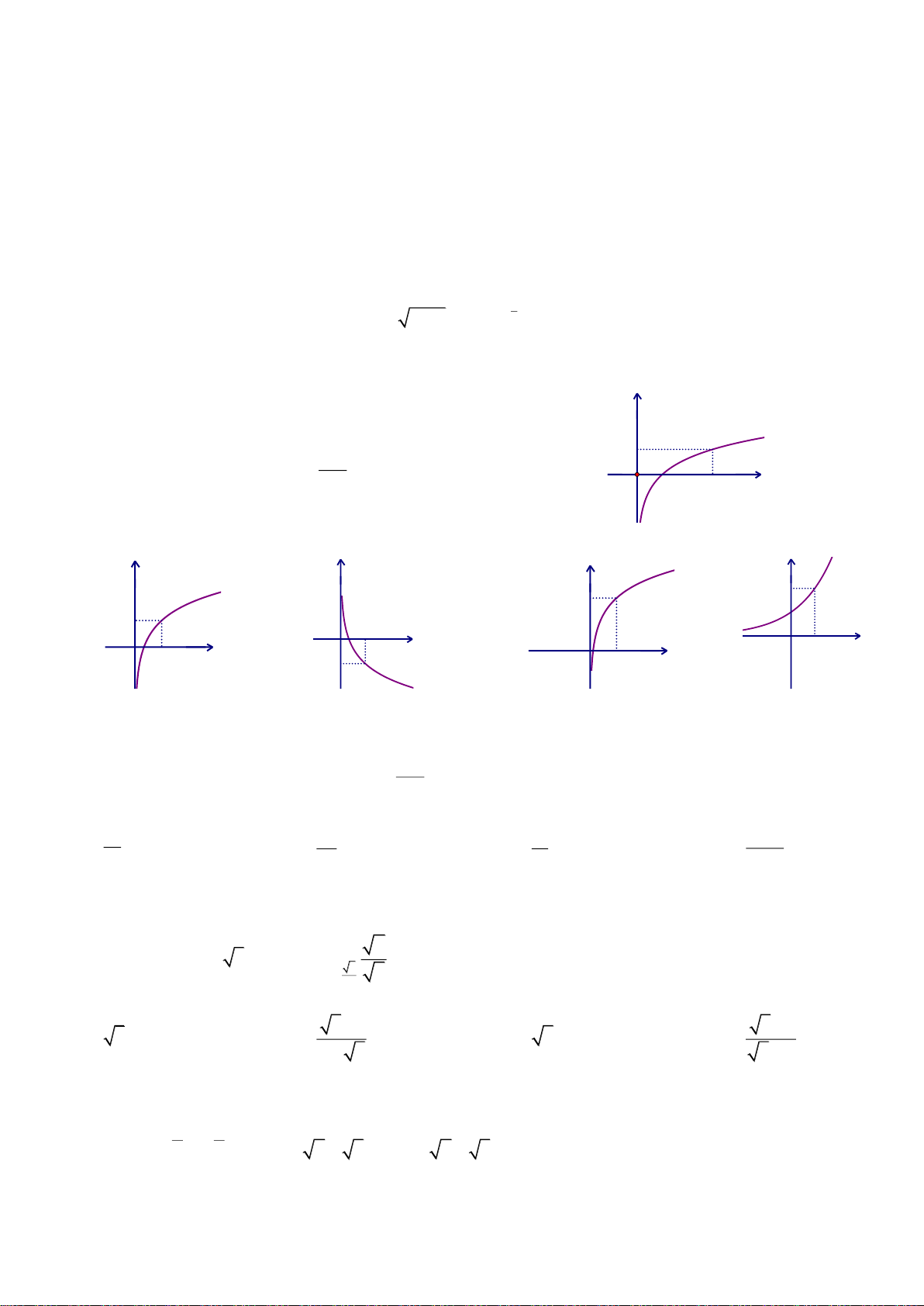
Preview text:

ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12 NĂM HỌC: 2018-2019 ĐỀ 1
PHẦN I: TRẮC NGHIỆM (6 điểm)Thời gian 60 phút-30 câu. Câu 1: Cho hàm số 4 2
y x  2x 1. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng   ;1  .
B. Hàm số đồng biến trên khoảng 0;  1 .
C. Hàm số nghịch biến trên khoảng  1   ;1 .
D. Hàm số đồng biến trên khoảng 1;2 .
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 2: Cho hàm số 3 2
y x mx  3x  1 với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số
đồng biến trên khoảng  ;   ? A. 6. B. Vô số. C. 7. D. 5.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… Câu 3: Hàm số 3 2
y x  3x  5 có giá trị cực đại bằng bao nhiêu? A. 0 . B. 2 . C. 5 . D.1 .
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 4: Cho hàm số y f x xác định và có đạo hàm liên tục trên khoảng a;b . Biết đồ thị của hàm số
y f  x trên khoảng a;b cắt trục hoành tại hai điểm có hoành độ lần lượt là x , x và tiếp xúc với 1 2
trục hoành tại hai điểm có hoành độ lần lượt là x , x như hình vẽ dưới đây. 3 4 y y f (  x) O a x x x x 1 2 3 4 b x
Hỏi trong khoảng a;b , hàm số y f x có bao nhiêu điểm cực trị? A. 4. B. 7. C. 5. D. 2.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………  Câu 5: x 1
Giá trị nhỏ nhất của hàm số y  1;1 bằng x  trên đoạn   2 A. 3 . B. 0 . C. 2
 . D. Không tồn tại.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 6: Với giá trị nào của tham số m thì giá trị lớn nhất của hàm số f x 2
 cos x  3cos x m trên đoạn 0;8  bằng 2? 1
A. m  4 . B. m  4  . C. m   . D. m  2  . 4
……………………………………………………………………………………………………….………… 1 Câu 7: x
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số 1 3 y  ? x  2 3 1 A. y   . B. y  1.
C. y  3 . D. y  . 2 2
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
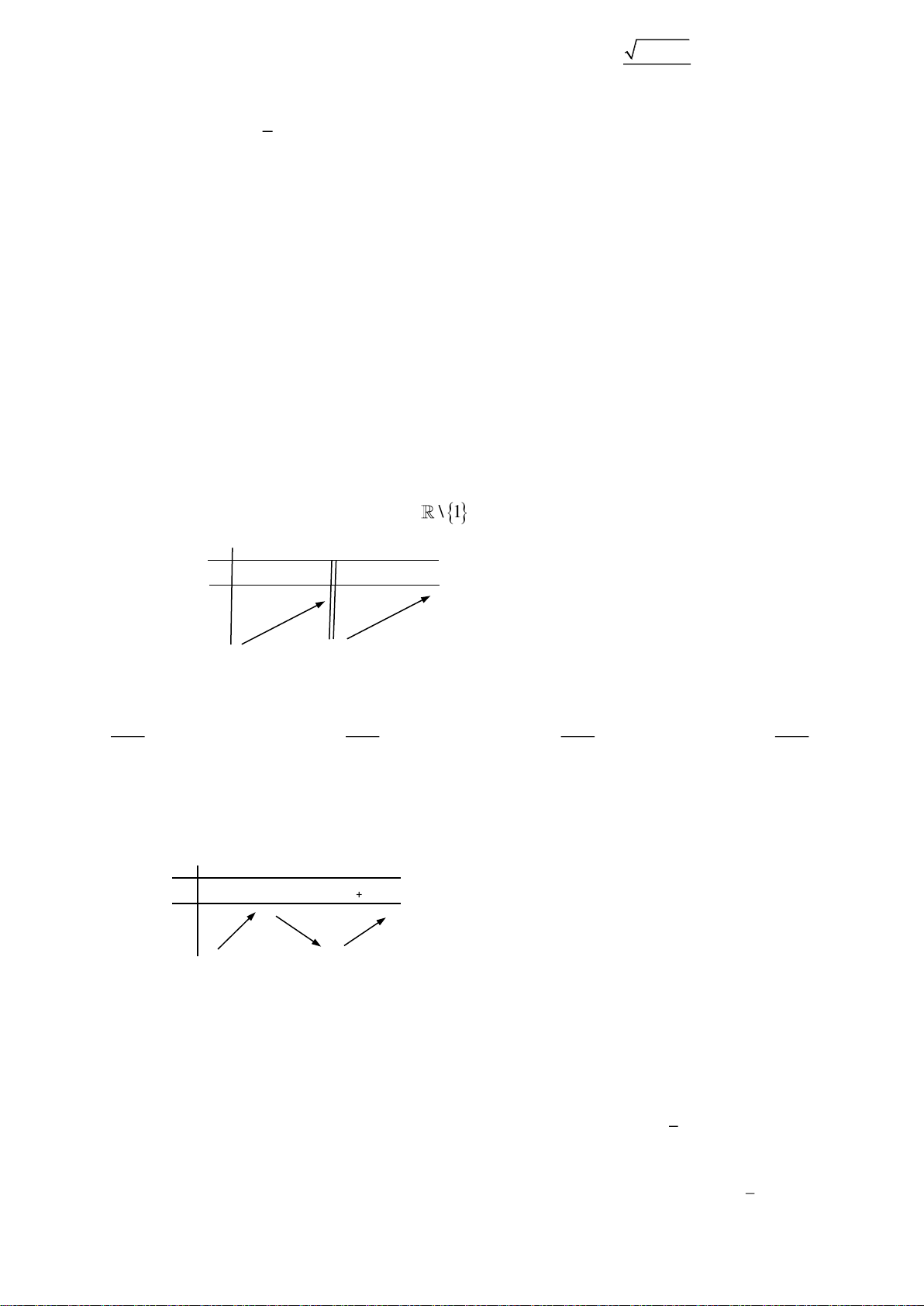
Câu 8: Cho hàm số y f x xác định và liên tục trên \  
1 thỏa lim f x  3 và lim f x   .   x 1  x 1 
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số đã cho có tiệm cận ngang và không có tiệm cận đứng.
B. Đồ thị hàm số đã cho có tiệm cận ngang là đường thẳng y  3.
C. Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng x  1 .
D. Đồ thị hàm số đã cho không có tiệm cận.
……………………………………………………………………………………………………….………… t1 x
  = x3 3∙x2 + 1
……………………………………………………………………………………………………….………… y
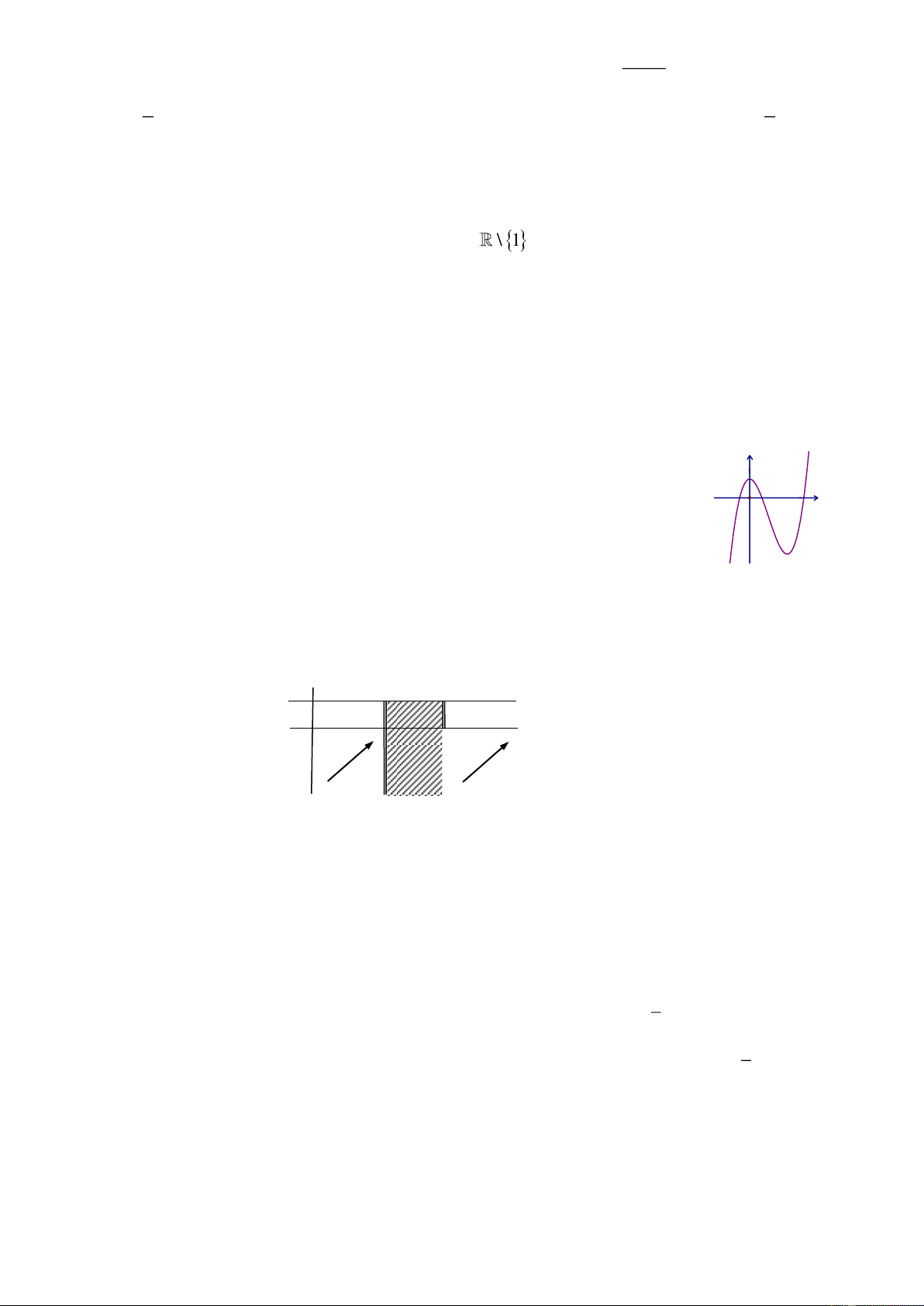
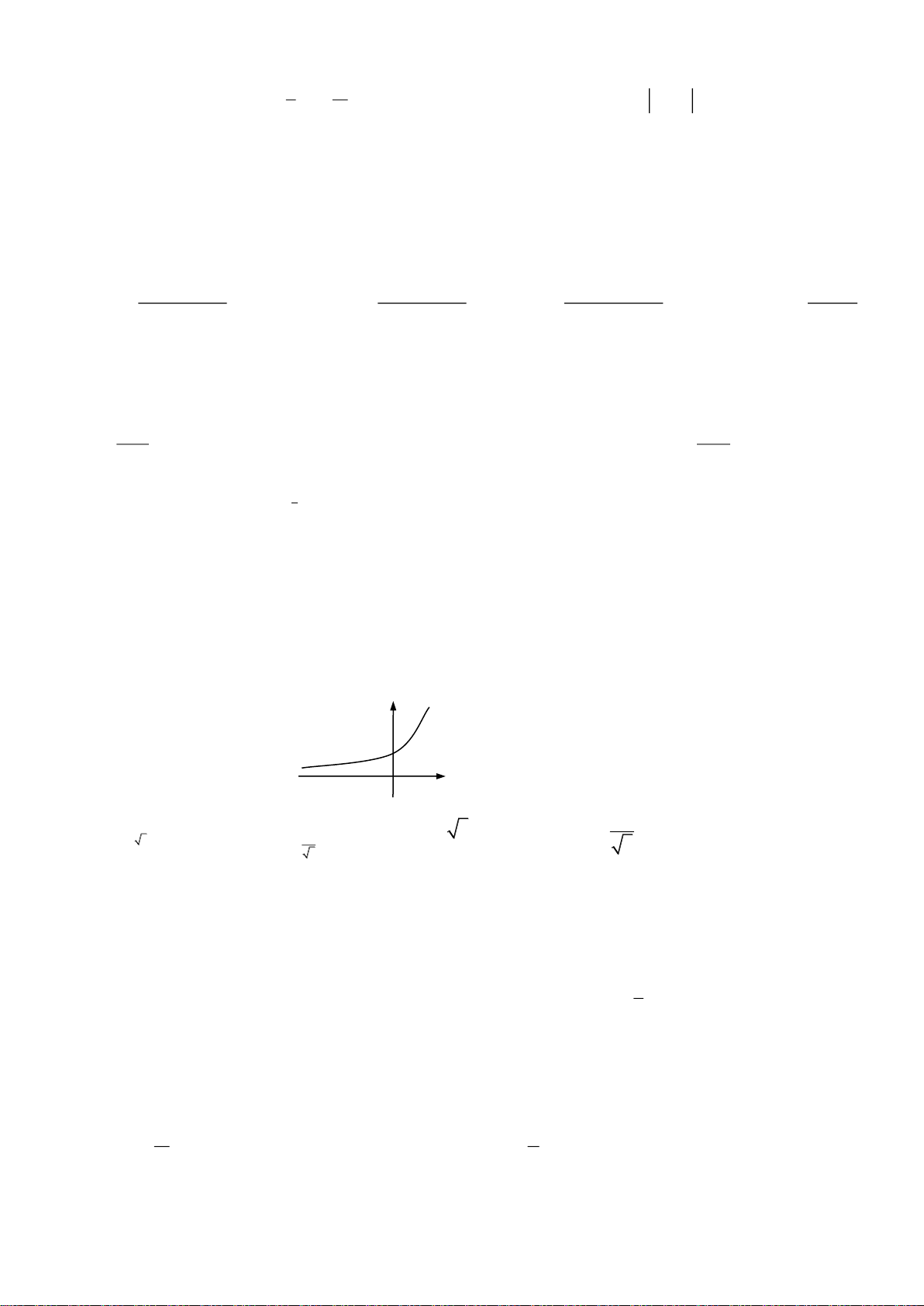
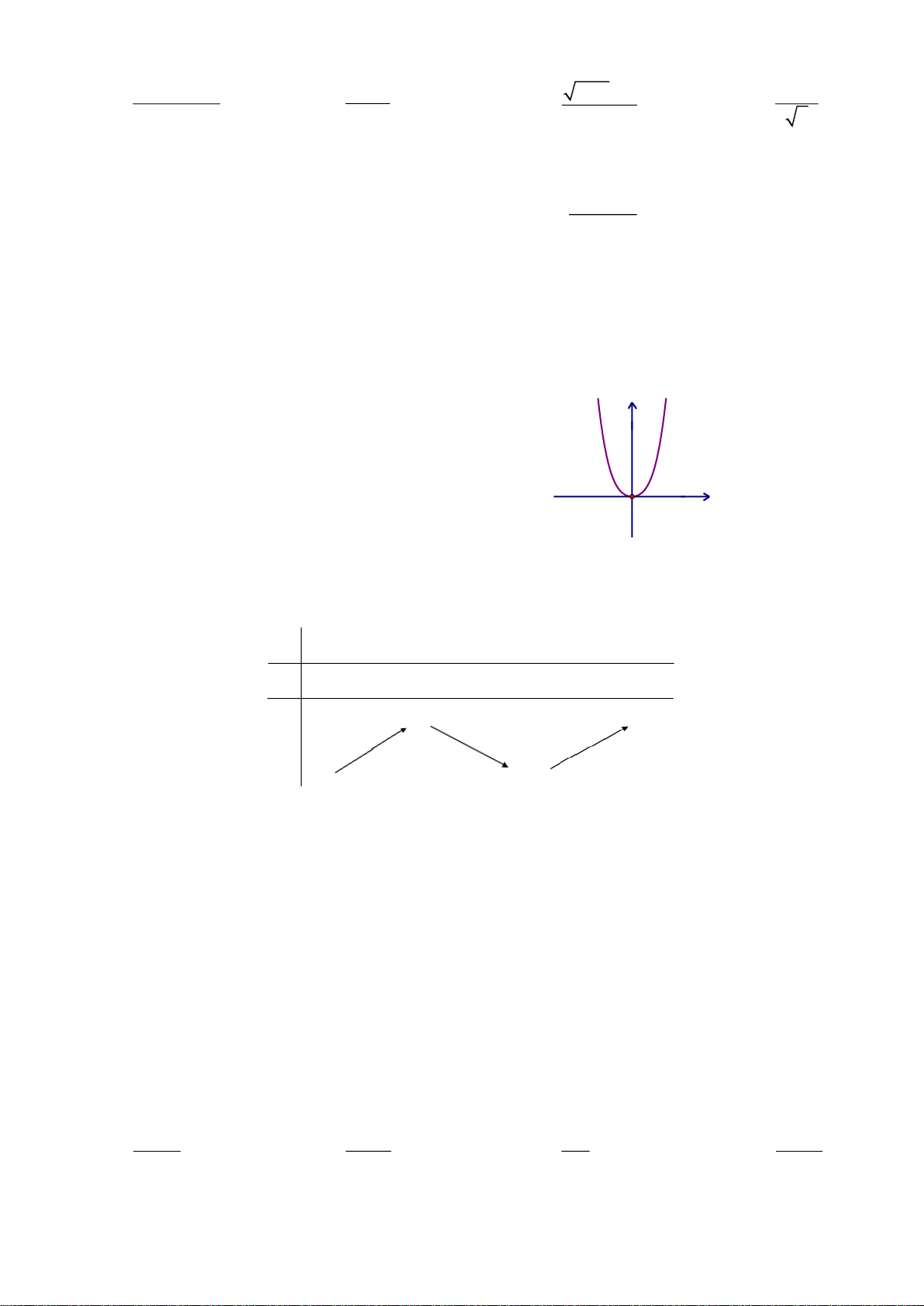
Câu 9: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. O x
Hàm số đó là hàm số nào? A. 3
y  x  4x . B. 3 2
y x  3x  1. C. 4 2
y x  3x  2 . D. 3 y x  1.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 10: Cho hàm số y f x có bảng biến thiên như hình bên. x – –5 2 + y’ + + + + y 6 5
Mệnh đề nào dưới đây đúng?
A. Hàm số có một điểm cực trị.
B. Đồ thị hàm số không có tiệm cận đứng.
C. Đồ thị hàm số không có tiệm cận ngang.
D. Hàm số có giá trị nhỏ nhất.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… Câu 11: 1
Hệ số góc tiếp tuyến của đồ thị hàm số y  ln x tại điểm có hoành độ bằng e 1 A. e . B. 0 . C. 1  . D. . e
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 12: Cho hàm số 4 2
y x x m – 1 ( m là tham số) thỏa mãn đồ thị của nó cắt trục hoành tại đúng 2 điểm ,
A B sao cho AB  2 . Mệnh đề nào sau đây đúng? A. m  0. B. m  4 .
C. 0  m  2 .
D. 2  m  4 . 2
Câu 13: Hàm số nào sau đây là đạo hàm của hàm số 2 x 1 y e   ? 2 x 1 e  2 x 1 2e A. 2 2 . x e e . B. 2 4 x e . C. . D. . ln 2 ln10
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… 
Câu 14: Tập xác định của hàm số y    x  2 2 16 4 là A.  2  ;2 . B.  ;  2   2; . C.  ;   . D. \  2  ;  2 .
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
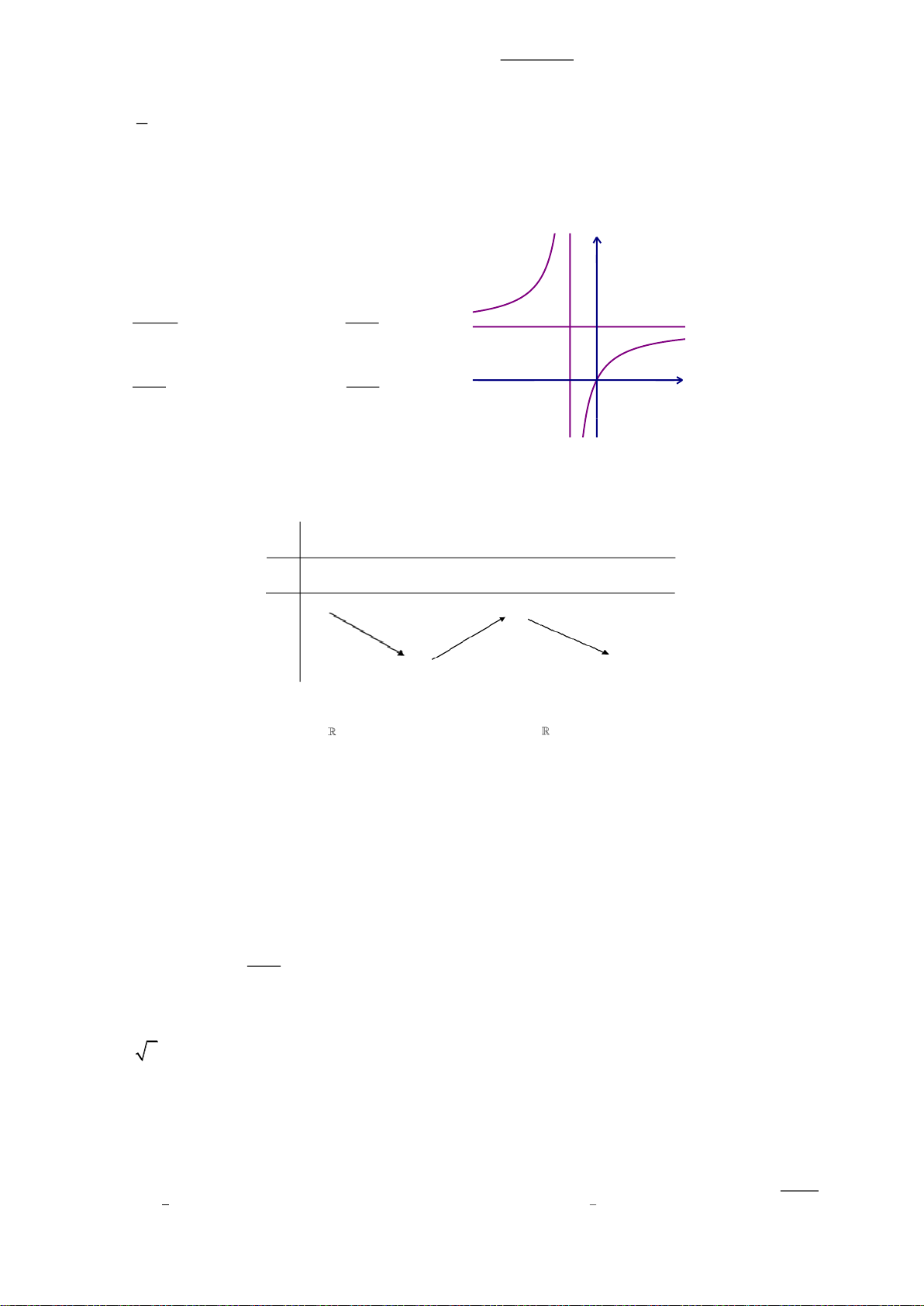
Câu 15: Hàm số nào trong các hàm số dưới đây có đồ thị là hình vẽ bên? y A. y  log x . B. y  log x . 3 1 3 O 1 x x x  1 
C. y   3 . D. y    .  3 
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 16: Cho a và b là hai số thực dương. Mệnh đề nào dưới đây đúng?
A. log a b  log .
a log b .
B. log ab  log a  log b .
C. log a b  log a  log b .
D. log ab  log .
a log b .
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 17: Cho log b  2 , giá trị biểu thức 8 2 log b a bằng 4 a   a 9 A. . B. 9 . C. 2 . D. 8 . 2
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… 2 2 1  
Câu 18: Cho a và b là hai số thực dương thỏa mãn  3 3 a b  3 3 a b   ab3 1 
. Giá trị lớn nhất của  
biểu thức a b bằng 1 1 A. . B. 1. C. 2 . D. . 2 4
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… 3
Câu 19: Cho phương trình 2
log x  2mlog x  3m  5  0 . Với giá trị của tham số thực m thì phương trình 2 2
có 2 nghiệm phân biệt x , x thỏa mãn x .x  8 ? 1 2 1 2 3 13 A. m .
B. m  3. C. m .
D. m  4 . 2 3
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 20: Sự tăng trưởng của một loại vi khuẩn tuân theo công thức  . rt S
A e , trong đó A là số lượng vi
khuẩn ban đầu, r là tỉ lệ tăng trưởng, t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là
100 con và sau 5 giờ có 500 con. Hỏi sau 2 giờ thì số lượng vi khuẩn gần với kết quả nào sau đây nhất? A. 190 con. B. 200 con. C. 195 con. D. 205 con.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 21: Trong các khối đa diện sau đây, khối nào có tâm đối xứng?
A. Khối tứ diện đều.
B. Khối lăng trụ tam giác đều.
C. Khối chóp tứ giác đều. D. Khối hộp.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 22: Cho hình chóp .
S ABC có SA vuông góc với mặt phẳng  ABC và SA a . Tam giác ABC vuông
tại B và AB a . Khoảng cách từ A đến mặt phẳng SBC bằng 3a 6a a 2 A. . B. . C. a 2 . D. . 3 3 2
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 23: Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật, AB a , AD  2a . Cạnh bên SA vuông
góc với mặt đáy và SA a . Thể tích của khối chóp . S ABC bằng 1 2 A. 3 a . B. 3 a . C. 3 a . D. 3 2a . 3 3
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 24: Cho hình chóp .
S ABC có ABC là tam giác đều cạnh a , tam giác SAB đều và nằm trong mặt
phẳng vuông góc với mặt phẳng  ABC. Gọi I là trung điểm SC . Thể tích của khối chóp SABI bằng 3 3a 3 3a 3 a 3 a A. . B. . C. . D. . 16 8 8 16
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… 4
Câu 25: Mặt phẳng  A B
D chia khối hộp chữ nhật ABC . D A BCD
  thành hai khối. Gọi V là thể tích của 1 khối chứa điểm V
A và V là thể tích của khối còn lại. Tỉ số 1 bằng 2 V2 1 1 2 3 A. . B. . C. . D. . 5 3 3 5
……………………………………………………………………………………………………….…………
Câu 26: Cho lăng trụ đều AB .
C A' B'C ' có cạnh đáy bằng a . Góc giữa đường thẳng BC ' và mặt  ABC  bằng 0
30 . Thể tích của khối lăng trụ đã cho bằng 3 a 3 3a 3 a 3 a A. . B. . C. . D. . 6 4 12 4
……………………………………………………………………………………………………….…………
Câu 27: Cho tam giác OAB vuông tại O có AB  2a, OB a . Quay tam giác OAB xung quanh cạnh
OA tạo thành khối tròn xoay. Thể tích của khối tròn xoay này bằng 3  3a 3 2 a 3  a A. 3  3a . B. . C. . D. . 3 3 2
……………………………………………………………………………………………………….…………
Câu 28: Cho hình chữ nhật ABCD có AB  6 và AD  10. Gọi M , N, ,
P Q lần lượt là trung điểm của , AB ,
CD AD và BC . P A D M N B C Q
Thể tích khối tròn xoay sinh ra khi quay phần gạch sọc trong hình vẽ bên quanh trục MN bằng
A. 60 . B. 30 . C. 90 . D. 120 .
……………………………………………………………………………………………………….…………
Câu 29: Cho hình lập phương có cạnh bằng a . Diện tích của mặt cầu nội tiếp hình lập phương bằng 2  a 2 4 a A. . B. 2  a . C. 2 4 a . D. . 3 3
Câu 30: Cho hình trụ mà thiết diện qua trục là hình chữ nhật có chu vi bằng 36cm . Khi đó, thể tích của
khối trụ đó có giá trị lớn nhất bằng bao nhiêu? A. 3 216 (cm ) . B. 3 432 (cm ) . C. 3 864 (cm ) . D. 3 464 (cm ) .
……………………………………………………………………………………………………….…………
PHẦN II: TỰ LUẬN (4.0 điểm) Thời gian 30 phút - 10 câu Câu 1: x m
Tìm tất cả giá trị tham số m để hàm số y
tăng trên từng khoảng xác định. x 1
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… 5 Câu 2: x 1
Tìm tất cả các đường tiệm cận ngang của đồ thị hàm số y  2 x  3
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 3: Tìm m để hàm số 3 2 2
y  x mx m x 1 đạt cực tiểu tại x 1.
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 4: Giải phương trình x 2 3 9 3  0 .
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 5: Giải phương trình log x  4  2 . 3  
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… 3x 1    Câu 6: 1 1 Giải bất phương trình    .  2  4
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 7: Giải bất phương trình log x  log  2 2x x 2 2 
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 8: Tính diện tích S của mặt cầu biết rằng thể tích của khối cầu bằng 36 .
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 9: Cho khối nón  N  có đường kính đáy bằng 8 và diện tích xung quanh bằng 15 . Tính thể tích
V của khối nón  N  .
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….…………
Câu 10: Cho khối trụ T  có bán kính đáy bằng 5 và diện tích xung quanh bằng 8 . Tính thể tích V của
khối trụ T .
……………………………………………………………………………………………………….…………
……………………………………………………………………………………………………….………… Hết 6
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12 NĂM HỌC 2018-2019 ĐỀ 2
PHẦN I: TRẮC NGHIỆM (6 điểm) Thời gian 60 phút-30 câu.
Câu 1: Cho hàm số 3 2
y x  3x 1. Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng 0  ;1 .
B. Hàm số đồng biến trên khoảng 1; 2 .
C. Hàm số nghịch biến trên khoảng  ;0  .
D. Hàm số đồng biến trên khoảng 1;  .
………………………….…………………………………………………………………………………………
Câu 2: Với giá trị nào của tham số thực của m thì hàm số 3
y x  m   2
1 x  3x 1 đồng biến trên khoảng  ;   ? A.  ;  4  2; B.  ;  4  2; C.  4  ;2 D.  4  ;2
………………………….………………………………………………………………………………………… Câu 3: Hàm số 4 2
y x  4x  4 đạt cực tiểu tại điểm nào?
A. x  2, x   2, x  0 B. x  2, x   2
C. x  2, x  0 D. x   2
………………………….…………………………………………………………………………………………
Câu 4: Cho số hàm số 3 2
y x  3mx  3mx  , m m
. Với giá trị nào của m thì đồ thị hàm số có hai điểm
cực trị và hai điểm đó cách đều đường thẳng x  3? A. m 1
B. m  3 C. m  2  D. m  0
………………………….…………………………………………………………………………………………
Câu 5: Giá trị nhỏ nhất của hàm số f x 4 2
x  2x  2 trên đoạn 0;2 bằng A. 10 B. 2 C. 1 D. 0
………………………….………………………………………………………………………………………… x m
Câu 6: Với giá trị nào của m thì giá trị lớn nhất của hàm số f x 2 1 
trên đoạn 1; 2 bằng 2? x 1 A. m 1 B. m  2 C. m  3
D. không có m
………………………….…………………………………………………………………………………………  x Câu 3 1
7: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y  ? x  2 A. x  2  B. y  2 C. y  3 D. x  3  1 x Câu 3
8: Với giá trị nào của tham số m thì tiệm cận đứng của đồ thị hàm số y
đi qua điểm A2;3 ? x m 1 A. m  3  B. m  1  C. m 1 D. m  3
………………………….…………………………………………………………………………………………
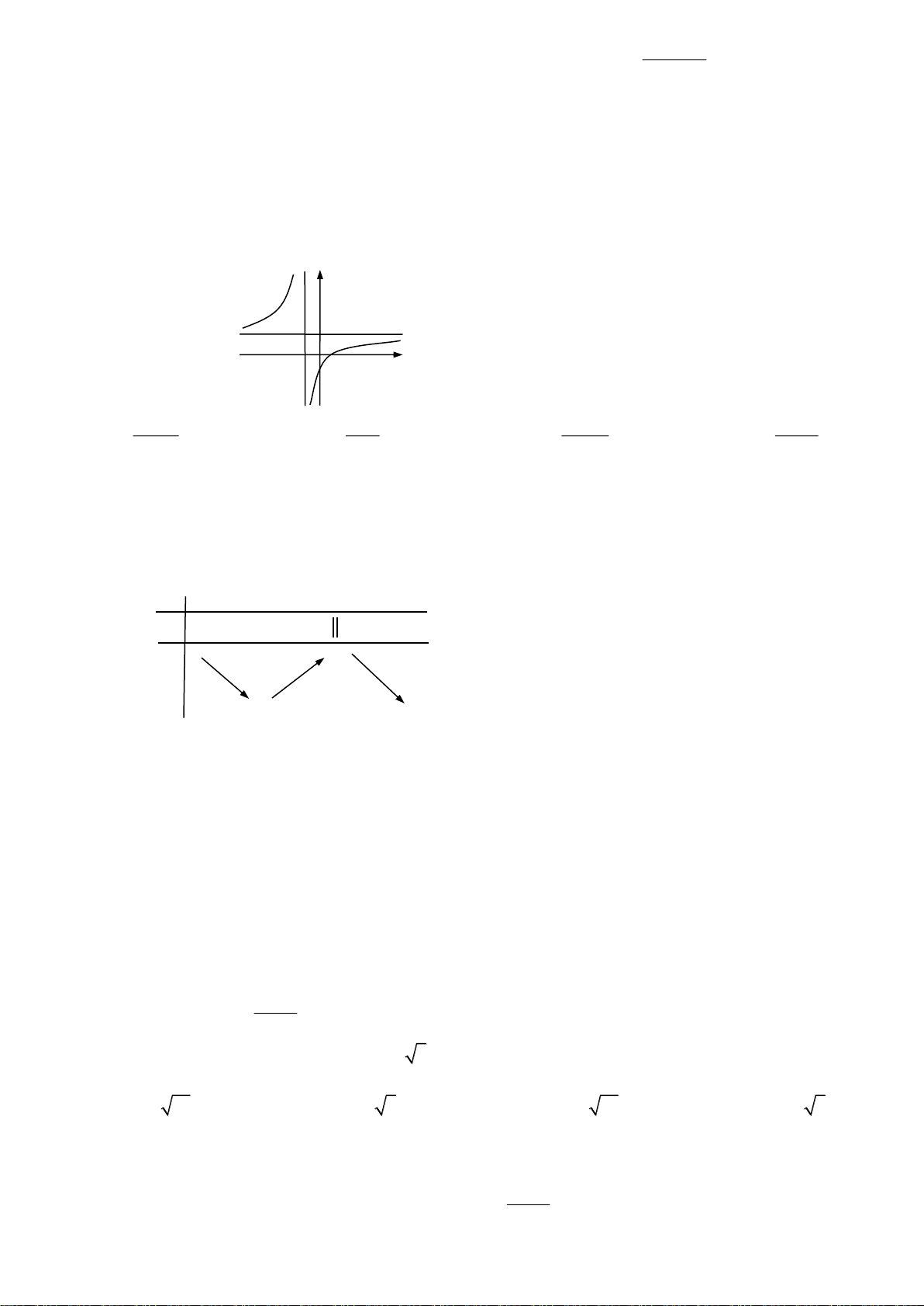
Câu 9: Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. y 1 O –1 x
Hỏi đó là hàm số nào? 2x  3 x 1 2x  2 2x 1 A. y B. y C. y D. y x 1 x 1 x 1 x 1
………………………….…………………………………………………………………………………………
Câu 10: Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây. Hỏi hàm số đã cho có bao nhiêu cực trị? x - 1 3 + y’ - 0 + - 0 8 y –4 4 A. 4 B. 1 C. 2 D. 3
………………………….…………………………………………………………………………………………
Câu 11: Phương trình nào sau đây là phương trình tiếp tuyến của đồ thị hàm số 3 y  2
x  8x  2 tại điểm có hoành độ bằng 0?
A. y  8x  2 B. y  2
C. y  2x 1
D. y  6x  2
………………………….………………………………………………………………………………………… x Câu 2 1
12: Cho hàm số y
có đồ thị C . Với các giá trị nào của m thì đường thẳng d  : y x m 1 x 1
cắt C tại hai điểm phân biệt ,
A B và AB  2 3 ?
A. m  4  10
B. m  4  3
C. m  2  10
D. m  2  3
………………………….…………………………………………………………………………………………   Câu 1
13: Hàm nào sau đây là đạo hàm của hàm số y  log ? 2   1 2x 2 2 2 2 2 A. y '  B. y '  C. y '  D. y '  x ln 4  ln 2 ln 2  x ln 4 x ln 2  ln 4 ln 4  x ln 2
………………………….…………………………………………………………………………………………
Câu 14: Tập nào sau đây là tập xác định của hàm số y  log  2 x  2x ? 7  A.  ;  2
 0; B.  2  ;0 C.  ;  2   D.  2;  
………………………….…………………………………………………………………………………………
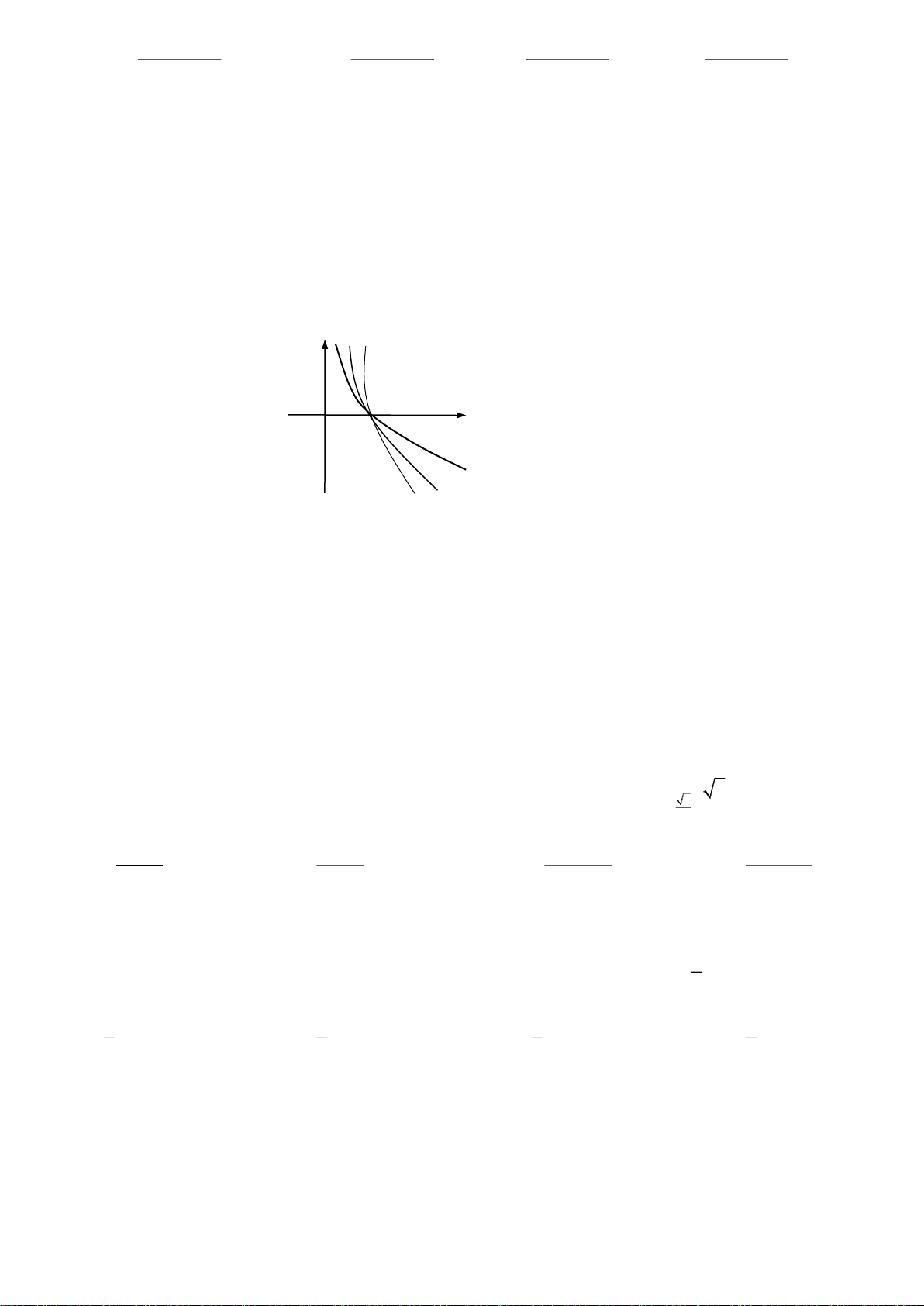
Câu 15: Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số y  log x, y  log x, y  log x được cho a b c trong hình vẽ bên. y 1 O x y= logbx y= logax y= logcx
Mệnh đề nào dưới đây đúng?
A. a c b .
B. a b c .
C. c a b .
D. b c a .
………………………….…………………………………………………………………………………………
Câu 16: Giá trị nhỏ nhất của hàm số   2    40 20 20 1283 x y x x e
trên tập số thực bằng A. 1238  B. 280 163.e C. 320 157.e D. 300 8.e
………………………….…………………………………………………………………………………………
Câu 17: Cho hai số thực dương a,b thỏa mãn log b  2000 . Giá trị biểu thức 3 log
b.a bằng aa b 4006 4006 2669999 2669999 A. B. C. D. 11997 11997 4 4
………………………….………………………………………………………………………………………… Câu a
18: Cho hai số thực dương a và b thỏa mãn log a  log b  log (a b). Tỉ số bằng 3 4 7 b 3 4 7 7 A. B. C. D. 4 7 4 3
………………………….………………………………………………………………………………………… Câu x x
19: Biết rằng phương trình 2 2 2 4  2
 6  m có đúng 3 nghiệm. Mệnh đề nào sau đây đúng? A. m  2
B. 2  m  3
C. 3  m  5 D. 5  m
………………………….………………………………………………………………………………………… 3
Câu 20: Bạn A là sinh viên của một trường Đại học, bạn muốn vay tiền ngân hàng với lãi suất ưu đãi để trang
trải kinh phí học tập hàng năm. Đầu mỗi năm học, bạn ấy vay ngân hàng số tiền 10 triệu đồng với lãi suất mỗi
năm là 4%. Số tiền mà A nợ ngân hàng sau 3 năm là bao nhiêu biết rằng trong 3 năm đó, ngân hàng không thay
đổi lãi suất (kết quả làm tròn đến nghìn đồng)? A. 32.464640 đồng B. 32.216.000 đồng
C. 30.216.464 đồng D. 31.200.000 đồng
………………………….…………………………………………………………………………………………
Câu 21: Hình lăng trụ tứ giác đều (không là hình lập phương) có bao nhiêu mặt phẳng đối xứng? A. 4 B. 5 C. 2 D. 3
………………………….…………………………………………………………………………………………
Câu 22: Cho hình chóp tứ giác .
S ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt phẳng đáy và SA  2a . Thể tích V của khối chóp . S ABCD bằng 3 2a 3 2a 3 2a A. B. C. 3 2a D. 6 4 3
………………………….…………………………………………………………………………………………
Câu 23: Cho khối tứ diện đều ABCD có cạnh bằng a. Gọi B ', C ' lần lượt là trung điểm của các cạnh AB và
AC. Thể tích V của khối tứ diện AB 'C ' D bằng 3 a 3 3 a 2 3 a 3 a 2 A. . B. . C. . D. . 48 48 24 24
………………………….…………………………………………………………………………………………
Câu 24: Cho hình chóp .
S ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy, mặt bên SBC  hợp 3 a 3
với đáy một góc bằng 60 ,
M là trung điểm của .
CD Biết thể tích khối chóp . S ABCD bằng , khoảng 3
cách từ M đến mặt phẳng SBC bằng a 3 a 3 a 3 A. B. C. D. a 3 6 4 2
………………………….…………………………………………………………………………………………
Câu 25: Cho lăng trụ đứng AB .
C A' B'C ' có các cạnh bằng a . Thể tích V khối tứ diện ABA'C ' bằng 3 a 3 3 a 3 3 a 3 a 3 A. B. C. D. 4 6 6 12
………………………….…………………………………………………………………………………………
Câu 26: Cho hình lăng trụ đều AB .
C A' B'C' có cạnh đáy bằng a , cạnh bên bằng a 3 . Thể tích của khối lăng trụ bằng 3 a 3 3 3a 3 a 3 3 a 7 A. B. C. D. 4 4 7 5 4
Câu 27: Trong không gian cho tam giác ABC vuông tại A , AB a và 0
ACB  30 . Thể tích của khối nón
nhận được khi quay tam giác ABC quanh cạnh AC bằng 3 3 a 3 3 a A. . B. 3 3 a . C. . D. 3  a . 3 9
………………………….…………………………………………………………………………………………
Câu 28: Một khối nón có thể tích bằng 30 . Nếu giữ nguyên chiều cao và tăng bán kính mặt đáy của khối nón
lên hai lần thì thể tích của khối nón mới bằng bao nhiêu? A. 120 B. 60 C. 40 D. 480
………………………….…………………………………………………………………………………………
Câu 29: Cho hình trụ có bán kính đáy bằng a, chu vi của thiết diện qua trục bằng 10 .
a Thể tích của khối trụ
giới hạn bởi hình trụ đã cho bằng A. 3 4 a . B. 3 3 a . C. 3  a . D. 3 5 a .
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 30:Một hình trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R. Diện tích xung
quanh của hình trụ bằng A. 2 2 R B. 2 2 R C. 2 2 2 R D. 2 4 R
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
PHẦN II: TỰ LUẬN (4 điểm)Thời gian 30 phút - 10 câu
Câu 1: Tìm m để hàm số 4
y x  m   2 2
4 x có 3 cực trị.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………  Câu 2: x 2
Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số y  2 x 1
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 3: Cho hàm số y f x biết y f 'x có bảng biến thiên như sau x – –5 1 2 + f’’ - 0 + f’ 3 3 -1 5
Hàm số y f x 3x đồng biến trên khoảng nào?
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 4: Giải phương trình x 2 2  4 2  0 .
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 5: Giải phương trình log x  4  3 . 2  
………………………….…………………………………………………………………………………………
………………………….………………………………………………………………………………………… 3x 1    Câu 6: 1 1 Giải bất phương trình    .  2  8
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 7: Giải bất phương trình x   2 ln ln 2x  3x
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 8: Tính diện tích S của mặt cầu biết rằng bán kính của mặt cầu bằng 2 .
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 9: Cho khối nón có đường kính đáy bằng 8 và thể tích bằng15 . Tính diện tích xung quanh của hình nón.
………………………….…………………………………………………………………………………………
………………………….…………………………………………………………………………………………
Câu 10: Cho khối trụ có thể tích bằng 1 5 và diện tích xung quanh bằng 8 . Tính bán kính đường tròn đáy của hình trụ.
………………………….…………………………………………………………………………………………
………………………….………………………………………………………………………………………… Hết 6
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12 NĂM HỌC 2017-2018 ĐỀ 3
PHẦN I: TRẮC NGHIỆM (6.0 điểm) Thời gian 60 phút-30 câu
Câu 1: Cho hàm số 4 2
y  x  2x 1. Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng 0  ;1 .
B. Hàm số đồng biến trên khoảng 1; 2 .
C. Hàm số nghịch biến trên khoảng  ;0  .
D. Hàm số đồng biến trên khoảng  2  ;  1 .
………………………….………………………………………………………………………………………
Câu 2: Tập tất cả các tham số thực nào của m thì hàm số 3 2
y mx mx  3x 1 đồng biến trên khoảng  ;   ? A. 0;9 B.  ;  09; C. 0;9 D. 9; 
………………………….……………………………………………………………………………………… Câu 3: Hàm số 3 2
y x  4x  4 có giá trị cực tiểu bằng bao nhiêu? 8 148 A. 0 B. C. 4 D.  3 27
………………………….………………………………………………………………………………………
Câu 4: Cho số hàm số 3 2
y x  3mx x có đồ thị C . Biết rằng đường thẳng y  3 cắt C tại 3 điểm A,
B, C thỏa mãn BA BC . Mệnh đề nào sau đây đúng? A. m  1  B. 0  m  3
C. 3  m  5 D. m  5
………………………….………………………………………………………………………………………  Câu x
5: Giá trị nhỏ nhất của hàm số f x 1 
trên đoạn 0;2 bằng x  2 1 1 A. 0 B. C.
D. không tồn tại. 2 4
………………………….………………………………………………………………………………………
………………………….………………………………………………………………………………………
Câu 6: Với tất cả các giá trị nào của m thì giá trị lớn nhất của hàm số f x 2
 cos x  4cos x m trên đoạn 0;8  bằng 2? A. m 1 B. m  3  C. m  4
D. không có m 1  x Câu 3 1
7: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y  ? x  2 1 A. x  2
B. x C. y  0
D. đồ thị không có tiệm cận ngang. 3
………………………….………………………………………………………………………………………
Câu 8: Cho hàm số y f x có lim f x  3 và lim f x  3
 . Khẳng định nào sau đây là khẳng định x x đúng?
A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x  3 và x  3  .
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y  3 và y  3
D. Đồ thị hàm số đã cho không có tiệm cận ngang.
………………………….………………………………………………………………………………………
Câu 9: Hàm số y f (x) xác định, liên tục trên \  
1 và có bảng biến thiên như hình dưới đây: – x 1 + A y’ + + 1 + y – 1
Hàm số f (x) là hàm nào sau đây? 1 x x 1 x 1 x 1 A. y B. y C. y D. y x 1 1 x x 1 x 1
………………………….………………………………………………………………………………………
Câu 10: Cho hàm số có bảng biến thiên như sau: x - –5 2 + + y’ 0 – 0 + 1 ∞ 3 2 y 0 –5
Mệnh đề nào dưới đây đúng?
A. Hàm số có bốn điểm cực trị.
B. Hàm số đạt cực tiểu tại x  2 .
C. Hàm số không có giá trị lớn nhất.
D. Hàm số đạt cực tiểu tại x  5  . Câu 1
11: Hệ số góc tiếp tuyến của đồ thị hàm số y  ln x 1 tại điểm có hoành độ bằng e 1 A. e B. 0 C. 1 D. e 2
………………………….……………………………………………………………………………………… Câu 1 m
12: Cho hàm số f x 3 2  x
x 1 có đồ thị C . Biết rằng đồ thị f x và trục hoành có một 3 2
điểm chung. Mệnh đề nào sau đây đúng? A. m  2 B. 2   m 1 C. 1 m  4 D. m  5
………………………….………………………………………………………………………………………
Câu 13: Hàm nào sau đây là đạo hàm của hàm số y  log ln 2x ? 2 1 1 1 A. y  . B. y  . C. y  . D. y  . x ln 2 . x ln10 x ln 2 . x ln10 2x ln 2 . x ln10 x ln 2x
………………………….………………………………………………………………………………………
Câu 14: Cho số thực x thỏa log log x  log log x . Giá trị biểu thức log x bằng 2 2018 2  8  8  2  1 1 A. . B. 1009 27 . C. 2018 27 . D. . 1009 3 2018 3 e
Câu 14: Hàm số y   2  x 2 16 4 có tập xác định là: A.  2  ;2 . B.  ;  2
 2; . C.  ;   . D. R \  2  ;  2
………………………….………………………………………………………………………………………
Câu 15: Hàm số nào trong các hàm số dưới đây có đồ thị là hình vẽ bên? y 1 O x x x  1  A. y  log x . B. y  log
x . C. y   3 . D. y    . 3 1  3  3
………………………….………………………………………………………………………………………
Câu 16: Giá trị nhỏ nhất của hàm số y f (x)  x ln x 1 trên 2 1  ;e  là:   1 A. 1 B. 2
2e 1 C. e 1 D.  1 e
………………………….………………………………………………………………………………………
Câu 17: Cho a là số dương khác 1, b là số dương và m là số thực bất kì. Mệnh đề nào dưới đây đúng ? 1 m 1 A. log b  log . b B. log m b mlog . b C. log b b D. log b m b m  log . m  log . a a m a a m a a a a
………………………….……………………………………………………………………………………… 3
Câu 18: Cho biểu thức 2 2 2
P (ln a  log )
e  ln a  log e , với a là số dương khác 1. Mệnh đề nào dưới đây a a đúng ? A. 2
P  2 ln a 1. B. 2
P  2 ln a . C. 2
P  ln a  2 . D. 2
P  2 ln a  2 .
………………………….………………………………………………………………………………………
Câu 19: Cho phương trình 9x  2( 1)3x m
 3m  4  0. Với giá trị thực nào của tham số m thì phương
trình có 2 nghiệm phân biệt x , x sao cho x x  3 ? 1 2 1 2 31 5 7 A. m B. m C. m
D. m  3. 3 2 3
………………………….………………………………………………………………………………………
Câu 20: Sự tăng trưởng của một loại vi khuẩn tuân theo công thức  . rt S
A e , trong đó A là số lượng vi
khuẩn ban đầu, r là tỉ lệ tăng trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban
đầu là 100 con và sau 5 giờ có 300 con. Để số lượng vi khuẩn ban đầu tăng gấp đôi thì thời gian tăng trưởng
t gần với kết quả nào sau đây nhất? A. 3 giờ 9 phút. B. 3 giờ 2 phút. C. 3 giờ 16 phút. D. 3 giờ 30 phút.
………………………….………………………………………………………………………………………
Câu 21: Hình lăng trụ có thể có số cạnh là số nào sau đây ? A. 2015 B. 2017 C. 2018 D. 2016
………………………….………………………………………………………………………………………
Câu 22: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC và SA  2a . Tam giác ABC vuông
cân tại B và AC a 2 . Sin góc  hợp bởi đường thẳng SB và mặt phẳng  ABC bằng 3 2 1 2 5 A. . B. . C. . D. . 2 2 2 5
………………………….………………………………………………………………………………………
Câu 23: Cho khối chóp S.ABC có SA vuông góc với đáy, SA  4, AB  6, BC 10 và CA  8 . Thể tích
của khối chóp S.ABC bằng A. 40 . B. 192. C. 32 . D. 24 .
………………………….………………………………………………………………………………………
Câu 24: Cho hình chóp S.ABC có đáy ABC là tam giác đều, mặt bên SAB vuông góc với mặt phẳng đáy
và tam giác SAB vuông tại S , SA a 3, SB a . Thể tích của khối chóp S.ABC bằng 1 1 1 1 A. 3 a .B. 3 a . C. 3 a . D. 3 a . 4 3 6 2 4
Câu 25: Cho khối lăng trụ AB . C A B
C có AB BC  5a, AC  6a . Hình chiếu vuông góc của  A trên mặt
phẳng  ABC  là trung điểm của AB và 133   a A C
. Thể tích của khối lăng trụ AB . C A B C bằng 2 A. 3 12a . B. 3 12 133a . C. 3 36a . D. 3 4 133a .
………………………….………………………………………………………………………………………
Câu 26: Cho lăng trụ đều AB .
C A' B'C ' có cạnh đáy bằng 2a . Diện tích xung quanh bằng 2 6 3a . Thể tích
của khối lăng trụ bằng 1 3 A. 3 a . B. 3 a . C. 3 a . D. 3 3a . 4 4
………………………….………………………………………………………………………………………
Câu 27: Cho tam giác OAB vuông tại O có AB  2a, OB a quay xung quanh cạnh AB tạo thành khối
tròn xoay. Thể tích của khối tròn xoay này bằng 3  a 3 3 4 a 3  a A. 3  a 3 . B. . C. . D. . 3 3 2
………………………….………………………………………………………………………………………
Câu 28: Cho một hình nón có bán kính đáy bằng a và góc ở đỉnh bằng 60. Diện tích xung quanh của hình nón đó bằng 2 2 3 a 2 4 3 a A. 2 4 a . B. . C. . D. 2 2 a . 3 3
………………………….………………………………………………………………………………………
Câu 29: Trong không gian, cho hình chữ nhật ABCD có AB  1 và AD  2 . Gọi M , N lần lượt là trung
điểm của AD và BC . Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Diện tích toàn
phần của hình trụ đó bằng A. 4 .
B. 2 . C. 6 . D. 10 .
………………………….………………………………………………………………………………………
Câu 30: Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có AB  3, AD  4, AA'  5 . Diện tích S của mặt cầu
ngoại tiếp khối chóp ACB' D' bằng
A . 100. B. 60. C. 50. D. 80.
………………………….……………………………………………………………………………………… 5
PHẦN 2: TỰ LUẬN (4 ĐIỂM)
Thời gian 30 phút - 10 câu Câu x 3
1: Tìm tiệm cận đứng của đồ thị hàm số y  . 2x 1
………………………………………………………………………………………………… Câu 2: 3
Tìm khoảng đồng biến của hàm số 2
y x  3x .
………………………………………………………………………………………………… Câu 3: Gọi 1
x , x , x lần lượt là các điểm cực trị của hàm số 4 2 y
x  2x 1 , trong đó x x x . Tính 1 2 3 2 1 2 3 giá trị biểu thức 3 3 3
A x x x . 1 2 3
……………………………………………………………………………………………… Câu 4:
Giải phương trình x 1 2  5  0 .
…………………………………………………………………………………………………
Câu 5: Giải phương trình log x  5  3 . 1   2
………………………………………………………………………………………………… 2x   Câu 6: 1 1 Giải bất phương trình    .  4  8
…………………………………………………………………………………………………
Câu 7: Giải bất phương trình x    2 log
1 log x x .
…………………………………………………………………………………………………
Câu 8: Quay một hình tròn có đường kính bằng 4 xung quanh một đường kính của nó.Tính thể tích khối tròn xoay thu được.
…………………………………………………………………………………………………
Câu 9: Cho khối nón có bán kính đáy bằng 3 và thể tích bằng16 . Tính diện tích xung quanh của hình nón.
…………………………………………………………………………………………………
Câu 10: Cho khối trụ có thể tích bằng 12 và diện tích xung quanh bằng 8 . Tính bán kính đường tròn đáy của hình trụ.
………………………….………………………………………………………………………………………
………………………….……………………………………………………………………………………… Hết 6
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12 NĂM HỌC 2018-2019 ĐỀ 4
PHẦN I: TRẮC NGHIỆM (6.0điểm)Thời gian 60 phút-30 câu
Câu 1: Hàm số nào sau đây đồng biến trên (0;  ) ? A. 4 2
y  x x . B. 4 2
y x x . C. 4 2
y  x x . D. 4 2
y x x .
………………………….……………………………………………………………………………………… Câu 1
2: Có bao nhiêu giá trị nguyên dương của tham số thực m để hàm số 3 2 y
x mx  4mx m đồng biến 3 trên khoảng  ;   ? A. 1. B. 2. C. 4. D. 3.
………………………….………………………………………………………………………………………
Câu 3: Trên đoạn [ 1  ;2] , hàm số 4 2
y x  2x có giá trị cực đại bằng A. 1.  B. 8. C. 1. D. 0.
………………………….………………………………………………………………………………………
Câu 4: Cho số hàm số 3 2
y  2x  9x 12x m . Với giá trị thực nào của tham số m thì đồ thị hàm số có hai điểm
cực trị và điểm cực tiểu nằm trên trục hoành? A. m  0.
B. m 1. C. m  5.  D. m  4. 
………………………….………………………………………………………………………………………
Câu 5: Giá trị nhỏ nhất của hàm số f x 2
x x  3 bằng 1 11 11 A. 0. B. . C. . D. . 2 4 2
………………………….………………………………………………………………………………………
Câu 6: Với tất cả các giá trị nào của tham số m thì giá trị nhỏ nhất của hàm số f x 2 2
 ln(x m 1) trên đoạn 1; 2 bằng ln3 ? A. 0  ;1 . B.  1  ;  0 . C.  1  ;  1 .
D. không có m .
………………………….……………………………………………………………………………………… 2x 1
Câu 7: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y  ? x  2 A. y  0. B. y  2. C. y  2. D. y  1. 1   Câu x 2m 1
8: Với giá trị nào của tham số m thì đồ thị hàm số y
không có đường tiệm cận đứng? x 1 1 A. m  . B. m  2. C. m  0. D. m  1.  2
………………………….………………………………………………………………………………………
Câu 9: Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. 2∙x y w1 x   = x + 1
Hỏi đó là hàm số nào? f2 x   = 2 g2 y   = 1 2x  3 2x A. y  . B. y  . 2 x 1 x 1 x 2x C. y  . y  . -1 O x x D. 1 x  1
………………………….………………………………………………………………………………………
Câu 10: Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây. Mệnh đề nào đúng? x - ∞ -1 1 + ∞ y' - 0 + || - + ∞ 5 y 4 - ∞ A. y  0. B. maxy  5. C. miny  4. D. y  5. CT CD
………………………….………………………………………………………………………………………
Câu 11: Phương trình nào sau đây là phương trình tiếp tuyến của đồ thị hàm số 3 2
y  2x  3x 12x 10 tại điểm
cực đại của đồ thị hàm số? A. y  17 . x B. y  10. C. y  10 . x D. y  17.
………………………….……………………………………………………………………………………… Câu x
12: Cho hàm số y
C . Với các giá trị nào của m thì đường thẳng d  : y  x m 1 cắt
x  có đồ thị   1
Ctại hai điểm phân biệt ,
A B và AB ngắn nhất? A. m  2. B. m 10. C. m  1.  D. m  0.
………………………….………………………………………………………………………………………
Câu 13: Hàm số y  log cos x có đạo hàm là 2   tan x
A. y '  log e.tan . x
B. y '  ln 2. tan . x
C. y '  log e.cot . x D. y '  . 1 1 ln 2 2 2 2
Câu 14: Tập nào sau đây là tập xác định của hàm số y  log x  22 ? 7 A.  ;  2
 7;. B.  2
 ; . C. 0; . D. \  2 .
………………………….……………………………………………………………………………………… t 1 x   = 2x ln x   u1 x   = y
Câu 15: Cho ba hàm số 2x y
, y x và y f (x) có đồ ln th (2) ị như hình bên. v1 x   = x y=2x y=x
Mệnh đề nào dưới đây đúng? y=f(x)
A. y f (x)  log . x
B. y f (x)  ln . x 1 2 O x
C. y f (x)  log . x
D. y f (x)  log . x 2
………………………….……………………………………………………………………………………… Câu 2
16: Giá trị nhỏ nhất của hàm số x 50 x 1000 y e   
trên tập số thực bằng A. 25 5 e . B. 25 e . C. 1000 e . D. 375 e .
………………………….……………………………………………………………………………………… Câu a
17: Cho hai số thực dương a, b và ab  1 thỏa mãn 1 log a  . Giá trị biểu thức log bằng ab 2018 ab b 504 504 1009 1009 A.  . B. . C.  . D. . 1009 1009 504 504
………………………….………………………………………………………………………………………
Câu 18: Có bao nhiêu giá trị nguyên của tham số m để hàm số 2
y  log (x  2mx  4) có tập xác định là ? 2 A. 3. B. 4. C. 2. D.1.
………………………….………………………………………………………………………………………
Câu 19: Tìm tất cả các giá trị của tham số m để phương trình x 4 2   m 2x
có 2 ngiệm phân biệt? 1 A. 2   m  1  . B. 1
  m  0.
C. 3  m  4.
D. m  3.
………………………….………………………………………………………………………………………
Câu 20: Sự tăng trưởng dân số được ước tính theo công thức tăng trưởng mũ  . nr S A e
, ( A dân số ban đầu, n
thời gian (năm), r tỷ lệ tăng trưởng). Biết rằng tỷ lệ tăng trưởng dân số thế giới hằng năm là 1.32% . Năm 2018,
dân số thế giới vào khoảng 7,5 tỷ người. Với mức tăng trưởng như trên thì dân số năm 2030 là bao nhiêu? A. 8,78 tỷ người. B. 7,78 tỷ người. C. 9,78 tỷ người. D. 6,78 tỷ người.
………………………….………………………………………………………………………………………
Câu 21: Hình chóp nào sau đây không nội tiếp được trong mặt cầu?
A. Hình chóp SABCD có đáy ABCD vuông.
B. Hình chóp SABCD có đáy ABCD thoi.
C. Hình chóp SABCD có đáy ABCD hình chữ nhật.
D. Hình chóp SABCD có 0
ABC CDA  180 . 3
Câu 22: Cho hình chóp tứ giác .
S ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng
đáy . Gọi M , N lần lượt là trung điểm BC , .
CD Biết thể tích của khối chóp .
S ABCD bằng V thì khi đó thể 0 tích khối . S AMN bằng 3 1 2 5 A. V . B. V . C. V . D. V . 0 8 0 4 0 3 0 8
………………………….………………………………………………………………………………………
Câu 23: Cho khối tứ diện đều ABCD có cạnh bằng a. Gọi M , N lần lượt là trung điểm của các cạnh AB và
AC, K là điểm trên AD sao cho AK  2KD . Thể tích của khối tứ diện AMNK 3 a 3 3 a 2 3 a 2 3 a 2 A. . B. C. . D. . 72 48 72 24
………………………….………………………………………………………………………………………
Câu 24: Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật , SA vuông góc với đáy, AB  2a, AD  4 . a 8 21
M là trung điểm SB , N là trung điểm SD . Biết khoảng cách từ S đền mặt phẳng ( AMN ) bằng a . 21 Thể tích khối chóp . S ABCD bằng 3 2 2a 3 64a 3 8a 3 a 21 A. . B. . C. . D. . 21 3 3 3 4
Câu 25: Cho lăng trụ ABC .
D A' B'C ' D' có đáy ABCD là hình vuông cạnh bằng a, tâm .
O Hình chiếu vuông
góc của B ' trên mặt phẳng (ABCD) là O . Góc hợp bởi BB ' và mặt phẳng (ABCD) bằng 0 60 . Thể tích V
khối tứ diện ABCD' bằng 3 a 6 3 a 6 3 a 6 3 a 3 A. . B. . C. . D. . 4 12 6 12
………………………….………………………………………………………………………………………
Câu 26: Cho hình lăng trụ đều AB .
C A' B 'C' có cạnh đáy bằng a , cạnh bên bằng a 3 . Thể tích của khối lăng trụ bằng 3 a 3 3a 3 a 3 a 5 A. . B. . C. . D. . 3 4 6 3
Câu 27: Hình nón tròn xoay có đường cao h  40 cm , bán kính đáy r  50cm . Một thiết diện qua đỉnh của hình
nón và khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24cm . Diện tích của thiết diện bằng A. 2 800 cm . B. 2 1600 cm . C. 2 2000 cm . D. 2 2200 cm . Câu 16
28: Một khối nón có thể tích bằng
 . Nếu chiều cao của khối nón bằng đường kính thì diện tích xung 3
quanh S của khối nón bằng xq 4 5 A. S  . B. S  5. C. S  2 5. D. S  4 5. xq 3 xq xq xq
Câu 29: Mặt phẳng (P) cắt hình cầu (S ) theo thiết diện là đường tròn có bán kính bằng 3. Biết khoảng cách từ
tâm mặt cầu đến mặt phẳng (P) bằng 4. Thể tích V của khối cầu (S ) bằng 500 400 100 50 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 30: Một hình trụ có diện tích một đáy bằng 8 , diện tích xung quanh 32 . Thể tích khối trụ là A. 50 2. B. 32 2. C. 72 2. D. 64 2.
PHẦN II: TỰ LUẬN (4 điểm)
Thời gian 30 phút - 10 câu
Câu 1: Tìm m để hàm số 4
y mx  m   2 2
4 x có hai cực đại và một cực tiểu.
……………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………… Câu 2: x 1
Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số y  ? x 1
……………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………… 5
Câu 3: Cho hàm số y f (x), y g(x) liên tục trên [2; 2] , biết đồ thị
v1(x) = x4 4∙ c x2 + ủa 2
hàm số f '(x), g '(x) như hình vẽ
w1(x) = x2 2
(đường đậm là đồ thị f '(x) ) . Tìm các khoảng đồng biến của hàm số y f (x)  g(x)? y
…………………………………………………………………………
……………………………………………………………………….… -2 -1 1 2 x O x
Câu 4: Giải phương trình 2 2 2x   2  0 .
……………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………… Câu 5: 1 Giải phương trình log x 1  log 3  . 2   2 4
……………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………… 1x   Câu 6: 2 9
Tìm tập nghiệm của bất phương trình    .  3  4
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 7: Giải bất phương trình ln 3 ln(x 1)  e
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 8: Cho hình chóp S.ABC , tam giác ABC vuông tại B , SA vuông góc mặt phẳng (ABC) . Xác định tâm
của mặt cầu ngoại tiếp hình chóp S.ABC .
……………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………… Câu 9: 1
Cho khối nón có diện tích đáy bằng
 , khoảng cách từ đỉnh của khối nón đến một điểm bất kỳ trên 2 đường tròn đáy bằ 10 ng
. Thể tích khối nón bằng bao nhiêu? 2
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
Câu 10: Cho khối trụ có diện tích toàn phần bằng 3 , chiều cao của khối trụ là 2 . Tính thể tích khối trụ đó.
……………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………… Hết 6
ĐỀ MẪU KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 12 NĂM HỌC 2018-2019 ĐỀ 5
PHẦN 1: Hình thức trắc nghiệm (6.0 điểm) 2
Câu 1: Cho hàm số y
. Mệnh đề nào dưới đây đúng ? x 1
A. Hàm số nghịch biến trên khoảng \{1}.
B. Hàm số đồng biến trên khoảng \{1}.
C. Hàm số nghịch biến trên khoảng  ;   1 .
D. Hàm số đồng biến trên khoảng 1;  .
………………………….………………………………………………………………………………………
Câu 2: Với giá trị nào của tham số thực của m thì hàm số 3 2 2
y  x  3mx  9mx m nghịch biến trên khoảng  ;   ?
A. 0  m  3.
B. 3  m  4. C. 1   m  0. D. m  4 .
………………………….……………………………………………………………………………………… 1
Câu 3: Hàm số y x x đạt cực tiểu tại điểm nào? 1 A. x  1. B. x  0. C. x  2. D. x  2. 
………………………….………………………………………………………………………………………
Câu 4: Cho số hàm số 3 2 2 y  2  x  ( 3
m  3m  27)x . Nếu tập hợp T là tập tất cả các giá trị của tham số m để
hàm số đạt cực tiểu tại x  3
 thì mệnh đề nào đúng? A. T   3  ;4.  
B. T  (0; 4].
C. T  ( 3;0].
D. T  [ 3;1).
………………………….……………………………………………………………………………………… 2
Câu 5: Cho hàm số f x 
1;3 , mệnh đề nào đúng? 2
x  . Với mọi x thuộc đoạn   1 1 1 A.
f (x)  1.
B. 1  f (x)  5 .
C. 1  f (x)  0 . D.
f (x)  2 . 2 5
………………………….………………………………………………………………………………………   Câu x mx 1
6: Với giá trị nào của m thì giá trị lớn nhất của hàm số f x 2  bằng 1? 2 x 1 A. m  2018. B. m  0. C. m .
D. Không có m .
………………………….………………………………………………………………………………………
………………………….………………………………………………………………………………………
………………………….……………………………………………………………………………………… 1
Câu 7: Đồ thị của hàm số nào sau đây có tiệm cận đứng ? 2 3x  5x  2 1 x  1  2 2x 1 A. y  . y  . y  . D. y  . x B. 2 2 x C. 2 x  3 x
………………………….………………………………………………………………………………………  Câu x m
8: Đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số y x m  tạo với hai trục tọa độ thành một 2
tứ giác có diện tích bằng 2 . Khi đó, phát biểu nào sau đây đúng? A. m  ;  5  . m 6;10 B. . C. m  5  ;  1 . D. m  1  ;5. t1 x
  = x4 + x2
………………………….………………………………………………………………………………………
Câu 9: Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? y A. 3 2
y x x . B. 2 y x  . x C. 4 2
y x x . D. 4 2
y x x . O x
Câu 10: Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây. x - ∞ -1 3 + ∞ y' + || - 0 + 6 + ∞ y -1 - ∞ Mệnh đề nào đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị lớn nhất bằng 6.
C. Hàm số có giá trị cực tiểu bằng 3.
D. Hàm số đạt cực đại tại x  1
 và đạt cực tiểu tại x  3.
………………………….………………………………………………………………………………………
Câu 11: Tiếp tuyến của đồ thị hàm số 5
y x  5x 1 tại M (2; 23) cắt hai trục tọa độ tại ,
A B . Khi đó diện tích
S của tam giác OAB ( với O là gốc tọa độ) bằng 16129 16129 127 16129 A. S  . B. S  . C. S  . D. S  . 150 75 25 151
………………………….………………………………………………………………………………………
………………………….……………………………………………………………………………………… 2
Câu 12: Đồ thị hàm số nào sau đây cắt trục hoành tại bốn điểm phân biệt? A. 4 2
y x  3x  2. B. 3 2
y x  3x  2. C. 4 2
y   x  3x  2. D. 4 2
y x  3x  2.
………………………….………………………………………………………………………………………
Câu 13: Hàm nào sau đây là đạo hàm của hàm số 2 x 2 y xee ? A. 2 '  (2 1) x y x e B. 2 '  (2 1) x y x e  2e . C. 2 '  2 x y xe  2e . D. 2 '  ( 1) x y x e .
………………………….……………………………………………………………………………………… ln(x) v1(x) = ln(3)
Câu 14: Tập xác định D của hàm số f x
x    x23 ( ) 2 3 là A. D  ( 3  ;2). B. D  ( 3  ;2]. C. D  ( ;  2]\  3 .
D. D   ;  2 \  0 . y
………………………….……………………………………………………………………………………… ln(3∙x) v ln(3∙x) 1(x) = ln(3) v v ( ) = 2x 1(x) = + 1 1 x ln(3) ln x 1 ln(x) w1(x) =
Câu 15: Đồ thị hàm số y f (x) 
được cho trong hình vẽ bên. ln(3) ln 3 O x 1 3
Đồ thị hàm số y f (3x) là đồ thị nào trong các đồ thị sau đây? y y y y 2 2 1 1 x 1 x O x 1 -1 1 x O A. B. C. D.
………………………….……………………………………………………………………………………… Câu x
16: Giá trị lớn nhất của hàm số f (x)  trên 3 [2;e ] bằng ln x 4 e 5 e 3 e 1339 A. . B. . C. . D. . 8 22 3 200
………………………….……………………………………………………………………………………… Câu a
17: Cho log b  3 . Giá trị log bằng a b b a 3 1 3 1 A. 3 1. B. . C. 3 1. D. . 2  3 3  2
………………………….……………………………………………………………………………………… 17 15 Câu 18: Nếu 3 8 a
a và log  2  5  log  2  3 thì b b  a  1 0  a  1 a  1 0  a  1 A.  . B.  . C.  . D.  . b  1 b   1 0  b  1 0  b 1 3 Câu   
19: Tổng tất cả các nghiệm của phương trình 2 2 x x 2 2
 2 x x  3 là A. 0. B. 2.  C. 1. D. 1. 
………………………….………………………………………………………………………………………
Câu 20: Ông A gửi vào ngân hàng 20 triệu đồng với lãi suất 0.75% mỗi tháng. Hằng tháng Ông A rút ra 300
nghìn đồng vào ngày tính lãi. Hỏi sau hai năm Ông A còn lại bao nhiêu tiền ( làm tròn đến 1000 đồng) ? A. 1.607.000 đồng.
B. 16.071.000 đồng.
C. 16.072.000 đồng.
D. 16.073.000 đồng.
………………………….………………………………………………………………………………………
Câu 21: Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành và có thể tích là V . Gọi M , N lần lượt là 0 trung điểm S ,
A SC . Mặt phẳng  BMN  cắt SD tại K . Tính thể tích khối S.BMKN theo V ? 0 2 2 1 1 A. V . B. V . C. V . D. V . 0 3 0 19 0 6 0 4
………………………….………………………………………………………………………………………
Câu 22: Cho hình chóp tứ giác .
S ABCD có đáy ABCD là chữ nhật, AB a, cạnh bên SA vuông góc với mặt 5
phẳng đáy và SA  5a , góc giữa mặt phẳng (SBD) và ( ABCD) bằng  , biết tan 
. Tính thể tích V của 2 khối chóp . S ABCD 3 2 3a 3 5 5a 3 2 5a 3 2 5a A. V  . B. V  . C. V  . D. V  . 5 2 5 3
………………………….………………………………………………………………………………………
Câu 23: Cho khối tứ diện đều S.ABC . Mặt phẳng (P) qua trung điểm M của SA và song song mặt phẳng V
( ABC) cắt SB, SC lần lượt tại N , K . Tỷ số thể tích SMNK bằng VSABC 2 1 3 1 A. . B. . C. . D. . 3 4 2 8
………………………….………………………………………………………………………………………
Câu 24: Cho hình chóp S.ABC có đáy ABC là là tam giác đều cạnh a . Hình chiếu vuông góc của S trên mặt
phẳng  ABC  là trung điểm của AB , góc giữa SC và mặt phẳng đáy bằng 0
30 . Tính thể tích V của khối chóp S.ABC ? 3 a 3 3 3 a 2 3 a 3 a 3 A. V  . B. V  . C. V  . D. V  . 4 24 2 24
Câu 25: Cho lăng trụ AB .
C A' B'C ' có A'.ABC là tứ diện đều cạnh bằng a . Thể tích V khối chóp A' BCC ' B' bằng 3 a 2 3 a 2 3 a 2 3 a 3 A. V  . B. V  . C. V  . D. V  . 6 4 12 6 4
Câu 26: Cho hình lăng trụ đứng AB .
C A' B'C ' tam giác ABC vuông tại B , BC a , 0
ACB  60 , A' B tạo với
mặt phẳng ( ABC) một góc 0
30 . Thể tích của khối lăng trụ AB .
C A' B'C ' bằng 3 3a 3 a 3 3 3 A. 3 a 3. B. . C. . D. 3 a . 2 3 3
………………………….………………………………………………………………………………………
Câu 27: Trong không gian cho tam giác ABC vuông tại A , AB a và 0
ACB  30 . Thể tích của khối nón
nhận được khi quay tam giác ABC quanh cạnh AC bằng 3 3 a 3 3 a A. . B. 3 3 a . C. . D. 3  a . 3 9
………………………….………………………………………………………………………………………
Câu 28: Một khối nón có thể tích bằng 30 . Nếu giữ nguyên chiều cao và tăng bán kính mặt đáy của khối nón
lên hai lần thì thể tích V của khối nón mới bằng bao nhiêu?
A. V 120 .
B. V  60 .
C. V  40 .
D. V  480 .
………………………….………………………………………………………………………………………
Câu 29: Thiết diện qua trục của hình trụ là một hình vuông cạnh bằng 2a . Gọi S , S lần lượt là diện tích xung 1 2
quanh và diện tích toàn phần của hình trụ đó. Mệnh đề nào đúng?
A. 4S  3S .
B. 3S  2S .
C. 2S S .
D. 2S  3S . 1 2 1 2 1 2 1 2
………………………….………………………………………………………………………………………
Câu 30: Cho tứ diện ABCD có tam giác ABC vuông tại B , cạnh DA vuông góc mặt phẳng (ABC) . Biết
AB  3a, BC  4a, DA  5a . Tính bán kính mặt cầu ngoại tiếp khối tứ diện ABCD theo a. 5 2 5 2 5 3 5 3 A. . a B. . a C. . a D. . a 2 3 2 8
………………………….………………………………………………………………………………………
Phần 2: Hình thức tự luận (4.0 điểm).
Thời gian 30 phút - 10 câu
Câu 1: Tìm điểm cực đại của đồ thị hàm số 3 2
y  x  3x 1 .
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….  Câu 2: x 2
Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số y  . 2 x x  6
……………………………………………………………………………………………………………….
………………………………………………………………………………………………………………. 5
Câu 3: Cho hàm số y f x biết y f 'x có đồ thị như hình vẽ bên
Hàm số y f x  x có mấy cực trị y s1 x
  = 2∙x4 4∙x2 + ( 0,5∙x) + 2 2 1 O x
Câu 4: Giải phương trình logx log 6 6  x 12 .
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 5: Giải phương trình log log x  4 1. 2  
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 6: Giải phương trình 8x 4 2 6.2 x  16  0 .
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 7: Tìm tập nghiệm bất phương trình 2
log x  log(x  2x 11)
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 8: Tính thể tích V khối cầu biết rằng bán kính của khối cầu cầu bằng 3.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 9: Cho khối nón có đường kính đáy bằng 8 và đường sinh bằng 10. Tính thể tích của khối nón.
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Câu 10: Thiết diện qua trục của khối trụ là hình vuông có chu vi bằng 10. Tính thể tích khối trụ đó ?
……………………………………………………………………………………………………………….
………………………………………………………………………………………………………………. Hết 6
Document Outline

  • MARIE-CURIE-de-mau-1-9159
  • MARIE-CURIE-de-mau-2-2939
  • MARIE-CURIE-de-mau-3-3618
  • MARIE-CURIE-de-mau-4-3658
  • MARIE-CURIE-de-mau-5-6854