Đề ôn tập môn Giải tích 1 số 4 | Đại học Bách Khoa Hà Nội

Câu 1. Diện tích mặt tròn xoay được sinh ra khi quay đồ thị hàm s ố 3
y ý x với 0 ó x ó 2 quanh tr c ụ Ox m t ộ
vòng là 2ð øa 145  bù, với a,b . Giá trị a  b là 17 1 8 1 A. . B. . C. . D. . 54 2 3 3
Lời giải
Nhận xét: Diện tích mặt tròn xoay được sinh ra khi quay đồ thị hàm s
ố y ý f ø xù với a ó x ó b quanh b
trục Ox một vòng được tính bởi công thức S ý ð f øxù  ù f  û øxù 2 2 1 ' ù dx û . a 2 16 ð 145 145 1 Áp d ng công th ụ ức ta được 3 4
S ý 2ð x . 1 9x dx ý . 1 9udu ý ð   . 2 27 0 0 145 1 8 Vậy a  b ý  ý . 54 54 3 1102 Câu 2. Cho hàm số ø ù ý .x f x
e sin x . Đặt ø ù a ý f
ø0ù . Khẳng định nào sau đây đúng? A. 163 a ü 10 . B. 165 166 10 ó a ü 10 . C. 166 167 10 ó a ü 10 . D. 163 165 10 ó a ü 10 .
Lời giải ø n ù   ü f øxù ýø 4  ùn 1 4 1 x
e . øsin x cos x ù ÿ ø4n2ù  ÿ f øxù ý 2.ø 4  ÿ ùn 1 . x e .cos x
Bằng phương pháp quy nạp ta chứng minh được n   . ù 3  ÿ f ø xù ý2.ø 4  ù n 1. x e .ø s
 in x cos xù ÿ ø4n4ù ÿ f þ øxù ý ø 4  ùn . x e .sin x Suy ra ø1102ù a ý f ø ù 549 0 ý 2
. Do 165 ü log a ü 166 nên 165 166 10 ó a ü 10 . 4 ø ù Câu 3. Cho hàm s
ố y ý f ø xù thoả mãn ý 3f x x
 f øxù với m i
ọ x  . Đặt a ý 11 f
 øxùdx . Khẳng định 1 nào sau đây đúng? A. a ü 17 .
B. 16 ó a ü 18 .
C. 17 ó a ü 19 .
D. 18 ó a ü 20 .
Lời giải d Nhận xét: x x . Suy ra f ø ù 1 ý 0, f ø 4ù ý 1. df
Ta có:  ø ùd ý ø ù d  ø ù ý ø ù f ø ù  ù3 x f x x xf x x f x xf x  f 
ø xùù df ø xù û û . 4 1 ù ù x 77 22
Khi đó a ý 11 f
 øxùdxý 11. ø4.11.0ù ø3  xùdx ý   ú ú 18,5 . 2 ln3 1 û 0 û 2
üÿx ý 2t t
Câu 4. Đường cong ý l i ồ trên khoảng nào? 3 ÿy þ ý 3t t A. t ü 1. B. t ü 1. C. t þ 1. D. t þ 2 .
Lời giải dyòx yò 3 3 Ta có: t d yò ý ý  t , t yò ý ý . x ø1 ù xò 2 x dx 4ø1tù t dt 2
üÿx ý 2t t
Nhận xét: với t ü 1 thì yò þ 0 , suy ra đường cong ý l i
ồ trên khoảng ø,1ù . x 3 ÿy ý þ 3t t
Câu 5. Khai triển Taylor c a ủ hàm số x
z ý y trong lân cận điểm ø1,1ù đến bậc hai là
A. 1 ø y  ù 1  2ø x  ù 1 ø y  ù 1 .
B. 1 ø y  ù 1  ø x  ù 1 ø y  ù 1 .
C. 1ø y  ù 1  2ø x  ù 1 ø y  ù 1 . D. 1   ø y  ù 1  2ø x  ù 1 ø y  ù 1 .
Lời giải x
üzò ý y .ln y ü x ø ù ò ÿ z ý x ø1, ù 1 0 ÿ
ÿzò ý y .xù ln y ù ÿzò ý xx ø1, ù 1 0 xx û ø ù 2 û ÿÿ ÿ Ta có: x1 y
 þ 0 :ýzò ý x.y suy ra ýzò ý . y ø1, ù 1 1 y ÿ ÿ
zò ý x. x  y  ÿ zò ý ÿ yy ø1, ù 1 0 yy ø ù x 2 1 . ÿ ÿ x1
zò ý zò ý y . 1 ù  ln y ù ý ý ÿ zò zò þ xy ø1, ù 1 yx ø1, ù 1 1 xy yx û ø ùû þ Khai triển Taylor c a ủ hàm s ố x
z ý y trong lân cận điểm ø1,1ù đến bậc hai là: 2
d f ø1 ñø x  ù 1 ,1ñø y  ù 1 ù
z ý 1 ø y  ù 1 ø x  ù 1 ø y  ù 1  . 2
Câu 6. Tính diện tích của hình phẳng giới hạn bởi đường cong 2 2 4 4
x  y ý x  y . ð 2 A. ð 2 . B. 2ð 2 . C. D. ð . 2
Lời giải
üx ý r ø ù.cos ÿ
ÿx ý r ø ù.sin
Giả sử tồn tại hàm số r ø ù : thoả mãn ý . Suy ra r ø ù 2 ý . 2 2 4 4
ÿx  y ý x  y 3  cos2 ÿ ,x y þ þ 0
Do hình phẳng giới hạn bởi đường cong 2 2 4 4
x  y ý x  y có tính đối xứng qua tr c
ụ Ox và trục Oy ð ð 2 2 r ø ù 2 1
nên diện tích của hình được tính bởi công th c ứ : S ý 4. d ý 8. d   . 2 3 cos 2 0 0  d Đặt t
t ý tan x , suy ra S ý 4. ý ð 2  . 2 1 2t 0 x b b a x e  e
Câu 7. Cho a,b þ 0 . Tính dx  . x a a b A. 0 . B. ab . C. . D. . E. ab e . F. 1 . b a
Lời giải x b b u u b b a b a x u a a u    Đặt ab e e e e ab e e u ý , ta có: S ý dx ý d ý  du ý S    . Suy ra S ý 0 . x x ab u u a b a u x t
Câu 8. Tìm tập giá trị của hàm f : ø1, ù  xác định bởi công th c ứ f øx ù d ý  . ln t x A. ø0,  ù . B . ø1,  ù. C. ø0, ù 1 . D. øln 2,  ù . ö ln 2 ö E. øln 2,ln 3ù . F. , ÷ . 2 ÷ ø ø
Lời giải  x d Nhận xét:  t x þ f ø ù x 1 1: ' x ý
þ 0, suy ra f øxùþ lim ý a  . x.ln x  x1 ln t x 3 2 1 1 Ta có:  þ t þ1: þ þ . 2
øt 1ùø3 t ù ln t t 1  x 2d x t d x t dt Khi đó: ln 2 ý lim  lim  lim ý ln 2    .    x1 t  t  t  t  x ø ù 1 ø3 ù x 1 ln x 1 1 x x x t
Vậy tập giá trị của hàm s ố f ø xù d ý  là øln 2,  ù. ln t x ð
Câu 9. Tìm cực trị c a
ủ hàm u ý sin xsin y sin z với x, y, z þ 0 thoả mãn x  y  z ý . 2 ö ð ð ð ö öð ð ð ö A. u đạt c c ự tiểu t m ại điể , , ÷ . B. u đạt c i ực đạ t m ại điể , , . 6 6 6 ÷ ÷ ÷ ø ø ø 6 6 6 ø ö ð ð ð ö öð ð ð ö C. u đạt c i ực đạ t m ại điể ÷ , , . D. u đạt c c ự tiểu t m ại điể ÷ , , . 8 8 4 ÷ ÷ ø ø ø 8 8 4 ø
Lời giải ö ð ð Xét hàm ö g ø ,
x y, z, Lù ý sin x sin y sin z  .
L x  y  z  ÷ và hàm hø ,
x y, zù ý x  y  z  ý 0 . 2 ÷ ø ø 2 üg ý 0 ÿ x ÿ c
ü os xsin y ý L ÿg ÿ ý 0 sinø ü 3 x  yù ý 0 ÿ  ÿ ÿL ý y ÿ ÿ
Ta có: hệ phương trình ý tương đương với 4 s
ý inø y zù ý 0 hay ý . g  ÿ ð ý 0 ÿ ÿ ÿ
x ý y ý z ý  ÿ ð z   ý ÿþ 6 ÿ x y z  ÿ g þ 2 ÿ ý 0 ÿþL ü öð ð ð 3 ö
ød xù2  ød yù2  ødzù2 3 d d x y d d y z d d 2 ø z xù ÿd g ÷ , , , ÷ ý  ÷ 6 6 6 4 ÷ ÿ 8 Nhận xét: ø ø ý . ÿ ö ð ð ð d ö h , ,
ý dx dy dz ý 0 ÿ ÷ þ ø 6 6 6 ÷ø ö ð ð ð 3 ö dx  dy  d 2 ø ù2 ø ù2 ø zù2 Suy ra d g÷ , , , ÷ ý  ü 0 ÷ . 6 6 6 4 ÷ 16 ø ø ö ð ð ð ö Vậy u đạt c i ực đạ t m ại điể , , ÷ . 6 6 6 ÷ ø ø
Câu 10. Cho hàm u ý xy  yz thoả mãn 2 2
x  y ý 2 và y  z ý 2 với x, y, z þ 0 . Khẳng định nào sau đây là đúng? A. u đạt c c ự tiểu tại ø1,1,1ù . B. u đạt c i ực đạ tại ø1,1, ù 1 .
C. u không có cực trị. D. u đạt c c ự tiểu tại ø0,0,0 ù. E. u đạt c i ực đạ tại ø0,0,0 ù .
Lời giải
Xét hàm g ø x, y, Lù ý xy  y ø2  yù  .
L h ø x, y ù , với h ø x yù 2 2 ,
ý x  y  2 ý 0 . ü g  ý0 ÿ x  ÿ ü 1 ÿ L ÿ ý Từ hệ phương trình g ý ý 0, kết hợp v u ki ới điề
ện x, y, z þ 0 c ta thu đượ nghiệm: ý 2 . y  ÿ ÿø ,x yù ý þ ø1, ù 1 ÿ g  ÿ ý 0 þ L  ü ö ö g
ý  ø x ù2  ø y ù2 2 1 d 1,1, d 3 d  ÿ ÷ ÷ dxdy Nhận xét: ý ø 2 ø . ÿdh
þ ø1,1ù ý 2dx  2dy ý 0 Suy ra ö ö g
ý  ø xù2  ø yù2 2 1 d 1,1, 2 d 3 d ü ÷ ÷ 0 . ø 2ø
Với x ý y ý 1 thì z ý 1. Vậy u đạt c i ực đạ t m ại điể ø1,1, ù 1 .
Câu 11. Tập giá trị của hàm số 2 2
z ý arccot 3  x  y là ùð ð ù ù ð ð ù A. ù 3, 3ù ù ù û û . B. , ú . C. , . D. 0, 3 3 2 ú û û ú 6 2 ú û û û û .
Lời giải
Tập xác định: D ý ø  x yù 2 , | , x y  ó 3 .
Nhận xét: với mọi x, y  D ta có 2 2
0 ó 3  x  y ó 3 . ð ð Suy ra 2 2
ý arccot 0  z ý arccot 3  x  y  arccot 3 ý . 2 6
Câu 12. Tìm tất cả các hàm số f ø xù thoả mãn f øx ù f øy ù ó sin øx  y ù x  y , x  , y  .
Lời giải
f øx ù  f øy ù sin øx y ù sin øx  y ù
Nhận xét: với mọi x  y : ó  1 và lim 1 ý 0 . x  y x  y y x x y
f øx ù f ø y ù Suy ra lim ý 0 hay x   ý 0 . y x x  y
Từ đó suy ra hàm f øx ù liên t c
ụ và khả vi trên . Khi đó c
họ ác hàm số f øx ù thoả mãn bài toán sẽ
có dạng: f øx ù ý C với C  .
Câu 13. Viết phương trình tiếp tuyến c ng ủa đườ r ý 1 cos t m
ại điể ứng với  ý 0 .
Lời giải üx
ÿ ø ù ý ø1 cos ùcos
Toạ độ của đường cong r ý 1 cos trong hệ toạ độ đề các là: ý , suy ra ÿy
þ ø ù ý ø1 cos ùsin
xòø0ù ý 0 và yòø0ù ý 2 . dy Nhận xét:
ø0ù ý  nên tiếp tuyến của đường r ý 1 cos tại điểm ng v ứ
ới  ý 0 sẽ vuông góc dx
với trục hoành và có dạng x ý a ø, a 
. Ta có xø0ù ý 2, suy ra a ý 2 .
Vậy phương trình tiếp tuyến của đường r ý 1 cos t m
ại điể ứng với  ý 0 là x ý 2 .
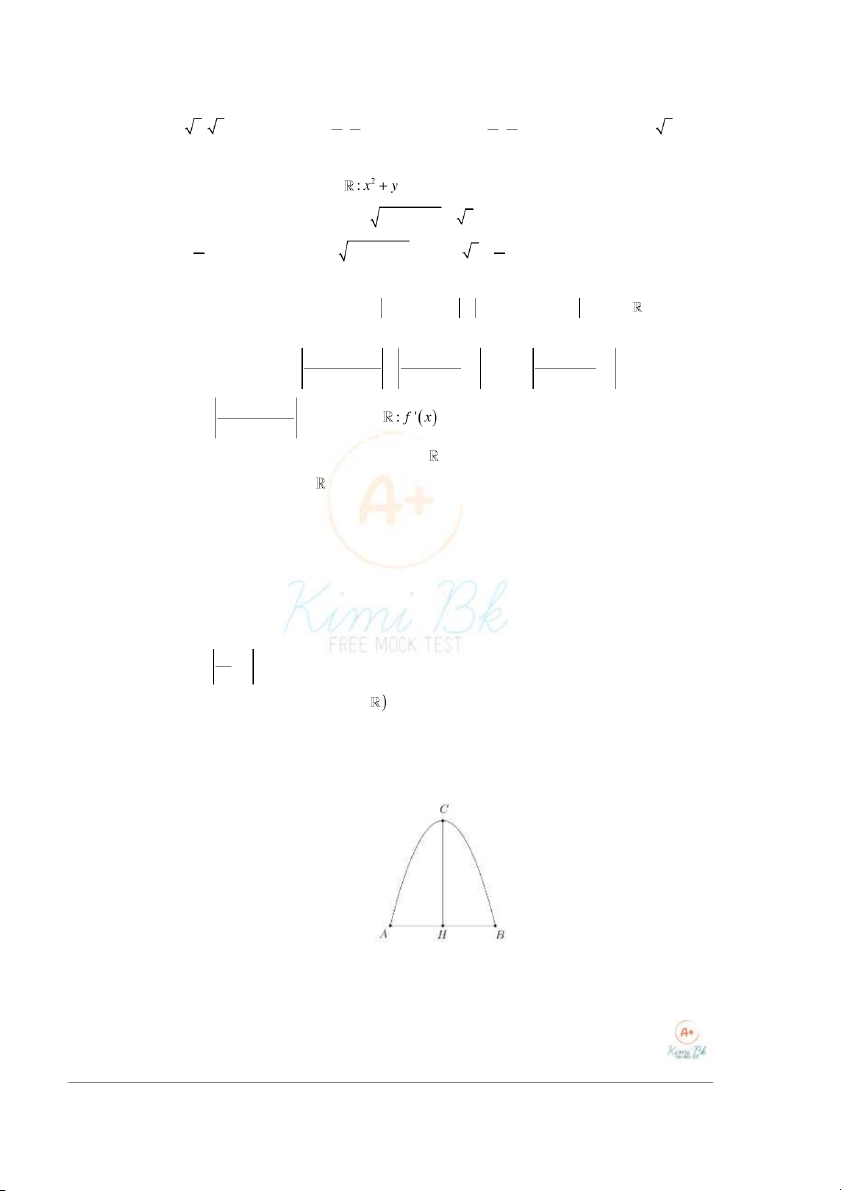
Câu 14. Tìm bán kính lớn nhất của một quả cầu có thể di chuyển vào được một c ng ổ hình parabol như hình vẽ
với CH ý AB ý 4m .
Lời giải
Xét hình tròn øS ù là mặt cắt d c ọ theo tr c ụ c a
ủ quả cầu. Để quả cầu di chuyển vào được c ng par ổ abol
thì hình øS ù phải nằm trong (hoặc tiếp xúc trong) hình c ng par ổ abol.
Hình øS ù có bán kính lớn nhất sẽ là hình tròn tiếp xúc với cạnh AB và parabol (?).
Ta sẽ đi tìm hình tròn øS ù thoả mãn điều kiện trên. Xét hệ tr c
ụ toạ độ Hxy với tia Hx trùng tia HB và tia Hy trùng tia HC . Khi đó parabol có phương trình 2
y ý 4  x . Giả s
ử đường tròn øS ù có tâm S , tiếp xúc với cạnh tại H và tiếp xúc với parabol tại điểm D có toạ độ ø 2
a, 4  a ù với 0 ü a ü 2 . Tiếp tuyến của parabol t m
ại điể D có phương trình: ød ù 2 : y ý 2
 ax  a  4 . 1 1 7
Đường thẳng vuông góc với ød tại D có phương trình: ød : ý   . 2ù 2 1 ù y x a 2a 2 ö 7 ö Toạ độ giao điểm c ng t ủa đườ hẳng ø với tr c ụ tung là 2  . 1 d ù ÷0, a ÷ ø 2 ø
Do tính chất của đường tròn øS ù nên giao điểm của đường thẳng ød với tr c ụ tung sẽ là tâm 1 ù S . Khi 2 1 ö7 ö
đó ta có SD ý SH hay 2 2 a  ý  a
. Suy ra a ý 2 , thoả mãn điều kiện. 4 ÷2 ÷ ø ø
Vậy bán kính lớn nhất cần tìm bằng SH ý 1,5m . ax s b in øsin xù
Câu 15. Tìm a, b  sao cho lim ý 1. 3 x0 x
Lời giải 3 Theo khai triển Taylor: x x ý x   oø 3 sin x ù. 3! 3 3 ù x ù x   o ú ø 3x ù 3 3 ú ö 3 ö 3 x û 3! ù ù Suy ra sinøsin ù ý   ø 3 ù û x   ÷   ú ø 3 ù x x x o x o x o x ÷ ý x   o ú ø 3x ù. 3! 3! ÷ 3! ÷ 3 û û ø ø a ü b ý 0
ax  bsin øsin xù ÿ a ü ý 3 Khi đó, để lim ý 1 thì ý hay ý . 3 b x 0 x  ý1 ÿ b ý 3  þ þ 3
Câu 16. Một cây cầu bắc qua một con kênh với mô hình toán học như hình vẽ. Phần mái vòm c a ủ chân cầu có
thể xem là một hàm bậc hai với 5 ó x ó 5 (đơn vị mét). Nếu chiều rộng của mặt cầu là 3m , tìm thể
tích lượng đá được sử dụng trong việc xây cầu.
Lời giải 2 x
Parabol trong hình vẽ có phương trình y ý 5  với 5  ó x ó 5 . 25 5 2 ö x ö 112
Diện tích mặt cắt của cây cầu là: S ý7.6.2  5  dx ý  ÷ ÷ ø 2 m ù . ø 25ø 3 5 3 112
Thể tích lượng đá được sử dụng trong việc xây cầu là: V ý dx ý 112  ø 3 m ù . 3 0
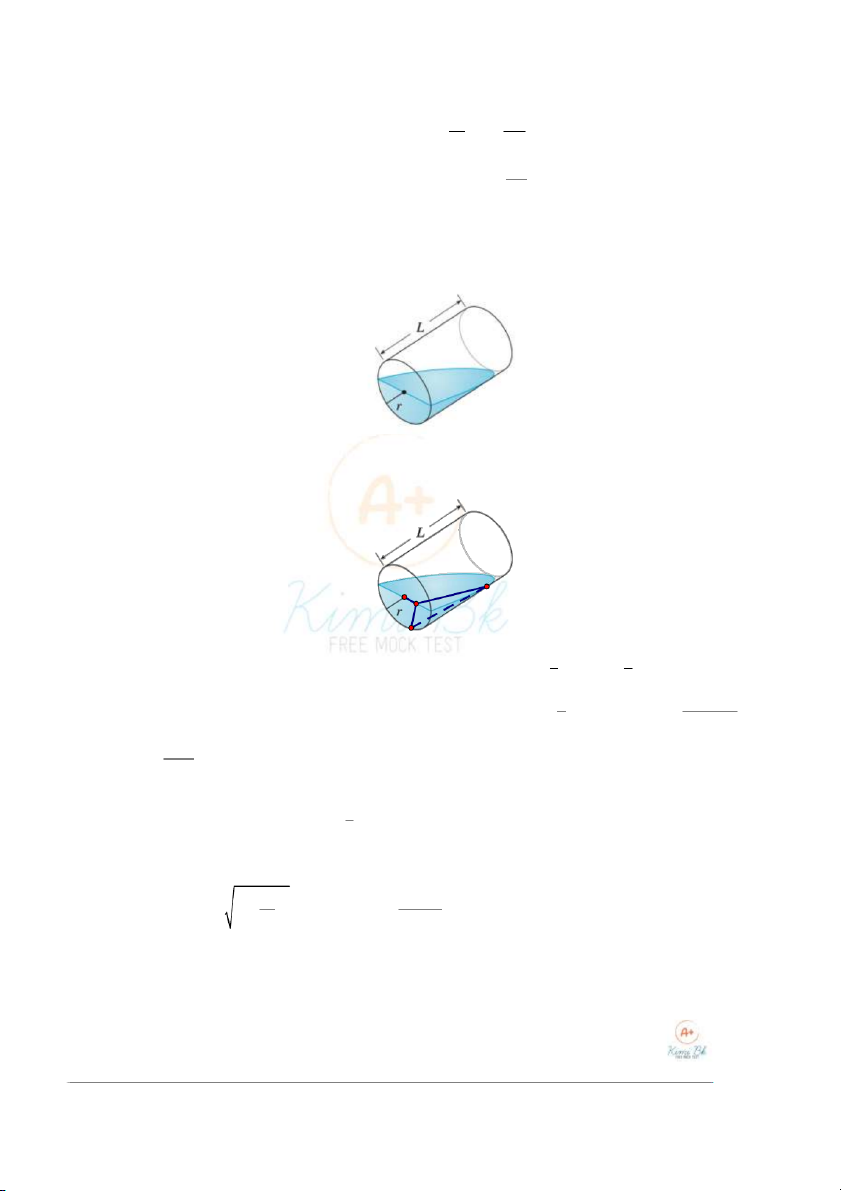
Câu 17. Một cốc nước hình trụ có bán kính đáy là r và chiều cao là L . Nghiêng cốc nước cho đến khi lượng
nước còn lại trong cốc vừa phủ n )
ửa đáy cốc (như hình vẽ . Tính thể c
tích lượng nướ bị chiếm chỗ.
Lời giải
Lấy O là tâm của đáy cốc nước, P là một điểm bất k t
ỳ rên đường kính đáy. Qua P d ng ự mặt phẳng
vuông góc với đường kính. Mặt phẳng này cắt đường tròn đáy tại M và cắt đường sinh của c c ố tại N (như hình vẽ). O P N M 1 1
Đặt OP ý x , ý�㕃  þ
ý  , suy ra L ý r.tan  . Diện tích MPN bằng MN.MP ý ø 2 2
r  x ù.tan . 2 2 r 1 2r .tan 
Thể tích lượng nước bị chiếm chỗ sẽ được tính bởi công thức V ý ør  x ù 3 2 2 .tan dx ý  2 3  r 2 2Lr ý . 3 1
Câu 18. Gọi L
là độ dài đường cong y ý cosh3x với 0 ó x ó 1 . Khẳng định nào sau đây là đúng? 3 A. L ü 4 . B. 3 ó L ü 5.
C. 4 ó L ó 6 .
D. 5 ó L ó 7 .
Lời giải 1 2 1 3 3 ö d ö  Ta có: y e e L ý 1  dx ý cosh 3 d x x ý   ÷ ÷ 3,34  . ø dx ø 6 0 0 ü2xyø 2 2 x  y ù 2 2 ÿ x   y  0
Câu 19. Cho f ø , x yù 2 2 ý ý x  y
. Đặt a ý f ò ø0,0 , tính 2 a  2 . xy ù ÿ 0 øx, y ù ý þ ø0,0ù A. 2 . B. 2 . C. 4 . D. 3.
Lời giải 2 2 ü 3 x  y 2 2 2 ÿ y  4 y . x  y  0
Nhận xét: f ò x y ý ý x  y . x ø , ù 2 2 ÿ 0 ø , x y ù ý ø0, 0 ù þ f ò 0, y   f ò 0,0 Suy ra a ý f ò ý ý  . Khi đó 2 a  2 ý 2 . xy ø0, 0 ù x ø ù x ø ù lim 2  y0 y