


Preview text:
Thuvienhoclieu.Com
ĐỀ KIỂM TRA CUỐI HỌC KỲ I-ĐỀ 5 MÔN TOÁN 12
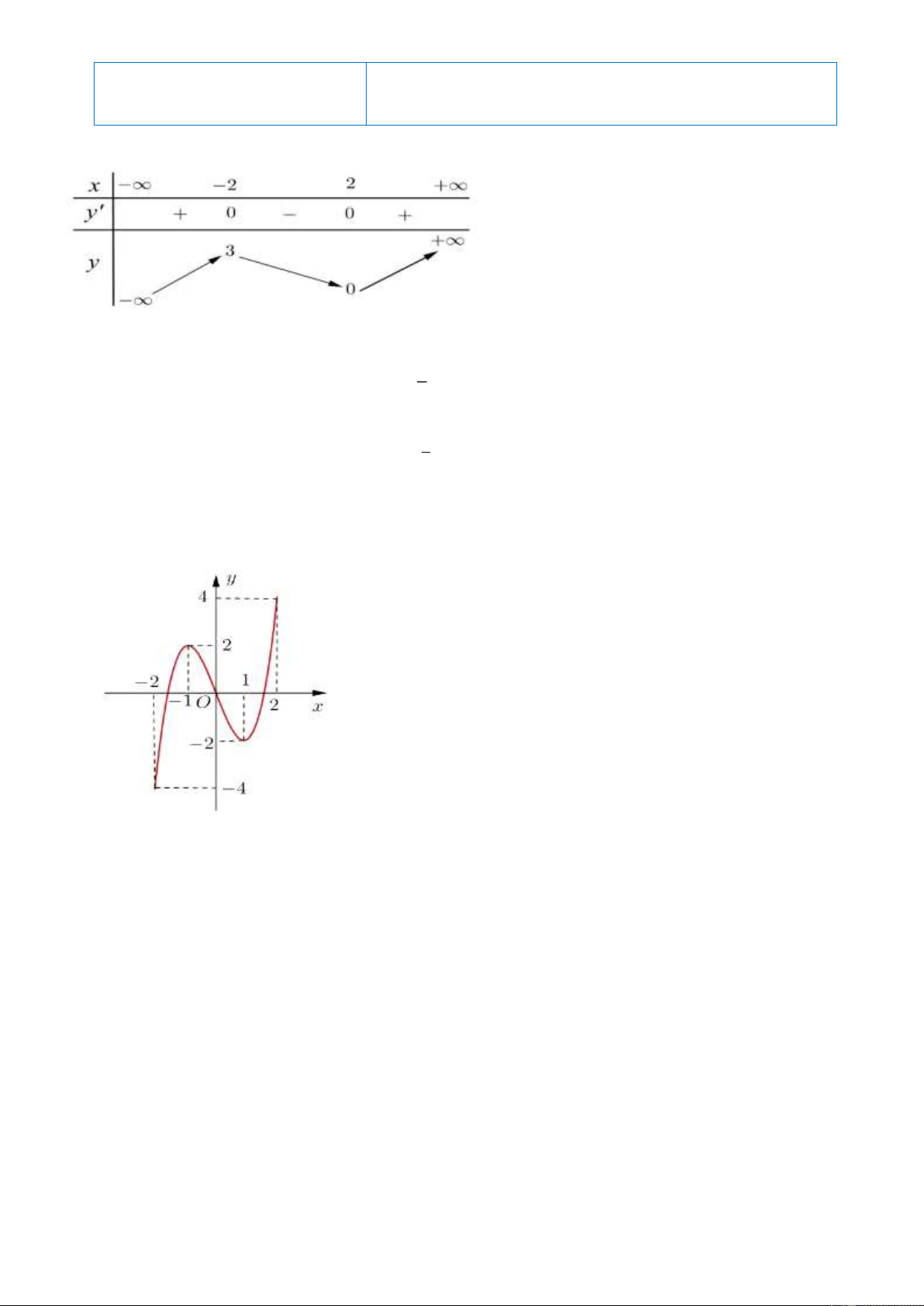
Câu 1: Cho hàm số y = f(x) có bảng biến thiên dưới đây:
Hàm số đồng biến trên khoảng :
A. (- ;3) B. (0;+ ) C. (-2;2) D. ( 2;+ ) 1
Câu 2: Tìm các khoảng đồng biến hàm số 3 2 y
x 2x 3x 1. 3
A. (;3). B. (1; ). C. (1;3). D. ( ; 1) và (3; ).
Câu 3: Tìm tất cả giá trị của m đề hàm số 1 3 y x m 2
–1 x (m 3)x 4 nghịch biến trên R. 3 m 2 m 2 A. 1
m 2 B. 1
m 2 C. D. m 1 m 1
Câu 4: Đồ thị hàm số y = f(x) như hình vẽ sau, đạt cực đại tại : .
A.x = -2 B. x=-1 C. x=1 D.x=2
Câu 5: Giá trị cực đại của hàm số 3 2 y 2
x 3x 1 là: A. y
0 B. y 1 C. y 1 D. y 4 CĐ CĐ CĐ CĐ
Câu 6: Đồ thị hàm số nào sau đây có 2 điểm cực trị: A. 2 y x 5 B. 4 2
y x 2x 1 C. 3 2
y x 3x 4 D. 4 2
y x 4x 5
Câu 7: Cho hàm số y f (x) có đồ thị như hình bên. Giá trị lớn nhất M và nhỏ nhất m của hàm số này trên đoạn 1; 4 bằng: Trang 1
A. M = 4, m = -1 B. M = 6, m = 1
C. M = 4, m = 1,5 D. M = 6, m = 0 4 2
Câu 8:Tìm giá trị lớn nhất của hàm số sau: y x x 8
16 trên đoạn 1; 3
A.9 B.16 C.0 D.25 2x 1
Câu 9: Đường tiệm cận đứng của đồ thị hàm số y x là 2
A.x = 2 B. x= -2 . C. y=2 D.y = -2
Câu 10: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây A. 4
y x 5x 1 B. 3
y 5x x 1 C. 3 2
y x x 5x 1 D. y 3 x 1
Câu 11: Tọa độ giao điểm của đồ thị các hàm số sau 3 2
y 2x 3x 1 và 2
y 2x 1 là: 1 3 1 3 A.(0;1); ( ; ) B. (0;1); (- ;
) C. (0;1); D. 2 2 2 2 1 3 (- ; ) 2 2
Câu12: Cho hàm số y f x . Đồ thị hàm số y f ' x như hình vẽ. Đặt
g x f x 3 3
x 3x m , với m là tham số thực. Điều kiện cần và đủ để
bất phương trình g x 0 nghiệm đúng với x 3; 3 là
A. m 3 f 3
B. m 3 f 0 C. m 3 f 1 D.
m 3 f 3 3 2 Câu 13: Hàm số y =
1 x có tập xác định là A. [-1; 1]
B. (-; -1] [1; +) C. R\{-1; 1} D. R Trang 2 5 Câu 14 : Kết quả 2
a a 0 là biểu thức rút gọn của phép tính nào sau đây? 3 7 a . a 4 5 a A. 5 a. a B. C. 5 a . a D. 3 a a
Câu 15: Cho a,b,c là các số thực dương và a 1 Mệnh đề nào dưới đây đúng ?
A.loga(bc) = logab.logac B.loga(b+c) = logab.logac
C. loga(bc) = logab+logac D. loga(b+c) = logab+logac 3
Tính B 2 log 15 log 3 log 9 4 2 8 Câu 16 : 2 6 4 B log (3 5 ) B log 15 B log 135 B 4log 15 2 B. 2 C. 2 D. 2 A.
y log (2x 1)
Câu 17: Tập xác định của hàm số là 3 1 1 A. ; B. 1
C. 1 ; D. ; ; 2 2 2 2
Một người gửi tiết kiệm 10 triệu đồng với lãi suất 0,5% một tháng và lãi hàng tháng được nhập vào Câu 18:
vốn. Hỏi sau 1 năm, người đó nhận được bao nhiêu tiền (cả vốn lẫn lãi ) biết rằng người đó không rút lãi ở tất
cả các định kỳ trước đó.
A.10616778đ B.10676000đ C.10600000đ D.10666667đ
Câu 19: Nghiệm của phương trình :log3(x+1) =log3(3-x) là
A.x= 2 B.x =1 C.x=0 D.x=-1 2x3 4x
Câu 20: Phương trình 4 8 có nghiệm là: 6 2 4 A. x = B. x = C. x = D. x =2 7 3 5
Câu 21: Tìm m để phương trình x 1 x2 4 2
m 0 có nghiệm thực
A. m 1 B. m 0 C. 0 m D. m 2
Câu 22: Tập nghiệm của bất phương trình : 2x 4 là:
A. (- ;4] B. [4;+ ) 4 C. [2 ; ) D. (- ;2] x x
Câu 23: Nghiệm của phương trình 9 2.3 3 0 là:
A.x=1 B.x=0. C.x=3 D.x=-1
Câu 24: Khối lập phương là khối đa diện đều loại:
A. {3;3} B. {3;4} C. {3;5} D. {4;3}
Câu 25: Mặt phẳng ( AB’C’) chia khối lăng trụ ABC.A’B’C’ thành các loại khối đa diện nào?
A. Hai khối chóp tam giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác. Trang 3
D. Hai khối chóp tứ giác.
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA ABCD và SA a 3 .
Thể tích của khối chóp S.ABCD là: a3 a3 3 a3 3 A. a3 3 B. C. D. 4 3 12
Câu 27 : Cho hình lăng trụ tam giác đều có các cạnh đều bằng a .Thể tích khối lăng trụ đều là: 3 2a 2 3 a 3 2a 3 a 3 A. B. C. D. 3 3 3 4
Câu 28: Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho SA' 1 SA . 3
Mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lần lượt tại B’, C’, D’. Khi đó
thể tích khối chóp S.A’B’C’D’ bằng: V V V V A. B. C. D. 3 9 27 81
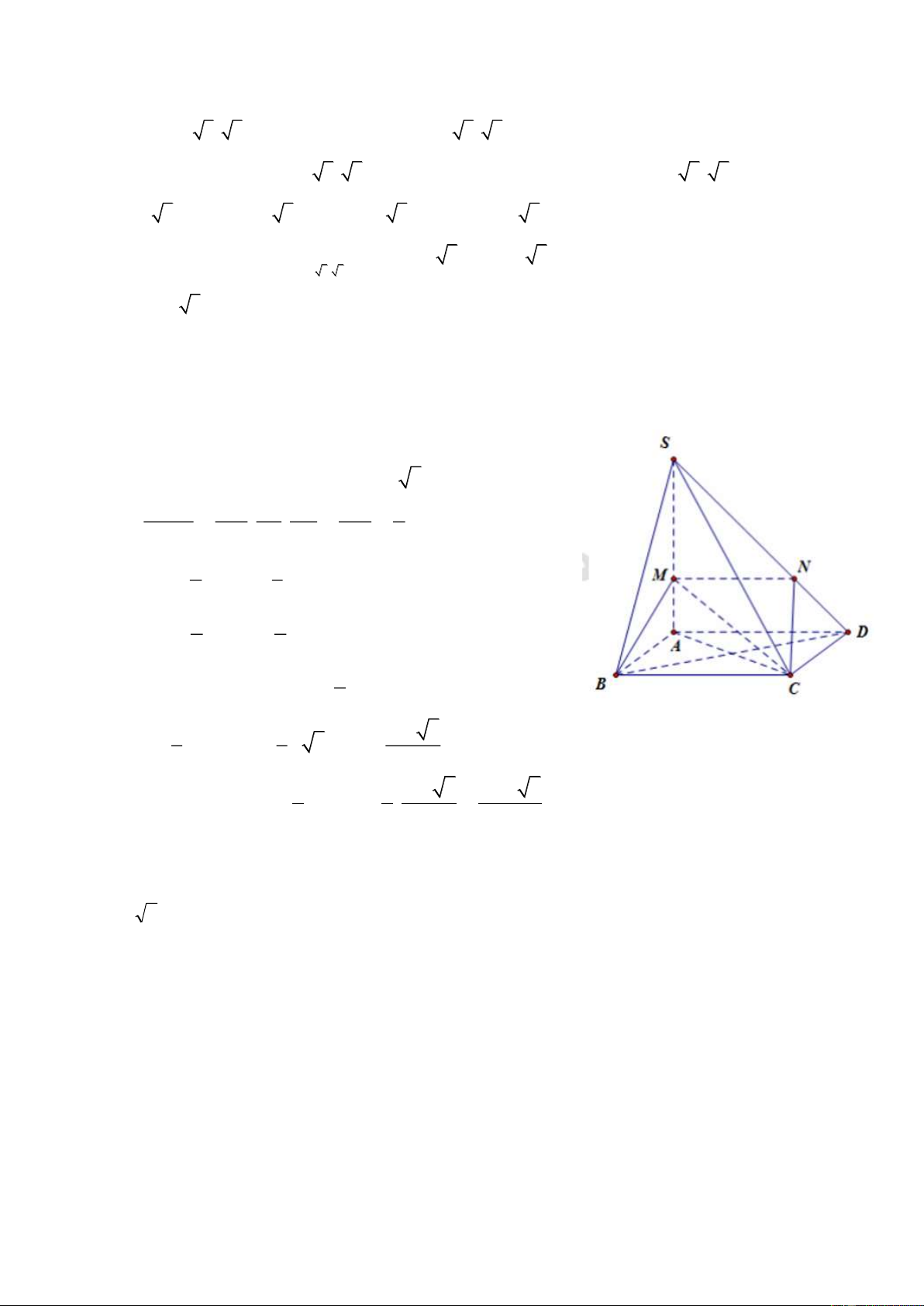
Câu 29 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a, AD 2a . Cạnh SA vuông góc với a 3
mặt phẳng đáy, cạnh bên SB tạo với mặt phẳng đáy góc 60°. Trên cạnh SA lấy điểm M sao cho AM , 3
mặt phẳng BCM cắt cạnh SD tại N. Thể tích khối chóp S.BCNM bằng: 3 10a 3 10a 3 10 3 3 10a 3 A. B. C. D. 27 9 27 27
Câu 30: Cho khối chóp SABC,SA vuông góc (ABC).SA =2a,Tam giác ABC vuông cân tại A có AB = a
2 .Tính bán kính mặt cầu ngoại tiếp khối chóp SABC.
A. a 2 B. a. C. 2a. D. 2a 2 ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A X X B X X X X X C X X D X X X X X X 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 A X X X X X B X X X C X X D X X X X X HƯỚNG DẪN GIẢI
Câu 12. Chọn đáp án A
Ta có: g x f x 3
x x m f x 3 3 3 0 3
x 3x m Điều kiện bài toán trở thành tìm m để f x 3 3
x 3x m, x 3; 3 .
Xét hàm h x f x 3 3
x 3x trên đoạn 3; 3 ta có: Trang 4
h x f x 2
x f x 2
x f x 2 ' 3 ' 3 3 3 ' 1 0 ' x 1 Dựng đồ thị hàm số 2
y x 1 cùng một hệ trục tọa độ với đồ thị hàm số y f ' x bài cho ta được:
Xét trên đoạn 3; 3 thì f x 2 ' x 1, x 3; 3 .
Do đó f x 2 '
x 1 0,x 3; 3
hay hàm số y hx đồng biến trên 3; 3 .
Suy ra h 3 h x h 3 hay 3 f 3 h x 3 f 3 .
Điều kiện bài toán thỏa m min h x h 3 3 f 3 . 3; 3
Vậy m 3 f 3 .
Câu 29 . Chọn đáp án D
Ta có SB ABCD
B và SA ABCD
SB, ABCD SB, AB SBA 60 SA A .
B tan SBA A .
B tan 60 a 3 V SM SB SC SM 2 Ta có S.MBC . . V SA SB SC SA 3 S . ABC 2 1 V V V S .MBC S . 3 ABC 3 ABCD 4 2 V V V S .MNC S . ADC S . 9 9 ABCD 5 V V V V . Ta có S .BCMN S .MBC S .MCN S . 9 ABCD 3 1 1 2a 3 V . SA S a 3. .2 a a S . ABCD 3 ABCD 3 3 3 3 5 5 2a 3 10a 3 Do đó ta suy ra V V . . S .BCMN S . 9 ABCD 9 3 27
Câu 30.Gọi M trung điểm BC Dựng trục của đáy
Dựng mặt phẳng trung trực cạnh SA cắt trục tại I R=AI= a 2 Trang 5




