Đề Ôn Thi Kỳ 1 Toán 12 Năm 2022-2023-Đề 4 (Có Đáp Án)

ĐỀ KIỂM TRA CUỐI HỌC KỲ I-ĐỀ 4 MÔN TOÁN 12
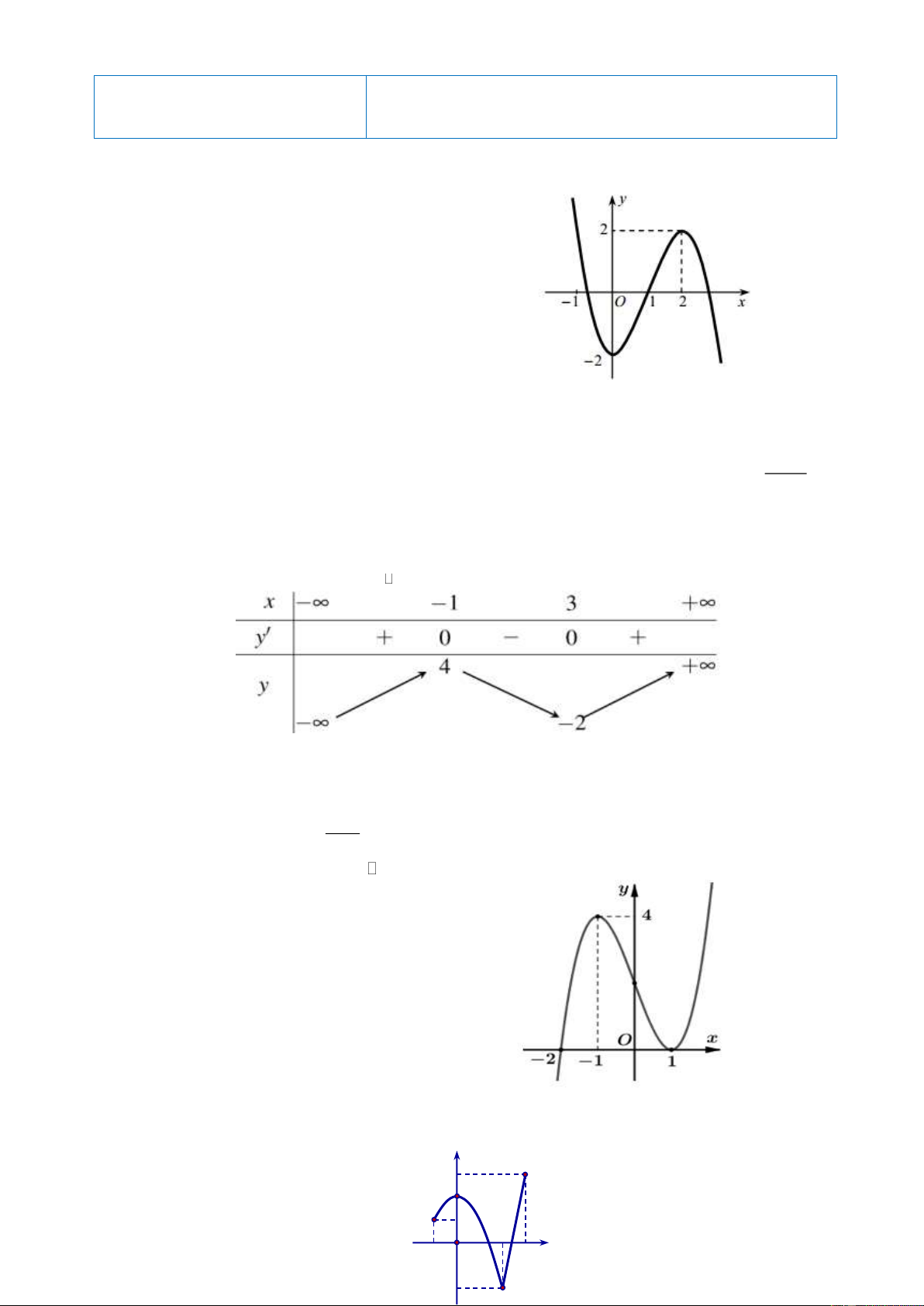
Câu 1. Cho đồ thị hàm số y  f  x có đồ thị như hình vẽ. Hàm số y  f  x đồng biến trên khoảng nào dưới đây? A.  2  ; 2 . B. 2;   . C.  ;  0 . D. 0; 2 .
Câu 2. Hàm số y = x3 – 6x2 + 9x nghịch biến trên tập nào trong các tập sau đây?
A. (0;3). B. (1; 3).
C. (–  ;1)  (3;+  ). D. (1;4). x  3
Câu 3. Có bao nhiêu giá trị nguyên của tham số m trên đoạn  2  021;202 
1 để hàm số y  x  đồng biến m
trên khoảng (1 ;  ) . A. 2023. B. 2022 . C. 2021. D. 4021.
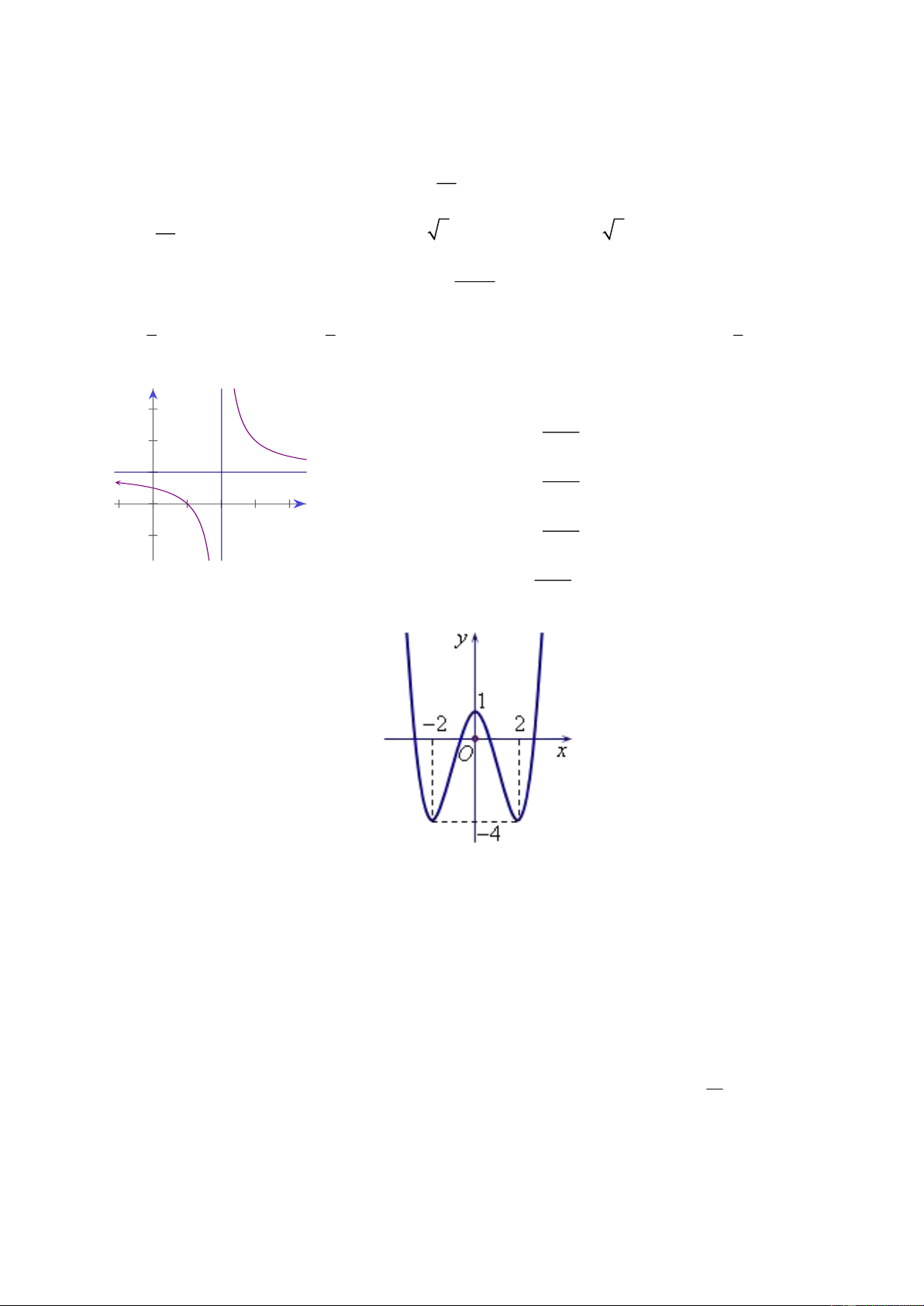
Câu 4. Cho hàm số y  f (x) xác định trên
, có bảng biến thiên như sau
Hàm số y  f (x) đạt cực đại tại điểm A. x  1  . B. x  2  . C. x  3 . D. x  4 .
Câu 5. Hàm số nào sau đây có hai điểm cực trị? x 1 A. 3 2
y  x  x  x 1. B. y  . C. 4 2
y  x  2x  3 . D. 3 2
y = x  x  2x 1. x  1
Câu 6. Cho hàm số y = f(x) liên tục trên , đồ thị của đạo
hàm f’(x) như hình vẽ bên. Tìm số điểm cực trị của hàm số g(x) = f(x2 − 3). A. 2. B. 3. C. 4. D. 5.
Câu 7. Cho hàm số y  f  x liên tục trên đoạn  1  ; 
3 và có đồ thị như hình vẽ sau. y 3 2 Trang 11 2 x 1 O 3 2 
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1  ; 
3 . Tính M  m . A. 5 . B. 4 . C. 3  . D. 5  . 4
Câu 8. Tìm giá trị nhỏ nhất của hàm số y  3x 
trên khoảng 0;  . 2 x 33 A. min y  B. 3 min y  2 9 C. 3 min y  3 9
D. min y  7 0; 5 0; 0; 0; 2x  3
Câu 9. Đường tiệm cận đứng của đồ thị hàm số y  là đường thẳng 2x  1 1 3 1 A. x   .
B. x  . C. y  1. D. y   . 2 2 2
Câu 10. Hàm số y  f (x) nào có đồ thị như hình vẽ sau : y x 1
A. y  f (x)  2 x  2 1 x 1
B. y  f (x)  x x  2 0 1 2 x 1
C. y  f (x)  x  2 x 1
D. y  f (x)  x  2
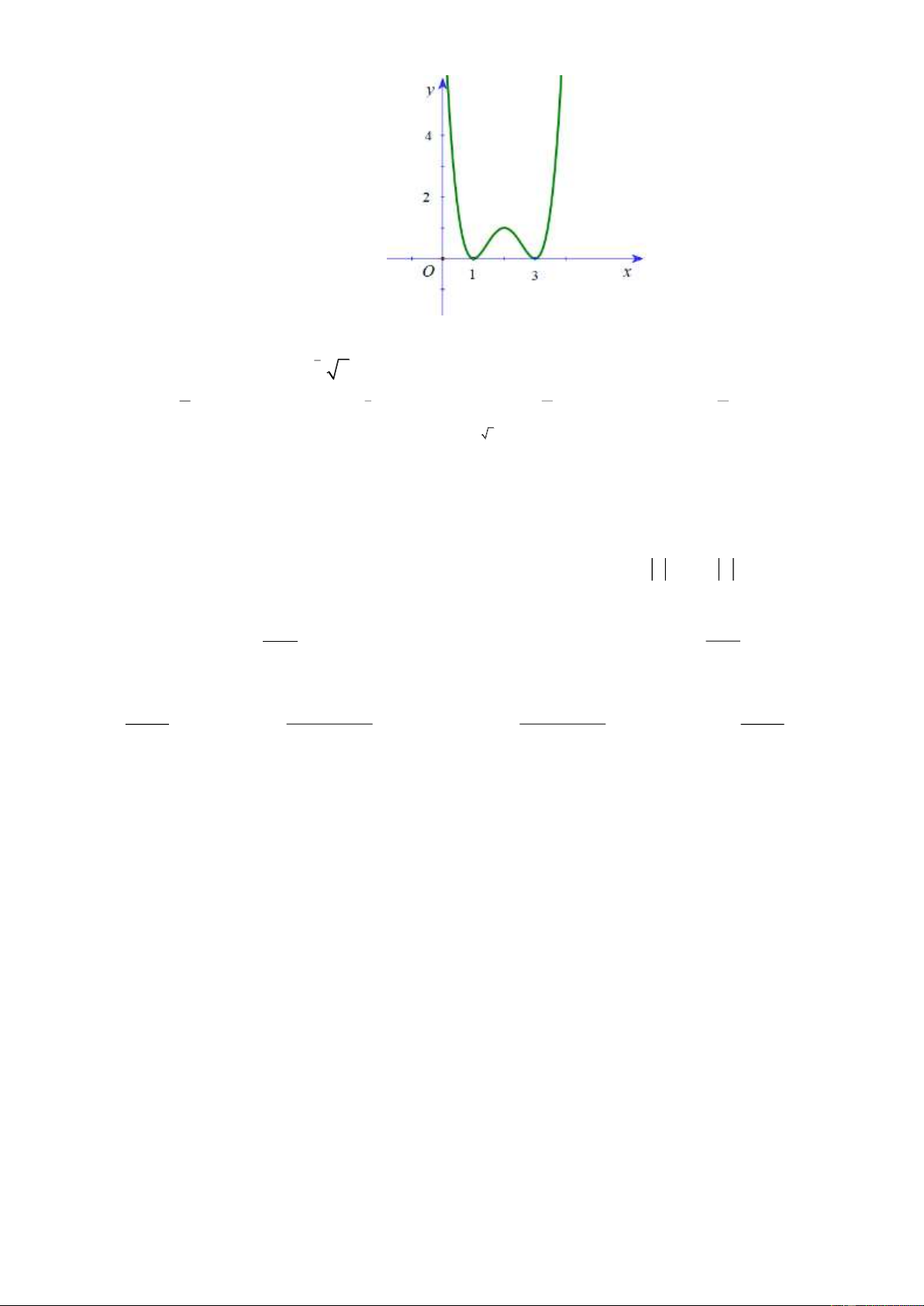
Câu 11. Cho hàm số bậc bốn y  f (x) có đồ thị như hình vẽ
Số nghiệm của phương trình 2 f (x) 1  0 là: A. 4. B. 3. C. 2. D. 1. x
Câu 12. Cho hàm số f  x có đồ thị f  x như hình vẽ dưới. Hàm số g  x  f  x 3 2
  2x 5x  2001 có 3
bao nhiêu điểm cực trị? Trang 2 A. 3 . B. 1. C. 2 . D. 0 . 3
Câu 13. Rút gọn biểu thức 2 5
P  x . x 13 4 3 17 A. 2 x . B. 7 x . C. 10 x . D. 10 x . 
Câu 14. Tìm tập xác định D của hàm số y    x1 3 2 .
A. D   ;  .
B. D   ;  2.
C. D   ;  2.
D. D  2;.
Câu 15. Cho a  0, a  1 và x, y là hai số thực khác 0. Khẳng định nào sau đây là khẳng định đúng? A. 2 log x  2log . x B. log xy  x  y a   log log . a a a a
C. log  x  y  log x  log . y D. log xy  x  y a   log log . a a a a a
Câu 16. Cho log 10  a . Tính log 20 theo ,
a ta được kết quả là 2 5 a  1 a 1 A. a  1. B. . C. a  1. D. . a 1 a  1
Câu 17. Tính đạo hàm của hàm số y  log 2x 1 . 2   2 2 1 1 A. y  . B. y  . C. y  . D. y  . 2x 1 2x   1 ln 2 2x   1 ln 2 2x 1
Câu 18. Ông A gởi 50 triệu đồng vào một ngân hàng theo hình thức lãi kép. Biết rằng lãi suất mỗi năm không
thay đổi và bằng 5,2%/năm. Hỏi sau tối thiểu bao nhiêu năm thì ông có được số tiền lãi hơn 45 triệu đồng ? A. 12 năm. B. 13 năm.
C. 14 năm. D. 15 năm.
Câu 19. Biết rằng phương trình 2 x 6 x3 8
 4096 có hai nghiệm x , x . Tính P  x .x . 1 2 1 2 A. P  9  . B. P  7
 . C. P  7 . D. P  9.
Câu 19. Biết rằng phương trình 2 x 6 x3 8
 4096 có hai nghiệm x , x . Tính P  x .x . 1 2 1 2 A. P  9  . B. P  7
 . C. P  7 . D. P  9.
Câu 20. Phương trình 2
log x - 5log x + 4 = 0 có 2 nghiệm x ,x .Tính tích x 2 2 1 2 1. x2
A. 32 B.22 C.16 D.36
Câu 21. Xác định m để phương trình: x x 2      4 2(m 1)2 m 4
0 có hai nghiệm phân biệt? A. m  2  B. m  2  m  2 C. m  1  D. m  2
Câu 22. Số nghiệm nguyên dương của bất phương trình 3x3 20197 2  2 x là: A. 200 . B. 100. C. 102 . D. 201.
Câu 23. Biết tập nghiệm của bất phương trình log
7.10x  5.25x  2x 1 là S = ( a; b). Tính T = 2a + b. 2   A. T =  2. B. T = 2 C. T = 5 D. T =  4.
Câu 24. Số cạnh của khối đa diện đầu loại {3; 5} là bao nhiêu? Trang 3 A. Mười hai. B. Mười sáu. C. Hai mươi. D. Ba mươi.
Câu 25. Mặt phẳng (A’BC) chia khối lăng trụ ABC.A’B’C’ thành các khối đa diện nào?
A. Ba khối tứ diện. B. Hai khối chóp tứ giác.
C. Hai khối chóp tam giác. D. Một khối chóp tam giác và một khối chóp tứ giác.
Câu 26. Cho khối lăng trụ có thể tích V =12 và chiều cao h = 4. Khi đó tính diện tích đáy S khối lăng trụ A. S = 9 B. S = 6 C. S = 3 D. S = 4.
Câu 27. Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA vuông góc với đáy, góc giữa SC và đáy bằng
450 . Tính thể tích V của khối chóp 3 3a 3 a 3 a 3 2a A. V = B. V = C. V = . D. V = 3 3 2 3
Câu 28. Tính thể tích khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a. Đường chéo
AC’ nằm trong mặt phẳng (AA’C’C) tạo với đáy (ABC) một góc 300. 3 a 3 a 3 a 3 3 a 3 A. B. C. D. 4 12 4 12
Câu 29. Một công ty cần sản xuất các thùng dạng hình hộp chữ nhật (có nắp), đáy là hình vuông và có
thể tích là 27dm3. Tính chiều cao h của hộp để ít tốn nguyên liệu sản xuất nhất. 9 3 4 A. h  dm . B. h  dm . C. h 
dm . D. h  3dm . 4 2 3
Câu 30. Một mặt cầu có diện tích 2
36 m . Thể tích của khối cầu này bằng: 4 A. 3  m B. 3 36 m C. 3 108 m D. 3 72 m 3
Câu 31. Cho hình trụ có bán kính đáy và chiều cao cùng bằng a. A, B lần lượt nằm trên hai đường tròn đáy. a
Biết khoảng cách giữa AB và trục hình trụ bằng
. Tính góc tạo bởi AB và trục hình trụ. 2 A. 300. B. 450. C. 600. D. 900.
Câu 32. Cho một hình nón đỉnh S, tâm đáy là O có chiều cao bằng 3, bán kính đáy bằng 4. SAB là một thiết
diện qua đỉnh hình nón có diện tích bằng 3 14 . Gọi I là trung điểm của AB, M là giao điểm của OI và hình
nón (IM < OM). N là trung điểm của SM. Tính khoảng cách từ N đến mp(SAB). 2 2 1 A. 1. B. . C. . D. . 3 3 2 2 ------Hết----- HƯỚNG DẪN GIẢI Câu 3: m  2  Câu 6:
Ta có g’(x) = 2x. f’(x2 – 3) x  0 g’(x) = 0   2 f '(x  3)  0( )  2 x 3  2  Xét ( )
 , từ đồ thị của f’(x) ta suy ra 2 : f '(x  3)  0   2 x  3 1(nghiêm kép) x  1    x  2  (nghiêm kép) Bảng biến thiên Trang 4 x −∞ –2 –1 0 1 2 +∞ f’(x) – 0 – 0 + 0 – 0 + 0 + +∞ f(0) +∞ f(x) f(-1) f(1)
Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị. Câu 12. Lời giải Chọn C
Có g x  f  x 2
 x  4x 5  gx   f x 2 0
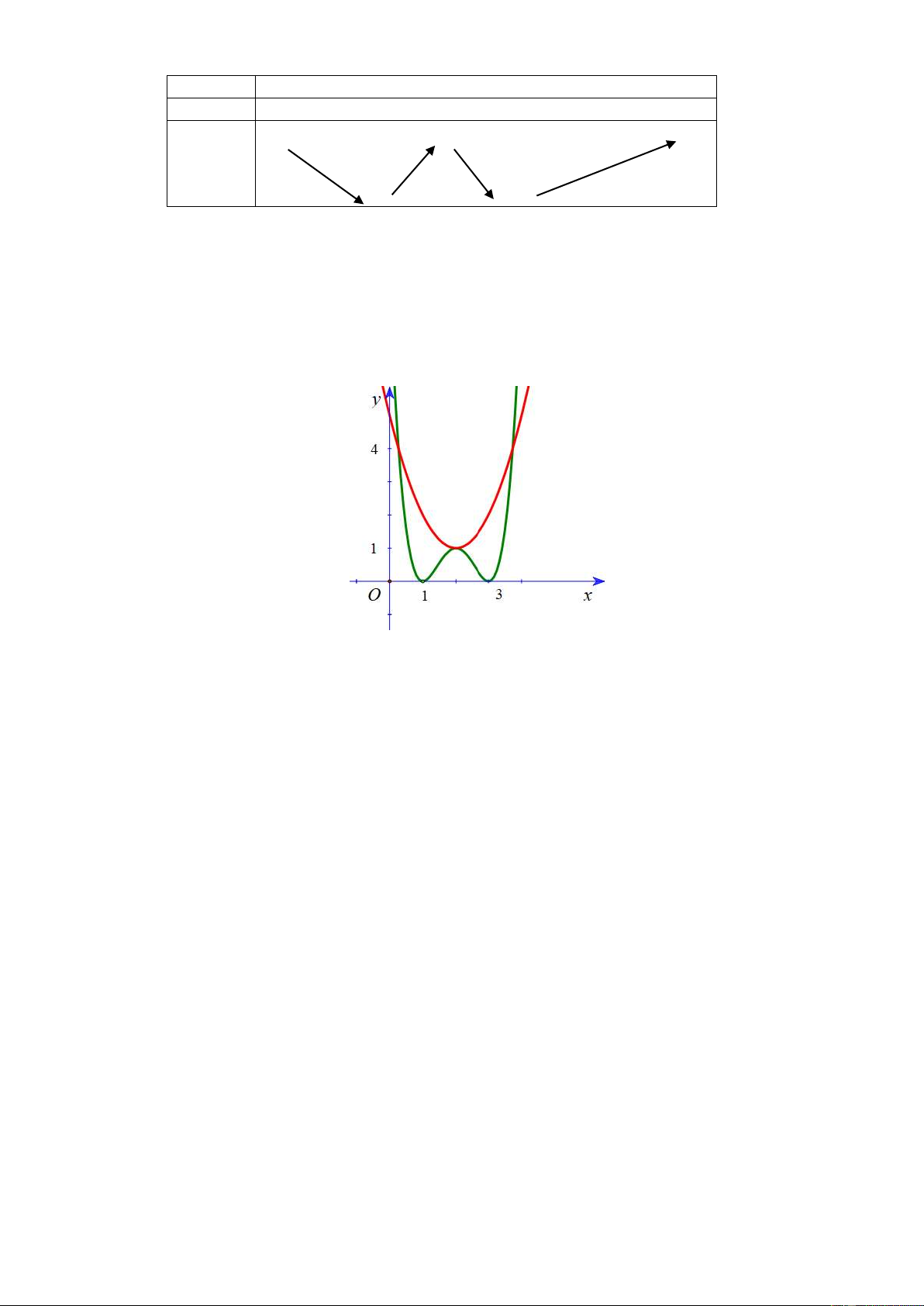
 x  4x  5 Ta có đồ thị hàm số 2
y  x  4x  5 và đồ thị hàm y  f  x như hình vẽ dưới
Quan sát hình vẽ ta thấy g x  0 có 3 nghiệm phân biệt trong đó chỉ có 1 nghiệm bội chẵn
Vậy hàm số g  x có 2 điểm cực trị. Trang 5