Đề tham khảo giữa kì 1 Toán 8 năm 2024 – 2025 phòng GD&ĐT Quận 3 – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THAM KHẢO GIỮA HỌC KÌ I
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2024-2025
TRƯỜNG TH, THCS VÀ THPT QUỐC TẾ Á CHÂU MÔN: TOÁN - KHỐI 8
(Thời gian làm bài: 90 phút, không tính thời gian giao đề)
Họ tên học sinh: ----------------------------------------------Lớp: -------------- SBD: -------------
(Học sinh lưu ý làm bài trên giấy thi, không làm trên đề)
PHẦN I: TRẮC NGHIỆM (3,0 điểm)
Câu 1. Trong các phát biểu sau, phát biểu nào đúng?
A. 2x là một đa thức.
B. Số 0 có bậc là 1. C. 2 3 2x y có bậc là 6. D. 2 2 2
5a b + 3ab − 2a b − 3a bcó bậc là 3.
Câu 2. Cho tứ giác MNPQ, cách đọc nào sau đây không đúng? A. Tứ giác NPQM. B. Tứ giác PQMN. C. Tứ giác QMNP. D. Tứ giác MPNQ.
Câu 3. Viết biểu thức 2
(x −1) thành đa thức? A. 2 x + 2x +1. B. 2 x − 2x +1. C. 2 x + 2x −1. D. 2 x − x +1.
Câu 4. Trong hình chóp tam giác đều, phát biểu nào sau đây sai?
A. Hình chóp tam giác đều có tất cả các mặt là tam giác đều.
B. Hình chóp tam giác đều có các cạnh bên bằng nhau.
C. Hình chóp tam giác đều có 4 mặt.
D. Hình chóp tam giác đều có 3 cạnh đáy bằng nhau.
Câu 5. Viết biểu thức 2 2
x − 9y dưới dạng tích:
A.(x − 9y)(x + 9y) .
B. (x − 3y)(x − 3y) .
C. (x + 3)(x − 3) .
D. (x − 3y)(x + 3y).
Câu 6. Cho tam giác MNP vuông tại P, khi đó: A. 2 2 2
MN + MP = NP . B. 2 2 2
MP + NP = MN . C. 2 2 2
MN + NP = MP .
D. MN + MP = NP .
Câu 7. Trong hình chóp tứ giác đều có mặt đáy là hình gì?
A. Hình tứ giác.
B. Hình bình hành.
C. Hình vuông.
D. Hình tam giác đều.
Câu 8. Kết quả của phép toán sau 2 2
(2ab − 5a ) − (3a + 2ab) A. 2 8 − a . B. 2 2a + 4ab . C. 2 8 − a + 4ab . D. 2 2a .
Câu 9. Cho tam giác DEF có 2 2 2
DE + FE = DF , phát biểu nào sau đây đúng?
A. Tam giác DEF vuông tại D.
B. Tam giác DEF vuông tại F.
C. Tam giác DEF vuông tại E.
D. Tam giác DEF cân tại D.
Câu 10. Khai triển hằng đẳng thức 3 3 a − b : A. 2 2
(a − b)(a + ab + b ) . B. 3 2 2 3
a − 3a b + 3ab − b . C. 2 2
(a + b)(a − ab + b ) . D. 3 2 2 3
a + 3a b + 3ab + b .
Câu 11. Cho tứ giác ABCD có A 30o = , B 211o = , C 15o = tìm số đo góc D? A. D 140o = . B. D 41o = . C. D 104o = . D. D 14o = .
Câu 12. Đẳng thức nào sau đây là lập phương một tổng?
A.x  y3 3 2 2 3
 x 3x y  3xy  y . C. 3 3     2 2 x y
x y x  xy  y .
B. x  y3 3 2 2 3
 x  3x y  3xy  y . D. 3 3     2 2 x y
x y x  xy  y .
PHẦN II: TỰ LUẬN (7,0 điểm)
Câu 1: (1,0 điểm) Cho đa thức sau 2 2 2 3
− a − 4ab + b + 3ab + 5a :
a) Thu gọn đa thức trên;
b) Tính giá trị của đa thức trên tại a = 1,b = 2 .
Câu 2: (2,0 điểm) Thực hiện phép tính: a) 2
2x(x − 3y) + 5x + 6xy ; b) 2 3 2
(15a b + 9ab − 5ab) : 3ab ; c) 2 3 3
(x + 2y) (x − 2y) + 2xy + 3x −8y   .
Câu 3: (1,5 điểm) Phân tích đa thức thành nhân tử a) 2 2 2
4a b − 6ab +16b b) 2
4x + 6xy −1+ 3y
Câu 4:(1,5 điểm) Chóp inox đặt trên đỉnh núi Fansipan
(Việt Nam) có dạng hình chóp tam giác đều cạnh 60cm
với diện tích đáy khoảng 1560cm2 và chiều cao khoảng
90cm. a) Cho biết chiều cao mặt bên khoảng 52cm. Hãy
tính diện tích xung quanh của chóp inox trên đỉnh núi Fansipan?
b) Tính thể tích của chóp inox trên đỉnh núi Fansipan (Việt Nam)?
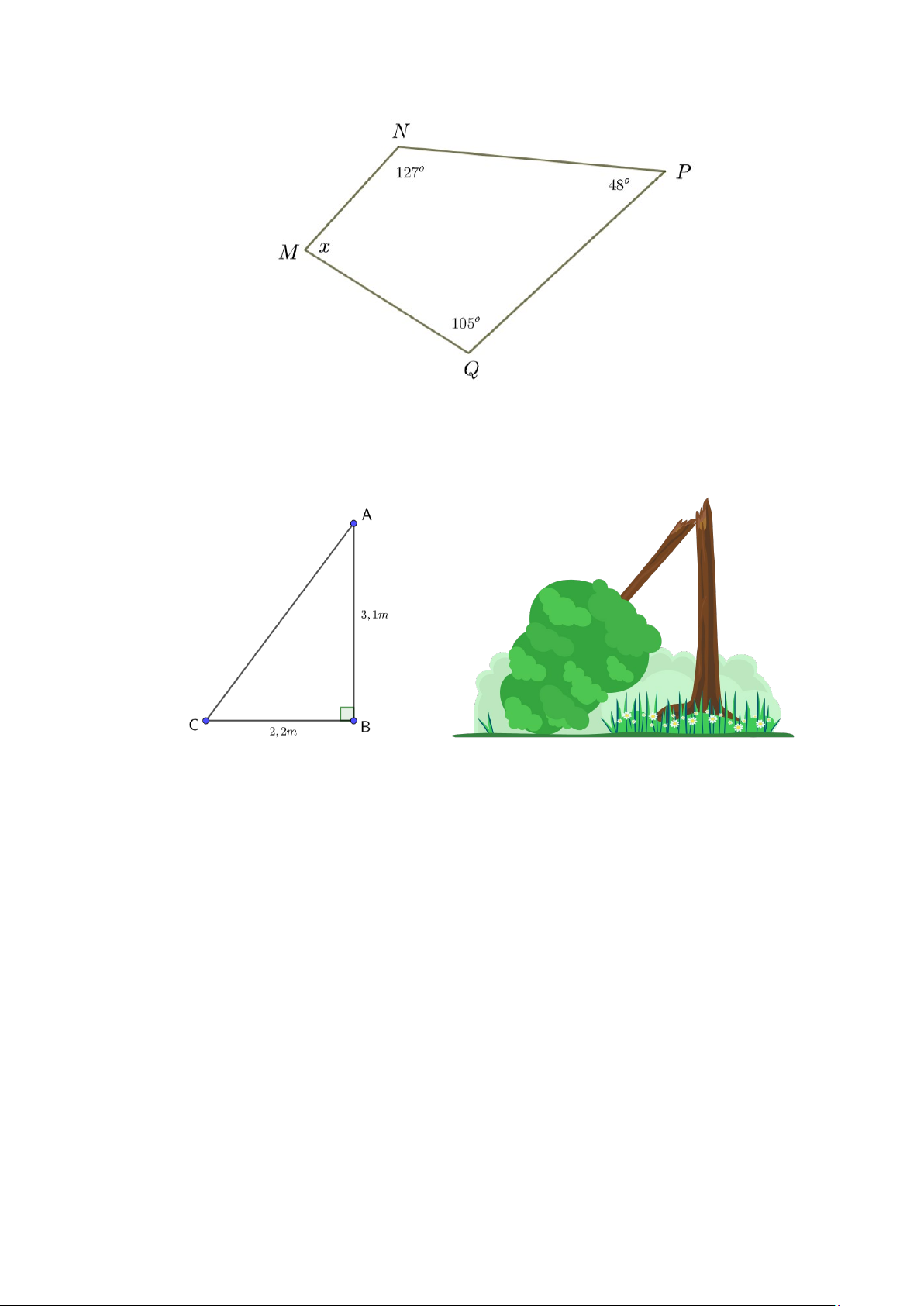
Câu 5: (0,5 điểm) Tính số đo góc M của tứ giác được cho như hình bên dưới.
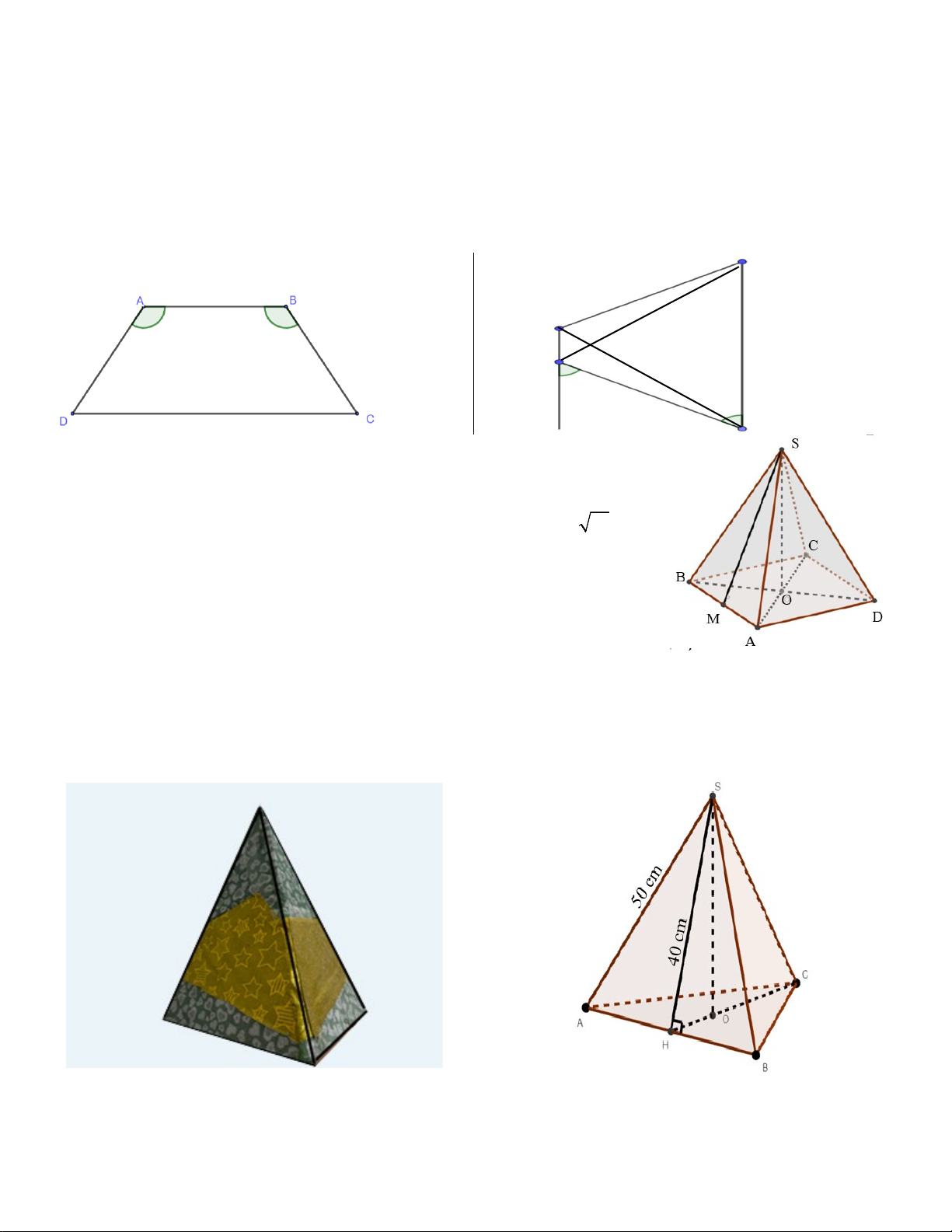
Câu 6: (0,5 điểm) Trong đợt bão, một cái cây đã bị gãy ngang thân (xem hình vẽ bên dưới),
ngọn cây chạm đất cách gốc 2,2m và chiều cao từ gốc cây đến chỗ cây bị gãy 3,1m. Em
hãy tính chiều cao (từ gốc đến ngọn) của cây đó? ---HẾT---
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm
HƯỚNG DẪN CHẤM ĐỀ THAM KHẢO GIỮA HỌC KÌ I NĂM HỌC 2024-2025 MÔN: TOÁN 8
PHẦN I: TRẮC NGHIỆM (3,0 điểm) 1 2 3 4 5 6 7 8 9 10 11 12 A D B A D B C A C A C B
II. PHẦN II : TỰ LUẬN (7 điểm) CÂU ĐÁP ÁN ĐIỂM Cho đa thức sau 2 2 2 A = 3
− a − 4ab + b + 3ab + 5a Câu 1 a) 2 2
A = 2a − ab + b 0.5
(1,0điểm) b) 2 2
A = 2.1 −1.2 + 2 = 20 0.5 a) 2
2x(x − 3y) + 5x + 6xy (0,5đ) 2 2
= 2x − 6xy + 5x + 6xy 0.25 2 = 7x 0.25 b) 2 3 2
(15a b + 9ab − 5ab) : 3ab (0,5đ) 2 5 Câu 2 = 5ab + 3b − 0,5 3
(2,0điểm) c) 2 3 3
(x + 2y) (x − 2y) + 2xy + 3x −8y   (1,0đ) 2 2 3 3
= (x + 2y)(x − 4xy + y + 2xy) + 3x − 8y 0.25 2 2 3 3
= (x + 2y)(x − 2xy + y ) + 3x − 8y 0.25 3 3 3 3
= x + 8y + 3x − 8y 0.25 3 = 4x 0.25 a) 2 2 2
4a b − 6ab +16b 2
= 2b(2a − 3ab + 8b) 0.5 b) 2
4x + 6xy −1+ 3y (1,0đ) Câu 3 2
= (4x −1) + 3y(2x +1) 0.25
(1,0điểm) =(2x+1)(2x−1)+3y(2x+1) 0.25
= (2x +1)[(2x −1) + 3y] 0.25
= (2x +1)(2x + 3y −1) Diện tích mặt bên: 1 2
S = × 60×52 =1560m 0.25 2 Câu 4 2 S = × = cm xq 1560 3 4680 0.5
(1,0điểm) 1 3
V = ×1560×90 = 46800cm 0.75 3 Câu 5
 +  +  +  = 360o M N P Q (0,5điểm) 0.25
360o (127o 48o 105o x = − + + ) 80o x = 0.25
Câu 6 Xét tam giác ABC vuông tại B, áp dụng định lý Pythagore: (0,5điểm) 2 2 2
AC = (3,1) + (2,2) =14,45 0.25 AC ≈ 3,8
Chiều cao của cái cây khoảng 3,8 + 3,1 = 6,9m 0.25 ---HẾT---
Học sinh giải cách khác nếu đúng thì vẫn được trọn điểm.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 3
KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THCS BẠCH ĐẰNG
NĂM HỌC 2023 – 2024
Môn: TOÁN – KHỐI 8
Thời gian làm bài: 60 phút
(Không kể thời gian phát đề)
Phần 1. Trắc nghiệm khách quan. (2,0 điểm)
Mỗi câu sau đây đều có 4 lựa chọn, trong đó chỉ có một phương án đúng.
Hãy khoanh tròn vào phương án mà em cho là đúng.
Câu 1: Biểu thức nào dưới đây không phải là đa thức? 2 A. 2 B. 2
x − y + xy C. 3 xy z D. x y z
Câu 2: Bậc của đa thức 2 3 3 2
5x y + 9x - 7y là: A. 3 B. 5 C. 7 D. 9
Câu 3: Số hạng tử của đa thức 5 3
5x + 2x y −1 là: A. 2 B. 3 C. 4 D. 5
Câu 4: Có bao nhiêu đơn thức trong các biểu thức sau đây: 4 2 2 ; ; xy x xy ;4; ;
x 3x − y π z A. 2 B. 3 C. 4 D. 5
Câu 5: Chiều cao của hình chóp tam giác đều là:
A. Độ dài đoạn thẳng nối từ đỉnh của hình chóp tới trung điểm của một cạnh đáy.
B. Chiều cao của mặt đáy.
C. Độ dài đường trung tuyến của một mặt bên của hình.
D. Độ dài đoạn thẳng nối từ đỉnh tới trọng tâm của tam giác đáy.
Câu 6: Số mặt của hình chóp tam giác đều là: A. 2 B. 3 C. 4 D. 5
Câu 7: Phát biểu nào sau đây là sai khi nói về chóp tứ giác đều S.ABCD?
A. Hình chóp tứ giác đều S.ABCD có đáy là tam giác đều.
B. Hình chóp tứ giác đều S.ABCD có 4 cạnh bên bằng nhau.
C. Hình chóp tứ giác đều S.ABCD có 4 mặt bên.
D. Hình chóp tứ giác đều S.ABCD có đỉnh là S.
Câu 8: Cho hình chóp tứ giác đều S.MNPQ có SM = 5 cm và MN = 4 cm. Khi đó: A. NP = PQ = SN = 4 cm; B. SN = SP = SQ =MP = 5cm; C. NP = PQ = QM = 4 cm; D. NP = PQ = 5cm.
Phần 2. Tự luận. (8,0 điểm)
Câu 1. (2 điểm) Rút gọn các biểu thức sau: a) 3 2
(x − 3) + x (9 − x) ; b) 2
(2x + 3)(2x − 3) − (2x +1) ;
Câu 2. (2 điểm) Phân tích các đa thức sau thành nhân tử: a) 3 2 4 3 2 2
6x y z − 4x y z − 2x y ; b) 4 3 2
x − x − x +1. Câu 3. (2 điểm)
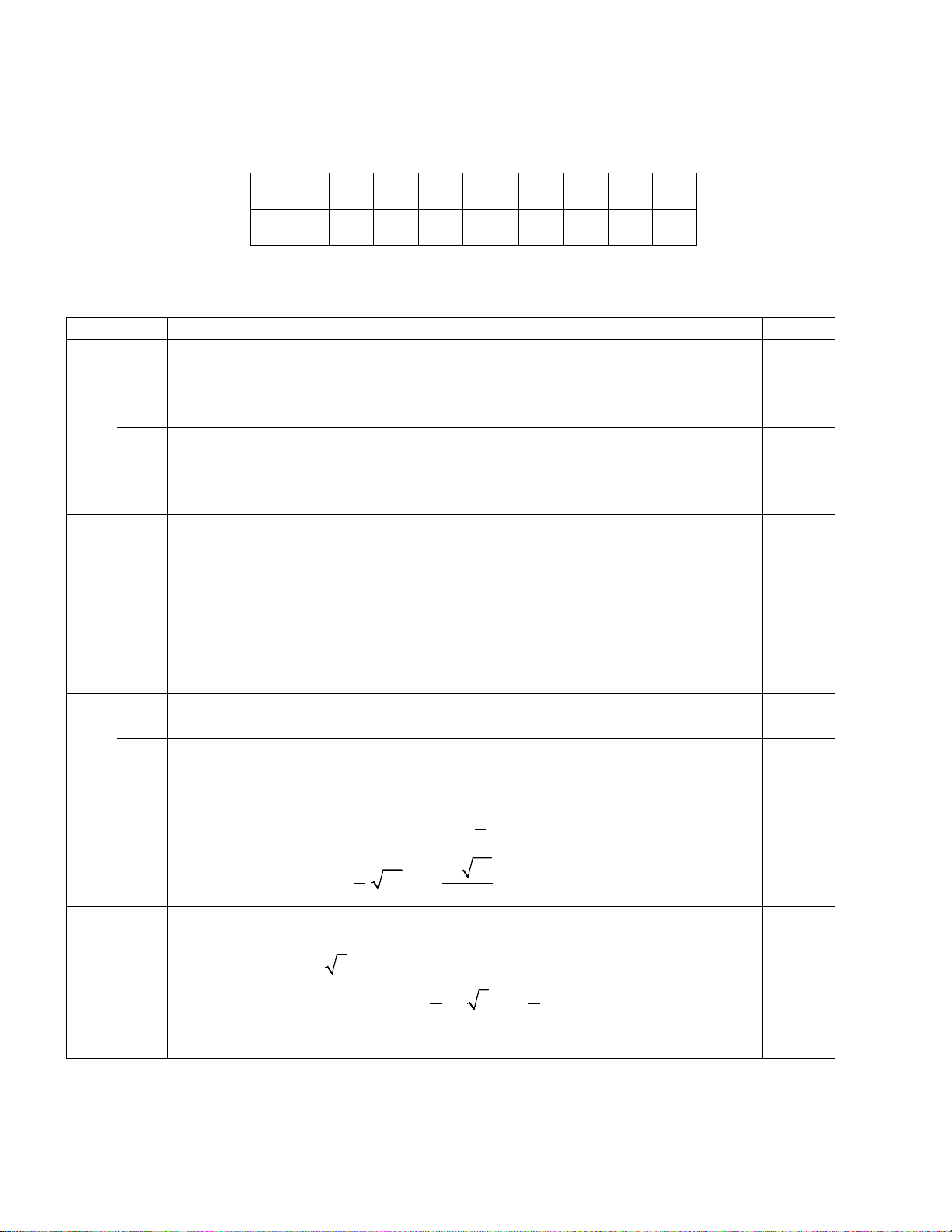
Tứ giác ABCD trong các trường hợp sau có phải hình thang cân không? Vì sao? a) AB // CD b) D AC = BD C B x A Câu 4. (1 điểm)
Cho hình chóp tứ giác đều S.ABCD như hình bên có đường cao mặt bên
SM = 5 cm, cạnh đáy AB = 4 cm và đường cao của hình chóp SO = 21 cm.
Hãy tính diện tích xung quanh và thể tích của hình.
Câu 5. (1 điểm) Trong tiết thực hành trải nghiệm chủ đề “Dùng vật liệu tái chế gấp hộp quà tặng”, nhóm bạn
Phương thực hiện gấp một hộp quà hình chóp tam giác đều từ thùng giấy cũ (Hình 1). Cho biết cạnh bên của
hộp quà có độ dài 50 cm và chiều cao của mặt bên có độ dài 40 cm (Hình 2). Tính diện tích toàn phần của hộp
quà (Biết rằng số đo các mép dán, độ dày của hộp là không đáng kể và kết quả làm tròn đến hàng đơn vị) S C A O H B Hình 1 Hình 2 - HẾT-
HƯỚNG DẪN CHẤM VÀ ĐÁP ÁN
I.TRẮC NGHIỆM: (2,0 điểm) Mỗi phương án chọn đúng ghi 0,25 điểm. Câu 1 2 3 4 5 6 7 8 Đ/án D B B C D B A C
II. TỰ LUẬN: (8,0 điểm) Câu Ý Lời giải Điểm 1 a 3 2
(x − 3) + x (9 − x) 3 2 2 3 0.25*2
= x − 9x + 27x − 27 + 9x − x = 27x − 27 0.5 b 2
(2x + 3)(2x − 3) − (2x +1) 2 2 0.25*2
= 4x − 9 − 4x − 4x −1 = 4 − x −10 0.5 2 a 3 2 4 3 2 2
6x y z − 4x y z − 2x y 2 2 2 0.25*4
= 2x y (3xz − 2x yz −1) b 4 3 2
x − x − x +1 3 2
= x (x −1) − (x −1) 0.25 3
= x (x −1) − (x −1)(x +1) 0.25 3
= (x −1)(x − x −1) 0.5 3
a Hình thang ABCD (AB // CD) có 𝐴𝐴̂ = 𝐵𝐵� nên ABCD là hình thang cân (hình 1.0
thang có hai góc kề một đáy bằng nhau là hình thang cân)
b Chứng minh NT // PM 0.5
Hình thang NTMP (NT // PM) có MN = PT nên ABCD là hình thang cân
(hình thang có hai đường chéo bằng nhau là hình thang cân) 0.5 4
Diện tích xung quanh của hình chóp: 1 4. .5.4 = 80 (cm2) 0.5 2 0.5
Thể tích của hình chóp: 1 2 16 21 . 21.4 = (cm3) 3 3 5 Tính được HB = 30 cm 0.25 Tính được AB = 60 cm Tính được CH = 30 3 0.25
Diện tích toàn phần của hộp quà: 1 1
.30 3.60 + .60.40.3 ≈ 5159 (cm2) 0.25*2 2 2
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
I-TRẮC NGHIỆM
Câu 1: Biểu thức nào sau đây là đơn thức? A. 5 ;
B. x  2y; C. xy x ; D. 2 5 3xy z . xy
Câu 2: Giá trị của biểu thức 2
6x y khi x = 3; y = −1 là: A. 54. B. -52. C. -54. D. 52 .
Câu 3 : Trong các đẳng thức dưới đây, đâu là đẳng thức đúng. A. ( A+ B)2 2 2
= A + 2AB + B C. ( + )2 2 2
A B = A + B B. ( + )2 2 2
A B = A + AB + B
D. ( A+ B)2 2 2
= A − 2AB + B
Câu 4: Kết quả phép toán là x  2 2
(x – 2x  4) A. 2 x  4. B. 3 x 8 . C. 2 x 4 . D. 3 x 8 .
Câu 5: Trong các phát biểu sau, phát biểu nào đúng? Hình chóp tứ giác đều có:
A. Các mặt bên là tam giác đều.
B. Các cạnh bên bằng nhau và đáy là hình vuông.
C. Tất cả các cạnh bằng nhau.
D. Các mặt bên là tam giác vuông.
Câu 6: Cho hình chóp tam giác đều có diện tích đáy bằng 42 cm2 và chiều cao bằng 8 cm.
Thể tích của hình chóp này là A. 111 cm3 . B. 112 cm3 C. 113 cm3. D. 114 cm3
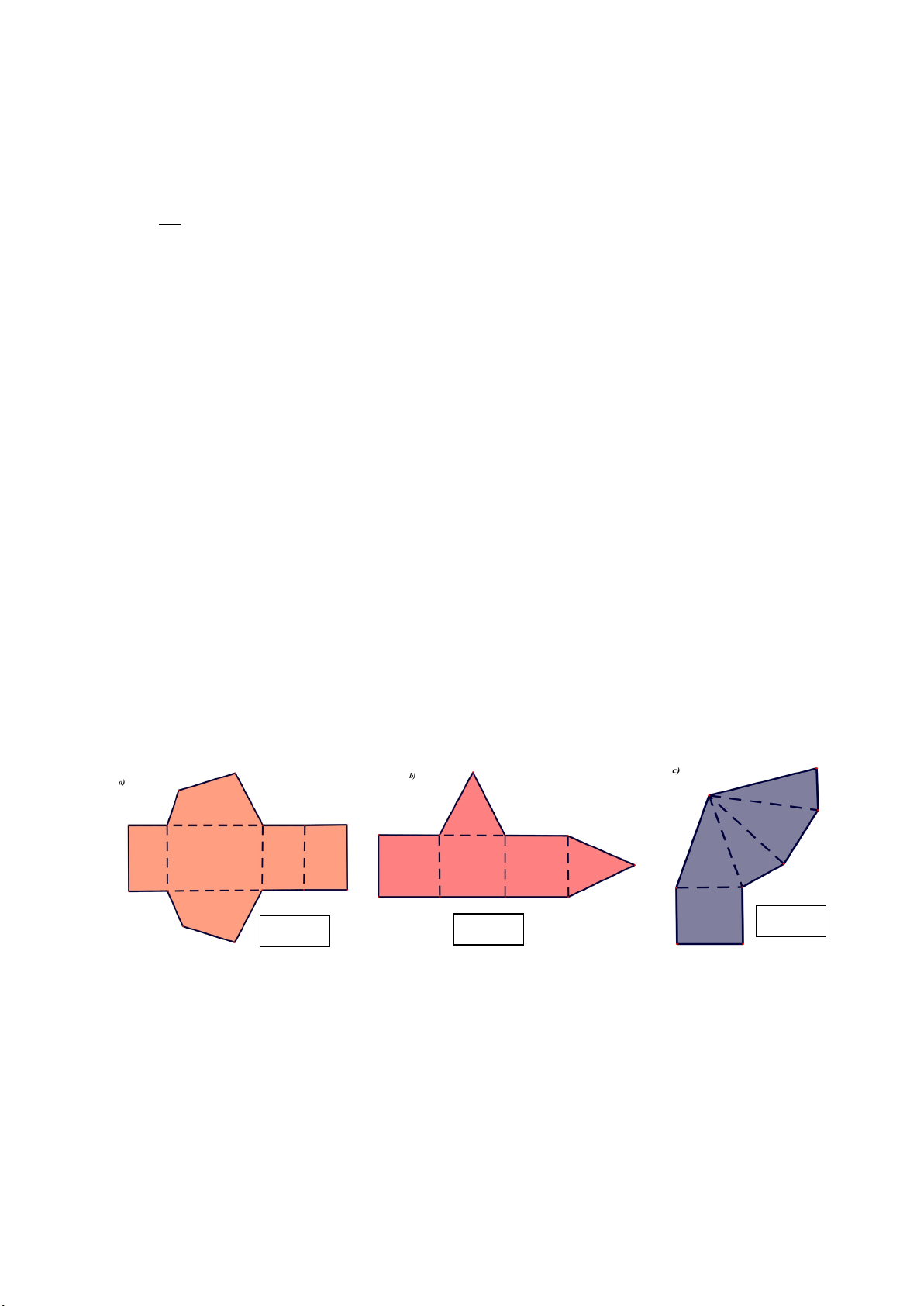
Câu 7: Trong các hình vẽ bên dưới hình nào có thể gấp theo nét đứt để được hình chóp tứ giác đều : Hình a Hình b Hình c
A. Hình b và c . B. Hình b . C. Hình a và c . D. Hình c .
Câu 8: Tổng số đo các góc của một tứ giác bằng bao nhiêu độ?
A. 180 B. 270 C. 360 D. 450 II- TỰ LUẬN:
Bài 1. Thu gọn biểu thức:
a) 5x2y 4x 3 y
b) (x −1)( y+1) − xy+ y c) ( 3 2 3 3
4x − 6x y + x y) : ( 2
2x ) d ) (x+ y)2 − (x − y)(x+ y)
Bài 2. Phân tích đa thức thành nhân tử: a) 2
2x 6xy 12x b) 2 9x −12x + 4 c) 2
4x − 25 d) x (x − 7)−3x + 21
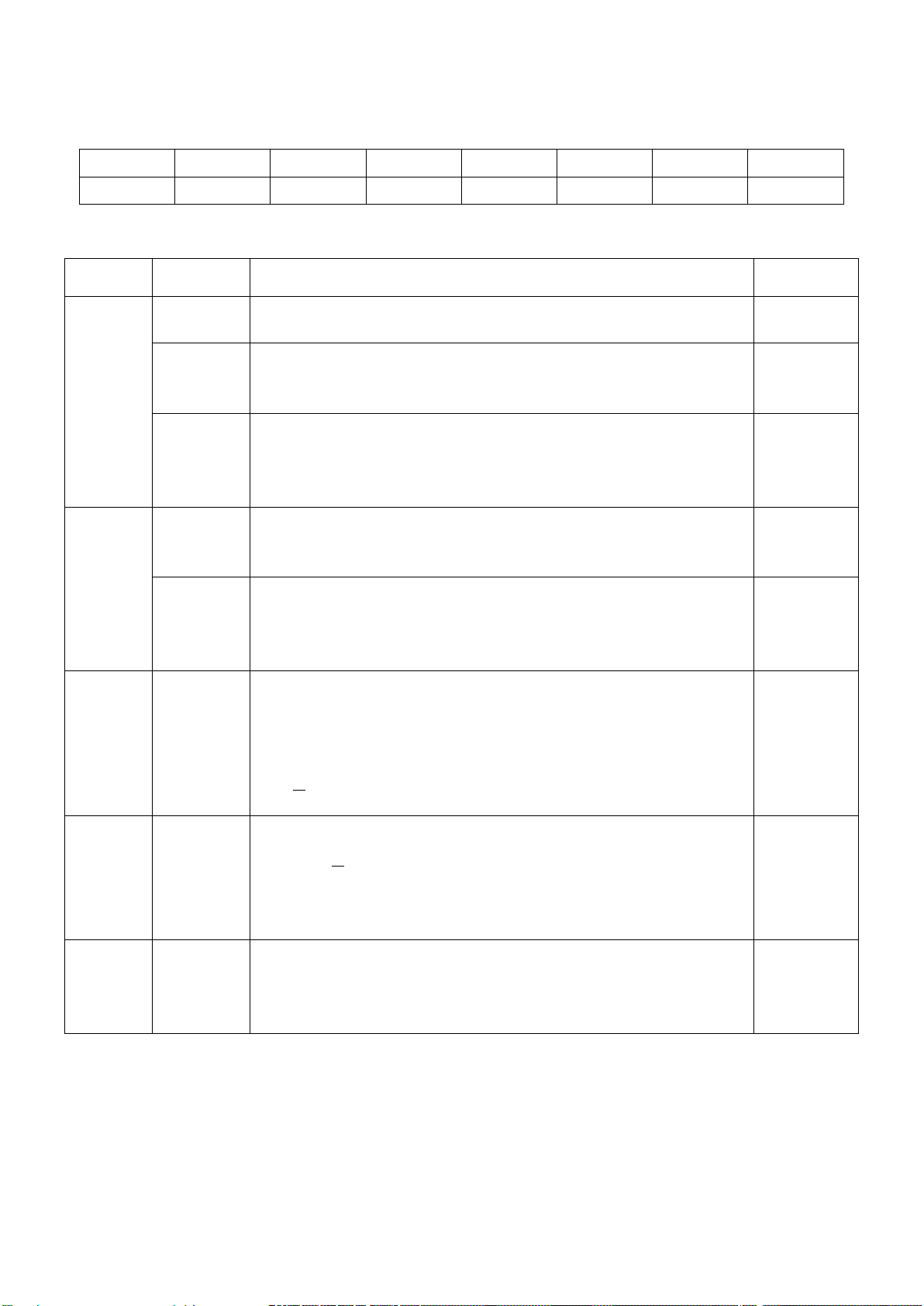
Bài 3. Một cửa hàng bán lều ngủ cho trẻ em có dạng hình chóp tứ giác đều, có đáy là một tấm
thảm hình vuông có cạnh dài 90cm và các mặt bên là những tấm vải hình tam giác cân có
chiều cao 120cm ( được mô tả bởi hình sau).
a) Tính diện tích vải các mặt xung quanh của lều.
b) Biết giá thảm 180 000 đồng/ 2
m , tiền vải các mặt bên là 120 000 đồng/ 2 m , phụ
kiện trang trí đi kèm có giá 50 000 đồng, Hỏi tổng số tiền vật liệu để làm nên mỗi cái lều là bao nhiêu ?
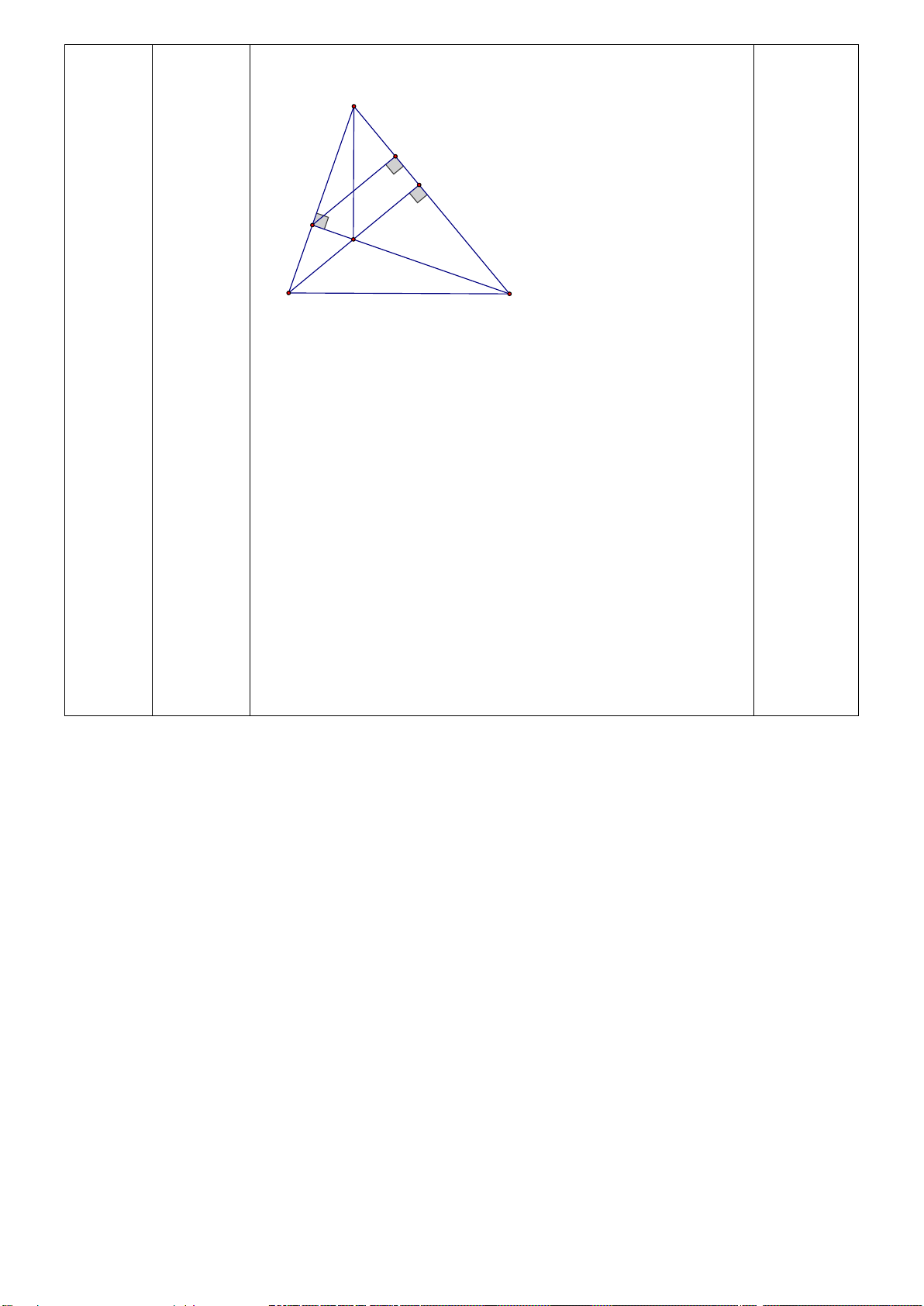
Bài 4. Một hồ bơi có dạng tứ giác ABCD được mô tả như
hình vẽ bên. Biết AC là tia phân giác góc  BAD và  0 DAC  40 . a) Tính số đo góc  BCD
b) Biết AB = 8 m và BC = 6 m. Một vận động viên bơi lội muốn bơi
từ A đến C trong 8 giây thì cần bơi với vận tốc (m/s) là bao nhiêu ?
Bài 5. (1điểm) Tìm giá trị nhỏ nhất của biểu thức 4 3 2
A  x  2x 3x  2x  2 — Hết —
HƯỚNG DẪN CHẤM KIỂM TRA GIỮA HỌC KỲ I
PHẦN I. TRẮC NGHIỆM: Câu 1 2 3 4 5 6 7 8 Đ.án D C A B B B D C
PHẦN II. TỰ LUẬN: Bài Đáp án
a)5x  2y  4x  3 y
 x 3y  3 b)x  1 y  +1  xy + y
 xy  x  y 1 xy  y  x 1 1 c) 3 2 3 3
4x 6x y + x y: 2 2x  3 1  2x 3y  y x 2
d)x+ y2 x yx+ y 2 2 2 2
 x  2xy  y  x  y 2  2y  2xy 2
a) 2x 6xy 12x
 2x(x 3y  6) 2 9x 12x  4 b) 2 2  (3x)  2.3 .2 x  2 2 2  (3x  2) a) 2 4x − 25 = ( )2 2 2x − 5 = (2x − 5)(2x + 5)
d) x (x − 7)−3x + 21
= x(x − 7) − 3(x − 7)
= (x − 7)(x − 3)
Diện tích vải các mặt xung quanh của lều.là: 3
4.120.90:2 = 21600 (cm2) = 2.16 (m2)
Giá vật liệu để làm nên mỗi cái lều là:
2.16. 120000  0,9.0,9.180000 50000  430.700 2 (đồng) a) Số đo góc  BCD là: 0 0 0 0 0 0
D  360 (90  90  40  40 ) 100 4
b) Xét tam giác ABC vuông tại B , theo định lí Pythagore ta có: 2 2 2 2 2
AC  AB  BC  6 8 100
 AC 10(m)
Vận tốc vận động viên bới lội cần phải bới là : 10:8 =1.25 (m/s) 4 3 2
A  x  2x  3x  2x  2 4 2 3 2
 (x  2x 1)  (2x  2x)  x 1 Ta có 2 2 2 2
 (x 1)  2x(x 1)  x 1 2 2
 (x  x 1) 1 5 1 2 3 2 [(x  )  ] 1 2 4 Ta có : 1 2
(x  )  0 x 2 Nên 1 2 3 2 25 [(x  )  ] 1 2 4 16 Vậy A min = 25 khi 1 1
x   0  x  16 2 2 ỦY BAN NHÂN DÂN QUẬN 3
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 TRƯỜNG THCS COLETTE
NĂM HỌC 2023 – 2024 MÔN : TOÁN 8 ĐỀ CHÍNH THỨC
Thời gian làm bài: 60 phút
(Đề có 2 trang)
(không kể thời gian phát đề) ĐỀ A
PHẦN I: TRẮC NGHIỆM (2,0 điểm)
Học sinh ghi vào giấy bài làm câu trả lời đúng (ví dụ: 1A; 2B; 3C; …)
Câu 1. Biểu thức nào dưới đây không là đơn thức? A. 2 B. 5x3y2z C. y D. 0 z
Câu 2. Biểu thức nào là đa thức trong các biểu thức sau? A. x2y – 3xy2 B. 1 − − 3x C. 2023x D. 2 y x
Câu 3. Kết quả của phép tính (3x + 2y)(3x – 2y) là: A. 3x2 – 2y2 B. (3x + 2y)2 C. (3x – 2y)2 D. 9x2 – 4y2
Câu 4. Giá trị của biểu thức xy (x – 2y) – y (x2 – xy) tại x = 2023, y = –1 là A. –1 B. 1 C. –2023 D. 2023 2
Câu 5. Thực hiện phép tính A : B với A = 2x6y4 và  1 2 B xy  = −  , ta được : 3    A. –18x4 B. 18x4 C. –18x4y D. 18x4y
Câu 6. Chiều dài của hình chữ nhật có diện tích bằng 10x2 – 4xy + 2x và chiều rộng bằng 2x là: A. 5x – 2y + 1 B. 5x – 2y C. 5x + 2y D. 5x – 2y + x
Câu 7. Cho tứ giác ABCD có  0 =  0 =  0
A 110 , B 93 , C = 100 . Số đo góc D bằng: A. 700 B. 800 C. 570 D. 70
Câu 8. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau A. 11cm; 4cm; 13cm B. 45m; 36m; 27m C. 3m; 5m; 7m D. 20dm; 30dm; 40dm
PHẦN II: TỰ LUẬN (8,0 điểm)
Bài 1. (2,5 điểm) Thực hiện phép tính: a) 3x (x2 – 2x + 5)
b) (2x + 1)(2x – 1) – x (1 + 4x)
c) (4x – 3)2 + (2x + 1) (5 – 8x)
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 3x3 – 12x2 + 12x b) x2 (x – 2y) + (2y – x)
Bài 3. (1,0 điểm) Tìm x biết: (2x + 3)2 – 4x(x + 5) = 5
Bài 4. (1,0 điểm)
Một cửa hàng bán lều ngủ cho trẻ em có dạng hình chóp tứ giác đều có đáy là một tấm
thảm hình vuông có cạnh dài 0,9 m và các mặt bên là những tấm vải hình tam giác cân có chiều cao 1,2 m. 1,2m 0,9m
a) Tính diện tích vải các mặt xung quanh của lều.
b) Biết tấm thảm lót có giá vốn là 180 000 đồng, tiền vải bọc các mặt bên có giá vốn là
150 000 đồng/1m2, tiền công và phụ kiện trang trí đi kèm có giá vốn là 190 000
đồng. Hỏi giá bán của mỗi cái lều là bao nhiêu để cửa hàng có lợi nhuận là 50% ?
Bài 5. (2,0 điểm)
Cho ∆ABC nhọn. Gọi H là giao điểm của hai đường cao BE, CF của ∆ABC. Vẽ FK vuông góc AC tại K.
a) Chứng minh: FKEB là hình thang vuông.
b) Chứng minh: AB2 + HC2 = BC2 + HA2. --- Hết ---
Học sinh không được sử dụng tài liệu
Giám thị coi kiểm tra không giải thích gì thêm.
HƯỚNG DẪN CHẤM ĐỀ A
KIỂM TRA GIỮA HK1 (2023-2024) - MÔN TOÁN 8
PHẦNI: TRẮC NGHIỆM (2,0 điểm) 1 2 3 4 5 6 7 8 C A D C B A C B
PHẦN II: TỰ LUẬN (8,0 điểm) BÀI Ý NỘI DUNG ĐIỂM a 3x (x2 – 2x + 5) (0,75 đ) = 3x3 – 6x2 + 15x 0,25đ x 3 b
(2x + 1)(2x – 1) – x (1 + 4x) 1
(0,75 đ) = 4x2 – 1 – x – 4x2 0,25đ x 2 (2,5 đ) = –x – 1 0,25đ
(4x – 3)2 + (2x + 1) (5 – 8x) c
= (4x)2 + 2.4x.3 + 32 + 10x – 16x2 + 5 – 8x 0,25đ x 2
(1,0 đ) = 16x2 – 24x + 9 + 10x – 16x2 + 5 – 8x 0,25đ = –22x + 14 0,25đ a 3x3 – 12x2 + 12x = 3x (x2 – 4x + 4) 0,5đ (0,75 đ) = 3x ( x – 2)2 0,25đ 2 x2 (x – 2y) + (2y – x) (1,5 đ) b
= x2 (x – 2y) – (x – 2y)
(0,75 đ) = (x – 2y) (x2 – 1) 0,25đ x 3
= (x – 2y) (x – 1) (x + 1) (2x + 3)2 – 4x(x + 5) = 5
4x2 + 12x + 9 – 4x2 – 20x = 5 0,25đ x 2 3 … (1,0 đ) –8x = –4 0,25đ 1 x = 0,25đ 2
Diện tích vải một mặt bên của lều là 1 4 a .0,9.1,2 = 0,54 (m2) (1,0 đ) (0,5 đ) 2 0,25đ x 2
Diện tích vải các mặt xung quanh của lều 0,54.4 = 2,16 (m2)
Số tiền vốn của 1 cái lều là: b
180 000 + 150 000. 2,16 + 190 000 = 694 000 (đồng)
(0,5 đ) Giá bán của mỗi cái lều để cửa hàng có lợi nhuận 50% 0,25đ x 2
694 000. 150% = 1 041 000 (đồng) A K E F H B C
------------------------------------------------------------------------
Chứng minh: FKEB là hình thang vuông. a
Chứng minh được FK // BE 5
(1,0 đ) ⇒ Tứ giác FKEB là hình thang (2,0 đ) = Mà  0 FKE 90 (gt)
⇒ Tứ giác FKEB là hình thang vuông. 4 x 0,25đ
------------------------------------------------------------------------
Chứng minh: AB2 + HC2 = BC2 + HA2. b Ta có: AB2 + HC2 (1,0 đ)
= AE2 + BE2 + HE2 + CE2 (định lý Pytago) = AE2 + HE2 + BE2 + CE2
= AH2 + BC2 (định lý Pytago) ⇒ đpcm 2 x 0,25đ 0,25đ 0,25đ Lưu ý:
Học sinh có cách giải khác nếu đúng thì giáo viên dựa trên thang điểm chung để chấm. ỦY BAN NHÂN DÂN QUẬN 3
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 TRƯỜNG THCS COLETTE
NĂM HỌC 2023 – 2024 MÔN : TOÁN 8 ĐỀ CHÍNH THỨC
Thời gian làm bài: 60 phút
(Đề có 2 trang)
(không kể thời gian phát đề) ĐỀ B
PHẦN I: TRẮC NGHIỆM (2,0 điểm)
Học sinh ghi vào giấy bài làm câu trả lời đúng (ví dụ: 1A; 2B; 3C; …)
Câu 1. Biểu thức nào dưới đây không là đơn thức? A. 0 B. 5x3y2z C. y D. 5 z
Câu 2. Kết quả của phép tính (2x + 3y)(2x – 3y) là: A. 2x2 – 3y2 B. (2x + 3y)2 C. (2x – 3y)2 D. 4x2 – 9y2
Câu 3. Biểu thức nào là đa thức trong các biểu thức sau? A. x3y – 2xy3 B. 1 2x − − C. 2022y D. 2 y x 2
Câu 4. Thực hiện phép tính A : B với A= 3x5y4 và  1 2 B xy  = −  , ta được : 2    A. –12x3 B. 12x3 C. –12x3y D. 12x3y
Câu 5. Giá trị của biểu thức xy (x2 – 3y) – y (x3 – 2xy) tại x = 2022, y = –1 là A. –1 B. 1 C. –2022 D. 2022
Câu 6. Chiều rộng của hình chữ nhật có diện tích bằng 9x2 – 6xy + 3x và chiều dài bằng 3x là: A. 3x – 2y + 1 B. 3x – 2y C. 3x + 2y D. 3x – 2y + x
Câu 7. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau A. 12cm; 4cm; 13cm B. 21dm; 31dm; 41dm C. 24m; 40m; 32m D. 3m; 5m; 7m
Câu 8. Cho tứ giác ABCD có  0 =  0 =  0
A 80 , B 97 , D = 110 . Số đo góc C bằng: A. 700. B. 730. C. 1000. D. 30.
PHẦN II: TỰ LUẬN (8,0 điểm)
Bài 1. (2,5 điểm) Thực hiện phép tính: a) 4x (x2 – 3x + 2)
b) (3x + 1)(3x – 1) – x (4 + 9x)
c) (4x – 3)2 + (2x + 1) (3 – 8x)
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 2x2y – 8xy + 8y b) x2 (3x – y) + (y – 3x)
Bài 3. (1,0 điểm) Tìm x biết: (3x + 2)2 – 9x(x + 3) = 10
Bài 4. (1,0 điểm)
Một cửa hàng bán lều ngủ cho trẻ em có dạng hình chóp tứ giác đều có đáy là một tấm
thảm hình vuông có cạnh dài 0,9 m và các mặt bên là những tấm vải hình tam giác cân có chiều cao 1,2 m. 1,2m 0,9m
a) Tính diện tích vải các mặt xung quanh của lều.
b) Biết tấm thảm lót có giá vốn là 200 000 đồng, tiền vải bọc các mặt bên có giá vốn
150 000 đồng/1m2, tiền công và phụ kiện trang trí đi kèm có giá vốn là 190 000
đồng. Hỏi giá bán của mỗi cái lều là bao nhiêu để của hàng có lợi nhuận là 40% ?
Bài 5. (2,0 điểm)
Cho ∆ABC nhọn. Gọi H là giao điểm của hai đường cao BD, CE của ∆ABC. Vẽ DI vuông góc AB tại I.
a) Chứng minh: IDCE là hình thang vuông.
b) Chứng minh: AC2 + HB2 = BC2 + HA2. --- Hết ---
Học sinh không được sử dụng tài liệu
Giám thị coi kiểm tra không giải thích gì thêm.
HƯỚNG DẪN CHẤM ĐỀ B
KIỂM TRA GIỮA HK1 (2023-2024) - MÔN TOÁN 8
PHẦNI: TRẮC NGHIỆM (2,0 điểm) 1 2 3 4 5 6 7 8 C D A B C A C B
PHẦN II: TỰ LUẬN (8,0 điểm) BÀI Ý NỘI DUNG ĐIỂM a 4x (x2 – 3x + 2) 0,25đ x 3 1 (0,75 đ) = 4x3 – 12x2 + 8x (2,5 đ) b
(3x + 1)(3x – 1) – x (4 + 9x)
(0,75 đ) = 9x2 – 1 – 4x – 9x2 0,25đ x 2 = –4x – 1 0,25đ
(4x – 3)2 + (2x + 1) (3 – 8x) c
= (4x)2 – 2.4x.3 + 32 + 6x – 16x2 + 3 – 8x 0,25đ x 2
(1,0 đ) = 16x2 – 24x + 9 + 6x – 16x2 + 3 – 8x 0,25đ = –26x + 12 0,25đ a 2x2y – 8xy + 8y = 2y (x2 – 4x + 4) 0,5đ (0,75 đ) = 2y (x – 2)2 0,25đ 2 x2 (3x – y) + (y – 3x) (1,5 đ) b
= x2 (3x – y) – (3x – y)
(0,75 đ) = (3x – y) (x2 – 1) 0,25đ x 3
= (3x – y) (x – 1) (x + 1) (3x + 2)2 – 9x(x + 3) = 10
9x2 + 12x + 4 – 9x2 – 27x = 10 0,25đ x2 3 … (1,0 đ) (1,0 đ) –15x = 6 0,25đ −2 x = 0,25đ 5
Diện tích vải một mặt bên của lều là 1 a .0,90.1,2 = 0,54 (m2) (0,5 đ) 2 0,25đ x 2 4
Diện tích vải các mặt xung quanh của lều (1,0 đ) 0,54.4 = 2,16 (m2)
Số tiền vốn của 1 cái lều là: b
200 000 + 150 000. 2,16 + 190 000 = 714 000 (đồng)
(0,5 đ) Giá bán của mỗi cái lều để của hàng có lợi nhuận 40% 0,25đ x 2
714 000. 140% = 999 600 (đồng) A I D E H B C
------------------------------------------------------------------------
Chứng minh: IDCE là hình thang vuông.
Chứng minh được DI // CE 5
⇒ Tứ giác IDCE là hình thang (2,0 đ) a Mà  0 CEI = 90 (gt)
(1,0 đ) ⇒ Tứ giác IDCE là hình thang vuông. 4 x 0,25đ
------------------------------------------------------------------------
Chứng minh: AC2 + HB2 = BC2 + HA2. Ta có: AC2 + HB2
= AE2 + CE2 + HE2 + BE2 (định lý Pytago) = AE2 + HE2 + BE2 + CE2 b
= AH2 + BC2 (định lý Pytago) (1,0 đ) ⇒ đpcm 0,25đ x 2 0,25đ 0,25đ Lưu ý:
Học sinh có cách giải khác nếu đúng thì giáo viên dựa trên thang điểm chung để chấm.