Đề tham khảo giữa kì 2 Toán 8 năm 2024 – 2025 phòng GD&ĐT Bình Thạnh – TP HCM có đáp án

UBND QUẬN BÌNH THẠNH
KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG TRUNG HỌC CƠ SỞ
NĂM HỌC: 2024 – 2025 CÙ CHÍNH LAN
MÔN: TOÁN – LỚP: 8 ĐỀ ĐỀ NGHỊ
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
A. Phần Trắc Nghiệm (3 điểm)
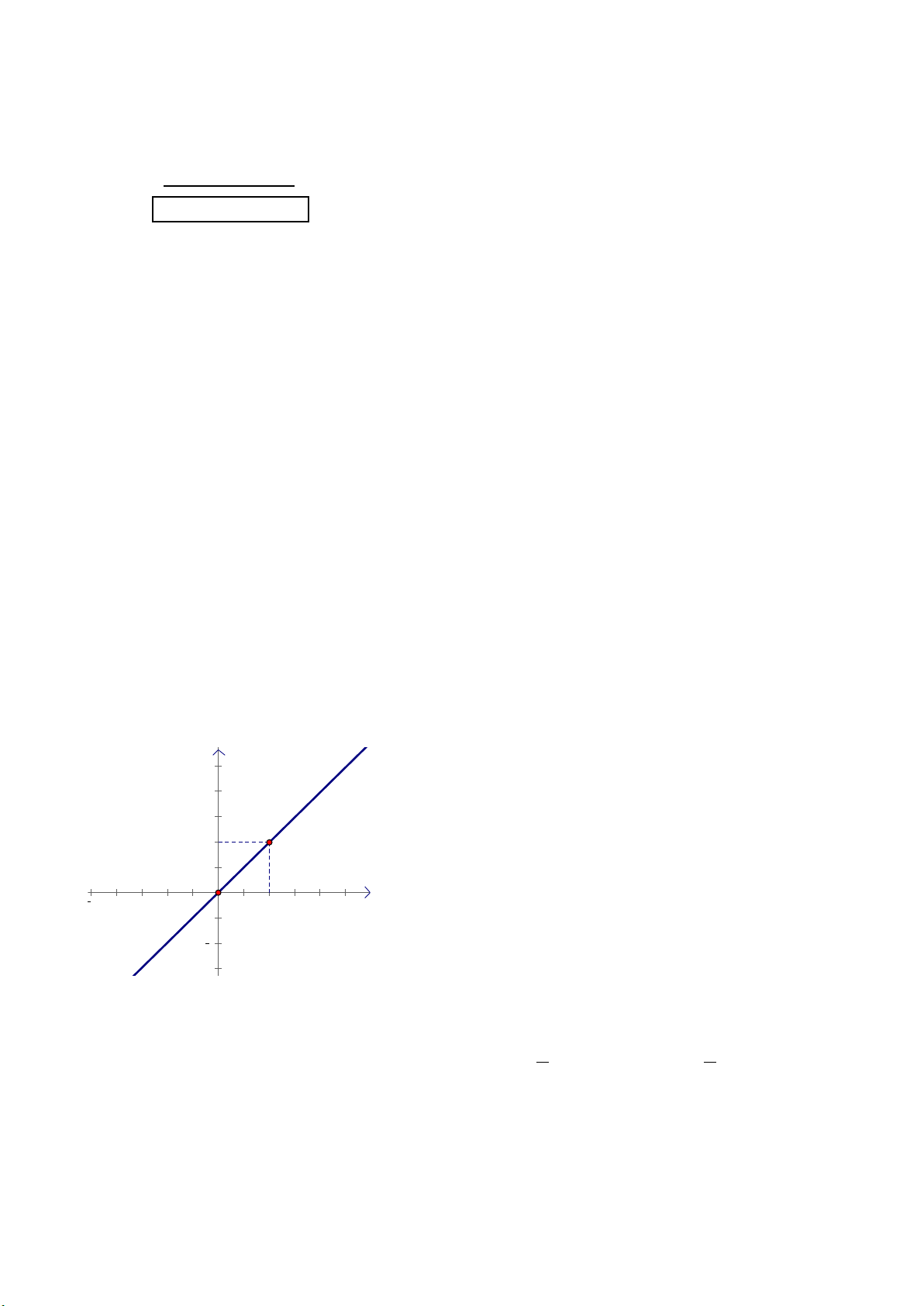
Câu 1. Cặp đường thẳng nào sau đây song song với nhau? A. y = 2
− x + 4 và y = 2 − x + 4
B. y = x + 7 và y = 7 + x C. y = 5
− x − 7 và y = 5x − 7
D. y = 4x + 4và y = 4x − 5
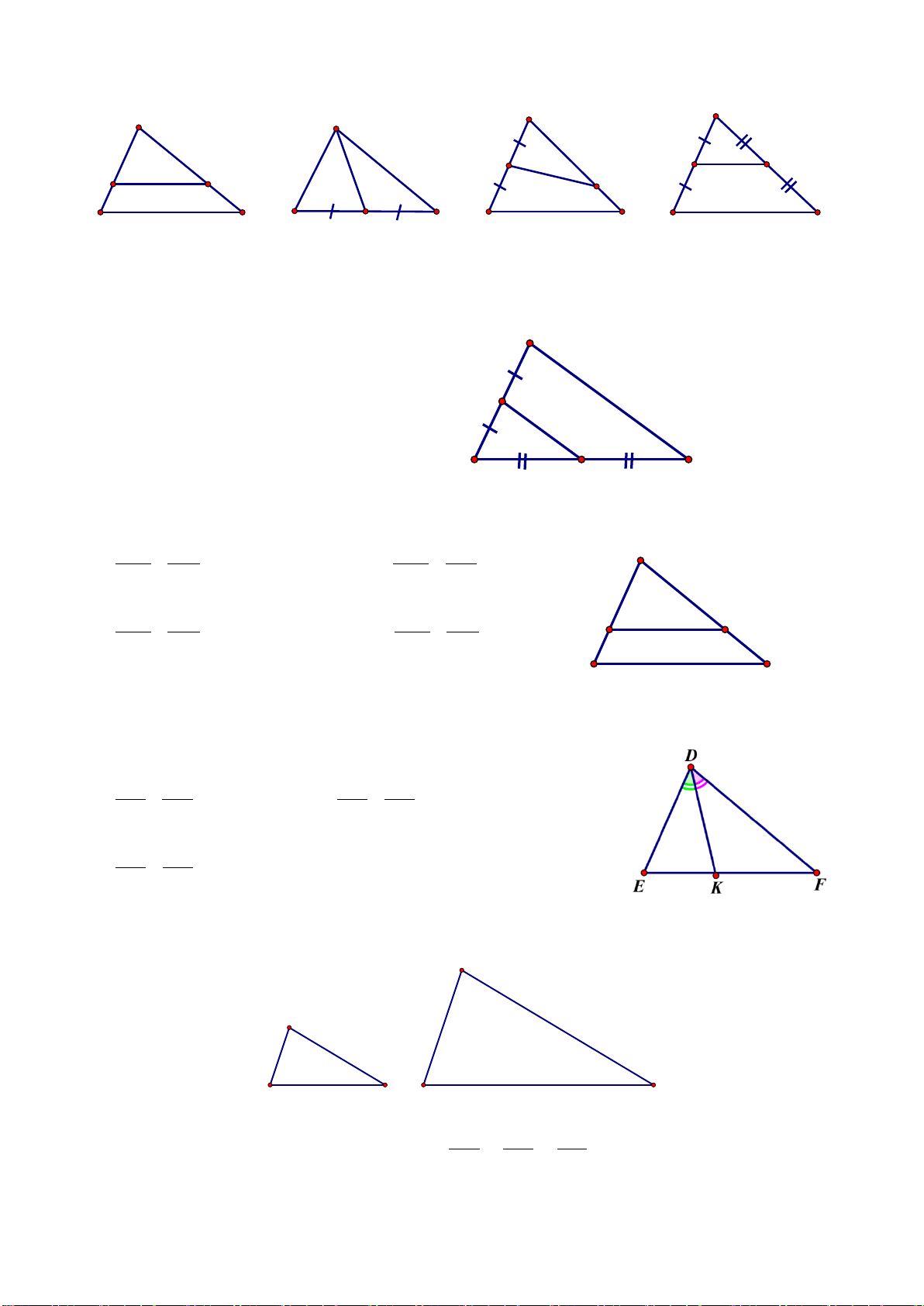
Câu 2. Cho DE là đường trung bình của tam giác ABC. Độ dài x là? A. 6 B. 12 B C. 15 x D. 10 D 6 cm A E C
Câu 3. Giá trị của x trong hình bên, biết BD là phân giác góc B B A. 20 3 x B. 3 5 20 C. 15 C 4 D 3 A 4 D. 4 15
Câu 4. Nếu ABC ∆ ∽ A
∆ 'B'C 'theo tỉ số 1 k = thì A
∆ 'B'C '∽ ABC ∆ theo tỉ số 3 A. 1 B. 1 C. 3 D. 9 3 9 Câu 5. Cho ABC ∆ ∽ DEF ∆ , biết  = ° 
A 75 , B = 50° . Khi đó số đo F bằng A. 65° B. 85° C. 55° D. 75°
Câu 6. Cho đường thẳng y = 7x + 4 và y = 7
− x + 4. Hai đường thẳng đã cho
A. cắt nhau tại điểm có hoành độ là 4 B. song song với nhau
C. cắt nhau tại điểm có tung độ là 4 D. trùng nhau
Câu 7. Đường thẳng song song với đường thẳng y = x và cắt trục tung tại điểm có tung độ bằng 1 là: A. y = x +1
B. y = −x −1 C. y = x −1
D. y = 3 − 2(1− x)
Câu 8. Hàm số nào dưới đây là hàm số bậc nhất A. 2 1 y − = 2x + B. 1 5 y = C. y = x − 4 D. y = x −1 4 x
Câu 9. Trong các điểm sau, điểm nào thuộc đồ thị hàm số y = x −1 A. ( 1; − 2) B. (2; ) 1 C. (2; ) 1 − D. ( 2; − − ) 1
Câu 10. Cho hàm số bậc nhất 1 1
y = − x + có hệ số góc là: 3 3 − A. 3 B. 3 − C. 1 D. 1 3 3
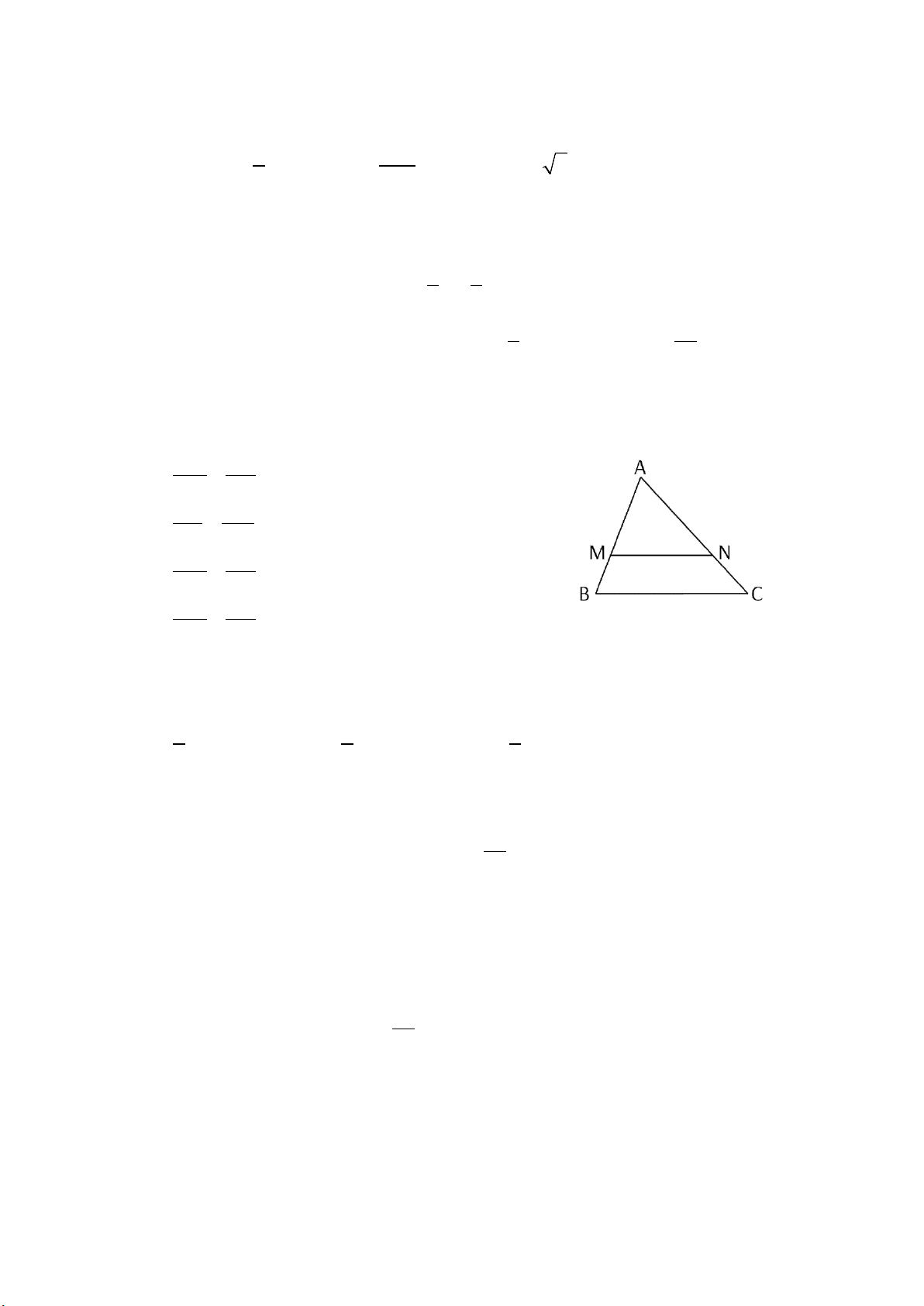
Câu 11. Cho tam giác ABC, biết MN // BC. Trong khẳng định sau, khẳng định nào đúng? A. AM AN = MB AC B. AN MN = NC BC C. AM AN = MB NC D. AM NC = MB AN
Câu 12. Cho hai đoạn thẳng MN = 6cmvà PQ =18cm . Tỉ số của đoạn thẳng MN và PQ là: A. 2 B. 3 C. 1 D. 3 3 2 3
B. Phần Tự Luận (7 điểm) Bài 1 (1,5 điểm).
a) Cho hàm số y = f (x) 2 = 2x +1. Tính  1 f −   và f (1) . 2   
b) Cho hàm số y = (m − 4) x − 9 . Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.
c) Tìm m để các hàm số bậc nhất y = 3mx −12 ( m ≠ 0 ) và y =15x + 8 có đồ thị là
những đường thẳng song song với nhau.
Bài 2 (2 điểm). Cho ( 1 d : y − =
x và (d : y = 3x −1 2 ) 1 ) 2
a) Vẽ (d và (d trên cùng hệ trục toạ độ Oxy . 2 ) 1 )
b) Xác định hàm số (d ) : y = ax + b (a ≠ 0) , sao cho (d) / /(d ) và (d ) đi qua điểm 2 M ( 2; − 4) .
Bài 3 (0,75 điểm). Một cửa hàng gạo nhập vào kho 480 tấn. Mỗi ngày bán đi 20 tấn.
Gọi y (tấn) là số gạo còn lại sau x (ngày) bán.
a) Viết công thức biểu diễn y theo x?
b) Tính số gạo còn lại sau 10 ngày bán.
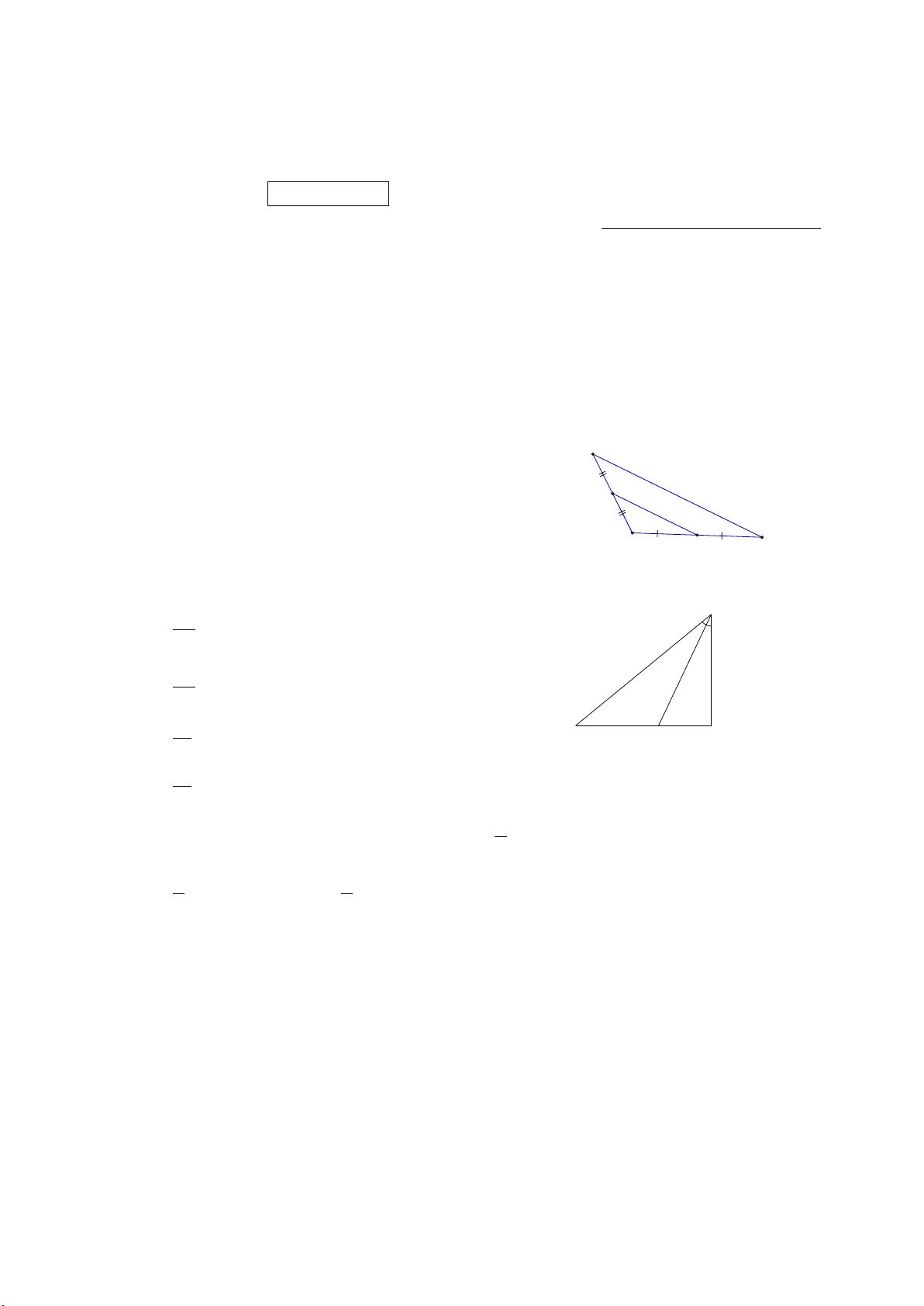
Bài 4 (0,75 điểm). Giữa hai địa điểm A và B là một hồ nước sâu (hình bên). Biết M, N
lần lượt là trung điểm của OA và OB, biết khoảng cách M và N là 300m. Tính khoảng cách AB . A B M N O
Bài 5 (2,0 điểm). Cho tam giác ABC có đường trung tuyến AI. Đường phân giác
của góc AIB cắt AB tại H. a) Cho AH = 7c ,
m HB = 8 cm và AI =14 cm . Tính BI .
b) Kẻ đường phân giác của góc AIC cắt cạnh AC tại K. Gọi M là giao điểm của HK
và AI. Chứng minh HK / /BC và M là trung điểm của HK.
-------------------------------------------HẾT--------------------------------------------- ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM (3,0 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đ.án D B A C C C A D B D C C
PHẦN TỰ LUẬN (7,0 ĐIỂM) Câu 1
d) Cho hàm số y = f (x) 2 = 2x +1. Tính  1 f −   và 2    f (1)
e) Cho hàm số y = (m − 4) x − 9 . Tìm điều kiện của m để 1,5đ
hàm số đã cho là hàm số bậc nhất.
f) Tìm m để các hàm số bậc nhất y = 3mx −12 ( m ≠ 0 )
và y =15x + 8 có đồ thị là những đường thẳng song song với nhau. 1a 2  1  1 −  3 0,25đ f − =  2. +   1 =   2   2  2 2 f (1) = 2.1 +1 = 3 0,25đ 1b Đk: m − 4 ≠ 0 0,25đ Vậy m ≠ 4 0,25đ 1c
Đk: a = a' và b ≠ b' 0,25đ 3m =15 và 12 − ≠ 8 0,25đ Vậy m = 5 Câu 2 2,0 điểm Cho ( 1 d : y − =
x và (d : y = 3x −1 2 ) 1 ) 2
c) Vẽ (d và (d trên cùng hệ trục toạ độ Oxy . 2 ) 1 )
d) Xác định hàm số (d ) : y = ax + b (a ≠ 0) , sao cho
(d) / /(d ) và (d ) đi qua điểm M ( 2; − 4) . 2 2a
Vẽ (d và (d trên cùng hệ trục toạ độ Oxy 2 ) 1 )
- Đúng một bảng giá trị của hàm số( 1 d : y − = x 1 ) 2 0,25đ
- Đúng một bảng giá trị của hàm số(d : y = 3x −1 2 ) 0,25đ -Vẽ đúng một đường( 1 d : y − = x 1 ) 2
-Vẽ đúng một đường(d : y = 3x −1 2 ) 0,25đ 0,25đ 2b
Vì (d) / /(d ) nên 0,5đ 2 a = 3
(d ) đi qua điểm M ( 2;
− 4) nên b = 4 −3.( 2) − = 10 0,25đ
Vậy (d ) : y = 3x +10 0,25đ Câu 3
Một cửa hàng gạo nhập vào kho 480 tấn. Mỗi ngày bán đi 0,75đ
20 tấn. Gọi y (tấn) là số gạo còn lại sau x (ngày) bán.
c) Viết công thức biểu diễn y theo x?
d) Tính số gạo còn lại sau 10 ngày bán. 3a
y = 480 − 20x 0,5đ 3b
Số tấn gạo còn lại sau 10 ngày bán là: 480-20.10=280 (tấn) 0,25đ Câu 4
Giữa hai địa điểm A và B là một hồ nước sâu (hình bên). 0,75đ
Biết M, N lần lượt là trung điểm của OA và OB, khoảng
cách M và N bằng 300m. Tính khoảng cách AB . A B M N O
CM: MN là đường trung bình 0,5đ AB=2MN= 2.300=600 0,25đ Câu 5
Cho tam giác ABC có đường trung tuyến AI. Đường 2,0đ
phân giác của góc AIB cắt AB tại H. c) Cho AH = 7c ,
m HB = 8 cm và AI =14 cm . Tính BI .
d) Kẻ đường phân giác của góc AIC cắt cạnh AC tại K.
Gọi M là giao điểm của HK và AI. Chứng minh
HK / /BC và M là trung điểm của HK. 5a Ta có: AH AI =
( Tính chất đường phân giác) 0,25đ HB IB . HB AI 8.14 BI = = = 16(cm) AH 7 0,25đ 5b Cm: AK AI = 0,5đ KC IC Mà IB=IC 0,25đ
Theo hệ quả Thales: HK / /BC
Cm: M là trung điểm của HK. 0,5đ
UBND QUẬN BÌNH THẠNH
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
TRƯỜNG TRUNG HỌC CƠ SỞ
NĂM HỌC: 2024 – 2025 CỬU LONG MÔN: TOÁN 8 ĐỀ ĐỀ NGHỊ Thời gian: 90 phút (Đề gồm 2 trang)
(không tính thời gian phát đề)
I. TRẮC NGHIỆM KHÁCH QUAN (12 câu): (3,0 điểm)
Câu 1. Cho hàm số y = − 2
5x − 3, em hãy chọn câu phát biểu đúng:
A. y là hàm số, x là biến số
B. y là hàm số, 2 5 − x là biến số
C. y là hàm số, 5 − là biến số
D. y là hàm số, 5; − 3 − là biến số
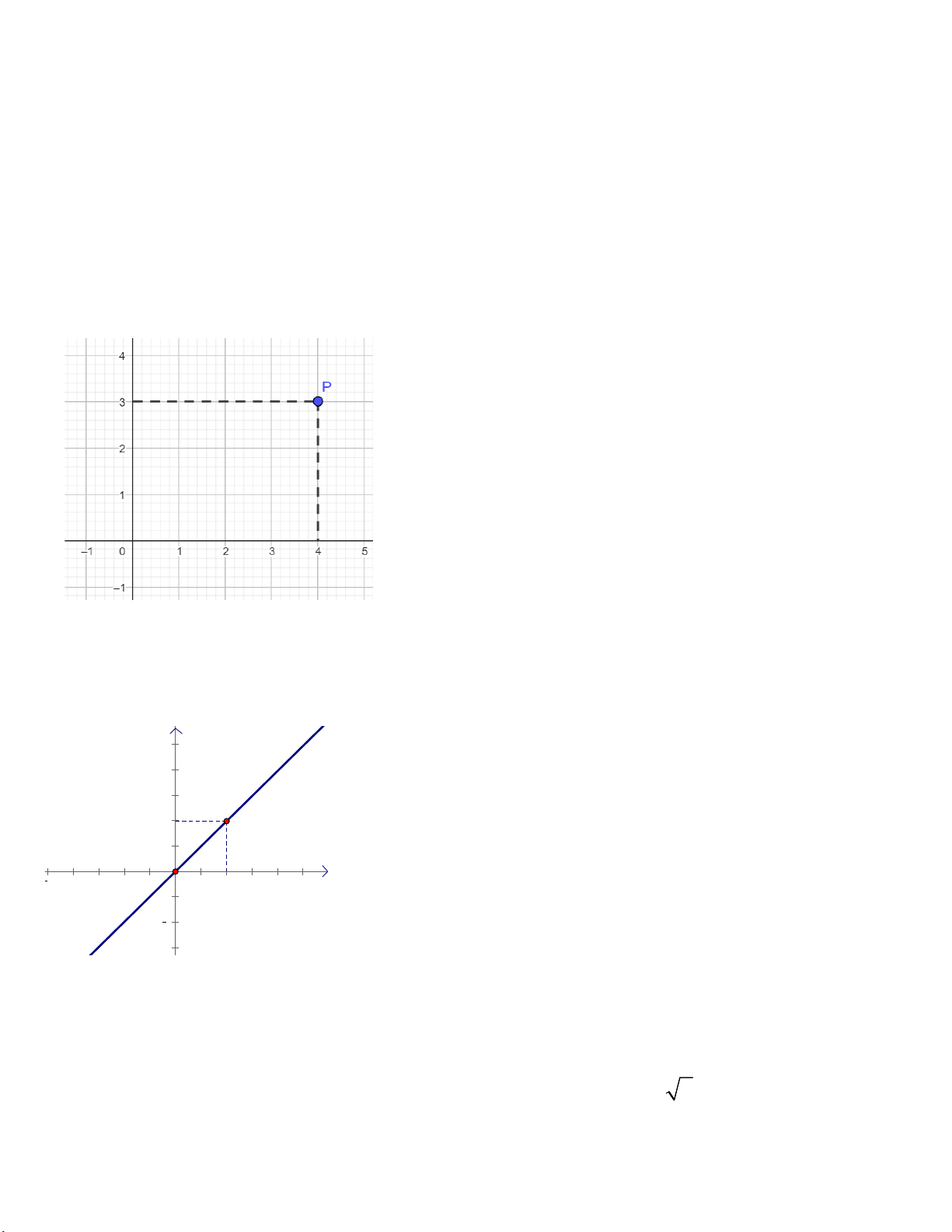
Câu 2. Cho hình vẽ. Tọa độ của điểm P là: A. P(4; 3) B. P(3; 4) C. P(4; 0) D. P(0; 3)
Câu 3. Cho hai đường thẳng (d) : y = 2x – 1 và (d’) : y = 2x + 3. Khi đó hai đường thẳng (d) và (d’): A. trùng nhau . B.song song. C.cắt nhau. D.vuông góc. Câu 4. y 4
Đường thẳng (d) là đồ thị của hàm số: (d) A.y = 2x B. y = 2x + 2 3 C. y = x D. y = x – 2 2 1 5 -4 -3 -2 -1 0 1 2 3 4 5 x -1 2 -3
Câu 5. Phương trình ax+b=0 là phương trình bậc nhất một ẩn nếu A. a = 0. B. b  0 . C. b = 0. D. a 0
Câu 6. Hàm số nào dưới đây là hàm số bậc nhất?
A. y = 4 + 0x B. 2 y = 4 + 5x C. 4 y = 4 − x
D. y = 2 + 3x
Câu 7. Trong các hình sau, hình nào MN là đường trung bình của tam giác ? A A A M M M N M N N B MN // BC C B N C B C B C hình 3 hình 4 hình 1 hình 2 A.Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Câu 8. Trong hình vẽ bên, biết M, N lần lượt là trung điểm của BC, AC và AB = 8 cm. Độ dài x của đoạn AB là: A A. 8cm B. 16cm C. 4cm D. 2cm 8 cm N x B M C
Câu 9. Cho hình vẽ, biết MN // BC. Trong các khẳng định sau, khẳng định nào đúng ? A A. AM AC = B. AM NC = AB AN AB AC C. AM AN = D. AM AN = AB AC MB AC M N B C
Câu 10. Cho tam giác ∆ABC và AM là đường phân giác của góc A (với M ∈ BC ). Khẳng định nào sau đây là đúng? A A. AB AC  B. AB AC  BM CM CM BM C. AB MC  D. MB AC  AC MB MC AB B M C
Câu 11. Cho HOT VND, 𝑂𝑂� = 530; 𝐷𝐷� = 470; 𝐻𝐻
� = 𝑥𝑥. Chọn kết quả đúng ? A. 0 x= 53 B. 0 x= 47 C. 0 x= 100 D. 0 x= 80
Câu 12. Cho KFC MNP và KF = 5cm; MN = 8cm ; MP = 9cm.
Vậy KFC MNP theo tỉ số đồng dạng k là: A. k = 5 B. k = 9 C. k = 5 D. k = 8 9 5 8 5
II. TỰ LUẬN: (7,0 điểm) Bài 1 (1,5 điểm)
a) Cho hàm số y = f (x) 2
= −x + Tính f (0); f ( 3 − ) 3
b) Cho hàm y = f (x) = (2m − 4)x +10 Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.
c) Cho đường thẳng d: y = (5m − 7)x −1. Với giá trị nào của m để đường thẳng d song song với đường thẳng d1: y = 2x + 5
Bài 2 (2,0 điểm) Cho hàm số y = 3
− x +1có đồ thị d1 và 1
y = x − 2 có đồ thị d 3 2
a) Vẽ d1 và d2 trên cùng một mặt phẳng tọa độ.
b) Xác định hàm số có đồ thị d3, biết d3 là đường thẳng song song với d1 và đi qua điểm A(2; 3).
Bài 3 (0,75 điểm) Một hãng máy bay có giá vé đi từ TP.Hồ Chí Minh ra Phú Yên là 1200 000 đồng/ 1 người.
Trong đó quy định mỗi khách hàng chỉ được mang lên sân bay tối đa 7 kg hành lý. Nếu vượt quá 7 kg hành lý trở
đi bắt đầu từ 7 kg trở đi cứ mỗi kg phải trả thêm 100 000 đồng cho tiền phạt hành lý.
Gọi y (đồng) là số tiền 1 người cần trả khi đặt vé đi máy bay từ TP. HCM ra Phú Yên, x (kg) là khối lượng hành lý người đó mang theo.
a/ Viết công thức y theo x. Cho biết y có phải là hàm số của x không ? Vì sao ?
b/ Một người đặt vé đi máy bay từ TP. HCM ra Phú Yên và mang theo 9kg hành lý . Hỏi người đó phải trả tổng cộng bao nhiêu tiền ?
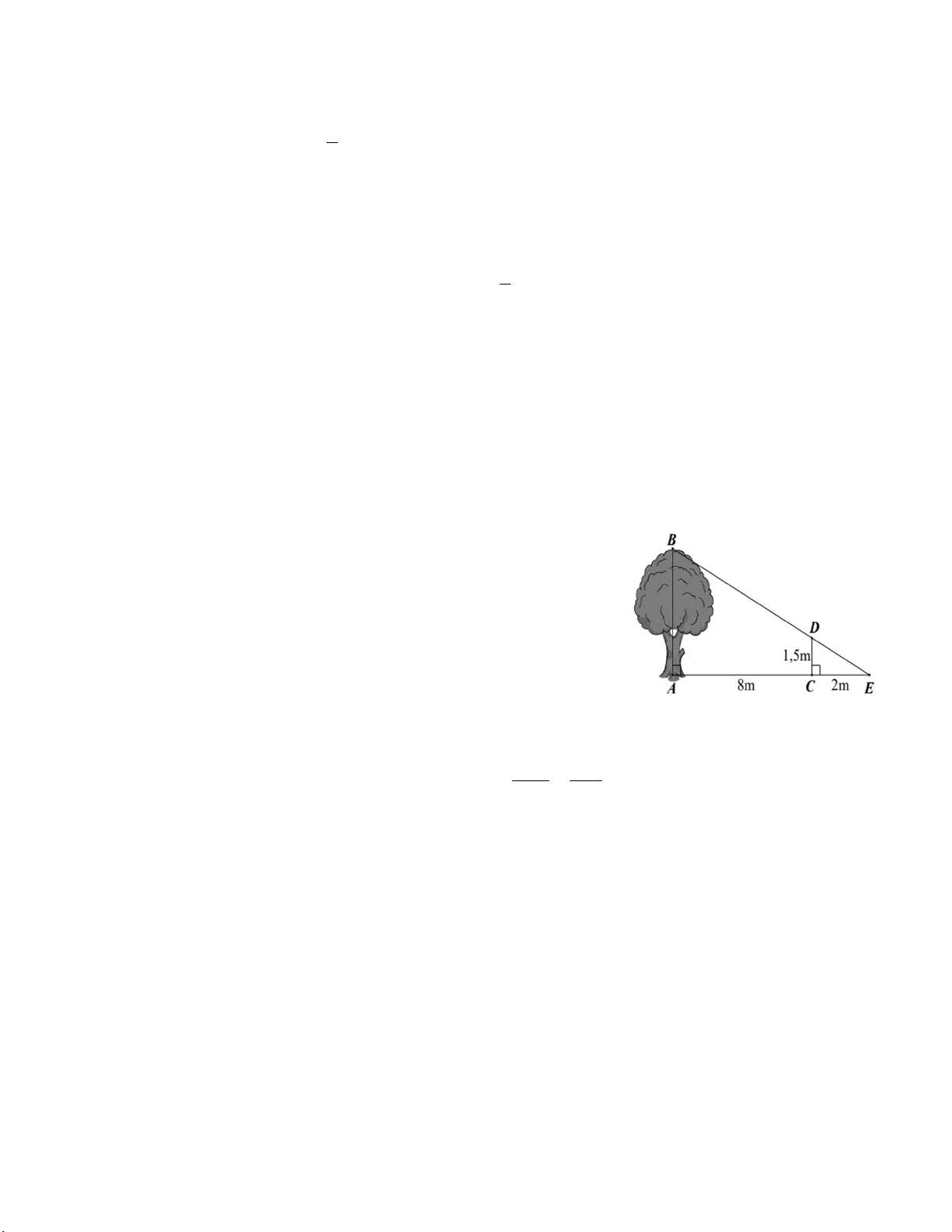
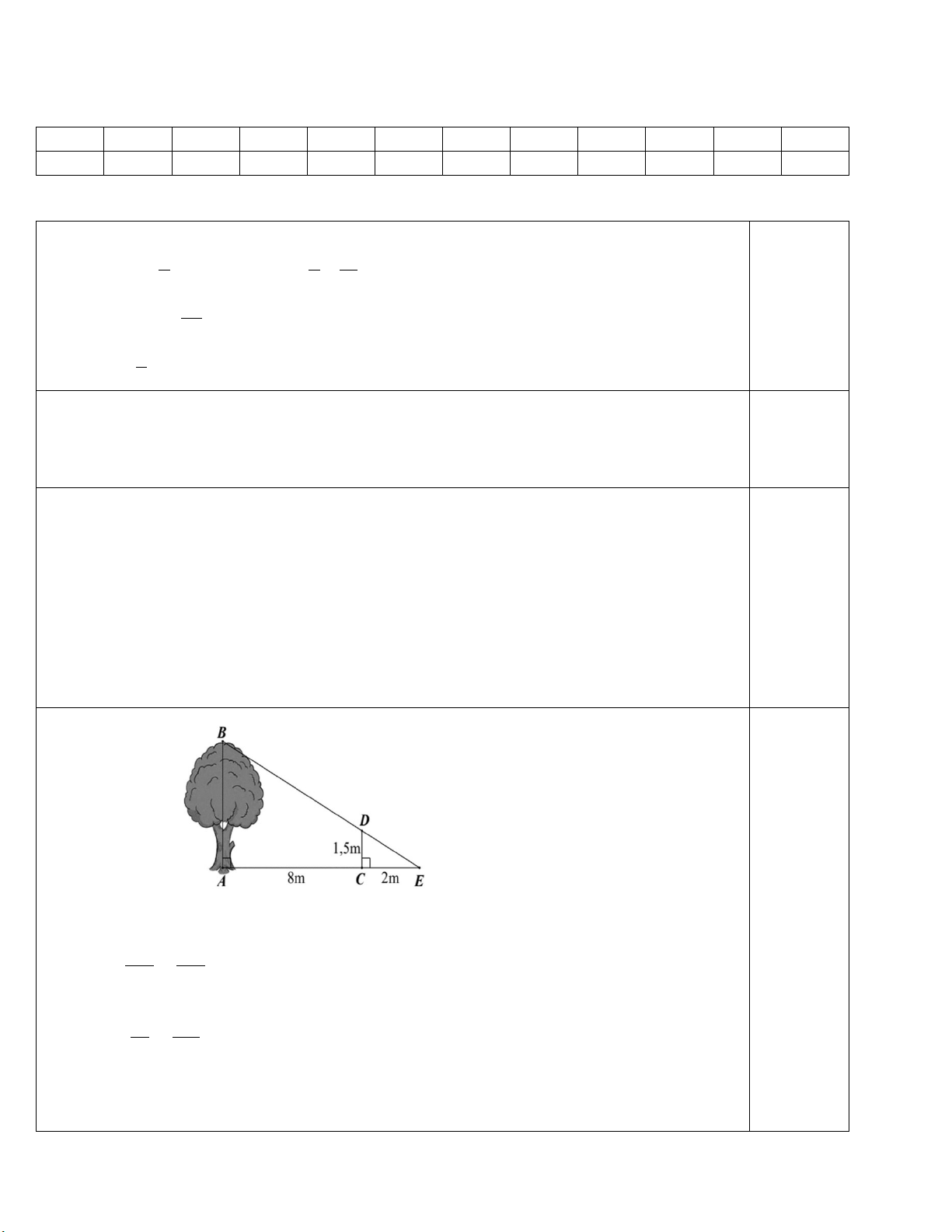
Bài 4 (0,75 điểm) Một người cắm một cái cọc vuông góc với mặt đất sao
cho bóng của đỉnh cọc trùng với bóng của ngọn cây (như hình vẽ). Biết cọc
cao 1,5 m so với mặt đất, chân cọc cách gốc cây 8 m và cách bóng của đỉnh
cọc 2 m. Tính chiều cao AB của cây.
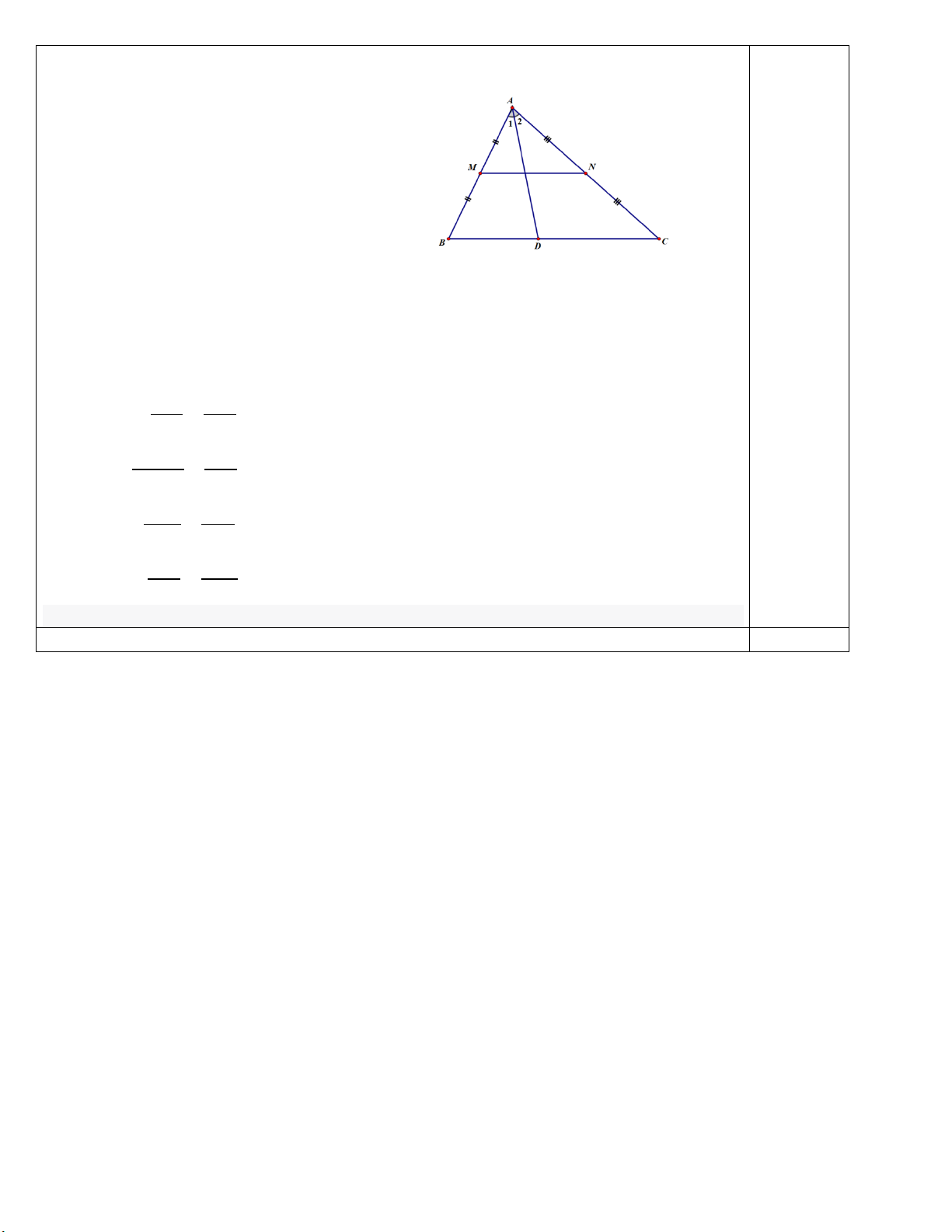
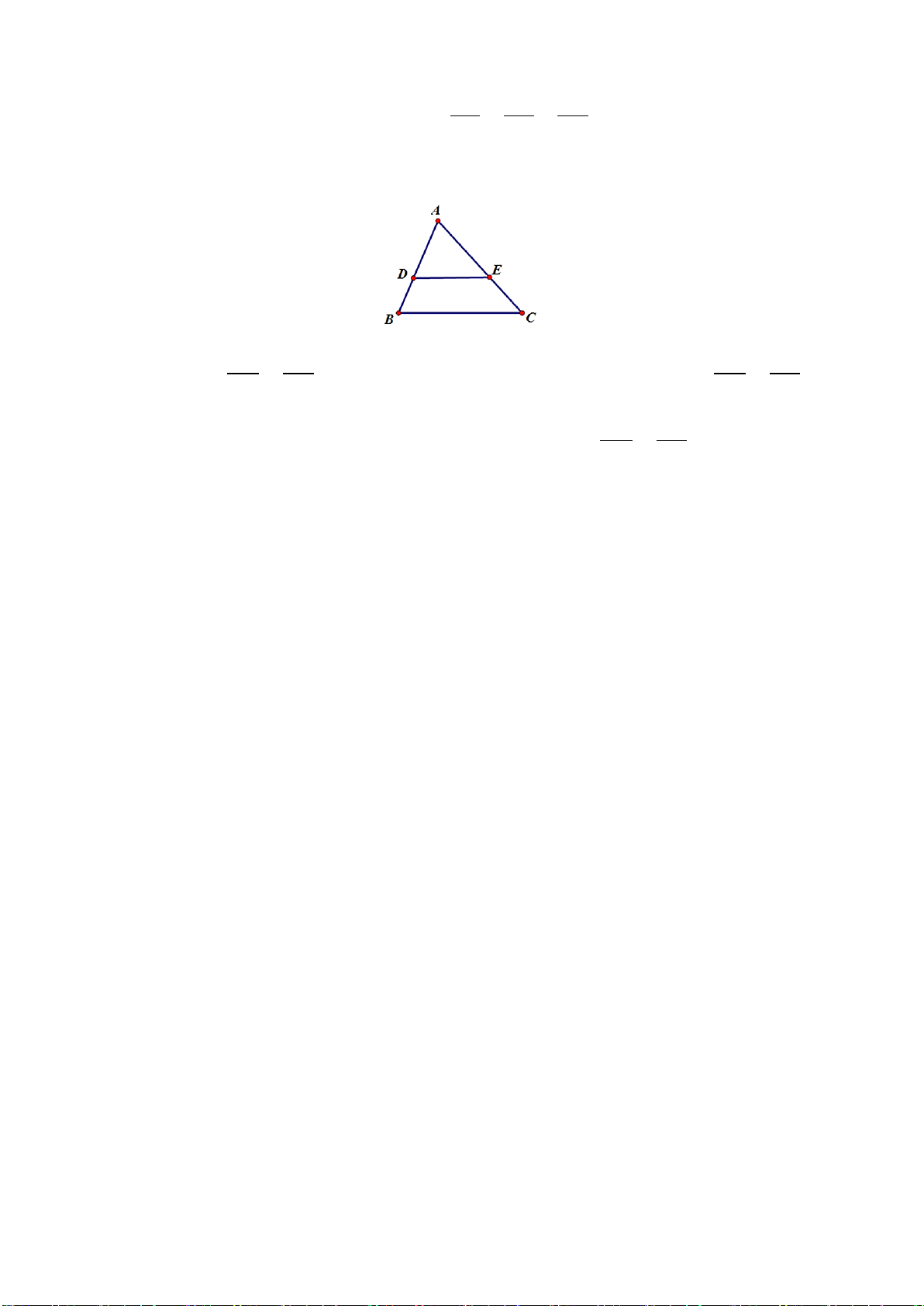
Bài 5 (2,0 điểm) Cho tam giác ABC có M, N lần lượt là trung điểm của AB, AC.
a) Chứng minh MN // BC. Biết MN = 10 cm, tính BC.
b) Vẽ AD là tia phân giác của  BAC . Chứng minh BD DC = . AM AN
------------------------------------------------------------HẾT------------------------------------------------------------------------ ĐÁP ÁN
PHẦN I. TRẮC NGHIỆM . Mỗi câu đúng : 0,25 đ. 1 2 3 4 5 6 7 8 9 10 11 12 A A B C D D D C C A D C PHẦN II. TỰ LUẬN Câu 1 a. 2 f (0) = , 2 11 f ( 3) − = −( 3) − + = 0,5đ 3 3 3 0,5đ b. 1 − m ≠ 2 y = x + 5 2 0,5đ c. 9 m ≠ 5 Câu 2.
a. Vẽ đúng mỗi đồ thị hàm số 0,5đ x2 b. y = 3 − x + 9 1,0đ Câu 3.
a/ Công thức y theo x là y = 1200 000 + (x – 7).100 000 (đồng)
y là hàm số của x. Vì mỗi giá trị của x chỉ xác định đúng một giá trị của y. 0,5đ b/
Một người đặt vé đi máy bay từ TP. HCM ra Phú Yên và mang theo 9kg hành 0,25đ
lý . Người đó phải trả tổng cộng số tiền là :
1200 000 + (9 – 7 ).100 000 = 1400 000 (đồng). Câu 4.
Xét tam giác EAB có : CD // AB (cùng vuông góc với AE) 0,25đ EC CD  
(hệ quả định lí Thales) EA AB 3 1,5 0,25đ    DB  7,5 10 AB AB = 7,5 (m)
Vậy chiều cao AB của cây là 7,5 m. 0,25đ Câu 5. a) Xét ∆ ABC ta có. M là trung điểm AB (gt) 0,25đ N là trung điểm AC (gt)
=> MN là đường trung bình ∆ ABC (đn) 0,25đ => MN // BC Và MN = BC : 2 0,25đ => BC= 2.MN Thay MN = 10 (cm) 0,25đ => BC= 2.10 = 20 (cm) b) Xét ∆ ABC ta có.
AD là đường phân giác của  BAC (gt) ⇒ AB = DB 0,25đ AC DC 2. 0,25đ ⇒ AM = DB 2.AN DC 0,25đ ⇒ AM = DB AN DC 0,25đ ⇒ DC = DB AN AM
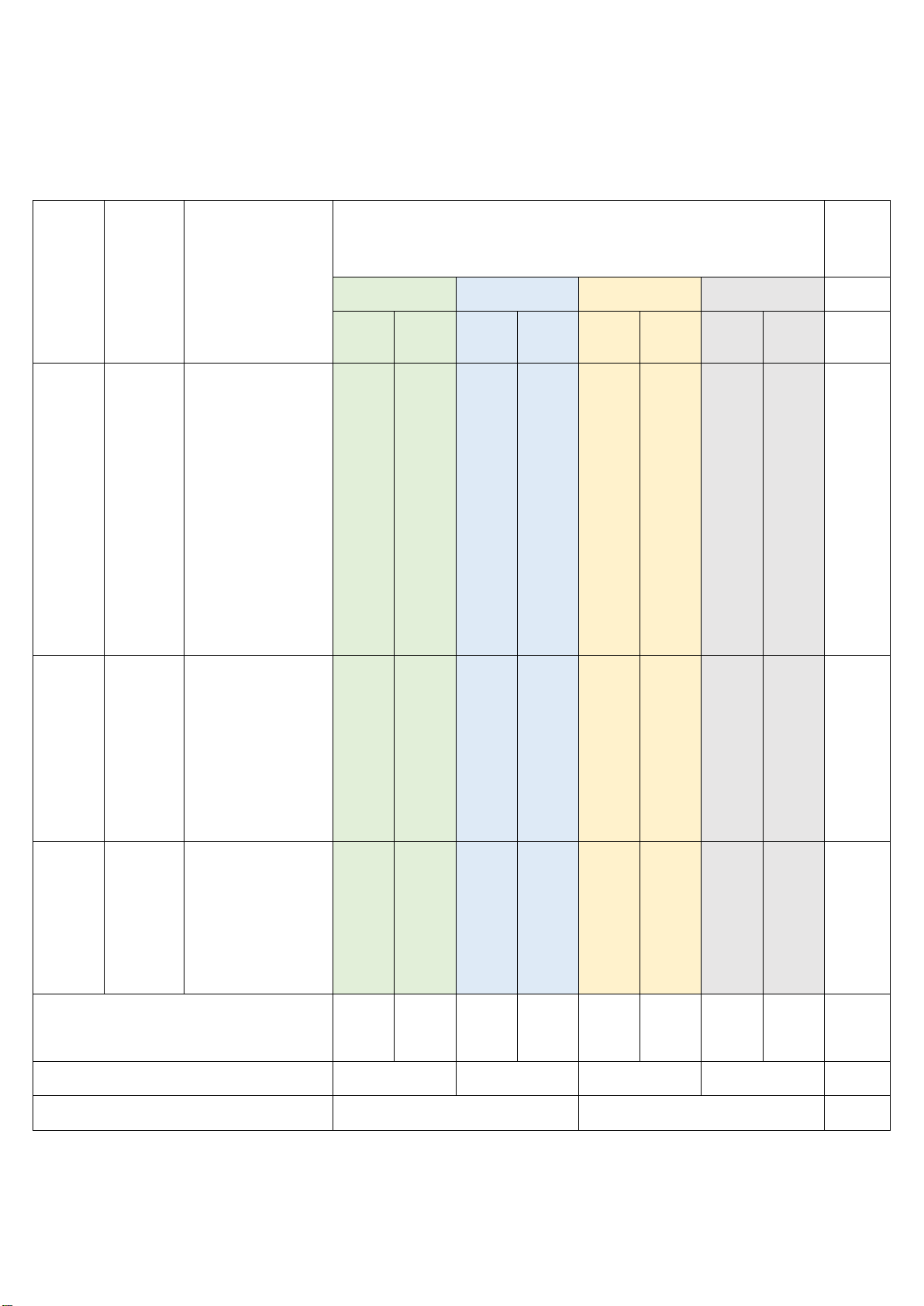
KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ – HỌC KÌ II MÔN TOÁN – LỚP 8
NĂM HỌC 2024 – 2025 Tổng
Mức độ đánh giá % TT
Chủ đề Nội dung/đơn vị điểm kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TNK Q TL TNK Q TL TNK Q TL TNK Q TL 1
Chủ đề 1/ Khái niệm hàm 1: số. Tọa độ của một điểm và đồ thị của Hàm số hàm số. và đồ 3 câu 2 câu thị 2/ Hàm số bậc nhất 2 câu y = ax + b (a ≠ 0) 4 câu (Bài 2 câu (Bài (Bài và đồ thị. 1c, 2a, 2b và 57,5% (1,0) 1a,b) (0,5) 3b) bài 3a) 3/ Hệ số góc của (1,0) (2,25) (1,0) đường thẳng y = ax + b. Hai đường thẳng song song, cắt nhau. 2
Chủ đề 1/ Định lí Thalès 2: trong tam giác. 1 câu 1 câu 1 câu Định lí 2/ Đường trung 2 câu 2 câu (Bài 4) Thalès bình của tam giác. (Bài (Bài 37,5% (0,5) (0,5) (0,75) 5a) 5b) 3/ Tính chất đường (1,0) (1,0) phân giác trong tam giác. 3 Chủ đề 3: Bài 1. Hai tam giác 5%
Hai tam đồng dạng. 2 câu giác (0,5) đồng dạng Tổng số câu 8 2 4 4 3 1 22 Tổng điểm 2,0 1,0 1,0 3,0 2,0 1,0 10,0 Tỉ lệ % 30% 40% 20% 10% 100% Tỉ lệ chung 70% 30% 100%
BẢN ĐẶC TẢ ĐỀ KIỂM TRA GIỮA KÌ – HỌC KÌ II MÔN TOÁN – LỚP 8
NĂM HỌC 2024 – 2025
Số câu hỏi theo mức độ nhận thức Chương/ Nội dung/Đơn TT
Mức độ đánh giá Vận Chủ đề vị kiến thức Nhận Thông Vận dụng biết hiểu dụng cao 1 Nhận biết: 1 TN 2 TN 2 TL
– Xác định được toạ độ của một điểm trên mặt phẳng TN8 TN7 TN5 toạ độ. 1 TL
Hàm số và đồ Thông hiểu (1a) thị
– Xác định điểm thuộc đồ thị hàm số
– Tính được giá trị của hàm số khi hàm số đó xác định
Hàm số và đồ thị bởi công thức.
Hàm số bậc nhất Nhận biết: 3 TN TL2b
y = ax + b (a ≠ 0)
– Nhận biết được khái niệm hàm số bậc nhất. TN1
và đồ thị. Hệ số TN2
góc của đường
– Nhận biết được khái niệm hệ số góc của đường TN4
thẳng y = ax + b thẳng y = ax + b (a ≠ 0). 1 TL
(a ≠ 0). (1b)
– Sử dụng được hệ số góc của đường thẳng để nhận
biết và giải thích được sự cắt nhau hoặc song song của
hai đường thẳng cho trước. Thông hiểu: 3 TL
– Thiết lập được bảng giá trị của hàm số bậc nhất y = (1c, 2a, 3a)
ax + b (a ≠ 0).
– Vẽ được đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0). Vận dụng: 1TL
– Vận dụng được hàm số bậc nhất và đồ thị vào giải quyết TL3b
một số bài toán thực tiễn (đơn giản, quen thuộc) (ví dụ:
bài toán về chuyển động đều trong Vật lí,...). Vận dụng cao:
– Vận dụng được hàm số bậc nhất và đồ thị vào giải quyết
một số bài toán (phức hợp, không quen thuộc) thuộc có
nội dung thực tiễn.
2 Định lí Thalès Định lí Thalès Nhận biết: 2 TN trong tam trong tam giác giác
– Nhận biết được định nghĩa đường trung bình của tam TN3 giác.
- Giải thích được tính chất đường trung bình của tam
giác (Đường trung bình của tam giác thì song song với
cạnh thứ ba và bằng nửa cạnh đó)
– Giải thích được định lí Thalès trong tam giác (định lí thuận và đảo).
– Giải thích được tính chất đường phân giác của tam TN11 giác. Thông hiểu: 2TN +1TL 1TL TN6 (5a)
– Giải thích các đoạn thẳng tỉ lệ bằng cách sử dụng định TN10
líThalès và tính chất đường phân giác của tam giác.
- Giải quyết được một số vấn đề thực tiễn (đơn giản, TL4
quen thuộc) gắn với việc vận dụng định lí Thalès, đường
trung bình, đường phân giác (ví dụ: tính khoảng cách giữa hai vị trí). Vận dụng cao: 1TL (5b)
– Giải quyết được một số vấn đề (phức hợp, không
quen thuộc) gắn với việc vận dụng định lí Thalès Tam
giác Tam giác đồng Nhận biết: 2TN đồng dạng dạng
– Mô tả được định nghĩa của hai tam giác đồng dạng. TN9 TN12 Tổng 12TN 3TL 2TL 2TL 1TL Tỉ lệ % 40% 30% 20% 10% Tỉ lệ chung 70% 30% UBND QUẬN BÌNH THẠNH
ĐỀ KIỂM TRA GIỮA KÌ – HỌC KÌ II
TRƯỜNG TRUNG HỌC CƠ SỞ
NĂM HỌC 2024 – 2025 LÊ VĂN TÁM
MÔN: TOÁN – LỚP: 8 ĐỀ THAM KHẢO
Thời gian: 90 phút (không kể thời gian phát đề)
PHẦN A. TRẮC NGHIỆM (3 điểm).
Câu 1. Trong các hàm số sau, hàm số nào là hàm số bậc nhất? A. 2 y  2x 1
B. y  3x  2
C. y 2 xx   3 D. 2
y  4x 2x
Câu 2. Cho điểm A1; 2. Khi đó:
A. Điểm A có toạ độ là 2;  1
B. Hoành độ điểm A là 1.
C. Hoành độ điểm A là 2
D. Tung độ điểm A là 1
Câu 3. Cho hai đường thẳng d: y  5x 3 và  
d’ : y  3x 5. Khi đó hai đường thẳng (d) và (d’): A. trùng nhau . B. song song. C. cắt nhau. D. không cắt nhau Câu 4. y 4 (d)
Đường thẳng (d) là đồ thị của hàm số: 3 2 A. y = 2x B. y = 2x + 2 1 5 -4 -3 -2 -1 0 1 2 3 4 5 x C. y = x D. y = x – 2 -1 2 -3
Câu 5. Hệ số góc a của đường thẳng y = 4x – 3 là: A. a = 4 B. a = – 3 C. a = 4 D. a = 3 3 4
Câu 6. Cho hàm số y = f(x) = 2x – 5. Giá trị của f(3) là: A. – 2 B. 6 C. 1 D. 4
Câu 7. Trong các hình sau, hình nào cho ta MN là đường trung bình của tam giác ABC ? A A A M M M N M N N B MN // BC C B N C B C B C hình 3 hình 4 hình 1 hình 2 A.Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Câu 8. Cho hình vẽ. Độ dài cạnh EF là : M A. 8cm B. 16cm C. 4cm D. 2cm 8cm E N F P
Câu 9. Cho hình vẽ, biết MN // BC. Trong các khẳng định sau, khẳng định nào đúng ? A A. AM AC = B. AM NC = AB AN AB AC C. AM AN = D. AM AN = M N AB AC MB AC B C
Câu 10. Cho tam giác DEF có DK là đường phân giác của góc EDF. Trong các khẳng định
sau, khẳng định nào đúng? A. DE EK = B. DE KE = DF EF DF KF C. DE KF = D. DK2 = KE . KF EK DE Câu 11. Cho A  BC ∽ DEF  , khẳng định đúng là: E B A C D F A.   ABC  EDF B. AC AB BC   DE DF EF C.   BCA  FED D. BC AB AC   EF DE DF Câu 12. Cho AB  C 
AB  AC như hình vẽ. Chọn khẳng định sai: A. Nếu AD AE  thì DE // BC.
B. Nếu DE // BC thì AD AE   AB AC AB AC
C. Nếu DE // BC thì AD  E ∽ AB  C. D. Nếu AD AE  thì DE // BC. DE ED
PHẦN B. TỰ LUẬN (7 điểm) Bài 1. (1,5 điểm)
a) Cho hàm số y  f x 2
 x 1. Tính f   3 ; f 2.
b) Tìm tất cả hàm số bậc nhất trong các hàm số dưới đây: 2
y  2x 3; y  3 x ; y  x 1;
y  2x   1 34x.
c) Cho hàm số bậc nhất y m  2x4 m  2 có đồ thị là đường thẳng d , tìm 1
điều kiện của tham số m để d song song với đường thẳng d : y  3x  4. 1 2 Bài 2. (2,0 điểm)
a) Vẽ đồ thị của hai hàm số y  2x và y  x 1 trên cùng mặt phẳng toạ độ Oxy.
b) Xác định hàm số bậc nhất y  ax b có đồ thị d song song với đường thẳng 1
d : y  2x 1 và đi qua điểm A1;4. 2
Bài 3. (0,75 điểm) Một chiếc xe đang chạy với vận tốc 10 m/s thì bắt đầu tăng tốc, khi cứ
mỗi giây xe chạy nhanh hơn 1,5 mét, xe chuyển động với vận tốc v (m/s) sau t (giây) là thời
gian kể từ lúc xe bắt đầu tăng tốc.
a) Lập công thức tính v theo t.
b) Nếu đoạn đường đó qui định vận tốc tối đa là 90 km/h, sau bao nhiêu giây kể từ
lúc bắt đầu tăng tốc thì xe đạt vận tốc tối đa theo qui định? Bài 4. (0,75 điểm)
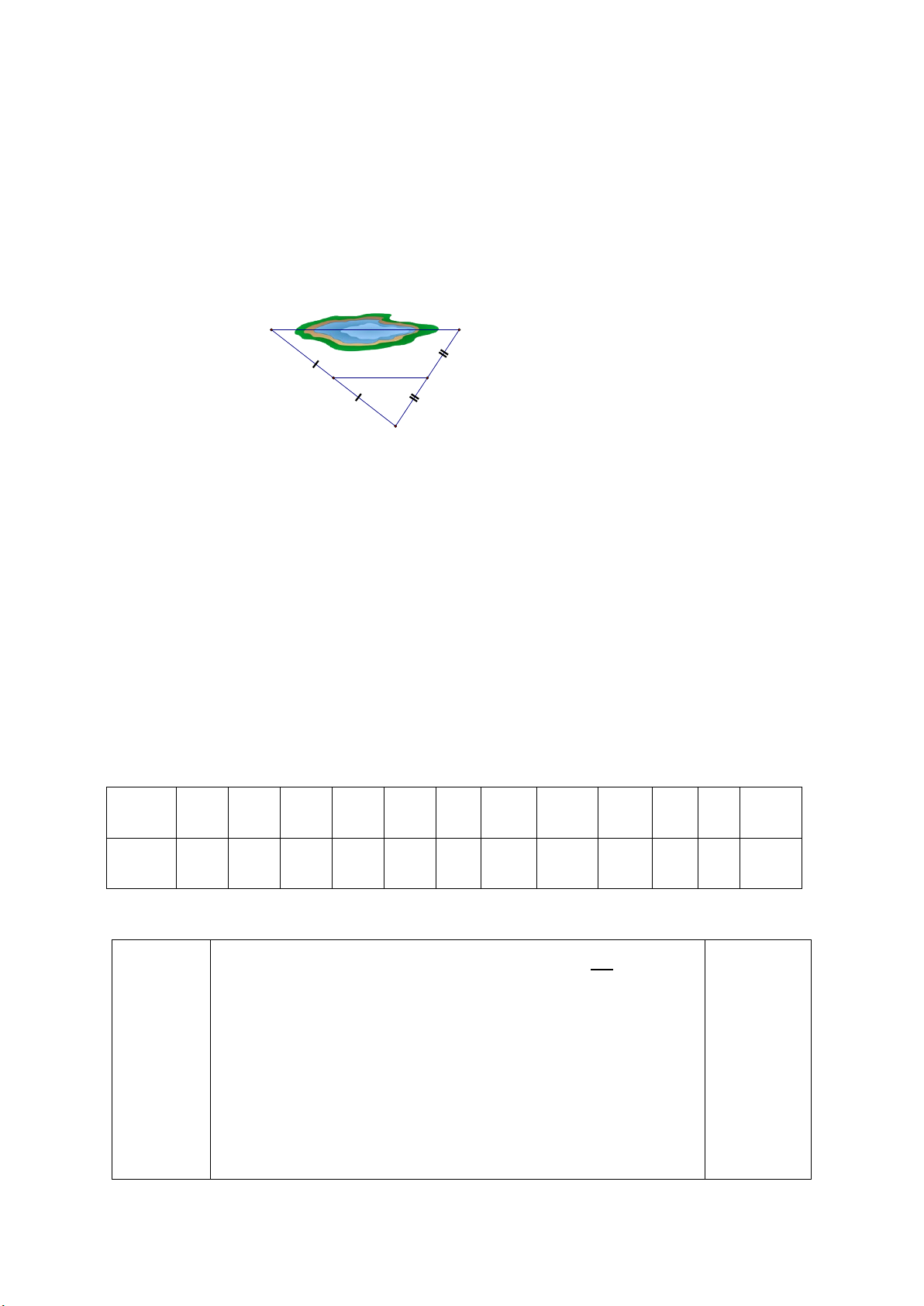
Để đo khoảng cách giữa hai điểm A và B bị ngăn cách
bởi một cái hồ người ta đóng các cọc ở vị trí A, B, C, D,
E như hình vẽ. Người ta đo được DE = 75m. Tính khoảng cách AB? Bài 5. (2 điểm) Cho AB 
C nhọn (AB < AC) có đường phân giác AE E  BC. Qua E vẽ
đường thẳng song song với AB cắt AC tại F. a/ Chứng minh: FA AB   FC AC
b/ Vẽ FH  AE tại H. Gọi K là trung điểm của EC. Chứng minh HK // AC.