Đề tham khảo (mẫu) môn Lý thuyết xác suất và thống kê toán | Trường Đại học Nam Cần Thơ

ĐỀ THAM KHẢO
Môn thi: Xác suất thống kê - TN010 Thời gian: 70 phút
Họ và tên: .............................................................................. Mã số sinh viên: ............................ PHẦN BÀI LÀM
A. Phần xác suất (12 câu) Câu 1 2 3 4 5 6 7 8 9 10 11 12 A B C D
B. Phần thống kê (16 câu) 13.
Gọi ............................................................... ............................................................................... 14.
Sai số ước lượng: ............ ................................ ............................................................................ 15.
Khoảng ước lượng: ........ ................................ ............................................................................
16. Số lô đất cần khảo sát: ... ................................ ............................................................................ 17.
Gọi ................................. ................................ ............................................................................
Chọn giả thiết: ............... ............................... ; đối thiết: ........................................................... 18.
Miền bác bỏ: ................. ................................ ............................................................................
20. Giá trị quan sát: ............. ..................................... ....................................................................... 21.
Kết luận: ........................ ..................................... ....................................................................... 22.
Gọi ................................. ................................ ............................................................................
Mẫu có n=…………………;f = .................... ............................................................................ 23.
Sai số ước lượng: ............ ................................ ............................................................................
24. Khoảng ước lượng: ........ ................................ ............................................................................ 25.
Gọi ............................... ..................................... .......................................................................
Chọn giả thiết: ............... ..................................... ;đối thiết: ...................................................... 26.
Miền bác bỏ: .................. ..................................... ....................................................................... 27.
Tính tham số các mẫu: n1= ............................ , x1 = …………………., s1= ............................ ,
n2= ............................. , x2 = …………………., s2 = ........................... ,
Giá trị quan sát: ....... ................................ ............................................................................
28. Kết luận: ........................ ................................ ............................................................................ NỘI DUNG ĐỀ A. Phần xác suất 1.
Cho hộp thứ nhất có 4 phiếu loại 30000đ và 6 phiếu loại 50000đ, hộp thứ hai có một phiếu loại
200000đ và 9 phiếu loại 20000đ. Người được thưởng được chọn 1 trong hai hộp và từ đó lấy ngẫu nhiên
một phiếu. Số tiền ghi trên phiếu sẽ là số tiền được thưởng. Người được thưởng nên chọn hộp nào thì có lợi hơn? A)
Hộp thứ nhất B) Hộp thứ hai C) Hai hộp có lợi như nhau 2.
Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất: X 1 2 3 4 P 0,15 a b 0,2
Cho biết E(X) = 2,65. Hãy tìm giá trị a, b. A)
a = 0,4; b = 0,25 B) a = 0,15; b = 0,5
C) a = 0,25; b = 0,4 D) a = 0,5; b = 0,15 3. Cho
hàm mật độ của biến ngẫu nhiên liên tục X như sau: 4.
Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất:
Giá trị mod(X) là ? A)0 B) 3/2 C) 3 D) 0 hoặc 3 5.
Một vùng dân cư có tỷ lệ người mắc bệnh sốt rét là 0,03. Cần chọn ngẫu nhiên ít nh ất bao nhiêu
người để kiểm tra để khả năng gặp ít nhất 1 người mắc bệnh sốt rét không dưới 99%? A) 151 B) 152 C) 153 D) 154 6.
Xác suất bắn trúng đích của mỗi viên đạn là 0,2. Tiến hành bắn 400 viên. Tính xác suất để có từ
30 đến 100 viên bắn trúng đích? A) 0,0062 B) 0,4838 C) 0,5 D) 0,9938 7.
Trong một lớp có 50 sinh viên trong đó có 20 nữ sinh. Cố vấn học tập cần chọn 5 sinh viên để
tham dự mitting hưởng ứng chiến dịch “ Giờ trái đất” năm 2015. Hãy tìm số nữ sinh trung bình được chọn tham dự mitting. A) 1 B) 2 C) 3 D) 5 8.
Cho X và Y là 2 biến ngẫu nhiên độc lập. Chọn kết luận đúng trong các kết luận sau:
9. Xác suất để mỗi con lợn khi tiêm phòng bằng một loại vắc xin được miễn dịch là 0,9. Có 50 con lợn
được tiêm phòng. Tìm số lợn được miễn dịch có khả năng xảy ra nhiều nhất? A) 42 con B) 43 con C) 44 con D) 45 con 10.
Cho X, Y là hai biến ngẫu nhiên với quy luật X ~ B(6; 0,4), Y ~ N(2; 1). Hãy tìm kỳ vọng của
T biết T = 2X + 3Y. A) 10,2 B) 25,8 C) 18 D) 4,4
Tuổi thọ của một loại sản phẩm sản xuất hàng loạt là biến ngẫu nhiên có phân phối chuẩn với 1000
giờ và 2 100 giờ2. Thời gian bảo hành của sản phẩm là 980 giờ. 11.
Tính tỷ lệ sản phẩm phải bảo hành? A) 0,0228 B) 0,4772 C) 0,9772 D) 0,5973 12.
Tính tỷ lệ sản phẩm có tuổi thọ ít nhất là 1020 giờ? A) 0,0228 B) 0,4772 C) 0,9772 D) 0,5973 B. Phần thống kê
Bài 1. Khảo sát năng suất lúa của 100 lô đất có diện tích như nhau được trồng một giống lúa mới, được số liệu: Năng suất (tấn) <5 5 - 6 6 - 7 7 - 8 8 - 9 9 - 10 >10 Số lô đất 8 15 21 23 16 9 8 Với độ tin cậy 95%, a)
Giả sử có rất nhiều lô đất được trồng giống lúa mới này, hãy ước lượng năng suất lúa trung bình trên mỗi lô. 13. Tính n, ,x s . 14. Độ chính xác ? 15. Khoảng ước lượng ? b)
Trong ước lượng trên, nếu muốn độ chính xác là 0,2 thì cần khảo sát năng suất lúa của bao nhiêu lô đất? 16.
Số lô đất cần khảo sát ?
Bài 2. Một công ty sản xuất các loại bánh kẹo sản xuất thử một loại chocolate có vị bạc hà. Trước khi
tung sản phẩm ra thị trường, công ty thực hiện một khảo sát để tìm hiểu thị hiếu của khách hàng. Một
mẫu 150 người lớn được cho dùng thử sản phẩm, kết quả cho thấy có 87 người rất thích loại chocolate
mới. Một mẫu khác gồm 200 trẻ em, kết quả cho thấy có 98 em thích sản phẩm mới. a)
Số liệu trên có chứng tỏ rằng người lớn thích loại chocolate mới này hơn trẻ em hay không?
Kết luận với mức ý nghĩa 1%. 17.
Đặt giả thiết, đối thiết? 18.
Tìm miền bác bỏ W ? 19.
Tính tỷ lệ các mẫu: f1, f2 và f ? 20. Tính giá trị quan sát? 21.
Kết luận: người lớn thích hơn hay không? b)
Với độ tin cậy 99%, hãy ước lượng tỷ lệ người ưa thích loại chocolate mới này. 22.
Tính tham số mẫu? 23. Tính độ chính xác? 24. Khoảng ước lượng?
Bài 3. Người ta muốn điều tra xem năng suất lúa tại một vùng sau khi sử dụng giống lúa mới. Tiến hành
kiểm tra trên diện tích 100ha trồng giống lúa mới tại vùng này và được bảng số liệu sau: Năng suất
[4,0 – 4,5) [4,5 – 5,0) [5,0 – 5,5) [5,5 – 6,0) [6,0 – 6,5) [6,5 – 7,0) [7,0 – 7,5) (tấn/ha) Vùng A (ha) 8 13 18 27 20 8 6 Vùng B (ha) 5 10 21 35 22 18 9
Với độ tin cậy 95%, có thể cho rằng giống lúa thích hợp trong ở vùng B hơn vùng A hay không? 25.
Đặt giả thiết, đối thiết? 26.
Tìm miền bác bỏ W ? 27.
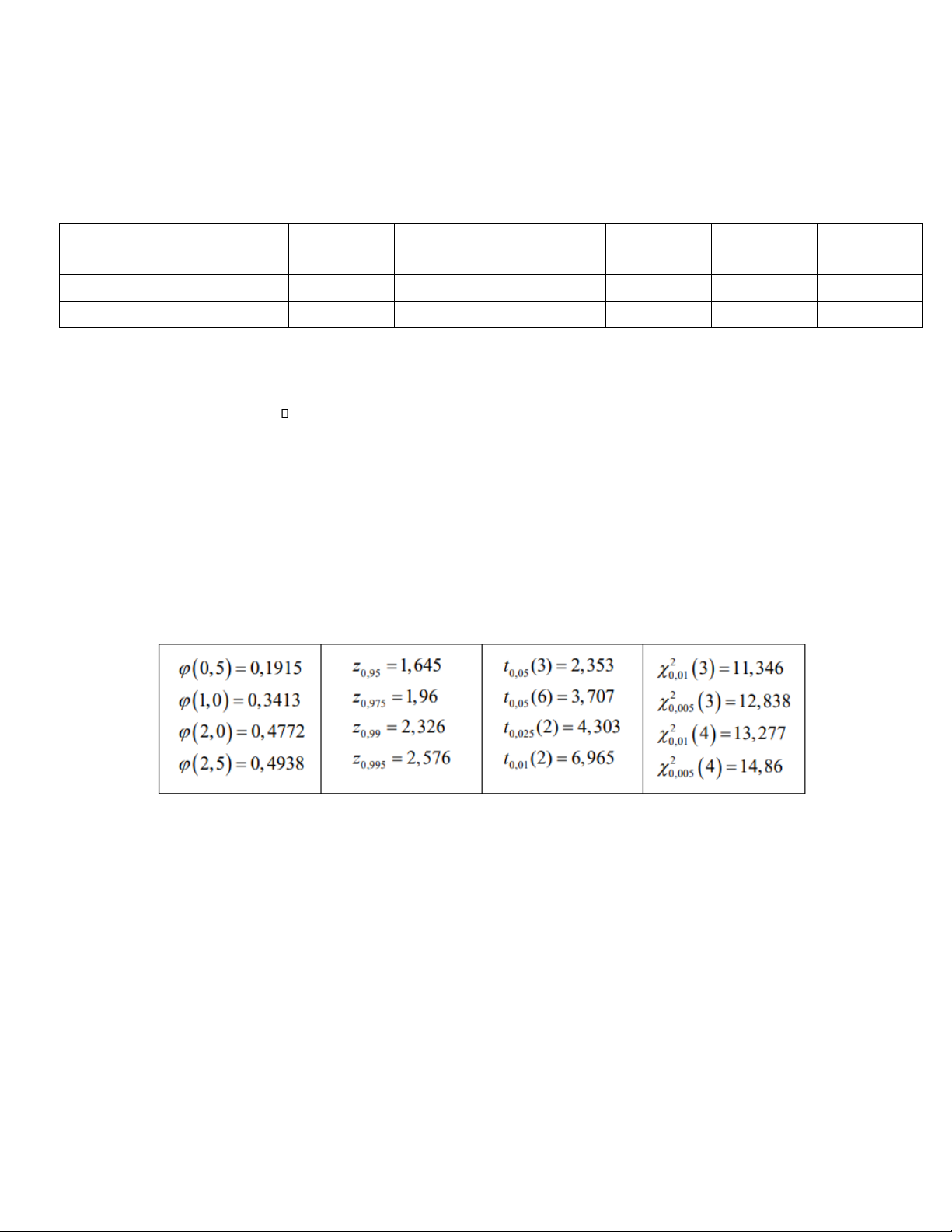
Tính tham số các mẫu và giá trị quan sát? 28. Kết luận? HẾT Cho biết: