Đề tham khảo tuyển sinh 10 năm 2023-2024

UBND …..
ĐỀ THAM KHẢO KỲ THI TUYỂN SINH 10
TRƯỜNG THCS …….
Năm học 2023 – 2024
Thời gian làm bài: 120 phút
(không kể thời gian phát đề) 1 1
Bài 1: (1,5 điểm) Cho hai hàm số: (P): 2 y 
x và đường thẳng (d): y   x  3 2 2
a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Bài 2: (1 điểm) Cho phương trình 2
2x  x  4  0 có hai nghiệm x , x . Không giải phương trình, 1 2 2x 2x
hãy tính giá trị của biểu thức 1 2 M   x x 2 1
Bài 3: (0,75 điểm) Quy tắc sau đây cho chúng ta biết được ngày a, tháng b, năm 2021 là ngày thứ
mấy trong tuần. Đầu tiên ta tính giá trị của biểu thức T = a + b + 4, với a là số ngày, ba là mã
tháng được cho trong bảng sau: Tháng 1,10 11, 2, 3 4, 7 5 6 8 9, 12 b 1 4 0 2 5 3 6
Sau đó lấy T chia cho 7 ta được số dư r (0 ≤ r ≤ 6).
Nếu r = 0 thì đó là ngày thứ Bảy. Nếu r = 1 thì đó là ngày Chủ Nhật
Nếu r = 2 thì đó là ngày thứ Hai. Nếu r = 3 thì đó là ngày thứ Ba
….Nếu r = 6 thì đó là ngày thứ Sáu
Ví dụ 1: Ngày 20/4/2021 có a = 20, b = 0  T = 20 + 0 + 4 = 24. Số 24 chia cho 7 có số dư là 3
nên ngày đó là ngày thứ 3.
a) Em hãy sử dụng quy tắc trên để xác định các ngày 23/05/2021 và 02/09/2021 là ngày thứ mấy.
b) Trong quá trình học lịch sử bạn An được biết rằng năm 2021 là năm kỉ niệm 110 năm
ngày sinh của Đại tướng Võ Nguyên Giáp nhưng lại không nhớ là ngày nào, bạn chỉ biết
ngày đó là thứ tư, nằm trong tháng 8 và là bội số của 5. Em hãy dùng quy tắc trên để xác
định ngày tháng năm sinh của Đại tướng Võ Nguyên Giáp
Bài 4: (0,75 điểm) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Mối
liên hệ giữa áp suất khí quyển P (mmHg) và độ cao h (mét) so với mực nước biển là một hàm
số bậc nhất có dạng P = a.h + b. Bạn Khang trong một lần đi Đà Lạt, tại thị trấn Bảo Lộc có
độ cao 900m so với mực nước biển, bạn đo được áp suất khí quyển tại nơi này là 688mmHg.
Khi lên đến Đà Lạt có độ cao 1,5km so với mực nước biển thì bạn Khang thấy áp suất khí
quyển tại đây là 640 mmHg. Xác định hệ số a và b.
Bài 5: (1 điểm) Một công ty có hai hình thức trả lương như sau:
- Hình thức 1: Trả lương theo tháng với mức lương 6 500 000 đồng/tháng. Trang 1
- Hình thức 2: Trả lương theo quý (một quý 3 tháng) với mức lương 16 000 000 đồng/quý và quý
sau sẽ tăng 15% so với quý trước.
Nếu anh Tuấn chỉ làm việc ở công ty 1 năm thì anh nên chọn hình thức trả lương nào để có
được số tiền nhiều hơn. Vì sao?
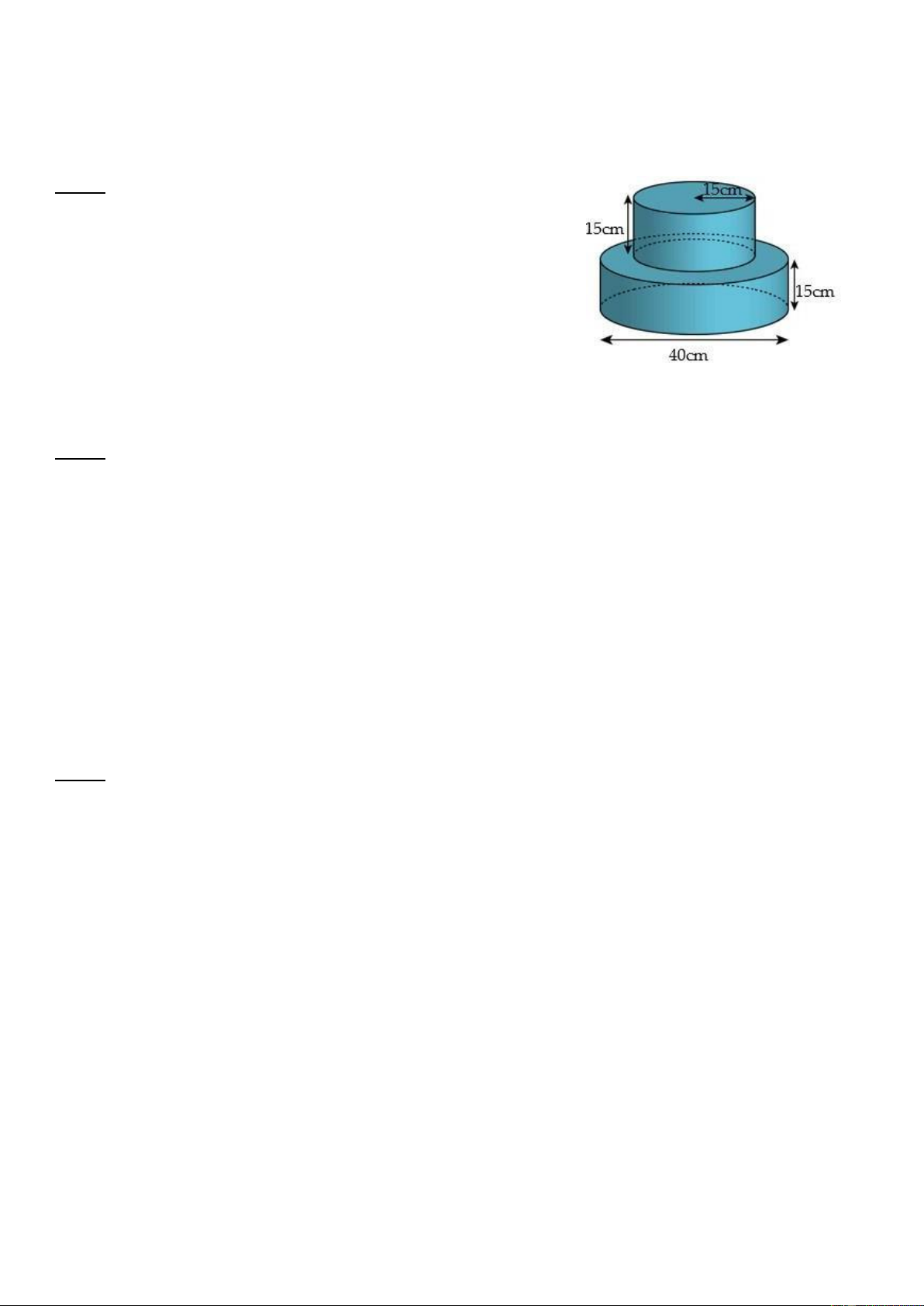
Bài 6: (1 điểm) Để tổ chức sinh nhật cho con gái, chị Thanh đã
đặt thợ làm bánh tại cửa hàng Bakery với yêu cầu bánh được làm
hai tầng, mỗi tầng cao 15cm, bán kính tầng trên là15cm, đường
kính tầng dưới là 40cm. Biết công thức tính thể tích hình trụ là V
 r2.h và diện tích xung quanh hình trụ là S  2r.h
a) Tính thể tích chiếc bánh. (Làm tròn kết quả đến hai chữ số thập phân)
b) Hỏi với kích thước yêu cầu của chị Thanh, khi chiếc bánh được hoàn thành thì người thợ có tất
cả bao nhiêu diện tích bề mặt để trang trí bánh? (Làm tròn kết quả đến hai chữ số thập phân).
Bài 7: (1 điểm) Nhân dịp cuối năm, ở các siêu thị đã đưa ra nhiều hình thức khuyến mãi.
- Ở siêu thị Big C giá áo sơ mi nữ nhãn hiệu Blue được giảm giá như sau: Mua áo thứ I giảm 15%
so với giá niêm yết, mua áo thứ II được giảm tiếp 10% so với giá đã giảm của áo thứ I, mua áo thứ
III sẽ được giảm thêm 12% so với giá đã giảm của áo thứ II nên áo thứ 3 chỉ còn 269.280.
- Ở siêu thị Maximax lại có hình thức giảm giá khác: Nếu mua 1 áo thì được giảm 50.000, mua
áo thứ II được giảm thêm 15% so với giá đã giảm ở áo thứ I, mua áo thứ III thì chỉ phải trả
250.000 đồng. Biết giá niêm yết của loại áo trên ở hai siêu thị là bằng nhau.
a) Tìm giá niêm yết của loại áo sơ mi trên.
b) Bạn Trang muốn mua 3 áo sơ mi thì nên chọn mua ở siêu thị nào để có lợi hơn và lợi hơn bao nhiêu tiền.
Bài 8: (3 điểm) Cho ABC nhọn (ABtại H. Vẽ đường kính AD của đường tròn (O). Qua H vẽ đường thẳng d vuông góc AD tại
K, d cắt AB, AC và đường thẳng BC lần lượt tại M, N và S.
a) Chứng minh 4 điểm A, E, H, K cùng thuộc một đường tròn. Xác định tâm I của đường tròn này.
b) Chứng minh AKM đồng dạng với ABD và SM.SN = SB.SC c) Chứng minh SI  OI -----HẾT----- Trang 2 UBND …..
ĐÁP ÁN KỲ THI TUYỂN SINH LỚP 10 TRƯỜNG THCS ……
Năm học 2023 – 2024
Thời gian làm bài: 120 phút
(không kể thời gian phát đề) Bài Nội dung Điểm
a) HS lập bảng giá trị (P) đúng 0.25 HS vẽ (P) đúng 0.25
HS lập bảng giá trị và vẽ (d) đúng 0.25
b) Phương trình hoành độ giao điểm 1 1 1 1 2 2 x  x  3  x  x  3  0 0.25 Bài 1: 2 2 2 2 1,5 x  2 0.25 điể  m  x  3
Với x  2  y  2 9
Với x  3  y  0.25 2  9 
Vậy tọa độ giao điểm của (P) và (d) là (2;2) và 3;     2   b  1
S  x  x    1 2  a 2
Theo hệ thức Vi-et ta có  0.5 c  P  x x   2  1 2  a Bài 2: 2 2 2 x  x  2 2 S  2 2 2 P x x  1 2  1 2 2S 4P 1 2      điể M 0.25 m x x x x P P 2 1 1 2 2  1  2  4.( 2  )    2  17 M    0.25 2 4
a) Ngày 23/05/2021  a  23,b  2  T  a  b  4  23 2  4  29 0.25
Vì 29 : 7 = 4 dư 1 nên ngày 23/05/2021 là ngày chủ nhật.
Ngày 02/09/2021  a  2,b  6  T  a  b  4  2  6  4  12 0.25
Vì 12 : 7 = 1 dư 5 nên ngày 02/09/2021 là ngày thứ năm.
b) Vì a là bội số của 5 và là một ngày trong tháng  a 5;10;15;20;25;30 Bài 3:
Vì sinh nhật của đại tướng Võ Nguyên Giáp nằm trong tháng 8 0,75 điể m
 b  3  T  a  3  4  a  7
Vì sinh nhật của đại tướng Võ Nguyên Giáp là vào thứ tư  T :7 dư 4 Xét các trường hợp, ta có bảng sau a 5 10 15 20 25 30 T = a+7 12 17 22 27 32 37 r 0 3 1 6 4 2
Vậy ngày tháng năm sinh của đại tướng Võ Nguyên Giáp là 25/08/1911 0.25
Bài 4: Đổi 1,5 km = 1500 m 0.25 Trang 3 0,75
Lần lượt thay các cặp số h  900, P  688 và h = 1500, P = 640 vào hàm số điểm
P  a.h  b ta có hệ phương trình 90
 0a  b  688  0.25 15
 00a  b  640  2 a   2  25 Vậy y  x  760 0.25  25 b  760
Số tiền anh Tuấn nhận được nếu trả lương theo hình thức 1:
6 500 000 . 12 = 78 000 000 đồng 0.25
Hình thức 2: quý 1: 16 000 000 đồng Bài 5:
Quý 2: 16 000 000 . (1 + 15%) = 18 400 000 đồng 0.25 1
Quý 3: 18 400 000 . (1 + 15%) = 21 160 000 đồng
điểm Quý 4: 21 160 000 . (1 + 15%) = 24 334 000 đồng
Số tiền anh Tuấn nhận được nếu trả lương theo hình thức 1:
16 000 000 + 18 400 000 + 21 160 000 + 24 334 000 = 79 894 000 đồng 0.25
Vậy anh Tuấn nên chọn hình thức 2 để có lợi hơn (79 894 000 > 78 000 000) 0.25 a) Thể tích bánh là 2 2 2 2 3
V   r .h   R .h  .15 .15  .20 .15  9375 29452, 43cm 0.5 Bài 6: 1
b) Diện tích bề mặt của chiếc bánh là điể m
S  2r.h  2R.h  R2 0.5
S  2.15.15  2.20.15  202  1450  4555, 31 cm2
a) Gọi x (đồng) là giá niêm yết của một chiếc áo, ta có phương trình 0.5
x.115%.110%.112%  269280  x  400000 đồng Bài 7:
b) Số tiền phải trả nếu mua ở siêu thị Big C 1
400000.115%  400000.115%.110%  269280  915 280 đồng 0.25 điểm
Số tiền phải trả nếu mua ở siêu thị Maximax 
400000 50000 400000  50000.115%  250000  897 500 đồng 0.25
Vậy bạn Trang nên mua ở siêu thị Maximax để có lợi hơn Bài 8: 3 điểm Trang 4 a) Xét tứ giác AHKE có 𝐴𝐸𝐻 ̂ = 900 0.5 (BE là đường cao) 𝐴𝐾𝐻 ̂ = 900 (gt)  𝐴𝐸𝐻 ̂  𝐴𝐾𝐻 ̂  900
 tứ giác AHKE nội tiếp đường tròn đường kính AH 0.25
 Tâm I là trung điểm AH 0.25 b) Ta có 𝐴𝐵𝐷
̂  900 (góc nội tiếp chắn nửa đường tròn) Xét AKM và ABD có 𝐵𝐴𝐷 ̂ chung 0.25  𝐴𝐾𝑀 ̂  𝐴𝐵𝐷 ̂  900 0.25  AKM ABD  𝐴𝑀𝐾 ̂  𝐴𝐷𝐵 ̂ 0.25 Mà 𝐴𝑀𝐾 ̂  𝑆𝑀𝐵
̂ (đối đỉnh) và 𝐴𝐷𝐵 ̂  𝑆𝐶𝑁 ̂ (cùng chắn cung AB)  𝐴𝑀𝐵 ̂  𝑆𝐶𝑁 ̂ 0.25 Xét SMB và SCN có S chung  𝐴𝑀𝐵 ̂  𝑆𝐶𝑁 ̂cmt  SMB SCN SM SB 0.25    SM .SN  . SB SC SC SN
c) Gọi L là giao điểm HD và BC
Cm được BHCD là hình bình hành, suy ra L là trung điểm HD. 0.25
Cm IL // AD, mà AD  SK  IL  SK
Cm H là trực tâm SIL LH  SI 0.25 Cm HD // IO  SI  IO 0.25 Trang 5