













Preview text:
SỞ GD&ĐT TPHCM
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT HUYỆN CẦN GIỜ
NĂM HỌC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Quận Cần Giờ- 1
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 1. (1,5 điểm). Cho P 2
: y x và đường thẳng d 1
: y x 1 . 2 2
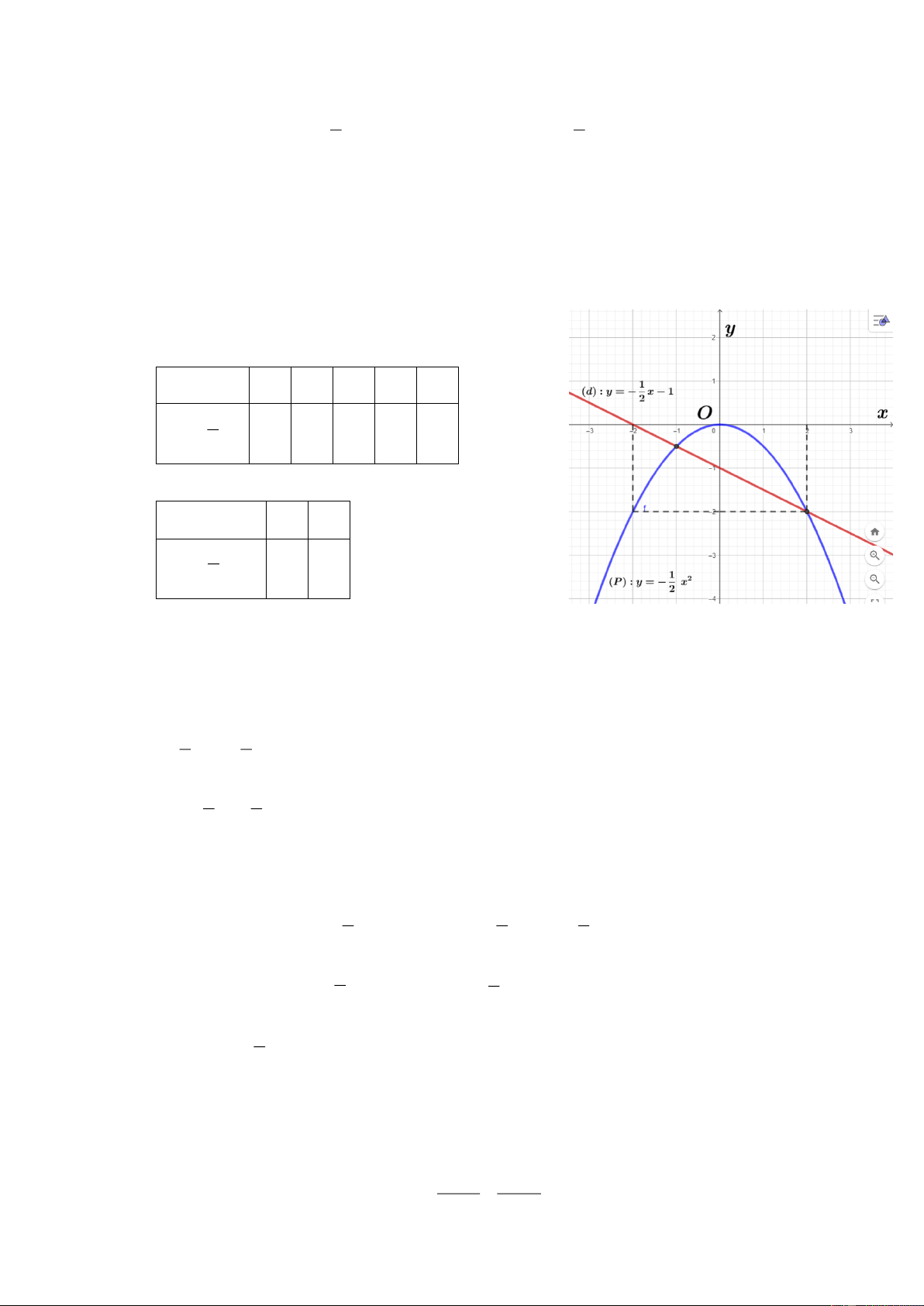
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Gọi x ,x là nghiệm (nếu có) của phương trình 2
x 3x 10 0 . Không giải 1 2 x 2 x 2
phương trình, hãy tính giá trị của biểu thức 1 2 A . x x 2 1
Câu 3. (1 điểm). Thực hiện chương trình khuyến mãi “Ngày chủ nhật vàng”, một cửa hàng điện
máy giảm giá 30% trên 1 tivi cho lô hàng tivi 50 cái với giá bán lẻ trước đó là 7 000000
đ/cái. Đến trưa cùng ngày thì cửa hàng đã bán được 20 cái và cửa hàng quyết định giảm
thêm 10%nữa (so với giá đã giảm lần 1) cho số tivi còn lại. Hỏi cửa hàng lời hay lỗ bao
nhiêu tiền khi bán hết lô hàng tivi đó, biết rằng giá vốn là 4 500 000 đ/cái tivi
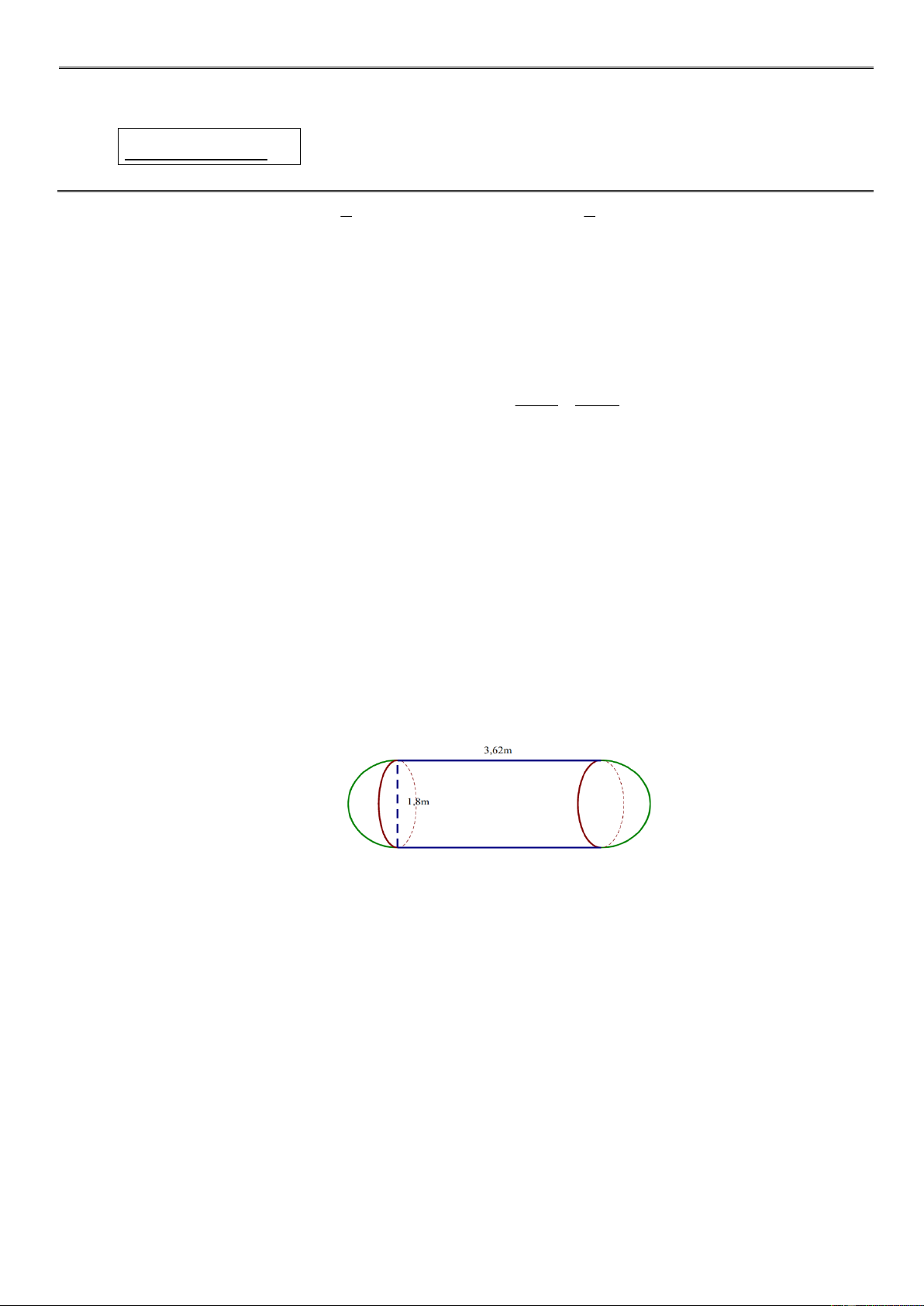
Câu 4. (0,75 điểm. Một xe bồn chở nước sạch cho một khu chung cư có 200 hộ dân. Bồn xe có kích
thước như hình vẽ, mỗi đầu của bồn xe là 1 nửa hình cầu. Xe chở đầy bồn nước và lượng
nước chia đều cho từng hộ dân. Tính xem mỗi hộ dân được nhận bao nhiêu nước sạch.
Câu 5. (1,25 điểm). Mục tiêu là để rèn luyện sức khỏe, anh An và anh Bình đề ra mục tiêu mỗi
ngày một người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở công viên và thấy
rằng, nếu cùng đi trong 2 phút thì anh An bước nhiều hơn anh Bình 20 bước. Hai người
cùng giữ nguyên tốc độ như vậy nhưng anh Bình đi trong 5 phút thì lại nhiều hơn anh An
đi trong 3 phút là 160 bước. Hỏi mỗi ngày anh An và anh Bình cùng đi bộ trong 1 giờ thì
họ đã đạt được số bước tối thiểu mà mục tiêu đề ra hay chưa? (Giả sử tốc độ đi bộ hàng
ngày của hai người không đổi).
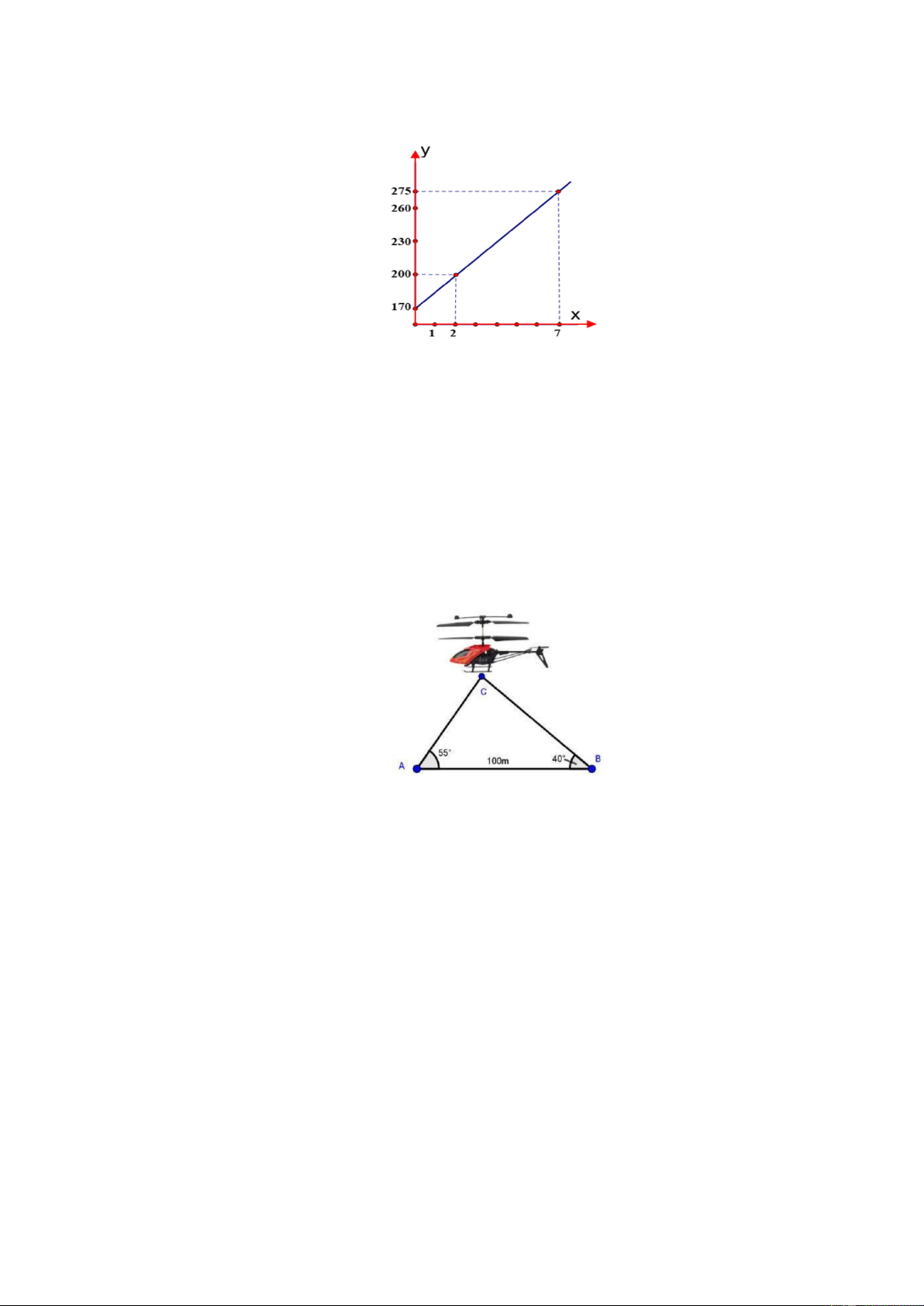
Câu 6. (1,25 điểm). Một công ty địa ốc sau 2 năm thay đổi đã bán được 200 căn nhà và sau 7 năm
thì bán được 275 căn nhà. Số lượng nhà bán được của công ty địa ốc sau khi thay đổi được Trang 1
cho bởi công thức: y ax b (trong đó: y là số lượng nhà bán được; x là số năm bán) và có đồ thị như hình bên.
a) Xác định hệ số a và b ?
b) Em hãy cho biết sau 10 năm công ty đó bán được bao nhiêu căn nhà?
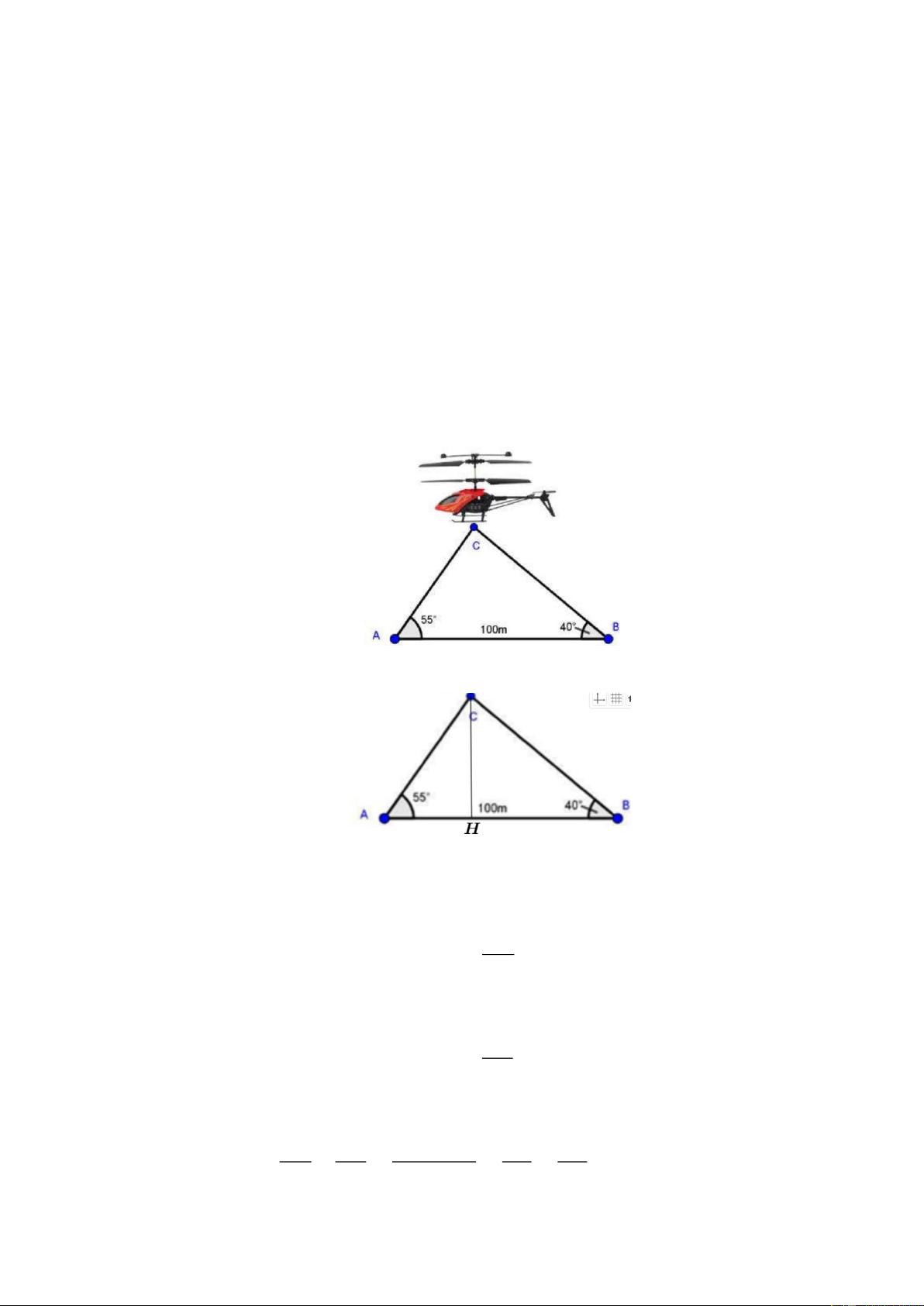
Câu 7. (0,75 điểm). Hai học sinh An (vị trí A ) và Bình (vị trí B ) đang đứng ở mặt đất bằng phẳng
cách nhau 100m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (vị trí C ). Biết góc
“nâng” để nhìn thấy máy bay tại vị trí A là 550 và góc “nâng” để nhìn thấy máy bay tại vị
trí B là 400 . Hãy tính độ cao của máy bay so với mặt đất (ghi kết quả gần đúng chính xác đến mét).
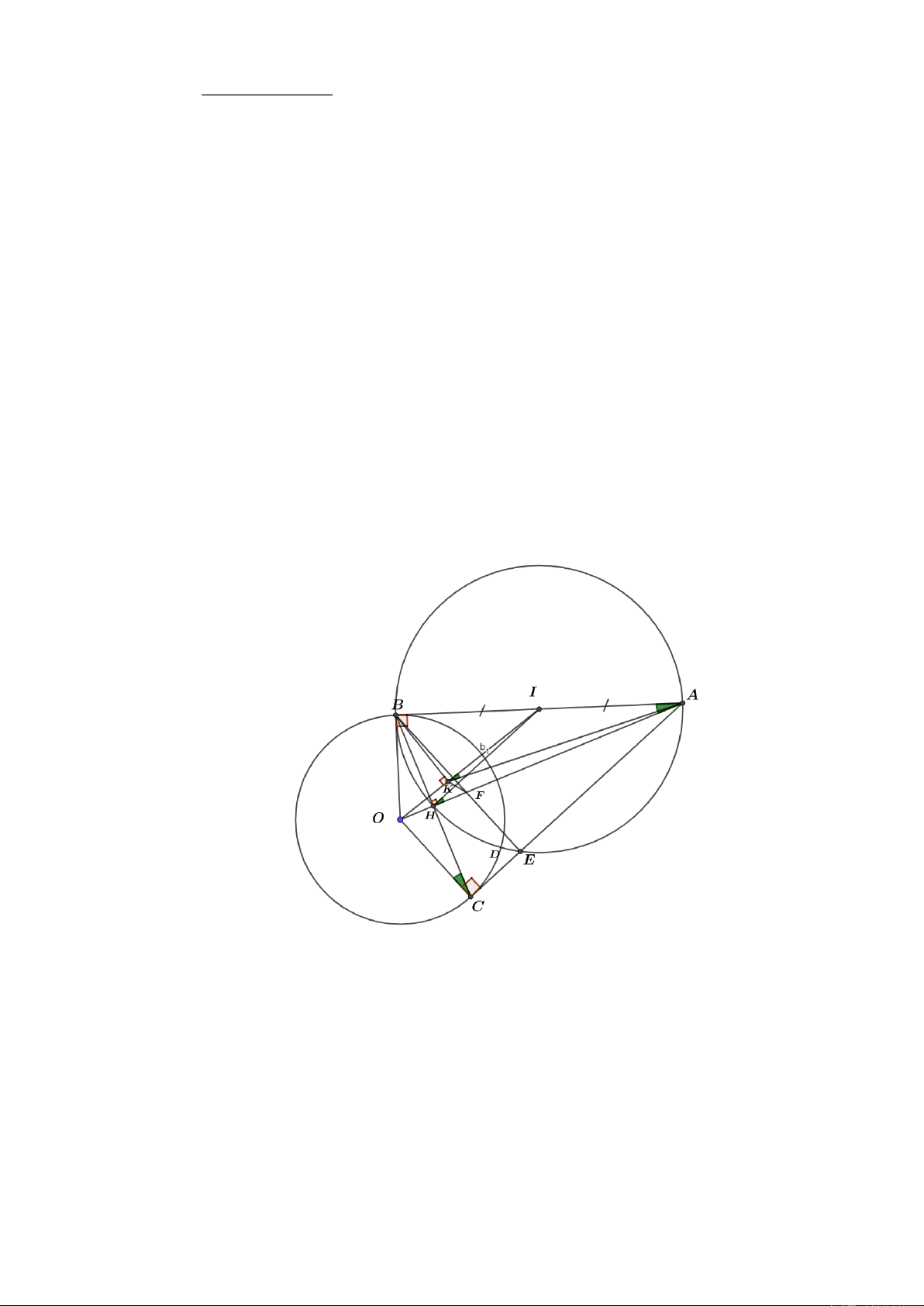
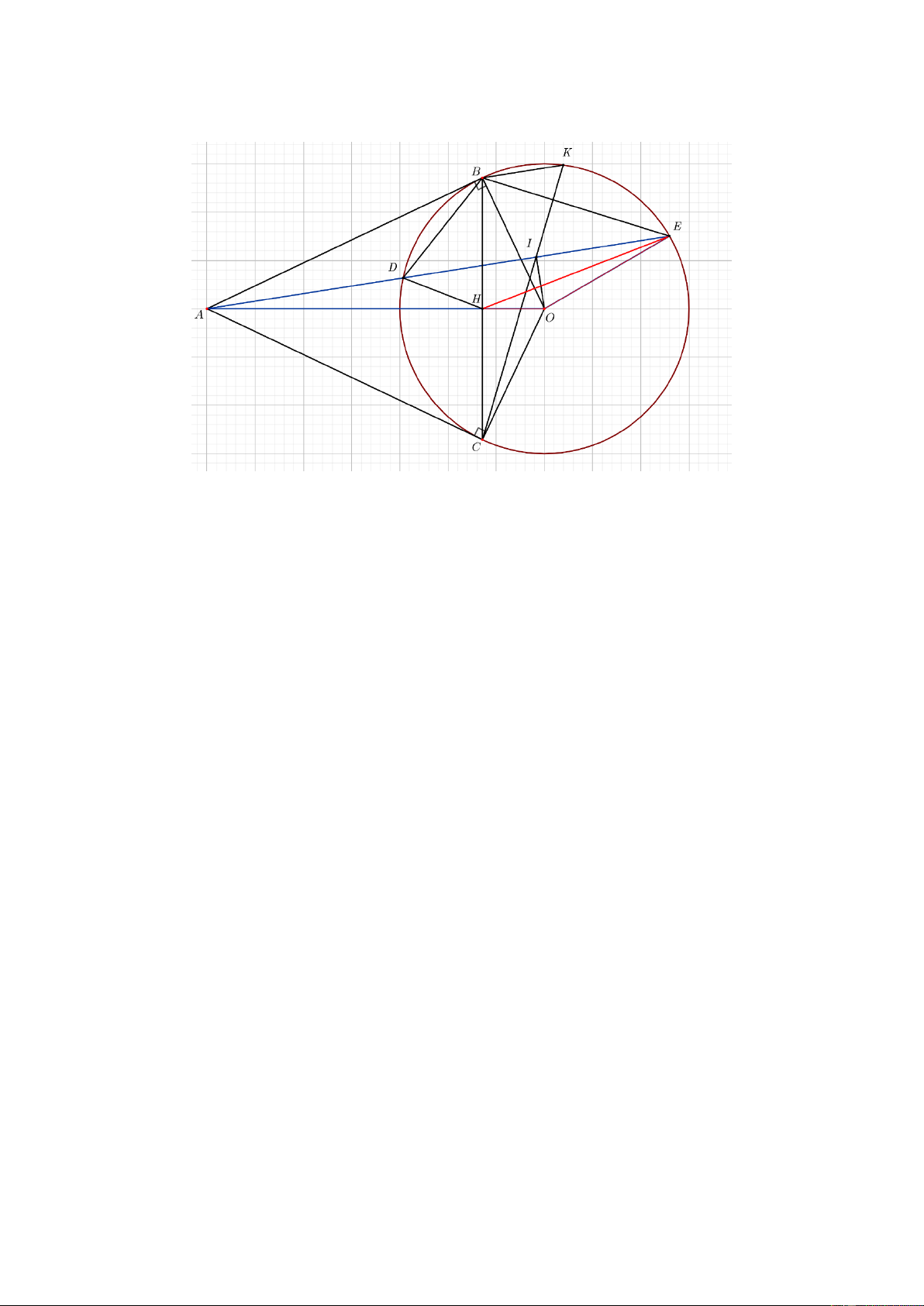
Câu 8. (2,5 điểm) Từ điểm A ở ngoài đường tròn O; R vẽ hai tiếp tuyến AB, AC đến đường tròn
với B,C là hai tiếp điểm. Gọi H là giao điểm của AO và BC . Gọi I là trung điểm của AB .
Từ B kẻ đường thẳng vuông góc với OI tại K , đường thẳng này cắt đường tròn O tại D ( D khác B ).
a) Chứng minh tứ giác ABOC nội tiếp vàO . K OI O . H OA .
b) Đường tròn tâm I đường kính AB cắt AC tại E . Gọi F là giao điểm của BE và AO .
Chứng minh F đối xứng với O qua H .
c) Chứng minh đường tròn ngoại tiếp tứ giác DAFB đi qua điểm K . ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI 1 1
Câu 1. (1,5 điểm). Cho P : y 2
x và đường thẳng d : y x 1 . 2 2
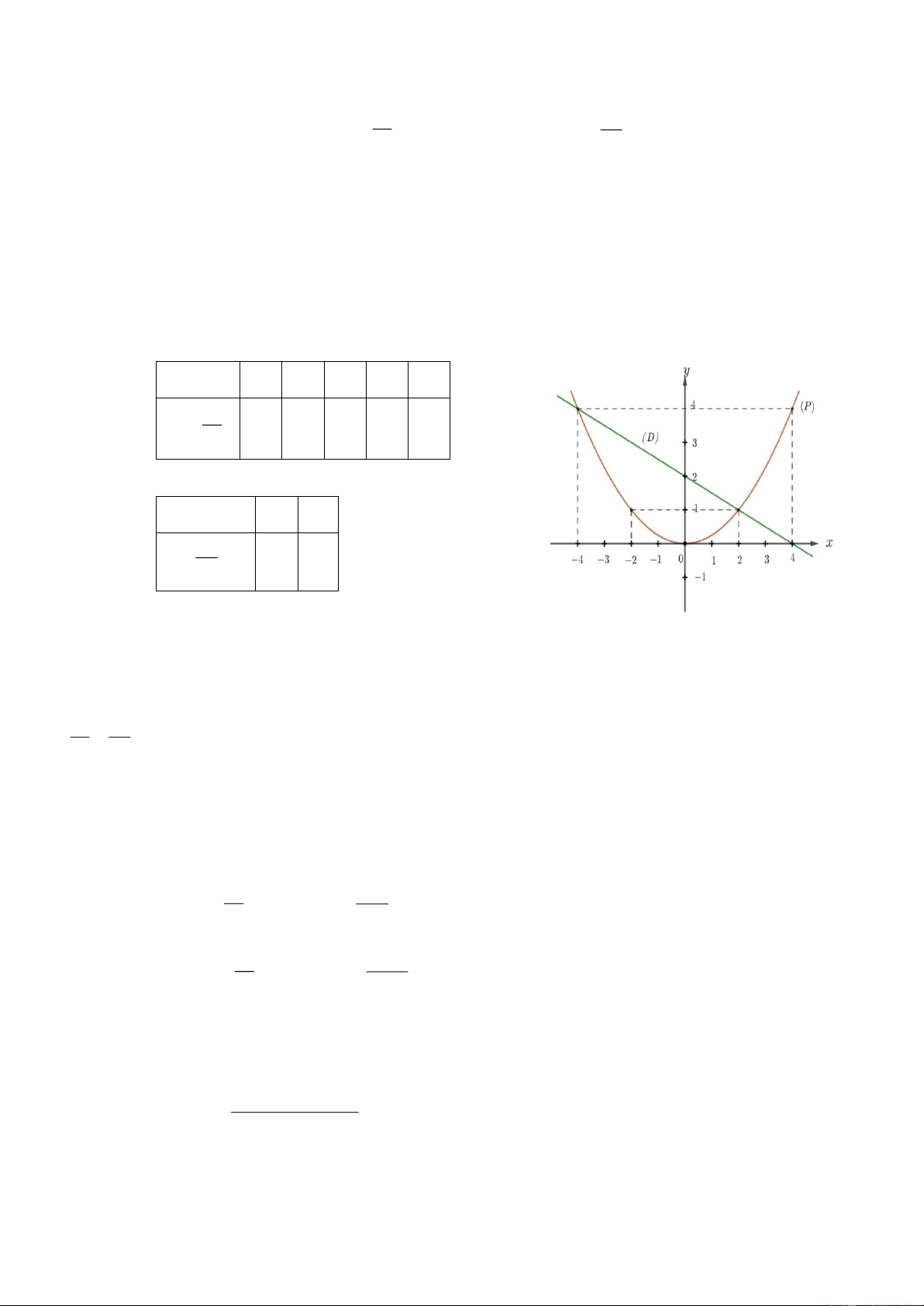
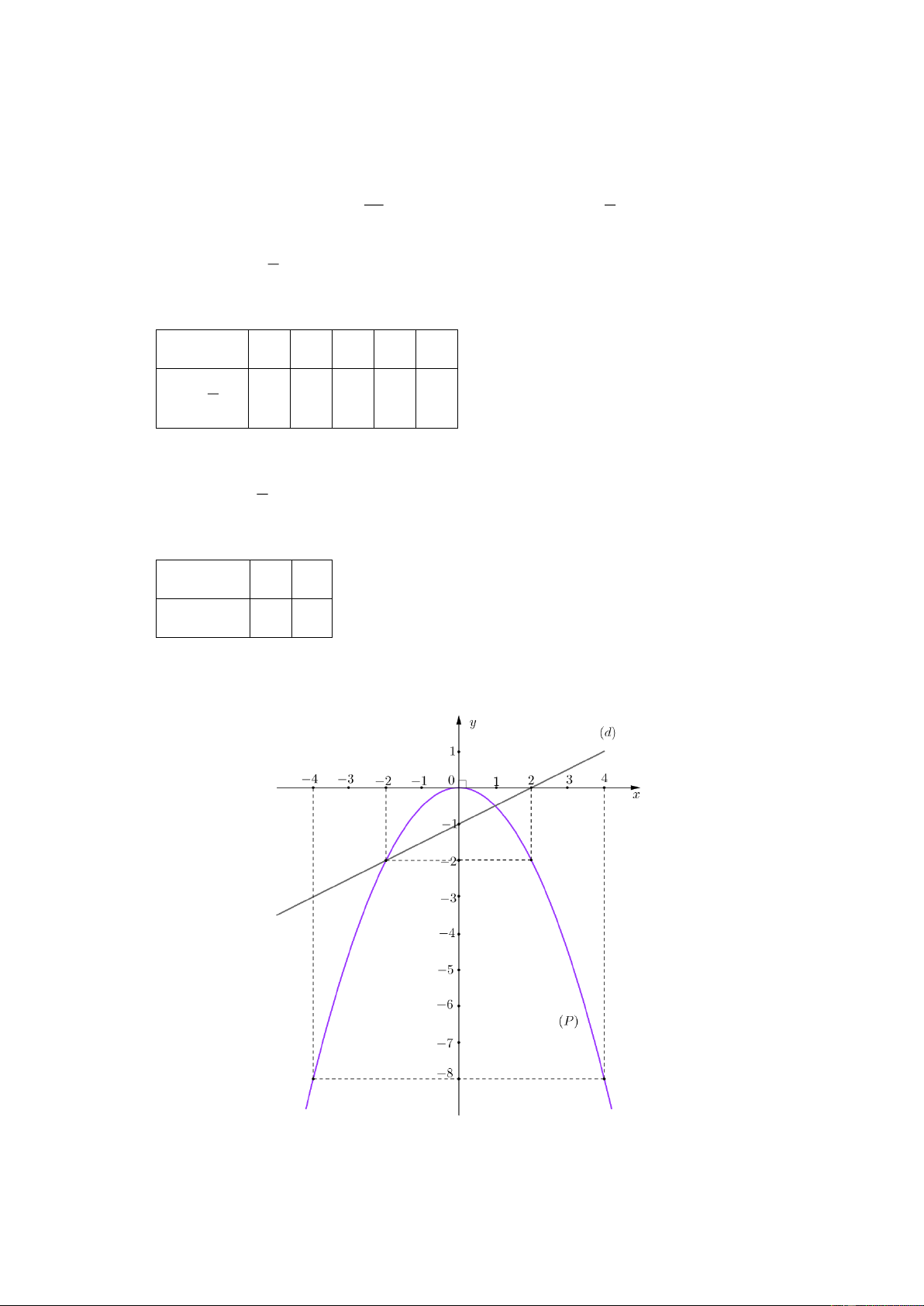
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: x 4 2 0 2 4 y 1 2 x 8 1 0 2 8 2 x 0 2
y 1 x 1 1 0 2
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 1 2
x 1 x 1 2 2 1 2
x 1 x 1 0 2 2 x 2 x 1 1 1 1
Thay x 1 vào y 2
x , ta được: y ( 2 1) . 2 2 2 1 1
Thay x 2 vào y 2
x , ta được: y 2 2 2 . 2 2 1 Vậy 1;
, 2;2 là hai giao điểm cần tìm. 2
Câu 2. (1 điểm). Gọi x , x là nghiệm (nếu có) của phương trình 2
x 3x 10 0 . Không giải phương 1 2 x 2 x 2
trình, hãy tính giá trị của biểu thức A 1 2 x x 2 1 Trang 3 Lời giải
Vì a.c = 1.(- 10) = - 10 < 0 Þ a,c trái dấu.
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b S x x 3 3 1 2
Theo định lí Vi-et, ta có: a 1 c P x .x 10 1 2 a x 2 x 2 Ta có: A 1 2 x x 2 1
x 2 x x 2 x 1 1 2 2 A x x 1 2 2 2
x x 2 x x 1 2 1 2 A x x 1 2
x x 2 2x x 2 x x 1 2 1 2 1 2 A x x 1 2
32 2.10 2.3 A 3 23 A . 3
Câu 3. (1 điểm). Thực hiện chương trình khuyến mãi “Ngày chủ nhật vàng”, một cửa hàng điện
máy giảm giá 30% trên 1 tivi cho lô hàng tivi 50 cái với giá bán lẻ trước đó là 7 000 000
đ/cái. Đến trưa cùng ngày thì cửa hàng đã bán được 20 cái và cửa hàng quyết định giảm
thêm 10% nữa (so với giá đã giảm lần 1) cho số tivi còn lại. Hỏi cửa hàng lời hay lỗ bao
nhiêu tiền khi bán hết lô hàng tivi đó, biết rằng giá vốn là 4 500 000 đ/cái tivi Lời giải
Giá 1 tivi sau khi giảm 30% là: 7000000.(1 - ) 30% = 4900000(đồng).
Số tiền sau khi bán được 20 tivi đầu tiên là: 4900000.20 = 98000000 (đồng).
Giá 1 tivi sau khi giảm thêm 10% là: 4900000.(1 - 10%) = 4410000 (đồng).
Số tiền sau khi bán được số tivi còn lại: 4410000.(50 - 20) = 132300000 (đồng).
Số tiền sau khi bán 50 tivi với giá vốn là:
4500000.50 = 225000000 (đồng).
Số tiền sau khi bán 50 tivi với giá khuyến mãi: 98000000 + 132300000 = 230300000 (đồng)
Vì 230300000 > 225000000nên cửa hàng lời. Số tiền lời là
230300000 - 225000000 = 5300000 (đồng). Trang 4
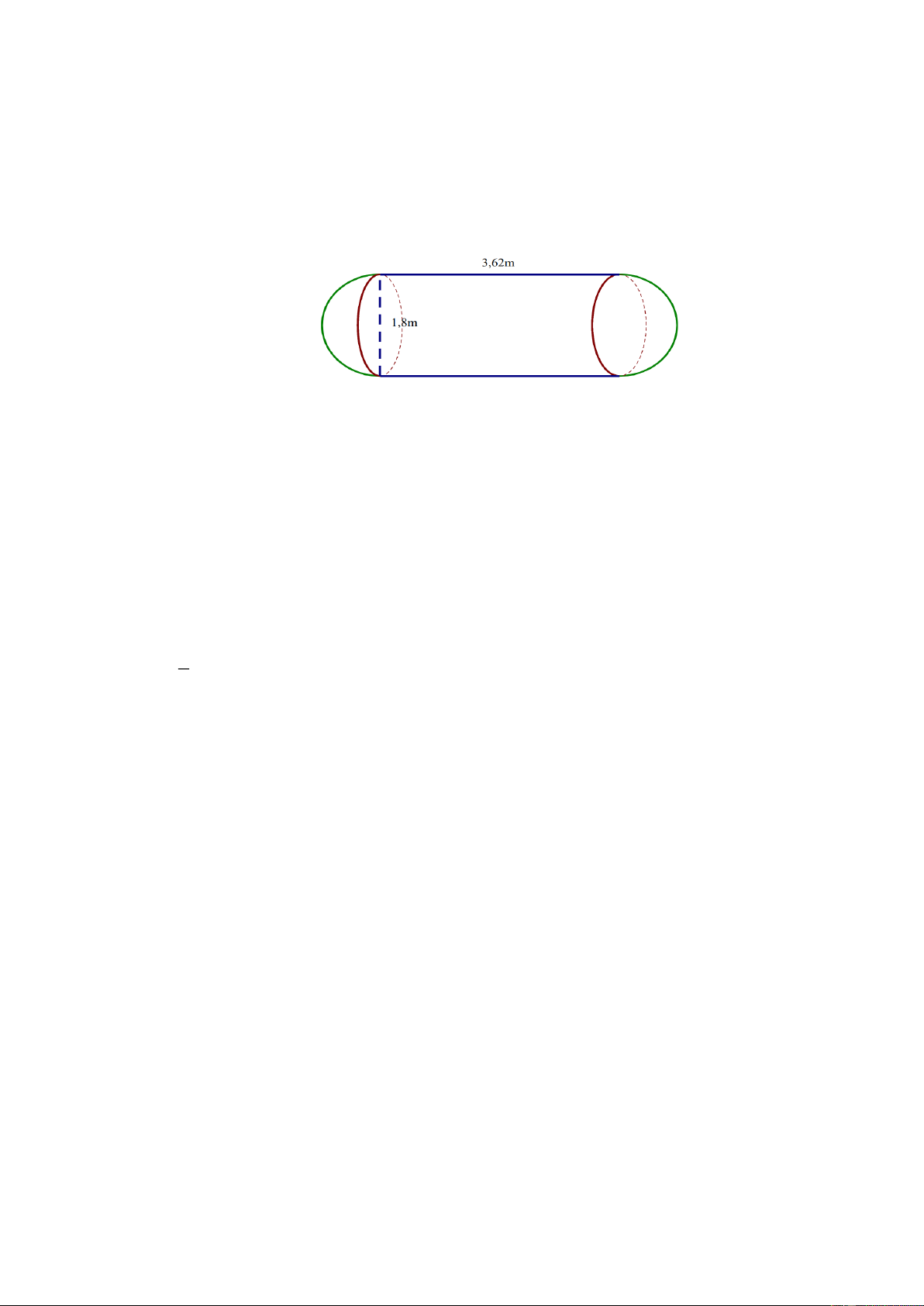
Câu 4. (0,75 điểm. Một xe bồn chở nước sạch cho một khu chung cư có 200 hộ dân. Bồn xe có kích
thước như hình vẽ, mỗi đầu của bồn xe là 1 nửa hình cầu. Xe chở đầy bồn nước và lượng
nước chia đều cho từng hộ dân. Tính xem mỗi hộ dân được nhận bao nhiêu nước sạch. Lời giải Bán kinh hình cầu là:
r = d : 2 = 1, 8 : 2 = 0, 9 (m ) Thể tích hình trụ là: 2
V = p.0, 9 .3, 62 = 2, 9322p ( 3 m ) 1
Thể tích của hai nửa hình cầu là: 4 3 V =
p.0, 9 = 0, 972p ( 3 m ) 2 3
Thể tích của xe chở bồn nước là:
V = V + V = 2, 9322p + 0, 972p = 3, 9042p ( 3 m ) 1 2
Số lít nước mỗi hộ dân sử dụng là: 3
3, 9042 : 200 » 0, 006m = 60 li’t
Vậy số nước mỗi hộ dân được sử dụng là 60 lít
Câu 5. (1,25 điểm). Mục tiêu là để rèn luyện sức khỏe, anh An và anh Bình đề ra mục tiêu mỗi ngày
một người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở công viên và thấy rằng, nếu
cùng đi trong 2 phút thì anh An bước nhiều hơn anh Bình 20 bước. Hai người cùng giữ
nguyên tốc độ như vậy nhưng anh Bình đi trong 5 phút thì lại nhiều hơn anh An đi trong 3
phút là 160 bước. Hỏi mỗi ngày anh An và anh Bình cùng đi bộ trong 1 giờ thì họ đã đạt
được số bước tối thiểu mà mục tiêu đề ra hay chưa? (Giả sử tốc độ đi bộ hàng ngày của hai người không đổi). Trang 5 Lời giải
Gọi x là mỗi bước anh An đi được trong 1 phút ( * x Î ¥ )
Gọi y là mỗi bước anh Bình đi được trong 1 phút ( * y Î ¥ )
Vì nếu đi trong 2 phút thì anh An nhiều hơn anh Bình 20 bước nên ta có phương trình: 2x - 2y = 20( ) 1
Vì nếu anh Bình đi trong 5 phút thì anh An đi trong 3 phút là 160 bước nên ta có phương trình: 5y - 3x = 160( ) 2 Từ ( ) 1 ,( ) 2 ta có hệ phương trình
ìï 2x - 2y = 20 ìï x = 105 ï ï (n ) í Û í ï - 3x + 5y = 160 ï y = 95 ïî ï (n ) ïî
Số bước anh An đi bộ trong 1 giờ là:105.60 = 6300 (bước)
Số bước anh An đi bộ trong 1 giờ là: 95.60 = 5700 (bước)
Vậy anh An đạt được mục tiêu đề ra, anh Bình chưa đạt mục tiêu đề ra.
Câu 6. Một công ty địa ốc sau 2 năm thay đổi đã bán được 200 căn nhà và sau 7 năm thì bán được
275 căn nhà. Số lượng nhà bán được của công ty địa ốc sau khi thay đổi được cho bởi công
thức: y = ax + b (trong đó: y là số lượng nhà bán được; x là số năm bán) và có đồ thị như hình bên.
a) Xác định hệ số a và b ?
b) Em hãy cho biết sau 10 năm công ty đó bán được bao nhiêu căn nhà? Lời giải
a) Thay x = 2;y = 200vào phương trình y = ax + b ta có phương trình:200 = 2a + b( ) 1
Thay x = 7;y = 275 vào phương trìnhy = ax + b ta có phương trình: 275 = 7a + b( ) 2 Từ ( ) 1 ,( ) 2 ta có hệ phương trình
ìï 2a + b = 200 ìïa = 15 ï ï í Û í ï 7a + b = 275 ïb = 170 ïî ïî
Vậy a = 15;b = 170 Trang 6
b) Thay a = 15;b = 170 vào y = ax + b
Þ y = 15x + 170
Số căn nhà công ty bán được sau 10 năm là: y = 15.10 + 170 = 320 (căn)
Vậy sau 10 năm công ty bán được 320 căn nhà.
Câu 7. (0,75 điểm).
Hai học sinh An (vị trí A ) và Bình (vị tríB ) đang đứng ở mặt đất bằng phẳng cách nhau
100m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (vị trí C ). Biết góc “nâng” để
nhìn thấy máy bay tại vị trí A là 550 và góc “nâng” để nhìn thấy máy bay tại vị trí B là 400 .
Hãy tính độ cao của máy bay so với mặt đất (ghi kết quả gần đúng chính xác đến mét). Lời giải
Dựng CH ^ A B Vậy độ cao máy bay so với mặt đất là CH
Xét tam giác CA H vuông tại H ta có: · A H 0 cot CA H = = cot 55 CH
Xét tam giác CBH vuông tại H ta có · BH 0 cot CBH = = cot 40 CH Ta có A H BH A H + BH A B o 100 0 cot 55 + cot 40 = + = = = CH CH CH CH CH Trang 7 100 Þ CH = » 53 (m ) 0 0 cot 55 + cot 40
Câu 8. (2.5 điểm)
Từ điểm A ở ngoài đường tròn (O;R )vẽ hai tiếp tuyến A B, A C đến đường tròn với B,C là
hai tiếp điểm. Gọi H là giao điểm của A O và B C . Gọi I là trung điểm củaA B . Từ B kẻ
đường thẳng vuông góc với OI tạiK , đường thẳng này cắt đường tròn (O )tại D (D khácB ).
a) Chứng minh tứ giác A BOC nội tiếp vàOK .OI = OH.OA .
b) Đường tròn tâm I đường kính A B cắt A C tại E . Gọi F là giao điểm của BE và A O .
Chứng minh F đối xứng với O quaH .
c) Chứng minh đường tròn ngoại tiếp DA FB đi qua điểm K Lời giải
a) Chứng minh tứ giác A BOC nội tiếp.
Xét tứ giác A BOC ta có ·
OB A = 90o ( A B là tiếp tuyến) ·
OCA = 90° ( A C là tiếp tuyến) · ·
Þ OBA + OCA = 90° + 90° = 180°
Vậy tứ giác A BOC nội tiếp đường tròn. Trang 8
Chứng minh OK .OI = OH.OA ta có
OB = OC = R
A B = A C (tính chất 2 tiếp tuyến cắt nhau)
Þ OA là đường trung trực của BC
Mà OA cắt B C tại H Nên BH ^ OA
Xét tam giác OBA vuông tại B có B H là đường cao 2
OB = OH .OA (tỷ số lượng giác )
Xét tam giác OBI vuông tại B có B K là đường cao: 2
OB = OK .OI (tỉ số lượng giác) Þ 2
OK .OI = OH .OA (= OB ) Þ OH OI = OK OA
b) Đường tròn tâm I đường kính A B cắt A C tại E . Gọi F là giao điểm của BE và A O .
Chứng minh F đối xứng với O quaH .
Ta có OF ^ BC tại H ( F Î OA )( ) 1 Mặt khác: Xét H V BF và DHCO · ·
BHF = OHC (đối đỉnh)
HB = HC ( H là trung điểm B C ) · ·
HBF = HCO (so le trong) Þ H
V BF = DHCO (g-c-g)
Þ HF = HO (2 cạnh tương ứng) (2) Từ ( )
1 và (2) Þ F đối xứng với O qua H (đpcm)
c) Chứng minh đường tròn ngoại tiếp DA FB đi qua điểm K xét O
V HK và DOIA : µ O : góc chung OH OI = (cmt) OK OA Trang 9
Þ DOHK ∽DOIA (g-g) Þ · ·
OK H = OA I ( 2 góc tương ứng)
Þ tứ giác HKIA nội tiếp (góc ngoài bằng góc đối trong) · · ·
Þ IKA = IHA = IA H ( DIHA cân tại I ) · ·
Mà IA H = B CO ( A BOC nội tiếp) · ·
Þ IKA = BCO ( ) 3
Xét D OHC vuông tại H : · 0 · ·
HOC = 180 - (BCO + OHC ) 0 · = 180 - ( 0 B CO + 90 ) · 0 ·
Mà HOC = 180 - OFE (2 góc trong cùng phía) · · 0
Þ OFE = BCO + 90 · ·
Mà OFE = BFA ( đối đỉnh) · · 0
Þ BFA = BCO + 90 (4) Từ ( ) 3 và (4) Þ · · 0 BFA = IKA + 90 · 0 · · ·
Mà IKA + 90 = IKA + BKI = BKA · · Þ BFA = BKA Þ BKFA nội tiếp
Vậy đường tròn ngoại tiếp DA FB đi qua điểm F (đpcm) ----HẾT---
SỞ GD&ĐT TP. HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT HUYỆN CẦN GIỜ
NĂM HỌC: 2023 - 2024 ĐỀ THAM KHẢO MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận.
Mã đề: Huyện Cần Giờ - 02
Thời gian: 120 phút (không kể thời gian phát đề) x x
Câu 1. (1,5 điểm). Cho Parabol P 2 : y
và đường thẳng D : y 2 . 4 2
a) Vẽ P và D trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép toán. Trang 10
Câu 2. (1,0 điểm). Cho phương trình 2
x 6x 1 0 . Không giải phương trình, hãy tính giá trị của 2 2
3x 5x x 3x biểu thức 1 1 2 2 A . 2 2 4x x 4x x 1 2 1 2
Câu 3. (1,0 điểm). Một nhà máy xay xát lúa đã nhập kho 35 tấn lúa ST25 để xay xát thành gạo
ST25 (loại gạo được vinh danh là gạo ngon nhất thế giới năm 2019 ). Mỗi ngày nhà máy xay
xát được 25 tạ lúa. Gọi y (tạ) là số lúa còn lại trong kho sau x (ngày) xay xát.
a) Hãy lập biểu thức biểu diễn y theo x .
b) Sau khi xay được 2 ngày nhà máy tăng năng suất xay xát lên 30 tạ 1ngày, hỏi nhà máy
đã xay hết 35 tấn lúa trên trong bao lâu.
Câu 4. (0,75 điểm). Còn một tuần nữa sẽ đến ngày 20 / 11, các bạn học sinh lớp 9A đăng kí thi đua
hoa điểm mười với mong muốn đạt thật nhiều điểm mười để tặng thầy cô giáo. Đến ngày
19 / 11 , lớp trưởng tổng kết số điểm mười của các bạn trong lớp và được như sau:
Không có bạn nào trong lớp không có điểm mười trong tuần vừa qua.
Có 20 bạn có ít nhất là 2 điểm mười.
Có 10 bạn có ít nhất là 3 điểm mười.
Có 5 bạn có ít nhất là 4 điểm mười.
Không có ai có nhiều hơn 4 điểm mười.
Hỏi cả lớp 9A đạt được bao nhiêu điểm mười trong lần thi đua? Câu 5.
(1,0 điểm) Trái bóng Telstar xuất hiện lần đầu tiên ở
World Cup 1970 ở Mexico do Adidas sản xuất có đường
kính 22,3cm . Trái bóng được may từ 32 múi da đen và
trắng. Các múi da màu đen hình ngũ giác đều, các múi da
màu trắng hình lục giác đều. Trên bề mặt trái bóng, mỗi múi da màu đen có diện tích 2
37cm . Mỗi múi da màu trắng có diện tích 2
55,9cm . Hãy tính trên trái bóng có bao nhiêu múi
da màu đen và màu trắng?
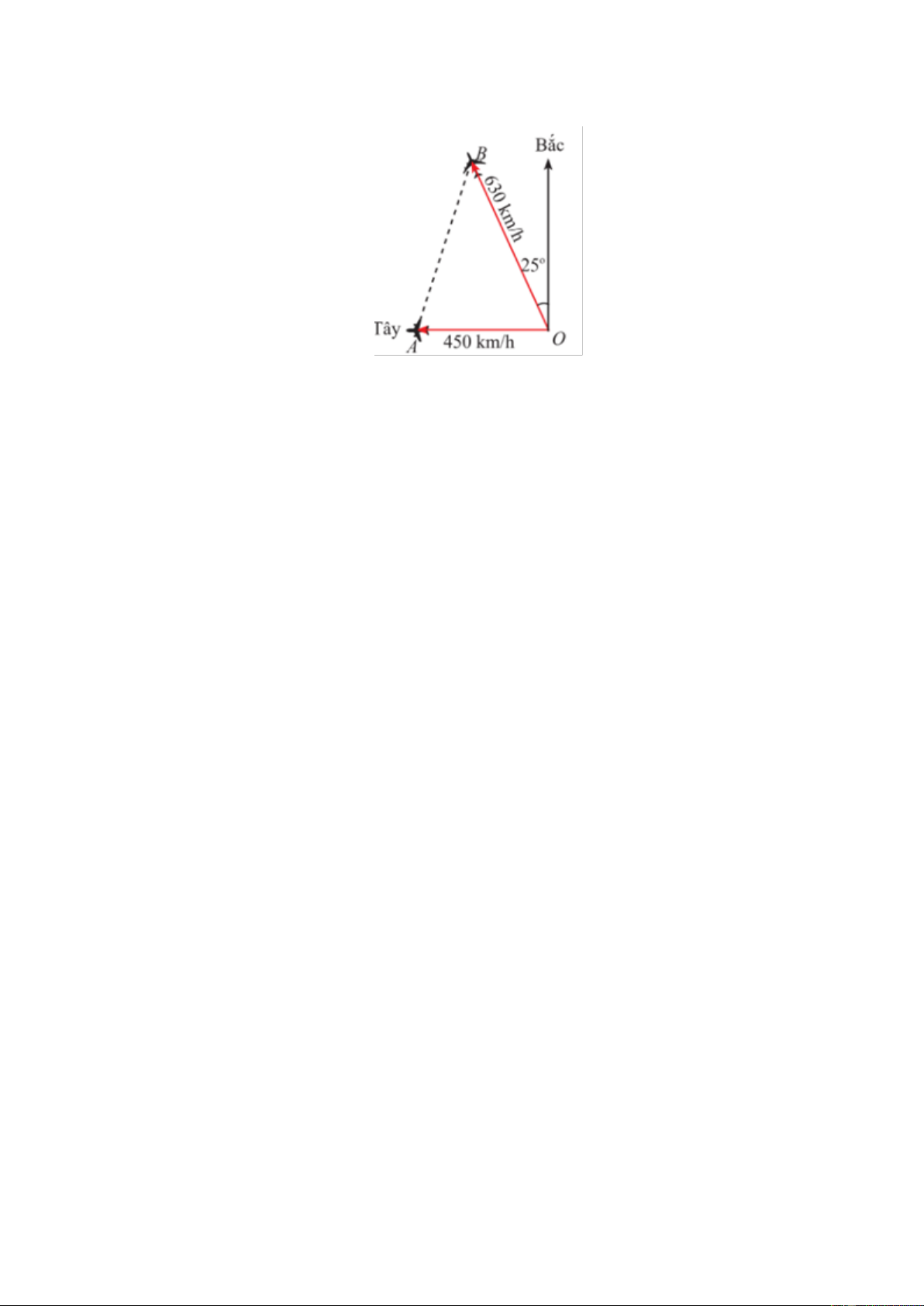
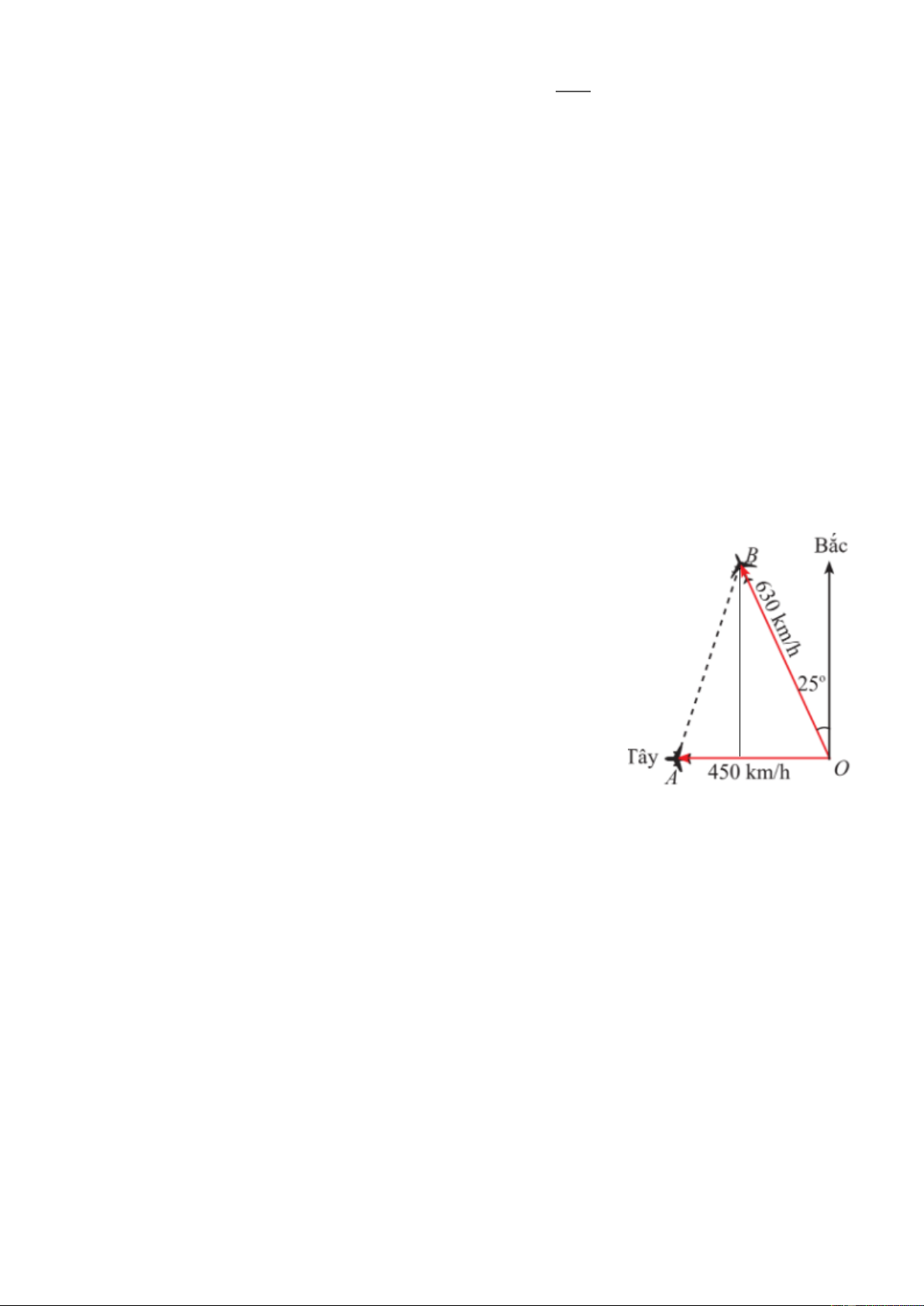
Câu 6. (1,0 điểm) Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau.
Một chiếc di chuyển với tốc độ 450km / h theo hướng tây và chiếc còn lại di chuyển theo
hướng lệch so với hướng bắc 25 về phía tây với tốc độ 630km / h (Hình vẽ). Sau 90 phút, Trang 11
hai máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ cao. (Kết quả làm
tròn đến hàng đơn vị) Câu 7.
(0,75 điểm) Vào tháng 5 năm 2021 , chỉ sau 26 giờ phát hành sản phẩm âm nhạc MV
“Trốn tìm” của rapper Đen Vâu đã chính thức dành Top 1 trending của YouTube Việt Nam.
Giả sử trong tất cả những người đã xem MV, có 60% số người đã xem 2 lượt và những
người còn lại mới chỉ xem 1 lượt. Hỏi đến thời điểm nói trên có bao nhiêu người đã xem MV,
biết rằng tổng số lượt xem là 6,4 triệu lượt?
Câu 8. (3,0 điểm) Cho tứ giác ABCD AD BC nội tiếp đường tròn (O) đường kính AB . Hai
đường chéo AC và BD cắt nhau tại E . Gọi H là hình chiếu của E trên AB .
a) Chứng minh ADEH là tứ giác nội tiếp.
b) Tia CH cắt đường tròn (O) tại điểm thứ hai là K . Gọi I là giao điểm của DK và AB . Chứng minh 2
DI AI.BI .
c) Khi tam giác DAB không cân, gọi M là trung điểm của EB , tia DC cắt tia HM tại N . Tia NB
cắt đường tròn ngoại tiếp tam giác HMB tại điểm thứ hai là F . Chứng minh F thuộc đường tròn (O) . ----HẾT--- Trang 12 HƯỚNG DẪN GIẢI 2 x x
Câu 1. (1,5 điểm) Cho Parabol P : y
và đường thẳng D : y 2 . 4 2
a) Vẽ P và D trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải
a) Vẽ P và D trên cùng mặt phẳng tọa độ. a) BGT: x 4 2 0 2 4 2 x y 4 1 0 1 4 4 x 4 2 x y 2 4 1 2
b) Tìm tọa độ giao điểm của P và D bằng phép toán.
Phương trình hoành độ giao điểm của P và D : 2 x x 2 4 2 2
x 2x 8 0 x 2 x 4 2 2 x 2
Thay x 2 vào y , ta được: y 1. 4 4 2 2 x 4 Thay x 4 vào y , ta được: y 4 . 4 4
Vậy 2; 1 , 4; 4 là hai giao điểm cần tìm.
Câu 2. (1,0 điểm) Cho phương trình 2
x 6x 1 0 . Không giải phương trình, hãy tính giá trị của 2 3x 5x x 2 3x biểu thức A 1 1 2 2 . 2 4x x 2 4x x 1 2 1 2 Lời giải
Vì b ac 2 2 4 6 4.1.1 32 0 Trang 13
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b S x x 6 1 2
Theo định lí Vi-et, ta có: a c P x .x 1 1 2 a Ta có: 2 3x 5x x 2 A 3x 1 1 2 2 2 4x x 2 4x x 3 1 2 1 2 2 x 2 x 5x x 1 2 A 1 2 4x x x x 1 2 1 2 3 x x 2x x 5x x 1 2 2 1 2 A 1 2 4x x x x 1 2 1 2 3x x 6x x 5x x 1 2 2 A 1 2 1 2 4x x x x 1 2 1 2 3x x x x 1 2 2 A 1 2 4x x x x 1 2 1 2 2 3.6 A 1 109 4.1.6 24 Câu 3.
(1,0 điểm). Một nhà máy xay xát lúa đã
nhập kho 35 tấn lúa ST25 để xay xát thành
gạo ST25 (loại gạo được vinh danh là gạo
ngon nhất thế giới năm 2019).
Mỗi ngày nhà máy xay xát được 25 tạ lúa. Gọi y
(tạ) là số lúa còn lại trong kho sau x (ngày) xay xát.
a) Hãy lập biểu thức biểu diễn y theo x.
b) Sau khi xay được 2 ngày nhà máy tăng năng suất xay xát lên 30 tạ 1 ngày, hỏi nhà máy
đã xay hết 35 tấn lúa trên trong bao lâu. Lời giải: 35 tấn = 350 tạ
a) Biểu thức: y = 350 – 25.x .
b) Số lúa còn lại trong kho sau 2 ngày xay xát:
y = 350 - 25.2 = 300 (tạ)
Do năng suất xay xát tăng lên 30 tạ / 1 ngày nên: Trang 14
Gọi y (tạ) là số lúa còn lại trong kho sau x (ngày) xay xát. Ta có: y = 300 – 30.x 1 1 1 1
Do xay hết lúa nên y = 0 nên: 0 = 300 – 30.x Þ x = 10 . 1 1 1
Vậy nhà máy đã xay xong 35 tấn lúa ST25 trên trong 12 ngày.
Câu 4. (0,75 điểm). Còn một tuần nữa sẽ đến ngày 20/11, các bạn học sinh lớp 9A đăng kí thi đua
hoa điểm mười với mong muốn đạt thật nhiều điểm mười để tặng thầy cô giáo. Đến ngày
19/11, lớp trưởng tổng kết số điểm mười của các bạn trong lớp và được như sau:
Không có bạn nào trong lớp không có điểm mười trong tuần vừa qua.
Có 20 bạn có ít nhất là 2 điểm mười.
Có 10 bạn có ít nhất là 3 điểm mười.
Có 5 bạn có ít nhất là 4 điểm mười.
Không có ai có nhiều hơn 4 điểm mười.
Hỏi cả lớp 9A đạt được bao nhiêu điểm mười trong lần thi đua? Lời giải
Vì lớp 9 A không có bạn nào không có điểm mười và có 20 bạn có từ 2 điểm mười trở lên nên số
học sinh chỉ có 1 điểm mười là
35 20 15 (học sinh.)
Vì có 10 bạn có ít nhất 3 điểm mười nên số học sinh chỉ có 2 điểm mười là
20 10 10 (học sinh)
Vì có 5 bạn có ít nhất 4 điểm mười nên số học sinh chỉ có 3 điểm mười là 10 5 5 (học sinh)
Vì không có học sinh nào có nhiều hơn 4 điểm 10 nên số học sinh đạt 4 điểm mười là 5 học sinh.
Vậy số điểm mười mà tuần vừa qua các bạn lớp 9 A đạt được là
15.1+ 10.2 + 5.3 + 5.4 = 70 (điểm mười)
Câu 5. (1,0 điểm) Trái bóng Telstar xuất hiện lần đầu tiên ở
World Cup 1970 ở Mexico do Adidas sản xuất có
đường kính 22,3cm. Trái bóng được may từ 32 múi da
đen và trắng. Các múi da màu đen hình ngũ giác đều,
các múi da màu trắng hình lục giác đều. Trên bề mặt
trái bóng, mỗi múi da màu đen có diện tích 37cm2. Mỗi
múi da màu trắng có diện tích 55,9cm2. Hãy tính trên
trái bóng có bao nhiêu múi da màu đen và màu trắng? Lời giải: Trang 15 22, 3
Trước tiên ta tính diện tích bề mặt trái bóng: 2
S 4 r với r 11,15 2 cm 2 Vậy S 2 1562, 28 cm
Gọi x, y (x,y Î ¥ )
* lần lượt là số múi da đen và trắng trên trái bóng Telstlar .
Khi đó vì 32 múi da đen và trắng phủ kín bề mặt trái bóng nên ta có biểu thức :
37x + 55, 9y = 1562, 28 ( ) 1
Lại có số múi da đen và trắng tổng cộng là 32 nên ta có : x + y = 32 (2) Từ ( )
1 và (2) ta có hệ phương trình: x y 32 x 12n .
37x 55,9y 1562,28 y 20n
Vậy có tất cả 12 múi da đen và 20 múi da trắng. Câu 6.
(1,0 điểm) Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo
hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo
hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng
bắc 250 về phía tây với tốc độ 630 km/h (Hình vẽ). Sau 90 phút, hai
máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ
cao.(Kết quả làm tròn đến hàng đơn vị) Giải H ·
Ta có: BOC = 90° - 25° = 65°. Sau 90 phút 1,5 giờ:
Máy bay thứ nhất đi được quãng đường OA là: 450.1, 5 = 675(km )
Máy bay thứ hai đi được quãng đường OB là: 630.1, 5 = 945(km ) Kẻ BH OA O
BH vuông tại H có OH = O .
B cos65° = 945.cos65° và BH O . B sin6 5 945.sin6 5
AH OA – OH 675 – 945. o c s6 5
ABH vuông tại H , theo định lí Pytago 2 = 2 + 2 A B A H BH Trang 16 AB 2 2 945.sin 65 675 945.cos 65 900km
Câu 7. (0,75 điểm) Vào tháng 5 năm 2021, chỉ sau 26 giờ phát hành sản phẩm âm nhạc MV “Trốn
tìm” của rapper Đen Vâu đã chính thức dành Top 1 trending của YouTube Việt Nam. Giả sử
trong tất cả những người đã xem MV, có 60% số người đã xem 2 lượt và những người còn lại
mới chỉ xem 1 lượt. Hỏi đến thời điểm nói trên có bao nhiêu người đã xem MV, biết rằng
tổng số lượt xem là 6,4 triệu lượt? Lời giải:
Gọi x là số người đã xem MV (triệu người) (x Î ¥ ) *
Khi đó số người đã xem 2 lượt là 60%x (người) và số người chỉ xem 1 lượt là 40%x (người).
Vì tổng số lượt xem là 6,4 triệu nên ta có phương trình:
60%x.2 + 40%x.1 = 6, 4 Û 1, 6x = 6, 4 x 4 (Nhận)
Vậy có 4 triệu người xem MV.
Câu 9. (3,0 điểm) Cho tứ giác A BCD (AD > BC )nội tiếp đường tròn (O) đường kính A B . Hai
đường chéo A C và B D cắt nhau tại E . Gọi H là hình chiếu của E trên A B .
a) Chứng minh A DEH là tứ giác nội tiếp.
b) Tia CH cắt đường tròn (O ) tại điểm thứ hai là K . Gọi I là giao điểm của DK và A B . Chứng minh 2 DI = A I .BI .
c) Khi tam giác DA B không cân, gọi M là trung điểm của EB , tia DC cắt tia HM tại N . Tia NB
cắt đường tròn ngoại tiếp tam giác HMB tại điểm thứ hai là F . Chứng minh F thuộc đường tròn (O ) . Lời giải D C E N M I O A B H F K Trang 17
a) Chứng minh ADEH là tứ giác nội tiếp. Ta có: ADB
90 (góc nội tiếp chắn nửa đường tròn)
EH AB AHE 90
Tứ giác ADEH có: ADB AHE 9 0 9 0 18 0
nên là tứ giác ADEH nội tiếp (đpcm)
a) Tia CH cắt đường tròn O tại điểm thứ hai là K . Gọi I là giao điểm của DK và AB . Chứng minh 2
DI AI.BI
Ta có: ADK ACK (hai góc nội tiếp cùng chắn cung A K ) 1
Xét tứ giác ECBH có: ECB ACB
90 (góc nội tiếp chắn nửa đường tròn) EHB
90 (do EH ^ A B )
ECB EHB 9 0 9 0 18 0
Do đó tứ giác ECBH nội tiếp (tứ giác có hai góc đối có tổng số đo bằng 180
ECH EBH (hai góc nội tiếp cùng chắn cung EH )
ACK DBA 2 Từ
1 và 2 suy ra ADK DBA ADI DBA
Lại có DBA DAB
90 nên ADI DAB
90 hay ADI DAI 90 DIA 18
0 ADI DAI 18 0 9 0 9 0
Þ DI ^ AB nên DI là đường cao trong tam giác vuông A DB . Vậy 2
DI = IA.IB (hệ thức giữa cạnh và đường cao trong tam giác vuông) (đpcm).
c) Khi tam giác DAB không cân, gọi M là trung điểm của EB , tia DC cắt tia HM tại N . Tia NB
cắt đường tròn ngoại tiếp tam giác HMB tại điểm thứ hai là F . Chứng minh F thuộc đường tròn
O .
Theo câu b, DK ^ BA tại I nên A B là đường trung trực của DK
Þ DA = AK Þ sđ AD = sđ AK
DCA ACK CA là tia phân giác của DCH
DCH 2.ECH 3
Tam giác EHB vuông tại H có M là trung điểm EB nên HM là đường trung tuyến Trang 18
Þ MH = MB Þ DMHB cân tại M .
⇒ DMH MHB MBH 2.MBH 2.EBH 4
Tứ giác ECBH có: ECB EHB 9 0 9 0 18 0
nên là tứ giác ECBH nội tiếp (tứ giác có tổng hai góc đối bằng 180 )
⇒ ECH EBH 5
Từ 3 4 và 5 suy ra DCH DMH .
Þ DCMH là tứ giác nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh đối diện các góc bằng nhau)
⇒ NCM NHD (góc ngoài bằng góc đối trong)
Xét DNCM và DNHD có: µ N chung
NCM NHD (chưng minh trên)
Þ DNCM ∽DNHD (g - g) NC NM (tỉ số đồng dạng) NH ND
Þ NC.ND = NM.NH 6
Tứ giác HMBF nội tiếp nên NMB NFH (góc ngoài bằng góc đối trong)
Xét D NMB và DNFH có: µ N chung
NMB NFH (chứng minh trên)
Þ DNMB ∽DNFH (g - g) NM NB ⇒ (tỉ số đồng dạng) NF NH
Þ NM .NH = NB.NF (7) NC NB
Từ 6 và 7 suy ra NC .ND = NF.NB NF ND
Xét DNBC và DNDF có: µ N chung
NC NB (chứng minh trên) NF ND
Þ DNBC ∽DNDF (c - g - c) Trang 19
⇒ NCB NFD BFD (góc tương ứng)
Mà NCB DCB 180 (kề bù)
Nên BFD DCB 0 180
Do đó tứ giác DCBF nội tiếp (tứ giác có tổng hai góc đối bằng 180 )
Vậy điểm F nằm trên đường tròn (O ) (đpcm). ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT HUYỆN CẦN GIỜ
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: SỐ 3
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). 1
a) Vẽ đồ thị hàm số P 2 : y
x và đường thẳng d 1 : y x 1 2 2
b) Tìm tọa độ giao điểm của P và D bằng phép toán.
Câu 2. (1 điểm). Cho phương trình: 2
2x 7x 6 0 có hai nghiệm là x ,x Không giải phương 1 2
trình trên, hãy tính giá trị của biểu thức: B 3x 2x 3x 2x . 1 2 2 1
Câu 3. (1 điểm). Một nhóm nhà sinh vật học thực hiện nghiên cứu, nhân giống một loại cây trong
nhà kính. Người ta đếm được hiện tại có khoảng 3000 gốc cây đang trong quá trình chăm
sóc. Số lượng gốc cây N được dự tính sẽ tăng qua mỗi năm theo công thức n
N n 0,2n 1 . K Trong đó
n là số lượng gốc cây tại thời điểm tính toán; N là số lượng gốc cây trong năm tiếp theo.
K là hệ số tiêu chuẩn của nhà kính: số lượng cây tối đa mà nhà kính có thể hỗ trợ để phát triển tốt nhất.
a) Tìm số lượng gốc cây sau 1 năm, nếu biết K 4000 .
b) Nếu nhà sinh vật học muốn số lượng gốc cây tăng lên từ 3000 của năm này đến 3360
của năm sau, thì nhóm nghiên cứu này phải điều chỉnh hệ số tiêu chuẩn của nhà kính là bao nhiêu?
Câu 4. (1 điểm). Qua nghiên cứu người ta nhận thấy rằng với mỗi người, trung bình nhiệt độ môi
trường giảm đi 1 C
thì lượng calo cần tăng thêm khoảng 30 calo. Tại 21 C một người làm
việc cần sử dụng khoảng 3000 calo mỗi ngày. Biết rằng mối liên hệ giữa calo y (calo) và
nhiệt độ x C
là một hàm số bậc nhất có dạng y ax b .
a) Xác định các hệ số a và b . Trang 20
b) Nếu một người thợ làm việc trong một xưởng nung thép phải tốn 2400 calo trong một
ngày. Hãy cho biết người thợ đó làm việc ở môi trường có nhiệt độ là bao nhiêu độ C ?
Câu 5. (1 điểm). Bạn Cường con của Bác Năm vừa tốt nghiệp trung học cơ sở, bạn Cường đã quyết
định qua trường nghề học nghề quản trị mạng. Để chuẩn bị cho việc học tập của con mình,
Bác Năm dự tính mua cho Cường một máy tính. Khi đến một công ty máy tính Bác Năm đã
tham khảo giá bán trả góp như sau: Kỳ hạn 6 tháng 12 tháng 18 tháng Lãi suất mỗi tháng 0.6% 0.8% 1%
Ghi chú: - Thanh toán trước 30% giá máy
Lãi suất tính trên nợ gốc ban đầu ( giá bán )
Tiền góp chia đều cho mỗi tháng
Hỏi nếu Bác Năm mua máy tính có giá là 12 000 000 đồng và chọn kỳ hạn là
12 tháng thì mỗi tháng Bác Năm phải góp bao nhiêu tiền?
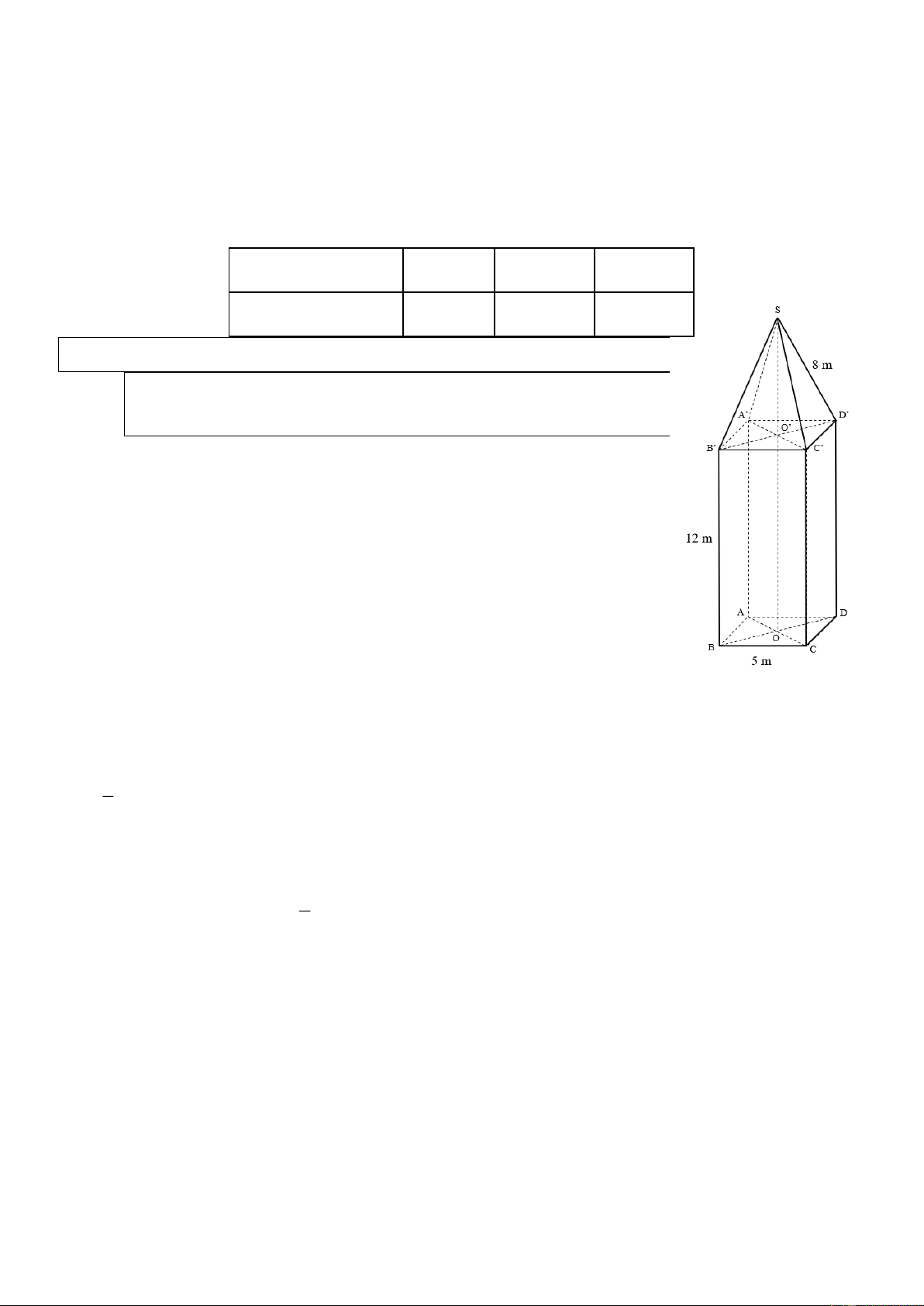
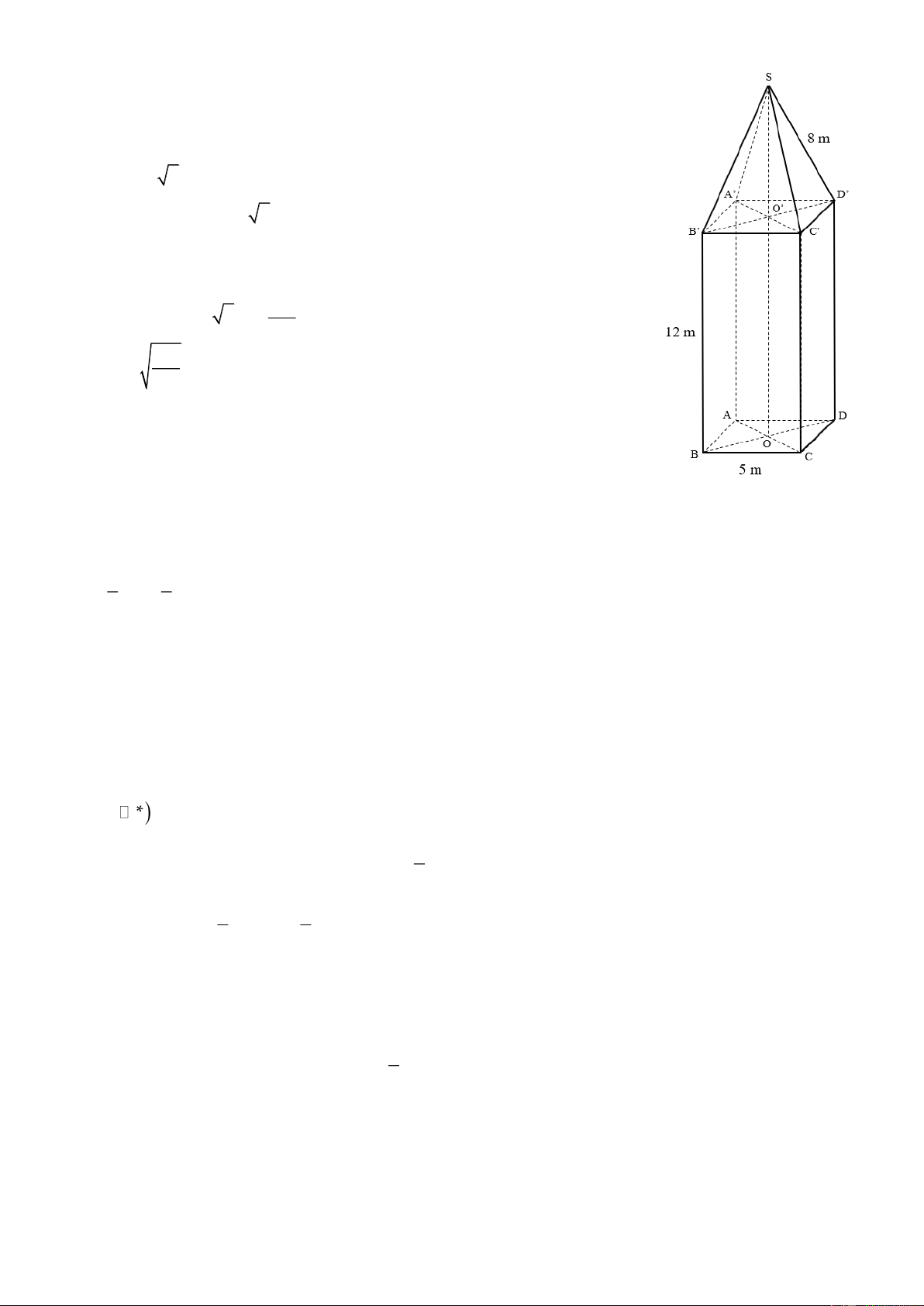
Câu 6. (1 điểm). Một tháp đồng hồ có phần dưới có dạng hình hộp chữ
nhật, đáy là hình vuông có cạnh dài 5 m , chiều cao của hình hộp
chữ nhật là 12 m . Phần trên của tháp có dạng hình chóp đều, các
mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của hình chóp dài 8 m .
a) Tính theo mét chiều cao của tháp đồng hồ? (làm tròn đến chữ số thập phân thứ nhất)
b) Cho biết thể tích của hình hộp chữ nhật được tính theo công thức V .
S h , trong đó S là diện tích
mặt đáy, h là chiều cao của hình hộp chữ nhật. Thể tích của hình chóp được tính theo công thức 1 V .
S h , trong đó S là diện tích mặt đáy, h là chiều cao của hình chóp. Tính thể tích của tháp 3
đồng hồ này? (Làm tròn đến hàng đơn vị).
Câu 7. (1 điểm). Trong kì thi tuyển sinh vào lớp 10 năm học 2021 2022 , số thí sinh vào trường 2 THPT chuyên bằng
số thí sinh thi vào trường PTDT Nội trú. Biết rằng tổng số phòng 3
thi của cả hai trường là 80 phòng thi và mỗi phòng thi có đúng 24 thí sinh. Hỏi số thí sinh
vào mỗi trường bằng bao nhiêu?
Câu 8. (3 điểm) Cho O và điểm A nằm ngoài đường tròn.Vẽ các tiếp tuyến A ; B AC và cát tuyến
ADEBD DC . Gọi I là trung điểm DE .
a) Chứng minh: A,B,I,O,C cùng nằm trên một đường tròn.
b) Tia CI cắt đường tròn O tại K . Chứng minh: BK // AE
c) Gọi H là giao điểm của OA và BC . Chứng minh: O
EH đồng dạng O AE. Từ đó suy
ra HB là phân giác của EHD . Trang 21 ----HẾT--- Trang 22 HƯỚNG DẪN GIẢI
Câu 8. (1,5 điểm) Lời giải 1
a) Vẽ đồ thị hàm số P 2 : y
x và đường thẳng d 1 : y x 1 2 2 1 Hàm số: 2
y x 2 Bảng giá trị x 4 2 0 2 4 1 2 y x 8 2 0 2 8 2 1 Hàm số: y x 1 2 Bảng giá trị x 2 0 y 3x 4 2 1 Vẽ:
b) Hoành độ giao điểm của P và d là nghiệm của phương trình: Trang 23 1 2 1 x x 1 2
x x 2 0 2 2
Vì 9 0 Phương trình có hai nghiệm phân biệt: x 1; x 2 . 1 2 1 1 1 Thay x 1 vào 2
y x , ta được: 2 y .1 . 2 2 2 1 1 Thay x 2 vào 2
y x , ta được: y . 2 2 2 . 2 2 1
Vậy d cắt P tại hai điểm phân biệt là 1; và 2 ; 2. 2
Câu 9. (1 điểm) Lời giải Vì 2 2
b 4ac 7 4.2.6 1 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 7
S x x 1 2
Theo định lí Vi - ét ta có: 2 . 6
P x .x 3 1 2 2 Ta có :
B 3x 2x 3x 2x 1 2 2 1 2 2
B 9x x 6x 6x 4x x 1 2 1 2 1 2 2 2
B 13x x 6 x x 1 2 1 2
B 13P 2 6 S 2P 2 7 B 1 . 3 3 6 2.3 2 153 B . 2
Câu 10. (1 điểm) Lời giải
a) Số lượng gốc cây sau 1 năm, nếu biết K 4000 là : 3000
N 3000 0,2.3000. 1 3150 (cây) 4000 Trang 24
b) Số lượng gốc cây tăng lên từ 3000 của năm này đến 3360 của năm sau thì hệ số tiêu
chuẩn của nhà kính là : 3000
3360 3000 0,2.3000. 1 K K 7500 .
Câu 11. (0,75 điểm) Lời giải
a) Xác định các hệ số a và b . Tại 21 C
một người làm việc cần sử dụng khoảng 3000 calo mỗi ngày nên ta có phương trình :
21.a b 3000 1
Trung bình nhiệt độ môi trường giảm đi 1 C
thì lượng calo cần tăng thêm khoảng 30 calo nên khi
nhiệt độ môi trường là 20 C
thì lượng tiêu thụ calo khoảng 3030 ta có phương trình :
20a b 3030 2
21.a b 3000 a 30 Từ
1 ,2 ta có hệ phương trình : . 20a b 3030 b 3630
Vậy số hệ số a là 30 và hệ số b là 3630 .
b) Một người thợ làm việc trong một xưởng nung thép phải tốn 2400 calo trong một ngày thì môi
trường có nhiệt độ là : 2400 3
0x 3630 x 41 C .
Vậy người thợ làm việc trong một xưởng nung thép phải tốn 2400 calo trong một ngày thì môi
trường có nhiệt độ là 41 C .
Câu 12. (1 điểm) Lời giải
Số tiền Bác Năm cần góp là :
12000000.(1 30%) 8400000 (đồng)
Số tiền góp Bác Năm cần phải trả là :
8400000.(1 0,8%.12) 9206400 ( đồng)
Số tiền góp Bác Năm cần phải trả trong 1 tháng là :
9 206 400 : 12 767 200 (đồng)
Câu 13. (1 điểm) Lời giải Trang 25
a) Ta có: A
'B'C' vuông tại A 2 2 2
B'D' A'B' A'D' (ĐL Pytago) 2 2 2
B'D' 5 5 50
B'D' 5 2 m
O'D' B'D' : 2 2,5 2 cm . Ta có: S
O'D' vuông tại O : 2 2 2
SO' S'D' D'O' (ĐL Pytago) SO 2 2 2 103 ' 8 2,5 2 2 103 SO' 7,18m. 2
Tổng chiều cao của tháp đồng hồ:
SO SO' OO' 12 7,18 19,18m .
b) Thể tích phần tháp hình hộp chữ nhật: 2 V .
S h 5 .12 300 3 m 1
Thể tích phần ngọn tháp hình chóp: 1 1 2 V .
S h .5 .7,18 59,83 3 m . 2 3 3
Thể tích của tháp đồng hồ: V V V 300 59,83 359,83 3 m . 1 2
Câu 14. (1 điểm) Lời giải
Gọi x,y ( thí sinh ) lần lượt là số thí sinh vào trường THPT chuyên và trường PTDT nội trú x,y * 2
Số thí sinh vào trường THPT chuyên bằng số thí sinh thi vào trường PTDT Nội trú nên ta có 3 2 2 phương trình : x
y x y 0 1 . 3 3
Tổng số phòng thi của cả hai trường là 80 phòng thi và mỗi phòng thi có đúng 24 thí sinh nên ta có
phương trình : x y 80.24 2 2 x y x 768
Từ 1 và 2 , ta có hệ phương trình: 3 ( nhận ) y 1152 x y 80.24
Vậy số thí sinh vào trường THPT chuyên là 768 (thí sinh).
số thí sinh vào trường PTDT nội trú là 1152 (thí sinh). Trang 26
Câu 15. (3 điểm) Lời giải
a) Chứng minh: A,B,I,O,C cùng nằm trên một đường tròn.
Xét tứ giác ABOC ta có :
ABO 90 ( AB là tiếp tuyến đường tròn O )
ACO 90 ( AC là tiếp tuyến đường tròn O )
ABO ACO 180
ABOC nội tiếp 1 Ta có :
OI là một phần đường kính đường tròn O
DE là dây cung đường tròn O
I là trung điểm DE
OI DE ( quan hệ đường kính dây cung )
Xét tứ giác ABIO ta có :
ABO 90 ( AB là tiếp tuyến đường tròn O )
AIO 90 ( OI DE )
ABO AIO 90
ABOI nội tiếp 2 Từ
1 ,2 A,B,I,O,C cùng nằm trên một đường tròn
b) Tia CI cắt đường tròn O tại K . Chứng minh: BK // AE Trang 27
Ta có : A,B,I,O,C cùng nằm trên một đường tròn cmt ABICnội tiếp
ABC AIC
Mà ABC BKC (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung)
AIC BKC
Mà 2 góc ở vị trí đồng vị AE / /BK
c) Gọi H là giao điểm của OA và BC . Chứng minh: O
EH đồng dạng O
AE. Từ đó suy ra HB là phân giác của EHD Ta có :
AB AC ( AB, AC là tiếp tuyến của đường tròn O )
OB OC (cùng là bán kính đường tròn O )
AO là đường trung trực BC AO BC Ta có : A
BO vuông tại B , BH là đường cao : 2
OH.OA OB htl
Mà OB OE(cùng là bán kính đường tròn O ) 2
OE OH.OA Xét OHE và O EA ta có : 2 OE O . H OA (cmt) AOE là góc chung O HE ∽ O A E
c g c Ta có : A
BO vuông tại B , BH là đường cao : 2
AH.AO AB htl 3 Xét A BD và A EB ta có : BAE góc chung
ABD AEB (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung) A BD ∽ A
EBg g 2 A .
D AE AB 4
Từ 3,4 A . H AO A . D AE Trang 28 Xét A DH và A OE ta có :
AH.AO A . D AE cmt EAO là góc chung A DH A
OE c g c
AHD AEO ( cặp góc tương ứng )
Mà AEO EHO O HE ∽ O EA
AHD EHO Ta có :
AHD DHB 90 O
HE BHE 90
Mà AHD OHE cmt
DHB BHE
BH là phân giác của EHD . ----HẾT--- Trang 29




