




















Preview text:
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT HUYỆN HÓC MÔN
NĂM HỌC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đề thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Huyện Hóc Môn - 1
Thời gian: 120 phút (không kể thời gian phát đề)
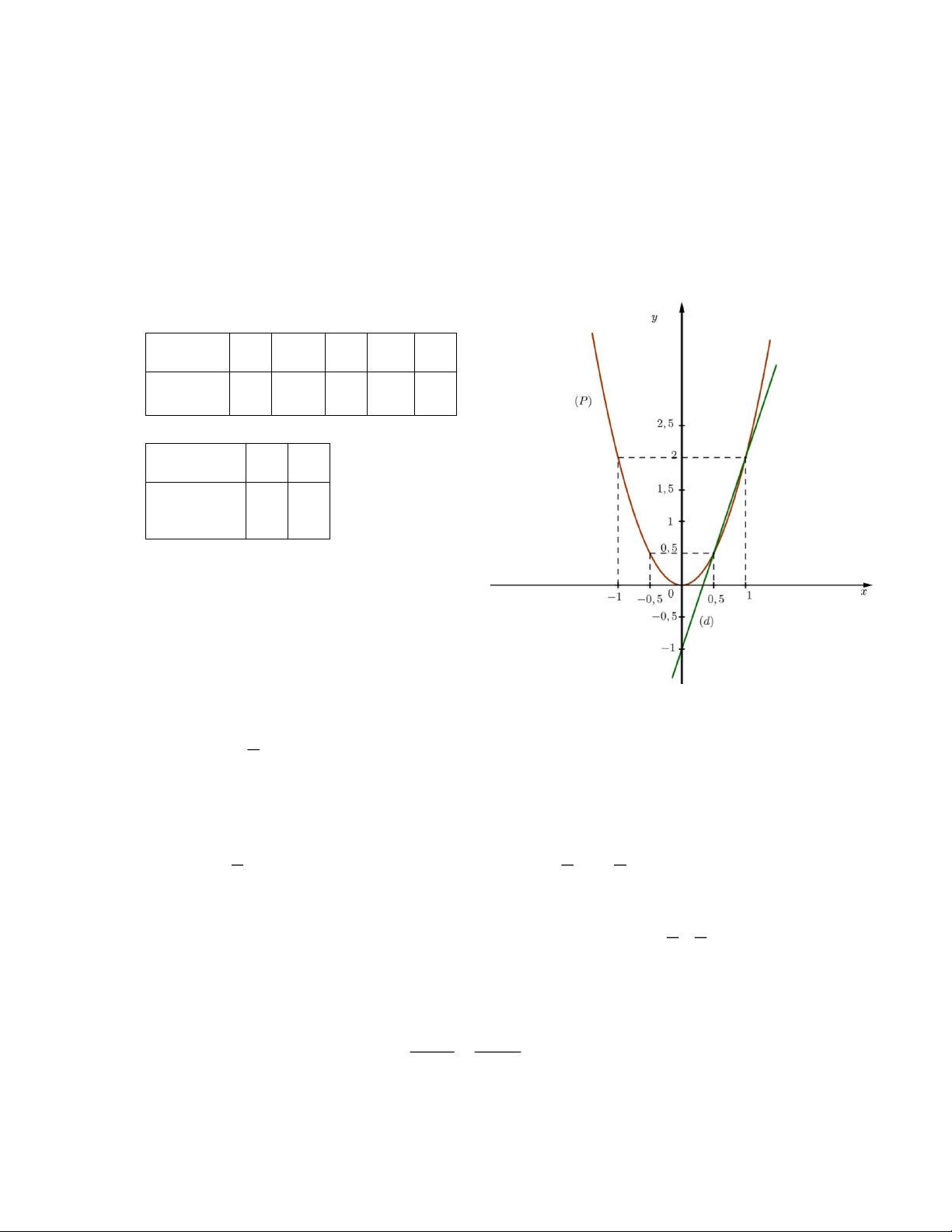
Câu 1. (1,5 điểm): Cho parabol P 2
: y 2x và đường thẳng d : y 3x 1
a) Vẽ P và d trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1,0 điểm): Cho phương trình 2
x 3x 5 0 có 2 nghiệm x ,x . Không giải phương trình, hãy 1 2 x x
tính giá trị của biểu thức 2 1 A x 1 x . 1 1 2
Câu 3. (1,0 điểm): Để tính nhẩm bình phương của một số tận cùng bằng 5 , bạn An thiết lập 1 công thức
bằng cách tính như sau: 2
Tính a5 , trong đó a là số chục, An viết: 2 a5 10a 52 2 2 100a 2.10. .5 a 5 2
100a 100a 25
100aa 1 25 2
Công thức: a5 100aa 1 25 Không dùng máy tính a) Hãy tính: 2 35 và 2 95 .
b) Hãy cho biết số 42025 là bình phương của số nào? Giải thích?
Câu 4. (0,75 điểm): Chị Lan mua một thùng nước ngọt (gồm 24 lon) của đại lý phân phối với giá
192 000 đồng và bán lẻ mỗi lon với giá 10 000 đồng.
a) Hỏi khi bán hết thùng nước ngọt đó thì chị Lan được lãi bao nhiêu phần trăm so với giá gốc?
b) Trong đợi khuyến mãi, do đại lý phân phối giảm giá nên chị Lan cũng chỉ bán mỗi lon nước
ngọt với giá 9 500 đồng và thu được lãi suất như cũ. Hỏi trong đợt này, chị Lan đã mua một
thùng nước ngọt với giá bao nhiêu?
Câu 5. (1,0 điểm): Bình xăng của một chiếc xe máy chứa 5 lít xăng. Trung bình, cứ chạy được 50km thì
xe máy tiêu thụ 1 lít xăng. Gọi y (lít) là số lít xăng còn lại trong bình xăng sau khi xe máy đi được
quãng đường là x km .
a) Viết công thức tính y theo x . Trang 1
b) Một người đổ đầy bình xăng cho xe máy trên rồi bắt đầu đi từ huyện Hóc Môn đến quận 7
với quãng đường dài 60km . Hỏi, sau khi đến nơi thì số lít xăng trong bình còn lại là bao nhiêu?
Câu 6. (1,0 điểm): Một cốc nước hình trụ cao12 cm , đường kính 7cm , độ dày cốc là 2mm , độ dày đáy là
5mm đang chứa 80ml nước. Người ta bỏ các viên đá bi có hình lập phương cạnh 2cm cho vào
cốc sao cho mực nước sau cùng cách miệng cốc không quá 1cm . Hỏi có thể bỏ được bao nhiêu
viên đá như thế vào cốc?
Câu 7. (0,75 điểm): Hai bạn Bảo và Minh rủ nhau đi mua đồ tết. Bạn bảo có nhiều hơn bạn Minh 50000
đồng. Khi vào cửa hàng, Bảo đã mua một quần jean và một áo thun hết 245000 đồng, còn Minh 5
mua 2 áo sơ mi hết 225000 đồng, khi đó số tiền còn lại của Minh chỉ bằng số tiền còn lại của 7
Bảo. Hỏi lúc đầu, mỗi bạn có bao nhiêu tiền?
Câu 8. (3,0 điểm): Cho A
BC nhọn ( A
B AC ) nội tiếp đường tròn (O; R). Vẽ đường cao AH của A
BC và đường kính AD của O .
a) Chứng minh hệ thức: A . B AC A . H AD
b) Vẽ BE và CF lần lượt vuông góc với AD ( ,
E F thuộc AD ). Chứng minh rằng: HE AC và HF AB .
c) Gọi M là trung điểm BC . Chứng minh rằng M là tâm đường tròn ngoại tiếp E HF . ---HẾT--- Trang 2 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm): Cho parabol 2
(P) : y 2x và đường thẳng (d ) : y 3x 1
a) Vẽ (P) và (d ) trên cùng một hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép tính. Lời giải a) Bảng giá trị: x 1 0,5 0 0,5 1 2 y 2 x 2 0,5 0 0,5 2 x 0 1 1 y 3x 1 2
b) Phương trình hoành độ giao điểm giữa P và d : 2 2x 3x 1 2
2x 3x 1 0 x 1 1 1 x 2 2
* Với x 1, thay vào 2
y 2 x ta được: 2 y 2.1 2 1 1 2 1 1 1
* Với x , thay vào 2
y 2 x ta được: y 2. 2 2 2 2 2 1 1
Vậy tọa độ giao điểm giữa (P) và (d ) là 2 điểm (1; 2) và ; 2 2
Câu 2. (1,0 điểm): Cho phương trình 2
x 3x 5 0 có 2 nghiệm x , x . Không giải phương 1 2 x x
trình, hãy tính giá trị của biểu thức 2 1 A x 1 x 1 1 2 Lời giải Trang 3 Vì phương trình 2
x 3x 5 0 có 2 nghiệm x , x . 1 2
Theo hệ thức Vi-ét, ta có: b 3
S x x 3 1 2 a 1 c 5
P x .x 5 1 2 a 1 Theo đề bài, ta có: x x x . x
1 x . x 2 2 1
x x x x 2 1 2 2 1 1 2 2 1 1 A x 1 x 1
x 1 . x 1
x .x x x 1 1 2 1 2 1 2 1 2
x x x x x x 2 2 2
2x .x x x 1 2 1 2 1 2 1 2 1 2
x .x x x 1
x .x x x 1 1 2 1 2 1 2 1 2 Từ Vi-ét, ta có: 2 2
S 2P S 3 2. 5 3 A 22 P S 1 5 3 1 Vậy A 22 .
Câu 3. (1,0 điểm): Để tính nhẩm bình phương của một số tận cùng bằng 5, bạn An thiết lập 1
công thức bằng cách tính như sau: 2
Tính a5 , trong đó a là số chục, An viết: 2 a5 10a 52 2 2 100a 2.10. .5 a 5 2
100a 100a 25
100a a 1 25 2
Công thức: a5 100a a 1 25
Không dùng máy tính a) Hãy tính: 2 35 và 2 95 .
b) Hãy cho biết số 42025 là bình phương của số nào? Giải thích? Lời giải 2
a) Theo công thức, ta có: 35 100.3.3 1 25 1225 Trang 4 2
Theo công thức, ta có: 95 100.9.9 1 25 9025
b) Ta có: 42025 => a = 4202 Theo công thức, ta có:
42025 100a a 1 25
100a a 1 42025 25
100a a 1 42000 a a 1 420 2
a a 420 0 a 2 1 l 1 a 20 n 2
Vậy số 42025 là bình phương của số 205 .
Câu 4. (0,75 điểm): Chị Lan mua một thùng nước ngọt (gồm 24 lon) của đại lý phân phối với
giá 192 000 đồng và bán lẻ mỗi lon với giá 10 000 đồng.
a) Hỏi khi bán hết thùng nước ngọt đó thì chị Lan được lãi bao nhiêu phần trăm so với giá gốc?
b) Trong đợi khuyến mãi, do đại lý phân phối giảm giá nên chị Lan cũng chỉ bán mỗi
lon nước ngọt với giá 9 500 đồng và thu được lãi suất như cũ. Hỏi trong đợt này,
chị Lan đã mua một thùng nước ngọt với giá bao nhiêu? Lời giải
a) Số tiền chị Lan bán hết 24 lon nước ngọt theo giá bán lẻ là: 10000.24 240000 đồng
Số tiền chị đã lãi được: 240000 192000 48000 đồng 48000
Số phần trăm mà chị đã lãi sau khi bán hết 24 lon nước ngọt: .100% 25% 192000
b) Số tiền bán 24 lon nước ngọt với giá bán lẻ 9500 đồng là: 24.9500 228000 đồng
Giá của một thùng nước ngọt mà chị Lan đã mua là: 228000.1 25% 171000 đồng Trang 5
Câu 5. (1,0 điểm): Bình xăng của một chiếc xe máy chứa 5 lít xăng. Trung bình, cứ chạy được
50km thì xe máy tiêu thụ 1 lít xăng. Gọi y (lít) là số lít xăng còn lại trong bình xăng sau khi xe
máy đi được quãng đường là x (km).
a) Viết công thức tính y theo x .
b) Một người đổ đầy bình xăng cho xe máy trên rồi bắt đầu đi từ huyện Hóc Môn đến
quận 7 với quãng đường dài 60km . Hỏi, sau khi đến nơi thì số lít xăng trong bình còn lại là bao nhiêu? Lời giải
a) Công thức tính y (lít) là số lít xăng còn lại trong bình theo x km là quãng đường 1
xe đi được là: y 5 x 50
b) Vì quãng đường từ Hóc Môn đến quận 7 dài 60 km : 1
x 60 thay vào công thức: y 5 x , ta có: 50 1 y 5 .60 3,8 (lít) 50
Vậy khi đi từ Hóc Môn đến quận 7 , trong bình xe còn 3,8 lít xăng
Câu 6. (1,0 điểm): Một cốc nước hình trụ cao 12 cm , đường kính 7cm , độ dày cốc là 2mm, độ
dày đáy là 5mm đang chứa 80ml nước. Người ta bỏ các viên đá bi có hình lập phương cạnh
2cm cho vào cốc sao cho mực nước sau cùng cách miệng cốc không quá 1cm . Hỏi có thể bỏ
được bao nhiêu viên đá như thế vào cốc? Trang 6 Lời giải
Đổi 2mm 0,2cm ; 5mm 0,5cm . 7
Bán kính của ly thủy tinh phần chứa nước: 0,2 3,3cm . 2
Chiều cao của ly thủy tinh phần chứa nước: 12 0,5 11,5cm .
Thể tích thực tế nếu ly thủy tinh mực nước cách miệng ly 1cm là: 2 2
V R h 3 . . .3,3 . 11,5 1 114,345 cm
Thể tích của một viên đá hình lập phương là: 3 3 3
V a 2 8cm
Số viên bi tối đa có thể bỏ vào cốc để mực nước sau cùng không quá 1cm là: 114,345 80 n 34 viên bi 8
Câu 7. (0,75 điểm): Hai bạn Bảo và Minh rủ nhau đi mua đồ tết. Bạn bảo có nhiều hơn bạn
Minh 50000 đồng. Khi vào cửa hàng, Bảo đã mua một quần jean và một áo thun hết 245000 5
đồng, còn Minh mua 2 áo sơ mi hết 225000 đồng, khi đó số tiền còn lại của Minh chỉ bằng 7
số tiền còn lại của Bảo. Hỏi lúc đầu, mỗi bạn có bao nhiêu tiền? Lời giải
Gọi x, y (đồng) là số tiền lúc đầu của Bảo và Minh x,y *
* Vì bạn Bảo có nhiều tiền hơn bạn Minh là 50000 đồng nên ta có phương trình:
x y 50000 1
- Số tiền còn lại của Bảo khi đã mua 1 quần jean và 1 áo thun là: x 245000 (đồng)
- Số tiền còn lại của Minh khi đã mua 2 áo sơ mi là: y 225000 (đồng) 5
* Do số tiền còn lại của Minh chỉ bằng số tiền còn lại của Bảo, nên ta có phương trình: 7 Trang 7 5 y 225000 . x 245000 7 5
x y 50000 2 7
x y 50000 x 350000 n Từ
1 và 2 , ta có hệ phương trình: 5 x y 5000 0 y 300000 n 7
Vậy lúc đầu Bảo mang theo 350000 đồng và Minh mang theo 300000 đồng
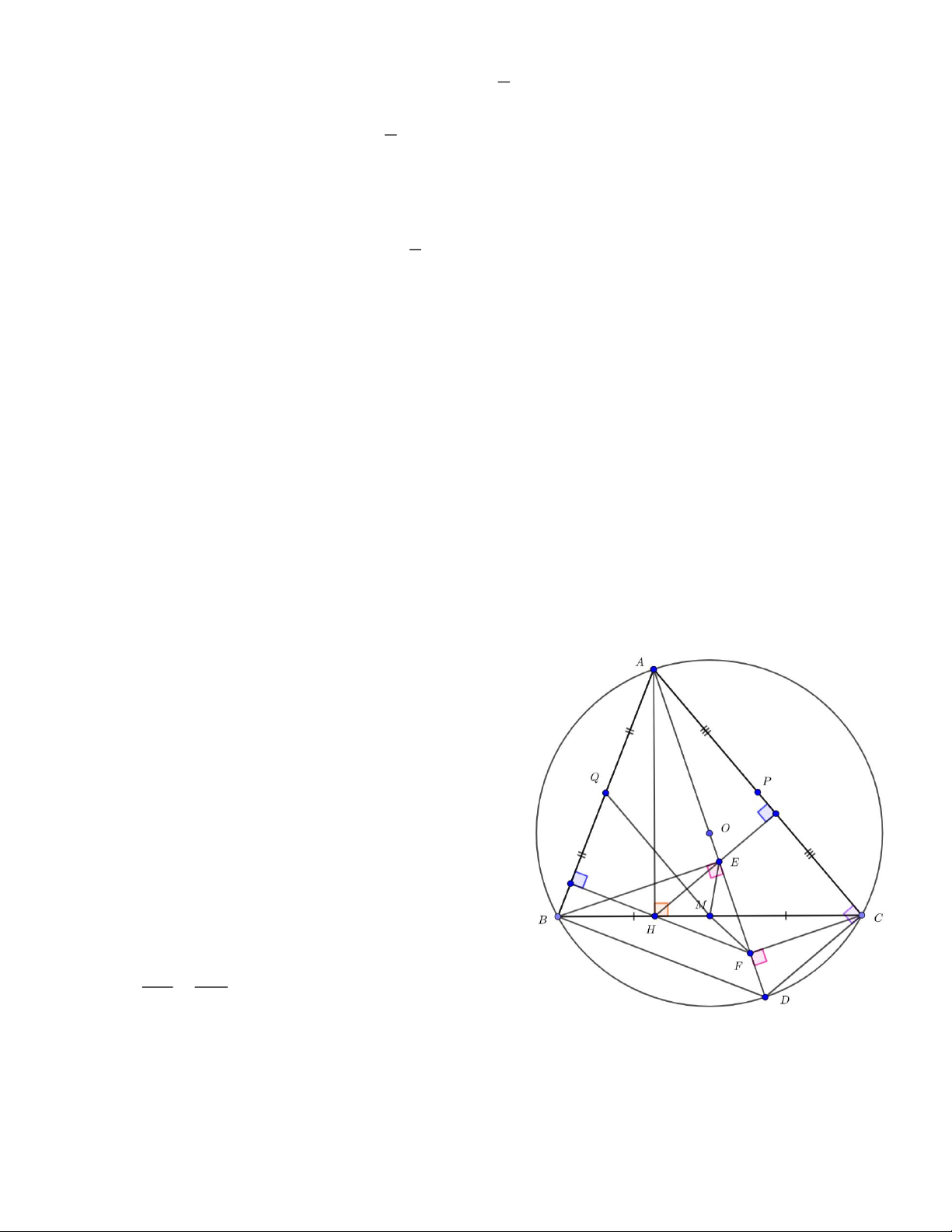
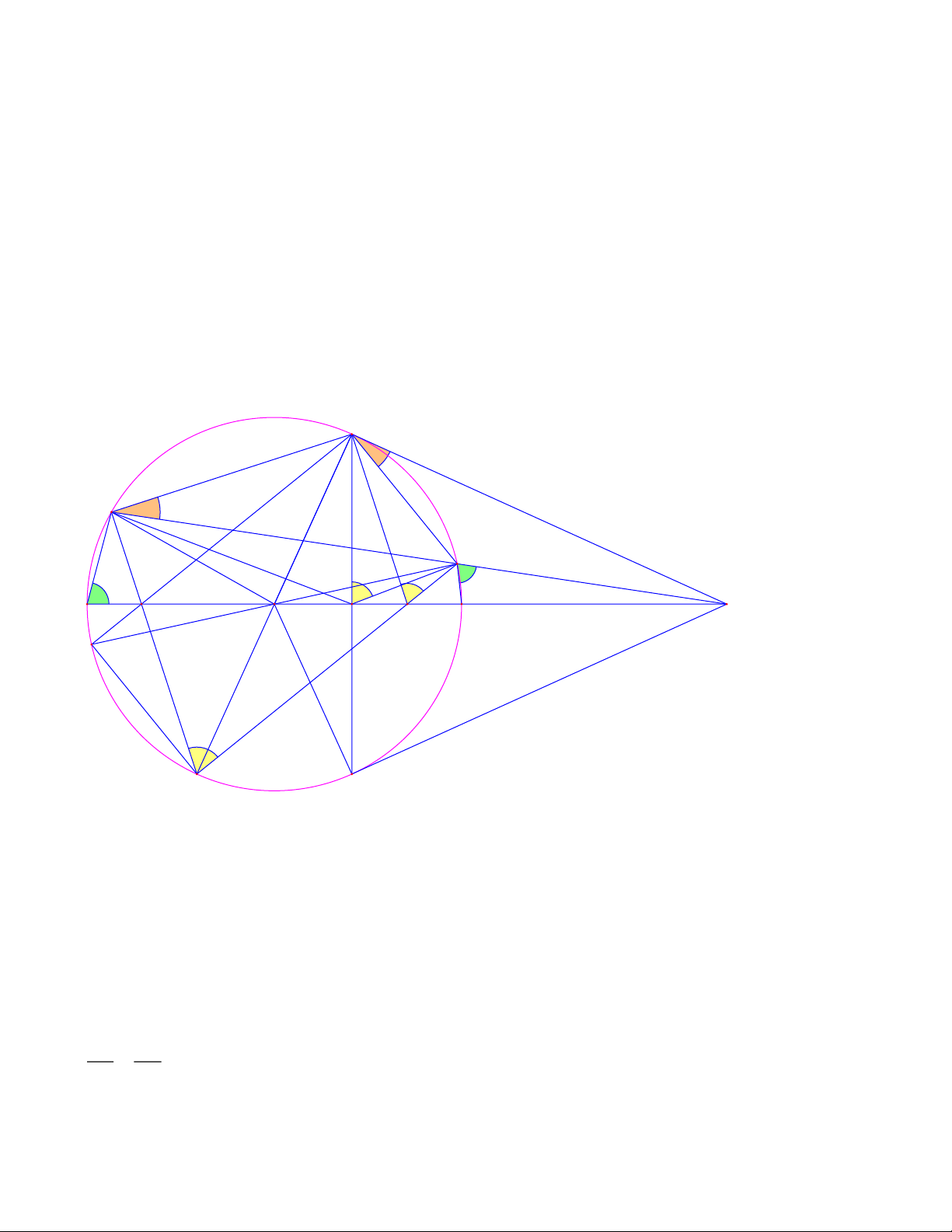
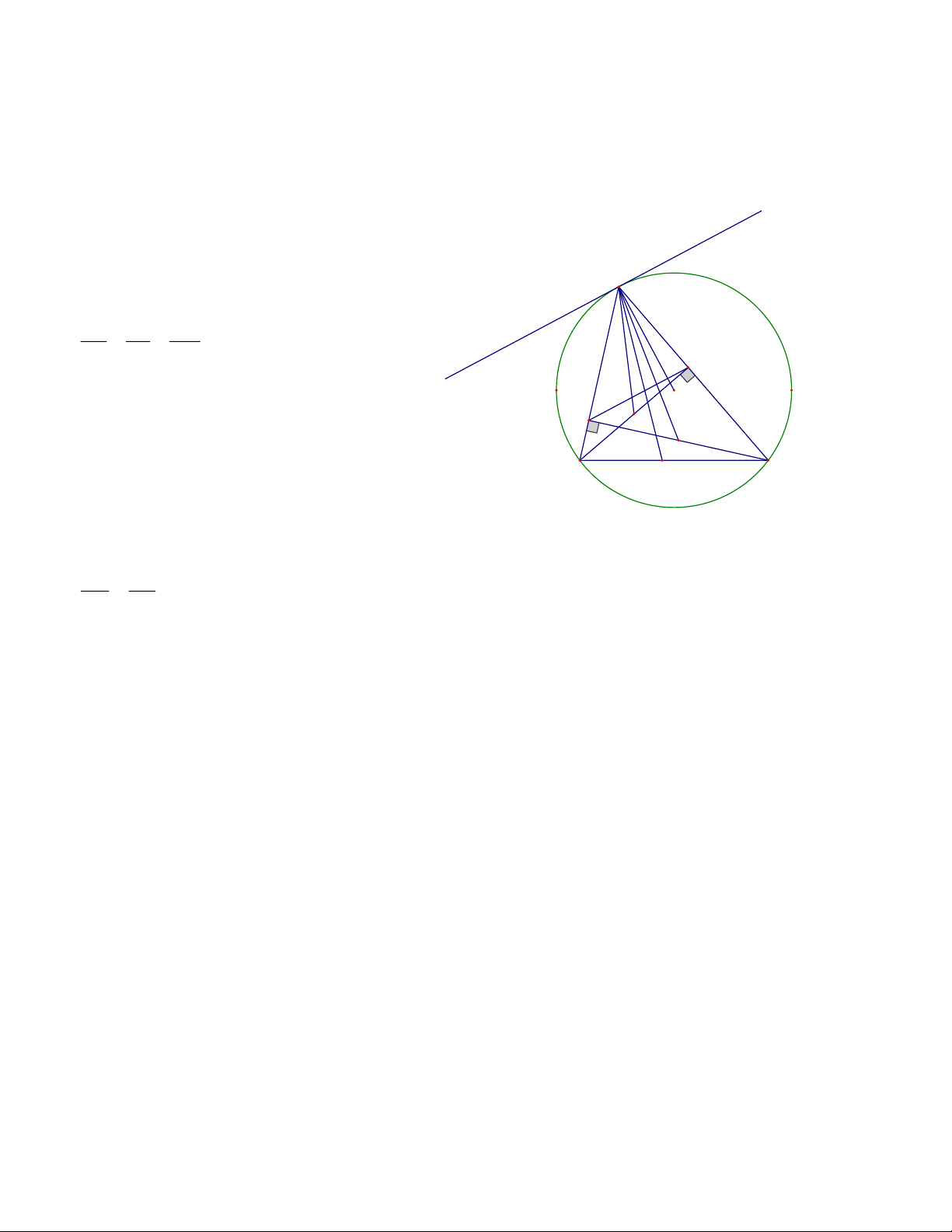
Câu 8. (3,0 điểm): Cho ABC
nhọn ( AB AC ) nội tiếp đường tròn (O; R). Vẽ đường cao AH của ABC
và đường kính AD của O .
a) Chứng minh hệ thức: A .
B AC AH.AD
b) Vẽ BE và CF lần lượt vuông góc với AD ( E, F thuộc AD ). Chứng minh rằng:
HE AC và HF AB
c) Gọi M là trung điểm BC . Chứng minh rằng M là tâm đường tròn ngoại tiếp E HF . Lời giải
a) Chứng minh hệ thức: A .
B AC AH.AD
Ta có: ACD 90 (góc nội tiếp chắn nữa
đường tròn đường kính AD )
Xét ABH và A DC , ta có:
AHB ACD 90
ABH ADC ( 2 góc nội tiếp cùng chắn AC ) A
BH” A DC g-g AB AH (yếu tố tương ứng) AD AC A .
B AC AH.AD
b) Vẽ BE và CF lần lượt vuông góc với AD ( E , F thuộc AD ). Chứng minh rằng:
HE AC và HF AB Trang 8
* Chứng minh HE AC :
Xét tứ giác ABHE , ta có:
AHB AEB 90 (gt)
ABHE là tứ giác nội tiếp đường tròn (tứ giác có 2 đỉnh liên tiếp cùng nhìn cạnh AB dưới 1 góc vuông
BAE EHC (góc trong bằng góc đối ngoài, tứ giác ABHE nội tiếp)
BAE BAD =EHC 1
Ta có: BAD BCD ( 2 góc nội tiếp cùng chắn cung BD ) 2 Từ
1 và 2 EHC BCD
Mà 2 góc này ở vị trí so le trong HE // CD
Lại có CD AC
HE AC (từ vuông góc đến song song)
* Chứng minh HF AB :
Ta có ABD 90 (góc nội tiếp chắn nữa đường tròn đường kính AD )
Ta có: AFH ACH ( 2 góc nội tiếp cùng chắn cung AH , tứ giác ABHE )
ADB ACB ( 2 góc nột tiếp cùng chắn cung AB )
Mà ACH ACB (góc chung)
ADB AFH
Mà 2 góc này ở vị trí đồng vị
BD // HF
Lại có: BD AB ( ABD 90 , cmt) Trang 9
HF AB (từ vuông góc đến song song)
c) Gọi M là trung điểm BC . Chứng minh rằng M là tâm đường tròn ngoại tiếp E HF .
Gọi Q, P lần lượt là trung điểm của AB, AC Xét ABC , ta có:
Q là trung điểm của AB (gt)
M là trung điểm của BC (gt)
MQ là đường trung bình của ABC
MQ // AC (tính chất đường trung bình)
Mà: HE AC (cmt)
MQ HE (từ vuông góc đến song song) 3 Mặt khác:
Tứ giác ABHE nội tiếp đường tròn (cmt) Lại có AEB vuông tại E
AB là đường kính của đường tròn ngoại tiếp tứ giác ABHE
Mà Q là trung điểm AB (gt)
Q là tâm của đường tròn ngoại tiếp tứ giác ABHE
QE QH
QM là đường trung tuyến của HE 4
Từ 3,4 , ta có: QM là đường trung trực của HE Xét ABC , ta có:
P là trung điểm của AC (gt)
M là trung điểm của BC (gt)
MP là đường trung bình của ABC Trang 10
MP // AB (tính chất đường trung bình)
Mà: HF AB (cmt)
MP HF (từ vuông góc đến song song) (5)
Xét tứ giác AHFC , ta có:
AHC AFC 90 (gt)
AHFC là tứ giác nội tiếp đường tròn đường kính AC (tứ giác có 2 đỉnh liên tiếp
cùng nhìn cạnh AC dưới 1 góc vuông
Mà P là trung điểm AC (gt)
P là tâm của đường tròn ngoại tiếp tứ giác AHFC
PH PF
PM là đường trung tuyến của HF 6
Từ 5,6 , ta có: PM là đường trung trực của HF Xét H EF , ta có:
QM là đường trung trực của HE (cmt)
PM là đường trung trực của HF (cmt)
M là tâm của đường tròn ngoại tiếp H EF ---HẾT---
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT HUYỆN HÓC MÔN
NĂM HỌC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Huyện Hóc Môn - 02
Thời gian: 120 phút (không kể thời gian phát đề) 2 x
Bài 1: Cho P : y
và d : y x 4 2
a) Vẽ đồ thị P,d trên cùng mặt phẳng tọa độOxy . Trang 11
b) Tìm tọa độ giao điểm của P và d .
Bài 2: Cho phương trình ẩn x : 2
3x 12x 2 0 có 2 nghiệm x ,x . Không giải phương trình, hãy tính giá 1 2
trị biểu thức sau: A x 2 x x x 2 x x . 1 1 2 2 2 1
Bài 3: Trong thời đại công nghệ 4.0 , con người làm việc và học tập ở mọi lúc mọi nơi trên các thiết bị
thông minh như máy tính, máy tính bảng, điện thoại,… Chính vì thế để đảm bảo cho sức khỏe về mắt thì
việc lựa chọn các thiết bị màn hình sắc nét được ưu tiên hàng đầu. Độ sắc nét của màn hình hay còn gọi là
"mật độ điểm ảnh" được đo bằng đơn vị PPI (Pixels Per Inch) thể hiện số lượng điểm ảnh. Số PPI càng cao
chứng tỏ các điểm ảnh trong hình càng nhiều, càng nhiều điểm ảnh thì màn hình càng sắc nét hơn. Tuy
nhiên, theo như Steve Jobs, cựu CEO Apple, mật độ điểm ảnh trên 300 PPI là đủ sắc nét so với mắt người thường.
Để tính mật độ điểm ảnh của màn hình, ta lấy căn bậc hai của tổng bình phương số điểm ảnh bề ngang và
bình phương số điểm ảnh chiều dọc, chia cho kích thước (đơn vị inch) của màn hình. 2 + 2 chieà u daø i chieà u roä ng maä t ñoäñieå m aû nh(PPI )= Ñöôø ng cheù o maø n hình(inch)
Ví dụ điện thoại Galaxy S21 có thông số màn hình là 1080 2400 điểm ảnh, kích thước 6,2 inch thì mật 2 2 1080 2400 độ điểm ảnh là: 424 PPI 6,2
Anh Hiểu Lâm đến cửa hàng An Nhiên thì được nhân viên giới thiệu chiếc điện thoại Iphone 14 có thông
số màn hình là 1170x2532 điểm ảnh, kích thước 6,1 inch và Iphone 14 Pro max có thông số màn hình là
1290 2796 điểm ảnh, kích thước 6,7 inch. Hãy giúp anh Hiểu Lâm tính xem chiếc điện thoại nào có mật độ điểm ảnh cao hơn?
Bài 4: Google Drive là dịch vụ lưu trữ và chỉnh sửa dữ liệu trực tuyến
hay còn gọi là lưu trữ đám mây (Cloud Storage). Khi đăng ký tài tài
khoản Google Drive, Google sẽ cho người dùng 15GB dung lượng
miễn phí cho bộ 3 ứng dụng Google Drive, Gmail và Google+ Ảnh
trên nền tảng “lưu trữ đám mây”. Dung lượng này chưa hẳn là lớn
nhưng cũng đủ dùng với người dùng thông thường, đặc biệt là dung
lượng ảnh trong phần Google+ Ảnh thì những ảnh nhỏ hơn kích thước 2048 2048 pixels thì Google cho
lưu trữ miễn phí. Nếu người dùng có nhu cầu cần thêm x GB dung lượng lưu trữ thì phải bỏ ra số tiền Trang 12
y (nghìn đồng). Mối liên hệ giữa hai đại lượng này phụ thuộc vào hàm số bậc nhất y ax b . Cụ thể, nếu
muốn có 100GB thì bạn sẽ phải trả 45 nghìn đồng một tháng, với 200GB là 69 nghìn đồng một tháng.
Anh Lưu Vĩnh muốn mua dung lượng lưu trữ 500GB thì cần phải trả số tiền là bao nhiêu cho mỗi tháng?
Bài 5: Decibel (viết tắt dB) là đơn vị đo cường độ âm thanh, tầm
nghe của con người là từ 0dB đến125dB , dưới 40dB thì khó nghe,
trên 105dB sẽ làm tai đau đớn. Nghe nhạc, mở to thời gian dài
cũng ảnh hưởng không tốt đến thính giác.
Ta thử tính xem cường độ âm thanh khi mở
nhạc to là bao nhiêu? biết rằng cường độ âm thanh khi mở nhạc to lớn hơn khi
nói chuyện bình thường là 50dB và ít hơn tiếng của máy bay phản lực là10dB , trong khi đó cường độ âm
thanh của tiếng máy bay phản lực nhiều gấp hai lần cường độ âm của tiếng nói chuyện bình thường.
Bài 6: Một căn phòng rộng 4m , dài 5,5m và cao 3,2m . Người ta muốn quét sơn lại trần nhà và bốn bức
tường. Biết tổng diện tích các cửa bằng 5% tổng diện tích bốn bức tường và trần nhà. Hãy tính chi phí
tiền công là bao nhiêu? Biết giá công sơn là 40 000 đồng/ m²
Bài 7: Tổng diện tích ba tỉnh có diện tích lớn nhất Việt Nam là Nghệ An – Gia Lai – Sơn La là 46128,1 ² km
. Diện tích Gia Lai nhiều hơn diện tích Sơn La là 1387,4 ²
km và ít hơn diện tích tỉnh Nghệ An là 982,8 ² km .
Hỏi diện tích mỗi tỉnh là bao nhiêu?
Bài 8: Từ điểm A nằm ngoài đường tròn O , kẻ hai tiếp tuyến AB,AC của đường tròn tâm O (với B,C
là hai tiếp điểm) và cát tuyến ADE sao cho D và C nằm ở hai nửa mặt phẳng đối nhau có bờ chứa tia
OA . Gọi H là giao điểm của OA và BC . Vẽ đường kính BK và DK cắt AO tại S . a)
Chứng minh: AB² A .
D AE và tứ giác OHDE nội tiếp
b) Tia AO cắt đường tròn O tại M và N ( M nằm giữa S và N ).
Chứng minh AM.NH MH.AN
c) Vẽ đường kính DR của O . Gọi I là giao điểm của AN và EK . Chứng minh ba điểm ,
B I,R thẳng hàng. Trang 13 HƯỚNG DẪN GIẢI 2 x
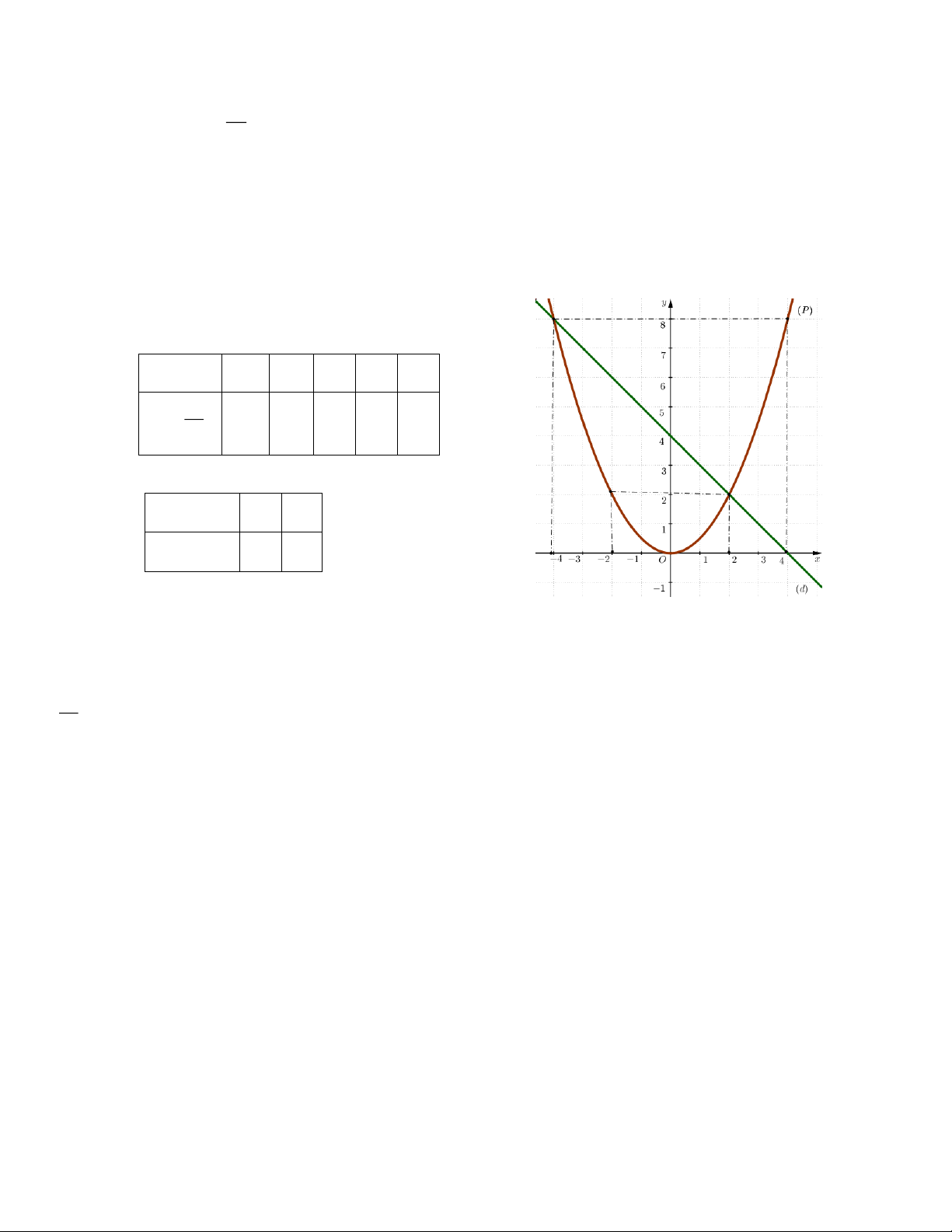
Bài 1. Cho(P ) : y
và(d) : y x 4 2
a) Vẽ đồ thị (P ),(d) trên cùng mặt phẳng tọa độOxy .
b) Tìm tọa độ giao điểm của (P ) và(d) . Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. a) BGT: x - 4 - 2 0 2 4 2 x y 8 1 0 2 8 2 x 0 1
y x 4 4 3
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2
x x 4 2 2
x 2x 8 0 x 2 x 4
Thay x 2 vào y x 4 , ta được: y 2 . Thay x 4
vào y x 4 , ta được: y 8 .
Vậy 2; 2 , 4; 8 là hai giao điểm cần tìm.
Bài 2: Cho phương trình ẩn 𝑥: 2
3x 12x 2 0 có 2 nghiệm 𝑥1; 𝑥2. Không giải phương trình,
hãy tính giá trị biểu thức sau: A x 2 x x x 2 x x 1 1 2 2 2 1 . Lời giải Trang 14 Ta có : D = b - ac = (- )2 2 4 12 - 4.3.2 = 120 > 0
Þ Phương trình đã cho có hai nghiệm phân biệt
ìï S = x + x = 4 ï 1 2 ï Theo Vi-et :í 2
ïï P = x .x = 1 2 ïî 3 2 2 2 3 3 3 3 Theo đề : A x x x x x x x x S 3PS 4 3. .4 54 1 1 2 2 2 1 1 2 3
Bài 3: Trong thời đại công nghệ 4.0 , con người làm việc và học tập ở mọi lúc mọi nơi trên các
thiết bị thông minh như máy tính, máy tính bảng, điện thoại,… Chính vì thế để đảm bảo cho
sức khỏe về mắt thì việc lựa chọn các thiết bị màn hình sắc nét được ưu tiên hàng đầu. Độ sắc
nét của màn hình hay còn gọi là "mật độ điểm ảnh" được đo bằng đơn vị PPI (Pixels Per Inch)
thể hiện số lượng điểm ảnh. Số PPI càng cao chứng tỏ các điểm ảnh trong hình càng nhiều,
càng nhiều điểm ảnh thì màn hình càng sắc nét hơn. Tuy nhiên, theo như Steve Jobs, cựu
CEO Apple, mật độ điểm ảnh trên 300 PPI là đủ sắc nét so với mắt người thường.
Để tính mật độ điểm ảnh của màn hình, ta lấy căn bậc hai của tổng bình phương số điểm ảnh
bề ngang và bình phương số điểm ảnh chiều dọc, chia cho kích thước (đơn vị inch) của màn hình. 2 + 2 chieà u daø i chieà u roä ng
maätñoäñieåmaûnh(PPI )= Ñöôø ng cheù o maø n hình(inch)
Ví dụ điện thoại Galaxy S21 có thông số màn hình là 1080´ 2400 điểm ảnh, kích thước 6, 2 2 2 1080 2400
inch thì mật độ điểm ảnh là: 424 PPI 6,2
Anh Hiểu Lâm đến cửa hàng An Nhiên thì được nhân viên giới thiệu chiếc điện thoại Iphone
14 có thông số màn hình là 1170x2532 điểm ảnh, kích thước 6,1 inch và Iphone 14 Pro max
có thông số màn hình là 1290´ 2796 điểm ảnh, kích thước 6, 7 inch. Hãy giúp anh Hiểu Lâm
tính xem chiếc điện thoại nào có mật độ điểm ảnh cao hơn? Trang 15 Lời giải 2 2 1170 2532
Mật độ điểm ảnh của Iphone 14: 457,7 (PPI) 6,1 2 2 1290 2796
Mật độ điểm ảnh của Iphone 14 Pro Max: 459,6 (PPI) 6,7
Vậy điện thoại có mật độ điểm ảnh cao hơn là Iphone 14 Pro Max vì 459,6 > 457,7
Bài 4: Google Drive là dịch vụ lưu trữ và chỉnh sửa dữ liệu
trực tuyến hay còn gọi là lưu trữ đám mây (Cloud Storage).
Khi đăng ký tài tài khoản Google Drive, Google sẽ cho người
dùng 15GB dung lượng miễn phí cho bộ 3 ứng dụng Google
Drive, Gmail và Google+ Ảnh trên nền tảng “lưu trữ đám
mây”. Dung lượng này chưa hẳn là lớn nhưng cũng đủ dùng với người dùng thông thường,
đặc biệt là dung lượng ảnh trong phần Google+ Ảnh thì những ảnh nhỏ hơn kích thước
2048 ´ 2048 pixels thì Google cho lưu trữ miễn phí. Nếu người dùng có nhu cầu cần thêm x
(GB ) dung lượng lưu trữ thì phải bỏ ra số tiền y (nghìn đồng). Mối liên hệ giữa hai đại lượng
này phụ thuộc vào hàm số bậc nhấty = ax + b . Cụ thể, nếu muốn có 100GB thì bạn sẽ phải
trả 45 nghìn đồng một tháng, với 200GB là 69 nghìn đồng một tháng. Anh Lưu Vĩnh muốn
mua dung lượng lưu trữ 500GB thì cần phải trả số tiền là bao nhiêu cho mỗi tháng? Lời giải
Thay x = 100, y = 45 vàoy = ax + b , ta được100a + b = 45 (1)
Thay x = 200, y = 69 vàoy = ax + b , ta được200a + b = 69 (2)
Từ (1) và (2) ta có hệ phương trình 1 00a b 45 2 00a b 69 a 0,24 ⇔ b 21
Khi đó ta có: y = 0, 24x + 21 Trang 16
Thay x = 500 vàoy = 0, 24x + 21 , ta được:
y = 0, 24.500 + 21 = 141
Vậy anh Lưu Vĩnh phải trả số tiền là 141 nghìn đồng khi mua dung lượng lưu trữ 500GB
Bài 5: Decibel (viết tắt dB) là đơn vị đo cường độ âm
thanh, tầm nghe của con người là từ 0dB đến125dB , dưới
40dB thì khó nghe, trên 105dB sẽ làm tai đau đớn.
Nghe nhạc, mở to thời gian dài cũng ảnh hưởng không tốt đến thính giác.
Ta thử tính xem cường độ âm thanh khi mở
nhạc to là bao nhiêu? biết rằng cường độ âm thanh khi mở nhạc to lớn hơn khi nói chuyện
bình thường là 50dB và ít hơn tiếng của máy bay phản lực là10dB , trong khi đó cường độ âm
thanh của tiếng máy bay phản lực nhiều gấp hai lần cường độ âm của tiếng nói chuyện bình thường. Lời giải
Gọi x (dB ) là cường độ âm thanh khi mở nhạc to và x > 50
Cường độ âm thanh khi nói chuyện bình thường là: x – 50(dB )
Cường độ âm thanh của tiếng máy bay phản lực là: x + 10(dB )
Vì cường độ âm thanh của tiếng máy bay phản lực nhiều gấp hai lần cường độ âm của tiếng nói chuyện bình thường
nên ta có phương trình: x + 10 = 2.(x – 5 ) 0 Û x = 110
Vậy cường độ âm thanh khi mở nhạc to là 110 dB
Bài 6: Một căn phòng rộng 4m , dài 5, 5m và cao 3, 2m . Người ta muốn quét sơn lại trần nhà và
bốn bức tường. Biết tổng diện tích các cửa bằng 5% tổng diện tích bốn bức tường và trần
nhà. Hãy tính chi phí tiền công là bao nhiêu? Biết giá công sơn là 40 000 đồng/ m ² Trang 17 Lời giải
Diện tích bốn bức tường và trần nhà: 2
2. 4 5,5 .3,24.5,5 82,8 (m ) Diện tích các cửa: 2 82,8 .5% 4,14 (m )
Ta có: (82,8 4,14). 40000 3146 400 3150000 (đồng)
Vậy chi phí sơn bốn bức tường và trần nhà khoảng 3150 000 đồng
Bài 7: Tổng diện tích ba tỉnh có diện tích lớn nhất Việt Nam là Nghệ An – Gia Lai – Sơn La là
46128,1km ² . Diện tích Gia Lai nhiều hơn diện tích Sơn La là 1387, 4km ² và ít hơn diện tích tỉnh
Nghệ An là 982, 8km ² . Hỏi diện tích mỗi tỉnh là bao nhiêu? Lời giải
Gọi x (km ²) là diện tích mỗi tỉnh Gia Lai
Diện tích tỉnh Sơn La là: x – 1387, 4(km²)
Diện tích tỉnh Nghệ An là: x + 982, 8(km ²)
Vì tổng diện tích ba tỉnh Nghệ An – Gia Lai – Sơn La là 46 128,1 km ² nên ta có phương trình:
x + 982, 8 + x + x – 1387, 4 = 46 128,1 Û 3x = 45723, 5 Û x = 15510, 9 Vậy
Diện tích tỉnh Gia Lai là 15510, 9km ²
Diện tích tỉnh Sơn La là 15510, 9 – 1387, 4 = 14123, 5km ²
Diện tích tỉnh Nghệ An là 15510, 9 + 982, 8 = 16493, 7km ²
Bài 8: Từ điểm A nằm ngoài đường tròn(O) , kẻ hai tiếp tuyến A B, A C của đường tròn tâm
O (với B,C là hai tiếp điểm) và cát tuyến A DE sao cho D và C nằm ở hai nửa mặt phẳng Trang 18
đối nhau có bờ chứa tiaOA . Gọi H là giao điểm của OA vàBC . Vẽ đường kính BK và DK
cắt A O tại S . a)
Chứng minh: A B ² = A D.A E và tứ giác OHDE nội tiếp
b) Tia A O cắt đường tròn (O) tại M và N (M nằm giữa S vàN ).
Chứng minh A M .NH = MH.A N
c) Vẽ đường kính DR của(O) . Gọi I là giao điểm của A N vàEK .
Chứng minh ba điểm B, I , R thẳng hàng. Lời giải B E D 0 N A I H S M R K C a)
Chứng minh A B ² = A D.A E và tứ giác OHDE nội tiếp
Xét A BD và A EB Ta có: BAE chung
ABD AEB (góc tạo bởi tiếp tuyến và dây cung cùng chắn cungBD ) ∾ nên DA BD DA EB ( . g g) AB AD Þ Þ AB² = A . (1) AE AB D AE
Ta có: OB = OC (bán kính) Trang 19
A B = A C (tính chất 2 tiếp tuyến cắt nhau)
nên OA là đường trung trực của đoạn thẳng BC
⇒ OA ^ BC tại H
Xét DOA B vuông tạiB , đường cao BH
Ta có: A B ² = A H .A O (hệ thức lượng) (2) Từ (1) và (2) Þ A .
D AE = AH.AO
Xét DA HD và DA EO Ta có: OAE chung AH AD (AH.AO AD.AE) AE AO ∾ nên DA HD DA EO ( . c . g c) ADH AOE
tứ giác OHDE nội tiếp (góc ngoài bằng góc đối trong)
b) Chứng minh A M .NH = MH .A N Ta có: ADH AOE ADM ANE 1 mà ANE AOE 2 1 nen ADM ADH 2
Þ DM là tia phân giác của ADH MA DA (3) MH DH Ta có: NDM 90
(góc nội tiếp chắn nửa đường tròn) Þ DM ^ DN
DN là phân giác ngoài của DADH NA DA (4) NH DH Trang 20 MA NA Từ (3) và (4) MH NH Þ M . A NH = N . A MH c)
Chứng minh 3 điểm B, I , R thẳng hàng
Gọi S là giao điểm của OA và DK Xét tứ giác BHSD Ta có: BHS 90
(OA ^ BC tạiH ) BDS 90
(góc nội tiếp chắn nửa đường tròn)
nên tứ giác BHSD nội tiếp (tổng hai góc đối bằng 180) ⇒ BHD BSD (5)
Ta có: EHO EDO (cùng chắn cung EO ) AHD AEO ∾ ( DA HD D A EO ) mà EDO AEO nên EHO AHD
mà EHO EHD AHD BHD 90 (OA ^ BC tạiH ) nên EHB BHD 1 ⇒ BHD DHE (6) 2 1
Từ (5) và (6) BSD DHE 2 1 mà DKE DOE 2 DOE DHE nên BSD DKE
mà BSD và DKE nằm ở vị trí so le trong nên BS / / EK ⇒ OBS OKI (so le trong) Trang 21
Xét D OBS và DOKI
Ta có: OBS OKI (( BS / / EK , 2 góc so le trong)
OB = OK (bán kính)
SOB IOK (2 góc đối đỉnh)
nên DOBS = DOKI ( . g . c g) Þ BS = IK
mà BS / / IK (BS / / EK )
nên tứ giác IKSB là hình bình hành
Þ BI / / SK (7) Xét tứ giác DKRB Ta có: RBD 90
(góc nội tiếp chắn nửa đường tròn) BOK 90
(góc nội tiếp chắn nửa đường tròn) RKD 90
(góc nội tiếp chắn nửa đường tròn)
nên tứ giác DKRB là hình chữ nhật Þ BR / / DK (8)
Từ (7) và (8) Þ 3 điểm B, I , R thẳng hàng
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT HUYEÄN HOÙC
NAÊM HOÏC: 2023 - 2024 MOÂN MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
Thời gian: 120 phút (không kể thời gian phát đề)
MÃ ĐỀ: Huyện Hóc Môn - 3
Câu 1. (1,5 điểm). Cho P 2
: y x và đường thẳng D : y x 2 .
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép toán.
Câu 2. (1 điểm). Cho phương trình 2
x 4x 5 0 có 2 nghiệm là x ,x . Không giải phương trình, hãy 1 2
tính giá trị của biểu thức A x 3x x 3x 7 1 2 2 1
Câu 3. (1 điểm). Tiền lương hằng tháng hiện nay của giáo viên được tính theo công thức Trang 22 A .
x m p1 t Trong đó:
A (đồng): là tiền lương một tháng p : Các phụ cấp (chức vụ, thâm niên,...)
x : hệ số lương t : tỉ lệ % phụ cấu ưu đãi.
m :lương tối thiểu cho một hệ số
Ví dụ: Anh Nguyễn Văn An là một giáo viên trung học có hệ số lương là 2,34 (không phụ cấp chức vụ,
thâm niên), lương tối thiểu là 1 490 000 đồng và giáo viên này được hưởng phụ cấp ưu đãi là 30%.
Tiền lương mỗi tháng của anh Nguyễn Văn An là A .
x m p1 t
2,34.1490000 01 30% 4532580 (đồng)
a) Anh Nguyễn Văn Bình là một giáo viên trung học có hệ số lương là 2,67 (không phụ cấp chức
vụ, thâm niên), lương tối thiểu là 1 490 000 đồng và giáo viên này được hưởng phụ cấp ưu đãi
là 30%. Hỏi lương của anh Bình mỗi tháng bao nhiêu?
b) Anh Nguyễn Văn Phúc cũng là một giáo viên hưởng ưu đãi như trên (không phụ cấp chức vụ,
thâm niên,…) lãnh lương một tháng với số tiền 9 646 260 đồng thì hệ số lương của anh Phúc là bao nhiêu?
Câu 4. (0,75 điểm). Bạn Nam mua hai đôi giày và bán lại với giá mỗi đôi là 1 232 000 đồng. Biết đôi giày
thứ nhất Nam lời được 12% so với giá đôi giày thứ nhất, đôi giày thứ hai Nam lỗ 12% so với giá
Nam đã mua đôi giày thứ hai. Hỏi sau khi bán hai đôi giày trên Nam lời hay lỗi bao nhiêu tiền?
Câu 5. (1 điểm). Hằng năm, sau khi kết thúc kiểm tra KHI, học sinh trường THCS A lại náo lức chào đón
ngày Hội Xuân với nhiều hoạt động ý nghĩa. Trong đó, các lớp sẽ mở gian hàng ẩm thực và học
sinh toàn trường sẽ mua sản phẩm số bằng phiếu do Ban tổ chức phát hành với số tiền 5000 đồng cho mỗi phiếu.
Năm nay, lớp 9A1 quyết định tổ chức gian hàng ẩm thực với số vốn là 1 612 000 đồng. Gọi x là số phiếu
lớp 9A1 thu được từ gian hàng và y (đồng) là số tiền nhận được tương ứng sau khi trừ vốn.
a) Viết công thức tính y theo x .
b) Lớp 9A1 phải thu vào ít nhất bao nhiêu phiếu để không bị lỗ vốn?
Câu 6. (1 điểm). Ông Năm làm lan can ban công của một ngôi nhà bằng một miếng kính cường lực.
Miếng kính này là một phần của mặt xung quanh hình trụ như hình bên dưới. Trang 23 4 m A B 150° 1,4 m E D C
Biết AB 4m , DA 1,4m , 0
AEB 150 . Tính diện tích của miếng kính?
Câu 7. (1 điểm). Hai lớp 9A và 9B có 86 học sinh. Trong đợt thu nhặt giấy vụn thực hiện kế hoạch nhỏ,
lớp 9A có một bạn góp được 5kg giấy vụn, còn các bạn còn lại góp được 4kg giấy vụn. Lớp 9B có
một bạn góp được 7kg giấy vụn, còn các bạn còn lại mỗi bạn góp được 8kg giấy vụn. Tính số học
sinh mỗi lớp biết cả hai lớp góp được 520kg giấy vụn.
Câu 8. (3 điểm) Cho tam giác ABC nhọn nội tiếp đường tròn O AB AC , có hai đường cao BE và CS.
a) Chứng minh tứ giác BSEC nội tiếp.
b) Chứng minh OA SE
c) Gọi M,N lần lượt là trung điểm của BE và CS. Tia phân giác của MAN cắt BC tại K . Chứng minh : K . B AC K . C AB ----HẾT--- HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm). Cho P 2
: y x và đường thẳng D : y x 2 .
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải y
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ. (D) BGT: (P) x 2 1 0 1 2 4 2 y x 4 1 0 1 4 3 2 x 0 1 1 y x 2 2 3 1 2 x -2 -1 Trang 24
b) Tìm tọa độ giao điểm của P và D bằng phép tính.
Phương trình hoành độ giao điểm của P và D : 2 x x 2 2
x x 2 0 x 2 x 1 Thay x 2 vào 2
y x , ta được: 2 y 2 4 . Thay x 1 vào 2
y x , ta được: y 2 1 1 . Vậy 2; 4 , 1 ;
1 là hai giao điểm cần tìm. Câu 2.
(1 điểm). Cho phương trình 2
x 4x 5 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A x 3x x 3x 7 1 2 2 1 Lời giải b 4
S x x 4 1 2
Theo định lí Vi-et, ta có: a 1 c 5
P x .x 5 1 2 a 1
Ta có: A x 3x x 3x 7 1 2 2 1 2 2
A x x 3x 3x 9x x 7 1 2 1
A 10x x 3 2 x x 1 2 2 2 7 1 2 1 2 2
A 10x x 3 x x 2x x 7 1 2 1 2 x 2 A 10. 5 3. 16 2. 5 7 A 135 Câu 3.
(1 điểm). Tiền lương hằng tháng hiện nay của giáo viên được tính theo công thức A .
x m p1 t Trong đó:
A (đồng): là tiền lương một tháng p : Các phụ cấp (chức vụ, thâm niên,...)
x : hệ số lương t : tỉ lệ % phụ cấu ưu đãi.
m :lương tối thiểu cho một hệ số Trang 25
Ví dụ: Anh Nguyễn Văn An là một giáo viên trung học có hệ số lương là 2,34 (không phụ cấp chức vụ,
thâm niên), lương tối thiểu là 1 490 000 đồng và giáo viên này được hưởng phụ cấp ưu đãi là 30%.
Tiền lương mỗi tháng của anh Nguyễn Văn An là A .
x m p1 t
2,34.1490000 01 30% 4532580 (đồng)
a. Anh Nguyễn Văn Bình là một giáo viên trung học có hệ số lương là 2,67 (không phụ cấp chức
vụ, thâm niên), lương tối thiểu là 1 490 000 đồng và giáo viên này được hưởng phụ cấp ưu đãi
là 30%. Hỏi lương của anh Bình mỗi tháng bao nhiêu?
b. Anh Nguyễn Văn Phúc cũng là một giáo viên hưởng ưu đãi như trên (không phụ cấp chức vụ,
thâm niên,…) lãnh lương một tháng với số tiền 9 646 260 đồng thì hệ số lương của anh Phúc là bao nhiêu? Lời giải
a. Tiền lương mỗi tháng của anh Bình là A .
x m p1 t
2,67.1490000 0.1 30% 5171000 (đồng)
b. Vì anh Phúc lãnh lương một tháng với số tiền là 9 646 260 đồng nên .1
x 490000 0.1 30% 9646260 9646 260 .1 x 490000 1 30% 9646 260 x : 1490000 1 30% x 4,98
Vậy hệ số lương của anh Phúc là 4,98 Câu 4.
(0,75 điểm). Bạn Nam mua hai đôi giày và bán lại với giá mỗi đôi là 1 232 000 đồng. Biết đôi
giày thứ nhất Nam lời được 12% so với giá đôi giày thứ nhất, đôi giày thứ hai Nam lỗ 12% so với
giá Nam đã mua đôi giày thứ hai. Hỏi sau khi bán hai đôi giày trên Nam lời hay lỗi bao nhiêu tiền? Lời giải
Gọi x (đồng), y (đồng) lần lượt là giá vốn của đôi giầy thứ nhất và đôi giầy thứ hai Đk: (0 ;
x y 1232 000)
- Vì đôi giầy thứ nhất anh Nam lời 12% nên: . x 112% 1232000 Trang 26 1232000 x 1100000 (đồng) 112%
- Vì đôi giầy thứ hai anh Nam lỗ 12% nên: . y 88% 1232000 1232000 y 1400000 (đồng) 88%
Giá vốn cả hai đôi giày là: 1 100 000 + 1 400 000 = 2 500 000 (đồng)
Số tiền anh Nam thu được khi bán cả hai đôi giầy là : 1 232 000.2 = 2 464 000 (đồng)
Vậy sau khi bánh ai đôi giầy anh Nam lỗ: 2 500 000 – 2 464 000 = 16 000 (đồng) Câu 5.
(1 điểm). Hằng năm, sau khi kết thúc kiểm tra KHI, học sinh trường THCS A lại náo lức
chào đón ngày Hội Xuân với nhiều hoạt động ý nghĩa. Trong đó, các lớp sẽ mở gian hàng ẩm thực
và học sinh toàn trường sẽ mua sản phẩm số bằng phiếu do Ban tổ chức phát hành với số tiền 5000 đồng cho mỗi phiếu.
Năm nay, lớp 9A1 quyết định tổ chức gian hàng ẩm thực với số vốn là 1 612 000 đồng. Gọi x là số phiếu
lớp 9A1 thu được từ gian hàng và y (đồng) là số tiền nhận được tương ứng sau khi trừ vốn.
a. Viết công thức tính y theo x .
b. Lớp 9A1 phải thu vào ít nhất bao nhiêu phiếu để không bị lỗ vốn? Lời giải
a. Số tiền lớp 9A1 thu được tương ứng sau khi trừ vốn là
y 5000.x 1 612 000 (đồng)
b. Để không bị lỗ vốn thì số tiền thu được phải lớn hơn hoặc bằng tiền vốn 5000x 1612000 1612000 x 322,4 5000
Vậy: để không bị lỗ vốn thì lớp 9A1 phải thu vào ít nhất 323 phiếu. Câu 6.
(1 điểm). Ông Năm làm lan can ban công của một ngôi nhà bằng một miếng kính cường lực.
Miếng kính này là một phần của mặt xung quanh hình trụ như hình bên dưới. 4 m A B 150° 1,4 m E D C Trang 27
Biết . AB 4m ., DA 1,4m , 0
AEB 150 . Tính diện tích của miếng kính? Lời giải
Gọi O là tâm của mặt đáy hình trụ chứa cung AB
Số đo cung lớn AB bằng 3000
Số đo cung nhỏ AB bằng 600 Suy ra 0 AOB 60 - Vì A
OB cân tại O (OA = OB) có 0 AOB 60 (cmt) A
OB là tam giác đều
R OA OB AB 4 (m)
Diện tích xung quanh của hình trụ chứa miếng kính là
S 2 rh 2 .4.1,4 11,2 (m2). xq
Diện tích của miếng kính làm lan can là 1 1
S S .11,2 5,9 (m2) 6 xq 6 Câu 7.
(1 điểm). Hai lớp 9A và 9B có 86 học sinh. Trong đợt thu nhặt giấy vụn thực hiện kế hoạch
nhỏ, lớp 9A có một bạn góp được 5kg giấy vụn, còn các bạn còn lại góp được 4kg giấy vụn. Lớp 9B
có một bạn góp được 7kg giấy vụn, còn các bạn còn lại mỗi bạn góp được 8kg giấy vụn. Tính số học
sinh mỗi lớp biết cả hai lớp góp được 520kg giấy vụn. Lời giải
Gọi x (học sinh), y(học sinh) lần lượt là số học sinh của lớp 9A và 9B (đk: 0 < x;y < 86 và x; y là các số nguyên)
- Vì hai lớp 9A và 9B có 86 học sinh nên x + y = 86 (1)
- Vì lớp 9A có một bạn góp được 5 kg giấy vụn còn các bạn còn lại mỗi bạn góp được 4kg giấy vụn nên số
kg giấy vụn lớp 9A góp được là: 5 + 4(x – 1) = 4x + 1 (kg).
- Vì lớp 9B có một bạn góp được 7 kg giấy vụn còn các bạn còn lại mỗi bạn góp được 8kg giấy vụn nên số
kg giấy vụn lớp 9B góp được là: 7 + 8.(y – 1) = 8y – 1 (kg)
- Vì cả hai lớp góp được 520 kg giấy vụn nên Trang 28 4x + 1 + 8y – 1 = 520 <=> 4x + 8y = 520 (2)
Từ (1) và (2) ta có hệ phương trình
x y 86 4x 8y 520 𝑥 = 42 (𝑛ℎậ𝑛) <=> { 𝑦 = 44 (𝑛ℎậ𝑛)
Vậy lớp 9A có 42 học sinh và 9B có 44 (học sinh) Câu 8.
(3 điểm) Cho tam giác ABC nhọn nội tiếp đường tròn O AB AC , có hai đường cao BE và CS.
a. Chứng minh tứ giác BSEC nội tiếp.
b. Chứng minh OA SE
c. Gọi M,N lần lượt là trung điểm của BE và CS. Tia phân giác của MAN cắt BC tại K . Chứng minh : K . B AC K . C AB Lời giải a) Xét tứ giác BSEC có: + 90o BSC
(vì CS là đường cao của A BC ) + 90o BEC
(vì BE là đường cao của A BC ) => ( 90o BSC BEC )
Vậy tứ giác BSEC nội tiếp b)
Kẻ tiếp tuyến xAy như hình
- Vì tứ giác BSEC nội tiếp (cmt)
nên ASE ACB (góc ngoài bằng góc đối diện bên trong)
Mà xAB ACB (cùng chắng cung AB)
=> ASE xAB Trang 29
Mà hai góc này ở vị trí so le trong => xy // SE
Mà OA xy (vì xy là tiếp tuyến của đường tròn (O)) y
=> OA SE c) A Chứng minh: A BE # A CS (g-g) BA BE BM CA CS CN x E Chứng minh: A BM # A CN (c-g-c) O S M BAM CAS N BAK CAK B K C
=> AK là đường phân giác của góc BAC - Xét A
BC có AK là đường phân giác (cmt) AB KB AC KC .
KB AC KC.AB ----HẾT--- Trang 30




