













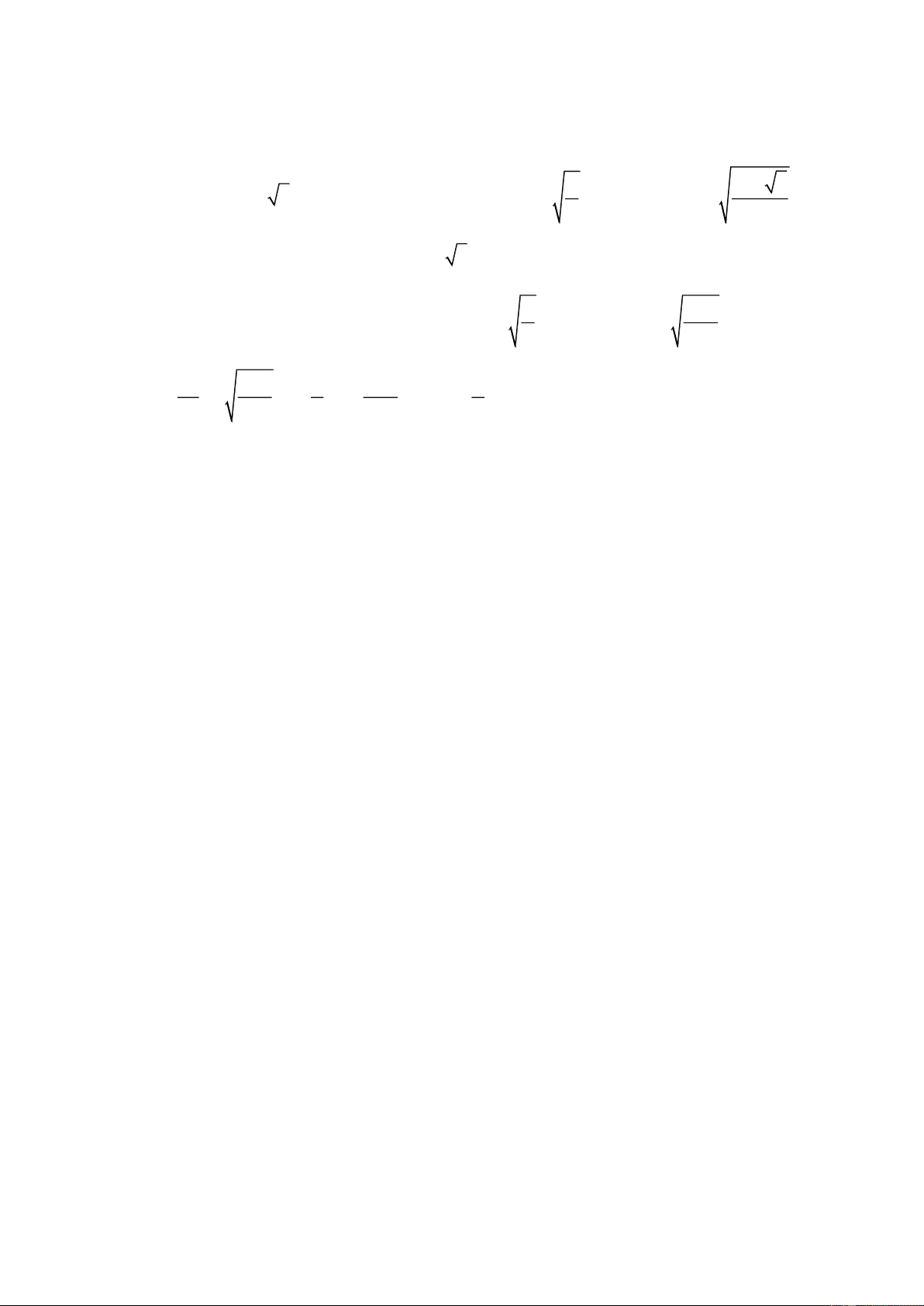


Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 1
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 1 - 1
Thời gian: 120 phút (không kể thời gian phát đề) 1 3
Câu 1. (1,5 điểm). Cho P : y 2
x và đường thẳng d : y x 2 . 4 2
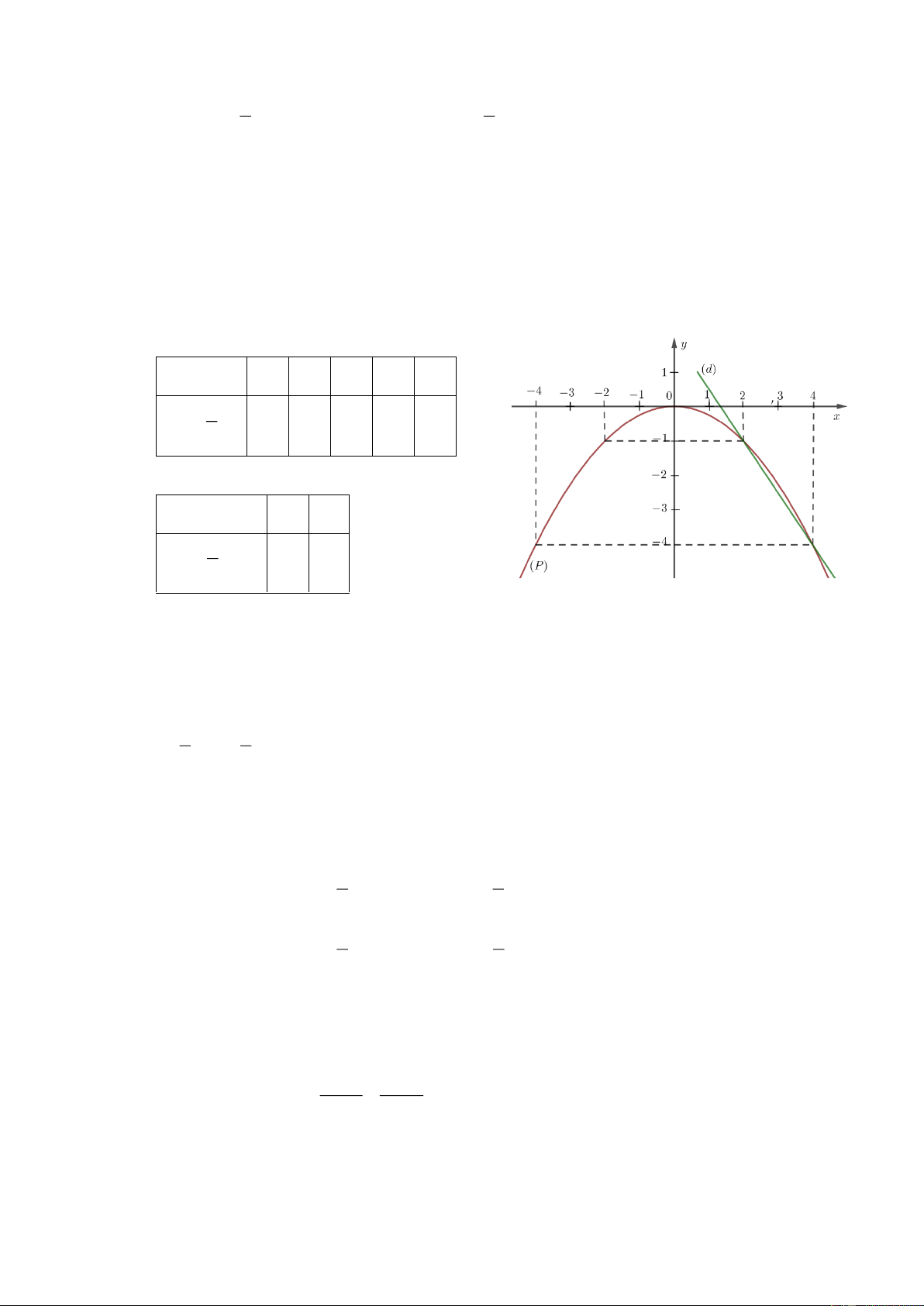
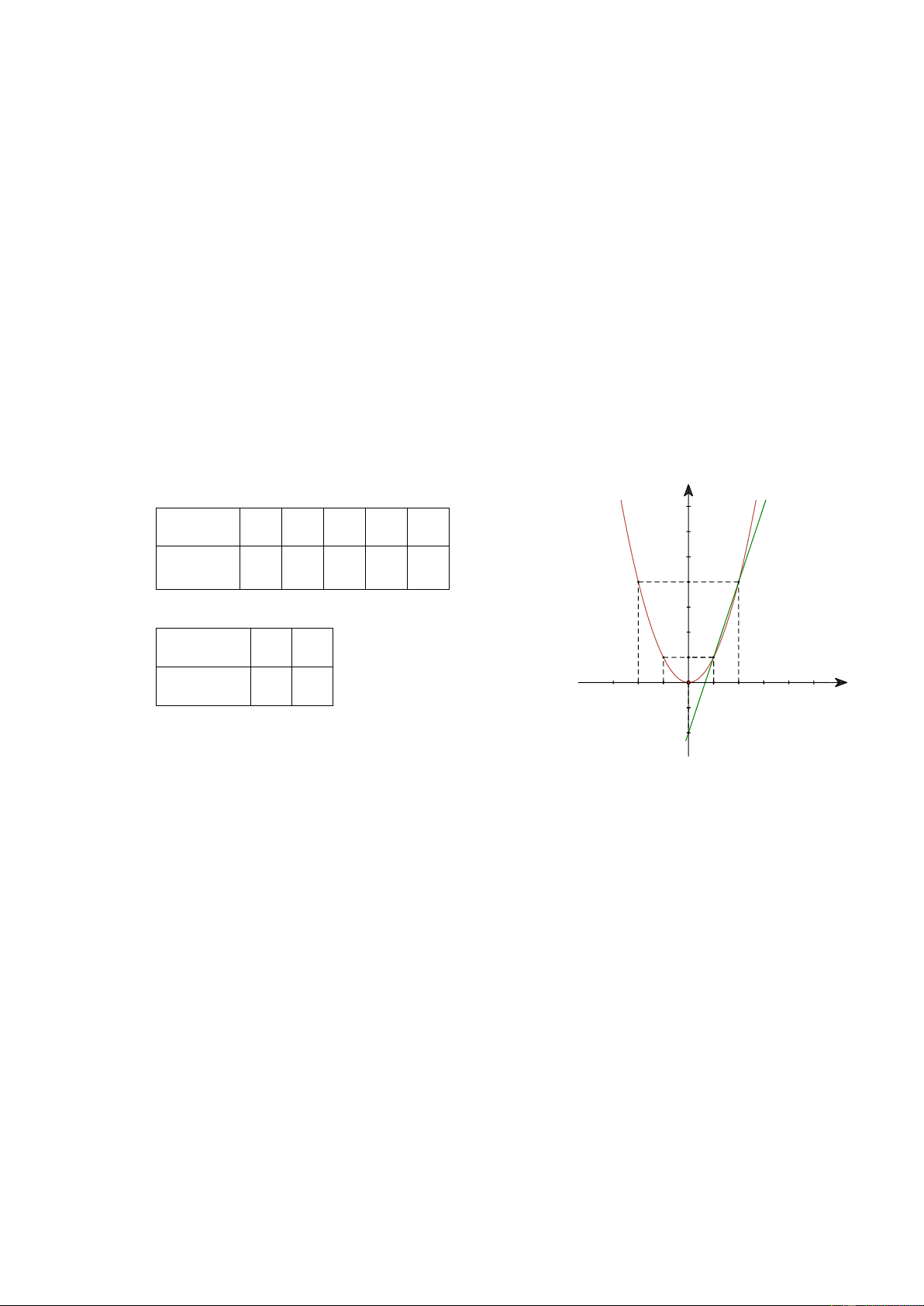
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
2x 6x 1 0 có 2 nghiệm là x ,x . Không giải phương 1 2 x 2 x 2
trình, hãy tính giá trị của biểu thức A 1 2 . x 1 x 1 2 1
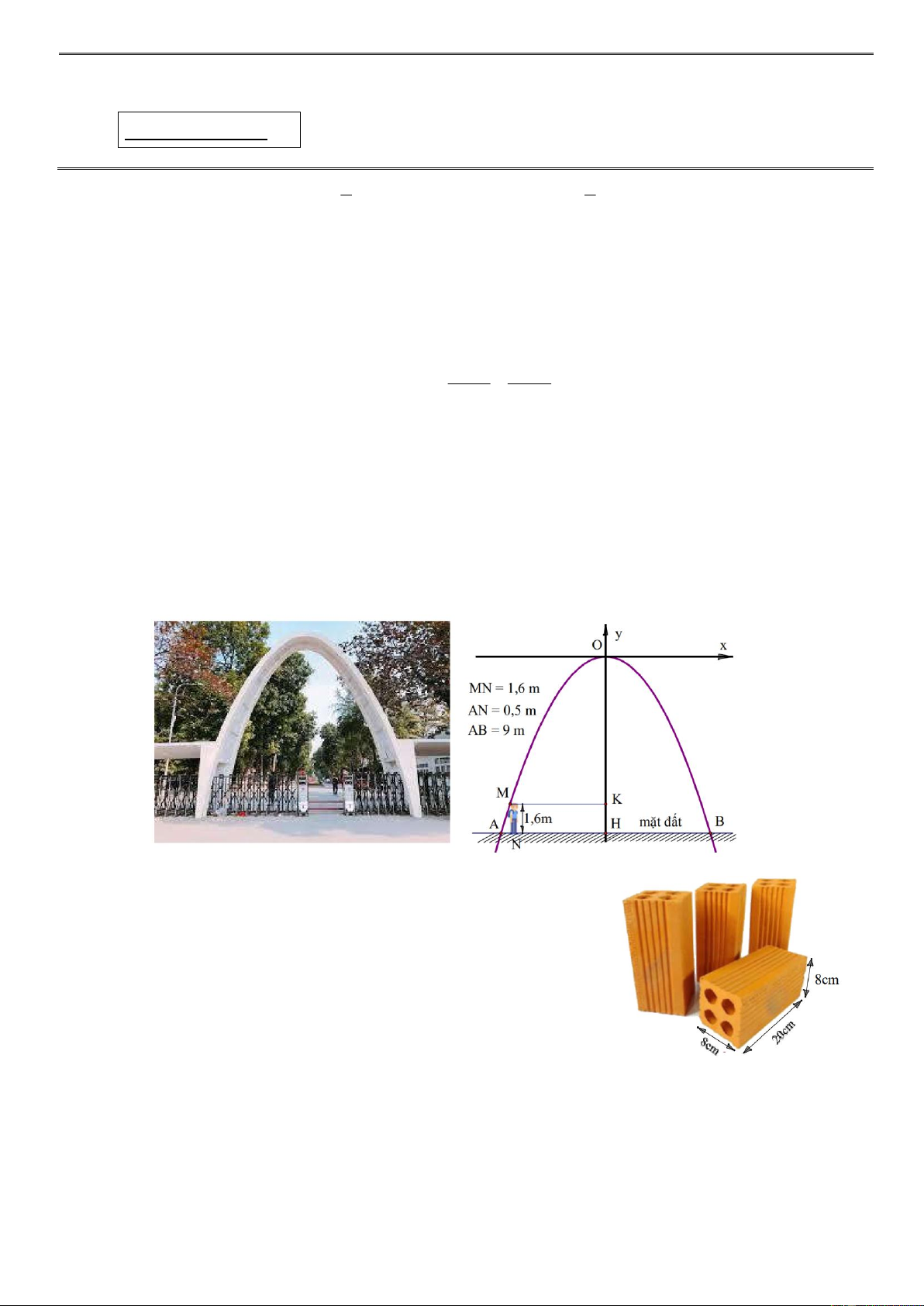
Câu 3. (1 điểm). Với thiết kế độc đáo, cổng Parabol trường Đại học Bách Khoa Hà Nội được xây
dựng cách đây hơn 50 năm và đã từng là niềm tự hào của tri thức thế hệ mới. Để đo chiều
cao của cổng một bạn sinh viên cao 1, 6m đứng cách chân cổng 0, 5m thì đỉnh đầu bạn ấy
vừa chạm vào cổng. Biết khoảng cách giữa hai chân cổng là 9m . Hãy tính chiều cao cổng
Parabol (làm tròn một chữ số thập phân)
Câu 4. (0,75 điểm). Gạch ống là một sản phẩm được tạo hình
thành từ đất sét và nước, được kết hợp lại với nhau theo
một công thức chung hợp lý mới có thể tạo ra hỗn hợp dẻo
quánh, sau đó chúng được đổ vào khuôn, rồi đem phơi
hoặc sấy khô và cuối cùng là đưa vào lò nung. Một viên
gạch hình hộp chữ nhật có kích thước dài 20cm , rộng
8cm . Bên trong có bốn lỗ hình trụ bằng nhau có đường kính 2, 5cm .
a) Tính thể tích đất sét để làm một viên gạch. (lấy p = 3,14 ) Trang 1
Theo toán học, bác Ba muốn xây một ngôi nhà phải mua 10 thiên gạch, giá một viên là 1100
đồng. Nhưng khi thi công, bác Ba phải mua dư 2% số gạch cần dùng dự phòng cho hư hao.
Tính số tiền bác Ba mua gạch để xây căn nhà, biết 1 thiên gạch là 1000 viên.
Câu 5. (1 điểm). Một nhóm học sinh tham gia hoạt động ngoại khóa được chia thành các tổ để sinh
hoạt. Nếu mỗi tổ có 7 nam và 7 nữ thì thừa 8 bạn nam. Nếu mỗi tổ có 6 nam và 5 nữ thì
thừa 12 nữ. Hỏi có bao nhiêu học sinh nam và bao nhiêu học sinh nữ?
Câu 6. (1 điểm). Trong một đợt khuyến mãi, siêu thị giảm giá cho mặt hàng A là 20% và mặt
hàng B là 15% so với giá niêm yết. Một khách hàng mua 2 món hàng A và 1 món hàng
B phải trả số tiền là 362 000 đồng. Nhưng nếu mua trong khung giờ vàng thì món hàng
A được giảm giá 30% còn món hàng B được giảm giá 25% so với giá niêm yết. Một
người mua 3 món hàng A và 2 món hàng B trong khung giờ vàng nên chỉ trả số tiền là
552 000 đồng. Tính giá niêm yết của mỗi món hàng A và B .
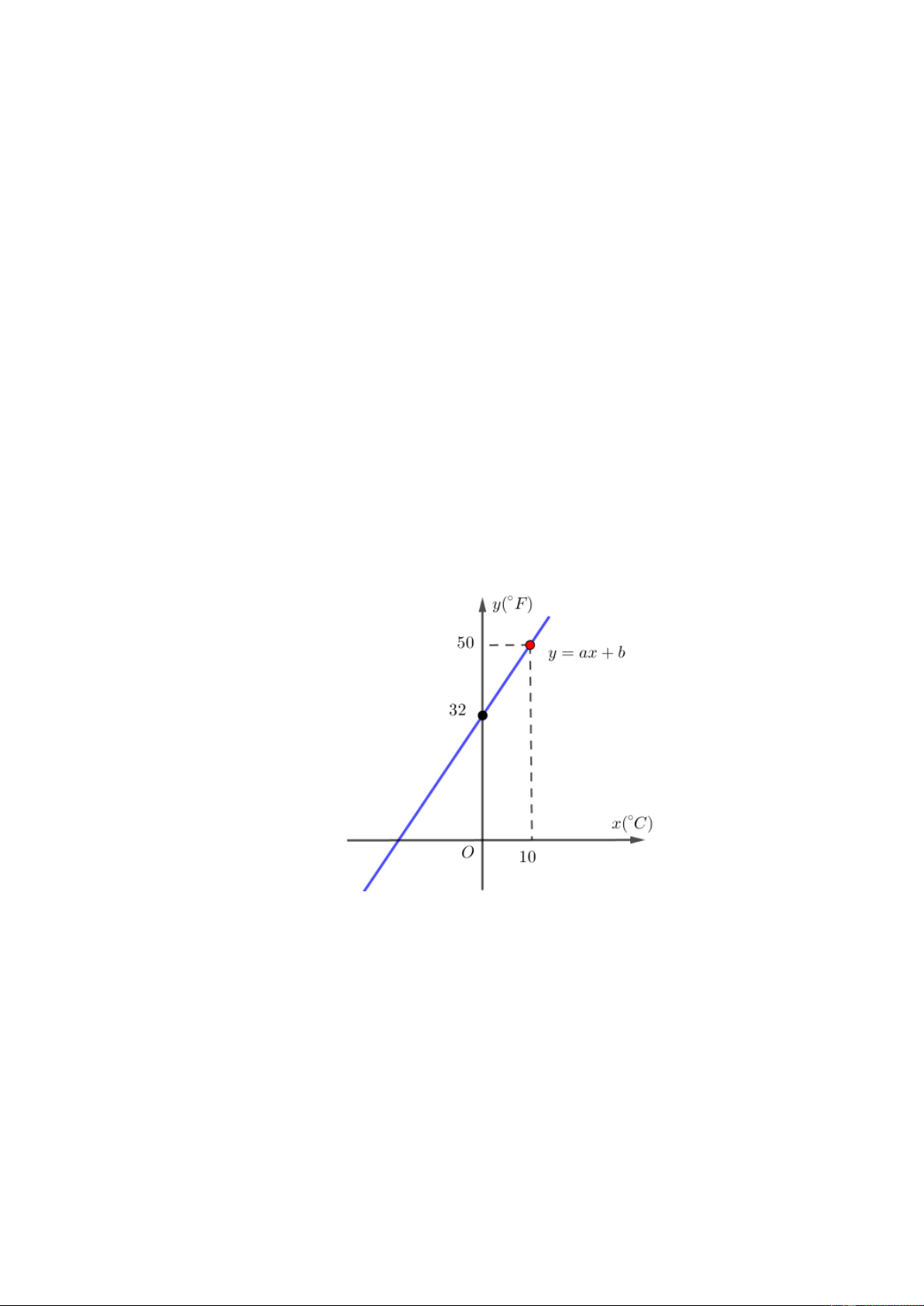
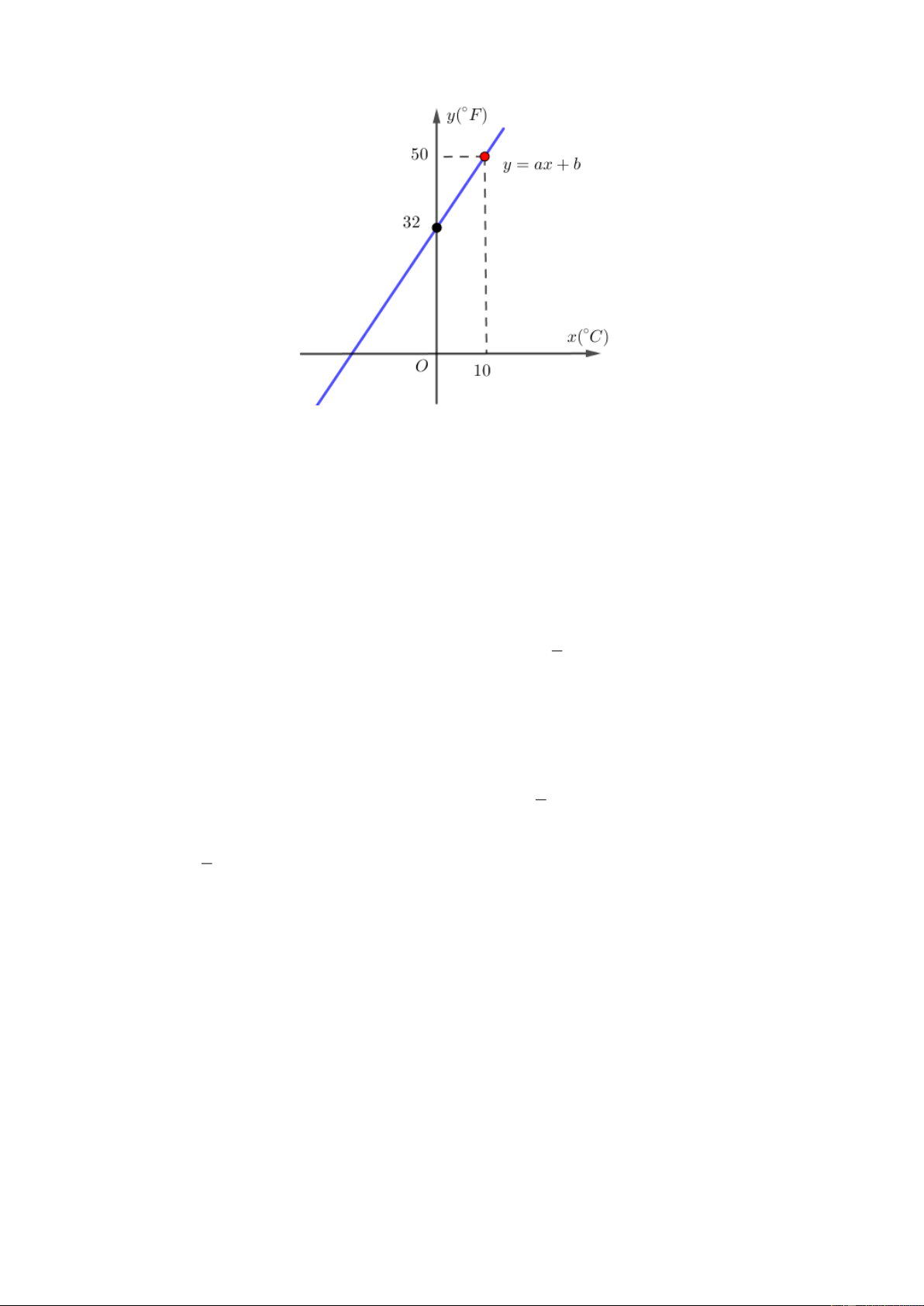
Câu 7. (1 điểm). Mối quan hệ giữa thang nhiệt độ y (độ F - Fahrenheit ) và thang nhiệt độ x (độ
C - Celsius ) được cho bởi hàm số bậc nhất y = ax + b .
a) Tìm a và b .
b) Trong không khí, tốc độ âm thanh v (tính bằng mét/giây) là một hàm số bậc nhất theo
nhiệt độ t (tính bằng C o
được cho bởi công thức: v = 0, 06t + 331 . Hãy tính tốc độ âm
thanh tại nơi có nhiệt độ không khí là 0 C ° , 77 F ° .
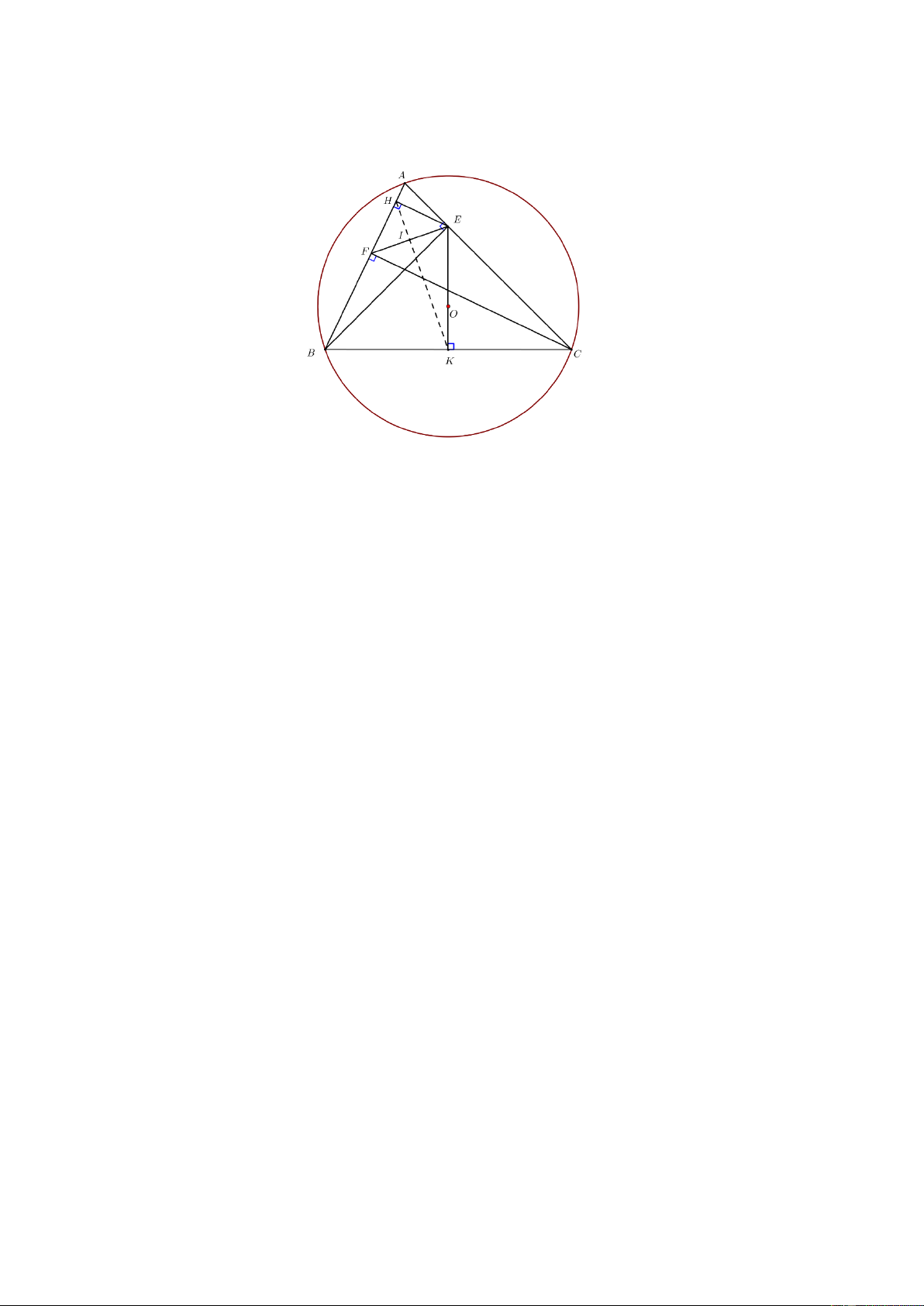
Câu 8. (3 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O , kẻ đường cao BE
của DA BC . Gọi H và K lần lượt là chân các đường vuông góc kẻ từ E đến A B và B C .
a) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
b) Chứng minh: BH .BA = BK .BC . Trang 2
c) Kẻ đường cao CF của tam giác A BC (F Î A B ) và I là trung điểm của EF . Chứng
minh ba điểm H , I , K thẳng hàng. ----HẾT--- Trang 3 HƯỚNG DẪN GIẢI 1 3
Câu 1. Cho P : y 2
x và đường thẳng d : y x 2 . 4 2
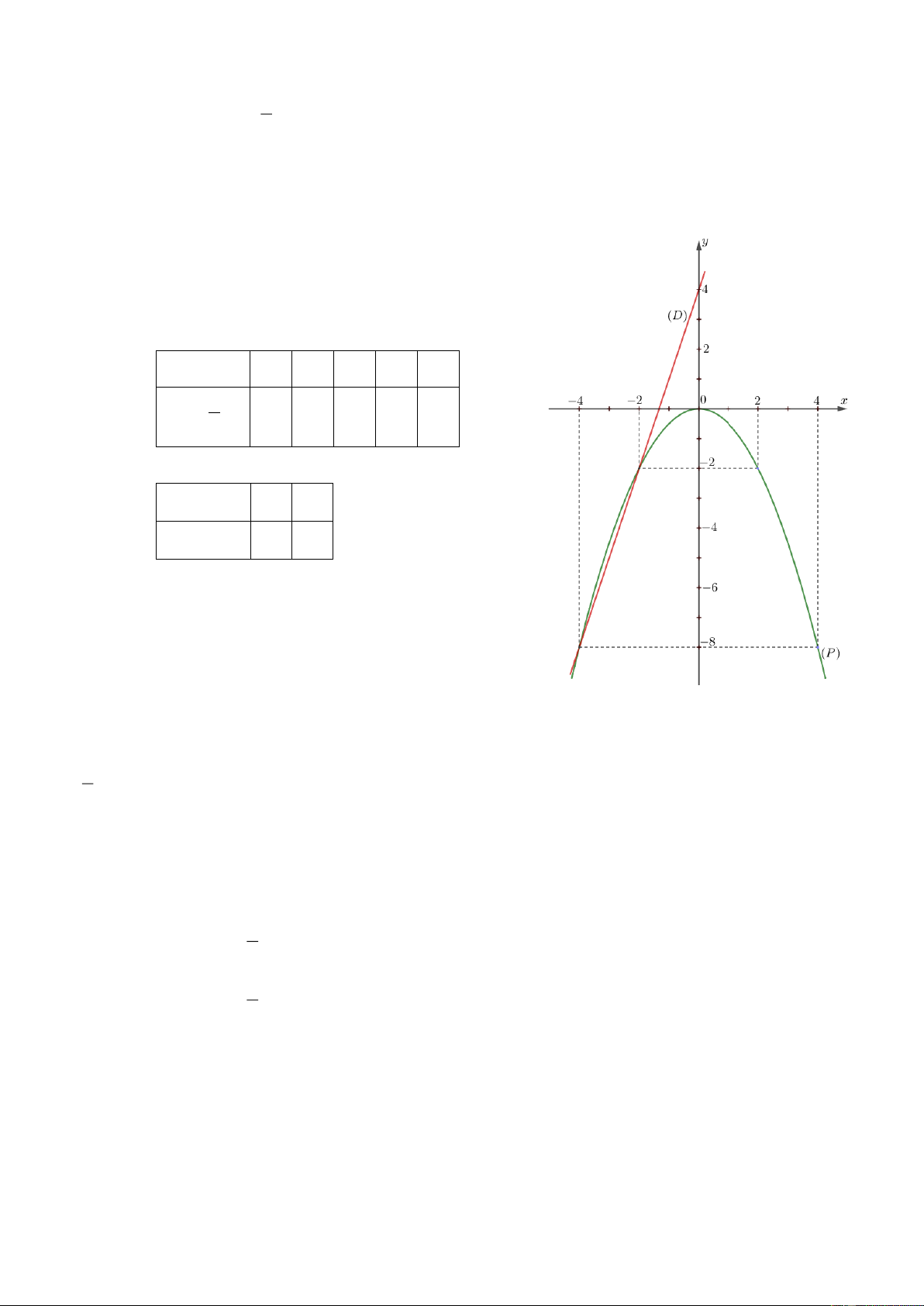
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. a) BGT: x 4 2 0 2 4 y 1 2 x 4 1 0 1 4 4 x 0 2
y 3 x 2 2 1 2
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 1 2
x 3 x 2 4 2 2
x 6x 8 0 x 4 x 2 1 1
Thay x 4 vào y 2
x , ta được: y 2 .4 4 . 4 4 1 1
Thay x 2 vào y 2
x , ta được: y 2 .2 1. 4 4
Vậy 4; 4 , 2;
1 là hai giao điểm cần tìm.
Câu 2. Cho phương trình 2
2x 6x 1 0 có 2 nghiệm là x ,x . Không giải phương trình, hãy tính 1 2 x 2 x 2
giá trị của biểu thức A 1 2 . x 1 x 1 2 1 Lời giải Ta có: ac = 2.(- )
1 < 0 nên phương trình có hai nghiệm phân biệt x ,x . 1 2 Trang 4 b 6
S x x 3 1 2
Theo định lí Vi-et, ta có: a 2 c
P x .x 1 1 2 a 2 x 2 x 2 Ta có: A 1 2 x 1 x 1 2 1 x 2 x A 2 1 2 x 1 x 1 2 1
x 2 x 1 x 2 x 1 1 1 2 2 x 1 x 1 2 1 2
x x 2x 2 2
x x 2x 2 1 1 1 2 2 2
x x x x 1 2 1 2 1 2 x 2 x 3 x x 4 1 2 1 2 x x x x 1 1 2 1 2 2
S 2P 3S 4 P S 1 1 2 3 2 3.3 4 2 1 31 2 2
Câu 3. Với thiết kế độc đáo, cổng Parabol trường Đại học Bách Khoa Hà Nội được xây dựng cách
đây hơn 50 năm và đã từng là niềm tự hào của tri thức thế hệ mới. Để đo chiều cao của
cổng một bạn sinh viên cao 1,6m đứng cách chân cổng 0,5m thì đỉnh đầu bạn ấy vừa chạm
vào cổng. Biết khoảng cách giữa hai chân cổng là 9m. Hãy tính chiều cao cổng Parabol
(làm tròn một chữ số thập phân) Lời giải A B Ta có: A H =
= 4, 5m ; MK = NH = A H - A N = 4, 5 - 0, 5 = 4m . 2
Đặt hệ trục Oxy như hình vẽ, ta thấy đồ thị của hàm số 2 y = ax
Đặt OH = h (h > ) 0 æ 9 ö ç ÷
Đồ thị của hàm số đi qua hai điểm A - ç ;- h÷ ç ÷
M - 4;- (h - 1, 6) ç và ( ) . è 2 ÷ ø
Thay hai điểm A và M vào hàm số ta có hệ phương trình: Trang 5 2 ìï ì æ ö ï 81 ï 9 ï ç ÷ ï ï - = . - ç ÷ ï - h = a h a ï ç ÷ ï ç ÷ 4 í è 2ø Û í ï ï 81 ï ï ï - ( - )= (- ï )2 ï a + 1, 6 = 16 1, 6 . 4 a h a ï ïî ïî 4 ìï 32 ïïa = - ï Ta giải tìm được 85 íï 648 ïï h = » 7, 6m ïïî 85
Vậy chiều cao cổng Parabol là 7, 6m .
Câu 4. Gạch ống là một sản phẩm được tạo hình thành từ đất sét và nước, được kết hợp lại với
nhau theo một công thức chung hợp lý mới có thể tạo ra hỗn hợp dẻo quánh, sau đó chúng
được đổ vào khuôn, rồi đem phơi hoặc sấy khô và cuối cùng là đưa vào lò nung. Một viên
gạch hình hộp chữ nhật có kích thước dài 20cm, rộng 8cm. Bên trong có bốn lỗ hình trụ
bằng nhau có đường kính 2,5cm.
a. Tính thể tích đất sét để làm một viên gạch. (lấy p = 3,14 )
b. Theo toán học, bác Ba muốn xây một ngôi nhà phải mua 10 thiên gạch, giá một viên
là 1100 đồng. Nhưng khi thi công, bác Ba phải mua dư 2% số gạch cần dùng dự
phòng cho hư hao. Tính số tiền bác Ba mua gạch để xây căn nhà, biết 1 thiên gạch là 1000 viên. Lời giải
a) -Thể tích đất sét làm viên gạch hình hộp chữ nhật chưa trừ bốn lỗ rỗng bên trong là: V = = ( 3 8.8.20 320 cm ) 2 2 æ , 5ö ç ÷
Thể tích của bốn lỗ hình trụ bằng nhau là: 2
V = pR h = 3, 14.ç ÷ .20 = 98,125 ç ÷ ( 3 cm 1 ) çè 2 ÷ø
Thể tích đất sét để làm một viên gạch là: V = V - V = 320 - 98,125 » 221, 9( 3 cm 2 1 )
b) Số viên gạch bác Ba cần mua là: 10.1000.(1 + 2 ) % = 10200 (viên gạch)
Số tiền bác Ba mua gạch để xây căn nhà là: 10200.1100 = 11220000 (đồng)
Câu 5. Một nhóm học sinh tham gia hoạt động ngoại khóa được chia thành các tổ để sinh hoạt.
Nếu mỗi tổ có 7 nam và 7 nữ thì thừa 8 bạn nam. Nếu mỗi tổ có 6 nam và 5 nữ thì thừa 12
nữ. Hỏi có bao nhiêu học sinh nam và bao nhiêu học sinh nữ? Lời giải
Gọi x, y (số tổ) lần lượt là số tổ trong trường hợp 1 và trường hợp 2 . Trang 6 Điều kiện: * x, y Î ¥
Nếu mỗi tổ có 7 nam và 7 nữ thì thừa 8 bạn nam nên số học sinh nam là 7x + 8 (học sinh) và
số học sinh nữ là 7x (học sinh).
Nếu mỗi tổ có 6 nam và 5 nữ thì thừa 12 nữ thì số học sinh nam là 6y (học sinh) và số học sinh
nữ là 5y + 12 (học sinh). ìï 7x + 8 = 6y ï
Ta có hệ phương trình: íï 7x = 5y + 12 ïî
Giải hệ phương trình ta được x = 16;y = 20 (nhận)
Vậy số học sinh nam là 120 học sinh, số học sinh nữ là 112 học sinh.
Câu 6. Trong một đợt khuyến mãi, siêu thị giảm giá cho mặt hàng A là 20% và mặt hàng B là 15%
so với giá niêm yết. Một khách hàng mua 2 món hàng A và 1 món hàng B phải trả số tiền là
362 000 đồng. Nhưng nếu mua trong khung giờ vàng thì món hàng A được giảm giá 30%
còn món hàng B được giảm giá 25% so với giá niêm yết. Một người mua 3 món hàng A và 2
món hàng B trong khung giờ vàng nên chỉ trả số tiền là 552 000 đồng. Tính giá niêm yết của mỗi món hàng A và B. Lời giải
Gọi x, y (đồng) lần lượt là giá niêm yết của món hàng A và món hàng B .
Điều kiện: x, y > 0 ìï 2.x ï
(1 - 20%)+ y (1 - 15%) = 362 000
Theo đề ta có hệ phương trình: íï 3.x. ï
(1 - 30%)+ 2.y.(1 - 25%) = 552 000 ïî
ìï 1, 6x + 0, 85y = 362 000 ï
Û íï 2,1x + 1,5y = 552000 ïî ì ï x = 120 000 ï Û í (n ) ï y = 200 000 ïî
Vậy giá niêm yết của món hàng A là 120 000 đồng, của món hàng B là 200 000 đồng.
Câu 7. Mối quan hệ giữa thang nhiệt độ y (độ F - Fahrenheit ) và thang nhiệt độ x
(độ C - Celsius ) được cho bởi hàm số bậc nhất y = ax + b .
a. Tìm a và b .
b. Trong không khí, tốc độ âm thanh v (tính bằng mét/giây) là một hàm số bậc nhất theo
nhiệt độ t (tính bằng C o
) được cho bởi công thức: v = 0, 06t + 331 . Hãy tính tốc độ âm
thanh tại nơi có nhiệt độ không khí là 0 C o , 77oF . Trang 7 Lời giải ìï x = 0 ï a) Thay íï
vào y = ax + b ta có: . a 0 + b = 32 ( ) 1 . y = 32 ïî ìï x = 10 ï Thay í 2 ï
vào y = ax + b ta có: .
a 10 + b = 50 ( ). y = 50 ïî 9 Từ ( )
1 và (2), giải hệ phương trình ta được: a = ;b = 32 . 5 b) Với t = 0 C o
thay vào công thức v = 0, 06t + 331 ta có v = 0, 06.0 + 331 = 331(m / s) 1 1 . 9
Với t = 77oF thay y = 77 vào công thức y = x + 32 ta có 2 5 9 77 =
x + 32 Û x = 25 C ° Þ t = 25 C ° 2 5 Thay t = 25 C
° vào công thức v = 0, 06t + 331ta có v = 0, 06.25 + 331 = 332, 5(m / s) 2 2 .
Vậy tốc độ âm thanh tại nơi có nhiệt độ không khí 0 C
° là 331m / s , tại nơi có nhiệt độ không khí 77 F
° là 332, 5m / s .
Câu 8. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O , kẻ đường cao BE của
DA BC . Gọi H và K lần lượt là chân các đường vuông góc kẻ từ E đến A B và B C .
a. Chứng minh tứ giác BHEK là tứ giác nội tiếp.
b. Chứng minh: BH .BA = BK .BC . Trang 8
c. Kẻ đường cao CF của tam giác A BC (F Î A B ) và I là trung điểm của EF . Chứng
minh ba điểm H , I , K thẳng hàng.
a) Chứng minh tứ giác BHEK nội tiếp
Xét tứ giác BHEK , có: BHE 90 EH AB EKB
90 EK BC
BHE EKB 180
Tứ giác BHEK nội tiếp vì có hai góc đối bù nhau.
b) Chứng minh BH .BA = BK .BC
Xét D A EB vuông tại E (BE ^ A C ), có EH là đường cao (EH ^ A B ) 2
EB BH.BA (HTL) ( ) 1
Xét DBEC vuông tại E (BE ^ A C ), có EK là đường cao (EK ^ BC ) 2
EB BK.BC (HTL) (2) Từ ( )
1 và (2), suy ra: BH BA = BK BC ( 2 . . = EB )
c) Kẻ đường cao CF của tam giác A BC (F Î AB ) và I là trung điểm của EF . Chứng
minh ba điểm H , I , K thẳng hàng. · · ¼
Ta có: tứ giác BHEK nội tiếp Þ BHK = BEK ( 2 góc nội tiếp cùng chắn BK )
D FHE vuông tại H (EH ^ A B ) có HI là đường trung tuyến ứng với cạnh EF Trang 9
( I là trung điểm của EF ) EF Þ HI = IF = 2 Þ D · ·
HIF cân tại I Þ FHI = IFH ( ) 3
Xét tứ giác BFEC có ·
BFC = 90o (CF ^ A B ) ·
BEC = 90o (BE ^ A C ) · ·
Þ BFC = BEC = 90o
Mà hai góc này liên tiếp cùng nhìn cạnh B C
Þ tứ giác BFEC nội tiếp · ·
Þ HFE = ECB (góc trong bằng góc đối ngoài) (4) · · ·
Mặt khác ECB = BEK (cùng phụ KEC ) (5) · · Từ ( )
3 , (4) và (5), suy ra: FHI = BEK ìï · · ï BHK = BEK ï (cmt ) · · Ta có: í ï · · Þ BHK = FHI
ï FHI = BEK (cmt ) ïî
Þ H , I , K thẳng hàng. ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 1
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 1 - 2
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 1. Cho P : y 2
x và đường thẳng d : y 3x 4 . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. Cho phương trình 2
x mx 2 2 2
m 0 ( m là tham số) 1
a) Tìm m để phương trình 1 có hai nghiệm x ; x ? 1 2
b) Với giá trị nào của m thì hai nghiệm x ; x của phương trình 1 thỏa x x 4 2x x 1 2 1 2 1 2 Trang 10
Câu 3. Trong lễ phát động phong trào trồng cây nhân dịp kỷ niệm ngày sinh Bác Hồ, lớp 9A
được giao trồng 360 cây. Khi thực hiện có 4 bạn được điều đi làm việc khác, nên mỗi học
sinh còn lại phải trồng thêm một cây so với dự định. Hỏi lớp 9A có bao nhiêu học sinh?
(Biết số cây trồng của mỗi học sinh như nhau)
Câu 4. Hai người A và B cùng ở một phía và cách thành phố Hồ Chí Minh 50km . Cả hai người
cùng nhau đi trên một con đường về phía ngược hướng với thành phố, người A đi với vận
tốc 30km / h và người B đi với vận tốc 45km / h . Gọi d km là khoảng cách từ thành phố
Hồ Chí Minh đến hai người A và B sau khi đi được t giờ.
a) Lập hàm số của d theo t đối với mỗi người.
b) Hỏi nếu hai người xuất phát cùng một lúc thì vào thời điểm nào kể từ lúc xuất phát,
khoảng cách giữa hai người là 30km .
Câu 5. Bà Tám vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời hạn 1 năm. Lẽ ra đúng
1 năm sau bà phải trả cả tiền vốn lẫn tiền lãi, song bà đã được ngân hàng cho kéo dài thời
hạn thêm 1 năm nữa, số tiền lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm
sau và lãi suất vẫn như cũ. Hết 2 năm bà tám phải trả tất cả 605 triệu đồng. Hỏi lãi suất
cho vay của ngân hàng đó là bao nhiêu phần trăm một năm?
Câu 6. Dây cu-roa là một trong những bộ truyền được sử dụng rộng rãi trong công nghiệp. Chiều d d d d 1 2 2 1 2
dài dây cu-roa được xác định theo công thức: L 2a 2 4a Trong đó:
L : Chiều dài dây cu-roa. a : Khoảng cách tâm của 2 pu-ly.
d : Đường kính của pu-ly 1 (hình tròn nhỏ màu vàng). 1
d : Đường kính của pu-ly 2 (hình tròn nhỏ màu vàng) 2 Trang 11
Cho d 10cm , d 20cm , a 60cm 1 2
Tính chiều dài của một đoạn dây cu-roa.
Gọi AB là chiều dài một đoạn dây cu-roa, trong đó A, B lần lượt là tiếp điểm trên dây cua-roa với
2 đường tròn tạo bởi mặt cắt của 2 pu-ly. Tính AB
Câu 7. Một bình đựng đầy nước có dạng hình nón (không có
đáy). Người ta thả vào đó một khối cầu có đường kính
bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là 3
18 dm . Biết rằng khối cầu tiếp xúc với tất
cả các đường sinh của hình nón và đúng một nửa của khối
cầu đã chìm trong nước ( hình dưới đây). Tính thể tích
nước còn lại trong bình.
Câu 8. Cho đường tròn tâm O đường kính AB . Kẻ dây cung CD
vuông góc với AB tại H ( H nằm giữa A và O , H khác A và O ). Lấy điểm G thuộc
CH ( G khác C và H ), tia AG cắt đường tròn tại E khác A . Gọi K là giao điểm của hai
đường thẳng BE và CD
a) Chứng minh tứ giác BEGH nội tiếp và K . C KD K . E KB .
b) Đoạn thẳng AK cắt đường tròn tâm tại F khác A . Chứng minh: G là tâm đường tròn
nội tiếp tam giác HEF
c) Gọi M, N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF . Chứng HE HF minh: 1 . MN ----HẾT--- Trang 12 HƯỚNG DẪN GIẢI 1
Câu 1. Cho P : y 2
x và đường thẳng d : y 3x 4 . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: x 8 2 0 2 4 y 1 2
x 8 2 0 2 8 2 x 0 2 y 3x 4 4 2
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 1 2 x 3x 4 2 2
x 6x 8 0 x 2 x 4 1
Thay x 2 vào y 2
x , ta được: y 2 . 2 1
Thay x 4 vào y 2
x , ta được: y 8 . 2
Vậy 2; 2 , 4; 8 là hai giao điểm cần tìm. Câu 2.
Cho phương trình 2
x mx 2 2 2
m 0 ( m là tham số) 1
a) Tìm m để phương trình 1 có hai nghiệm x ; x ? 1 2 Trang 13
b) Với giá trị nào của m thì hai nghiệm x ; x của phương trình 1 thỏa 1 2
x x 4 2x x 1 2 1 2 Lời giải
a) Tìm m để phương trình 1 có hai nghiệm x ; x ? 1 2 2
Ta có: m 2 ' 2 m 4m 4
Để phương trình có có hai nghiệm x ; x thì ' 0 4m 4 0 m 1 1 2
b) Với giá trị nào của m thì hai nghiệm x ; x của phương trình 1 thỏa 1 2
x x 4 2x x 1 2 1 2
Khi m 1 , áp dụng hệ thức Vi-et ta có: b S x x 4m 4 1 2 a c P x x 2 m 1 2 a
Ta có: x x 4 2x x 1 2 1 2 4m 4 4 2 2m 2 2m 4m 2 2m 4m
khi 1 m 0 2 2m 4m khi 0 m
m 0; m 2 khi 1 m 0
m 0; m 2 khi 0 m m 0
Câu 3. Trong lễ phát động phong trào trồng cây nhân dịp kỷ niệm ngày sinh Bác Hồ, lớp 9A
được giao trồng 360 cây. Khi thực hiện có 4 bạn được điều đi làm việc khác, nên mỗi học
sinh còn lại phải trồng thêm một cây so với dự định. Hỏi lớp 9A có bao nhiêu học sinh?
(Biết số cây trồng của mỗi học sinh như nhau) Lời giải
Gọi số học sinh của lớp 9A là x x N * 360
Số cây trồng mà mỗi học sinh phải trồng dự định là: x 360
Sau khi 4 bạn được điều đi làm việc khác, nên mỗi học sinh còn lại phải trồng: x 4 360 360 Ta có: 1 x x 4 Trang 14
360x 4 xx 4 360x 2
x 4x 1440 0 x 36 L 1 x 40 N 2
Vậy lớp 9A có 40 học sinh
Câu 4. Hai người A và B cùng ở một phía và cách thành phố Hồ Chí Minh 50km . Cả hai người
cùng nhau đi trên một con đường về phía ngược hướng với thành phố, người A đi với vận
tốc 30km / h và người B đi với vận tốc 45km / h . Gọi d km là khoảng cách từ thành phố
Hồ Chí Minh đến hai người A và B sau khi đi được t giờ.
a) Lập hàm số của d theo t đối với mỗi người.
b) Hỏi nếu hai người xuất phát cùng một lúc thì vào thời điểm nào kể từ lúc xuất phát,
khoảng cách giữa hai người là 30km . Lời giải
a) Hàm số của d theo t đối với người A là: d 30t 50
Hàm số của d theo t đối với người B là: d 45t 50
b) Nếu khoảng cách giữa hai người là 30km thì: 45t 50 30t 50 30 t 2
Hai người xuất phát cùng một lúc thì sau 2h kể từ lúc xuất phát, khoảng cách giữa hai người là 30km .
Câu 5. Bà Tám vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời hạn 1 năm. Lẽ ra đúng
1 năm sau bà phải trả cả tiền vốn lẫn tiền lãi, song bà đã được ngân hàng cho kéo dài thời
hạn thêm 1 năm nữa, số tiền lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm
sau và lãi suất vẫn như cũ. Hết 2 năm bà tám phải trả tất cả 605 triệu đồng. Hỏi lãi suất
cho vay của ngân hàng đó là bao nhiêu phần trăm một năm? Lời giải
Gọi lãi suất của ngân hàng là %
x /năm x 0 .
Số tiền phải trả của bà Tám sau một năm là: 500.1 %
x 500 5x .
Số tiền phải trả của bà Tám sau hai năm là:
x x x x 2 500 5 1 % 500 5 5 0,05x . Trang 15
Theo đề: sau hai năm bà Tám phải trả tất cả 605 triệu đồng nên ta có: 2
0,05x 10x 500 605 2
0,05x 10x 105 0
x 210 L 1 x 10 N 2
Vậy lãi suất cho vay của ngân hàng đó là 10%/năm.
Câu 6. Dây cu-roa là một trong những bộ truyền được sử dụng rộng rãi trong công nghiệp. Chiều d d d d 1 2 2 1 2
dài dây cu-roa được xác định theo công thức: L 2a 2 4a Trong đó:
L : Chiều dài dây cu-roa.
a : Khoảng cách tâm của 2 pu-ly.
d : Đường kính của pu-ly 1 (hình tròn nhỏ màu vàng) 1
d : Đường kính của pu-ly 2 (hình tròn nhỏ màu vàng) 2
Cho d 10cm , d 20cm , a 60cm 1 2
Tính chiều dài của một đoạn dây cu-roa.
Gọi AB là chiều dài một đoạn dây cu-roa, trong đó A, B lần lượt là tiếp điểm trên dây cua-roa với
2 đường tròn tạo bởi mặt cắt của 2 pu-ly. Tính AB Lời giải d d d d 1 2 2 1 2
Thay d 10cm , d 20cm , a 60cm vào L 2a 1 2 2 4a 2 10 20 20 10 L 2.60 2 4.60 2 10 20 20 10 .20 .10 2.60
Chiều dài đoạn AB là: 2 4.60 2 2 60,21cm 2
Vậy chiều dài đoạn AB là 60,21cm. Trang 16
Câu 7. Một bình đựng đầy nước có dạng hình nón (không có
đáy). Người ta thả vào đó một khối cầu có đường kính
bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là 3
18 dm . Biết rằng khối cầu tiếp xúc với tất
cả các đường sinh của hình nón và đúng một nửa của khối
cầu đã chìm trong nước ( hình dưới đây). Tính thể tích
nước còn lại trong bình. Lời giải
Gọi R là bán kính của khối cầu. 1 4
Thể tích nước tràn ra là: 3 R
18 R 3dm . 2 3
Chiều cao của bình nước là: h 2R 6dm . 1 1 1
Gọi r là bán kính đáy của bình hình nón thì
r 2 3dm . 3 2 2 r h R 1
Thể tích bình hình nón: V 2 r h 3 24 dm . 3
Thể tích nước tràn ra là: 3 24 18 6 dm .
Câu 8. Cho đường tròn tâm O đường kính AB . Kẻ dây cung CD vuông góc với AB tại H ( H
nằm giữa A và O , H khác A và O ). Lấy điểm G thuộc CH ( G khác C và H ), tia AG
cắt đường tròn tại E khác A . Gọi K là giao điểm của hai đường thẳng BE và CD
a) Chứng minh tứ giác BEGH nội tiếp và K . C KD K . E KB .
b) Đoạn thẳng AK cắt đường tròn tâm tại F khác A . Chứng minh: G là tâm đường tròn
nội tiếp tam giác HEF
c) Gọi M, N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF . Chứng HE HF minh: 1. MN Trang 17
a) Chứng minh tứ giác BEGH nội tiếp và K . C KD K . E KB .
Xét tứ giác BEGH , có: BHG 90 GT BEG
90 AB 2R
BHG BEG 180
Mà BHG ; BEG đối nhau
Tứ giác tứ giác BEGH nội tiếp.
Xét KDE và KCB ta có:
KBC KDE (cùng chắn EC ) K chung
KDE# KBC g g
KD KE (tỉ số đồng dạng) KB KC K . D KC K . E KB.
b) Đoạn thẳng AK cắt đường tròn tâm tại F khác A . Chứng minh: G là tâm đường tròn
nội tiếp tam giác HEF
Ta có: KAB có ba đường cao AE,BF,KH đồng quy tại G . Suy ra G là trực tâm của KAB .
Ta có: GHE GBE 1 sdGE ( trong đường tròn BEGH ) 2
Ta có: GBE GAF 1 sdEF 2
Ta có: GAF GHF 1 sdEG (tứ giác AFGH nội tiếp) 2 Trang 18
Suy ra: GHE GHF HG là tia phân giác của EHF
Tương tự EG là tia phân giác của FEG Ta có: E
HF có 2 tia phân giác HG và EG nên G là tâm đường tròn nội tiếp EHF .
c) Gọi M, N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF . Chứng HE HF minh: 1 . MN
Gọi Q là giao điểm của tia EH và O
Ta có: EOB 2BFE sdE ;
B 2BFE EFO (do FG là tia phân giác của EFH )
EOB EFH tứ giác EFHO nội tiếp
FOH FEH 1 sdQE 1 FOQ FOH 1 FOQ 2 2 2
OH là tia phân giác của FOQ
Ta có: OFH ; OQH có OH chung, OF OQ, FOH QOH
OFH OQH HF HQ
Do đó: HE HF HE HQ EQ
Ta có: AMN MNT NTA 90 tứ giác AMNT là hình chữ nhật, nên AT MN
AQ FA ET AE//QT mà AETQ nội tiếp O
AETQ là hình thang cân EQ AT MN HE HF HE HF MN hay 1 MN
SỞ GD&ĐT TP. HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 1
NĂM HỌC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 1- 3
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 9. (1,5 điểm). Cho P y 2 :
x và đường thẳng d : y 3x 2 .
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Trang 19
Câu 10. (1 điểm). Cho phương trình x x 2 3 4
2x 1 có 2 nghiệm là x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức A 2 x 2 x 3x x . 1 2 1 2
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 11. (1 điểm). Nước biển là dung dịch có nồng độ muối là 3, 5% (giả sử không có tạp chất). Có
10kg nước biển. Hỏi phải thêm bao nhiêu kg nước (nguyên chất) để được dung dịch có nồng độ 2%.
Câu 12. (0,75 điểm). Nhân dịp Lễ giỗ tổ Hùng Vương, một siêu thị điện máy đã giảm giá nhiều mặt
hàng để kích cầu mua sắm. Giá niêm yết một tủ lạnh và một máy giặt có tổng số tiền là
25, 4 triệu đồng nhưng trong dịp này giá một tủ lạnh giảm 40% giá bán và giá một máy
giặt giảm 20% giá bán nên cô Liên đã mua hai món đồ trên với tổng số tiền là 16, 77 triệu
đồng. Hỏi giá mỗi món đồ trên khi chưa giảm giá là bao nhiêu tiền?
Câu 13. (1 điểm). Người ta nuôi cá trong một bể xây, mặt bể là hình chữ nhật chiều dài 60m , chiều
rộng 40m . Trên mỗi đơn vị diện tích mặt bể người ta thả 12 con cá giống, đến mỗi kỳ thu
hoạch, trung bình mỗi con cá cân nặng 240g . Khi bán khoảng 30000 đồng/kg và thấy lãi
qua kỳ thu hoạch này là 100 triệu. Hỏi vốn mua cá giống và các chi phí trong đợt này
chiếm bao nhiêu phần trăm so với giá bán (làm tròn 1 chữ số thập phân).
Câu 14. (1 điểm). Để tính toán thời gian một chu kỳ đong đưa (một chu kỳ đong đưa dây đu được
tính từ lúc dây đu bắt đầu được đưa lên cao đến khi dừng hẳn) của một dây đu, người ta L
sử dụng công thức T = 2p
. Trong đó, T là thời gian một chu kỳ đong đưa (s), L là g
chiều dài của dây đu (m ), 2
g = 9, 81 m / s .
a) Một sợi dây đu có chiều dài 2 +
3 m , hỏi chu kỳ đong đưa dài bao nhiêu giây?
b) Một người muốn thiết kế một dây đu sao cho một chu kỳ đông đưa kéo dài 4 giây. Hỏi
người đó phải làm một sợi dây đu dài bao nhiêu?
Câu 15. (1 điểm). Máy kéo nông nghiêp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh
xa sau có đường kính là 1, 672m và bánh xe trước có đường kính là 88cm . Hỏi khi bơm
căng, bánh xe sau lăn được 10 vòng thì bánh xe trước lăn được mấy vòng?
Câu 16. (3 điểm) Cho tam giác ABC AB AC có ba góc nhọn nội tiếp đường tròn O . Các
đường cao AD, BE, CF cắt nhau tại H . Tia EF cắt tia CB tại K .
a) Chứng minh tứ giác BFEC nội tiếp và K . F KE K . B KC . Trang 20
b) Đường thẳng KA cắt (O ) tại M . Chứng minh tứ giác A EFM nội tiếp.
c) Gọi N là trung điểm của BC . Chứng minh M, H , N thẳng hàng. ----HẾT--- HƯỚNG DẪN GIẢI
Câu 3. (1,5 điểm) Cho P y 2 :
x và đường thẳng d : y 3x 2 .
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
c) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. b) BGT: y x 2 1 0 1 2 2 y x 4 1 0 1 4 4 x 0 1 1 x
y 3x 2 2 1 –2 –1 0 1 2
d) Tìm tọa độ giao điểm của P và d bằng phép tính. –2
Phương trình hoành độ giao điểm của P và d : 2 x 3x 2 2
x 3x 2 0 x 1 x 2 Thay x 1 vào 2 y
x , ta được: y 2 1 1 . Thay x 4 vào 2 y
x , ta được: y 2 2 4 . Vậy 1;
1 , 2; 4 là hai giao điểm cần tìm.
Câu 4. (1 điểm) Cho phương trình x x 2 3 4
2x 1 có 2 nghiệm là x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức A 2 x 2 x 3x x . 1 2 1 2 Lời giải
Ta có: x x 2 3 4 2x 1 Trang 21 2 3x 4x 2 2x 1 2 3x 4x 2 2x 1 0 2
x 4x 1 0 a 1, b 4, c 1
Vì a.c < 0 nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b
S x x 4 4 1 2
Theo định lí Vi-et, ta có: a 2 c
P x x 1 . 1 1 2 a 1 Ta có: A 2 x 2 x 3x x 1 2 1 2 A 2
S 2P 3P A 2 S P A 2 4 1 A 15
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ
số thập phân, số đo góc làm tròn đến phút.
Câu 5. (0,75 điểm). Nước biển là dung dịch có nồng độ muối là 3, 5% (giả sử không có tạp chất).
Có 10kg nước biển. Hỏi phải thêm bao nhiêu kg nước (nguyên chất) để được dung dịch có nồng độ 2%? Lời giải
Khối lượng muối trong dung dịch nước biển 10kg là: 3, 5%.10 = 0, 35(kg).
Khối lượng nước biển có nồng độ 2% là: 0, 35 : 2% = 17, 5(kg).
Khối lượng nước được thêm vào để được dung dịch có nồng độ 2% là: 17, 5 - 10 = 7, 5(kg).
Câu 6. (0,75 điểm) Nhân dịp Lễ giỗ tổ Hùng Vương, một siêu thị điện máy đã giảm giá nhiều mặt
hàng để kích cầu mua sắm. Giá niêm yết một tủ lạnh và một máy giặt có tổng số tiền là 25, 4
triệu đồng nhưng trong dịp này giá một tủ lạnh giảm 40% giá bán và giá một máy giặt giảm
20% giá bán nên cô Liên đã mua hai món đồ trên với tổng số tiền là 16, 77 triệu đồng. Hỏi
giá mỗi món đồ trên khi chưa giảm giá là bao nhiêu tiền? Lời giải
Gọi x, y (đồng) lần lượt là số tiền của một tủ lạnh, một máy giặt khi chưa giảm giá (x,y > ) 0 Trang 22
Vì giá niêm yết một tủ lạnh và một máy giặt có tổng số tiền là 25, 4 triệu đồng nên có
phương trình x + y = 25, 4 (1)
Vì trong dịp này giá một tủ lạnh giảm 40% giá bán và giá một máy giặt giảm 20% giá bán
nên cô Liên đã mua hai món đồ trên với tổng số tiền là 16, 77 triệu đồng nên có phương trình (1 - 40 ) % x + (1 - 20 )
% y = 16, 77 Û 0, 6x + 0, 8y = 16, 77 (2) Từ ( )
1 và (2) ta có hệ phương trình
ìï x + y = 25, 4
ìï x = 17,75 (n) ï ï í Û í .
ï 0, 6x + 0, 8y = 16, 77 ï y = 7, 65 (n) ïî ïî
Vậy số tiền của một tủ lạnh khi chưa giảm giá là 17, 75 triệu đồng, số tiền của một tủ lạnh
chưa giảm giá là 7, 65 triệu đồng.
Câu 7. (1 điểm) Người ta nuôi cá trong một bể xây, mặt bể là hình chữ nhật chiều dài 60m , chiều
rộng 40m . Trên mỗi đơn vị diện tích mặt bể người ta thả 12 con cá giống, đến mỗi kỳ thu
hoạch, trung bình mỗi con cá cân nặng 240g . Khi bán khoảng 30000 đồng/kg và thấy lãi
qua kỳ thu hoạch này là 100 triệu. Hỏi vốn mua cá giống và các chi phí trong đợt này chiếm
bao nhiêu phần trăm so với giá bán (làm tròn 1 chữ số thập phân). Lời giải
Diện tích của bể nuôi cá là: = ( 2 60.40 2400 m ).
Số con cá giống được thả vào bể là: 2400.12 = 28800 (con ).
Số kg cá được bán là: 240.28800 = 6912000(g) = 6912(kg).
Số tiền bán cá là: 6912.30000 = 207360000 (đồng) = 207, 36 (triệu đồng).
Số tiền vốn và các chi phí là: 207, 36 - 100 = 107, 36 (triệu đồng).
Phần trăm vốn mua cá giống và các chi phí so với giá bán chiếm:
107, 36 : 207, 36 » 0, 518 = 51, 8% .
Câu 8. (1 điểm) Để tính toán thời gian một chu kỳ đong đưa (một chu kỳ đong đưa dây đu được
tính từ lúc dây đu bắt đầu được đưa lên cao đến khi dừng hẳn) của một dây đu, người ta sử L
dụng công thức T = 2p
. Trong đó, T là thời gian một chu kỳ đong đưa (s), L là chiều g
dài của dây đu (m ), 2
g = 9, 81 m / s .
a) Một sợi dây đu có chiều dài 2 +
3 m , hỏi chu kỳ đong đưa dài bao nhiêu giây? Trang 23
b) Một người muốn thiết kế một dây đu sao cho một chu kỳ đông đưa kéo dài 4 giây. Hỏi
người đó phải làm một sợi dây đu dài bao nhiêu? Lời giải L 2 + 3 c) Thay L = 2 +
3, g = 9, 81 vào công thức T = 2p
, ta được T = 2p » 3, 9 g 9, 81
Vậy một sợi dây đu có chiều dài 2 +
3 m có chu kỳ đong đưa dài khoảng 3, 9 giây. L L
d) Thay T = 4, g = 9, 81 vào công thức T = 2p , ta được 4 = 2p g 9, 81 2 2 4 L 2 æ ö L 2 æ ö ç ÷ ç ÷ Û = Û ç ÷ =
Û L = ç ÷ .9, 81 » 4 ç ÷ ç ÷ ç ÷ (m ) 2p 9, 81 èp ø 9, 81 çèp ÷ø
Vậy một người muốn thiết kế một dây đu sao cho một chu kỳ đông đưa kéo dài 4 giây,
người đó phải làm một sợi dây đu dài khoảng 4m .
Câu 9. (1 điểm) Máy kéo nông nghiêp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh
xe sau có đường kính là 1, 672m và bánh xe trước có đường kính là 88cm . Hỏi khi bơm
căng, bánh xe sau lăn được 10 vòng thì bánh xe trước lăn được mấy vòng? Lời giải
Đổi đơn vị: 1, 672m = 167, 2cm .
Chu vi của bánh xe sau là: C = d
p = p.162, 7 = 162, 7p (cm ).
Chu vi của bánh xe trước là: C = d
p = p.88 = 88p (cm ).
Quãng đường xe di chuyển được là: 10.167, 2p = 1672p (cm ).
Số vòng mà bánh xe trước lăn được là: 1672p : 88p = 19 (vòng).
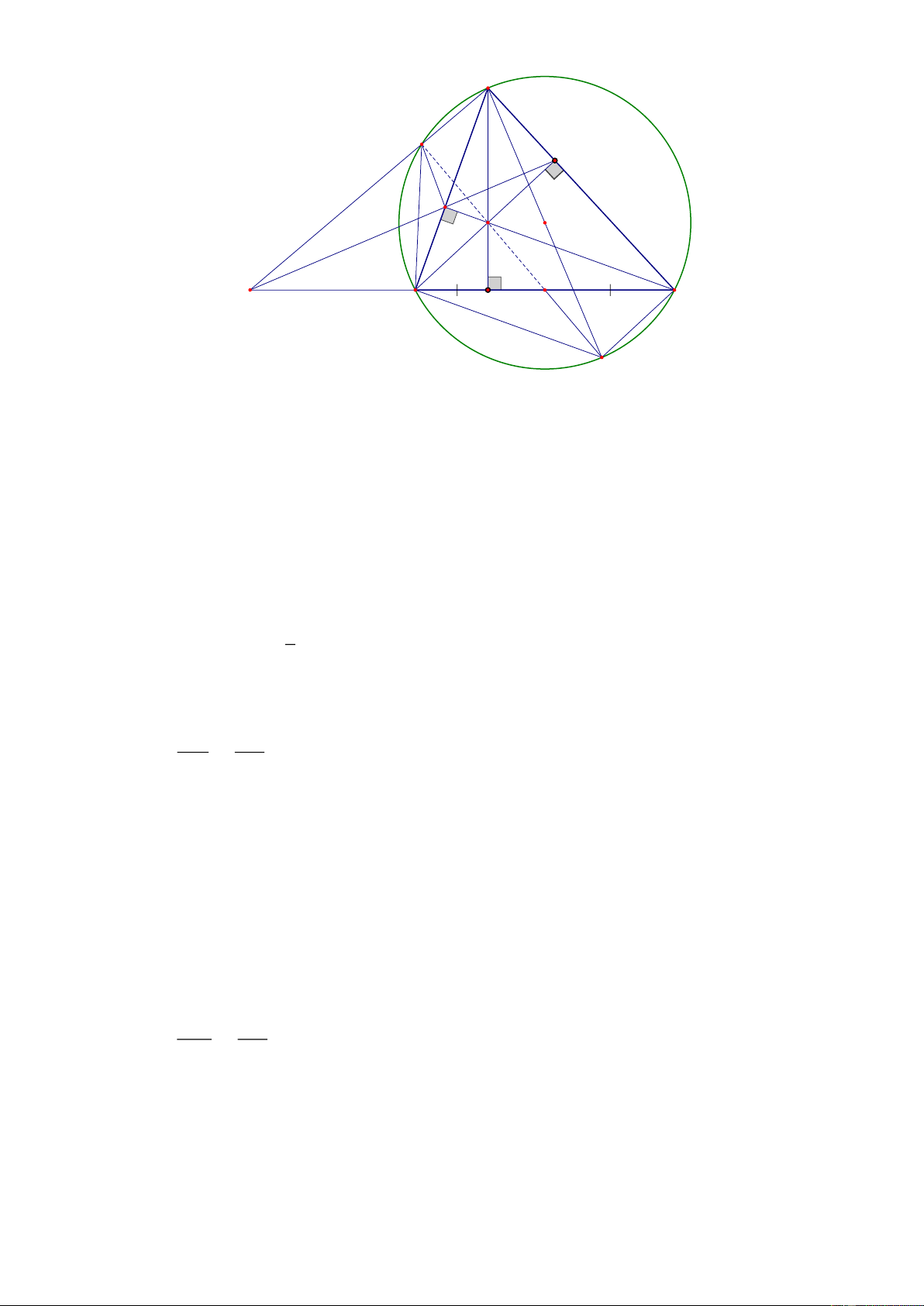
Câu 8. (3 điểm) Cho tam giác ABC AB AC có ba góc nhọn nội tiếp đường tròn O . Các đường
cao AD, BE, CF cắt nhau tại H . Tia EF cắt tia CB tại K .
a) Chứng minh tứ giác BFEC nội tiếp và K . F KE K . B KC .
b) Đường thẳng KA cắt (O ) tại M . Chứng minh tứ giác A EFM nội tiếp.
c) Gọi N là trung điểm của BC . Chứng minh M, H , N thẳng hàng. Lời giải Trang 24 A M E F O H K B C D N L
a) Chứng minh tứ giác BFEC nội tiếp và K . F KE K . B KC . · ·
Xét tứ giác BFEC có BEC = BFC = 90° ( BE ,CF là đường cao)
Suy ra tứ giác BFEC nội tiếp (2 đỉnh liền kề cùng nhìn cạnh BC ).
Xét KEB và KCF có: µ K là góc chung · · 1 » KEB = KCF =
Sđ BF (tứ giác BFEC nội tiếp) 2
Vậy KEB # KCF (g.g). K E K B Þ =
Û KE .KF = KB.KC . K C K F
b) Đường thẳng KA cắt (O ) tại M . Chứng minh tứ giác A EFM nội tiếp.
Xét KMB và KCA có: µ K là góc chung · ·
K MB = K CA (góc ngoài bằng góc đối trong của tứ giác AMBC nội tiếp)
Vậy KMB # KCA (g.g). KM KB Þ =
Û KM .KA = KB.KC . KC KA
Mà KE .KF = KB.KC (cmt )
Suy ra KM .KA = KE .KF .
Xét KMF và KEA có: Trang 25 µ K là góc chung KM KF =
(KM .KA = KE.KF ) KE KA
Vậy KMF # KEA (g.g) · ·
Þ KMF = KEA (2 góc tương ứng)
Vậy tứ giác A EFM nội tiếp (góc ngoài bằng góc đối trong).
c) Gọi N là trung điểm của BC . Chứng minh M, H , N thẳng hàng.
Kẻ đường kính A L của đường tròn (O )
ABL 90 ; ACL 90 (góc nội tiếp chắn nửa đường tròn)
AB BL, AC CL
Ta có: A B ^ BL,CF ^ A B Þ BL / / CF
A C ^ CL, BE ^ A C Þ CL/ / BE
Tứ giác BHCL là hình bình hành
Mà N là trung điểm của B C
N là trung điểm của HL
H,N ,L thẳng hàng (1)
Xét tứ giác A FHE có · ·
A FH = A EH = 90° (CF, BE là đường cao) · ·
Þ A FH + A EH = 90° + 90° = 180°
Vậy tứ giác A FHE nội tiếp
Mà tứ giác A EFM nội tiếp (cmt)
5 điểm A,M,F,H,E cùng thuộc 1 đường tròn.
Tứ giác AMHE nội tiếp
AMH AEH 90 HM ^ AM
Mà A M ^ ML ( vì LMA 90 là góc nội tiếp chắn nửa đường tròn)
M ,H,L thẳng hàng (2) Trang 26 Từ ( )
1 , (2) suy ra H, M , N thẳng hàng. ----HẾT--- Trang 27




