
















Preview text:
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 4
NĂM HỌC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đề thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 4-1
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). Cho parabol P y = 2 ( ) :
x và đường thẳng ( )
d : y = x + 2 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình: 2
2x + 6x - 3 = 0 có hai nghiệm x , x . Không giải phương 1 2 2 2 6029
trình, hãy tính giá trị của biểu thức B = + - . 2 2 x x x + x 1 2 1 2
Câu 3. (0.75 điểm). Anh An làm việc cho một công ty sản xuất hàng cao cấp, anh được trả năm
triệu bảy trăm sáu mươi ngàn đồng cho 48 tiếng làm việc trong một tuần. Sau đó để tăng
thêm thu nhập, anh An đã đăng ký làm thêm một số giờ nữa trong tuần, mỗi giờ làm thêm
này anh An được trả bằng 150% số tiền mà mỗi giờ anh An được trả trong 48 giờ đầu.
Cuối tuần sau khi xong việc, anh An được lãnh số tiền là bảy triệu hai trăm ngàn đồng. Hỏi
anh An đã làm thêm bao nhiêu giờ trong tuần đó?
Câu 4. (0,75 điểm). Công ty FPA cung cấp dịch vụ Internet với mức chi phí ban đầu là 400 000
đồng và chi phí trả hàng tháng là 272 000 đồng. Công ty VNPB cung cấp dịch vụ Internet
không tính chi phí ban đầu, nhưng chi phí trả hàng tháng là 320 000 đồng. Anh Minh đã
đăng ký dịch vụ Internet của công ty FPA. Hỏi anh Minh phải sử dụng dịch vụ Internet của
công ty FPA ít nhất trong bao nhiêu tháng thì tổng chi phí sử dụng sẽ rẻ̉ hơn sử dụng của công ty VNPB?
Câu 5. (1 điểm). Hai người A và B cùng ở một phía và cách thành phố Hồ Chí Minh 50km . Cả
hai người cùng nhau đi trên một con đường về phía ngược hướng với thành phố, người A
đi với vận tốc trung bình là 60 km / h và người B đi với vận tốc trung bình là 50 km / h . Gọi d(k )
m là khoảng cách từ thành phố Hồ Chí Minh đến hai người A , B sau khi đi được t (giờ).
a) Lập hàm số của d theo t đối với mỗi người.
b) Hỏi nếu hai người xuất phát cùng một lúc thì vào thời điểm nào kể từ lúc xuất phát,
khoảng cách giữa hai người là 20km . Trang 1
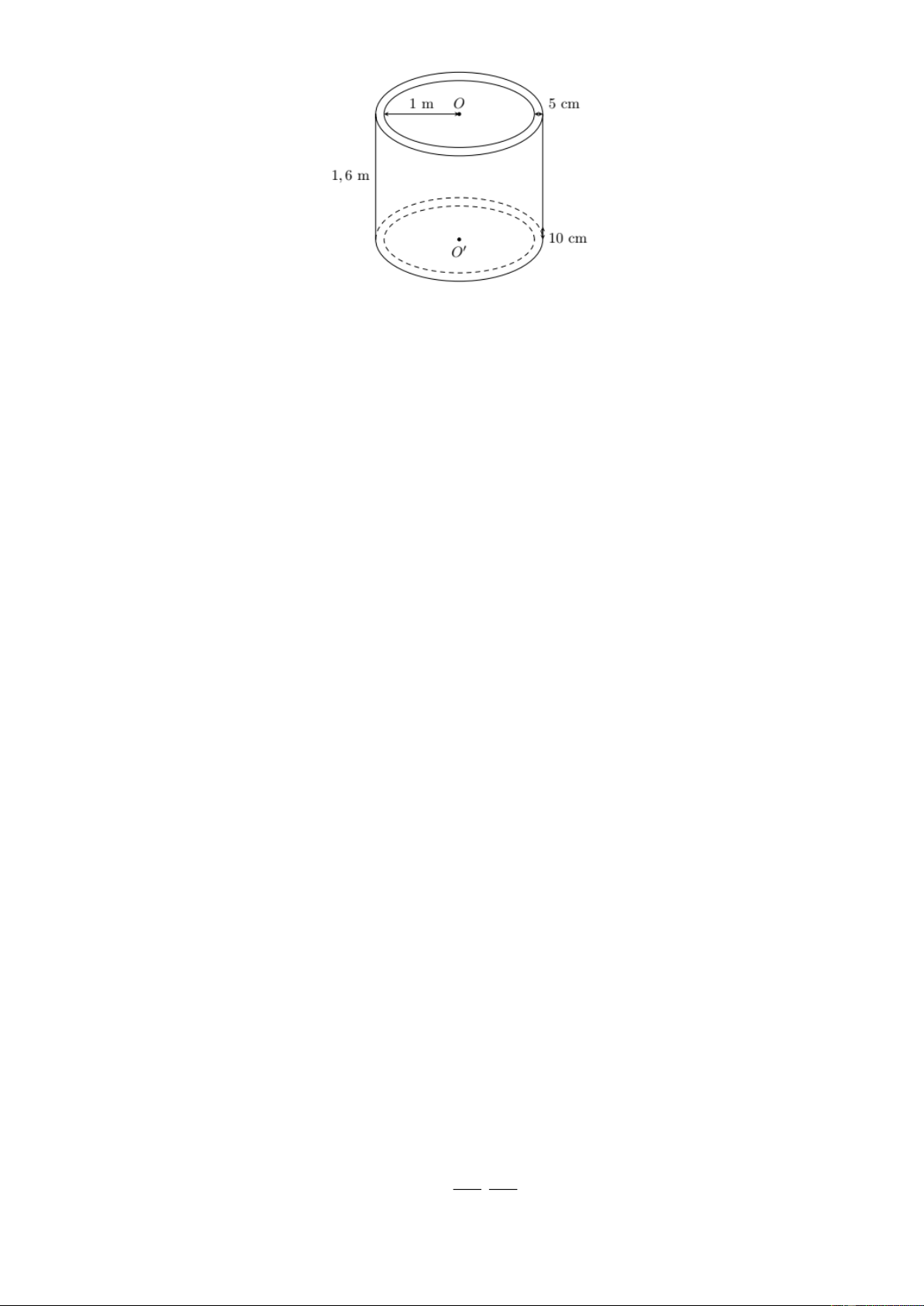
Câu 6. (1 điểm). Chú Hòa muốn xây một bể nước bê tông hình trụ có chiều cao là 1,6 m ; bán kính
lòng bể (tính từ tâm bể đến mép trong của bế) là r = 1m , bề dày của thành bể là 10 cm và
bề dày của đáy bể là 5 cm . Hỏi:
a) Bể có thể chứa được nhiều nhất bao nhiêu lít nước (biết thể tích hình trụ bằng = 2 V pr h
với r là bán kính đáy; h là chiều cao hình trụ; p » 3,14 ) .
b) Được biết một khối bê tông cần: 5 bao xi măng loại 50 kg/bao, 3 0,5 m cát, 3 0,9 m đá, 185
lít nước. Hỏi chú Hòa cần bao nhiêu kg xi măng? Bao nhiêu 3
m cát và bao nhiêu lít nước
để xây bể? (các kết quả được làm tròn đến chữ số thập phân thứ ba).
Câu 7. (1 điểm). Hạt tiêu đen thường được dùng làm gia vị trong nấu ăn vì ngoài tăng vị ngon của
thức ăn, tiêu còn có nhiều tác dụng tốt cho sức khỏe như tốt cho dạ dày, giảm cân, sức khỏe
da, chống oxy hóa và các tác dụng khác. Được biết tỉ lệ nước trong hạt tiêu xanh còn tươi là
68% và hạt tiêu khô là 2% .
a) Vậy nếu đem đi phơi khô một tạ tiêu xanh còn tươi thì thu được khối lượng hạt tiêu khô
là bao nhiêu? (làm tròn đến chữ số thập phân thứ hai) Giả sử lượng tiêu hao hụt trong quá trình là 5%.
b) Biết giá hồ tiêu thời điểm 11 / 4 / 2022 như sau: Tiêu khô có giá 55000 Vnđ/kg và tiêu
xanh còn tươi giá 13750 Vnđ/kg. Bác An có 10 tấn tiêu tươi và dự định thuê 2 công
nhân phơi khô trong 10 ngày với tiền công 400 000 Vnđ/ngày. Hỏi bác An làm như vậy
sẽ lời hay lỗ so với bán tiêu tươi bao nhiêu tiền?
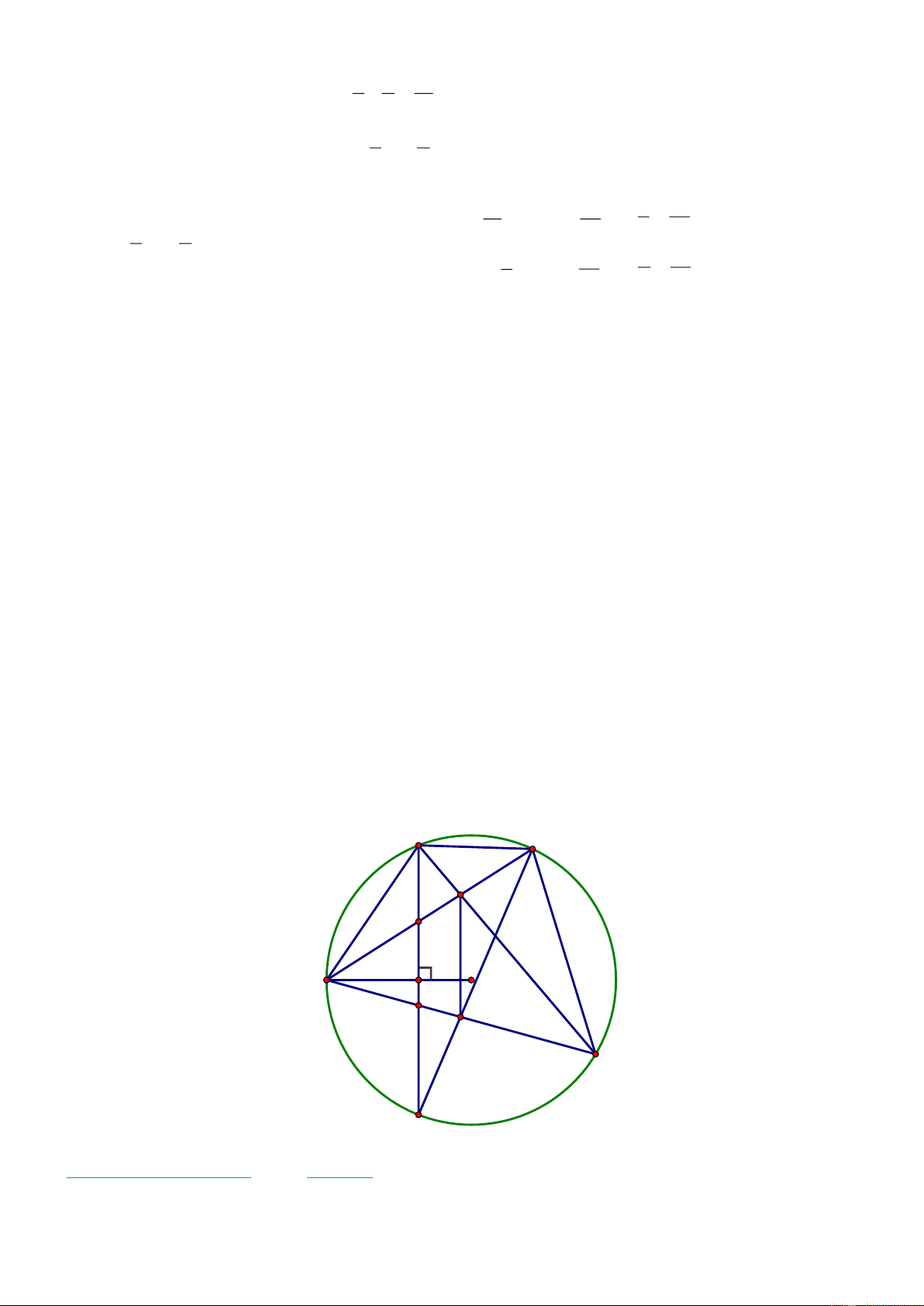
Câu 8. (3 điểm) Cho đường tròn (O) và điểm M nằm ngoài đường tròn (O). Từ M vẽ 2 tiếp
tuyến MA , MB của đường tròn (O) ( A và B là 2 tiếp điểm). Gọi H là giao điểm của MO
và AB . Qua M vẽ cát tuyến MCD của đường tròn (O) (C và D thuộc đường tròn (O))
sao cho đường thẳng MD cắt đoạn thẳng HB . Gọi I là trung điểm dây cung CD .
a) Chứng minh OI ^ CD tại và tứ giác MAOI nội tiếp. b) Chứng minh 2
MA = MC.MD và tứ giác OHCD nội tiếp.
c) Trên cung nhỏ AD lấy điểm N sao cho DN = DB . Qua C vẽ đường thẳng song song
với DN cắt đường thẳng MN tại E và cũng qua C vẽ đường thẳng song song với BD
cắt cạnh AB tại F . Chứng minh: Tam giác CEF cân. ----HẾT--- Trang 2 Trang 3 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm). Cho parabol P y = 2 ( ) :
x và đường thẳng ( )
d : y = x + 2 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
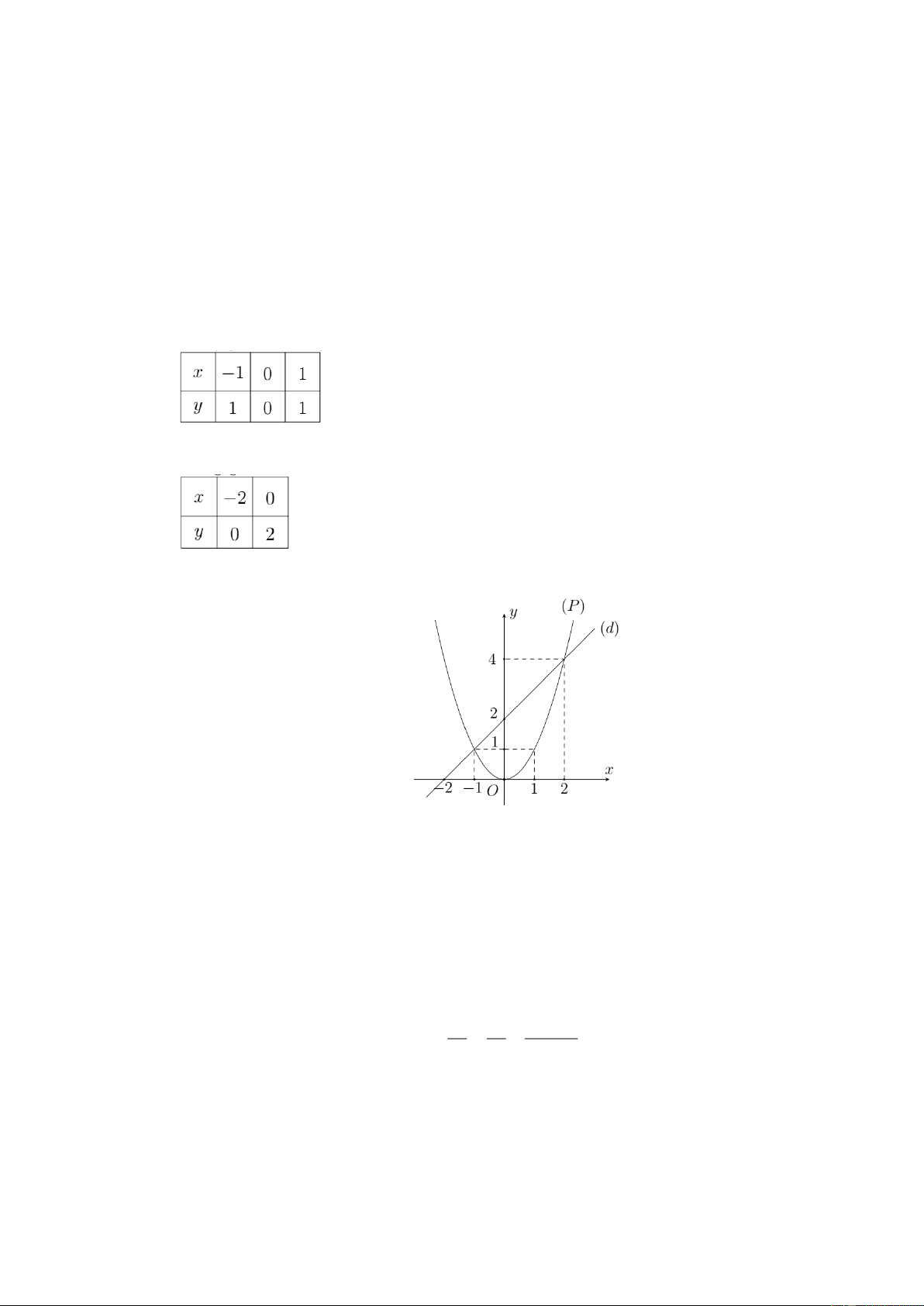
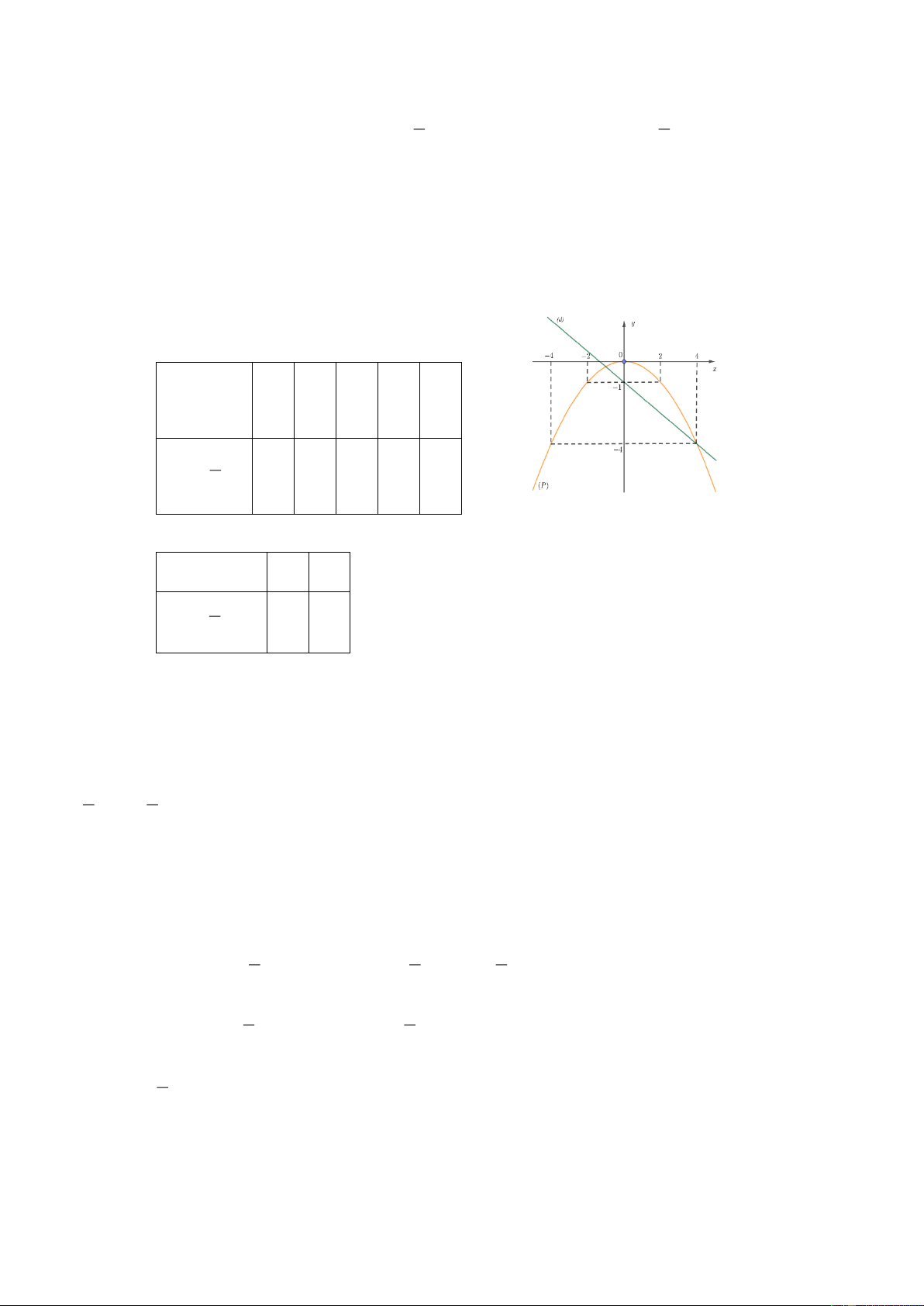
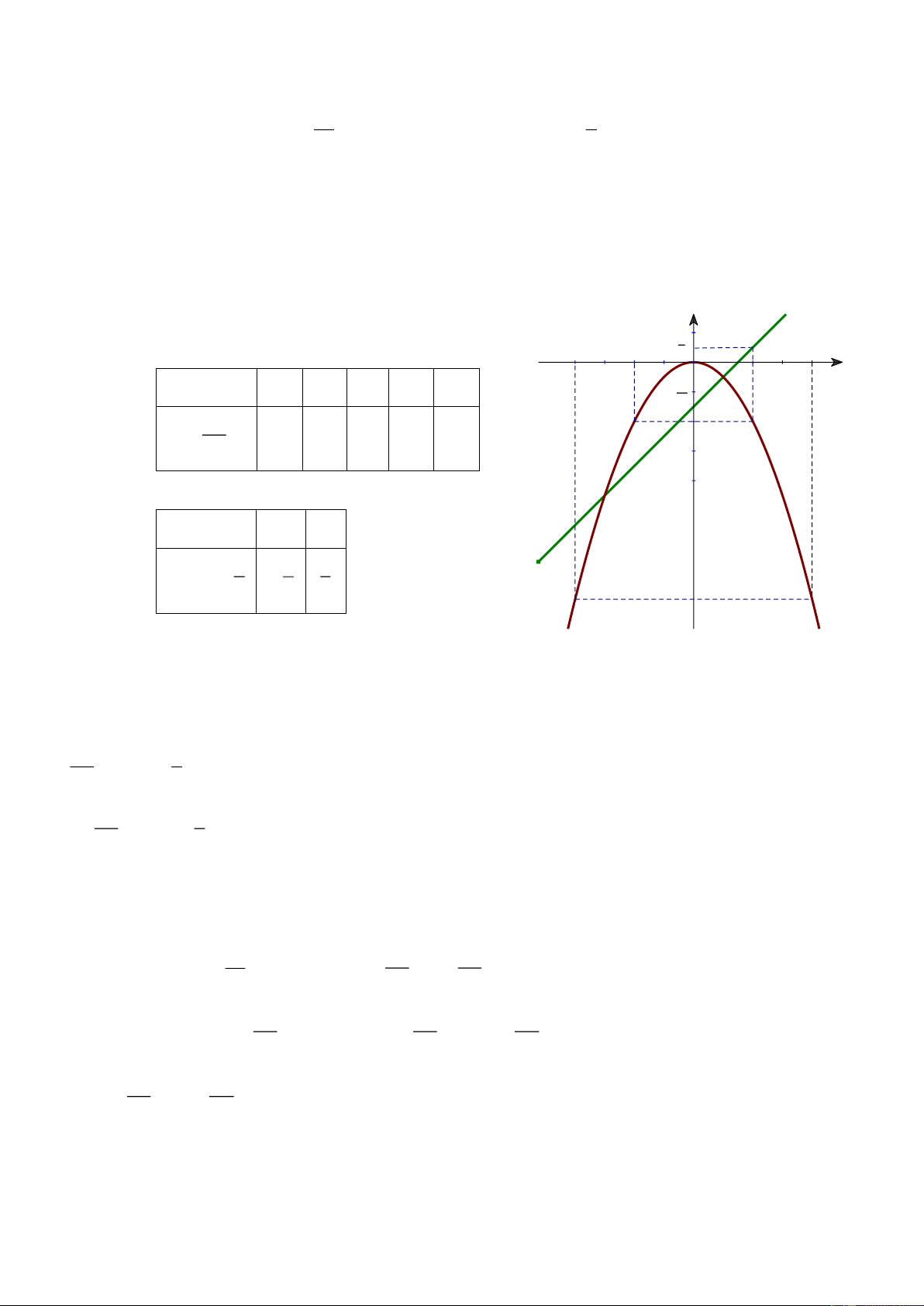
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ
Bảng giá trị hàm số P y = 2 ( ) : x
Bảng giá trị hàm số ( )
d : y = x + 2 Đồ thị:
b) Phuong trình hoành độ giao điểm của (P) và (d):
éx = - 1Þ y = 1 2 x = x + 2 Û 2
x - x - 2 = 0 Û ê 1 1 ê x = 2 Þ y = ë 4 2 2
Vậy tọa độ giao điểm của (P) và (d) là (- 1; ) 1 , (2; ) 4 .
Câu 2. (1 điểm). Cho phương trình: 2
2x + 6x - 3 = 0 có hai nghiệm x , x . Không giải phương 1 2 2 2 6029
trình, hãy tính giá trị của biểu thức B = + - . 2 2 x x x + x 1 2 1 2 Lời giải
Ta thấy a = 2 , c = - 3 , do đó a , c trái dấu nên phương trình có hai nghiệm phân biệt. Trang 4 ìïï b
ï S = x + x = - = - ï 3 ï 1 2
Áp dụng định lý Vi-ét ta có: í a ï ï c 3 ï P = x x = = - ïïî 1 2 a 2 é 2 2 2 ù x x x x 2 2 6029 ( 2 2 x x ) 2 ( ê + 2 2 1 2 ) - ú + 6029 êë 1 2 1 2 úû 6029 B = + - = - = - 2 2 x x x + 2 2 x x x x + x x x 1 2 1 2 1 2 1 2 (x x 1 2 )2 + 1 2 é 2 æ ù ö 3 2 ( ê- ) ç ÷ 3 - 2. - ú ç ÷ ê ç ÷ú ÷ è 2ø ë û 6029 6061 = - = . æ ö2 - ç ÷ 3 3 3 - ç ÷ ç ÷ è 2ø
Câu 3. (0.75 điểm). Anh An làm việc cho một công ty sản xuất hàng cao cấp, anh được trả năm
triệu bảy trăm sáu mươi ngàn đồng cho 48 tiếng làm việc trong một tuần. Sau đó để tăng
thêm thu nhập, anh An đã đăng ký làm thêm một số giờ nữa trong tuần, mỗi giờ làm thêm
này anh An được trả bằng 150% số tiền mà mỗi giờ anh An được trả trong 48 giờ đầu.
Cuối tuần sau khi xong việc, anh An được lãnh số tiền là bảy triệu hai trăm ngàn đồng. Hỏi
anh An đã làm thêm bao nhiêu giờ trong tuần đó? Lời giải
Gọi x (giờ) là số giờ anh An làm thêm ( x > 0 ). 5760000 Ta có 5760000 + . x
.150% = 7 200000 Û x = 8 (thỏa mãn). 48
Vậy trong tuần đó anh An đã làm thêm 8 giờ.
Câu 4. (0,75 điểm). Công ty FPA cung cấp dịch vụ Internet với mức chi phí ban đầu là 400 000
đồng và chi phí trả hàng tháng là 272 000 đồng. Công ty VNPB cung cấp dịch vụ Internet
không tính chi phí ban đầu, nhưng chi phí trả hàng tháng là 320 000 đồng. Anh Minh đã
đăng ký dịch vụ Internet của công ty FPA. Hỏi anh Minh phải sử dụng dịch vụ Internet của
công ty FPA ít nhất trong bao nhiêu tháng thì tổng chi phí sử dụng sẽ rẻ̉ hơn sử dụng của công ty VNPB? Lời giải
Gọi x (tháng) là thời gian sử dụng dịch vụ ( x > 0 ).
Số tiền phải trả khi sử dụng dịch vụ FPA là 272000x + 400000 .
Số tiền phải trả khi sử dụng dịch vụ VNPB là 322000x .
Khi đó ta có phương trình Trang 5 x + = x Û x = 25 272000 400000 320000 » 8,3 . 3
Vậy kể từ tháng thứ 9 trở đi sử dụng dịch vụ FPA rẻ hơn sử dụng dịch vụ VNPB.
Câu 5. (1 điểm). Hai người A và B cùng ở một phía và cách thành phố Hồ Chí Minh 50km . Cả
hai người cùng nhau đi trên một con đường về phía ngược hướng với thành phố, người A
đi với vận tốc trung bình là 60 km / h và người B đi với vận tốc trung bình là 50 km / h . Gọi d(k )
m là khoảng cách từ thành phố Hồ Chí Minh đến hai người A , B sau khi đi được t (giờ).
a) Lập hàm số của d theo t đối với mỗi người.
b) Hỏi nếu hai người xuất phát cùng một lúc thì vào thời điểm nào kể từ lúc xuất phát,
khoảng cách giữa hai người là 20km . Lời giải
a) Hàm số của d theo t của người thứ nhất là (d ): d = 60t . 1
Hàm số của d theo t của người thứ hai là (d ): d = 50t + 50 . 2 é é 10t - 50 = 20 t = 7
b) Ta có 60t - 50t - 50 = 20 Û ê Û ê ê ê 10t - 50 = - 20 t = ë ë 3.
Vậy kể từ lúc xuất phát đến khi hai xe cách nhau 20km là 3 giờ và 7 giờ.
Câu 6. (1 điểm). Chú Hòa muốn xây một bể nước bê tông hình trụ có chiều cao là 1,6 m ; bán kính
lòng bể (tính từ tâm bể đến mép trong của bế) là r = 1m , bề dày của thành bể là 10 cm và
bề dày của đáy bể là 5 cm . Hỏi:
a) Bể có thể chứa được nhiều nhất bao nhiêu lít nước (biết thể tích hình trụ bằng = 2 V
pr h với r là bán kính đáy; h là chiều cao hình trụ; p » 3,14 ) .
b) Được biết một khối bê tông cần: 5 bao xi măng loại 50 kg/bao, 3 0,5 m cát, 3 0,9 m đá,
185 lít nước. Hỏi chú Hòa cần bao nhiêu kg xi măng? Bao nhiêu 3 m cát và bao nhiêu
lít nước để xây bể? (các kết quả được làm tròn đến chữ số thập phân thứ ba). Lời giải Trang 6
a) Thể tích nước mà bể có thể chứa là V = 2 pr h = 2 p.1 ( . 1,6 - 0,0 ) 5 = 3,14. , 1 55 = 3 4,867 m .
b) Gọi V , V , V lần lượt là thể tích của khối trụ lớn, thể tích phần chứa nước, thể tích 1 2 3 khối bê tông. 2
V = V - V = p ( . 1+ 0, ) 1 .1,6 - 2 p.1 ( . 1,6 - 0,0 ) 5 = 3 1,212 m . 3 1 2
Khối lượng xi măng cần là 2,212.50.5 = 303kg . Thể tích cát là = 3 1.212.0,9 1,091m .
Thể tích nước sử dụng là 1.212.185 = 224,220 lít.
Câu 7. (1 điểm). Hạt tiêu đen thường được dùng làm gia vị trong nấu ăn vì ngoài tăng vị ngon của
thức ăn, tiêu còn có nhiều tác dụng tốt cho sức khỏe như tốt cho dạ dày, giảm cân, sức khỏe
da, chống oxy hóa và các tác dụng khác. Được biết tỉ lệ nước trong hạt tiêu xanh còn tươi là
68% và hạt tiêu khô là 2% .
a) Vậy nếu đem đi phơi khô một tạ tiêu xanh còn tươi thì thu được khối lượng hạt tiêu
khô là bao nhiêu? (làm tròn đến chữ số thập phân thứ hai) Giả sử lượng tiêu hao hụt trong quá trình là 5% .
b) Biết giá hồ tiêu thời điểm 11 / 4 / 2022 như sau: Tiêu khô có giá 55000 Vnđ/kg và tiêu
xanh còn tươi giá 13750 Vnđ/kg. Bác An có 10 tấn tiêu tươi và dự định thuê 2 công
nhân phơi khô trong 10 ngày với tiền công 400000 Vnđ/ngày. Hỏi bác An làm như
vậy sẽ lời hay lỗ so với bán tiêu tươi bao nhiêu tiền? Lời giải
a) Khối lượng một tạ tiêu nguyên chất là 100.68% = 68 kg .
Khối lượng một tạ tiêu chứa 2% nước và hao hụt 5% là 100 95 68. . » 65,92 kg . 98 100 Trang 7
b) Số tiền bán 10 tấn tiêu tươi là
13750.10000 = 137 500000 Vnđ.
Số tiền bán 10 tấn tiêu khi phơi khô là 65,92 55000.10000. = 362 560 000 Vnđ. 100
Số tiền thuê nhân công phơi là 40000.10.2 = 8000000 Vnđ.
Số tiền bác An thu về khi bán tiêu khô và trừ nhân công là
362 560000 - 8000000 = 354 560000 Vnđ.
Như vậy bác An bán tiêu khô lời hơn bán tiêu tươi là
354 560000 - 137 500000 = 217 060000 Vnđ.
Câu 8. (3 điểm) Cho đường tròn (O) và điểm M nằm ngoài đường tròn (O). Từ M vẽ 2 tiếp
tuyến MA , MB của đường tròn (O) ( A và B là 2 tiếp điểm). Gọi H là giao điểm của MO
và AB . Qua M vẽ cát tuyến MCD của đường tròn (O) (C và D thuộc đường tròn (O))
sao cho đường thẳng MD cắt đoạn thẳng HB . Gọi I là trung điểm dây cung CD .
a) Chứng minh OI ^ CD tại và tứ giác MAOI nội tiếp. b) Chứng minh 2
MA = MC.MD và tứ giác OHCD nội tiếp.
c) Trên cung nhỏ AD lấy điểm N sao cho DN = DB . Qua C vẽ đường thẳng song
song với DN cắt đường thẳng MN tại E và cũng qua C vẽ đường thẳng song song
với BD cắt cạnh AB tại F . Chứng minh: Tam giác CEF cân. Lời giải
a) Do I là trung điểm của CD nên OI ^ CD (tính chất đường kính và dây cung) Trang 8 · ·
Xét tứ giác MAOI có OAM = OIM = ° 90 · ·
Þ OAM + OIM = 9 ° 0 + 9 ° 0 = 18 ° 0 .
Suy ra tứ giác MAOI nội tiếp (tổng hai góc dối bằng ° 180 ). · ·
b) Xét DMCB và DMBD có BMC = DMC · ·
MCB = MDB (liên hệ giữa góc nội tiếp và góc giữa tia tiếp tuyến và dây cung)
Suy ra DMCB"DMBD (g-g)
Þ MC = MB Û MC MD = 2 MB Û MC MD = 2 . . MA . ( ) 1 MB MD
ìï OA = OB = R Ta có ïí Þ AB
AH là đường cao trong tam ï
MO là trung trực của Þ MA = ïî MB(tc2tt)
giác MAO vuông tại A nên 2
MA = MH.MO . (2) MH MC Từ ( )
1 và (2) Þ MH.MO = MC.MD Û = . MD MO · · MH MC
Xét DMHC và DMDO có HMC = DMO và = nên MD MO
DHMC"DDMO (c-g-c). · ·
Suy ra MHC = ODC nên tứ giác OHCD nội tiếp (góc ngoài bằng góc đối trong không kề)
c) Gọi P là giao điểm của AB và MD . MC CE
Ta có CE//DN nên = . ( ) 1 MD DN PC CF
Ta có CF//BD nên = . (2) PD BD · · ·
Do tứ giác OHCD nội tiếp, suy ra MHC = ODC = OCD . · · Mà OCD = OHD . · ·
Nên MHC = OHD .
Mặt khác HP ^ OM .
Lúc này ta có HP là phân giác trong, HM là phân giác ngoài của tam giác HCD nên MC PC
áp dụng tính chất phân giác ta có = ( ) 3 MD PD CE CF Từ ( ) 1 , (2) và ( ) 3 suy ra =
mà DB = DN Þ CE = CF . DN BD
Vậy tam giác CEF cân tại C . Trang 9 ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 4
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 4 - 2
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 1. (1,5 điểm): Cho Parabol (P ) 2 : y = -
x và đường thẳng (D) 3 : y = - x - 1. 4 4
a) Vẽ (P ) và (D) trên cùng một hệ trục tọa độ 0xy .
b) Bằng phép toán xác định tọa độ giao điểm của (P ) và (D).
Câu 2. (1 điểm) Cho phương trình: 2
x 11x 5 0
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt x , x rồi tính tổng và tích hai 1 2
nghệm x , x của phương trình. 1 2 2 2
b) Không giải phương trình hãy tính giá trị của biểu thức: A
x x 1 2 x x 2 1
Câu 3. (0,75 điểm) Để đạt kết quả tốt nhất trong kì thi tuyển sinh lớp 10 THPT vào ngày
02 / 6 / 2021 , sau khi tổ chức Hội trại truyền thống vào thứ Sáu ngày 26 / 3 / 2021 , học
sinh khối 9 đã đề ra kế hoạch học tập môn Toán cụ thể như sau: "Mỗi học sinh bắt đầu từ
ngày 27 / 3 / 2021 đến hết tháng ba mỗi ngày làm 3 bài toán, mỗi ngày trong tháng tư làm
4 bài toán, mỗi ngày trong tháng năm làm 5 bài toán". Biết tháng ba và tháng năm là
những tháng có 31 ngày, tháng tư có 30 ngày. Hỏi:
a) Theo kế hoạch, mỗi học sinh làm được bao nhiêu bài toán?
b) Ngày thi 02 / 6 / 2021 là thứ mấy? Giải thích vì sao? 2
Câu 4. (0,75 điểm) Một lon nước ngọt có giá 10000 đồng. Một quyển tập có giá bằng giá một lon 5
nước ngọt, một hộp bút có giá gấp 3 lần giá một lon nước ngọt. Bạn An cần mua một số
quyển tập và một hộp bút.
a) Gọi x là số quyển tập An mua và y là số tiền An phải trả (bao gồm tiền mua tập và một
hộp bút). Viết công thức biểu diễn y theo x . Trang 10
b) Nếu An bán 2 thùng nước ngọt, mỗi thùng gồm 24 lon với giá đã nêu trên để mua tập
và một hộp bút thì tối đa bạn An mua được bao nhiêu quyển tập?
Câu 5. (1 điểm) Một công ty giao cho cửa hàng 100 hộp bánh để bán ra thị trường. Lúc đầu cửa
hàng bán 24 hộp bánh với giá bán một hộp bánh là 200000 đồng. Do nhu cầu của thị
trường nên từ hộp bánh thứ 25 đến hộp bánh thứ 80 mỗi hộp bánh có giá bán tăng 15%
so với giá bán lúc đầu, từ hộp bánh thứ 81 đến hộp bánh thứ 100 mỗi hộp bánh có giá bán
giảm 10% so với giá bán lúc đầu.
a) Hỏi số tiền thu cửa hàng được khi bán 100 hộp bánh là bao nhiêu?
b) Biết rằng: Với số tiền thu được khi bán 100 hộp bánh, sau khi trừ đi 10% tiền thuế giá
trị gia tăng VAT cửa hàng vẫn lãi 1152000 đồng. Hỏi mỗi hộp bánh công ty giao cho
cửa hàng có giá là bao nhiêu?
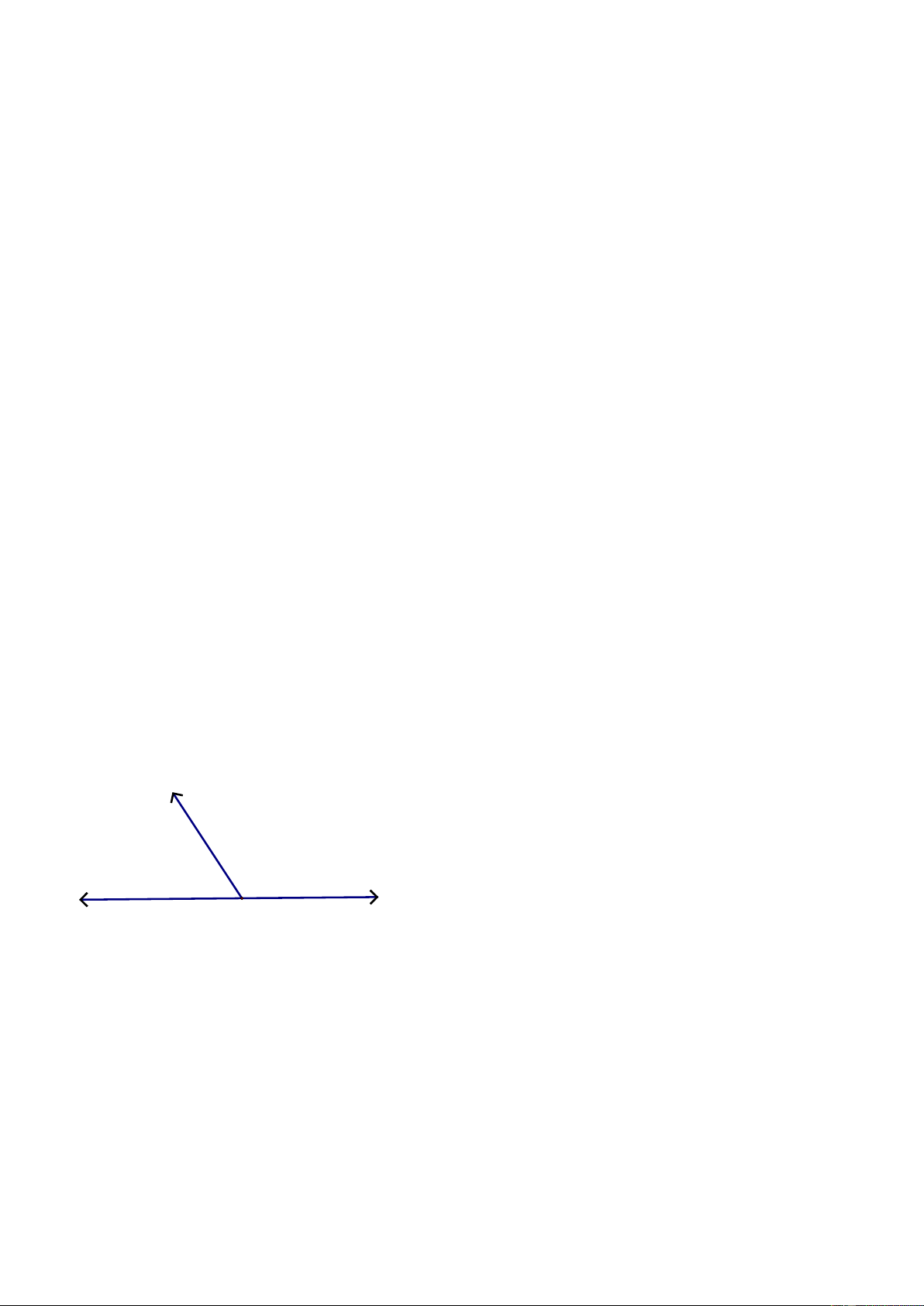
Câu 6. (1 điểm) Ba xe máy cùng xuất phát từ O đi theo ba hướng Ox, y O , z
O trong đó Ox và Oz
ngược hướng nhau như hình vẽ. y x O z
Xe thứ nhất đi theo hướng Ox , xe thứ hai đi theo hướng Oy , xe thứ ba đi theo hướng Oz , cả ba xe
cùng chạy với vận tốc không đổi là 50 km / giờ. Sau 2 giờ xe thứ nhất và xe thứ hai ở cách nhau
107 km. Hỏi lúc đó xe thứ hai và xe thứ ba ở cách nhau bao nhiêu ki-lô-mét? (làm tròn kết quả đến chữ số hàng đơn vị).
Câu 7. (1 điểm)Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thợ thứ
nhất làm trong 3 giờ, người thợ thứ hai làm trong 6 giờ thì hoàn thành 25% công việc. Hỏi
mỗi người thợ chỉ làm một mình thì trong bao lâu làm xong công việc?
Câu 8. (3 điểm)Cho đường tròn tâm O bán kính OA và dây cung MN vuông góc OA( A nằm trên
cung nhỏ MN) . Vẽ dây cung AB và dây cung AC sao cho AB cắt MN tại I, AC cắt MN
tại K theo thứ tự M, I, K, N .
a) Chứng minh: Tứ giác BIKC nội tiếp.
b) Gọi R là giao của AB và MC,S là giao của AC và BN . Chứng minh: MN // RS và A . B IR A . C KS .
c) Chứng minh: MA là tiếp tuyến của đường tròn ngoại tiếp M
BI và đường tròn ngoại tiếp M
BI tiếp xúc với đường tròn ngoại tiếp M CK . ----HẾT--- Trang 11 HƯỚNG DẪN GIẢI 1 3
Câu 1. 1,5 điểm): Cho Parabol 2 (P) : y
x và đường thẳng (D) : y x 1. 4 4
a) Vẽ (P) và (D) trên cùng một hệ trục tọa độ 0xy.
b) Bằng phép toán xác định tọa độ giao điểm của (P) và (D). Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: 4 2 4 x 2 0 – 4 2 4 1 4 1 1 4 2 y x 0 4 – 4 – 1 – 1 – 4 x 0 4 3 y x 1 1 4 4
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 1 3 2
x x 1 4 4 2
x 3x 4 0 x 1 x 4 1 1 1 Thay x 1 vào 2 y
x , ta được: y 2 1 4 4 4 1 1 Thay x 4 vào 2 y
x , ta được: y .42 4 4 4 1 Vậy 1;
, 4; 4 là hai giao điểm cần tìm. 4
Câu 2. Cho phương trình: 2
x 11x 5 0 Trang 12
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt x , x rồi tính tổng và tích hai 1 2
nghệm x , x của phương trình. 1 2 2 2
b) Không giải phương trình hãy tính giá trị của biểu thức: A
x x 1 2 x x 2 1 Lời giải
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt x , x rồi tính tổng và tích hai nghệm 1 2
x , x của phương trình. 1 2 2 Vì 2
b 4ac 1 1 4.1.5 101 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b S x x 11 1 2 a
Theo định lí Vi-et, ta có: c P x .x 5 1 2 a 2 2
b) Không giải phương trình hãy tính giá trị của biểu thức: A
x x 1 2 x x 2 1 2 2 Ta có: A
x x 1 2 x x 2 1
2x 2x 1 2 A
x x 1 2 x x 1 2 x x 2 1 2 A 2 x x 1 2 2 2
x 2x x x 1 1 2 2 A 2 x x 1 2
x x 2 2x x 2x x 1 2 1 2 1 2 A 2 x x 1 2
x x 2 4x x 1 2 1 2 A 2 x x 1 2 2 11 4.5 202 A 2 5 5
Câu 3. (0,75 điểm) Để đạt kết quả tốt nhất trong kì thi tuyển sinh lớp 10 THPT vào ngày
02/6/2021, sau khi tổ chức Hội trại truyền thống vào thứ Sáu ngày 26/3/2021, học sinh
khối 9 đã đề ra kế hoạch học tập môn Toán cụ thể như sau: "Mỗi học sinh bắt đầu từ ngày
27 / 3 / 2021 đến hết tháng ba mỗi ngày làm 3 bài toán, mỗi ngày trong tháng tư làm 4 bài Trang 13
toán, mỗi ngày trong tháng năm làm 5 bài toán". Biết tháng ba và tháng năm là những
tháng có 31 ngày, tháng tư có 30 ngày. Hỏi:
a) Theo kế hoạch, mỗi học sinh làm được bao nhiêu bài toán?
b) Ngày thi 02/6/2021 là thứ mấy? Giải thích vì sao? Lời giải
a) Số ngày từ 27 / 3/ 2021 đến 31/ 3/ 2021
Số bài toán mỗi học sinh làm được theo kế hoạch là:
4.3 30.4 51.5 287 (bài toán)
b) Số ngày từ ngày 26 / 3 / 2021 đến ngày 02 / 6 / 2021 là: 5 + 30 + 31 + 2 = 68 (ngày)
Ta có: 68 : 7 = 9 (dư 5 ) mà ngày 26 / 3 / 2021 là thứ sáu nên ngày 02 / 6 / 2021 là ngày thứ tư. 2
Câu 4. (0,75 điểm) Một lon nước ngọt có giá 10000 đồng. Một quyển tập có giá bằng giá 5
một lon nước ngọt, một hộp bút có giá gấp 3 lần giá một lon nước ngọt. Bạn An cần mua
một số quyển tập và một hộp bút.
a) Gọi x là số quyển tập An mua và y là số tiền An phải trả (bao gồm tiền mua
tập và một hộp bút). Viết công thức biểu diễn y theo x .
b) Nếu An bán 2 thùng nước ngọt, mỗi thùng gồm 24 lon với giá đã nêu trên để
mua tập và một hộp bút thì tối đa bạn An mua được bao nhiêu quyển tập? Lời giải 2
a) Giá tiền một quyển tập là: 10000 4000 (đồng) 5
Giá tiền một hộp bút là: 310000 30000 (đồng)
Công thức biểu diễn y theo x là: y 4000x 30000
b) Số tiền bán 2 thùng nước ngọt là: 2.24.10000 480000 (đồng)
Thế y = 480000 vào y 4000x 30000 , ta được:
480000 4000x 30000 4000x 450000 x 112, 5
Vậy bạn An mua được tối đa 112 quyển tập
Câu 5. (1 điểm) Một công ty giao cho cửa hàng 100 hộp bánh để bán ra thị trường. Lúc đầu
cửa hàng bán 24 hộp bánh với giá bán một hộp bánh là 200000 đồng. Do nhu cầu của thị
trường nên từ hộp bánh thứ 25 đến hộp bánh thứ 80 mỗi hộp bánh có giá bán tăng 15% Trang 14
so với giá bán lúc đầu, từ hộp bánh thứ 81 đến hộp bánh thứ 100 mỗi hộp bánh có giá bán
giảm 10% so với giá bán lúc đầu.
a) Hỏi số tiền thu cửa hàng được khi bán 100 hộp bánh là bao nhiêu?
b) Biết rằng: Với số tiền thu được khi bán 100 hộp bánh, sau khi trừ đi 10% tiền thuế
giá trị gia tăng VAT cửa hàng vẫn lãi 1152000 đồng. Hỏi mỗi hộp bánh công ty giao
cho cửa hàng có giá là bao nhiêu? Lời giải
a) Số tiền thu được khi bán 24 hộp bánh đầu là: 24.200000 4800000 (đồng)
Số tiền thu được khi bán được từ hộp bánh thứ 25 đến hộp bánh thứ 80 là:
56.200000(115%) 12880000 (đồng)
Số tiền thu được khi bán được từ hộp bánh thứ 81 đến hộp bánh thứ 100 là:
20.200000110% 3600000 (đồng)
Số tiền thu cửa hàng được khi bán 100 hộp bánh là:
4800000 12880000 3600000 21280000 (đồng)
b) Số tiền thuế giá trị gia tăng VAT là 10%.21280000 2128000(đồng)
Số tiền mỗi hộp bánh công ty giao cho cửa hàng có giá là: 212800002128000 1152000:100 180000 (đồng)
Câu 6. (1 điểm) Ba xe máy cùng xuất phát từ O đi theo ba hướng Ox, y O , z O trong đó Ox và
Oz ngược hướng nhau như hình vẽ. y x O z
Xe thứ nhất đi theo hướng Ox , xe thứ hai đi theo hướng Oy , xe thứ ba đi theo hướng Oz , cả
ba xe cùng chạy với vận tốc không đổi là 50 km / giờ. Sau 2 giờ xe thứ nhất và xe thứ hai ở cách
nhau 107 km. Hỏi lúc đó xe thứ hai và xe thứ ba ở cách nhau bao nhiêu ki-lô-mét? (làm tròn kết
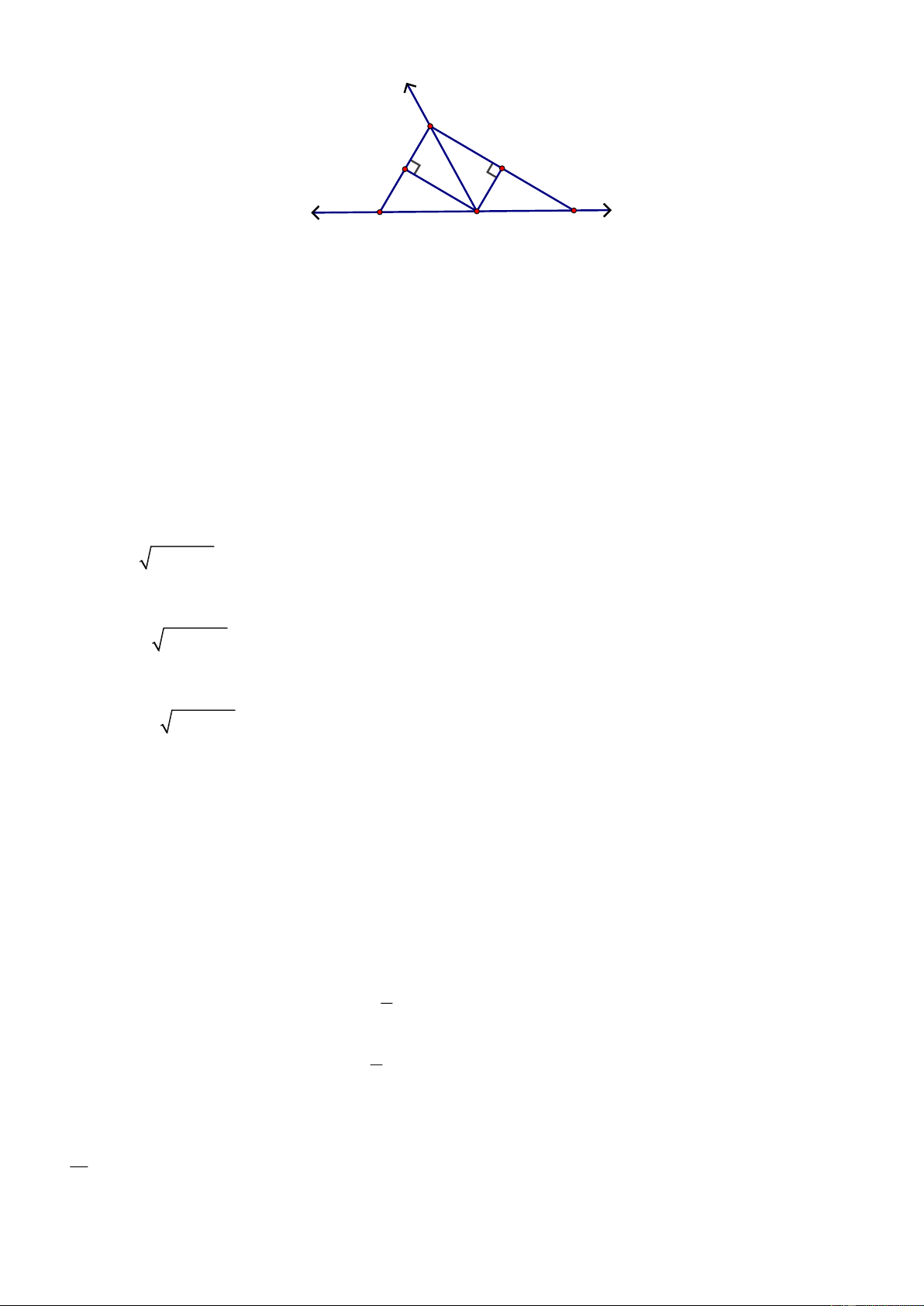
quả đến chữ số hàng đơn vị). Lời giải Trang 15 y B H K A C z x O
Gọi A , B , C lần lượt là các vị trí mà xe thứ nhất, xe thứ hai, xe thứ ba sau khi xuất phát được 2 giờ.
Vẽ OH vuông góc với AB tại H và OK vuông góc với BC tại K .
Ta chứng được H là trung điểm của AB và K là trung điểm của BC .
Ta dễ tính được OA OB OC 100km; AC 200km ; BH 53, 5km Xét HOB
vuông tại H , ta có: 2 2 2
OH BH OB (định lí Pitago) 2 2 2 OH 53,5 100 2 OH 7137,75 OH 7137,75
Mà OH BK (tứ giác OHBK là hình chữ nhật) Nên BK 7137, 75
Mặt khác: BC 2BK (vì K là trung điểm của BC )
Nên BC 2 7137, 75 169 km
Câu 7. (1 điểm)Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thợ
thứ nhất làm trong 3 giờ, người thợ thứ hai làm trong 6 giờ thì hoàn thành 25% công
việc. Hỏi mỗi người thợ chỉ làm một mình thì trong bao lâu làm xong công việc? Lời giải
Gọi x (giờ) là thời gian người thứ nhất làm xong công việc một mình x 16
y (giờ) là thời gian người thứ hai làm xong công việc một mình y 16 1
Trong mỗi giờ người thứ nhất làm được: (công việc) x 1
Trong mỗi giờ người thứ hai làm được: (công việc) y
Vì hai người thợ cùng làm một công việc trong 16 giờ thì xong nên mỗi giờ cả hai người làm được 1 (công việc) 16 Trang 16 1 1 1 x y 16
Theo đề bài, ta có hệ phương trình: 1 1 3 6 25% x y 1 1 1 1 a b a 1 1 16 24 x 24 x 24 Đặt a ;b
. Hệ phương trình trở thành: x y 1 1 1 1 y 48 3a 6b b 4 48 y 48
KL: Vậy người thợ thứ nhất chỉ làm một mình trong 48 giờ thì xong công việc
người thợ thứ hai chỉ làm một mình trong 24 giờ thì xong công việc.
Câu 8. (3 điểm)Cho đường tròn tâm O bán kính OA và dây cung MN vuông góc OA( A nằm
trên cung nhỏ MN) . Vẽ dây cung AB và dây cung AC sao cho AB cắt MN tại I, AC cắt
MN tại K theo thứ tự M, I, K, N .
a) Chứng minh: Tứ giác BIKC nội tiếp.
b) Gọi R là giao của AB và MC,S là giao của AC và BN . Chứng minh: MN // RS và A . B IR A . C KS .
c) Chứng minh: MA là tiếp tuyến của đường tròn ngoại tiếp M
BI và đường tròn ngoại tiếp M
BI tiếp xúc với đường tròn ngoại tiếp M CK . Lời giải M B R I A K S C N
a) Chứng minh: Tứ giác BIKC nội tiếp. Xét O , ta có: Trang 17
OA laø baùn kính gt
MN laø daây cunggtA laø ñieåm chính giöõa MN OA NM gt Ta có: 1 AIN sñMB
sñANgoùc coù ñænh beân trong ñöôøng troøn chaén MB vaø AN 2 sñAN
sñAM A laø ñieåm chính giöõa MN 1 AIN sñMBsñAM 2 1 AIN sñAB 2 Mà 1 ACB
sñABgoùc noäi tieáp chaén AB cuûa O 2 Nên ACB AIN
Tứ giác BIKC nội tiếp (Tứ giác có góc ngoài bằng góc đối trong)
b) Gọi R là giao của AB và MC,S là giao của AC và BN . Chứng minh: MN // RS và AB.IR AC.KS. Ta có: RBC 1
sñAN goùc noäi tieáp chaén AN cuûa O 2 1
RCS sñAM goùc noäi tieáp chaén AM cuûa O 2 sñAN
sñAM A laø ñieåm chính giöõa MN RBC RCS
Tứ giác BCSR nội tiếp (Tứ giác có 2 đỉnh liên tiếp cùng nhìn 1 cạnh dưới 2 góc bằng nhau) IRS BCS Maø
BCS AIK Tö ùgiaùc BCKI noäi tieáp Neâ n IRS AIK MN // R S 2 goù c naø y ôû vò trí ñoà ng v ò
Xét AIK và ACB, ta có: Trang 18 AIK
ACBtöù giaùc BCKI noäi tieáp IAK CABgoùc chung
AIK ∽ ACBg g AI AK TSÑD AC AB AI.AB AK.AC
Chứng minh tương tự ta có: AR.AB AS.AC Ta có: AR.AB AS.AC cmt AI.AB AK.AC
AR.AB AI.AB AS.AC AK.AC
ABAR AI ACAS AK AB.IR AC.KS
c) Chứng minh: MA là tiếp tuyến của đường tròn ngoại tiếp MBI và đường tròn ngoại tiếp MBI
tiếp xúc với đường tròn ngoại tiếp MCK .
Gọi E , F lần lượt là tâm MBI ;MCK Ta có:
AMI MBI 2 goùc noäi tieáp chaén 2 cung AM vaø AN baèng nhau cuûa O
MA là tiếp tuyến của MBI tại M
AM ME tại M (2)
Chứng minh tương tự ta có: AM MF tại M (2) Từ ( )
1 và (2) ME MF M , E , F thẳng hàng E nằm giữa F và M FE MF ME
Mà FE là khoảng cách 2 tâm của MBI ;MCK , MF, ME là bán kính của MBI ;MCK
Đường tròn ngoại tiếp MBI tiếp xúc với đường tròn ngoại tiếp MCK ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 4
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ THAM KHẢO Trang 19
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 4 – 3
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 9. (1,5 điểm). Cho P : y 2
x và đường thẳng d 3 : y x . 2 2
a) Vẽ P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép toán.
Câu 10. (1 điểm). Cho phương trình 2
2x 5x 9 0
a) Chứng tỏ phương trình luôn có nghiệm. 1 1
b) Không giải phương trình, tính N = + . x - 1 x - 1 1 2
Câu 11. (0,75 điểm). Quy tắc sau đây cho biết CAN, CHI của năm X nào đó.
Để xác định CAN, ta tìm số dư r trong phép chia X cho 10 và tra vào bảng 1
Để xác định CHI, ta tìm số dư s trong phép chia X cho 12 và tra vào bảng 2
Ví dụ: Năm 2020 có CAN là Canh, có CHI là Tí. Bảng 1 r 0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Bảng 2 s 0 1 2 3 4 5 6 7 8 9 10 11 CHI Thân Dậu Tuất Hợi Tí Sửu Dần Mẹo Thìn Tỵ Ngọ Mùi
a) Em hãy sử dụng quy tắc trên để xác định CAN CHI của năm 2023 ?
b) Lý Thái Tổ (Lý Công Uẩn) là vị vua đầu tiên đã mở nên triều đại Lý phồn thịnh trong
suốt trong 200 năm. Ông lên ngôi vào năm Kỷ Dậu đầu thế kỷ X I . Em hãy cho biết ông lên ngôi vào năm nào?
Câu 12. (0,75 điểm). Với sự phát triển của khoa học kỹ thuật, người ta tạo ra nhiều mẫu xe lăn đẹp
và tiện dụng cho người khuyết tật. Công ty A đầu tư và sản xuất ra những chiếc xe lăn cho
người khuyết tật với số vốn ban đầu là 450 000 000 đồng, chi phí để sản xuất ra 1 chiếc xe
lăn là 2 000 000 đồng, giá bán ra mỗi chiếc là 3 500 000 đồng.
a) Gọi x là số xe được sản xuất ra và y là tổng số tiền đã đầu tư (gồm vốn ban đầu và chi
phí sản xuất). Hãy lập công thức y theo x .
b) Công ty A phải bán bao nhiêu chiếc xe mới thu hồi được vốn?
Câu 13. (1 điểm). Một cửa hàng bánh pizza có chương trình khuyến mãi giảm 70% cho bánh pizza
thứ 2 cùng size có giá bằng hoặc thấp hơn pizza thứ nhất. Biết bánh pizza có giá ban đầu là 210 000 đồng.
a) Hỏi nếu khách hàng mua 10 bánh pizza thì phải trả bao nhiêu tiền? Trang 20
b) Cửa hàng có chương trình khuyến mãi thêm, nếu hóa đơn trên 2 000 000 đồng thì được
giảm thêm 5% trên tổng số tiền phải trả. Hỏi nếu khách hàng mua 15 bánh pizza thì
phải trả bao nhiêu tiền?
Câu 14. (1 điểm). Một bồn nước hình trụ có bán kính đáy là 3m , chiều cao là 4m . Người ta đổ nước
vào trong bồn sao cho chiều cao của nước bằng đúng một nửa chiều cao của bồn và tiếp tục
đặt vào trong bồn một phao nước có dạng hình cầu bằng kim loại không thấm nước có bán
kính là 50cm và chìm hoàn toàn trong nước.
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ ba)?
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 30, 0024
lít cho mỗi giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)?
Câu 15. (1 điểm). Một công ty có 100 xe chở khách gồm hai loại, loại xe chở được 30 khách và loại
xe chở được 50 khách. Nếu dùng tất cả số xe đó thì tối đa công ty chở một lần được 4300
khách. Hỏi mỗi loại công ty đó có mấy xe?
Câu 16. (3 điểm) Cho DA BC AB AC nội tiếp (O;R ) đường kính BC , trên cung nhỏ A C lấy
điểm D , B D cắt A C tại E , từ E vẽ EF ^ BC tại F .
a) Chứng minh tứ giác BA EF nội tiếp đường tròn.
b) Chứng minh DB là phân giác góc A DF .
c) Gọi M là trung điểm EC . Chứng minh DM .CA = CF .CO . ----HẾT--- Trang 21 HƯỚNG DẪN GIẢI 1
Câu 3. (1,5 điểm) Cho P 2 : y
x và đường thẳng d 3 : y x . 2 2
a) Vẽ P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải
c) Vẽ P và d trên cùng hệ trục tọa độ. y (d) BGT: 1 -4 -2 2 4 2 0 x x - 4 - 2 0 2 4 -3 2 - 1 2 y = x - 8 - 2 0 - 2 - 8 -2 2 x 0 2 3 3 1 y = x - - 2 2 2 -8 (P)
d) Tìm tọa độ giao điểm của P và d bằng phép toán.
Phương trình hoành độ giao điểm của P và d : - 1 3 2 x = x - 2 2 - 1 3 2 Û x - x + = 0 2 2 x é = 1 ê Û x ê = - 3 êë 1 - 1 - 1 Thay x 1 vào 2 y x , ta được: 2 y = .1 = . 2 2 2 - 1 - - Thay x = - 3 vào 2 y =
x ta được: y = (- )2 1 9 . 3 = . 2 2 2 æ 1ö - æ 9ö - Vậy ç ÷ ç ÷ 1 ç ; ÷ ç ÷; - ç 3;
÷ là hai giao điểm cần tìm. ç ç ÷ è 2 ÷ ø çè 2 ÷ ø
Câu 4. (1 điểm) Cho phương trình 2
2x + 5x - 9 = 0 . Trang 22
a) Chứng tỏ phương trình luôn có nghiệm. 1 1
b) Không giải phương trình, tính N = + . x - 1 x - 1 1 2 Lời giải Vì 2 2
b 4ac 5 4.2. 9 97 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b 5
S x x 1 2
Theo định lí Vi-et, ta có: a 2 c 9
P x .x 1 2 a 2 1 1 Ta có: N = + x - 1 x - 1 1 2 - 5 - 2 x - 1 + x - 1 (x + x - 2 1 2 ) S - 2 9 2 1 N = = = 2 = = . (x - 1 x - 1 x x - x + x + 1 P - S + 1 - 9 - 5 2 1 2 ( 1 2 ) 1 )( 2 ) - + 1 2 2
Câu 5. (0,75 điểm) Quy tắc sau đây cho biết CAN, CHI của năm X nào đó.
Để xác định CAN, ta tìm số dư r trong phép chia X cho 10 và tra vào bảng 1
Để xác định CHI, ta tìm số dư s trong phép chia X cho 12 và tra vào bảng 2
Ví dụ: Năm 2020 có CAN là Canh, có CHI là Tí. Bảng 1 r 0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Bảng 2 s 0 1 2 3 4 5 6 7 8 9 10 11 CHI Thân Dậu Tuất Hợi Tí Sửu Dần Mẹo Thìn Tỵ Ngọ Mùi
a) Em hãy sử dụng quy tắc trên để xác định CAN CHI của năm 2023 ?
b) Lý Thái Tổ (Lý Công Uẩn) là vị vua đầu tiên đã mở nên triều đại Lý phồn thịnh trong
suốt trong 200 năm. Ông lên ngôi vào năm Kỷ Dậu đầu thế kỷ 11. Em hãy cho biết
ông lên ngôi vào năm nào? Lời giải Trang 23
a) Em hãy sử dụng quy tắc trên để xác định CAN CHI của năm 2023 ?
Vì 2023 : 10 = 202 dư 3 nên sau khi tra vào bảng 1 , ta được CAN là Quý.
Vì 2023 : 12 = 168 dư 7 nên sau khi tra vào bảng 2 , ta được CHI là Mẹo.
Vậy năm 2023 có CAN CHI là Quý Mẹo.
b) Em hãy cho biết ông lên ngôi vào năm nào?
Gọi X là năm Lý Thái Tổ lên ngôi.
Vì năm X ở thế kỷ 11 nên 1001 £ X £ 1100
Tra vào bảng 1 ta được r = 9 ; tra vào bảng 2 ta được s = 1
Vì năm X là năm Kỷ Dậu nên:
X : 10 dư 9 Þ X = {1019;1029;1039;1049;1059;1069;1079;1089; } 1099
X : 12 dư 1 Þ X = 1069
Vậy Lý Thái Tổ lên ngôi nào năm 1069 .
Câu 6. (0,75 điểm). Với sự phát triển của khoa học kỹ thuật, người ta tạo ra nhiều mẫu xe lăn đẹp và
tiện dụng cho người khuyết tật. Công ty A đầu tư và sản xuất ra những chiếc xe lăn cho
người khuyết tật với số vốn ban đầu là 450 000 000 đồng, chi phí để sản xuất ra 1 chiếc xe
lăn là 2 000 000 đồng, giá bán ra mỗi chiếc là 3 500 000 đồng.
a) Gọi x là số xe được sản xuất ra và y là tổng số tiền đã đầu tư (gồm vốn ban đầu và chi
phí sản xuất). Hãy lập công thức y theo x .
b) Công ty A phải bán bao nhiêu chiếc xe mới thu hồi được vốn? Lời giải
a) Hãy lập công thức y theo x .
Công thức y theo x là: y = 2 000 000x + 450 000 000 (đồng)
b) Công ty A phải bán bao nhiêu chiếc xe mới thu hồi được vốn?
Số tiền thu được khi bán x chiếc xe là: 3 500 000x (đồng)
Để công ty A thu hồi vốn thì 3 500 000x = 2 000 000x + 450 000 000
Û 1500 000x = 450 000 000 Û x = 300
Vậy công ty A phải bán 300 chiếc xe mới thu hồi được vốn. Trang 24
Câu 7. (1 điểm) Một cửa hàng bánh pizza có chương trình khuyến mãi giảm 70% cho bánh pizza
thứ 2 cùng size có giá bằng hoặc thấp hơn pizza thứ nhất. Biết bánh pizza có giá ban đầu là 210 000 đồng.
a) Hỏi nếu khách hàng mua 10 bánh pizza thì phải trả bao nhiêu tiền?
b) Cửa hàng có chương trình khuyến mãi thêm, nếu hóa đơn trên 2 000 000 đồng thì được
giảm thêm 5% trên tổng số tiền phải trả. Hỏi nếu khách hàng mua 15 bánh pizza thì
phải trả bao nhiêu tiền? Lời giải
a) Hỏi nếu khách hàng mua 10 bánh pizza thì phải trả bao nhiêu tiền?
Giá một bánh pizza sau khi được khuyến mãi 70% là: 210 000.(1 - 70 ) % = 63 000 (đồng).
Nếu khách hàng mua 10 bánh pizza thì phải trả tiền mua 5 bánh pizza với giá 210 000
đồng/bánh và trả tiền mua 5 bánh pizza còn lại với giá 63 000 đồng/bánh.
Số tiền khách hàng phải trả nếu mua 10 bánh pizza là:
5.210 000 + 5.63 000 = 2 730 000 (đồng).
b) Hỏi nếu khách hàng mua 15 bánh pizza thì phải trả bao nhiêu tiền?
Nếu khách hàng mua 15 bánh pizza thì phải trả tiền mua 8 bánh pizza với giá 210 000
đồng/bánh và trả tiền mua 7 bánh pizza với giá 63 000 đồng/bánh.
Số tiền khách hàng phải trả nếu mua 15 bánh pizza mà chưa áp dụng chương trình khuyến mãi thêm là:
8.210 000 + 7.63 000 = 2121000 (đồng).
Vì 2121000 > 2 000 000 nên khách hàng trên được áp dụng chương trình khuyến mãi thêm là
giảm 5% trên tổng số tiền phải trả.
Vậy số tiền khách hàng phải trả khi mua 15 bánh pizza là: 2121000(1 - 5 ) % = 2 014 950 (đồng).
Câu 8. (1 điểm) Một bồn nước hình trụ có bán kính đáy là 3m , chiều cao là 4m . Người ta đổ nước
vào trong bồn sao cho chiều cao của nước bằng đúng một nửa chiều cao của bồn và tiếp tục Trang 25
đặt vào trong bồn một phao nước có dạng hình cầu bằng kim loại không thấm nước có bán
kính là 50cm và chìm hoàn toàn trong nước.
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ ba)?
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có lưu lượng nước chảy là
30, 0024 lít cho mỗi giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)? Lời giải
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ ba)?
Một nửa chiều cao của bồn bằng: 4 : 2 = 2 (m ).
Đổi: 50cm = 0, 5m .
Thể tích của phao nước là: 2 4p.0, 5 = p ( 3 m ). p 19
Chiều cao của mực nước trong bồn cao là: + 2 = » 2,111 (m ). 2 p.3 9
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 30, 0024
lít cho mỗi giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)? æ 19ö
Thể tích phần không chứa nước trong bồn là: 2 ç ÷ p.3 . 4 ç - ÷= 17p 3 ç ÷ (m ). çè 9 ÷ ø
Đổi: 30, 0024 lít/giây = 1, 800144 3 m /phút.
Bồn đầy nước sau: 17p : 1, 800144 » 30 (phút).
Câu 9. (1 điểm) Một công ty có 100 xe chở khách gồm hai loại, loại xe chở được 30 khách và loại xe
chở được 50 khách. Nếu dùng tất cả số xe đó thì tối đa công ty chở một lần được 4300
khách. Hỏi mỗi loại công ty đó có mấy xe? Lời giải
Gọi x , y (xe) là số xe loại chở được 30 khách và loại chở được 50 khách. (x,y Î ¥ )
Vì công ty có 100 xe chở khách nên ta có: x + y = 100 . ( ) 1
Vì nếu dùng tất cả số xe thì tối đa công ty chở một lần được 4300 khách nên ta có:
30x + 50y = 4300 . (2) Trang 26 ìï x + y = 100 ì ï ï x = 35 ï Từ ( )
1 và (2), ta có hệ phương trình: í Û í (nhận)
ï 30x + 50y = 4300 ï ï î y = 65 ïî
Vậy công tay có 35 xe loại chở được 30 khách và 65 xe loại chở được 50 khách. Câu 10.
(3 điểm) Cho DA BC AB AC nội tiếp (O;R ) đường kính BC , trên cung nhỏ A C lấy
điểm D , B D cắt A C tại E , từ E vẽ EF ^ BC tại F .
a) Chứng minh tứ giác BA EF nội tiếp đường tròn.
b) Chứng minh DB là phân giác góc A DF .
c) Gọi M là trung điểm EC . Chứng minh DM .CA = CF.CO . Lời giải D A E M B C F O
a) Chứng minh tứ giác BA EF nội tiếp đường tròn.
Xét tứ giác BA EF , ta có: ·
B FE = 90° ( EF ^ BC tại F ) ·
B A E = 90° (góc nội tiếp chắn nửa (O )) · ·
Þ BFE + BA E = 180°
Þ Tứ giác BA EF nội tiếp (Tứ giác có hai góc đối bù nhau)
b) Chứng minh DB là phân giác góc A DF .
Xét tứ giác CDEF , ta có: ·
CDE = 90° (góc nội tiếp chắn nửa (O )) ·
B FE = 90° (cm câu a) Trang 27 · · Þ BFE = CDE
Þ Tứ giác CDEF nội tiếp (Tứ giác có góc ngoài bằng góc trong của đỉnh đối diện) · · Þ EDF = BCA · ·
Mà BCA = A DB (hai góc nội tiếp cùng chắn cung A B của (O)) · · Nên EDF = ADB
Þ DB là tia phân giác của góc A DF .
c) Chứng minh DM .CA = CF.CO .
Xét DCDE vuông tại D , ta có: DM là đường trung tuyến (M là trung điểm của CE ) 1 Þ DM =
CE Þ CE = 2DM . 2
Xét D CEF và D CBA , ta có: µ C là góc chung · ·
CFE = CA B (= 90 ) °
Þ DCEF ∽DCBA (g - g) CE CF Þ = (tỉ số đồng dạng) CB CA
Þ CE.CA = CF.CB
Mà CE = 2DM và CB = 2CO ( B C là đường kính của (O))
Nên 2DM .CA = CF.2CO
Þ DM.CA = CF.CO . ----HẾT--- Trang 28




