




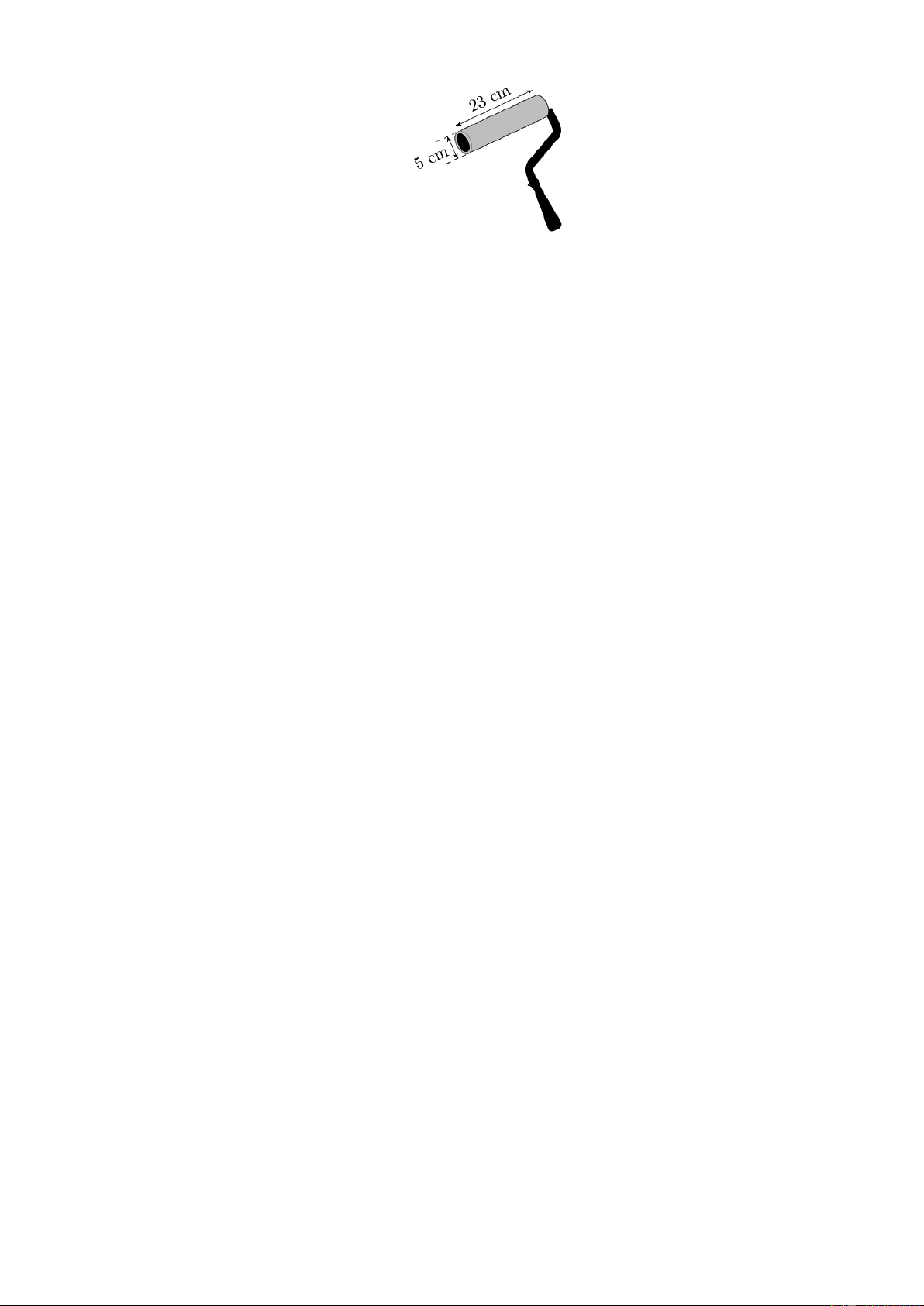








Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 5
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 5 - 1
Thời gian: 120 phút (không kể thời gian phát đề) x x
Câu 1. (1,5 điểm). Cho P 2 : y
và đường thẳng d : y 2 . 4 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Gọi x , x là hai nghiệm của phương trình 2
x 5x 6 0 . Không giải phương 1 2
1x x 1x x 1 2 2
trình, tính giá trị của các biểu thức: 1 A . x x 1 2
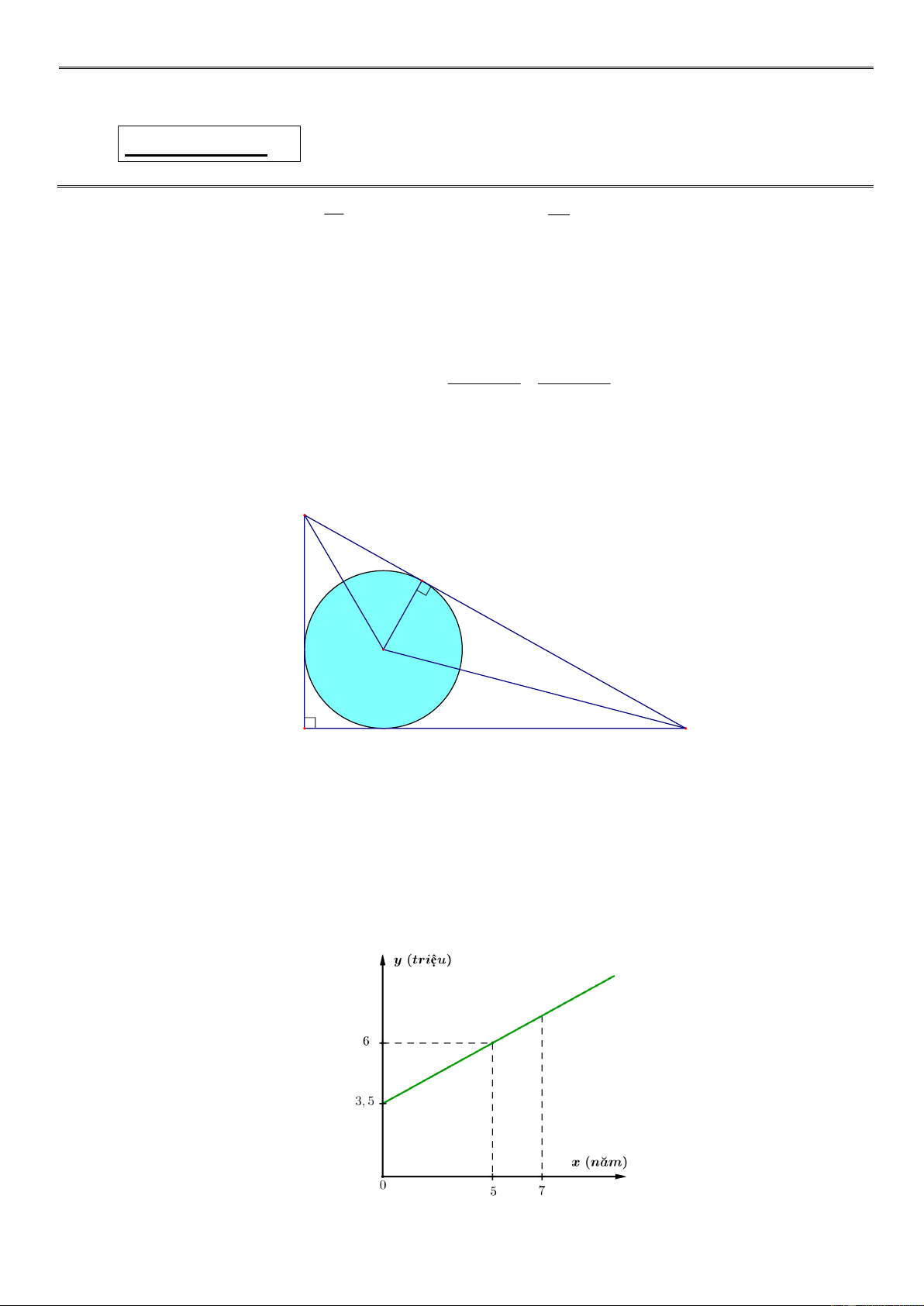
Câu 3. (1 điểm). Áp Cho tam giác ABC vuông tại A có cạnh AC 40cm . Đường tròn O; 4 cm
nội tiếp tam giác ABC . Tính độ dài cạnh AB của tam giác ABC . B N 4 cm O C A 40 cm
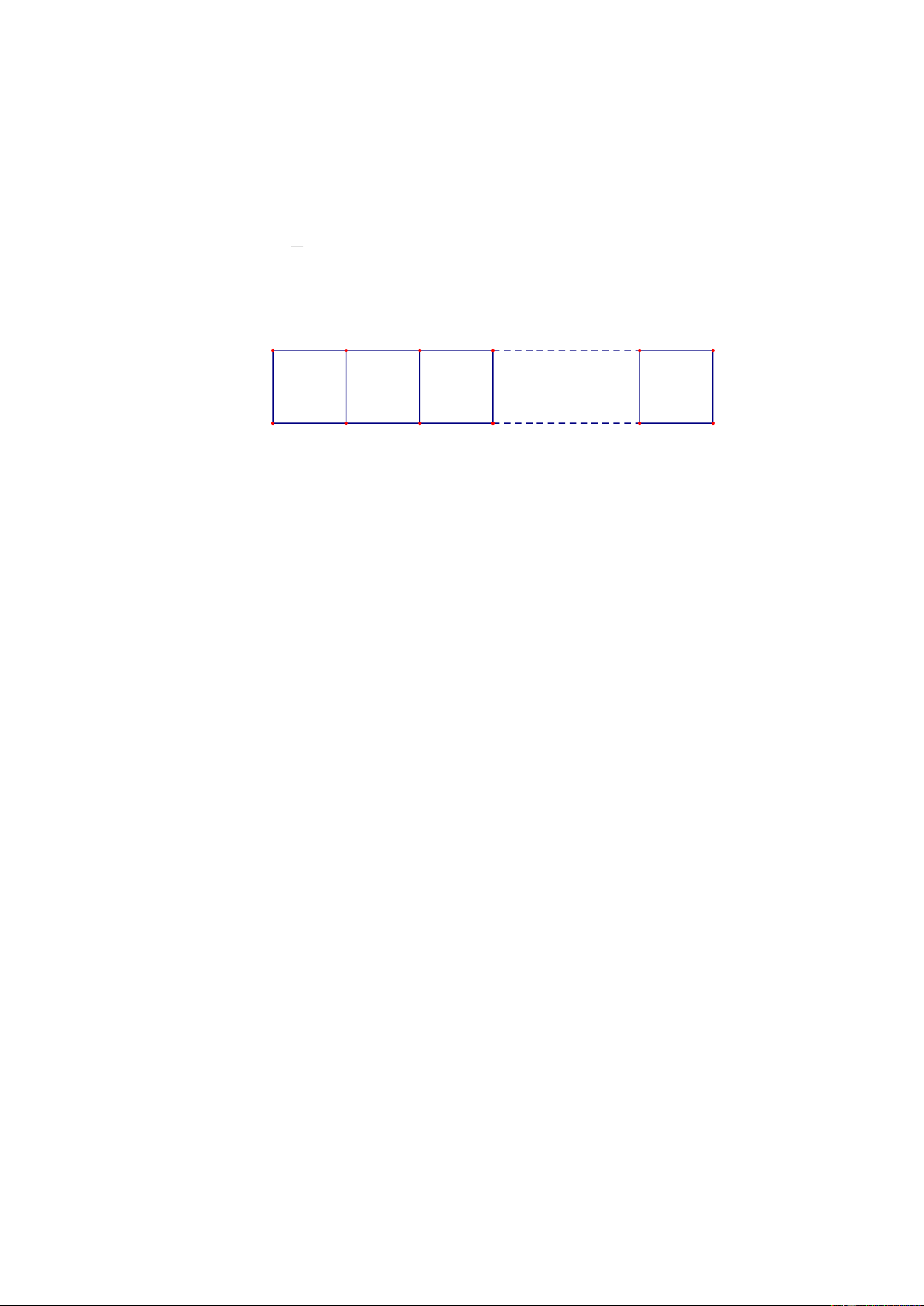
Câu 4. (1 điểm). Anh Bình là công nhân trong một công ty may có vốn đầu tư nước ngoài. Lương
cơ bản khởi điểm khi vào làm là 3,5 triệu đồng. Công ty có chế độ tính thâm niên cho công
nhân làm lâu năm, cứ mỗi năm được tăng một khoản nhất định. Vì thế khi làm được 5
năm thì lương cơ bản của anh Bình là 6 triệu đồng. Không tính các khoản phụ cấp, thưởng
và các khấu trừ khác thì ta thấy mối liên hệ giữa lương cơ bản và số năm làm việc là một
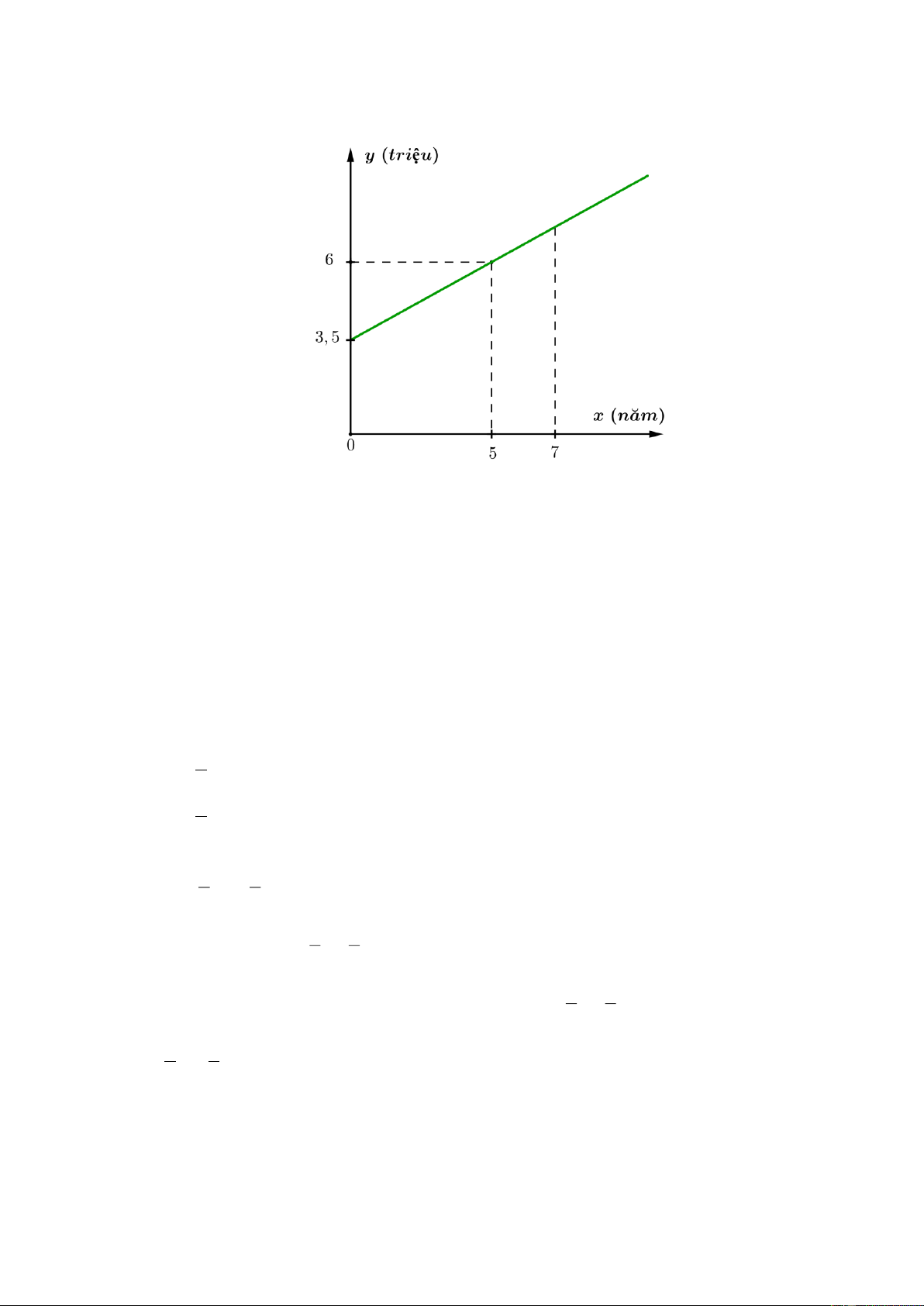
hàm số bậc nhất y ax b ( a khác 0 ) có đồ thị như hình bên. Trang 1
a) Xác định hệ số a, b .
b) Nếu thâm niên là 7 năm làm việc thì lương cơ bản của anh Bình là bao nhiêu?
Câu 5. (1 điểm). Có ba thùng dầu đựng tổng cộng 123 lít dầu. Nếu đổ từ thùng thứ nhất sang
thùng thứ hai 5 lít, rồi đổ từ thùng thứ hai sang thùng thứ ba 7 lít, tiếp tục đổ từ thùng
thứ ba sang thùng thứ nhất 9 lít thì số dầu ở thùng thứ nhất sẽ ít hơn số dầu ở thùng thứ 2 hai là 4 lít và bằng
số dầu ở thùng thứ ba. Tính số lít dầu ở mỗi thùng lúc đầu. 3
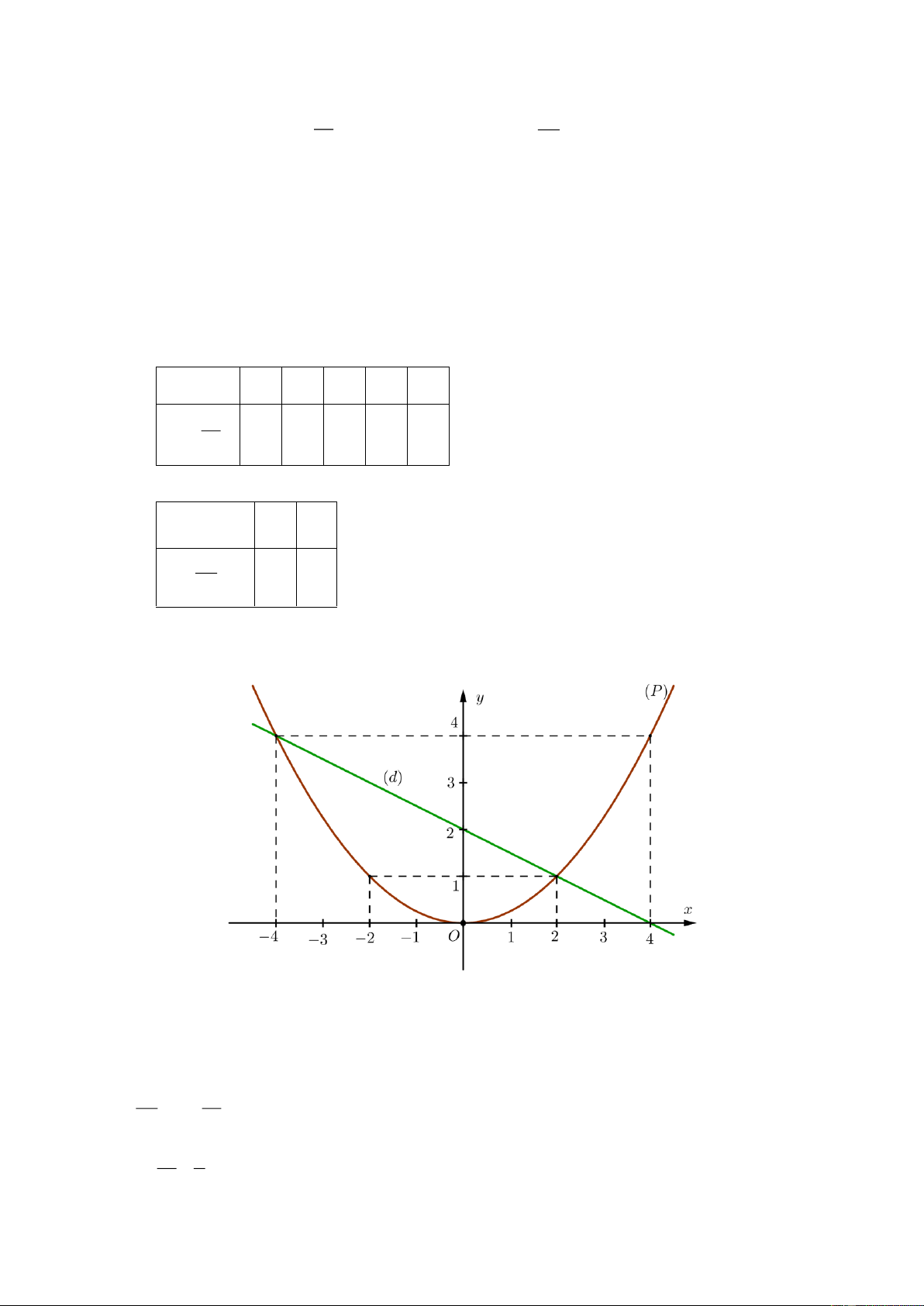
Câu 6. (1 điểm). Bạn Khôi dùng những que tính có độ dài 4 cm để ghép lại thành các hình vuông
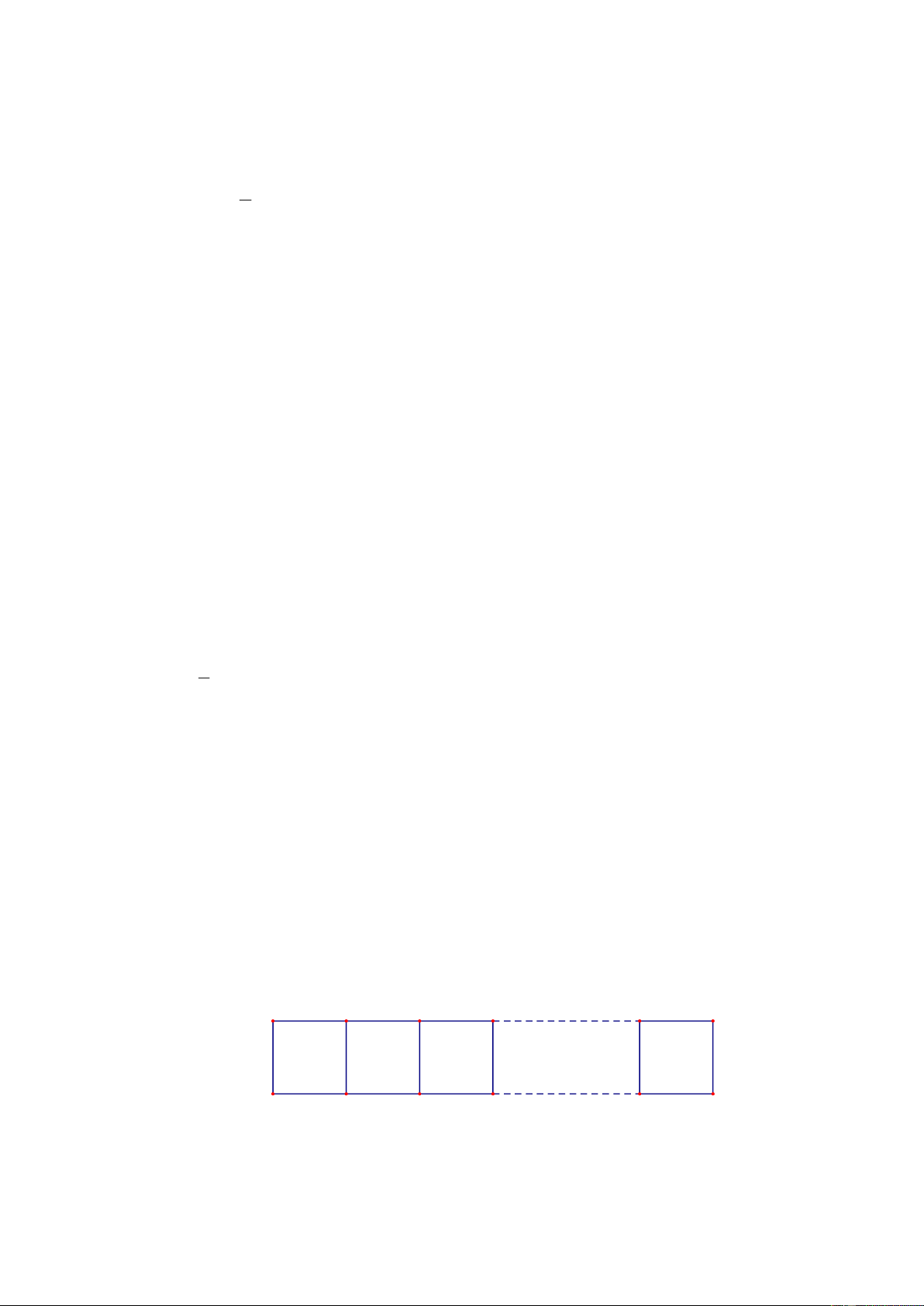
như hình vẽ dưới đây: B A
a) Nếu cạnh AB dài 48 cm thì bạn Khôi đã dùng tất cả bao nhiêu que tính để ghép được hình trên?
b) Nếu bạn Khôi dùng tất cả 61 que tính thì cạnh AB có độ dài là bao nhiêu cm ?
Câu 7. (1 điểm). Một cửa hàng điện máy thực hiện chương trình khuyến mãi giảm giá tất cả các
mặt hàng 10% theo giá niêm yết, và nếu hóa đơn khách hàng trên 10 triệu sẽ được giảm
thêm 2% số tiền trên hóa đơn, hóa đơn trên 15 triệu sẽ được giảm thêm 3% số tiền trên
hóa đơn, hóa đơn trên 40 triệu sẽ được giảm thêm 6% số tiền trên hóa đơn. Ông Nam
muốn mua một ti vi với giá niêm yết là 9 200 000 đồng và một tủ lạnh với giá niêm yết là
8100000 đồng. Hỏi với chương trình khuyến mãi của cửa hàng, ông Nam phải trả bao nhiêu tiền?
Câu 8. (2,5 điểm) Cho hình thang ABCD đáy lớn AD , nội tiếp trong một đường tròn tâm O . Các
cạnh bên AB và CD cắt nhau tại I . Tiếp tuyến với đường tròn tâm O tại B và D cắt nhau tại K .
a) Chứng minh tam giác IAD cân và BID 180 BOD .
b) Chứng minh năm điểm O, ,
B I, K, D cùng thuộc một đường tròn và IK // AD .
c) Vẽ hình bình hành BDKM . Đường tròn tâm O cắt đường tròn ngoại tiếp tam giác BKM
tại N (N khác B) . Chứng minh rằng ba điểm M, N , D thẳng hàng. ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI x x
Câu 1. (1,5 điểm) Cho P 2 : y
và đường thẳng d : y 2 . 4 2
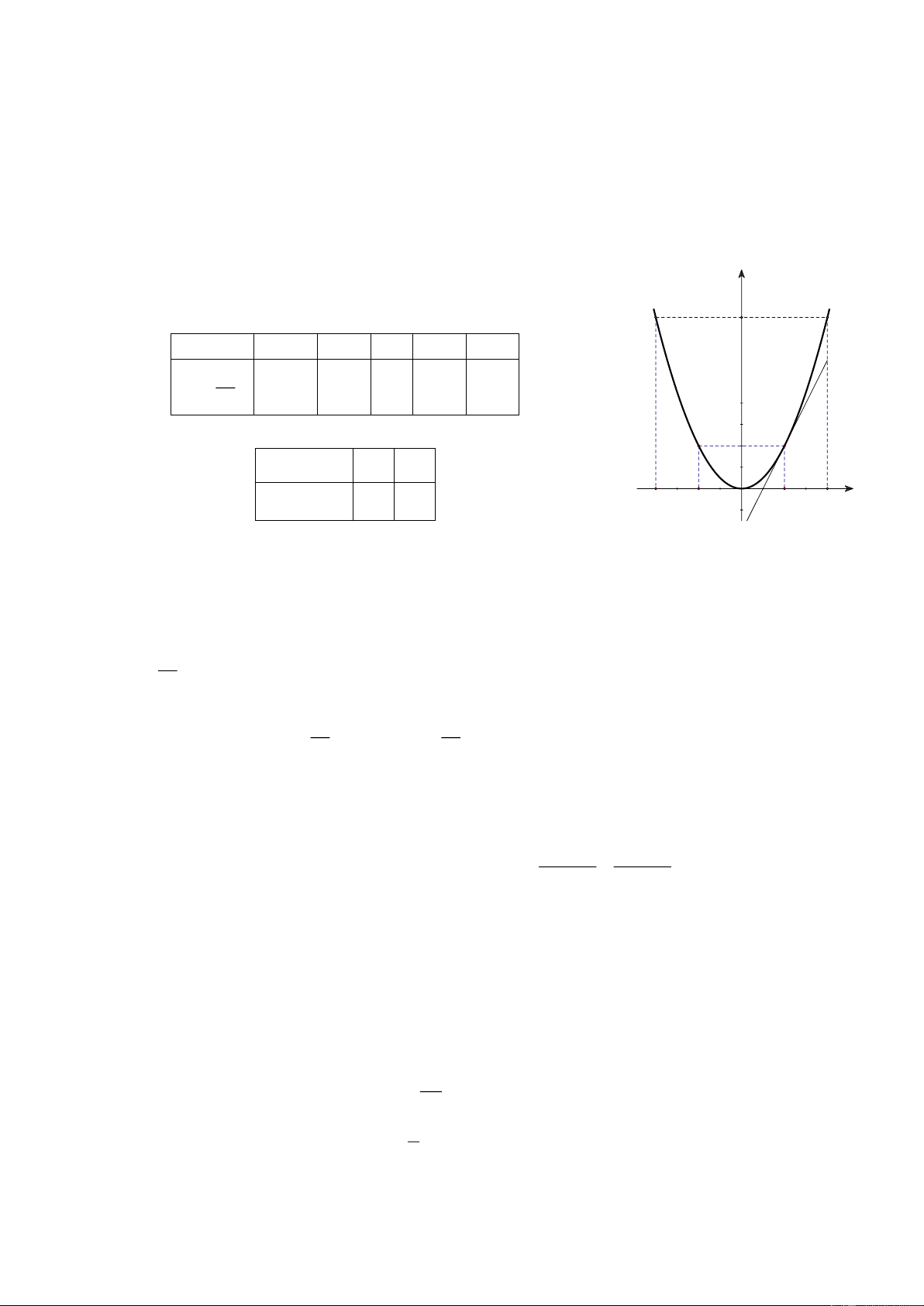
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
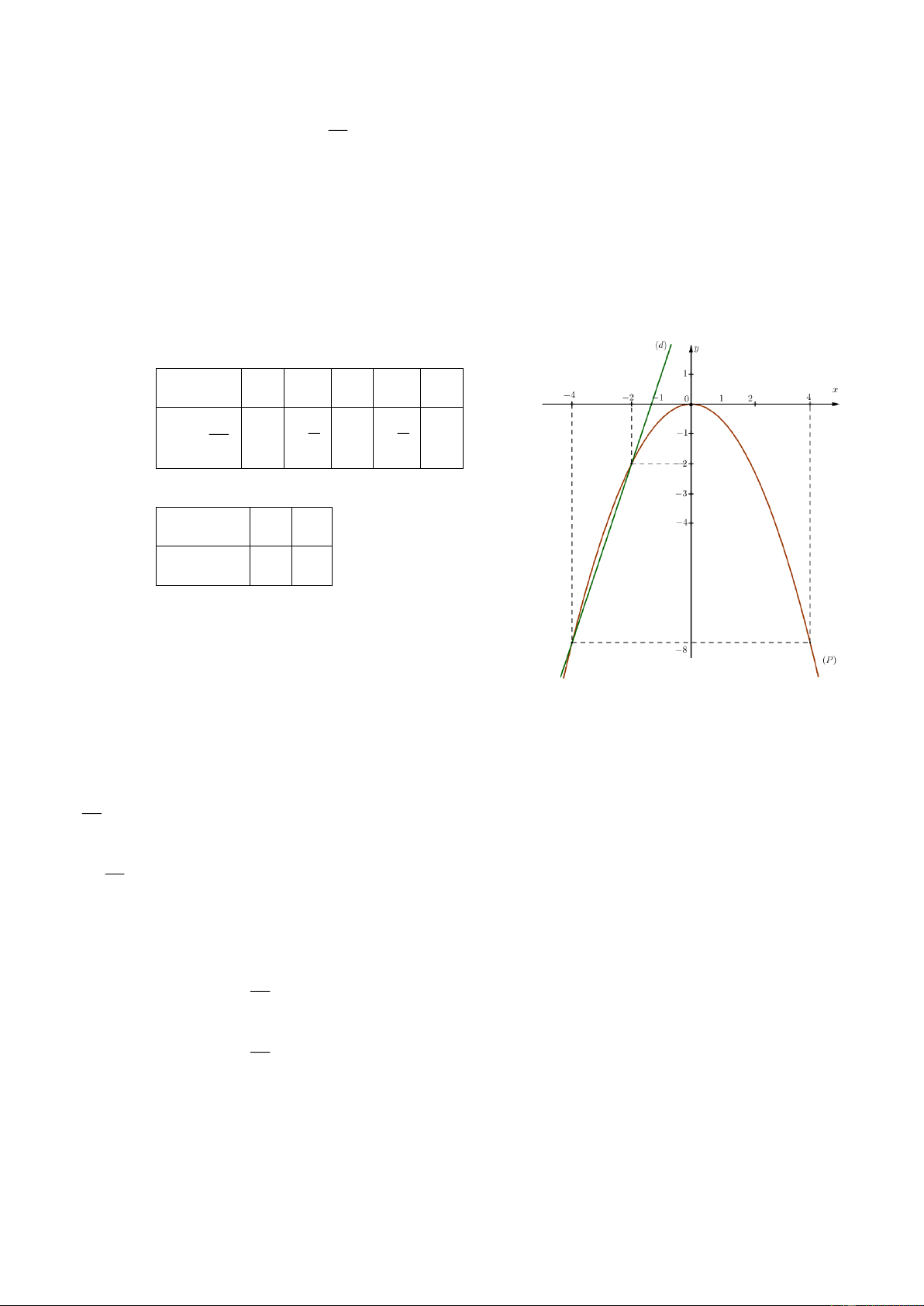
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. Bảng giá trị: x 4 2 0 2 4 2 x y 4 1 0 1 4 4 x 0 2 x y 2 2 1 2 Đồ thị:
a) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2 x x 2 2 4 2 x x 2 0 4 2 Trang 3 x 2 4 2 x 2 2
Thay x 2 vào y , ta được: y 1. 4 4 2 x 2 4 Thay x 4 vào y , ta được: y 4 . 4 4 Vậy 2;1 và 4
;4 là hai giao điểm cần tìm.
Câu 2. (1 điểm) Gọi x , x là hai nghiệm của phương trình 2
x 5x 6 0 . Không giải phương 1 2
1x x 1x x 1 2 2
trình, tính giá trị của các biểu thức: 1 A . x x 1 2 Lời giải 2 Vì 2
b 4ac 5 4.1. 6 49 0
Nên phương trình có 2 nghiệm phân biệt x , x . 1, 2 b 5 S
x x 5 1 2
Theo định lý Vi-et, ta có: a 1 c 6
P x .x 6 1 2 a 1 Ta có:
1x x 1x x 1 2 2 1 A x x 1 2 1 x x 1 x x 1 2 2 2 2 1 A x x x x 1 2 1 2 2 2 2 2
x x x x x x 2 1 2 1 1 2 A x x 1 2
x x 2 2x x x x x x 1 2 1 2 1 2 1 2 A x x 1 2 2 5 2. 6 6 .5 67 A . 6 6
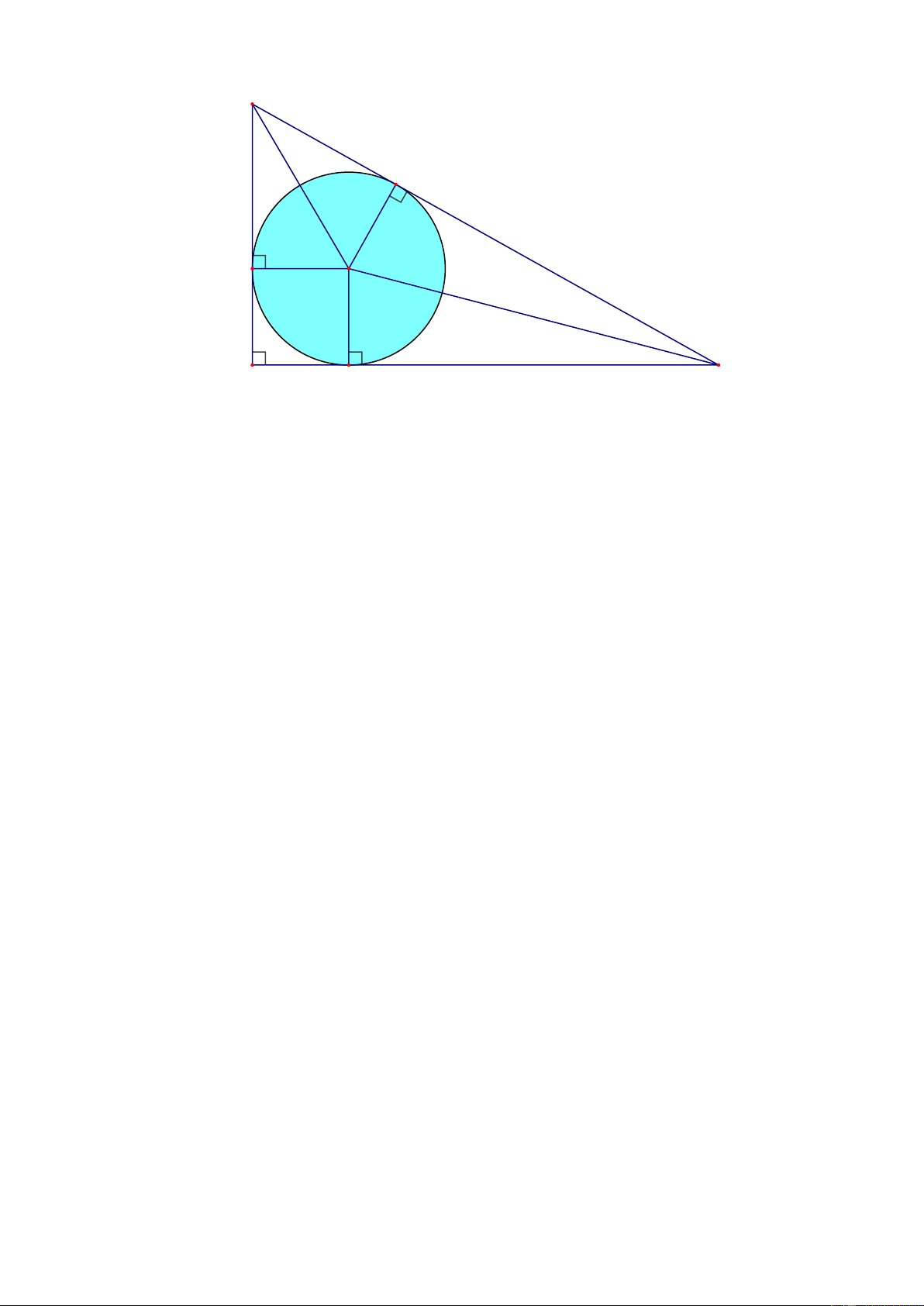
Câu 3. (1 điểm). Cho tam giác ABC vuông tại A có cạnh AC 40cm . Đường tròn O; 4 cm nội
tiếp tam giác ABC . Tính độ dài cạnh AB của tam giác ABC . Lời giải Trang 4 B N 4 cm M O C A P 40 cm
Gọi M, N , P lần lượt là hình chiếu của O lên các cạnh AB, BC, AC . Ta có:
+ OM ON OP 4cm,
+ AMOP là hình vuông, suy ra AM AP 4 m c .
+ BM BN , CN CP (tính chất hai tiếp tuyến cắt nhau).
* AB AC AM MB AP PC
AM AP MB PC
2.4 BN CN 8 BC .
AB 40 8 BC
BC AB 32
Mặc khác: tam giác ABC vuông tại A suy ra 2 2 2
BC AB AC
Thay BC AB 32 vào, ta được AB 2 2 2 32 AB 40 64.AB 576 AB 9 .
Vậy độ dài cạnh AB của tam giác ABC là 9 cm .
Câu 4. (1 điểm). Anh Bình là công nhân trong một công ty may có vốn đầu tư nước ngoài. Lương
cơ bản khởi điểm khi vào làm là 3,5 triệu đồng. Công ty có chế độ tính thâm niên cho công
nhân làm lâu năm, cứ mỗi năm được tăng một khoản nhất định. Vì thế khi làm được 5 năm
thì lương cơ bản của anh Bình là 6 triệu đồng. Không tính các khoản phụ cấp, thưởng và Trang 5
các khấu trừ khác thì ta thấy mối liên hệ giữa lương cơ bản và số năm làm việc là một hàm
số bậc nhất y ax b ( a khác 0 ) có đồ thị như hình bên.
a) Xác định hệ số a, b .
b) Nếu thâm niên là 7 năm làm việc thì lương cơ bản của anh Bình là bao nhiêu? Lời giải
a) Xác định hệ số a, b .
Đồ thị hàm số qua 2 điểm 0; 3,5, 5;6 nên ta có hệ phương trình:
0.a b 3,5 5.a b 6 1 a 2 7 b 2 1 7 Vậy a , b . 2 2 1 7
Hàm số đã cho là: y x . 2 2 1 7
b) Thâm niên là 7 năm thì x 7 , thay vào hàm số y x , ta có: 2 2 1 7 y .7 2 2 y 7
Vậy nếu thâm niên là 7 năm là việc thì lương cơ bản của anh Bình là 7 triệu đồng. Trang 6
Câu 5. (1 điểm). Có ba thùng dầu đựng tổng cộng 123 lít dầu. Nếu đổ từ thùng thứ nhất sang
thùng thứ hai 5 lít, rồi đổ từ thùng thứ hai sang thùng thứ ba 7 lít, tiếp tục đổ từ thùng thứ
ba sang thùng thứ nhất 9 lít thì số dầu ở thùng thứ nhất sẽ ít hơn số dầu ở thùng thứ hai là 2 4 lít và bằng
số dầu ở thùng thứ ba. Tính số lít dầu ở mỗi thùng lúc đầu. 3 Lời giải
Gọi x (lít), y (lít) lần lượt là số lít dầu ở thùng thứ nhất, thùng thứ hai lúc đầu.
(ĐK : x, y 0; x 123; y 123)
Do đó, số lít dầu ở thùng thứ ba lúc đầu là: 123 x y (lít).
Nếu đổ từ thùng thứ nhất sang thùng thứ hai 5 lít, rồi đổ từ thùng thứ hai sang thùng thứ
ba 7 lít, tiếp tục đổ từ thùng thứ ba sang thùng thứ nhất 9 lít. Số lít dầu ở:
+ Thùng thứ nhất là: x 5 9 x 4 (lít)
+ Thùng thứ hai là: y 5 7 y 2 (lít)
+ Thùng thứ ba là: 123 x y 7 9 121 x y (lít)
Theo đề, ta có hệ phương trình:
x 4 y 2 4 2
x 4 121 x y 3
x y 10 5x 2y 230 x 30 (nhận) y 40
Vậy lúc đầu, thùng thứ nhất chứa là 30 lít dầu, thùng thứ hai chứa 40 lít dầu, thùng thứ
ba chứa 123 30 40 53 lít dầu.
Câu 6. (1 điểm). Bạn Khôi dùng những que tính có độ dài 4 cm để ghép lại thành các hình vuông
như hình vẽ dưới đây: B A
a) Nếu cạnh AB dài 48 cm thì bạn Khôi đã dùng tất cả bao nhiêu que tính để ghép được hình trên? Trang 7
b) Nếu bạn Khôi dùng tất cả 61 que tính thì cạnh AB có độ dài là bao nhiêu cm ? Lời giải
a) Số que tính cần để ghép cạnh AB dài 48 cm là: 48 : 4 12 (que tính)
Số que tính cần để ghép hình có cạnh AB dài 48 cm là:
12212 1 37 (que tính)
b) Số que tính trên một cạnh AB là:
61 1: 3 20 (que tính)
Độ dài cạnh AB là: 20 4 80 cm
Vậy cần 37 que tính và chiều dài cạnh AB là 80 cm .
Câu 7. (1 điểm). Một cửa hàng điện máy thực hiện chương trình khuyến mãi giảm giá tất cả các
mặt hàng 10% theo giá niêm yết, và nếu hóa đơn khách hàng trên 10 triệu sẽ được giảm
thêm 2% số tiền trên hóa đơn, hóa đơn trên 15 triệu sẽ được giảm thêm 3% số tiền trên
hóa đơn, hóa đơn trên 40 triệu sẽ được giảm thêm 6% số tiền trên hóa đơn. Ông Nam
muốn mua một ti vi với giá niêm yết là 9 200 000 đồng và một tủ lạnh với giá niêm yết là
8100000 đồng. Hỏi với chương trình khuyến mãi của cửa hàng, ông Nam phải trả bao nhiêu tiền? Lời giải
Giá tiền của một ti vi sau khi giảm giá 10% là:
9200000.100% 10% 8280000 (đồng)
Giá tiền của một tủ lạnh sau khi giảm giá 10% là:
8100000.100% 10% 7 290000 (đồng)
Tổng số tiền ông Nam phải trả trước khuyến mãi theo hóa đơn là:
8 280000 7 290000 15570000 (đồng)
Vì hóa đơn trên 15000 000 đồng nên ông Nam được áp dụng khuyến mãi giảm thêm 3%
trên tổng hóa đơn. Số tiền ông Nam thực tế phải trả là:
15570000.100% 3% 15102900 (đồng) Trang 8
Vậy, với chương trình khuyến mãi của cửa hàng, ông Nam phải trả cho cửa hàng số tiền 15102900 (đồng).
Câu 8. (2,5 điểm) Cho hình thang ABCD đáy lớn AD , nội tiếp trong một đường tròn tâm O . Các
cạnh bên AB và CD cắt nhau tại I . Tiếp tuyến với đường tròn tâm O tại B và D cắt nhau tại K .
a) Chứng minh tam giác IAD cân và BID 180 BOD .
b) Chứng minh năm điểm O, ,
B I, K, D cùng thuộc một đường tròn và IK // AD .
c) Vẽ hình bình hành BDKM . Đường tròn tâm O cắt đường tròn ngoại tiếp tam giác BKM
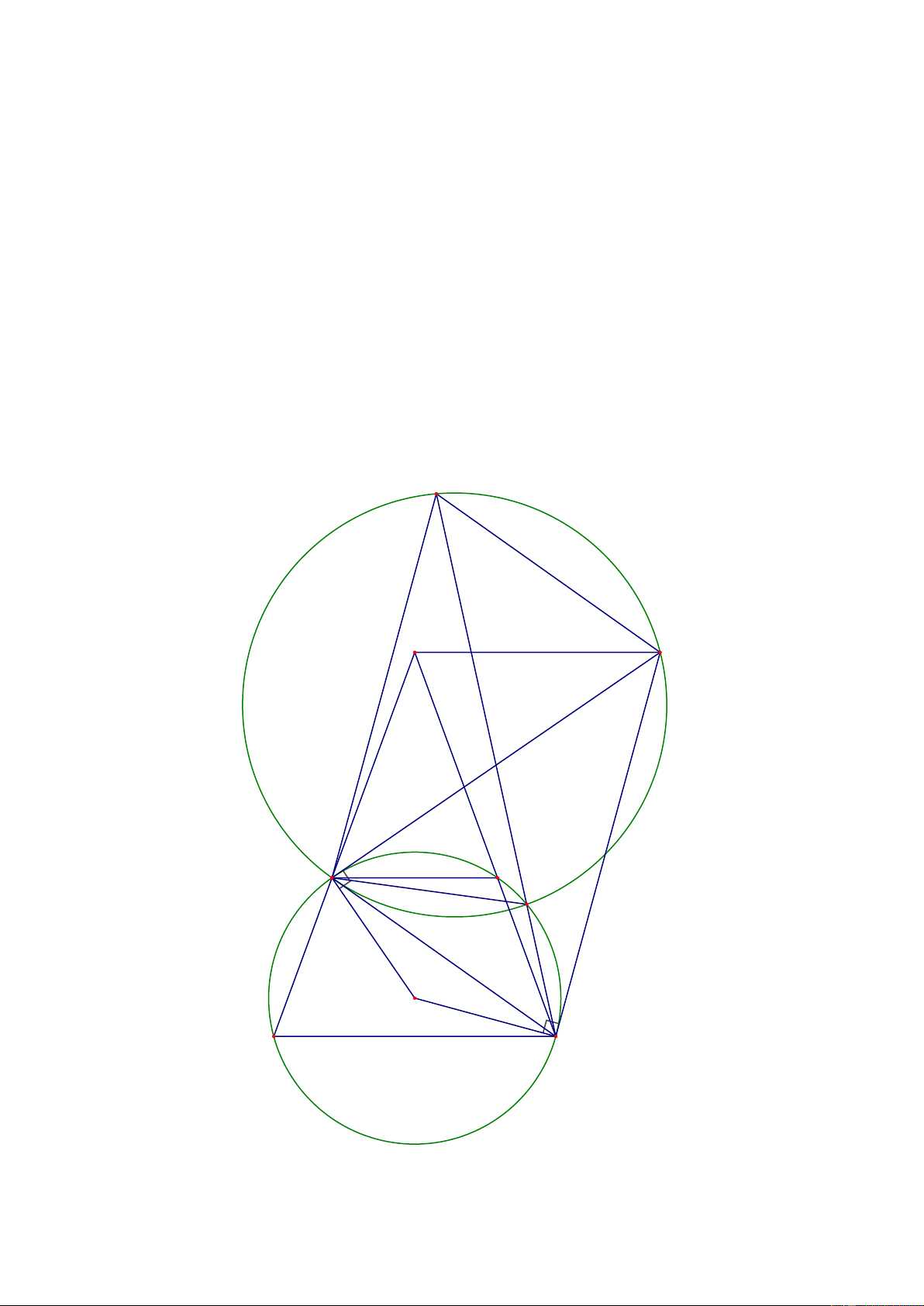
tại N (N khác B) . Chứng minh rằng ba điểm M, N , D thẳng hàng. Lời giải M I K C B N O A D
a) Chứng minh tam giác IAD cân và BID 180 BOD . Trang 9
* Chứng minh tam giác IAD cân:
Tứ giác ABCD nội tiếp đường tròn tâm O , suy ra ABC ADC 180
Mà ABC DAB 180 (hai góc trong cùng phía do BC // AD )
Nên ADC DAB
Suy ra tam giác IAD cân tại I .
* Chứng minh BID 180 BOD .
+ BOD 2BAD sđ BD (góc nội tiếp và góc ở tâm cùng chắn cung BD .
+ Tam giác IAD cân tại I
BID 2BAD 180
BID BOD 180 (do BOD 2BAD )
BID 180 BOD .
b) Chứng minh năm điểm O, ,
B I, K, D cùng thuộc một đường tròn và IK // AD .
* Chứng minh năm điểm O, ,
B I, K, D cùng thuộc một đường tròn:
+ BK, BD là 2 tiếp tuyến của O nên OBK ODK 90, suy ra tứ giác OBKD nội tiếp
được đường tròn (tổng hai góc đối bằng 180 ) 1
+ tứ giác OBKD nội tiếp được đường tròn
BKA BOD 180 hay BKD 180 BOD
BKD BID (do BID 180 BOD )
Tứ giác BIKD có hai đỉnh I , K cùng nhìn cạnh BD dưới một góc bằng nhau nên BIKD
nội tiếp được đường tròn. 2
Từ 1 và 2 suy ra năm điểm O, ,
B I, K, D cùng thuộc một đường tròn.
* Chứng minh IK // AD :
+ Tứ giác BIKD nội tiếp được đường tròn (chứng minh trên)
KID KBD 1 sđ KD (hai góc nội tiếp cùng chắn cung KD ) 3 2 1
+ KBD BAD
sđ BD (góc tạo bởi tiếp tuyến KB và dây BD và góc nội tiếp chắn 2 cung BD ) 4
+ BAD IAD ADI (tam giác IAD cân tại I ) 5 Trang 10
Từ 3, 4, 5 suy ra KID ADI , mà hai góc này ở vị trí so le trong nên IK // AD .
c) Vẽ hình bình hành BDKM . Đường tròn tâm O cắt đường tròn ngoại tiếp tam giác BKM
tại N (N khác B) . Chứng minh rằng ba điểm M, N , D thẳng hàng.
Ta chứng minh BND BNM 180 . Ta có:
BAD KBD (chứng minh trên)
KBD BKM (so le trong do MK // BD )
BKM BNM (hai góc nội tiếp cùng chắn cung BM của BKM )
BAD BNM
* Tứ giác BNDA nội tiếp O
BND BAD 180
BND BNM 180
Suy ra ba điểm M, N , D thẳng hàng. ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 5
NAÊM HOÏC: 2021 - 2022 MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 5 - 2
Thời gian: 120 phút (không kể thời gian phát đề) x
Câu 9. (1,5 điểm). Cho hàm số P 2 : y và đường thẳng ( )
d : y 2x 2 . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 10. (1 điểm). Cho phương trình 2
x 5x 4 0 . 5x x x 5x
Không giải phương trình, hãy tính giá trị biểu thức 1 2 1 2 A . x x 1 2
Câu 11. (1 điểm). Lúc 6 giờ sáng, một xe ô tô ở vị trí cách thành phố Hồ Chí Minh 50km và khởi
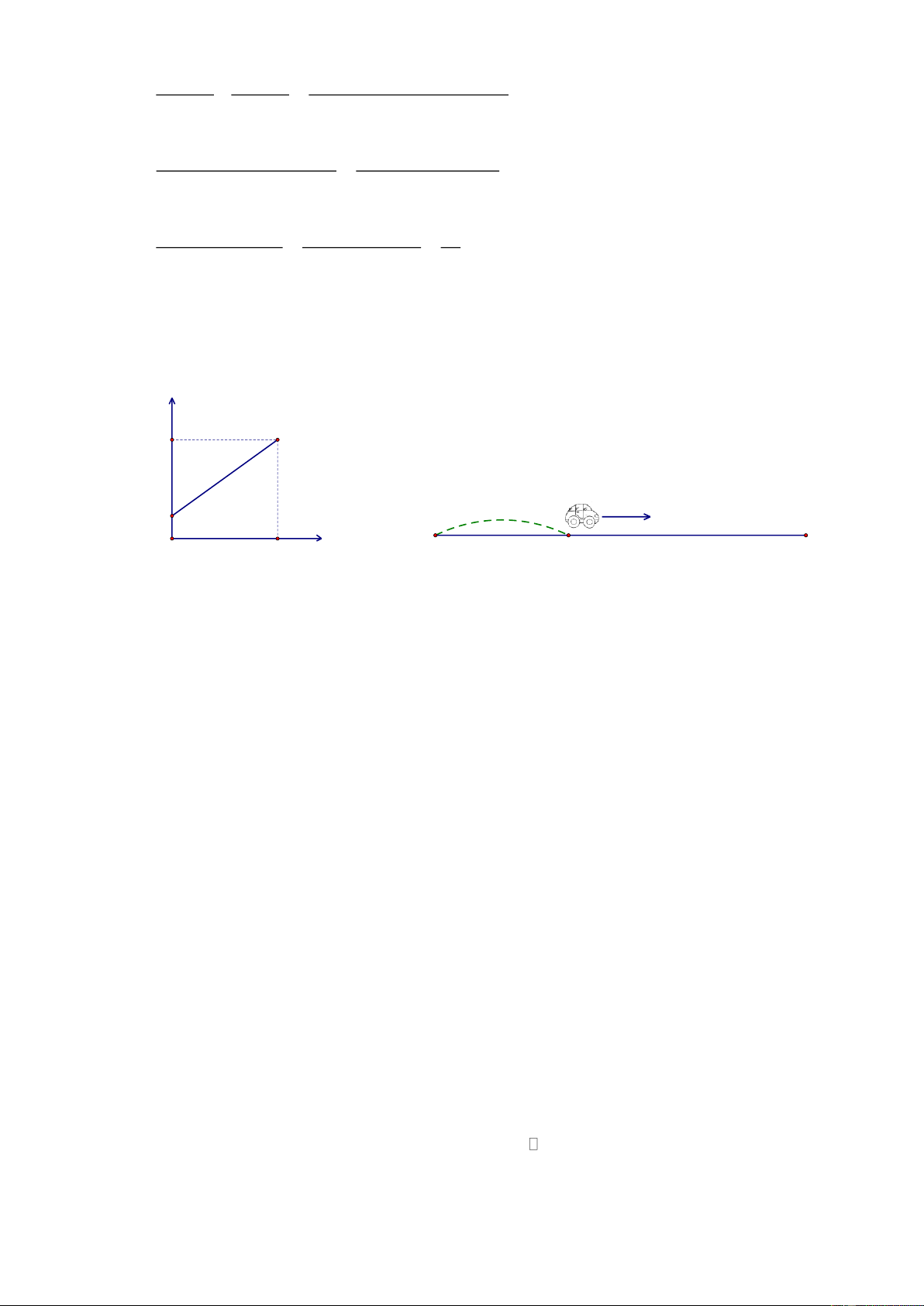
hành đi Hà Nội (ở ngược chiều với TPHCM). Gọi y ax b là hàm số biểu diễn độ dài
quãng đường từ TPHCM đến vị trí của xe ô tô sau x giờ theo đồ thị ở hình sau. Trang 11 y (km) 230 50 50 km 0 3 x (giờ) TPHCM Hà Nội
a) Tìm a và b .
b) Vào lúc mấy giờ thì xe ô tô cách TPHCM 410km ?
Câu 12. (1 điểm). Hai xí nghiệp theo kế hoạch phải làm tổng cộng 360 dụng cụ. Trên thực tế, xí
nghiệp A vượt mức 12%, xí nghiệp B vượt mức 10% do đó cả hai xí nghiệp làm tổng
cộng 400 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm.
Câu 13. (0,75 điểm). Một giải bóng đá gồm 6 đội bóng thi đấu theo thể thức vòng tròn 1 lượt. Đội
thắng được 3 điểm, hoà được 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng số điểm của cả 6 đội là 41 điểm.
a) Hỏi giải đấu có bao nhiêu trận?
b) Tính số trận hòa của giải đấu?
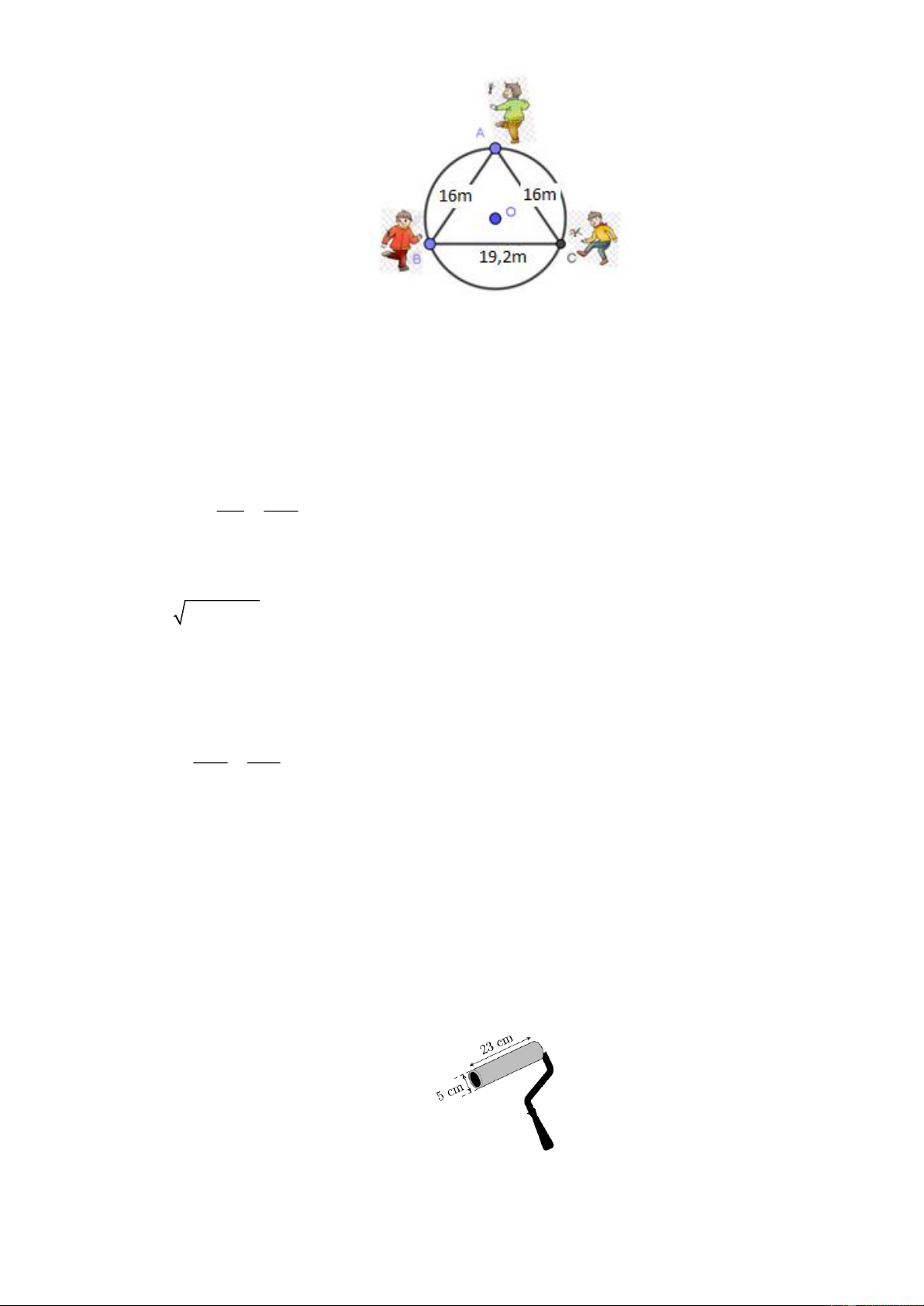
Câu 14. (1 điểm). Ba bạn Dũng, Tài và Trí đứng ở ba vị trí A , B , C trên một đường tròn tâm O để
chơi trò truyền cầu. Biết khoảng cách từ Dũng đến Tài bằng khoảng cách từ Dũng đến Trí
là 16m ( AB AC 16m), khoảng cách từ Tài đến Trí là 19,2m ( BC 19,2m ) (Hình bên).
Em hãy tính bán kính của đường tròn O .
Câu 15. (0,75 điểm). Bạn An đi mua giúp bố cây lăn sơn ở cửa hàng nhà bác Toàn. Một cây lăn sơn
tường có dạng một khối trụ với bán kính đáy là 5 cm và chiều cao là 23 cm (hình vẽ bên).
Nhà sản xuất cho biết sau khi lăn 1000 vòng thì cây sơn tường có thể bị hỏng. Hỏi bạn An
cần mua ít nhất mấy cây lăn sơn tường biết diện tích tường mà bố bạn An cần sơn là 2 100 m ? Trang 12
Câu 16. (3 điểm) Cho A
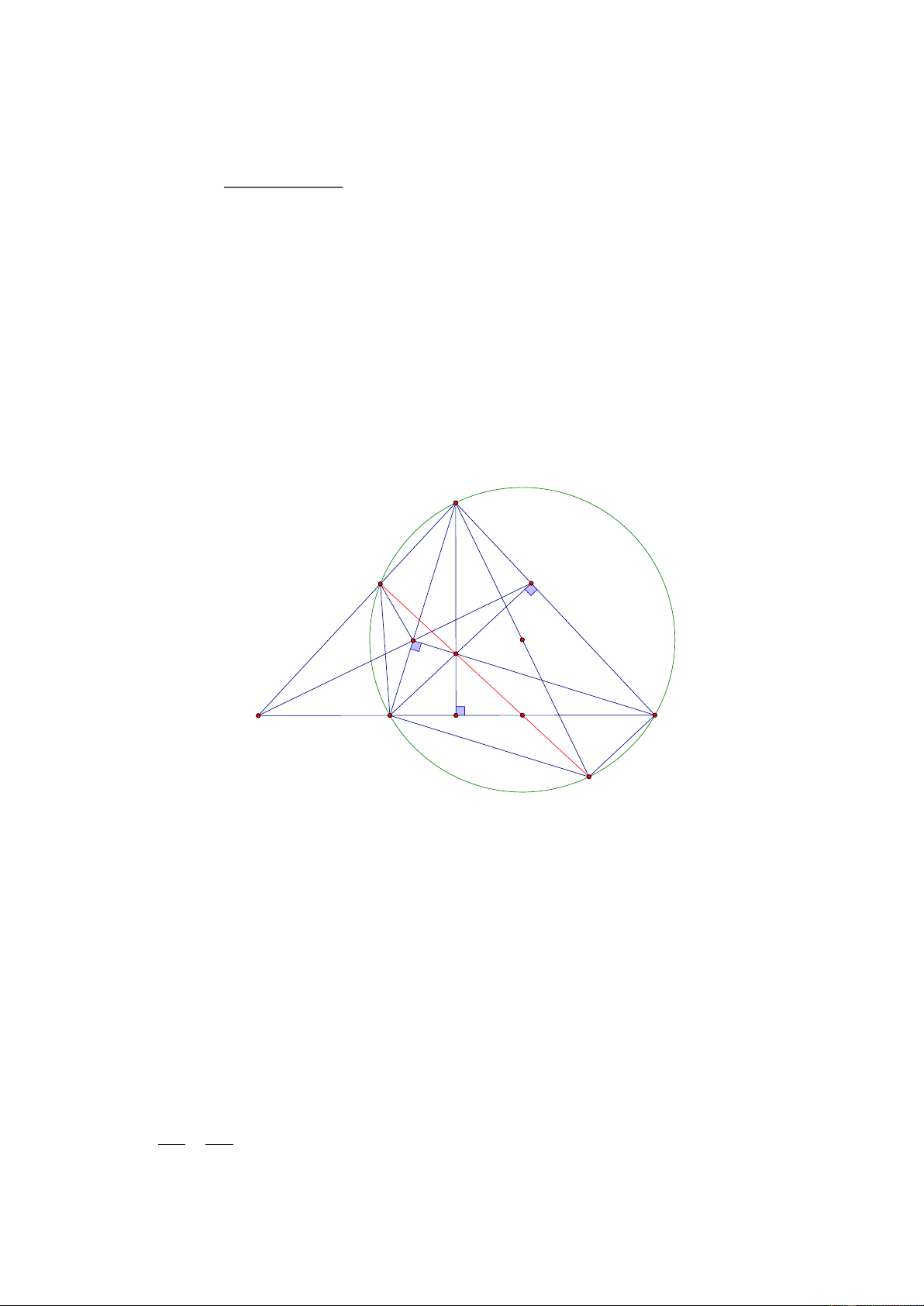
BC nhọn ( AB AC ) nội tiếp đường tròn O . Các đường cao AD , BE ,
CF cắt nhau tại H . Tia EF cắt tia CB tại K .
a) Chứng minh tứ giác BFEC nội tiếp và K . E KF K . B KC .
b) Đường thẳng KA cắt O tại M . Chứng minh tứ giác AEFM nội tiếp.
c) Gọi N là trung điểm của BC . Chứng minh M, H ,N thẳng hàng. ----HẾT--- Trang 13 HƯỚNG DẪN GIẢI
Câu 9. (1,5 điểm) Cho P 2
: y x và đường thẳng d : y 3x 4 .
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
b) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. y BGT: 8 x 4 2 0 2 4 2 x y 8 2 0 2 8 2 2 x 1 2 y 2x 2 0 2 -4 -2 O 1 2 x 4
c) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2 x 2
2x 2 x 4x 4 0 x 2. 2 2 x 2 2
Thay x 2 vào y , ta được: y 2. 2 2
Vậy 2; 2 là giao điểm cần tìm.
Câu 10. (1 điểm) Cho phương trình 2
x 5x 4 0 . 5x x x 5x
Không giải phương trình, hãy tính giá trị biểu thức 1 2 1 2 A . x x 1 2 Lời giải 2
x 5x 4 0 . Vì 2 2
b 4ac ( 5 ) 4.1.4 9 0 .
Nên phương trình có hai nghiệm phân biệt x , x . 1 2 b
S x x 5 1 2 Theo đị a nh lí Vi-et, ta có: . c
P x .x 4 1 2 a Trang 14 5x x x 5x
5x x .x x 5x .x 1 2 1 2 1 2 2 1 2 1 A x x x .x 1 2 1 2 10x . 5 . 5 . x 2 2 2 2 x x x x x x x x 1 2 1 2 1 2 2 1 1 2 A x .x x .x 1 2 1 2 P 2 S P 2 10. 2. 10.4 5 2.4 23 A . P 4 4
Câu 11. (1 điểm) Lúc 6 giờ sáng, một xe ô tô ở vị trí cách thành phố Hồ Chí Minh 50km và khởi hành
đi Hà Nội (ở ngược chiều với TPHCM). Gọi y ax b là hàm số biểu diễn độ dài quãng đường
từ TPHCM đến vị trí của xe ô tô sau x giờ theo đồ thị ở hình sau. y (km) 230 50 50 km 0 3 x (giờ) TPHCM Hà Nội
a) Tìm a và b .
b) Vào lúc mấy giờ thì xe ô tô cách TPHCM 410km ? Lời giải
a) Tìm a và b . 50 .0
a b b 50 . 230 .3
a 50 x 60 .
b) Vào lúc mấy giờ thì xe ô tô cách TPHCM 410km ?
Xe ô tô cách TPHCM 410 km y 410 .
Thay vào ta có x 6 (giờ).
Vậy lúc 12 giờ thì xe ô tô cách TPHCM 410km .
Câu 12. (1 điểm). Hai xí nghiệp theo kế hoạch phải làm tổng cộng 360 dụng cụ. Trên thực tế, xí nghiệp
A vượt mức 12% , xí nghiệp B vượt mức 10% do đó cả hai xí nghiệp làm tổng cộng 400 dụng
cụ. Tính số dụng cụ mỗi xí nghiệp phải làm. Lời giải
Gọi x (dụng cụ) là số dụng cụ xí nghiệp A làm; y (dụng cụ) là số dụng cụ xí nghiệp B làm. (ĐK: * ,
x y N ).(sai kí hiệu tập hợp số tự nhiên * x, y ).
Vì theo kế hoạch phải làm tổng cộng là 360 dụng cụ nên ta có phương trình: Trang 15
x y 360 1
Vì trên thực tế, xí nghiệp A vượt mức 12% , xí nghiệp B vượt mức 10% do đó cả hai xí nghiệp
làm tổng cộng 400 dụng cụ nên ta có phương trình:
112%.x 110%.y 400 2
x y 360 x 200 (N) Từ
1 và 2 , ta có hệ phương trình: 11
2%.x 110%.y 400
y 160 (N)
Vậy xí nghiệp A làm được 200 dụng cụ; xí nghiệp B làm được 160 dụng cụ.
Câu 13. (0,75 điểm) Một giải bóng đá gồm 6 đội bóng thi đấu theo thể thức vòng tròn 1 lượt. Đội
thắng được 3 điểm, hoà được 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng số điểm của cả 6 đội là 41 điểm.
a) Hỏi giải đấu có bao nhiêu trận?
b) Tính số trận hòa của giải đấu? Lời giải
a) Hỏi giải đấu có bao nhiêu trận?
Số trận đấu của giải là:
5 4 3 2 1 15 (trận).
b) Tính số trận hòa của giải đấu?
Gọi x (trận) là số trận hòa của giải đấu (ĐK: x *)
Vì một trận thắng được 3 hòa được 1 điểm và có tổng cộng là 41 điểm nên ta có phương trình:
2.x 3.15 x 41 x 4 (nhận).
Vậy số trận hòa của giải đấu là 4 .
Câu 14. (1 điểm) Ba bạn Dũng, Tài và Trí đứng ở ba vị trí A , B , C trên một đường tròn tâm O để
chơi trò truyền cầu. Biết khoảng cách từ Dũng đến Tài bằng khoảng cách từ Dũng đến Trí là 16 m
( AB AC 16 m), khoảng cách từ Tài đến Trí là 19, 2 m ( BC 19, 2m ) (Hình bên). Em hãy tính
bán kính của đường tròn O . Trang 16 Lời giải
+ Đường thẳng AO cắt BC và O lần lượt tại H và D . ABD
vuông tại B và H là trung điểm của BC .
+ Ta có: H là trung điểm của BC . BC 19, 2 HB HC 9,6m . 2 2 + ABH vuông tại H có: 2 2
AH 16 9, 6 12,8m + ABD
vuông tại B có BH là đường cao. 2
AB AH.AD (hệ thức lượng). 2 2 AB 16 AD 20m . AH 12,8
Vậy bán kính của O là: R AD: 2 20: 2 10m .
Câu 15. (0,75 điểm)
Bạn An đi mua giúp bố cây lăn sơn ở cửa hàng nhà bác Toàn. Một cây lăn sơn tường có dạng
một khối trụ với bán kính đáy là 5 cm và chiều cao là 23 cm (hình vẽ bên). Nhà sản xuất cho biết
sau khi lăn 1000 vòng thì cây sơn tường có thể bị hỏng. Hỏi bạn An cần mua ít nhất mấy cây lăn
sơn tường biết diện tích tường mà bố bạn An cần sơn là 2 100 m ? Lời giải
+ Diện tích xung quanh của cây lăn sơn: Trang 17 2 4 2 S 2 .
R h 2. .2,5.23 115 cm 115.10 m .
+ Số cây lăn sơn cần mua để sơn được 2 100 m : 100 2,77 3 cây. 4 115. .10 .1000
Câu 16. (3 điểm) Cho ABC
nhọn ( AB AC ) nội tiếp đường tròn O . Các đường cao AD , BE ,
CF cắt nhau tại H . Tia EF cắt tia CB tại K .
a) Chứng minh tứ giác BFEC nội tiếp và K . E KF K . B KC .
b) Đường thẳng KA cắt O tại M . Chứng minh tứ giác AEFM nội tiếp.
c) Gọi N là trung điểm của BC . Chứng minh M , H , N thẳng hàng. Lời giải A M E F O H K B D N C I
a) Chứng minh tứ giác BFEC nội tiếp và K . E KF K . B KC .
+ Xét tứ giác BFEC , có: BFC 90 CF AB BEC 90 BE AC
BFEC là tứ giác nội tiếp.
KFB KCE .
Mà EKC là góc chung. K BF ∽ K
EC g.g KB KF
( 2 cạnh tương ứng tỉ lệ) KE KC K . B KC K . E KF (1) Trang 18
b) Đường thẳng KA cắt O tại M . Chứng minh tứ giác AEFM nội tiếp.
+ Ta có AMBC nội tiếp O .
KMB KCA .
Mà AKC là góc chung. K MB∽ K
CA g.g . KB KM
( 2 cạnh tương ứng tỉ lệ). KA KC K .
B KC KM.KA 2 . Từ
1 và 2 KM.KA K . E KF . KM KF . KE KA
Mà AKE là góc chung. K MF ∽ K EA . c g.c
KMF KEA ( 2 góc tương ứng bằng nhau).
AEFM là tứ giác nội tiếp.
c) Gọi N là trung điểm của BC . Chứng minh M , H , N thẳng hàng.
+ Xét tứ giác AFHE , ta có: HFA 90o HF AB . HEA 90o HE AC
Suy ra: AFHE nội tiếp đường tròn đường kính AH .
+ Mà AEFM nội tiếp (chứng minh trên) ,
A M , F, H , E cùng thuộc đường tròn đường kính AH .
AHFM là tứ giác nội tiếp.
HMA HFA 90 HM AM 3
+ Kẻ AI là đường kính của O .
AMI 90 ; ACI 90 . AM MI 4 CI AC Trang 19
Từ 3 và 4 M , H , I thẳng hàng. 5 Ta có :
+ IC∥ BH (vì cùng AC ).
+ IB∥ CH (vì cùng AB )
BHCI là hình bình hành.
Mà N là trung điểm của BC (gt).
N là trung điểm của HI .
H, N, I thẳng hàng 6
Từ 5 và 6 M , H , N thẳng hàng (đpcm). ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 5
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 5 - 3
Thời gian: 120 phút (không kể thời gian phát đề) 2 x
Câu 1. (1,5 điểm). Cho P : y
và đường thẳng d : y 3x 4 . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm).
Chứng minh phương trình : 2
2x 5x 1 0 có hai nghiệm là x , x . 1 2 x x
Không giải phương trình, hãy tính giá trị của biểu thức: A 1 2 x x 1 2 x x 2 1
Câu 3. (1 điểm). Công thức YMCA dùng để đo lượng “mỡ thừa” trong cơ thể dựa vào cân nặng và
a 4,15.m 0,082.n số đo vòng 2 như sau: n
Trong đó: Hệ số a 98,42 nếu là nam và a 76,76 nếu là nữ; m là số đo vòng 2 tính bằng inch,
n là cân nặng tính bằng pound. ( 1inch 2,54cm ; 1 kg 2,2 pound )
Bảng phân loại đánh giá lượng “mỡ thừa” trong cơ thể Xếp loại Nữ ( % chất béo) Nam ( % chất béo) Tối thiểu 10% 13% 2% 5% Ít mỡ 14% 20% 6% 13% Bình thường 21% 24% 14% 17% Thừa cân 25% 31% 18% 25% Trang 20 Béo phì 32% 26%
a) Anh Hoàng có số đo vòng 2 là 78cm , nặng 74kg . Dựa vào cách tính trên hãy đánh giá
lượng “mỡ thừa” trong cơ thể của anh Hoàng.
b) Chị Hoa cân nặng 60kg . Chị Hoa nên có số đo vòng 2 bao nhiêu để % chất béo chỉ từ 21% đến 24% .
Câu 4. (0,75 điểm). Qua nghiên cứu người ta nhận thấy rằng với mỗi người trung bình nhiệt độ
môi trường giảm đi 1 C thì lượng calo cần tăng thêm khoảng 30 calo. Tại 21 C , một người
làm việc cần sử dụng khoảng 3000 calo mỗi ngày. Người ta thấy mối quan hệ giữa hai đại
lượng này là một hàm số bậc nhất y ax b ( x : đại lượng biểu thị cho nhiệt độ môi
trường và y: đại lượng biểu thị cho lượng calo).
a) Xác định hệ số a,b .
b) Nếu một người làm việc ở sa mạc Sahara trong nhiệt độ 50 C thì cần bao nhiêu calo?
Câu 5. (1 điểm). Một người có 100 triệu đồng muốn gởi vào ngân hàng A có hai lựa chọn: Người
gửi có thể nhận lại suất 5% /năm và 2000000 đồng tiền thưởng nếu gởi bằng tiền Việt Nam
hoặc lãi suất 2%/năm nếu gởi bằng đồng đô la Mỹ. Nếu giá đô la ở thời điểm gởi vào và
lấy ra sau cùng một năm lần lượt là: 21500 đồng/đô la và 21800 đồng/đô la. Nếu người đó
gởi có kỳ hạn một năm thì nên chọn giải pháp nào có lợi hơn (tính theo tiền đồng Việt Nam).
(Làm tròn đến hàng trăm nghìn)
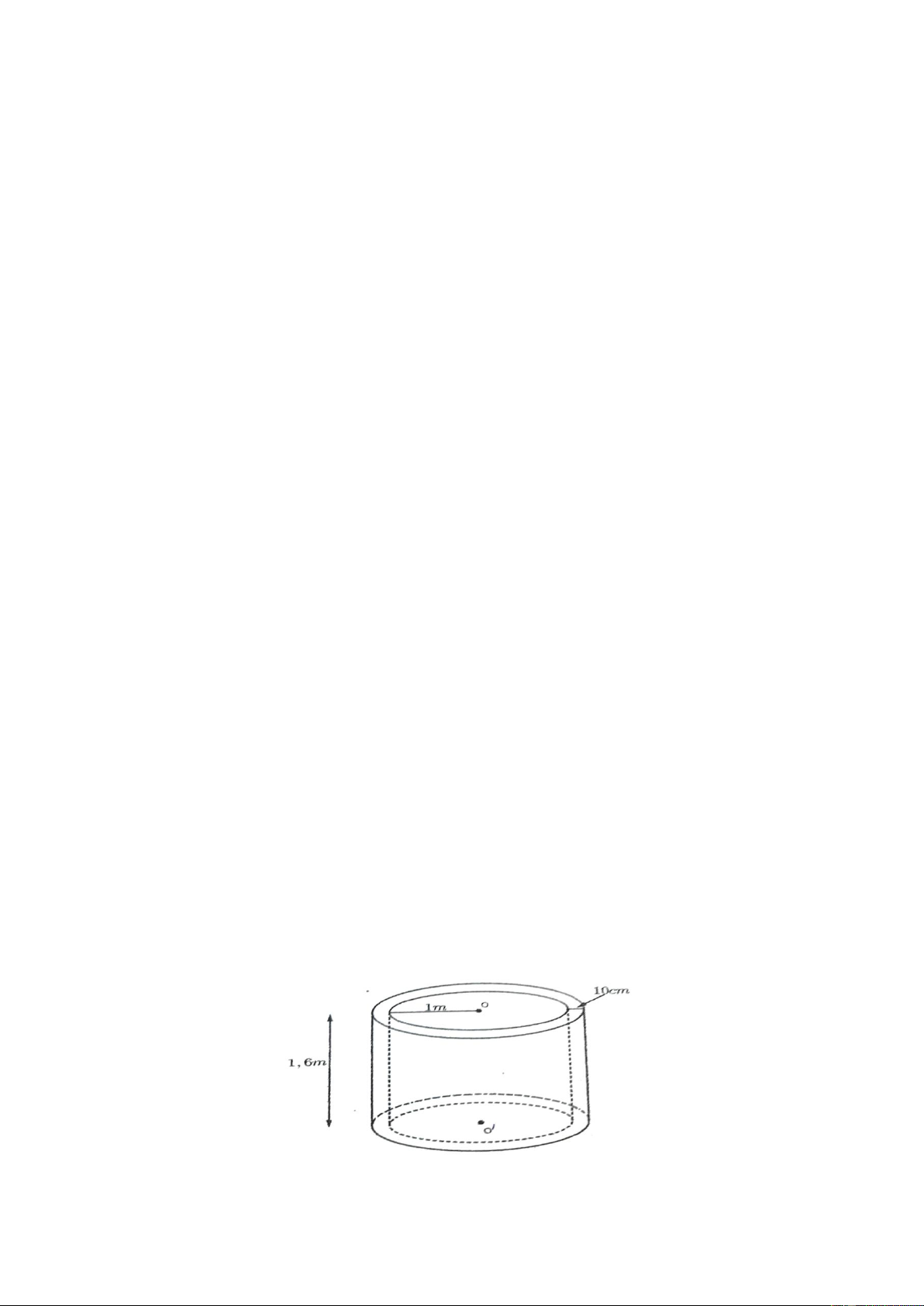
Câu 6. (1 điểm). Để làm cống thoát nước cho một khu vực dân cư người ta cần đúc 500 ống cống
bê tông hình trụ có đường kính trong là 2 m và chiều dài mỗi ống là 1,6 m , độ dày thành
ống là 10 cm . Hỏi các công nhân phải chuẩn bị bao nhiêu bao xi măng để làm đủ số ống
nói trên ?. Biết mỗi mét khối bê tông cần 7 bao xi măng.
Câu 7. (1 điểm). Vào ngày lễ “Black Friday”, cửa hàng đồng loạt giảm giá toàn bộ sản phẩm trong
cửa hàng. Một áo thể thao giảm 10%, một quần thể thao giảm 20% , một đôi giày thể thao
giảm 30% . Đặc biệt nếu mua đủ bộ bao gồm 1 quần, 1áo, 1đôi giày thì sẽ được giảm tiếp
(tính theo giá trị của 3 mặt hàng trên sau khi giảm giá). Bạn An vào cửa hàng mua 3 áo Trang 21
giá 300000 VNĐ/cái, 2 quần giá 250000 /cái, 1 đôi giày giá 500000 VNĐ/ đôi (giá trên là
giá chưa giảm). Vậy số tiền bạn An phải trả là bao nhiêu?
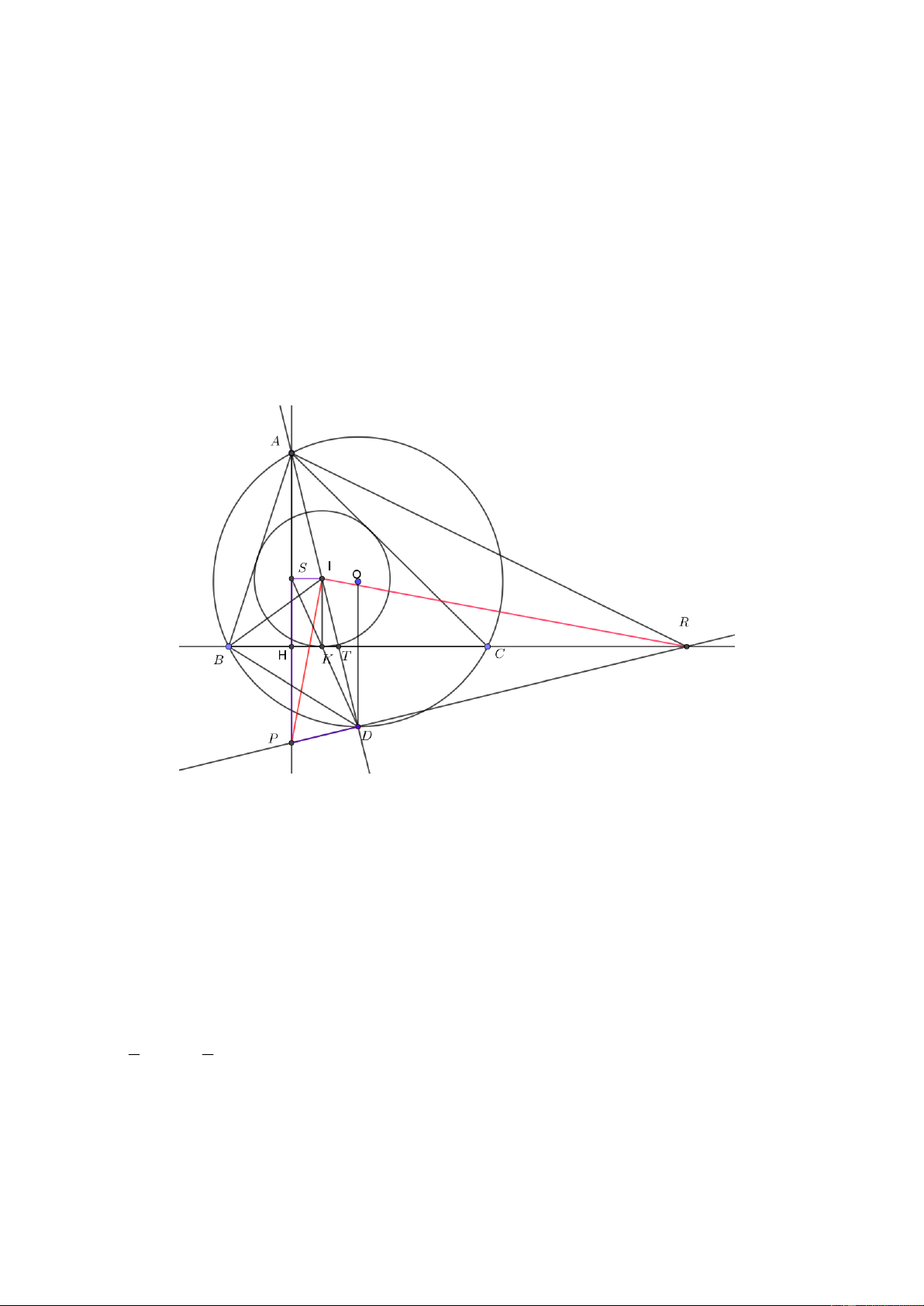
Câu 8. (3 điểm) Cho ABC AB AC nhọn nội tiếp O có AH là đường cao và I là tâm đường
tròn nội tiếp ABC . Gọi T,D lần lượt là giao điểm của AI với BC và O .
a) Chứng minh: OD vuông góc với BC và tam giác IBD cân.
b) Qua D vẽ đường thẳng vuông góc với AD , cắt AH và BC lần lượt tại P,R. Chứng
minh: IP IR .
c) Vẽ IK BC tại K,DK cắt AH tại S . Chứng minh: tứ giác SIDP nội tiếp. ----HẾT--- Trang 22 HƯỚNG DẪN GIẢI 2 x
Câu 1. (1,5 điểm) Cho P : y
và đường thẳng d : y 3x 4 . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. a) BGT: x 2 1 0 1 2 2 x y 2 1 0 1 2 2 2 2 x 0 1 y 3x 4 4 7
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2
x 3x 4 2 2
x 3x 4 0 2 x 2 x 4 2 x
Thay x 2 vào y
, ta được: y 2 . 2 2 x Thay x 4 vào y
, ta được: y 8 . 2
Vậy 2; 2 , 4; 8 là hai giao điểm cần tìm.
Câu 2. (1 điểm)
a) Chứng minh phương trình : 2
2x 5x 1 0 có hai nghiệm là x , x . 1 2 Trang 23 x x
b) Không giải phương trình, hãy tính giá trị của biểu thức: A 1 2 x x 1 2 x x 2 1 Lời giải 2 Vì 2
b 4ac 5 4.2.1 17 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b S x x 5 1 2 a 2
Theo định lí Vi-et, ta có: c P x .x 1 1 2 a 2 x x
Ta có: A 1 2 x x 1 2 x x 2 1 2 x 2 A x 1 2 x x 1 2 x x 1 2 x x 2x x 1 2 2 A 1 2 x x 1 2 x x 1 2 5 2 1 2. 2 A 2 1 1 2 2 A 10
Câu 3. (1 điểm). Công thức YMCA dùng để đo lượng “mỡ thừa” trong cơ thể dựa vào cân nặng
a 4,15.m 0,082.n
và số đo vòng 2 như sau: n
Trong đó: Hệ số a 98,42 nếu là nam và a 76,76 nếu là nữ; m là số đo vòng 2 tính bằng inch,
n là cân nặng tính bằng pound. (1inch = 2,54cm; 1 kg = 2,2 pound)
Bảng phân loại đánh giá lượng “mỡ thừa” trong cơ thể Xếp loại Nữ (% chất béo) Nam (% chất béo) Tối thiểu 10% - 13% 2% - 5% Ít mỡ 14% - 20% 6% - 13% Bình thường 21% - 24% 14% - 17% Thừa cân 25% - 31% 18% - 25% Béo phì 32%+ 26%+ Lời giải
a) Anh Hoàng có số đo vòng 2 là 78cm, nặng 74kg. Dựa vào cách tính trên hãy đánh giá
lượng “mỡ thừa” trong cơ thể của anh Hoàng. Trang 24 3900
Đổi đơn vị: 78 cm
inch; 74 kg 162,8 pound . 1 7 2
Lượng mỡ thừa trong cơ thể anh Hoàng là: 3900 9 8,42 4,15. 0,082.162,8
a 4,15.m 0, 082.n = 127 0,1 10 % n 162,8
Vậy anh Hoàng thuộc loại ít mỡ.
b) Chị Hoa cân nặng 60kg . Chị Hoa nên có số đo vòng 2 bao nhiêu để % chất béo chỉ từ
21% đến 24% .
Đổi đơn vị: 60 kg 132 pound ;
Lượng mỡ thừa trong cơ thể chị Hoa là:
a 4,15.m 0, 082.n 21% 24% n 7
6,76 4,15.m 0,082.132 0, 21 0, 24 132 4,15.m 119, 264 11 5,304 4,15.m
27, 784 m 28, 738inch
70,572 m 72,995(cm)
Câu 4. (0,75 điểm). Qua nghiên cứu người ta nhận thấy rằng với mỗi người trung bình nhiệt độ môi
trường giảm đi 1˚C thì lượng calo cần tăng thêm khoảng 30 calo. Tại 21˚C, một người làm
việc cần sử dụng khoảng 3000 calo mỗi ngày. Người ta thấy mối quan hệ giữa hai đại lượng
này là một hàm số bậc nhất y = ax + b (x: đại lượng biểu thị cho nhiệt độ môi trường và y: đại
lượng biểu thị cho lượng calo).
a) Xác định hệ số a, b.
b) Nếu một người làm việc ở sa mạc Sahara trong nhiệt độ 50˚C thì cần bao nhiêu calo? Lời giải a) Theo đề bài:
Tại 21˚C, một người làm việc cần sử dụng khoảng 3000 calo mỗi ngày, thay vào hàm số
y = ax + b ta có: 21a b 3000 ( ) 1
Nhiệt độ môi trường giảm đi 1˚C thì lượng calo cần tăng thêm khoảng 30 calo, ta có:
20a b 3030 (2) Trang 25 Từ ( ) 1 , (2)ta có hpt:
21a b 3000
20a b 3030
Giải hpt ta có: a = - 30; b = 3630
b). Nếu người đó ở sa mạc Sahara trong nhiệt độ 50 C
þ thì người đó cần năng lượng là:
y = - 30.50 + 3630 = 2130 (calo)
Câu 5. (1 điểm) Một người có 100 triệu đồng muốn gởi vào ngân hàng A có hai lựa chọn: Người gửi
có thể nhận lại suất 5%/năm và 2 000 000 đồng tiền thưởng nếu gởi bằng tiền Việt Nam hoặc
lãi suất 2%/năm nếu gởi bằng đồng đô la Mỹ. Nếu giá đô la ở thời điểm gởi vào và lấy ra sau
cùng một năm lần lượt là: 21 500 đồng/đô la và 21 800 đồng/đô la. Nếu người đó gởi có kỳ
hạn một năm thì nên chọn giải pháp nào có lợi hơn (tính theo tiền đồng Việt Nam).
(Làm tròn đến hàng trăm nghìn) Lời giải
Đổi 100 (triệu đồng) 4651 (đô la)
Với lãi suất 2%/năm ta được: 4651.1 2% 4744 (đô la)
Đổi ra tiền Việt ở thời điểm lấy ra, ta được:
4744 . 21 800 103 400 000 (đồng)
Nếu gởi bằng tiền Việt Nam, ta được:
100 000 000.105% 2 000 000 107 000 000 (đồng).
Như vậy, gởi bằng tiền Việt Nam sẽ có lợi hơn (giải thích)
Câu 6. (1 điểm) Để làm cống thoát nước cho một khu vực dân cư người ta cần đúc 500 ống cống bê
tông hình trụ có đường kính trong là 2 m và chiều dài mỗi ống là 1,6 m, độ dày thành ống là
10 cm. Hỏi các công nhân phải chuẩn bị bao nhiêu bao xi măng để làm đủ số ống nói trên ?.
Biết mỗi mét khối bê tông cần 7 bao xi măng. Lời giải Trang 26 Đổi 10c
m 0,1 m . Bán kính trong ’ R 1m Bán kính ngoài :
R 0,1 1 1,1 m
Lượng bê tông cần dùng cho một ống cống hình trụ là : V 2 R h 2
R h h 2 2 R R 2 2 3 – ’ – ’ .1,6. 1,1 1 0,336 m
Lương bê tông cần dùng cho 500 ống cống là: 3 500 . 0,366 168 m
Số bao xi măng để làm đủ số ông cống trên là : 16 8 .7 3695 (bao)
Câu 7. (1 điểm) ). Vào ngày lễ “Black Friday”, cửa hàng đồng loạt giảm giá toàn bộ sản phẩm
trong cửa hàng. Một áo thể thao giảm 10%, một quần thể thao giảm 20%, một đôi giày thể
thao giảm 30% . Đặc biệt nếu mua đủ bộ bao gồm 1 quần, 1áo, 1đôi giày thì sẽ được giảm tiếp
(tính theo giá trị của 3 mặt hàng trên sau khi giảm giá). Bạn An vào cửa hàng mua 3 áo giá
300 000 VNĐ/cái, 2 quần giá 250 000 /cái, 1 đôi giày giá 500 000 VNĐ/ đôi (giá trên là giá chưa
giảm). Vậy số tiền bạn An phải trả là bao nhiêu? Lời giải
Số tiền bạn An phải trả khi mua 3 áo là :
3.300000.90% 810000 ( đồng)
Số tiền bạn An phải trả khi mua 2 quần là :
2.250000.80% 400000 ( đồng)
Số tiền bạn An phải trả khi mua 1 đôi giầy là :
500000.70% 350000 ( đồng)
Số tiền bạn An được giảm khi mua đủ bộ là :
(810000 : 3 400000 : 2 350000).5% 41000 ( đồng)
Vậy, số tiền bạn An phải trả là :
810000 400000 350000 41000 1519000 ( đồng) Trang 27
Câu 8. (3 điểm)
Cho ΔABC (AB < AC) nhọn nội tiếp (O) có AH là đường cao và I là tâm đường tròn nội tiếp ΔABC.
Gọi T, D lần lượt là giao điểm của AI với BC và (O).
a) Chứng minh: OD vuông góc với BC và tam giác IBD cân.
b) Qua D vẽ đường thẳng vuông góc với AD, cắt AH và BC lần lượt tại P, R. Chứng minh rằng: IP vuông góc IR.
c) Vẽ IK ⏊ BC tại K, DK cắt AH tại S. Chứng minh: tứ giác SIDP nội tiếp. Lời giải
a) * C/m: OD BC
I là tâm đường tròn nội tiếp ABC
nên AD là tia phân giác BAC
D là điểm chính giữa BD OD BC
* C/m: DBI cân tại D .
BID ABI BAI ABI IBC
( BI là phân giác ABC )
BAI 1 sdBD 1 sdBD DBC 2 2
BID IBC DBC IBD
BID cân tại D
b) C/m: IP IR .
Dễ dàng chứng minh được: DBT ∽ DA ( B g g) Trang 28 2
DB DT.DA 2
DI DT.DA ( BID cân tại D ) ( ) 1
Chứng minh dễ dàng: Tứ giác AHDR nội tiếp
PAD PRT
DRT ∽ DA ( P g g)
DT.DA D . P DR (2) Từ ( ) 1 , (2)ta có: 2 DI . DP DR
DIP ∽ DRI(g g) IPD DIR
IPD DIP 90o( I DP vuong i ta D) 90o DIR DIP
hay IP IR (đpcm) c) Ta có:
PSD IKS (hai góc so le trong)
IKS DRI (tứ giác IKDR nội tiếp)
DRI DIP (cùng phụ IPR )
Suy ra: PSD DIP
Suy ra: tứ giác SIDP là tứ giác nội tiếp. Trang 29




