Đề tham khảo tuyển sinh 10 năm 2023-2024 môn toán Phòng GD Quận 7 mã đề Quận 7-1 (có đáp án và lời giải chi tiết)
Tổng hợp Đề tham khảo tuyển sinh 10 năm 2023-2024 môn toán Phòng GD Quận 7 mã đề Quận 7-1 (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 7
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 7 - 1
Thời gian: 120 phút (không kể thời gian phát đề) 2 x
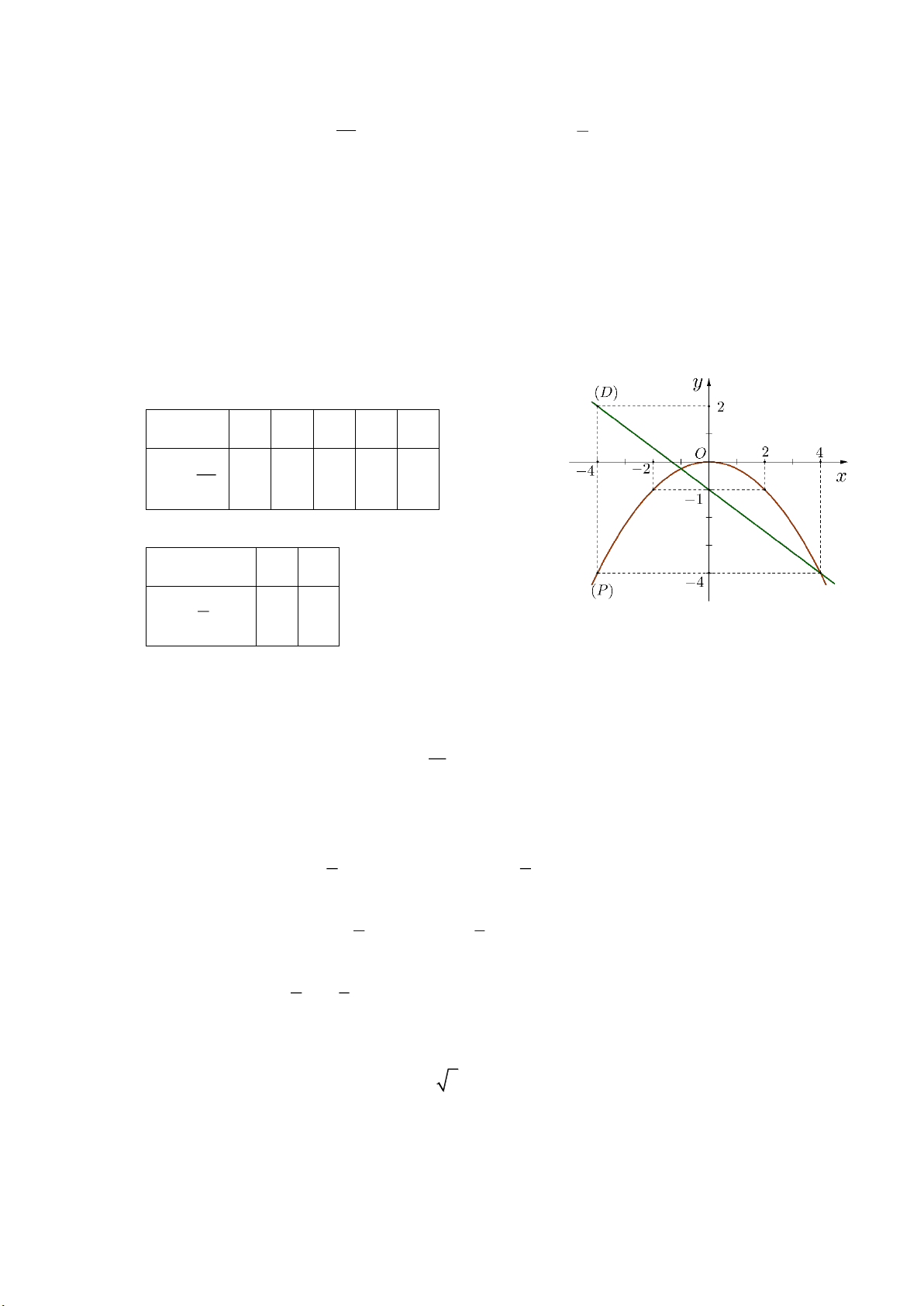
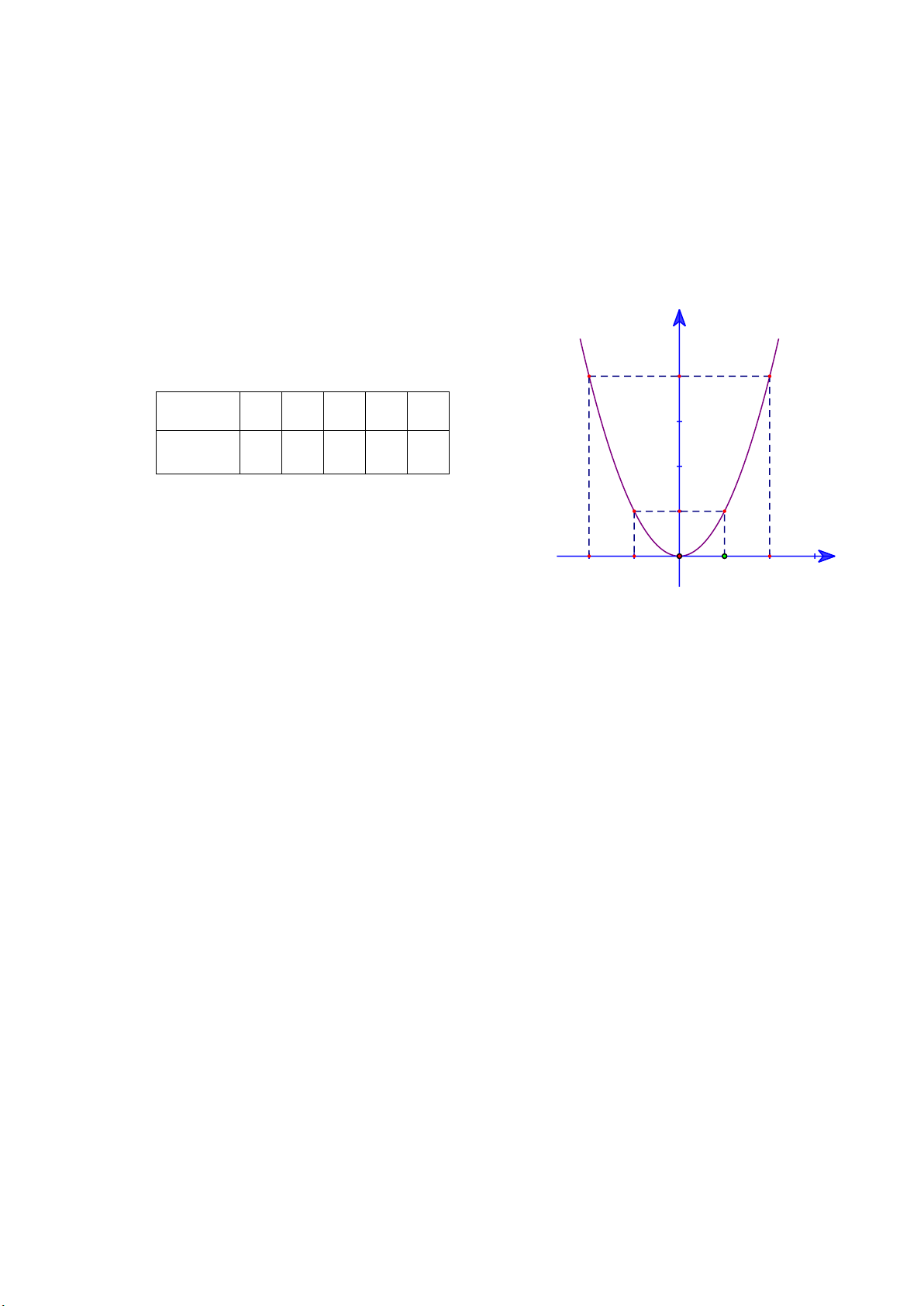
Câu 1. (1,5 điểm). Cho P : y
và đường thẳng D 3
: y x 1 . 4 4
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ.
b) Viết phương trình đường thẳng (D song song với (D) và đi qua điểm A thuộc (P ) có 1 ) hoành độ bằng 2 .
Câu 2. (1 điểm). Cho phương trình 2 x - 3x - 5 + 1 = 0 .
Không giải phương trình, hãy tính giá trị của biểu thức 2 2
M = 2x x - x x - 3x - 3x . 1 2 1 2 1 2
Câu 3. (1 điểm). Đầu năm học, một trường THPT tuyển được 75 học sinh vào 2 lớp chuyên Văn
và chuyên Sử. Nếu chuyển 15 học sinh từ lớp chuyên Văn sang lớp chuyên Sử thì số học 8
sinh lớp chuyên Sử bằng
số học sinh lớp chuyên Văn. Hãy tính số học sinh của mỗi lớp. 7
Câu 4. (1 điểm). Xí nghiệp may Việt Tiến hàng tháng phải chi 410 000 000 đồng để trả lương cho
công nhân, mua vật tư và các khoản phí khác. Mỗi chiếc áo được bán với giá 350 000 đồng.
Gọi số tiền lời (hoặc lỗ) mà xí nghiệp thu được sau mỗi tháng là T và mỗi tháng xí nghiệp
bán được x chiếc áo.
a) Lập hàm số của T theo x .
b) Cần phải bán trung bình bao nhiêu chiếc áo mỗi tháng để
sau 1 năm, xí nghiệp thu được tiền lời là 1380 000 000 đồng.
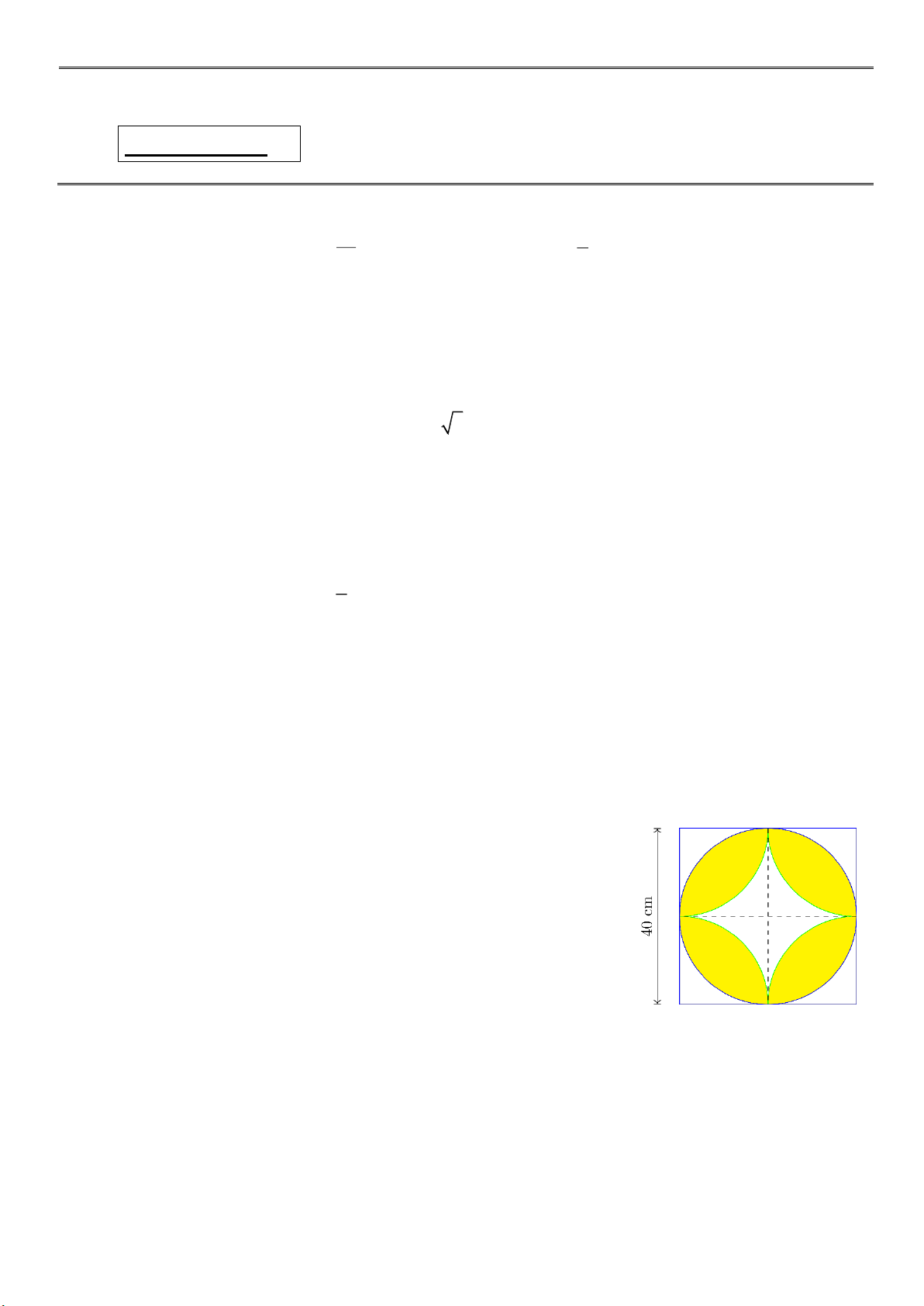
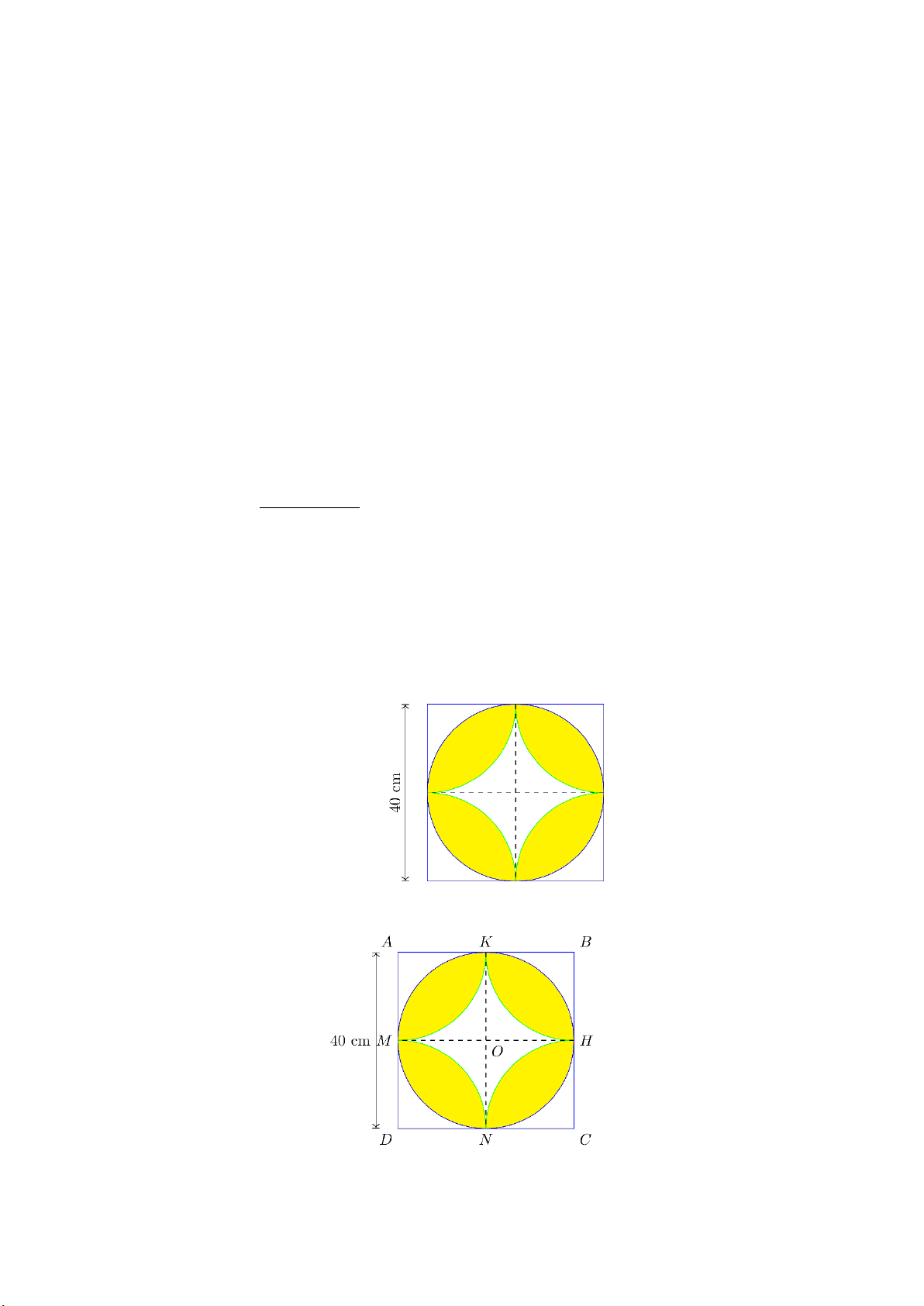
Câu 5. (0,75 điểm). Một viên gạch hình vuông ( 40cm ´ 40cm ) được
trang trí hoạ tiếp như trên hình, tính diện tích phần tô màu.
Câu 6. (0,75 điểm). Mỗi công nhân của công ty Cổ phần ABC có số tiền thưởng tết năm 2018 là 1
tháng lương. Đến năm 2019 , số tiền thưởng tết của họ được tăng thêm 6% so với số tiền
thưởng tết của năm 2018 . Vào năm 2020 , số tiền thưởng tết của họ được tăng thêm 10%
so với số tiền thưởng tết của năm 2019 , ngoài ra nếu công nhân nào được là công đoàn
viên xuất sắc sẽ được thưởng thêm 500 000 đồng. Anh Ba là công đoàn viên xuất sắc của Trang 1
năm 2019 , nên anh nhận được số tiền thưởng tết là 6 330 000 đồng. Hỏi năm 2018 , tiền
lương 1 tháng của anh Ba là bao nhiêu?
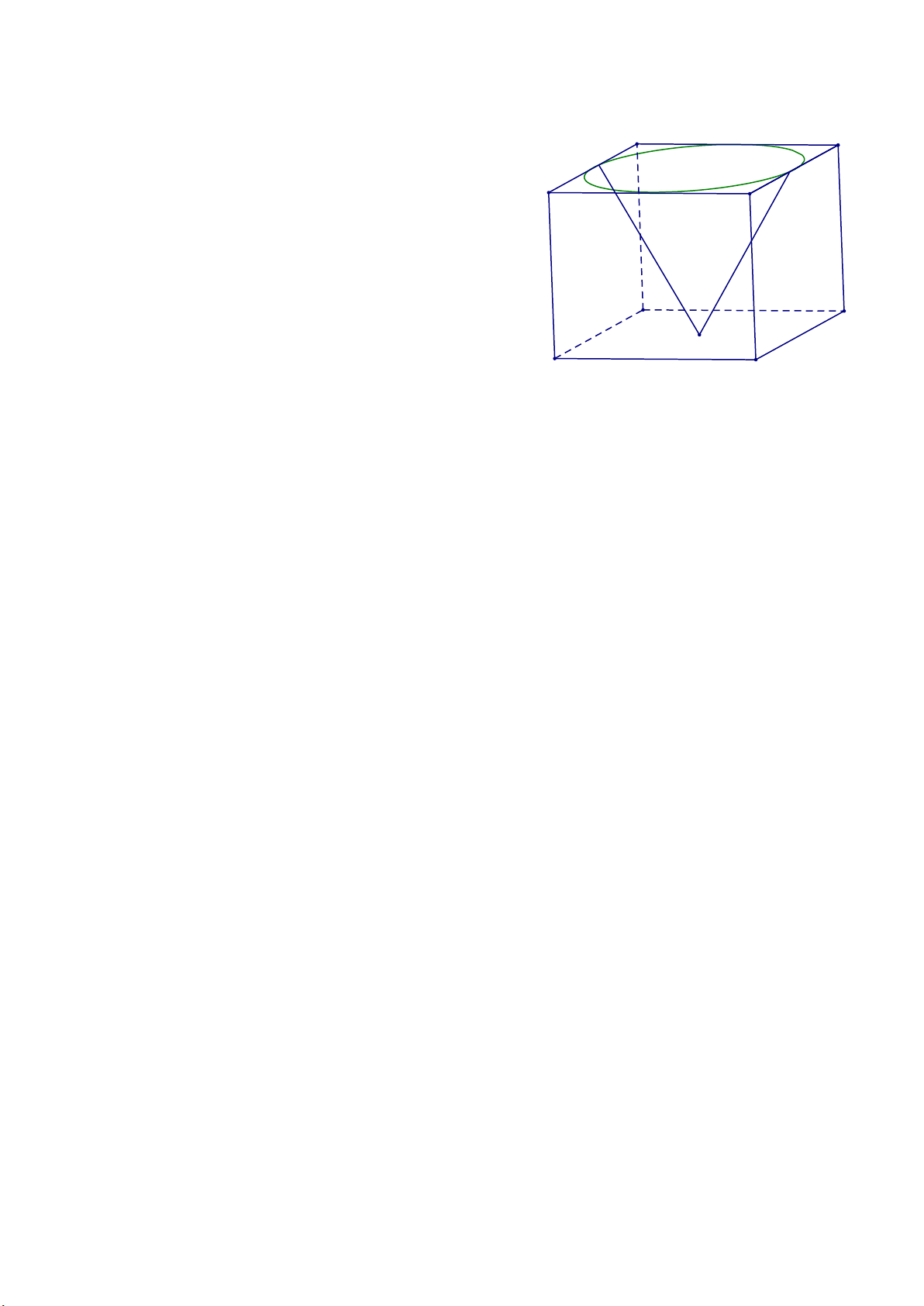
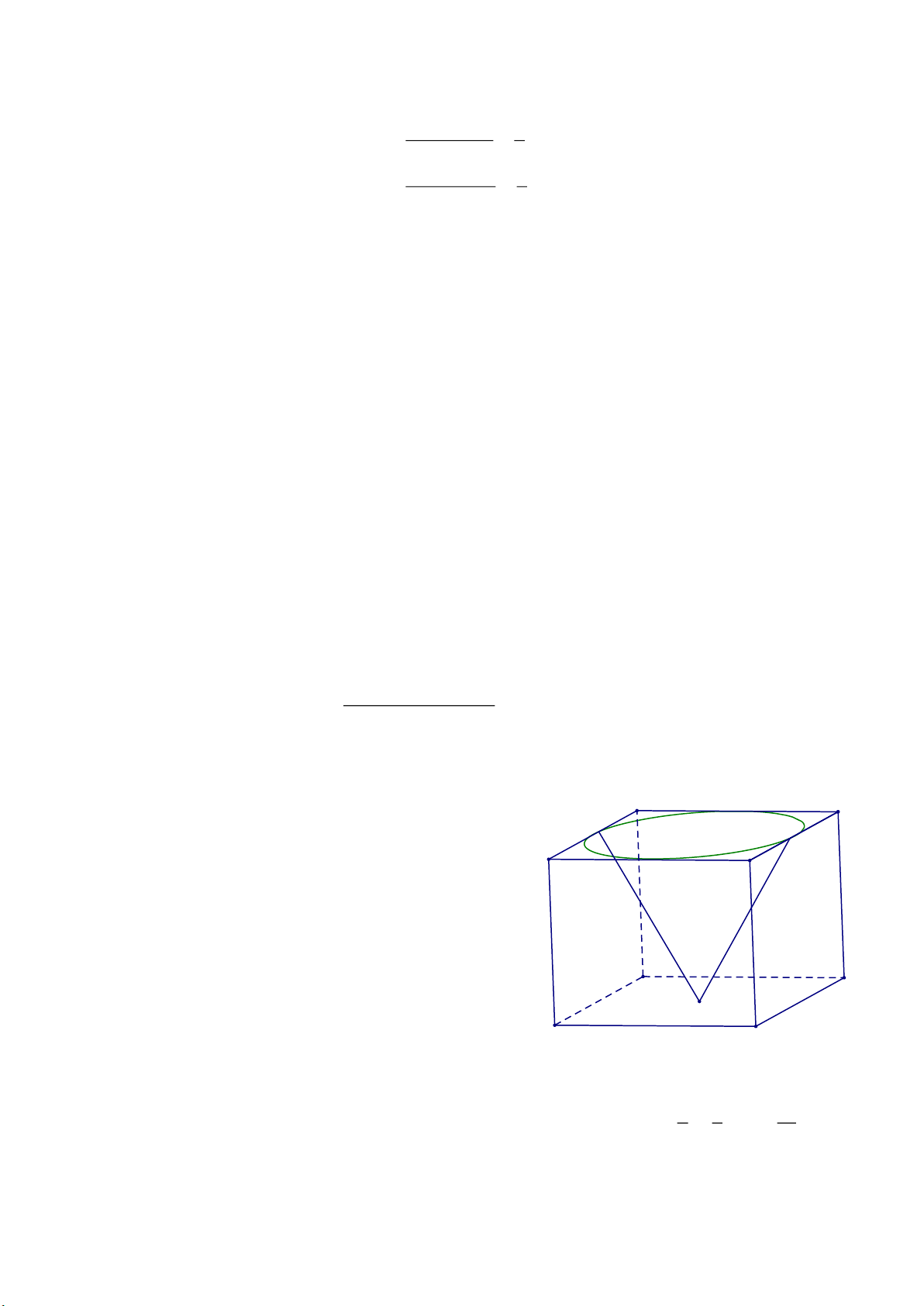
Câu 7. (1 điểm). Một khối lập phương có cạnh 1m chứa
đầy nước. Đặt vào trong khối đó một khối nón có
đỉnh trùng với tâm một mặt của lập phương, đáy
khối nón tiếp xúc với các cạnh của mặt đối diện
(xem hình vẽ bên). Tính tỉ số thể tích của lượng
nước tràn ra ngoài và lượng nước ban đầu trong khối hộp.
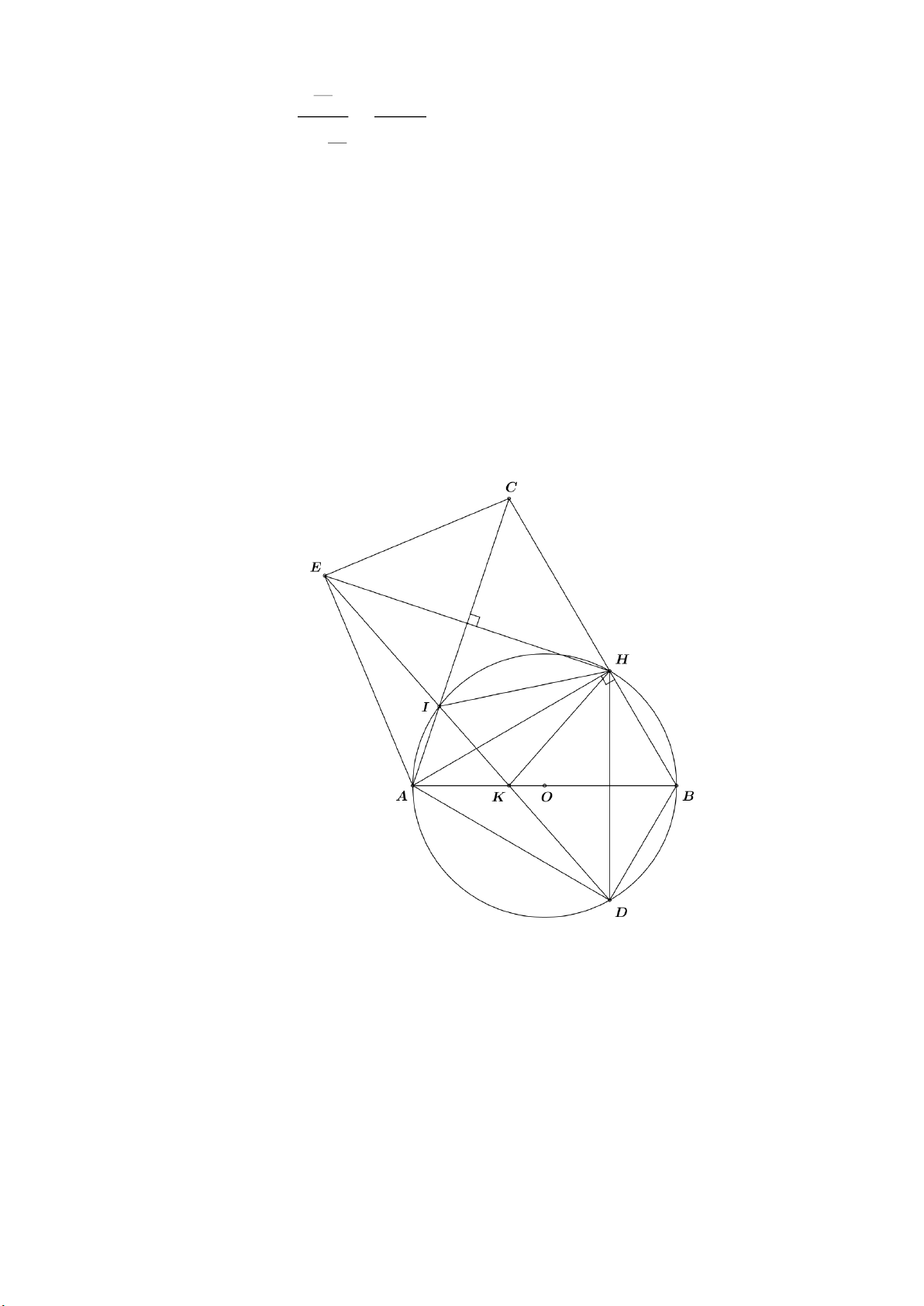
Câu 8. (3.0 điểm) Cho tam giác ABC AB AC có đường cao A H . Vẽ đường tròn tâm (O ) đường
kính A B cắt A C tại I . Gọi E là điểm đối xứng của H qua A C , EI cắt A B tại K và cắt
(O) tại điểm thứ hai là D .
a) Chứng minh tứ giác ADBH nội tiếp và AD AE . ·
b) Chứng minh DH ^ A B . Suy ra HA là phân giác của góc IHK .
c) Chứng minh năm điểm A , E , C , H , K cùng thuộc đường tròn. ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI 2 x 3
Câu 1. (1,5 điểm). Cho P : y
và đường thẳng D : y x 1 . 4 4
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ.
b) Viết phương trình đường thẳng (D song song với (D) và đi qua điểm A thuộc (P ) có 1 ) hoành độ bằng 2 . Lời giải
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ. BGT: x 4 2 0 2 4 2 x y 4 1 0 1 4 4 x 0 4
y 3 x 1 1 2 4
b) Viết phương trình đường thẳng (D song song với (D) và đi qua điểm A thuộc (P ) có 1 ) hoành độ bằng 2 . 2 2
Gọi A (2;a)Î (P ), nên ta có a = - = - 1 . 4 Suy ra A (2;- ) 1 . 3 3
Vì (D / / D : y = -
x - 1 nên (D : y = -
x + c với c ¹ - 1. 1 ) 1 ) ( ) 4 4 3 1
Vì A Î (D nên - 1 = - .2 + c Û c = (nhận). 1 ) 4 2 3 1 Vậy (D : y = - x + . 1 ) 4 2
Câu 2. (1 điểm). Cho phương trình 2 x - 3x - 5 + 1 = 0 .
Không giải phương trình, hãy tính giá trị của biểu thức 2 2
M = 2x x - x x - 3x - 3x . 1 2 1 2 1 2 Lời giải Trang 3
Vì a.c = 1.(- 5 + )
1 < 0 nên phương trình có hai nghiệm x và x . 1 2 b S x x 3 1 2
Theo định lí Vi-et, ta có: a c P x .x 5 1 1 2 a Ta có: 2 2
M = 2x x - x x - 3x - 3x 1 2 1 2 1 2
M 2x x 2 x x 3 x x 1 2 1 2 1 2
M 2 5 12 5 1 3.3
M 26 2 5 5 10 2 3 5 Vậy M = 2 - 3 5 .
Câu 3. (1 điểm). Đầu năm học, một trường THPT tuyển được 75 học sinh vào 2 lớp chuyên Văn
và chuyên Sử. Nếu chuyển 15 học sinh từ lớp chuyên Văn sang lớp chuyên Sử thì số học 8
sinh lớp chuyên Sử bằng
số học sinh lớp chuyên Văn. Hãy tính số học sinh của mỗi lớp. 7 Lời giải
Gọi x là số học sinh lớp chuyên Văn lúc đầu ( 0 < x < 75 , x Î ¥ * ) (học sinh).
Gọi y là số học sinh lớp chuyên Sử lúc đầu ( 0 < x < 75 , x Î ¥ * ) (học sinh).
Vì tổng số học sinh lúc đầu của hai lớp là 75 học sinh nên ta có phương trình x + y = 75 ( ) 1
Số học sinh lớp chuyên Văn lúc sau là x - 15 (học sinh).
Số học sinh lớp chuyên Sử lúc sau là y + 15 (học sinh). 8
Vì số học sinh lớp chuyên Sử lúc sau bằng
số học sinh lớp chuyên Văn lúc sau nên ta có 7 phương trình 8 y + = (x - ) 8 225 15 15 Û x - y = (2) 7 7 7 ìï x + y = 75 ï ìï x = 50 ï ï Từ ( )
1 và (2), ta có hệ phương trình í 8 225 Û í ï (nhận). x - y ï = y = 25 ï ïî ïî 7 7
Vậy số học sinh lớp chuyên Văn là 50 (học sinh).
Số học sinh lớp chuyên Sử là 25 (học sinh). Trang 4
Câu 4. (1 điểm). Xí nghiệp may Việt Tiến hàng tháng phải chi 410 000 000 đồng để trả lương cho
công nhân, mua vật tư và các khoản phí khác. Mỗi chiếc áo được bán với giá 350 000 đồng.
Gọi số tiền lời (hoặc lỗ) mà xí nghiệp thu được sau mỗi tháng là T và mỗi tháng xí nghiệp
bán được x chiếc áo.
a) Lập hàm số của T theo x .
b) Cần phải bán trung bình bao nhiêu chiếc áo mỗi tháng để sau 1 năm, xí nghiệp thu được
tiền lời là 1380 000 000 đồng. Lời giải
a) Hàm số T = 350 000x - 410 000 000 .
b) Xí nghiệp thu được tiền lời là 1380 000 000 đồng nên ta có phương trình
1 380 000 000 = 350000x - 410000000 Û x = 1500 (chiếc áo). 12
Vậy cần bán ít nhất là 1500 chiếc áo mỗi tháng thì xí nghiệp thu được tiền lời là 1380 000 000 đồng.
Câu 5. (0,75 điểm). Một viên gạch hình vuông ( 40 cm x 40 cm) được như trên hình, tính diện tích phần tô màu. Lời giải
Diện tích phần tô màu bằng 8 lần diện tích hình viên phân BKH . Trang 5
Diện tích hình viên phân = S - S quat D BKH 2 KB 90 1 BK BN 360 2 2 20 90 1 20 20 360 2 100 200
Vậy diện tích cần tìm là 8 2 100 200 913cm .
Câu 6. (0,75 điểm). Mỗi công nhân của công ty Cổ phần ABC có số tiền thưởng tết năm 2018 là 1
tháng lương. Đến năm 2019 , số tiền thưởng tết của họ được tăng thêm 6% so với số tiền
thưởng tết của năm 2018 . Vào năm 2020 , số tiền thưởng tết của họ được tăng thêm 10%
so với số tiền thưởng tết của năm 2019 , ngoài ra nếu công nhân nào được là công đoàn
viên xuất sắc sẽ được thưởng thêm 500 000 đồng. Anh Ba là công đoàn viên xuất sắc của
năm 2019 , nên anh nhận được số tiền thưởng tết là 6 330 000 đồng. Hỏi năm 2018 , tiền
lương 1 tháng của anh Ba là bao nhiêu? Lời giải
Số tiền lương một tháng vào năm 2018 của anh Ba là
6 330 000 - 500 000 = 5000000(đồng) (1 + 10 ) % (1 + 6 ) %
Vậy tiền lương một tháng vào năm 2018 của anh Ba là 5 000 000 (đồng)
Câu 7. (1 điểm). Một khối lập phương có cạnh 1 m chứa
đầy nước. Đặt vào trong khối đó một khối nón có
đỉnh trùng với tâm một mặt của lập phương, đáy
khối nón tiếp xúc với các cạnh của mặt đối diện
(xem hình vẽ bên). Tính tỉ số thể tích của lượng
nước tràn ra ngoài và lượng nước ban đầu trong khối hộp. Lời giải 2 1 1 æ ö ç ÷ p
Thể tích lượng nước tràn ra bằng với thể tích khối nón nên V = p ç ÷ .1 = 3 m . non ç ÷ 3 2 ç ÷ è ø 12
Thể tích khối lập phương là 3 V = 1 = 1 3 m . lp Trang 6 p p
Vậy tỉ số cần tìm là 12 = . p 12 - p 1 - 12
Câu 8. (3.0 điểm) Cho tam giác ABC AB AC có đường cao A H . Vẽ đường tròn tâm (O )
đường kính A B cắt A C tại I . Gọi E là điểm đối xứng của H qua A C , EI cắt A B tại
K và cắt (O ) tại điểm thứ hai là D .
a) Chứng minh tứ giác ADBH nội tiếp và AD AE . ·
b) Chứng minh DH ^ A B . Suy ra HA là phân giác của góc IHK .
c) Chứng minh năm điểm A , E , C , H , K cùng thuộc đường tròn. Lời giải
a) Ta có: DA HB vuông tại H
Þ H thuộc đường tròn đường kính A B hay thuộc đường tròn (O).
Þ ADBH nội tiếp đường tròn (O). · · »
Ta có: A DI = A HI (cùng chắn cung A I ) 1
Vì E và H đối xứng qua A C nên A C là đường trung trực của EH
Þ AE = AH và IE = IH .
Xét DA IE và DA IH có: Trang 7 A I chung. A E = A H IE = IH
Þ DAIE = DAIH (c – c – c) · · Þ A EI = A HI 2 · · Từ ( )
1 và (2) Þ AEI = ADI Þ DAED cân tại A Þ AD = AE . ·
b) Ta có: A DB = 90° (góc nội tiếp chắn nửa đường tròn)
Xét DA HB và DA DB có:
A H = A D (= AE )
A B là cạnh chung · ·
A HB = A DB (= 90 ) °
Þ DAHB = DADB (cạnh huyền – cạnh góc vuông)
Þ BH = BD mà A H = A D Þ AB là đường trung trực của HD Þ AB ^ HD
Vì A B là đường trung trực của HD nên KH = KD .
Xét DA KH và DA KD có: A H = A D
A K là cạnh chung KH = KD
Þ DAKH = DAKD (c – c – c) · · Þ · · · ·
A HK = A DK mà A DI = A HI Þ A HK = A HI ·
Þ HA là tia phân giác của IHK .
c) Xét DA EC và DA HC có:
A E = A H (A C là đường trung trực của EH )
CE = CH (A C là đường trung trực của EH )
A C là cạnh chung
Þ DAEC = DAHC (c – c – c) · ·
Þ A EC = A HC = 90° · ·
Þ A EC + A HC = 180o Þ tứ giác A ECH nội tiếp đường tròn 3 · · · · · ·
Ta có: A HK = A HI mà A HI = A EI Þ A HK = A EI Trang 8
Þ Tứ giác A EHK nội tiếp đường tròn 4
Từ 3 và 4 Þ năm điểm A , E , C , H , K cùng thuộc đường tròn. ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 7
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 7 - 2
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). Trong mặt phẳng tọa độ Oxy , cho parabol P 2
: y x và đường thẳng
d: y mx3 (m là tham số).
a) Vẽ parabol P .
b) Khi m 2 , tìm tọa độ giao điểm của P và d bằng phép toán.
Câu 2. (1 điểm). Cho phương trình 2
x x 13 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A x 2x 2x x 1 2 1 2
Câu 3. (1 điểm). Tổng số học sinh của hai lớp 9A và 9B ở một trường THCS là 76 học sinh.
Hưởng ứng phong trào ủng hộ trang thiết bị y tế trong đợt phòng dịch Covid-19, cả hai lớp
đã quyên góp ủng hộ 189 chiếc khẩu trang. Biết rằng mỗi học sinh lớp 9A ủng hộ 3 chiếc
khẩu trang, mỗi học sinh lớp 9B ủng hộ 2 chiếc khẩu trang. Tính số học sinh của mỗi lớp.
Câu 4. (1 điểm). Hãng taxi A quy định giá thuê xe cho những chuyến đi đường dài (trên 50 km ).
Mỗi km là 16 nghìn đồng đối với 50 km đầu tiên và 9 nghìn 5 trăm đồng đối với các km tiếp theo.
a) Một khách thuê xe taxi đi quãng đường 75 km thì phải trả số tiền thuê xe là bao nhiêu nghìn đồng?
b) Gọi y (nghìn đồng) là số tiền khách thuê xe taxi phải trả sau khi đi x km . Khi ấy mối liên
hệ giữa hai đại lượng này là một hàm số bậc nhất y ax b . Hãy xác định hàm số này khi x 50 ?
Câu 5. (1 điểm). Một trường học cần đưa 510 học sinh đi tham quan Vũng Tàu. Có hai cách để
thuê xe: Cách 1 là thuê xe 45 chỗ, giá thuê đi và về cho mỗi xe là 1800000 đồng; cách 2 là
thuê xe 29 chỗ, giá thuê đi về cho mỗi xe là 950000 đồng. Nếu chỉ thuê một loại xe cho cả
đoàn thì nhà trường thuê loại xe nào sẽ tiết kiệm hơn? Trang 9
Câu 6. (0,75 điểm). Một vé xem phim có giá 60000 đồng. Khi có đợt giảm giá, mỗi ngày số lượng
người xem tăng lên 50% , do đó doanh thu cũng tăng 25% . Hỏi giá vé khi được giảm là bao nhiêu?
Câu 7. (1 điểm). Nhà hát Cao Văn Lầu, Trung
tâm triển lãm văn hóa nghệ thuật tỉnh
Bạc Liêu có hình dáng ba chiếc nón lá
lớn nhất Việt Nam, mái nhà hình nón
làm bằng vật liệu composite và được
đặt hướng vào nhau. Em hãy tính thể
tích của một mái nhà hình nón biết đường kính là 45m và chiều cao là 45m (lấy 3,14 ,
kết quả làm tròn đến hàng đơn vị, ba hình nón có bán kính bằng nhau).
Câu 8. (3 điểm) Cho tam giác nhọn ABC AB AC nội tiếp đường tròn tâm O . Hai tiếp tuyến
tại B và C của đường tròn O cắt nhau tại M , tia AM cắt đường tròn O tại điểm D .
a) Chứng minh rằng tứ giác OBMC nội tiếp được đường tròn. b) Chứng minh 2 MB M . D MA .
c) Gọi E là trung điểm của đoạn thẳng AD ; tia CE cắt đường tròn O tại điểm F Chứng
minh rằng: BF / /AM . ----HẾT--- Trang 10 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol P y 2 :
x và đường thẳng
d: y mx3 (m là tham số).
a. Vẽ parabol P .
b. Khi m 2 , tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. y (P) BGT: 4 x 2 1 0 1 2 2 y x 4 1 0 1 4 1 x
b) Khi m 2 , tìm tọa độ giao điểm của P và d -2 -1 O 1 2 bằng phép toán.
Phương trình hoành độ giao điểm của P và d : 2 x 2x 3 2
x 2x 3 0 x 1 x 3 2
Thay x 1 vào 2 y
x , ta được: y 1 1 . 2 Thay x 3 vào 2 y
x , ta được: y 3 9 . Vậy 1;
1 , 3; 9 là hai giao điểm cần tìm. Câu 2.
(1 điểm) Cho phương trình 2
x x 13 0 có 2 nghiệm là x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức A x 2x 2x x . 1 2 1 2 Lời giải 2 Vì 2
b 4ac
1 4.1.13 53 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 Trang 11 b S x x 1 1 2 a
Theo định lí Vi-et, ta có: c P x .x 13 1 2 a
Ta có: A x 2x 2x x 1 2 1 2 A 2
2x x x 4x x 2 2x 1 1 2 1 2 2 A 2 2 x 2 x 5x x 1 2 1 2 A 2 x x 2x x 5x x 1 2 2 1 2 1 2
A 2x x 9x x 1 2 2 1 2
A 212 9.13 119
Câu 3. (1 điểm) Tổng số học sinh của hai lớp 9A và 9B ở một trường THCS là 76 học sinh.
Hưởng ứng phong trào ủng hộ trang thiết bị y tế trong đợt phòng dịch Covid-19, cả hai
lớp đã quyên góp ủng hộ 189 chiếc khẩu trang. Biết rằng mỗi học sinh lớp 9A ủng hộ 3
chiếc khẩu trang, mỗi học sinh lớp 9B ủng hộ 2 chiếc khẩu trang. Tính số học sinh của mỗi lớp. Lời giải
Gọi số học sinh của lớp 9A , 9B lần lượt là x,y ( x y * , )
Số chiếc khẩu trang lớp 9A đã ủng hộ là: 3x (chiếc)
Số chiếc khẩu trang lớp 9B đã ủng hộ là: 2y (chiếc)
Vì tổng số học sinh của hai lớp là 76 học sinh nên ta có phương trình x y 76 1
Vì cả hai lớp ủng hộ 189 chiếc khẩu trang nên ta có phương trình: 3x 2y 189 2
x y 76 x 37
Từ 1 và 2 , ta có hệ phương trình: (thỏa mãn)
3x 2y 189 y 39
Vậy số học sinh của lớp 9A và 9B lần lượt là 37 học sinh và 39 học sinh Câu 4.
(0,75 điểm). Hãng taxi A quy định giá thuê xe cho những chuyến đi đường dài
(trên 50 km ). Mỗi km là 16 nghìn đồng đối với 50 km đầu tiên và 9 nghìn 5 trăm đồng
đối với các km tiếp theo.
a) Một khách thuê xe taxi đi quãng đường 75 km thì phải trả số tiền thuê xe là bao nhiêu nghìn đồng? Trang 12
b) Gọi y (nghìn đồng) là số tiền khách thuê xe taxi phải trả sau khi đi x km . Khi ấy mối liên
hệ giữa hai đại lượng này là một hàm số bậc nhất y ax b . Hãy xác định hàm số này khi x 50 ? Lời giải
a) Số tiền thuê xe đi quãng đường 75 km :
16000.50 9500.25 1037500 (đồng)
b) Hàm số biểu thị khi x 50 :
y 50.16000 x – 50.9500 9500 x 325000
Câu 5. (1 điểm) Một trường học cần đưa 510 học sinh đi tham quan Vũng Tàu. Có hai cách để
thuê xe: Cách 1 là thuê xe 45 chỗ, giá thuê đi và về cho mỗi xe là 1800000 đồng; cách 2 là
thuê xe 29 chỗ, giá thuê đi về cho mỗi xe là 950000 đồng. Nếu chỉ thuê một loại xe cho cả
đoàn thì nhà trường thuê loại xe nào sẽ tiết kiệm hơn? Lời giải
Số xe 45 chỗ cần thuê để đưa 510 học sinh đi tham quan: 510 11,33 (xe) 45
Vậy nhà trường phải thuê 12 (xe)
Số tiền thuê xe 45 chỗ là:
12.1800000 21600000 (đồng)
Số xe 29 chỗ cần thuê để đưa 510 học sinh đi tham quan: 510 17,58(xe) 29
Vậy nhà trường phải thuê 18 (xe)
Số tiền thuê xe 29 chỗ là:
18.950000 17100000 (đồng)
Vì 17100000 21600000 nên thuê xe loại 29 chỗ sẽ tiết kiệm hơn cho nhà trường.
Câu 6. (1 điểm) Một vé xem phim có giá 60000 đồng. Khi có đợt giảm giá, mỗi ngày số lượng
người xem tăng lên 50% , do đó doanh thu cũng tăng 25% . Hỏi giá vé khi được giảm là bao nhiêu? Lời giải
Gọi x là số lượng khán giả đi xem phim lúc chưa giảm giá ( x *) Trang 13
Số tiền thu được lúc chưa giảm giá là 60000x (đồng)
Số lượng khán giả sau khi giảm giá là: . x 150%
Số tiền thu được sau khi giảm giá là: 60000 . x 125% 60000 .125 x %
Vậy giá tiền số vé lúc giảm: 50000 (đồng) .150% x
Câu 7. (1 điểm) Nhà hát Cao Văn Lầu, Trung
tâm triển lãm văn hóa nghệ thuật tỉnh
Bạc Liêu có hình dáng ba chiếc nón lá
lớn nhất Việt Nam, mái nhà hình nón
làm bằng vật liệu composite và được
đặt hướng vào nhau. Em hãy tính thể tích của một mái nhà hình nón biết đường kính là
45m và chiều cao là 45m (lấy 3,14 , kết quả làm tròn đến hàng đơn vị, ba hình nón có bán kính bằng nhau). Lời giải 45
Mái nhà hình nón đường kính là 45m suy ra bán kính R m . 2
Thể tích của một mái nhà hình nón là 2 1 1 45 2 V R h 3,14. .24 12717 3 m 3 3 2
Câu 8. (3 điểm) Cho tam giác nhọn ABC AB AC nội tiếp đường tròn tâm O . Hai tiếp
tuyến tại B và C của đường tròn O cắt nhau tại M , tia AM cắt đường tròn O tại điểm D .
a) Chứng minh rằng tứ giác OBMC nội tiếp được đường tròn. b) Chứng minh 2 MB M . D MA .
c) Gọi E là trung điểm của đoạn thẳng AD ; tia CE cắt đường tròn O tại điểm F Chứng
minh rằng: BF // AM . Lời giải
a) Chứng minh rằng tứ giác OBMC nội tiếp được đường tròn.
Xét O có: MB,MC là các tiếp tuyến của đường tròn O tại B vàC
MBO MCO 90
Xét tứ giác OBMC , có: MBO MCO 180 Trang 14
Tứ giác OBMC nội tiếp vì có hai góc đối bù nhau. A F O E B C D M b) Chứng minh 2 MB M . D MA
Xét MBD và MAB
MBD MAB 1 sdBD 2 BMA chung M BD ” M AB (g – g
MB MD 2 MB M . A MD . MA MB
c) Gọi E là trung điểm của đoạn thẳng AD ; tia CE cắt đường tròn O tại điểm F
Chứng minh rằng: BF / /AM .
Ocó E là trung điểm của dây AD không qua tâm (gt)
OE AD tại E OEM 90
Xét tứ giác OEMC , có: MEO MCO 9
0 MEO MCO 18 0
Tứ giác OEMC nội tiếp vì có hai góc đối bù nhau.
CEM COM (cùng chắn MC ) Trang 15 1
Mà BOM COM
sd BC (tính chất hai tiếp tuyến cắt nhau) 2 1 Và BFC
sd BC (tính chất góc nội tiếp) 2
Do đó: CEM BFC mà hai góc này ở vị trí đồng vị
BF // AM (đpcm) ----HẾT----
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 7
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 7 - 3
Thời gian: 120 phút (không kể thời gian phát đề) 2 x x
Câu 9. Cho y
P và y 2 D . 4 2
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép toán.
Câu 10. Cho phương trình 2
x 2x 3 1 0 . Không giải phương trình, hãy tính giá trị của biểu thức 2 2
M x x 2x x x x 1 2 1 2 1 2
Câu 11. Bạn Bình và mẹ dự định di du lịch Hội An và Bà Nà (Đà Nẵng) trong 6 ngày. Biết rằng chi
phí trung bình mỗi ngày tại Hội An là 1500 000 đồng, còn tại Bà Nà là 2 000 000 đồng. Tìm
số ngày nghỉ tại mỗi địa điểm, biết số tiền mà họ phải chi cho toàn bộ chuyến đi là 10 000 000 đồng.
Câu 12. Trong 130 con bò của gia đình ông Hiệp ở huyện Mộc Châu, tỉnh Sơn La có 75 con sinh
sản (hiện có 42 con đang vắt sữa), còn lại bê và bò tơ, tổng giá trị đàn bò không dưới 6 tỷ
đồng. Sản lượng sữa hằng ngày ông thu khoảng 1,2 tấn, bán cho nhà máy được 15 triệu
đồng, trừ chi phí ông Hiệp còn lãi 40% so với doanh thu.
a) Hỏi mỗi ngày 1 con bò vắt được bao nhiêu kg sữa?
b) Mỗi tháng (khoảng 30 ngày) gia đình ông Hiệp thu được tiền lãi là bao nhiêu từ sản lượng sữa bò?
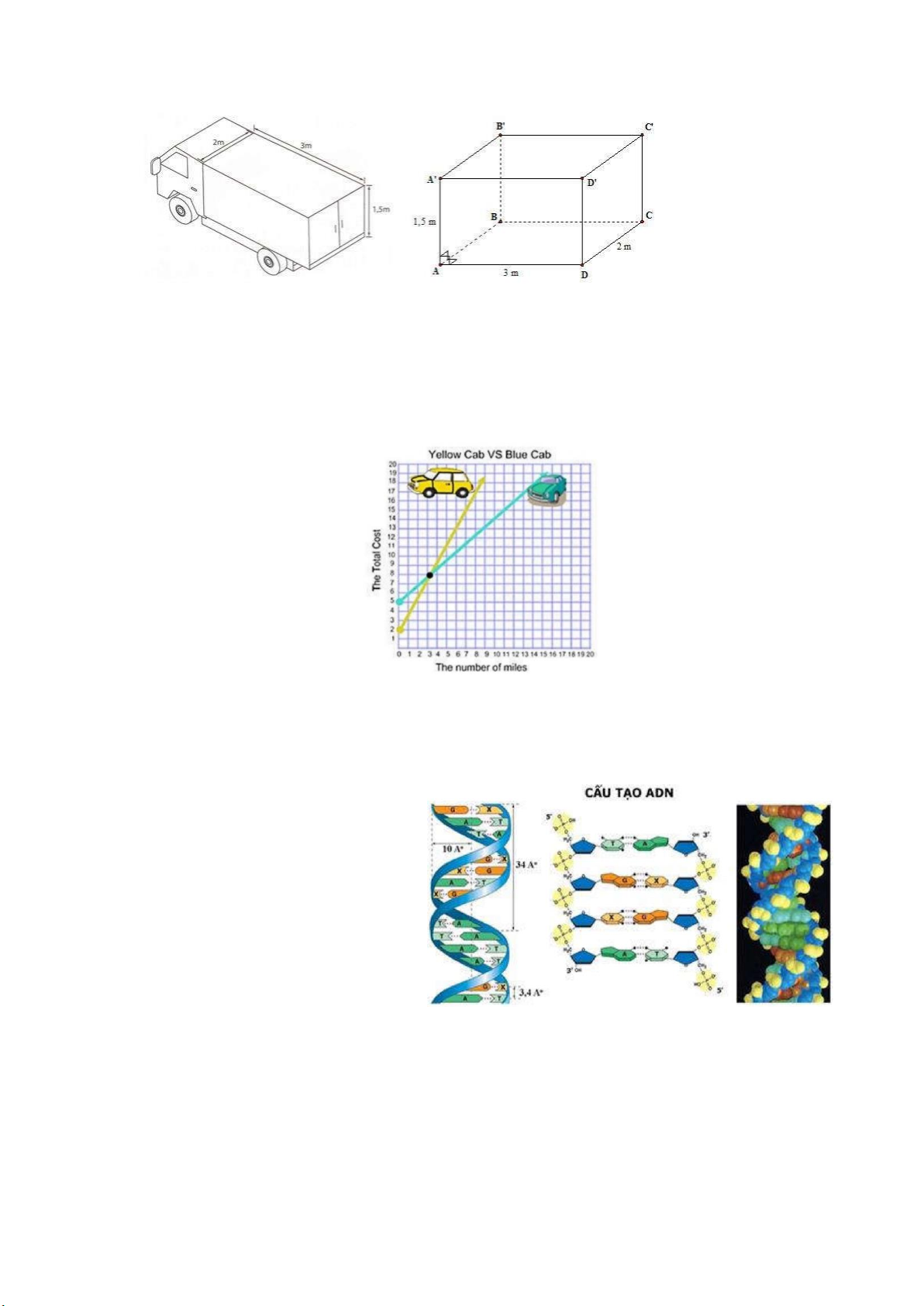
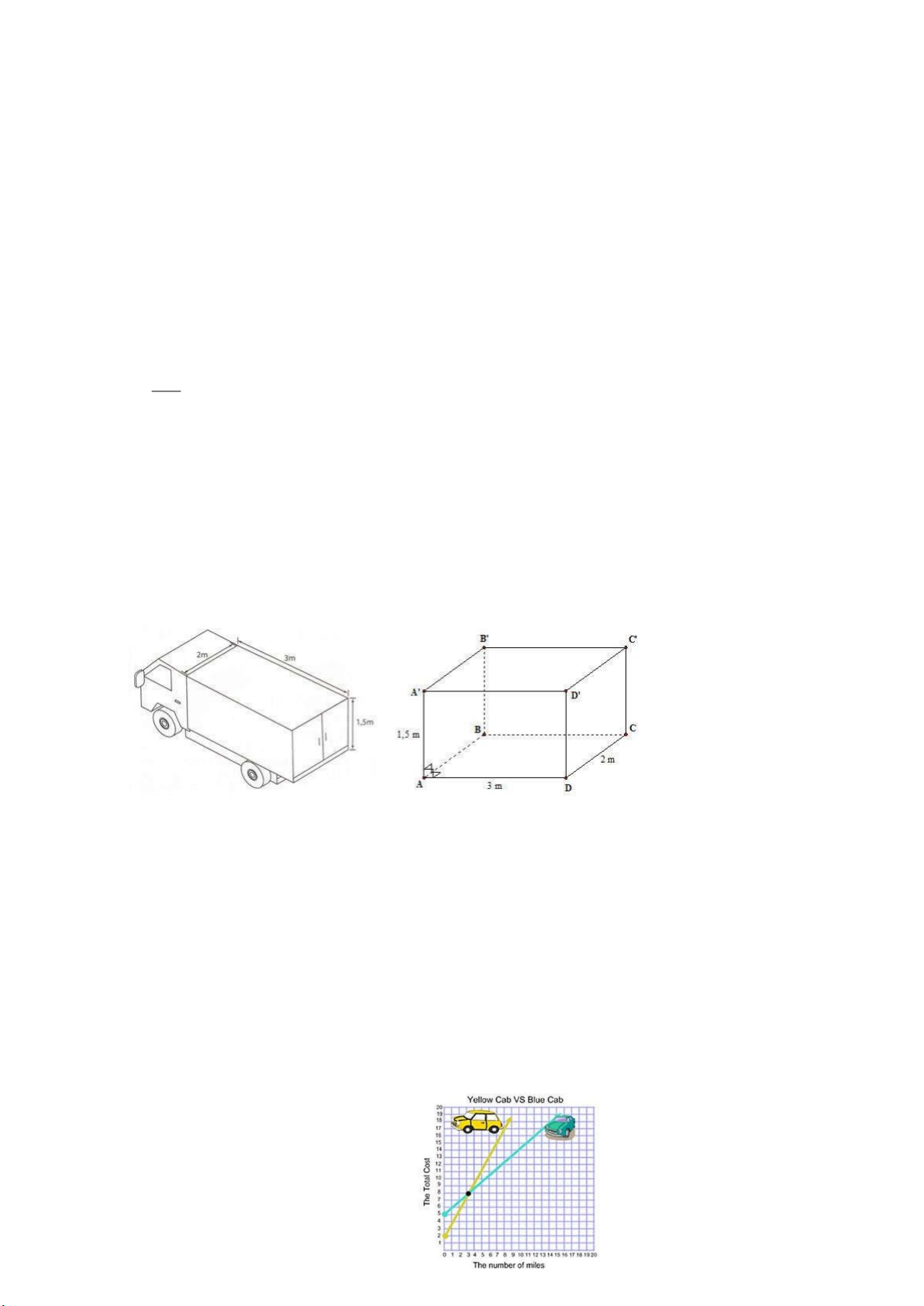
Câu 13. Một xe tải đông lạnh chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như
hình bên. Bạn hãy tính giúp thể tích của thùng xe và diện tích phần Inox đóng thùng xe Trang 16 (tính luôn sàn).
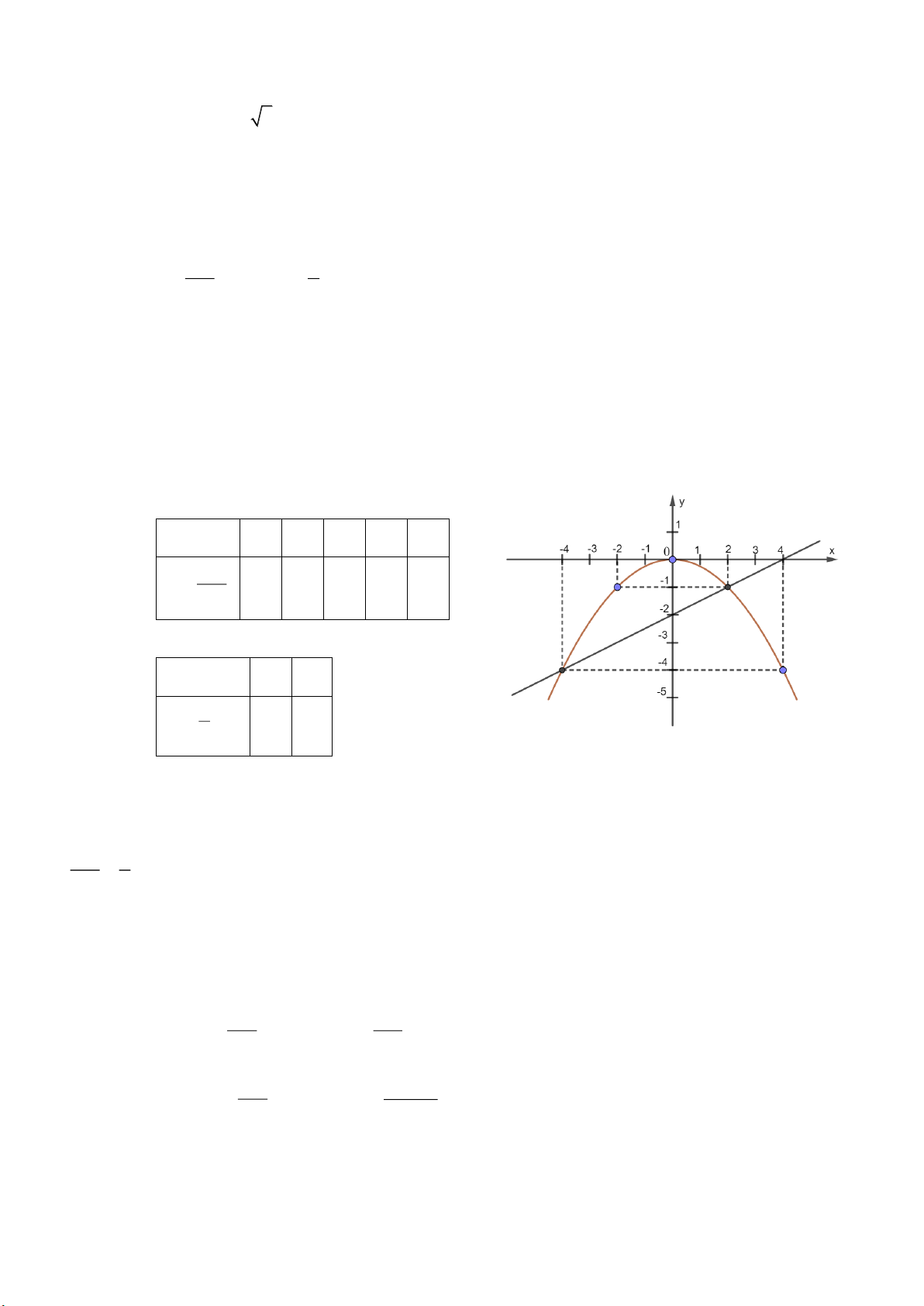
Câu 14. Dưới đây là đồ thị biểu diễn quãng đường đi được giá tiền tương ứng mà khách hàng phải
trả cho hãng taxi Blue Cap và Yellow Cab.
Trục hoàng biểu diễn số km mỗi xe đi được (mỗi đơn vị: 1km ), trục tung biểu diễn số tiền
phải trả tương ứng (mỗi đơn vị: 7 ngàn đồng). Quan sát đồ thị và cho biết:
a) Anh Du di chuyển quãng đường 3km với xe của hãng Yellow Cab, anh phải trả bao nhiêu tiền?
b) Cô Hạ cần di chuyển quãng đường 8 km , cô nên chọn hãng nào để tiết kiệm chi phí?
Câu 15. Gen B có 3600 liên kết Hidro và có
hiệu giữa Nucleotit loại T với loại
Nucleotit không bổ sung với nó là
300 Nucleotit. Tính số Nucleotit
từng loại của gen B .
Biết rằng, để tính số lượng
Nucleotit ( A,T,G,X ) trong phân
tử ADN, ta áp dụng nguyên tắc bổ
sung: “ A liên kết với T bằng 2 liên kết Hidro và G liên kết với X bằng 3 liên kết Hidro”
và %A %T , %G %X .
Tổng số Nucleotit trong gen B : N A T G X 2A 2G 2T 2X .
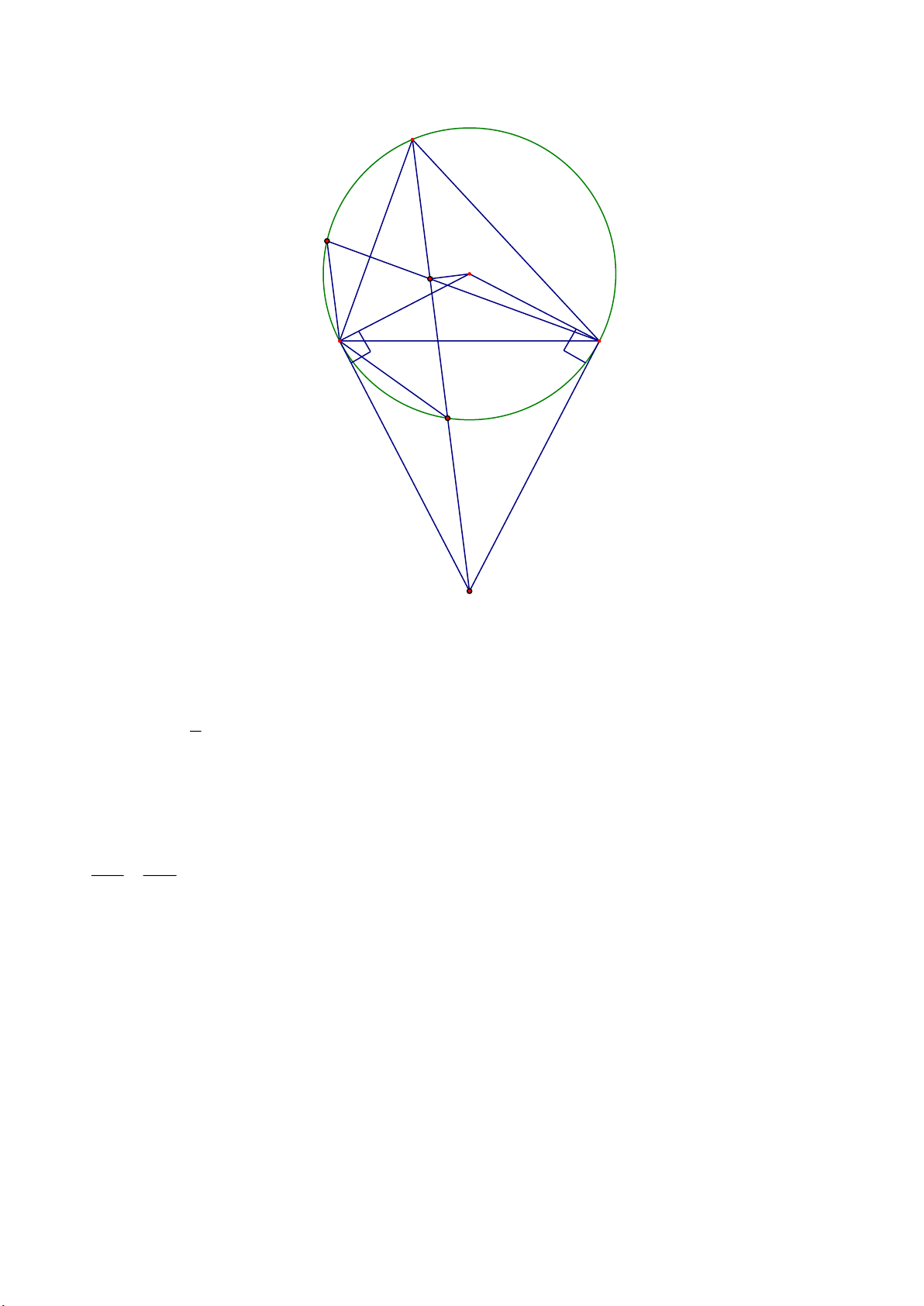
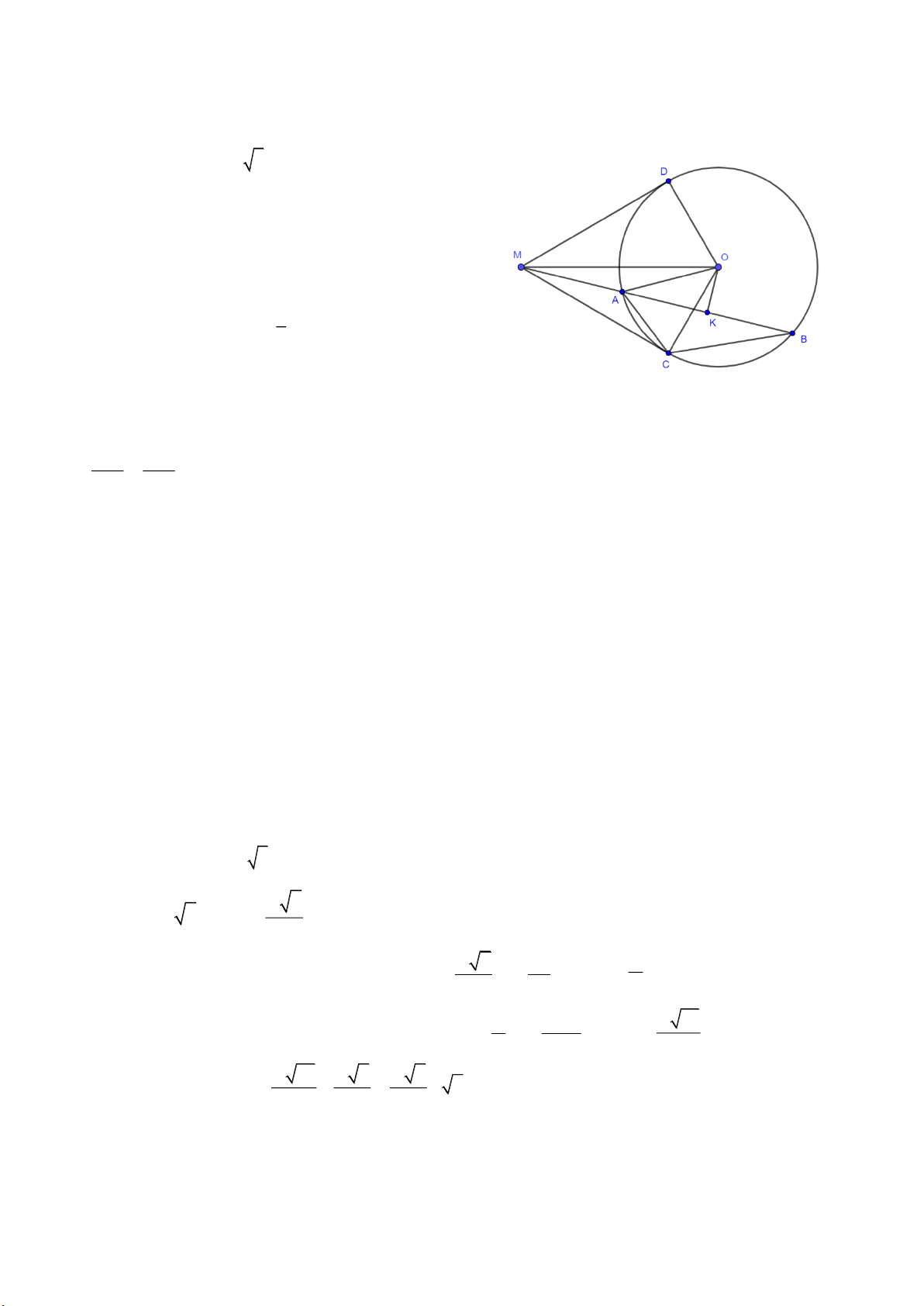
Câu 16. Cho đường tròn O; R , M là một điểm nằm ngoài đường tròn sao cho OM 2R. Từ M
kẻ 2 tiếp tuyến MC, MD đến đường tròn ( C, D là tiếp điểm) và cát tuyến MAB . a) Chứng minh: 2 MC M . A MB Trang 17
b) Gọi K là trung điểm AB , chứng minh 5 điểm M,C,K,O,D cùng thuộc một đường tròn.
c) Cho AB R 3 . Tính MA theo R . ----HẾT--- HƯỚNG DẪN GIẢI 2 x x
Câu 1. Cho y
P và y 2 D . 4 2
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải
c) Vẽ đồ thị P và D trên cùng hệ trục tọa độ. BGT: x 4 2 0 2 4 2 x y 4 1 0 1 4 4 x 0 2 x y 2 2 1 2
d) Tìm tọa độ giao điểm của P và D bằng phép toán.
Phương trình hoành độ giao điểm của P và D : 2 x x 2 4 2 2
x 2x 8 0 x 2 x 4 2 x 2 2
Thay x 2 vào y , ta được: y 1 . 4 4 2 2 x 4 Thay x 4 vào y , ta được: y 4 . 4 4 Vậy 2;
1 , 4; 4 là hai giao điểm cần tìm. Trang 18
Câu 2. Cho phương trình 2
x 2x 3 1 0 . Không giải phương trình, hãy tính giá trị của biểu thức M 2 2
x x 2x x x x 1 2 1 2 1 2 Lời giải 2 Vì 2
b 4ac 2 4.1. 3 1 4 3 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b 2
S x x 2 1 2
Theo định lí Vi-et, ta có: a 1 c 3 P x x 1 . 1 3 1 2 a 1 Ta có: M 2 2
x x 2x x x x 1 2 1 2 1 2 M x x 2x x x x 1 2 2 1 2 1 2 2
M 1 3 2.1 3 2 M 0
Câu 3. Bạn Bình và mẹ dự định di du lịch Hội An và Bà Nà (Đà Nẵng) trong 6 ngày. Biết rằng chi
phí trung bình mỗi ngày tại Hội An là 1500000 đồng, còn tại Bà Nà là 2000000 đồng. Tìm số
ngày nghỉ tại mỗi địa điểm, biết số tiền mà họ phải chi cho toàn bộ chuyến đi là 10 000 000 đồng. Lời giải
Gọi thời gian nghỉ tại Hội An là x (ngày), thời gian nghỉ tại Bà Nà là y
(ngày) 0 x 6;0 y 6 .
Vì bạn Bình và mẹ dự định đi du lịch tại Hội An và Bà Nà (Đà Nẵng) trong 6 ngày nên ta có
phương trình x y 6 1
Chi phí ở Hội An là 1500000x (đồng), chi phí ở Bà Nà là 2000000y (đồng)
Vì tổng chi phí cho toàn bộ chuyến đi là 10000000 đồng nên ta có phương trình
1500000x 2000000y 10000000 3x 4y 20 2
x y 6 x 4
Từ 1 và 2 ta có hệ phương trình (thỏa mãn điều kiện) 3x 4y 20 y 2
Vậy Bình và mẹ nghỉ tại Hội An 4 ngày và nghỉ tại Bà Nà 2 ngày.
Câu 4. Trong 130 con bò của gia đình ông Hiệp ở huyện Mộc Châu, tỉnh Sơn La có 75 con sinh
sản (hiện có 42 con đang vắt sữa), còn lại bê và bò tơ, tổng giá trị đàn bò không dưới 6 tỷ Trang 19
đồng. Sản lượng sữa hằng ngày ông thu khoảng 1,2 tấn, bán cho nhà máy được 15 triệu
đồng, trừ chi phí ông Hiệp còn lãi 40% so với doanh thu.
a) Hỏi mỗi ngày 1 con bò vắt được bao nhiêu kg sữa?
b) Mỗi tháng (khoảng 30 ngày) gia đình ông Hiệp thu được tiền lãi là bao nhiêu từ sản lượng sữa bò? Lời giải
a) 1,2 tấn 1200kg .
Khối lượng sữa mỗi ngày 1 con bò vắt được: 200 1200: 42 kg 28,6kg 7
b) Số tiền lãi gia đình ông hiệp thu được mỗi tháng từ sản lượng sữa bò:
15.40%.30 180 triệu đồng.
Câu 5. Một xe tải đông lạnh chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình
bên. Bạn hãy tính giúp thể tích của thùng xe và diện tích phần Inox đóng thùng xe (tính luôn sàn). Lời giải
Thể tích thùng xe tải: V 3 3.2.1,5 9 m
Diện tích phần Inox đóng thùng xe: S S S 2 2. 3 2 .2.1,5 2.3.2 27m tp xq day
Câu 6. Dưới đây là đồ thị biểu diễn quãng đường đi được giá tiền tương ứng mà khách hàng phải
trả cho hãng taxi Blue Cap và Yellow Cab.
Trục hoàng biểu diễn số km mỗi xe đi được (mỗi đơn vị: 1 km), trục tung biểu diễn số tiền phải trả Trang 20
tương ứng (mỗi đơn vị: 7 ngàn đồng). Quan sát đồ thị và cho biết:
a) Anh Du di chuyển quãng đường 3 km với xe của hãng Yellow Cab, anh phải trả bao nhiêu tiền?
b) Cô Hạ cần di chuyển quãng đường 8 km, cô nên chọn hãng nào để tiết kiệm chi phí? Lời giải
a) Số tiền anh Du phải trả khi di chuyển quãng đường 3km với xe của hãng Yellow Cab: 8.7 56 nghìn đồng.
b) Quan sát đồ thị, ta thấy khi di chuyển quãng đường lớn hơn 3km thì số tiền phải trả
khi đi xe Blue Cab sẽ nhỏ hơn xe Yellow Cab.
Câu 7. Gen B có 3600 liên kết Hidro và có
hiệu giữa Nucleotit loại T với loại
Nucleotit không bổ sung với nó là
300 Nucleotit. Tính số Nucleotit từng loại của gen B.
Biết rằng, để tính số lượng Nucleotit (A, T,
G, X) trong phân tử ADN, ta áp dụng
nguyên tắc bổ sung: “A liên kết với T bằng 2 liên kết Hidro và G liên kết với X bằng 3 liên kết
Hidro” và %A %T , %G %X .
Tổng số Nucleotit trong gen B: N A T G X 2A 2G 2T 2X . Lời giải
Gọi A,G lần lượt là số Nucleotit loại A , loại G A,G * .
Số liên kết hidro là 3600 nên ta có phương trình 2A 3G 3600 1
Số Nucleotit loại T bằng số Nucleotit loại A . Nucleotit không bổ sung với T là G hoặc X
Số Nucleotit loại T trừ số Nucleotit loại không bổ sung bằng 300 nên ta có phương trình:
A G 300 2
2A 3G 3600 A 900 Từ
1 , 2 ta có hệ phương trình: (thỏa mãn điều kiện) A G 300 G 600
Vậy số nu loại A,T là 900, loại G,X là 600.
Câu 8. Cho đường tròn O; R , M là một điểm nằm ngoài đường tròn sao cho OM 2R. Từ M kẻ 2
tiếp tuyến MC, MD đến đường tròn ( C, D là tiếp điểm) và cát tuyến MAB . Trang 21 a) Chứng minh: 2 MC M . A MB
b) Gọi K là trung điểm AB , chứng minh 5 điểm M,C,K,O,D cùng thuộc một đường tròn.
c) Cho AB R 3 . Tính MA theo R . Lời giải d) Chứng minh : 2 MC M . A MB
Xét tam giác MAC và tam giác MCB có: 1
MCA MBC (cùng bằng sđ AC ). 2 M chung
DMA C ” DMCB (g-g)
MC MB 2 MC M . A MB . MA MC
e) Gọi K là trung điểm AB , chứng minh 5 điểm M,C,K,O,D cùng thuộc một đường tròn.
Gọi K là trung điểm AB
OK AB MKO 90
K thuộc đường tròn đường kính MO 1 .
Mà MCO MDO
90 ( MC,MD là tiếp tuyến của O;R )
C,D thuộc đường tròn đường kính MO 2 . Từ
1 , 2 suy ra: 5 điểm M,C,K,O,D cùng thuộc một đường tròn.
f) Cho AB R 3 . Tính MA theo R . R Ta có AB R AK 3 3 và OM 2R. 2 2 2 R R 3 R
OAK vuông tại K có: 2 OK 2 AO 2 AK 2 R OK . 2 4 2 2 2 2 R 15R R
MOK vuông tại K có: 2 2 2 MK MO OK 2R MK 15 . 2 4 2 R 15 R 3 R 3
Suy ra: MA MK AK . 5 1 . 2 2 2 ----HẾT--- Trang 22