













Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 8
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 8 - 1
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). Cho hàm số 2
y 2x có đồ thị P và hàm số y x 3 có đồ thị d .
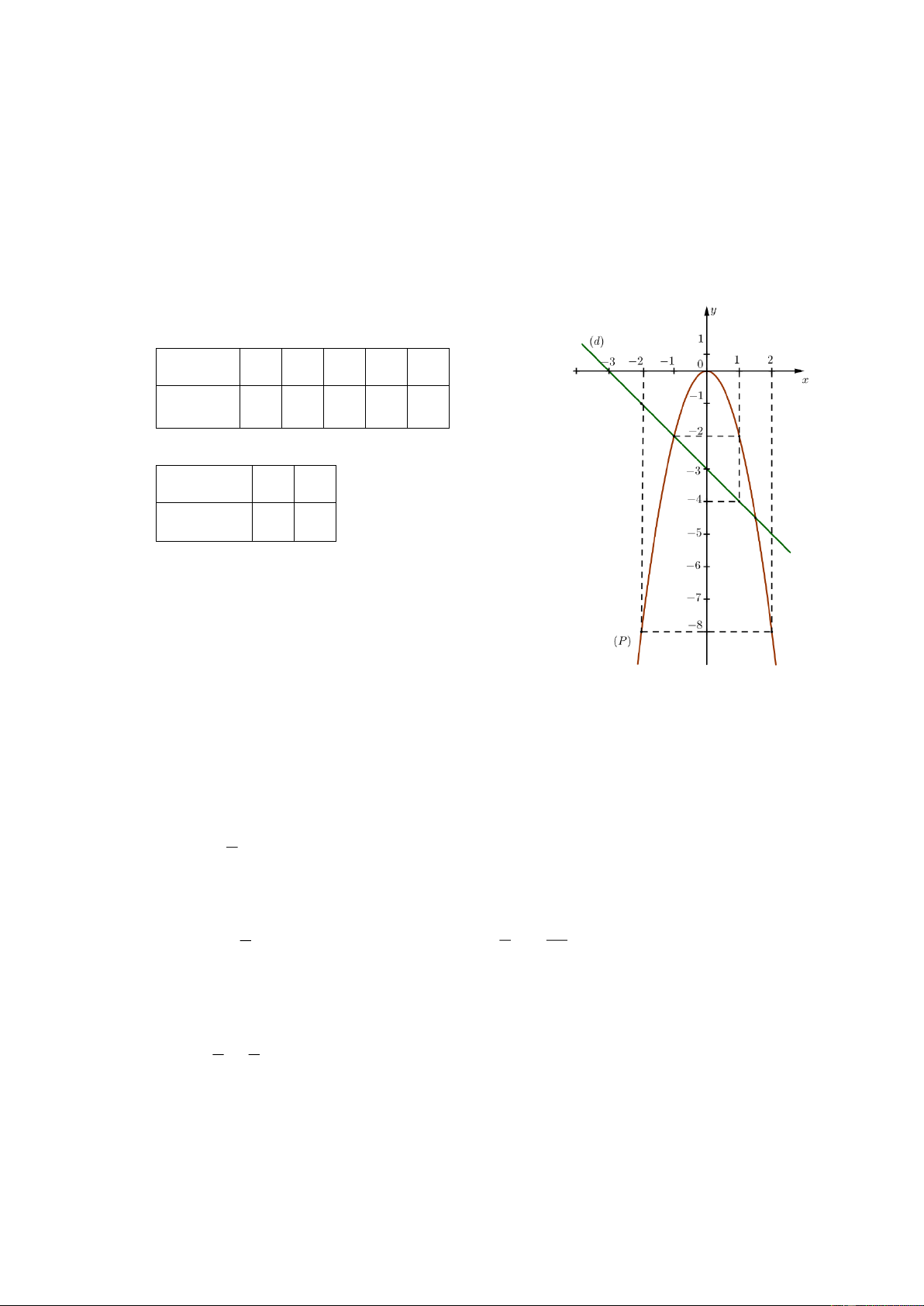
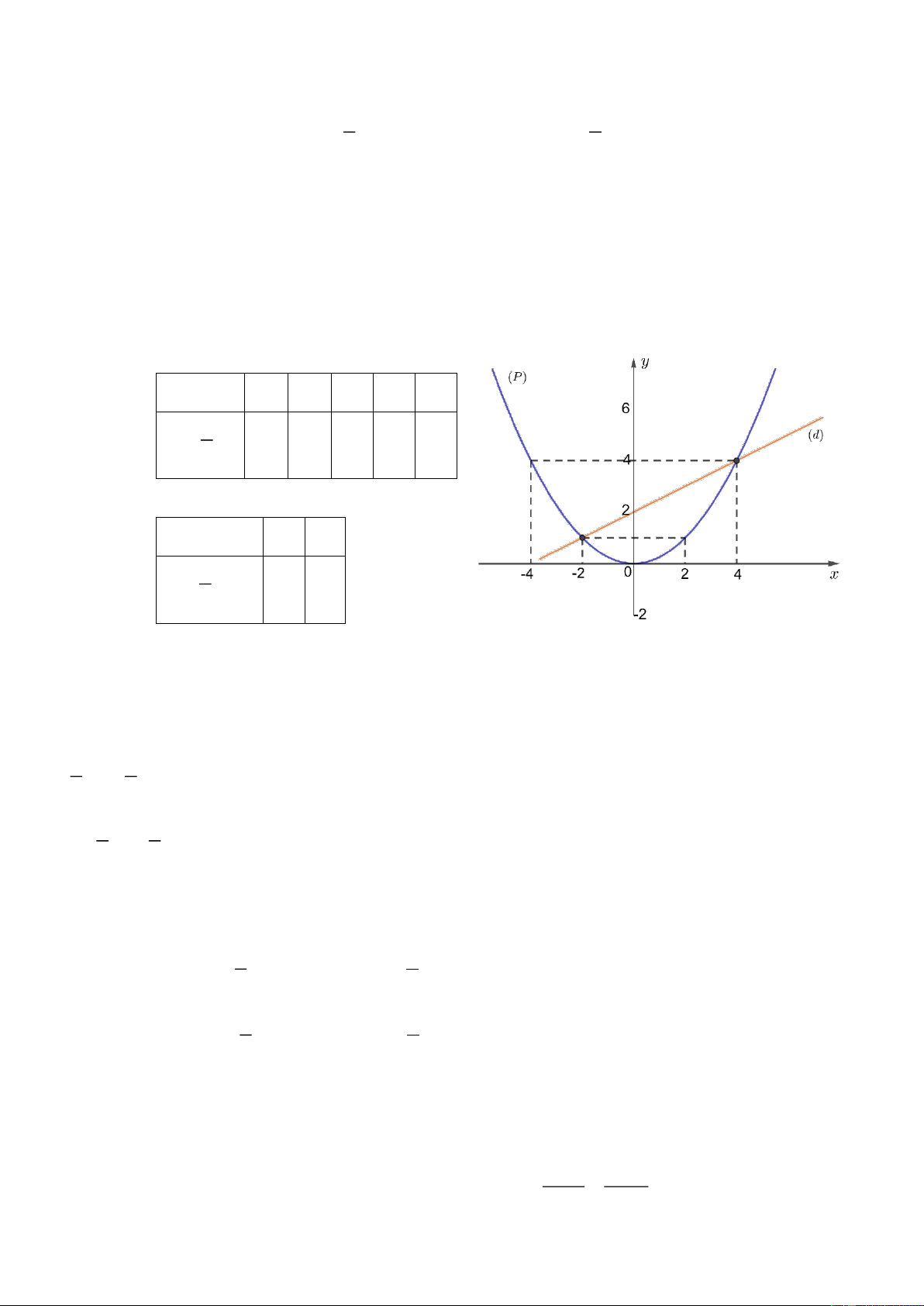
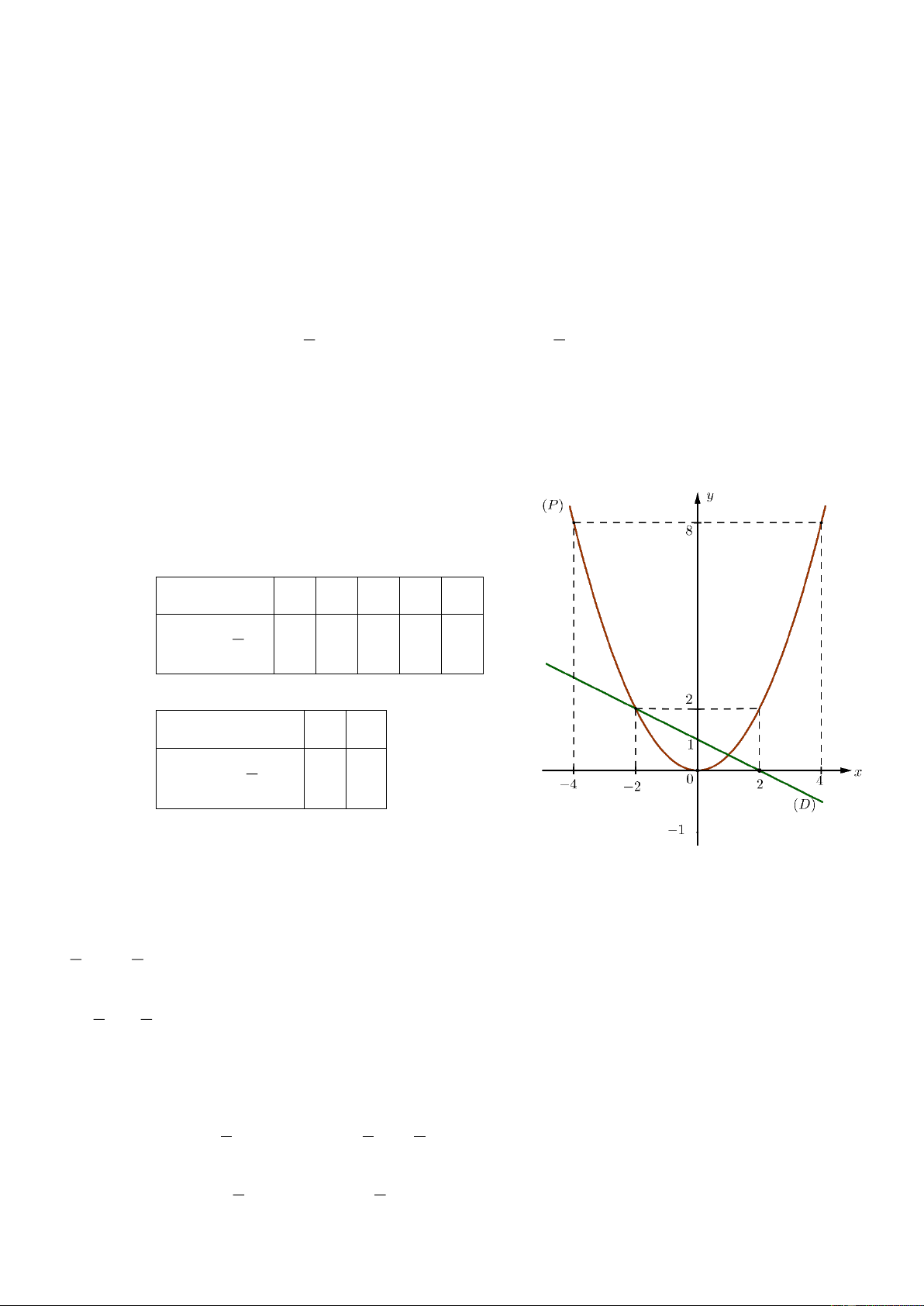
a) Vẽ P và d trên cùng một hệ trục tọa độ.
b) Tìm toạ độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình: 2
20x – 23x – 24 0 có hai nghiệm x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức: 2 2
A x x x x . 1 2 2 1
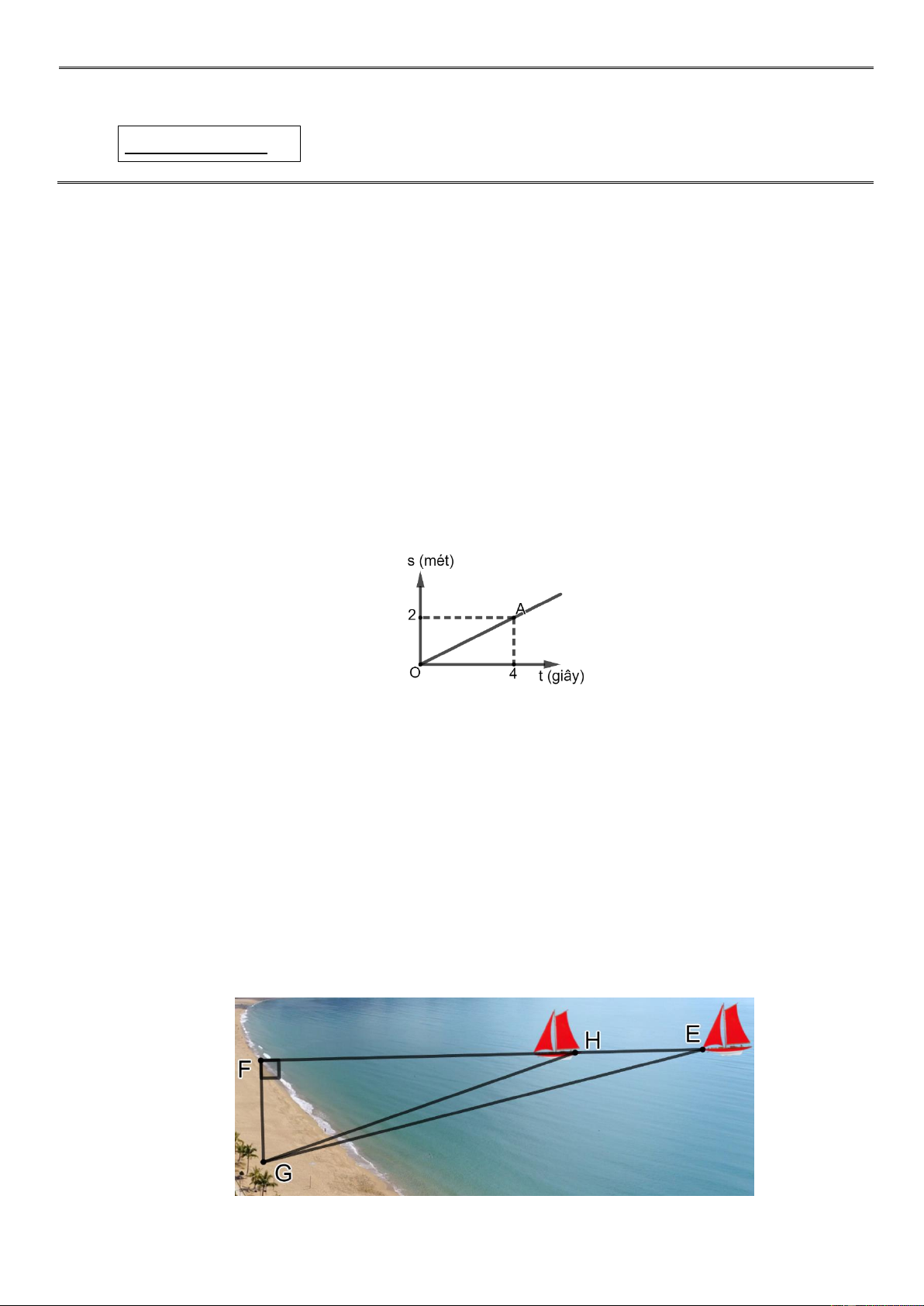
Câu 3. (0,75 điểm). Một vật chuyển động đều, quãng đường chuyển động smét của vật trong
thời gian t giây được biểu diễn theo hàm số s .
a t . Biết đồ thị chuyển động của vật được cho như hình bên.
a) Hãy tìm hệ số a .
b) Trong bao lâu thì vật chuyển động được 5 mét
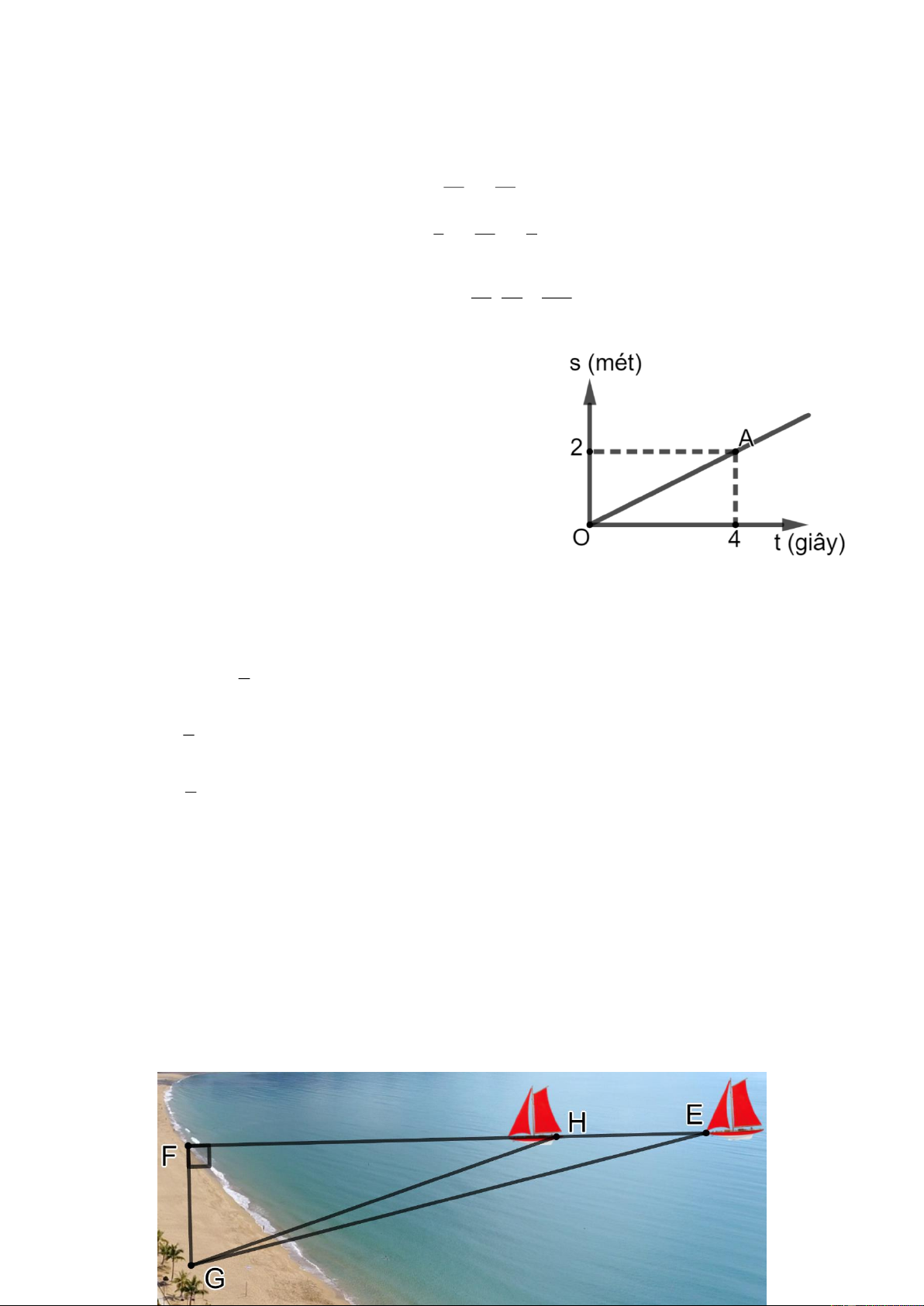
Câu 4. (1 điểm). Trong một buổi hoạt động trải nghiệm ứng dụng thực tế tỉ số lượng giác của góc
nhọn, một nhóm học sinh lớp 9A có thể tính được khoảng cách giữa hai thuyền trên biển
bằng cách dùng thước cuộn, eke, cọc và giác kế để xác định được các vị trí G,F,H,E như
hình vẽ bên dưới. Học sinh đã đo đoạn FG 20 mét, góc FGH bằng 70 , góc FGE bằng
77. Em hãy cho biết học sinh lớp 9A đã tính được khoảng cách giữa hai thuyền là bao
nhiêu ? (Làm tròn kết quả đến chữ số hàng đơn vị) Trang 1
Câu 5. (1 điểm). Một cửa hàng cần bán một lô hàng gồm 32 sản phẩm cùng loại với giá bán ban
đầu là 2 400 000 đồng. Nhân dịp lễ Noel, cửa hàng giảm 10% so với giá bán ban đầu thì
bán được 12 sản phẩm. Vào dịp tết Tây, mỗi sản phẩm được giảm 200000 đồng (so với giá
đã giảm ở dịp lễ Noel) thì cửa hàng bán được hết số sản phẩm còn lại. Sau khi bán hết thì
cửa hàng lãi được 60% so với tổng số tiền bỏ ra gồm giá vốn của các sản phẩm và giá vận
chuyển 2 000 000 đồng. Hỏi giá vốn của mỗi sản phẩm trong lô hàng cần bán là bao nhiêu tiền?
Câu 6. (1 điểm). Trong một trò chơi Toán học có 50 câu trắc nghiệm, mỗi câu có 4 đáp án
A,B,C,D và mỗi câu chỉ có một đáp án đúng. Khi người chơi chọn được đáp án đúng thì
câu đó sẽ được 20 điểm, khi đáp án sai thì câu đó sẽ bị trừ đi 5 điểm. Bạn An đã tham gia
trò chơi Toán học đó. Sau khi kết thúc trò chơi, bạn An được 550 điểm. Hỏi bạn An đã trả
lời bao nhiêu câu đúng, bao nhiêu câu sai ?
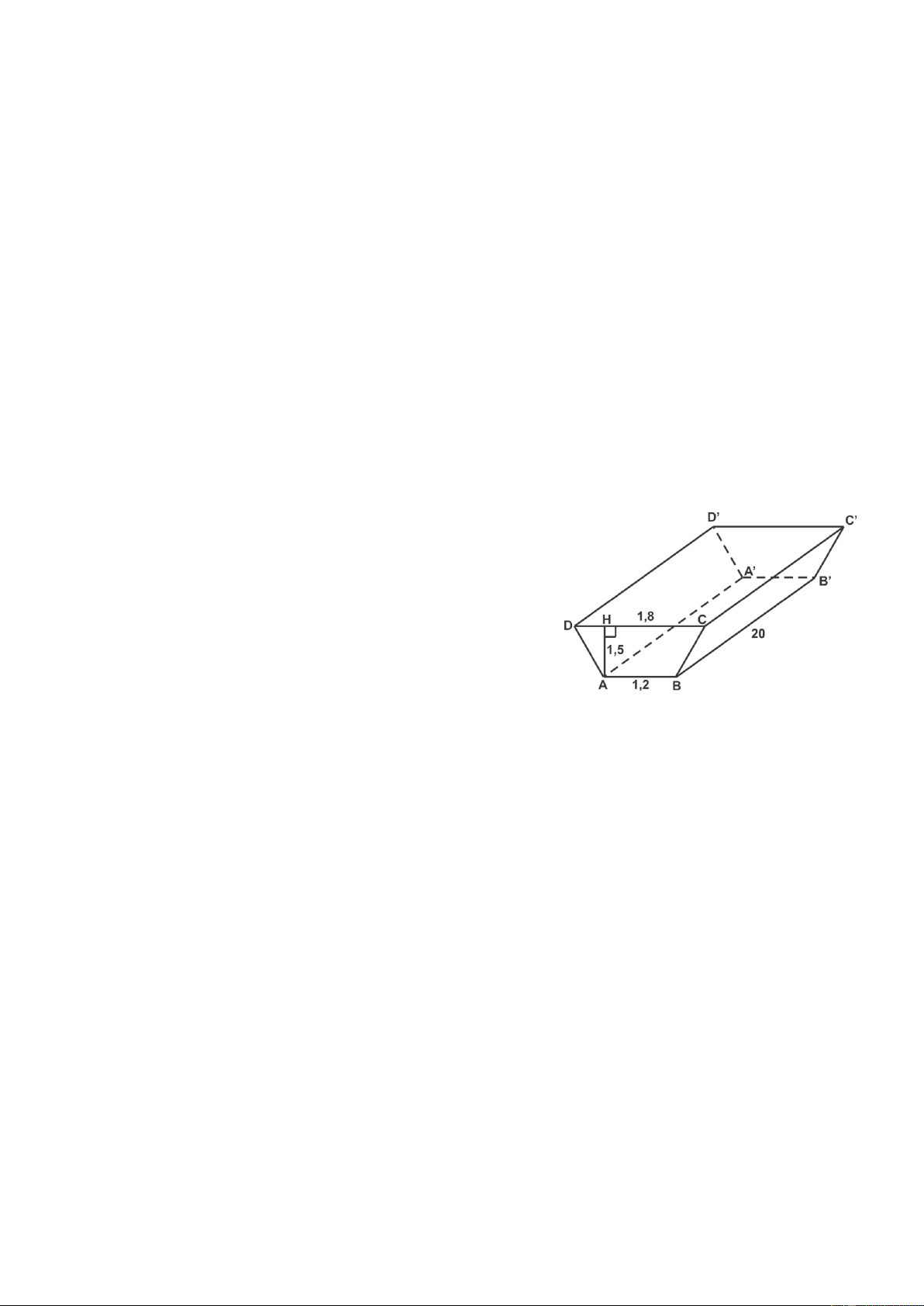
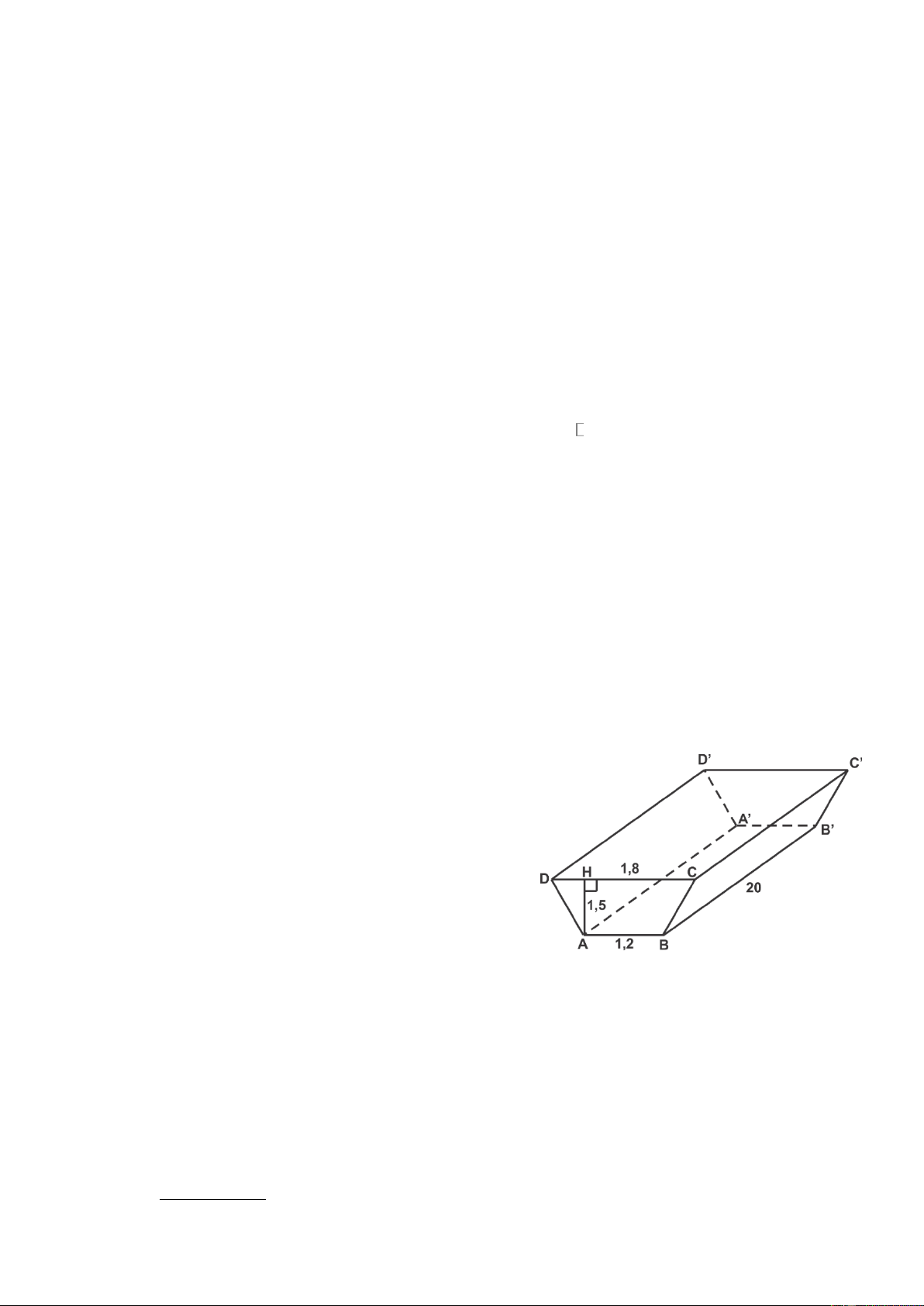
Câu 7. (0,75 điểm). Người ta đào một đoạn mương dài 20m
, sâu 1,5m . Trên bề mặt có chiều rộng 1,8m và đáy
mương là 1,2m (xem hình minh họa bên) . Người ta
chuyển toàn bộ khối đất đi để rải lên một miếng đất
hình chữ nhật có kích thước 12m và 15m . Số đất
được chuyển bằng một chiếc ô tô chở mỗi chuyến 3 6m .
a) Tính bề dày của lớp đất rải lên miếng đất hình chữ nhật (biết lớp đất được rải đều,
không có chổ cao chổ thấp).
b) Cần bao nhiêu chuyến ô tô để tải hết khối đất.
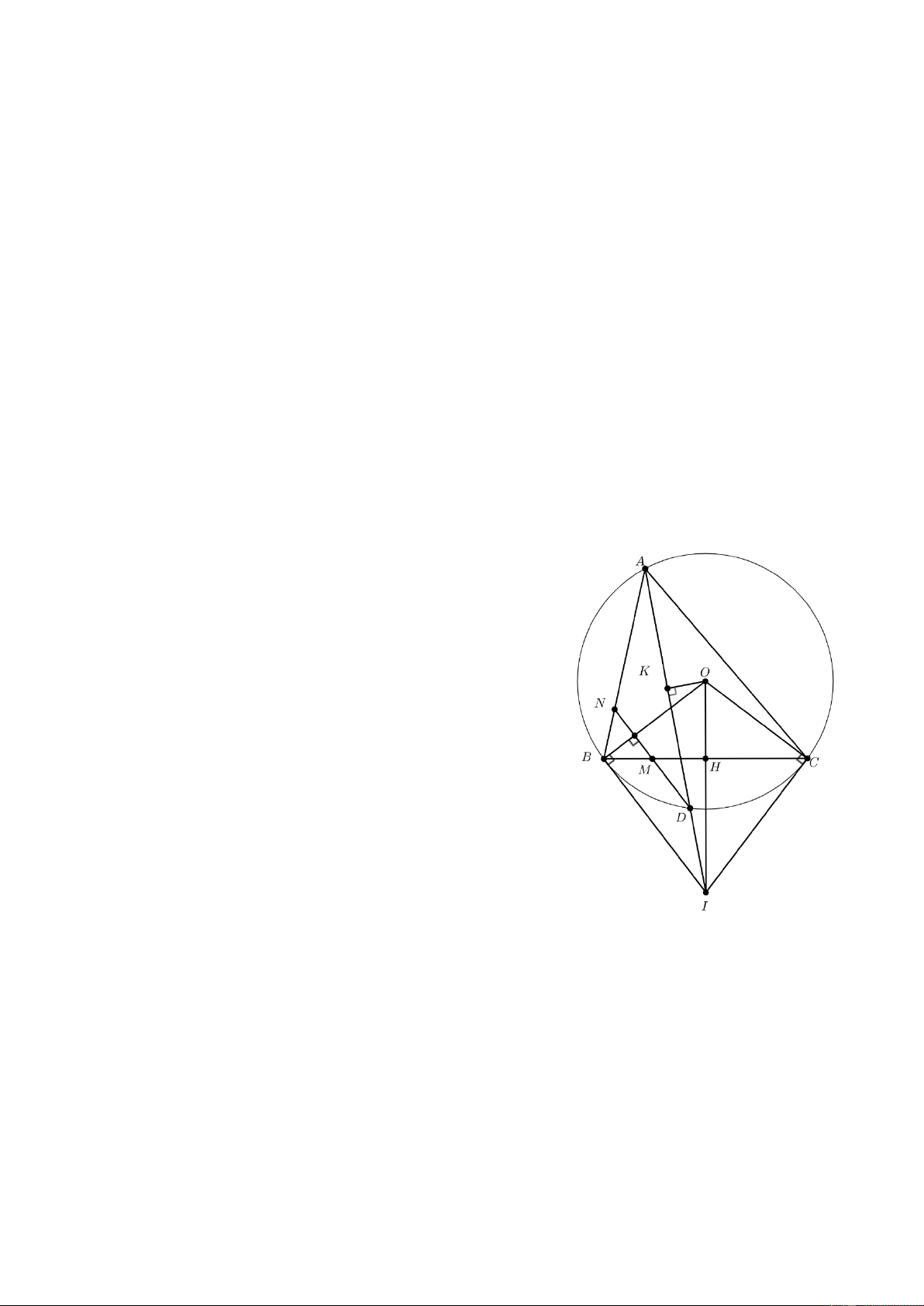
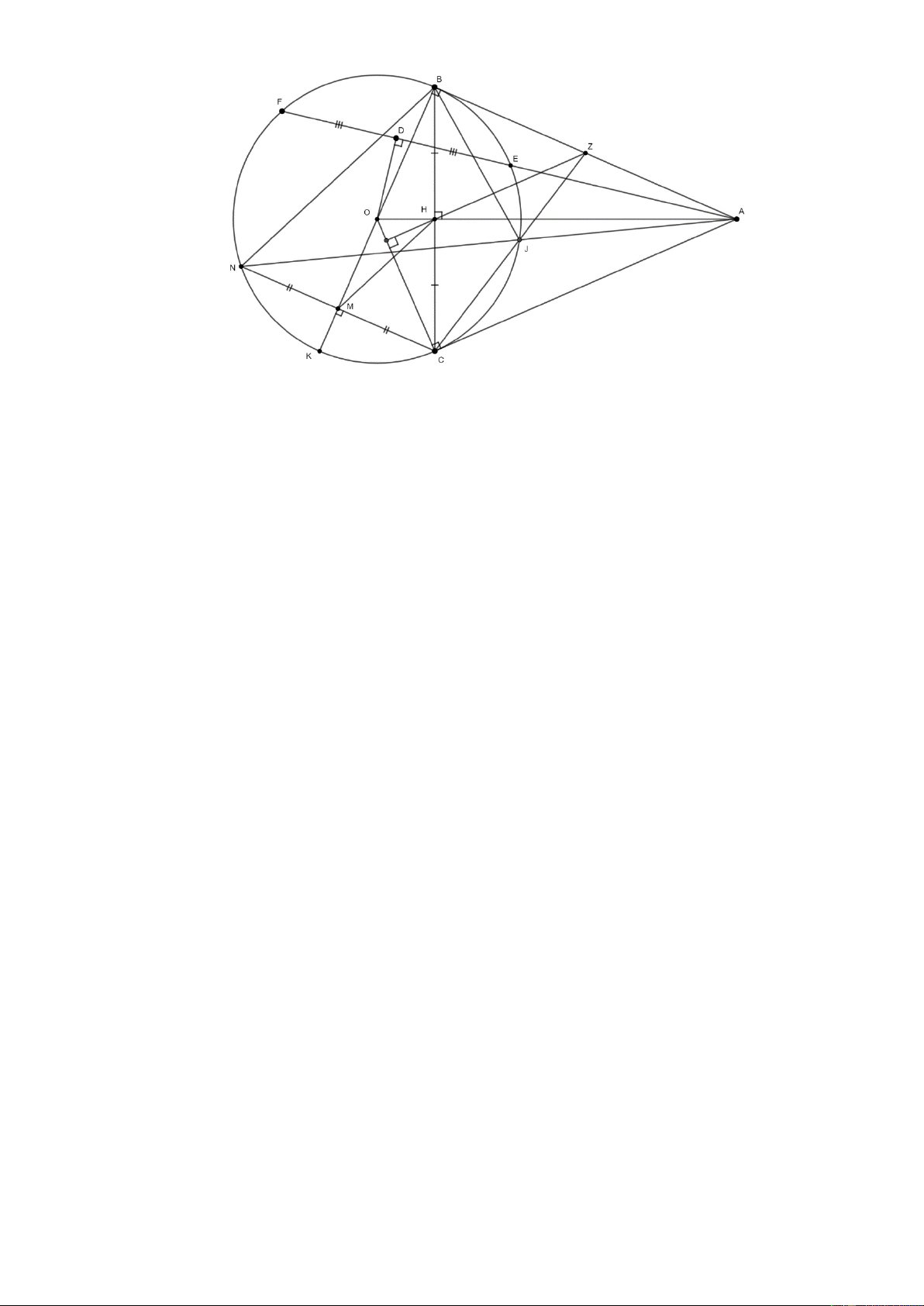
Câu 8. (3 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp O,R . Tiếp tuyến tại B và C của O
cắt nhau tại I . Đường thẳng AI cắt O tại điểm thứ hai là D (khác A ). Đoạn thẳng OI
cắt BC tại H .
a) Chứng minh : OI vuông góc với BC và H . B HC H . O HI
b) Vẽ OK vuông góc với AD . Chứng minh 5 điểm I,B,K,O,C cùng thuộc một đường tròn
c) Từ D kẻ đường thẳng vuông góc với OB , đường thẳng này cắt BC tại M và cắt AB tại
N . Chứng minh : M là trung điểm của DN . ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm). Cho hàm số y 2
2x có đồ thị P và hàm số y x 3 có đồ thị d .
a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ.
b) Tìm toạ độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: x 2 1 0 1 2 y 2
2x 8 2 0 2 8 x 0 1
y x 3 3 4
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d: 2
2x x 3 2
2x x 3 0 x 3 2 x 1 2 3 9
Thay x 3 vào y 2
2x , ta được: y 2 . 2 2 2 2
Thay x 1 vào y 2
2x , ta được: y 2 1 2 . 3 9 Vậy ;
, 1; 2 là hai giao điểm cần tìm. 2 2
Câu 2. (1 điểm). Cho phương trình: 2
20x – 23x – 24 0 có hai nghiệm x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức: A 2 x x 2 x x 1 2 2 1 Lời giải Trang 3 2 Vì 2
b 4ac 23 4.20.24 2449 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b S x x 23 1 2
Theo định lí Vi-et, ta có: a 20 c P x .x 24 6 1 2 a 20 5 23 6 69 Ta có: A 2 x x 2
x x x x (x x ) P.S 1 2 2 1 1 2 1 2 20 5 50
Câu 3. (0,75 điểm). Một vật chuyển động đều, quãng
đường chuyển động smét của vật trong thời gian
tgiây được biểu diễn theo hàm số s . a t . Biết đồ
thị chuyển động của vật được cho như hình bên.
a) Hãy tìm hệ số a .
b) Trong bao lâu thì vật chuyển động được 5 mét Lời giải
a) Thay t 4 ; s 2 ; vào phương trình s . a t 2 . a 4 a 1 2 b) s 1 .t 2 1 5 t 2 t 10
Vậy trong 10 giây thì vật chuyển động được 5 mét
Câu 4. (1 điểm). Trong một buổi hoạt động trải nghiệm ứng dụng thực tế tỉ số lượng giác của góc
nhọn, một nhóm học sinh lớp 9A có thể tính được khoảng cách giữa hai thuyền trên biển
bằng cách dùng thước cuộn, eke, cọc và giác kế để xác định được các vị trí G,F,H,E như
hình vẽ bên dưới. Học sinh đã đo đoạn FG 20 mét, góc FGH bằng 0 70 , góc FGE bằng 0
77 . Em hãy cho biết học sinh lớp 9A đã tính được khoảng cách giữa hai thuyền là bao Trang 4
nhiêu ? (Làm tròn kết quả đến chữ số hàng đơn vị) Lời giải
Xét FGH vuông tại F FH tanFGH FG FH tan70 20
FH 20.tan70 54,95m
Xét FGE vuông tại F FE tanFGE FG FE tan77 20
FE 20.tan77 86,63m
HE EF HF 86,63 54,95 32m
Khoảng cách giữa hai thuyền là 32 mét
Câu 5. (1 điểm). Một cửa hàng cần bán một lô hàng gồm 32 sản phẩm cùng loại với giá bán ban
đầu là 2 400 000 đồng. Nhân dịp lễ Noel, cửa hàng giảm 10% so với giá bán ban đầu thì
bán được 12 sản phẩm. Vào dịp tết Tây, mỗi sản phẩm được giảm 200000 đồng (so với giá
đã giảm ở dịp lễ Noel) thì cửa hàng bán được hết số sản phẩm còn lại. Sau khi bán hết thì
cửa hàng lãi được 60% so với tổng số tiền bỏ ra gồm giá vốn của các sản phẩm và giá vận
chuyển 2 000 000 đồng. Hỏi giá vốn của mỗi sản phẩm trong lô hàng cần bán là bao nhiêu tiền? Lời giải
Giá tiền 1 sản phẩm khi được giảm 10%
2400000110% 2160000(đồng)
Số tiền bán được sau khi bán hết 32 sản phẩm:
12 2160000 32 122160000 200000 65120000 (đồng)
Gọi x (đồng) là số tiền vốn của mỗi sản phẩm, x 0
Số tiền vốn và lãi sau khi bán 32 sản phẩm là:
32x2000000160% 1,632x2000000 Ta có phương trình: Trang 5
1,632x 2000000 65120000
x 1209 375 (đồng)
Vậy giá vốn của mỗi sản phẩm là 1209 375 đồng
Câu 6. (1 điểm). Trong một trò chơi Toán học có 50 câu trắc nghiệm, mỗi câu có 4 đáp án
A,B,C,D và mỗi câu chỉ có một đáp án đúng. Khi người chơi chọn được đáp án đúng thì
câu đó sẽ được 20 điểm, khi đáp án sai thì câu đó sẽ bị trừ đi 5 điểm. Bạn An đã tham gia
trò chơi Toán học đó. Sau khi kết thúc trò chơi, bạn An được 550 điểm. Hỏi bạn An đã trả
lời bao nhiêu câu đúng, bao nhiêu câu sai ? Lời giải
Gọi x là số câu trả lời đúng, y là số câu trả lời sai x, y *
Có 50 câu trắc nghiệm: x y 50
Bạn An được 550 điểm: 20x 5y 550 Ta có hệ phương trình:
x y 50 20x5y 550 x 32n y 18 n
Vậy bạn An trả lời được 32 câu đúng, 18 câu sai
Câu 7. (0,75 điểm). Người ta đào một đoạn mương dài
20m , sâu 1,5m . Trên bề mặt có chiều rộng 1,8m
và đáy mương là 1,2m (xem hình minh họa bên)
. Người ta chuyển toàn bộ khối đất đi để rải lên
một miếng đất hình chữ nhật có kích thước 12m
và 15m . Số đất được chuyển bằng một chiếc ô tô chở mỗi chuyến 3 6m .
a) Tính bề dày của lớp đất rải lên miếng đất hình chữ nhật (biết lớp đất được rải đều,
không có chổ cao chổ thấp).
b) Cần bao nhiêu chuyến ô tô để tải hết khối đất. Lời giải
a) Thể tích của khối đất được đào lên: 1,21,8.1,5 20. 45 3 m 2 Trang 6 Bề dày của lớp đất:
45 : 12.15 0,25m
b) Số chuyến ô tô chở đất là: 45 : 6 7,5
Vậy cần chở 8 chuyến ô tô để tải hết chổ đất.
Câu 8. (3 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp O,R . Tiếp tuyến tại B và C của O
cắt nhau tại I . Đường thẳng AI cắt O tại điểm thứ hai là D (khác A ). Đoạn thẳng OI
cắt BC tại H .
a) Chứng minh : OI vuông góc với BC và H . B HC H . O HI
b) Vẽ OK vuông góc với AD . Chứng minh 5 điểm I,B,K,O,C cùng thuộc một đường tròn
c) Từ D kẻ đường thẳng vuông góc với OB, đường thẳng này cắt BC tại M và cắt AB tại
N . Chứng minh : M là trung điểm của DN . Lời giải
a) Chứng minh OI vuông góc với BC
OB = OC = R
IB = IC (tính chất hai tiếp tuyến cắt nhau tại I )
Þ OI thuộc đường trung trực của BC
Þ OI ^ BC tại H .
Xét D OBI vuông tại B đường cao B H Þ 2
B H = HO.HI
Mà BH = CH ( H Î OI )
Þ BH.CH = H . O HI
b) Chứng minh được chứng minh 5 điểm
I , B, K ,O,C cùng thuộc một đường tròn. · 0
OK ^ A D Þ OIK = 90 · · · 0
Þ OBI = OKI = OCI = 90
Vậy 5 điểm I , B, K ,O,C cùng thuộc một đường tròn.
c) Chứng minh : M là trung điểm của DN .
Ta có DN / / BI (cùng vuông góc OB ) · ·
Þ A DN = KIB (đồng vị) · · ¼
Mà KCB = KIB (cùng chắn B K ) Trang 7 · ·
Þ KCM = KDM (cùng nhìn MK )
Þ Tứ giác KCDM nội tiếp · · ·
Þ KMC = KDC = A BC (đồng vị)
Þ KM / / A B Þ KM / / A N
Mà K là trung điểm A D
Þ M là trung điểm DN ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 8
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đề thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 8 - 2
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 1. (1,5 điểm). Cho P 2 : y
x và đường thẳng d 1 : y x 2 . 4 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
x x 12 0 có 2 nghiệm là x ,x . 1 2 x 1 x 1
Không giải phương trình, hãy tính giá trị của biểu thức 1 2 A . x x 2 1
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 3. (0,75 điểm). Mối quan hệ giữa lợi nhuận và số sản phẩm bán được trong một tháng tại một
cửa hàng tính theo công thức T 20n 500 . Trong đó T là số tiền lợi nhuận tính theo ngàn
đồng, n là số sản phẩm bán được trong tháng.
a) Nếu trong tháng 9 cửa hàng bán được 5000 sản phẩm thì lợi nhuận thu về là bao nhiêu?
b) Mối quan hệ giữa số tiền lợi nhuận và số nhân viên làm việc là T 9000.k với k là số nhân viên * k
, T là lợi nhuận tính theo đơn vị ngàn đồng. Vậy nếu cửa hàng có 8
nhân viên thì một tháng bán được bao nhiêu sản phẩm?
Câu 4. (1 điểm). Nhằm động viên, khen thưởng các em đạt danh hiệu “học sinh giỏi cấp thành
phố” năm học 2021 2022 , trường THCS A tổ chức chuyến tham quan ngoại khóa tại một
điểm du lịch với mức giá ban đầu là 375 000 đồng/người. Biết công ty du lịch giảm 10%
chi phí cho mỗi giáo viên và giảm 30% chi phí cho mỗi học sinh. Số học sinh tham gia gấp
4 lần số giáo viên và tổng chi phí tham quan (sau khi giảm giá) là 12 487 500 đồng. Tính
số giáo viên và số học sinh đã tham gia chuyến đi?
Câu 5. (1 điểm). Bà Năm nuôi tất cả 10 con heo, mỗi con 70 kg. Đến ngày xuất chuồng bà bán
được 4 con với giá lúc ổn định là 58 000 đồng/1kg heo hơi (cân heo hơi là heo vẫn còn Trang 8
sống, cân tại chuồng). Tháng sau, gặp trận dịch bệnh bà Năm phải bán với giá giảm 40%
so với giá khi ổn định. Biết giá vốn bà đầu tư lúc ban đầu nuôi heo là 32 000 đồng/ 1kg heo hơi.
a) Sau khi bán hết 10 con heo thì sẽ bà Năm lời bao nhiêu tiền?
b) Một người buôn bán heo ở chợ đã mua 2 con heo của bà Năm với giá lúc ổn định. Người
đó muốn lời 60% so tổng số tiền vốn bỏ ra gồm số tiền mua heo và chi phí vận chuyển
heo là 2 triệu đồng, thì người đó cần bán lẻ mỗi kg heo bao nhiêu tiền ? (Làm tròn kết quả
đến chữ số hàng nghìn)
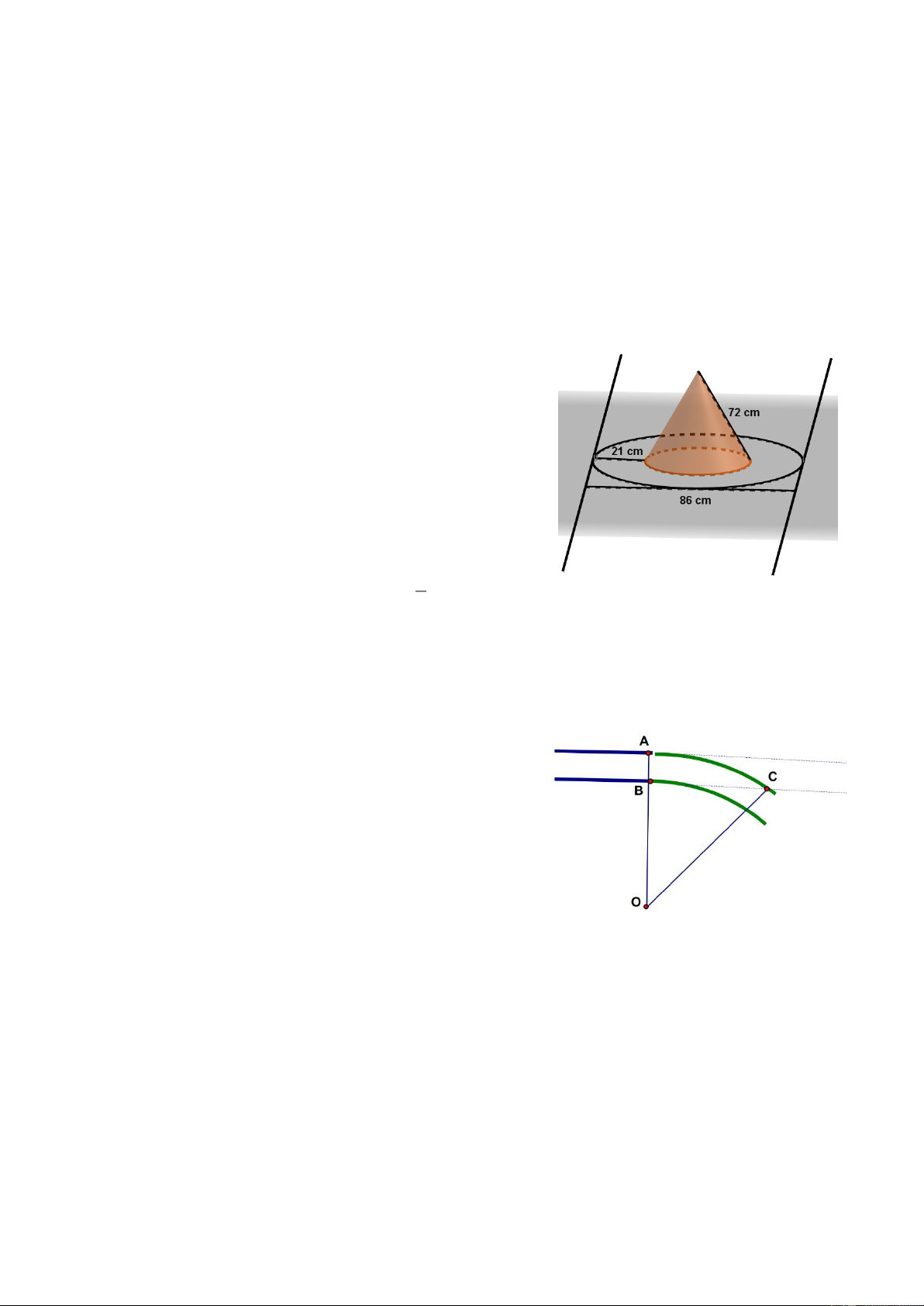
Câu 6. (1 điểm). Cái mũ có vành của chú hề với các kích thước cho theo hình vẽ
a) Hãy tính tổng diện tích vải cần có để làm nên cái
mũ của chú hề (không kể riềm, mép, phần thừa).
b) Chú hề dự định mua bột đổ đầy nón để làm ảo
thuật. Chú hề cần mua khối lượng bột là bao
nhiêu (làm tròn đến hàng đơn vị)? (biết rằng khối
lượng riêng của loại bột đó là 3
1gam / cm nghĩa là 3
1cm tương ứng với 1gam ). 1
Cho công thức tính thể tích hình nón: 2
V R .h 3
Công thức tính dện tích xung quanh hình nón là S . . R l
Trong đó h là chiều cao hình nón, R là bán kính đáy, l là đường sinh. Lấy 3,14
Câu 7. (0,75 điểm). Để giúp xe lửa chuyển từ một đường
ray từ hướng này sang một đường ray theo hướng
khác, người ta làm xen giữa một đoạn đường ray
hình vòng cung (hình vẽ minh họa bên). Biết chiều
rộng của đường ray là AB 1,1m , đoạn
BC 28,4m , BC vuông góc với AO . Hãy cho biết
số đo cung AC (làm tròn kết quả đến độ).
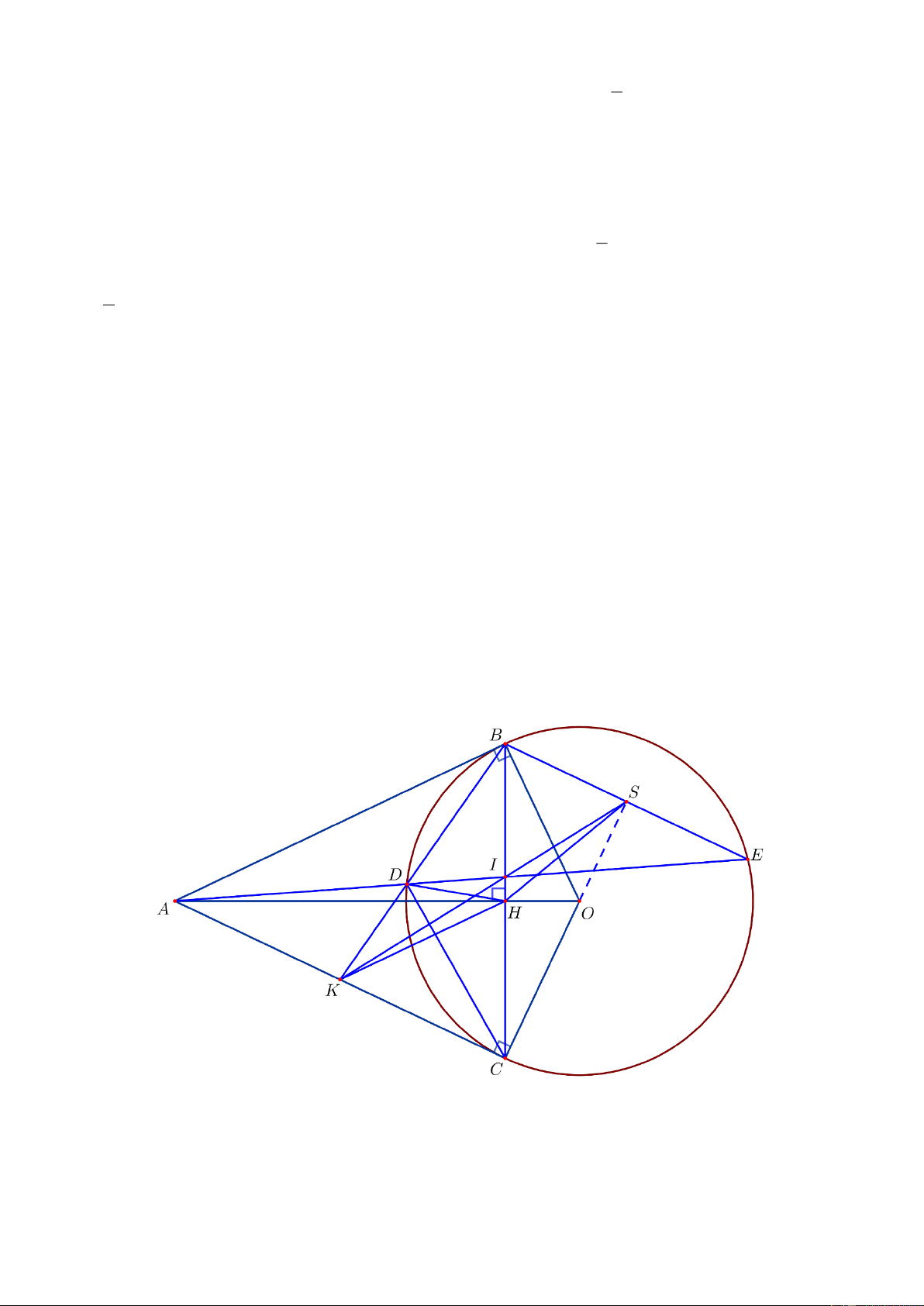
Câu 8. (3 điểm) Cho đường tròn O,R . Qua điểm A ở ngoài đường tròn, ta vẽ các tiếp tuyến AB
và AC tới đường tròn ( B và C là các tiếp điểm), AO cắt BC tại H . Vẽ cát tuyến AEF (
E, B cùng thuộc một nửa mặt phẳng bờ OA ). Gọi D là trung điểm của EF .
a) Chứng minh: tứ giác ODBC nội tiếp.
b) Vẽ đường kính BK của O . Gọi M là hình chiếu của C trên BK , AK cắt CM tại I .
Chứng minh I là trung điểm của CM .
c) Tia CM cắt O tại điểm thứ hai N , AN cắt O tại điểm thứ hai J , CJ cắt AB tại Z .
Chứng minh ZH vuông góc với OC . ----HẾT--- Trang 9 HƯỚNG DẪN GIẢI 1
Câu 1. (1,5 điểm). Cho P 2 : y
x và đường thẳng d 1 : y x 2 . 4 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: x 4 2 0 2 4 1 2 y x 4 1 0 1 4 4 x 0 2 1 y x 2 2 3 2
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 1 1 2 x x 2 4 2 1 1 2
x x 2 0 4 2 x 4 x 2 1 1
Thay x 4 vào y
x 2 , ta được: y .4 2 4 . 2 2 1 1 Thay x 2
vào y x 2, ta được: y .2 2 1. 2 2 Vậy 4;4 , 2 ;
1 là hai giao điểm cần tìm.
Câu 2. (1 điểm). Cho phương trình 2
x x 12 0 có 2 nghiệm là x , x . 1 2 x 1 x 1
Không giải phương trình, hãy tính giá trị của biểu thức 1 2 A x x 2 1 Trang 10 Lời giải 2 Vì 2
b 4ac 1 4.1. 1 2 49 0
Nên phương trình có hai nghiệm phân biệt x , x . 1 2 b
S x x 1 1 2 a
Theo định lí Vi-et, ta có: c
P x .x 12 1 2 a Ta có: x 1 x 1 1 2 A x x 2 1
x 1 .x x 1 .x 1 1 2 2 A x . x 1 2 2 2
x x x x 1 1 2 2 A x . x 1 2 2 2 x x x x 1 2 1 2 A x . x 1 2 2
S 2P S A P 2 1 2. 1 2 1 13 A 12 6
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 3. (0,75 điểm) Mối quan hệ giữa lợi nhuận và số sản phẩm bán được trong một tháng tại
một cửa hàng tính theo công thức T 20n 500 . Trong đó T là số tiền lợi nhuận tính
theo ngàn đồng, n là số sản phẩm bán được trong tháng.
a) Nếu trong tháng 9 cửa hàng bán được 5000 sản phẩm thì lợi nhuận thu về là bao nhiêu?
b) Mối quan hệ giữa số tiền lợi nhuận và số nhân viên làm việc là T 9000.k với k là số nhân viên * k
, T là lợi nhuận tính theo đơn vị ngàn đồng. Vậy nếu cửa hàng
có 8 nhân viên thì một tháng bán được bao nhiêu sản phẩm? Lời giải a) Ta có n 5000
T 20.5000 500 99 500 (ngàn đồng) Trang 11
Vậy trong tháng 9 , lợi nhuận của cửa hàng là 99 500 (ngàn đồng). b) Ta có k 8
T 9000.8 72 000
Mà T 20n 500
72 000 20n 500 n 3625
Vậy nếu cửa hàng có 8 nhân viên, mỗi tháng sẽ bán được 3625 sản phẩm.
Câu 4. (1 điểm). Nhằm động viên, khen thưởng các em đạt danh hiệu “học sinh giỏi cấp thành
phố” năm học 2021 2022 , trường THCS A tổ chức chuyến tham quan ngoại khóa tại
một điểm du lịch với mức giá ban đầu là 375 000 đồng/người. Biết công ty du lịch giảm
10% chi phí cho mỗi giáo viên và giảm 30% chi phí cho mỗi học sinh. Số học sinh tham
gia gấp 4 lần số giáo viên và tổng chi phí tham quan (sau khi giảm giá) là 12 487 500
đồng. Tính số giáo viên và số học sinh đã tham gia chuyến đi? Lời giải Gọi ;
x y (người) lần lượt là số học sinh và số giáo viên tham gia chuyến đí * x; y x 4y Theo đề, ta có: 1 30%
.375000.x 110%.375000.y 12487500 x 36 (nhận) y 9
Vậy: Số học sinh tham gia chuyến đi là 36 (học sinh)
Số giáo viên tham gia chuyến đi là 9 (giáo viên).
Câu 5. (1 điểm) Bà Năm nuôi tất cả 10 con heo, mỗi con 70kg. Đến ngày xuất chuồng bà bán
được 4 con với giá lúc ổn định là 58 000 đồng/1kg heo hơi (cân heo hơi là heo vẫn còn
sống, cân tại chuồng). Tháng sau, gặp trận dịch bệnh bà Năm phải bán với giá giảm 40%
so với giá khi ổn định. Biết giá vốn bà đầu tư lúc ban đầu nuôi heo là 32 000 đồng/1kg heo hơi.
a) Sau khi bán hết 10 con heo thì sẽ bà Năm lời bao nhiêu tiền?
b) Một người buôn bán heo ở chợ đã mua 2 con heo của bà Năm với giá lúc ổn định.
Người đó muốn lời 60% so tổng số tiền vốn bỏ ra gồm số tiền mua heo và chi phí
vận chuyển heo là 2 triệu đồng, thì người đó cần bán lẻ mỗi kg heo bao nhiêu tiền ?
(Làm tròn kết quả đến chữ số hàng nghìn) Trang 12 Lời giải
a) Số tiền bà Năm thu được sau khi bán 10 con heo là:
4.70.58000 6.70.(1 40%).58000 30856000 (đồng)
Số tiền đầu tư lúc đầu là:
10.70.32000 22400000 (đồng) Số tiền lời là:
30856000 22400000 8456000 (đồng)
b) Số tiền mua hai con heo và chi phí vận chuyển là:
2.70.58000 2000000 10120000 (đồng)
Số tiền bán mỗi kg heo là:
10120000.1 60% : 2.70 116000 (đồng)
Câu 6. (1 điểm) Cái mũ có vành của chú hề với các kích thước cho theo hình vẽ
a) Hãy tính tổng diện tích vải cần có để làm nên cái mũ của chú hề (không kể riềm, mép, phần thừa).
b) Chú hề dự định mua bột đổ đầy nón để làm ảo thuật. Chú hề cần mua khối lượng bột là
bao nhiêu (làm tròn đến hàng đơn vị)? (biết rằng khối lượng riêng của loại bột đó là 3
1gam / cm nghĩa là 3
1cm tương ứng với 1gam ). 1
Cho công thức tính thể tích hình nón: 2
V R .h 3
Công thức tính dện tích xung quanh hình nón là S . . R l
Trong đó h là chiều cao hình nón, R là bán kính đáy, l là đường sinh. Lấy 3,14 Lời giải 86 21.2
a) Bán kính hình nón: r 22cm 2
Diện tích xung quanh: S rl 2 3,14.22.72 4973, 76 cm xq 2 86 Diện tích vành nón: 2 S .
.22 4286,1 cm vn 2 2
Diện tích cần tìm: S S S 2 4973, 76 4286,1 9259,86 cm xq vn b) Chiều cao hình nón: 2 2 h
72 22 10 47 cm Trang 13 1 1 Thể tích hình nón: 2 2
V . R h .3,14.22 .10 47 34729,8 3 cm 3 3
Vậy số bột cần để đổ đầy nón là: 34730 g
Câu 7. (0,75 điểm) Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray
theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (hình vẽ
minh họa bên). Biết chiều rộng của đường ray là AB 1,1m , đoạn BC 28, 4m , BC
vuông góc với AO. Hãy cho biết số đo cung AC (làm tròn kết quả đến độ). Lời giải
- Thanh ray trùng với BC tiếp xúc với đường tròn ,
O OB tại B nên là tiếp tuyến của đường tròn ,
O OB BC OB
- OA cắt đường tròn O,OA tại điểm D D A AD 2R
- Tam giác ACD nội tiếp đường tròn O,OA có đường kính AD nên là tam giác vuông tại C .
- Xét tam giác ACD vuông tại C , đường cao BC , ta có: 2 CB A .
B BD (hệ thức lượng trong tam giác vuông) 2 CB A .
B AD AB 2 CB A .
B 2R AB 2
- Thay số, ta có: 28, 4 1,1.2R 1,
1 2R 807, 77 R 367, 2m
Câu 8. (3 điểm) Cho đường tròn ,
O R . Qua điểm A ở ngoài đường tròn, ta vẽ các tiếp tuyến AB
và AC tới đường tròn ( B và C là các tiếp điểm), AO cắt BC tại H . Vẽ cát tuyến AEF (
E, B cùng thuộc một nửa mặt phẳng bờ OA). Gọi D là trung điểm của EF .
a) Chứng minh: tứ giác ODBC nội tiếp.
b) Vẽ đường kính BK của O . Gọi M là hình chiếu của C trên BK , AK cắt CM tại I .
Chứng minh I là trung điểm của CM .
c) Tia CM cắt O tại điểm thứ hai N , AN cắt O tại điểm thứ hai J , CJ cắt AB tại
Z . Chứng minh ZH vuông góc với OC . Lời giải Trang 14
a) Chứng minh tứ giác ODBC nội tiếp Xét O có: FE là dây cung
D là trung điểm của FE OD FE
Xét tứ giác ODBC có:
ODA OBA 90
Mà hai góc cùng nhìn cạnh OA
Tứ giác ODBC nội tiếp (Hai đỉnh liên tiếp cùng nhìn một cạnh dưới hai góc bằng nhau)
b) Chứng minh: I là trung điểm MC O
B OC R Ta có: AB AC , O A cách đều , B C
OA là đường trung trực của BC
OA BC tại H
Do M là hình chiếu của C trên BK
CM BK tại M
Xét tứ giác MOHC có:
OMC 90CM BK OHC 90
OA BCH
OMC OHC 90 90 180
Tứ giác MOHC nội tiếp (Tổng hai góc đối bằng 180) Trang 15
OMH OCH (chắn OH )
Mà OCH OBH ( O
CB cân tại O , OB OC R )
OMH OBH B
HM cân tại H BH HM
Mà BH HC ( OA là đường trung trực BC ) HM HC M
HC cân tại H
HMC HCM Xét H IM và H IC có: HI là cạnh chung
HM HC (cmt)
HMC HCM (cmt) H IM H
IC c g c IM IC
I là trung điểm MC .
c) Chứng minh: ZH vuông góc với OC Ta có:
AB BK ( AB là tiếp tuyến của O )
CN BK tại M (cmt) AB / /CN
CNA NAB (sole trong)
Mà CNA ZCA (chắn JC )
NAB ZCA Xét Z JA và Z AC có: CZA chung
NAB ZCA (cmt)
ZJA” ZAC g g ZJ ZA 2
ZA ZJ.ZC 1 ZA ZC Trang 16 Xét Z BJ và Z JC có BZJ chung
JBZ BCZ (chắn BJ )
ZBJ ” ZCBg g ZB ZJ 2
ZB ZJ.ZC 2 ZC ZB Từ 1 và 2 2 2
ZA ZB ZJ.ZC ZA ZB
Z là trung điểm AB Xét ABC có:
Z là trung điểm AB (cmt)
H là trung điểm BC (cmt)
ZH là đường trung bình ZH / / AC
Mà AC OC ( AC là tiếp tuyến của O ) ZH OC . ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 8
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 8 - 3
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 9. (1,5 điểm). Cho P 2 : y
x và đường thẳng D 1
: y x 1 . 2 2
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép tính.
Câu 10. (1 điểm). Cho phương trình 2
20x 5x 2020 0 có 2 nghiệm là x ,x . Không giải 1 2 x x
phương trình, hãy tính giá trị của biểu thức 1 A 1x 2 1 x . 2 1 x x 2 1 Trang 17
Câu 11. (1 điểm). Một ô tô có bình chứa xăng chứa được nhiều nhất là 40 lít xăng. Cứ chạy 100 km
thì ô tô tiêu thụ hết 8 lít xăng. Gọi xkm là quãng đường ô tô đi được và y (lít) là số lít xăng tiêu thụ.
a) Hãy lập công thức tính y theo x.
b) Khi ô tô chạy từ TPHCM đến Đà Lạt quãng đường dài 290km thì số lít xăng trong bình
còn lại bao nhiêu lít nếu lúc đầu bình đầy.
Câu 12. (1 điểm). Một nền nhà hình nhật có lích thước 4m và 12m .Người ta nhờ thợ xây dựng lát
hết nền nhà bằng loại gạch hình vuông cạnh 60cm . Khi lát gạch nền, do tính thẩm mĩ của
thợ xây phải dùng máy cắt bỏ một phần của những viên gạch lát cuối trong trường hợp
viên gạch đó bị hư và không sử dụng phần cắt bỏ của viên gạch đó. Cho rằng hao phí khi
lát gạch là 3% trên số tổng gạch lát nền và phải để dành 5 viên gạch để dự trữ sau này để
thay thế các viên gạch bị hỏng (nếu có). Hỏi người ta cần phải mua bao nhiêu viên gạch loại nói trên?
Câu 13. (1 điểm). Trong đợt dịch Covid-19, học sinh hai lớp 9A và 9B trường THCS X ủng hộ 217
chiếc khẩu trang cho những nơi cách ly tập trung. Biết rằng số học sinh lớp 9A nhiều hơn
số học sinh lớp 9B là 4 học sinh và mỗi học sinh lớp 9A ủng hộ 3 chiếc khẩu trang, mỗi
học sinh lớp 9B ủng hộ 2 chiếc khẩu trang. Tính số học sinh mỗi lớp.
Câu 14. (1 điểm). Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r 10cm , chiều cao gấp
hai lần bán kính (đơn vị: cm ). Người ta khoét rỗng hai nữa hình cầu có kích thước bằng
nhau như hình dưới (phần tiếp xúc có bề dày không đáng kể). Hãy tính diện tích bề mặt
của khối gỗ còn lại (diện tích cả trong lẫn ngoài). (Làm tròn kết quả đến chữ số hàng đơn vị)?
Biết diện tích xung quanh hình trụ là S 2 rh với r là bán kính đường tròn đáy, h là chiều cao. xq
Diện tích hình cầu có bán kính là r là 2 S 4 r .
Câu 15. (1 điểm). Lúc 8 giờ sáng, một xe máy đi từ tỉnh A đến tỉnh B cách nhau 270km với vận
tốc trung bình là 40km / h . Sau khi xe máy đi được 90 phút thì một ô tô xuất phát đi từ B
về A với vận tốc trung bình là 50km / h . Hỏi 2 xe gặp nhau trên quãng đường AB lúc mấy giờ?
Câu 16. (3 điểm). Từ điểm A nằm ngoài đường tròn O OA 2R . Vẽ hai tiếp tuyến AB và AC
và cát tuyến ADE của O . Gọi K trung điểm AC , OA cắt BC tại H . Trang 18
Sửa đề: Từ điểm A nằm ngoài đường tròn O OA 2R . Vẽ hai tiếp tuyến AB và AC của O .
Gọi K trung điểm AC , BK cắt O tại D , OA cắt BC tại H .
a) Chứng minh HK∥ AB và tứ giác CHDK nội tiếp.
b) Tia AD cắt O tại E . Chứng minh 2 KC .
KD KB và BE∥ AC .
c) Gọi I là giao điểm của BC và AE , tia KI cắt BE tại S . Chứng minh 2 . BD BK 2HS . ----HẾT--- HƯỚNG DẪN GIẢI 1 1
Câu 9. (1,5 điểm) Cho P : y 2
x và đường thẳng D : y x 1 . 2 2
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép tính. Lời giải
c) Vẽ đồ thị P và D trên cùng hệ trục tọa độ. BGT: x 4 2 0 2 4
P: y 1 2x 8 2 0 2 8 2 x 0 2
D y 1 : x 1 1 0 2
d) Tìm tọa độ giao điểm của P và D bằng phép tính.
Phương trình hoành độ giao điểm của P và D : 1 2
x 1 x 1 2 2 1 2
x 1 x 1 0 2 2 x 1 x 2 1 1 1
Thay x 1 vào y 2
x , ta được: y 2 .1 . 2 2 2 1 1 2
Thay x 2 vào y 2
x , ta được: y .2 2 . 2 2 Trang 19 1
Vậy 1; , 2; 2 là hai giao điểm cần tìm. 2 Câu 10.
(1 điểm) Cho phương trình 2
20x 5x 2020 0 có 2 nghiệm là x ,x . Không giải 1 2 x x
phương trình, hãy tính giá trị của biểu thức A 1 1 x 2 1 x . 2 1 x x 2 1 Lời giải Vì 2 b ac 2 4
5 4.20.2020 161625 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b S x x 1 1 2
Theo định lí Vi-et, ta có: a 4 c P x .x 101 1 2 a x x
Ta có: A 1 1 x 2 1 x 2 1 x x 2 1 A x x
1 2 x x 1 2 x x 2 1 2 x 2 A x 1 2 x x 1 2 x x 1 2 x x 2x x 1 2 2 A
1 2 x x 1 2 x x 1 2 1 2 2. 101 4 1 A 2829 . 101 4 1616 Câu 11.
(1 điểm) Một ô tô có bình chứa xăng chứa được nhiều nhất là 40 lít xăng. Cứ chạy 100km
thì ô tô tiêu thụ hết 8 lít xăng. Gọi (
x km) là quãng đường ô tô đi được và y (lít) là số lít xăng tiêu thu.
a) Hãy lập công thức tính y theo x.
b) Khi ô tô chạy từ TPHCM đến Đà Lạt quãng đường dài 290km thì số lít xăng trong bình
còn lại bao nhiêu lít nếu lúc đầu bình đầy. Lời giải
a) Hãy lập công thức tính y theo x. Theo đề bài, ta có: x 0 Với
0 0.a . 1 y b 0 Trang 20 x 100 Với
8 100.a . 2 y b 8 a b a 2 0 0
Từ 1 và 2 ta có hệ phương trình: . 100a b 25 8 b 0
Vậy: a 2 , b 0 và y 2 x . 25 25
b) Khi ô tô chạy từ TPHCM đến Đà Lạt quãng đường dài 290km thì số lít xăng trong bình
còn lại bao nhiêu lít nếu lúc đầu bình đầy. 2
Số lít xăng trong bình còn lại là: 40 .290 16,8 (lít). 25 Câu 12.
(1 điểm) Một nền nhà hình nhật có lích thước 4m và 12m . Người ta nhờ thợ xây dựng
lát hết nền nhà bằng loại gạch hình vuông cạnh 60cm . Khi lát gạch nền, do tính thẩm mĩ của
thợ xây phải dùng máy cắt bỏ một phần của những viên gạch lát cuối trong trường hợp viên
gạch đó bị hư và không sử dụng phần cắt bỏ của viên gạch đó. Cho rằng hao phí khi lát gạch
là 3% trên số tổng gạch lát nền và phải để dành 5 viên gạch để dự trữ sau này để thay thế
các viên gạch bị hỏng (nếu có). Hỏi người ta cần phải mua bao nhiêu viên gạch loại nói trên? Lời giải Diện tích nền nhà là: 2 4.12 48m .
Diện tích viên gạch là: 2 2 cm 2 60 3600 0,36m .
Số viên gạch lát nền nhà chưa tính hao phí là: 48 : 0,36 134 (viên).
Số viên gạch lát nền nhà đã tính hao phí là: 134.1 3% 139 (viên).
Số viên gạch cần mua là: 139 5 144 (viên). Câu 13.
(1 điểm) Trong đợt dịch Covid-19, học sinh hai lớp 9A và 9B trường THCS X ủng hộ 217
chiếc khẩu trang cho những nơi cách ly tập trung. Biết rằng số học sinh lớp 9A nhiều hơn số
học sinh lớp 9B là 4 học sinh và mỗi học sinh lớp 9A ủng hộ 3 chiếc khẩu trang, mỗi học
sinh lớp 9B ủng hộ 2 chiếc khẩu trang. Tính số học sinh mỗi lớp. Lời giải
Gọi x và y lần lượt là số học sinh lớp 9A và 9B ( x y * , )
Số học sinh lớp 9A nhiều hơn số học sinh lớp 9B là 4 học sinh nên ta có phương trình:
x y 4. 1 Trang 21
Tổng số khẩu trang ủng hộ của hai lớp 9A và 9B là 217 chiếc khẩu trang nên ta có phương trình:
3x 2y 217. 2 x y 4 x 45
Từ 1 và 2 ta có hệ phương trình: n
3x 2y 217 y . ( ) 41
Vậy số học sinh lớp 9A và 9B lần lượt là 45 và 41 học sinh. Câu 14.
(1 điểm) Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r 10cm , chiều cao gấp
hai lần bán kính (đơn vị: cm ). Người ta khoét rỗng hai nữa hình cầu có kích thước bằng nhau
như hình dưới (phần tiếp xúc có bề dày không đáng kể). Hãy tính diện tích bề mặt của khối
gỗ còn lại (diện tích cả trong lẫn ngoài). (Làm tròn kết quả đến chữ số hàng đơn vị)?
Biết diện tích xung quanh hình trụ là S
2 rh với r là bán kính đường tròn đáy, h là chiều cao. xq
Diện tích hình cầu có bán kính là r là S 2 4 r . Lời giải
Diện tích xung quanh khối gỗ: S rh 2 2 2 .10. 2.10 400 cm . xq
Diện tích hình cầu là: S 2 r 2 2 4 4 .10 400 cm .
Vậy diện tích bề mặt khối gỗ còn lại là: S 2 400 400 800 2513 cm . Câu 15.
(1 điểm) Lúc 8 giờ sáng, một xe máy đi từ tỉnh A đến tỉnh B cách nhau 270km với vận
tốc trung bình là 40km / h . Sau khi xe máy đi được 90 phút thì một ô tô xuất phát đi từ B về
A với vận tốc trung bình là 50km / h . Hỏi 2 xe gặp nhau trên quãng đường AB lúc mấy giờ? Lời giải
Gọi C là vị trí xe máy sau khi đi được 90 phút; D là vị trí hai xe gặp nhau.
Gọi x là thời gian đi được của hai xe (tính từ lúc xe máy đã đi được 90 phút) đến lúc hai xe gặp nhau. ( x 0, ) h . Trang 22 3
Quãng đường xe máy đi từ vị trí A đến C sau 90 phút là: S 40. km A 60 . C 2
Quãng đường xe máy đi từ vị trí C đến D là: S 40.x km . C D
Quãng đường ô tô đi từ vị trí B đến D là: S 50.xkm. B D
Khi hai xe gặp nhau ta có phương trình: x x x 7 40 50 270 60 n. 3 7 Đổi giờ 2 giờ 20 phút. 3
Vậy hai xe gặp nhau lúc 11giờ 50 phút.
Câu 8. (3 điểm) Từ điểm A nằm ngoài đường tròn O OA 2R . Vẽ hai tiếp tuyến AB và AC và
cát tuyến ADE của O . Gọi K trung điểm AC , OA cắt BC tại H .
Sửa đề: Từ điểm A nằm ngoài đường tròn O OA 2R . Vẽ hai tiếp tuyến AB và AC của O .
Gọi K trung điểm AC , BK cắt O tại D , OA cắt BC tại H .
a. Chứng minh HK∥ AB và tứ giác CHDK nội tiếp.
b. Tia AD cắt O tại E . Chứng minh 2 KC .
KD KB và BE∥ AC .
c. Gọi I là giao điểm của BC và AE , tia KI cắt BE tại S . Chứng minh BD BK 2 . 2HS Lời giải
d) Chứng minh HK//AB và tứ giác CHDK nội tiếp.
Ta có: OB OC (bán kính); AB AC (Tính chất hai tiếp tuyến cắt nhau)
OA là đường trung trực của BC
H là trung điểm của BC . Trang 23
Xét tam giác ABC có HK là đường trung bình HK//AB.
Ta có: HKD ABD ( hai góc so le trong)
BCD ABD (gnt và góc tạo bởi tia tt và dây cung cùng chắn BD )
HKD BCD
HKD HCD
Xét tứ giác CHDK , có:
HKD HCD (cmt)
Tứ giác CHDK nội tiếp vì có hai đỉnh kề cùng nhìn một cạnh dưới hai góc bằng nhau.
e) Tia AD cắt O tại E . Chứng minh 2 KC .
KD KB và BE//AC .
Ta có: KCD DBC (gnt và góc tạo bởi tia tt và dây cung cùng chắn DC )
KCD KBC
Xét KCD và KBC có: K chung KCD KBC (cmt)
KCD∽KBC (g – g)
KC KD (tỉ lệ cạnh tương ứng) KB KC 2 KC . KD KB
Ta có: K trung điểm AC nên 2 KB 2 KC . KD KB
Dễ dàng chứng minh được KAD∽KBA (c – g- c)
Suy ra: KAD KBA (hai góc tương ứng)
Suy ra: KAD DBA
Mà BED DBA (gnt và góc tạo bởi tia tt và dây cung cùng chắn BD )
Suy ra: BED KAD
Suy ra: BE∥ AC (hai góc so le trong).
f) Gọi I là giao điểm của BC và AE , tia KI cắt BE tại S . Chứng minh BD BK 2 . 2HS IS SB
Dễ dàng Cm: ISB∽IKC (g – g) 1 IK KC IS SE
Dễ dàng Cm: ISE∽IKA (g – g) 2 IK KA Trang 24 SB SE Suy ra: KC KA
Suy ra: S trung điểm BE .
Suy ra: OS EB (liên hệ đường kính và dây cung)
Suy ra: C,S,O thẳng hàng (do OC AC; EB∥ AC ).
Suy ra: CSB vuông tại S có SH là đường trung tuyến
Suy ra: HS HB HC (đường trung tuyến ứng với cạnh huyền) BH BD
Dễ dàng cm: BHD∽BKC (g – g)
BH.BC BK.BD BK BC
Suy ra: HS HS BK BD 2 .2 . 2HS B . K B . D ----HẾT--- Trang 25




