




















Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN TAÂN
NAÊM HOÏC: 2023 - 2024 PHUÙ MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
Thời gian: 120 phút (không kể thời gian phát đề) MÃ ĐỀ: Quận 11-1
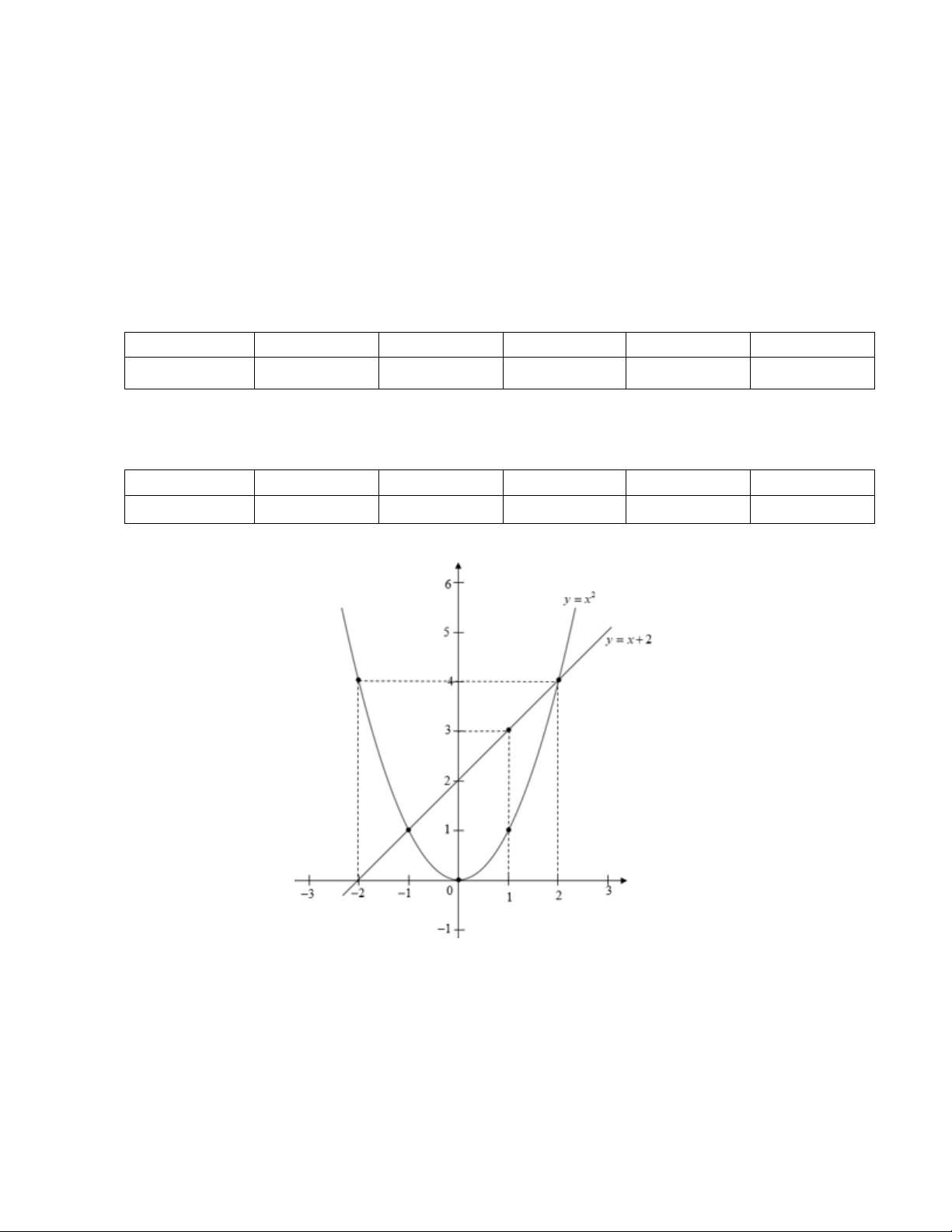
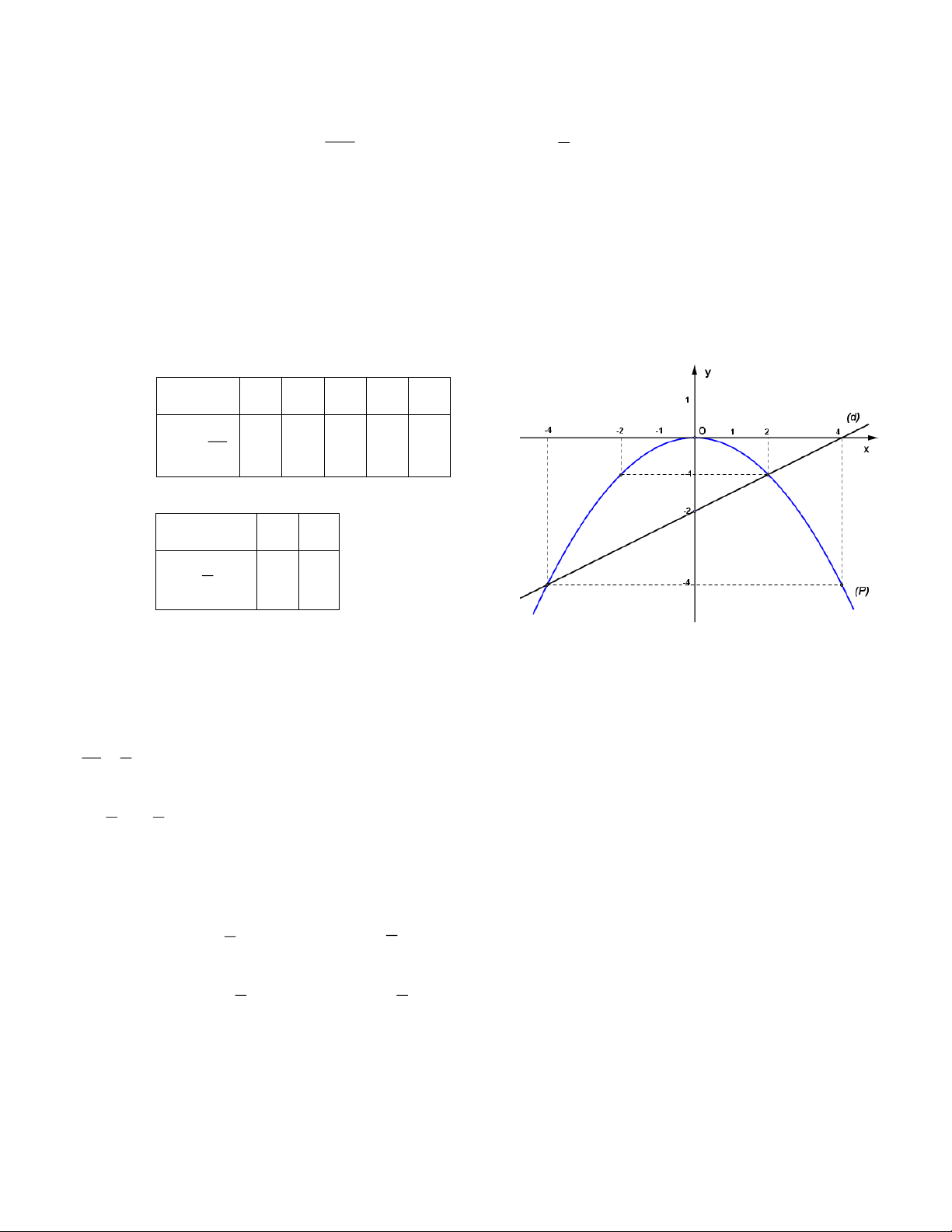
Câu 1. Trong mặt phắng tọa độ Oxy cho Parabol P 2
: y x và đường thẳng d : y x 2 .
a) Vẽ P và d trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. Cho phương trình: 2
2x x 3 0 có 2 nghiệm là x ,x . Không giải phương trình, hãy tính giá 1 2 trị của biểu thức 2 2 2 2
A x x x x 2024 . 1 2 1 2
Câu 3. Hợp tác xã A chuyên trồng hoa màu để bán. Nhưng năm nay chịu đợt sâu hại nên số lượng
hoa màu dự định bán ra đã hư 30% và phần còn lại cũng ảnh hưởng nên chỉ bán được với giá 3 bán bằng
giá bán dự định lúc đầu. Nếu bán hết phần còn lại này với giá như trên thì số tiền 4
sẽ ít hơn 152 triệu đồng so với dự tính lúc đầu. Hỏi nếu không bị hư hại và không giảm giá thì
theo dự tính, hợp tác xã này sẽ thu về bao nhiêu tiền từ hoa màu?
Câu 4. Một vé xem phim có mức giá là 60000 đồng. Trong dịp khuyến mãi cuối năm 2019, số lượng
người xem phim tăng thêm 45% nên tổng doanh thu cũng tăng 8,75% . Hỏi rạp phim đã giảm
giá mỗi vé bao nhiêu phần trăm so với giá ban đầu?
Câu 5. Có 2 đội công nhân cùng làm 1 công trình. Lần thứ nhất: đội 1 làm trong 6 ngày, đội 2 làm
trong 4 ngày thì xong công trình. Lần thứ hai: đội 1 làm trong 4 ngày, đội 2 làm trong 8 ngày
thì xong công trình. Hỏi nếu làm một mình thì mỗi đội công nhân làm trong bao lâu hoàn thành công trình? Trang 1
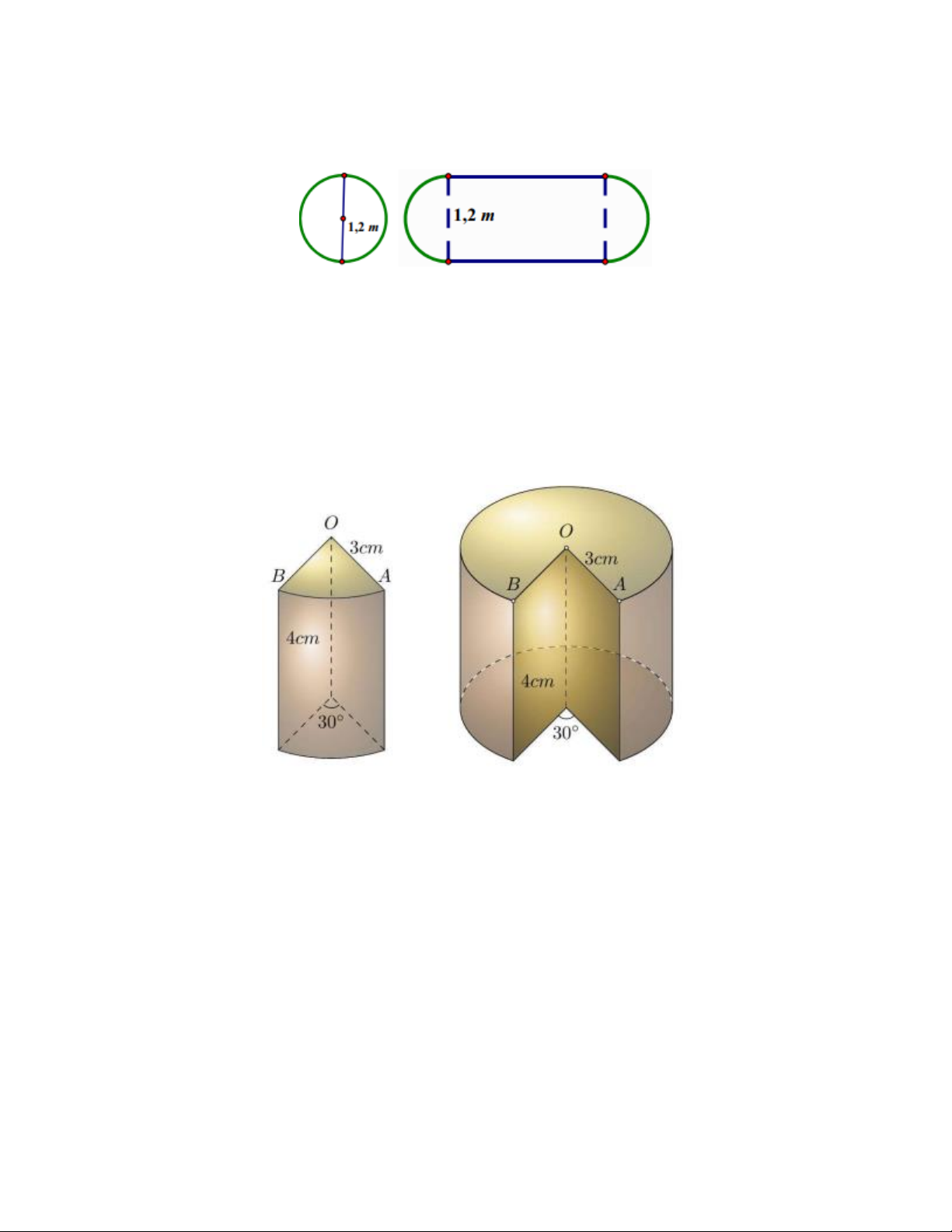
Câu 6. Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính 1,2 m . Người ta muốn
nới rộng mặt bàn bằng cách ghép thêm vào giữa một mặt hình chữ nhật có 1 kích thước là
1,2 m như hình vẽ dưới.
a) Kích thước kia của hình chữ nhật phải là bao nhiêu để diện tích mặt bàn tăng gấp ba sau khi nới?
b) Kích thước kia của hình chữ nhật phải là bao nhiêu để chu vi mặt bàn tăng gấp đôi sau khi nới?
Câu 7. Một khối gỗ hình trụ có bán kính đáy là 3 cm , chiều cao 4 cm được đặt đứng trên mặt bàn. Một
phần của khối gỗ bị cắt rời theo các bán kính OA,OB và theo chiều dài thẳng đứng từ trên
xuống dưới với AOB 30 như hình vẽ bên dưới:
a) Tính thể tích của khối gỗ còn lại sau khi bị cắt rời.
b) Diện tích toàn phần của khối gỗ còn lại sau khi đã bị cắt. Câu 8. Cho A
BC nội tiếp trong đường tròn O;R . Ba đường cao AD,BE,CF cắt nhau tại H .
a) Chứng minh các tứ giác AEHF,BCEF nội tiếp.
b) Kẻ đường kính AK của O . Chứng minh A . B AC 2 . R AD .
c) Gọi M là trung điểm của BC,I là giao điểm EF và BC . Chứng minh tứ giác EFDM nội tiếp và I . B IC I . D IM . ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI
Câu 1. Trong mặt phắng tọa độ Oxy cho Parabol P 2
: y x và đường thẳng d : y x 2 .
a) Vẽ P và d trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải a) P 2 : y x x 2 1 0 1 2 2 y x 4 1 0 1 4
d : y x 2 x 2 1 0 1 2
y x 2 0 1 2 3 4
b) Tọa độ giao điểm P và d . Phương trình hoành độ giao điểm P và d 2 x x 2 2
x x 2 0
x 2x 1 0 Trang 3 x 2 0 x 1 0
Thế x 2 vào P 2 y x 2 y 2 4
Vậy tọa độ giao điểm P và d là 2; 4
Câu 2. Cho phương trình: 2
2x x 3 0 có 2 nghiệm là x , x . 1 2
Không giải phương trình, hãy tính giá trị của biểu thức 2 2 2 2
A x x x x 2024 . 1 2 1 2 Lời giải 2
2x x 3 0
a 2;b 1 ;c 3 2
b 4ac 2 1 4.2 3 1 24 25 0
Vì 0 nên phương trình có 2 nghiệm phân biệt
Áp dụng định lý Vi-et ta có: b 1 x x 1 2 a 2 c 3 x x 1 2 a 2 Ta có: 2 2 2 2
A x x x x 2024 2 1 1
A x x 2 2x x x x 2 2014 1 2 1 2 1 2 2 2 1 3 3 A 2 . . 2024 2 2 2 1 9 A 3 2024 4 4 A 2023 Trang 4
Vậy giá trị của biểu thức A là 2023
Câu 3. Hợp tác xã A chuyên trồng hoa màu để bán. Nhưng năm nay chịu đợt sâu hại nên số lượng hoa
màu dự định bán ra đã hư 30% và phần còn lại cũng ảnh hưởng nên chỉ bán được với giá bán bằng
3 giá bán dự định lúc đầu. Nếu bán hết phần còn lại này với giá như trên thì số tiền sẽ ít hơn 152 4
triệu đồng so với dự tính lúc đầu. Hỏi nếu không bị hư hại và không giảm giá thì theo dự tính, hợp
tác xã này sẽ thu về bao nhiêu tiền từ hoa màu? Lời giải
Gọi x là số hoa dự định bán và y là giá tình dự định bán ( * x , y 0 )
Số tiền theo dự tính xã A nhận được khi bán hết hoa là: xy (đ)
Số lượng hoa còn lại sau khi hư 30% : x(100% 30%) 0.7x (hoa) 3
Giá bán của hoa lúc sau: y 4
Nếu bán hết phần còn lại với giá như trên thì ít hơn 152 triệu đồng so với dự tính lúc đầu: 3 0, 7 . x
y xy 152 (triệu) 4 21
xy xy 152 (triệu) 40 19
xy 152 (triệu) 40
xy 320 (triệu)
Vậy nếu không bị hư hại và không giảm giá trị thì theo dự tính sẽ thu về 320 triệu đồng.
Câu 4. Một vé xem phim có mức giá là 60000 đồng. Trong dịp khuyến mãi cuối năm 2019, số lượng
người xem phim tăng thêm 45% nên tổng doanh thu cũng tăng 8,75% . Hỏi rạp phim đã giảm giá
mỗi vé bao nhiêu phần trăm so với giá ban đầu? Trang 5 Lời giải
Gọi x là số lượng người xem trước khi khuyến mãi (người, * x )
Doanh thu lúc đó : 60000x (đ)
Vì khi có đợt khuyễn mãi số lượng người xem tăng thếm 45%
x(100% 45%) 1, 45x
Doanh thu đợt khuyến mã:
60000x(100% 8, 75%) 65250x (đ)
Giá vé lúc sau: 65250x :1, 45x 45000 (đ)
Gọi y là % giảm giá cho mỗi vé xem phim (%, y 0 )
Theo đề bài ta có: 60000100% y% 45000
100% y% 0, 75 y% 0, 25 y 0, 25%
Vậy phần trăm giảm giá cho mỗi vé là 25%
Câu 5. Có 2 đội công nhân cùng làm 1 công trình. Lần thứ nhất: đội 1 làm trong 6 ngày, đội 2 làm trong
4 ngày thì xong công trình. Lần thứ hai: đội 1 làm trong 4 ngày, đội 2 làm trong 8 ngày thì xong
công trình. Hỏi nếu làm một mình thì mỗi đội công nhân làm trong bao lâu hoàn thành công trình? Lời giải
Gọi x là thời gian đội 1 làm một mình xong công việc ( x 0)
Gọi y là thời gian đội 2 làm một mình xong công việc ( y 0 )
Vì lần thứ nhất đội 1 làm 6 ngày , đội 2 làm 4 ngày thì xong công việc nên: 6 4 1 (1) x y
Vì lần thứ nhất đội 2 làm 4 ngày , đội 2 làm 8 ngày thì xong công việc nên: Trang 6 4 8 1 (2) x y 6 4 1 x y Từ (1), (2) 4 8 1 x y 1 1
Đặt a ; b x y
6a 4b 1
4a 8b 1 1 4b a 6 41 4b 8b 1 6 1 4b a 6 4 16b 48b 6 6 6 6 1 4b a 6
4 16b 48b 6 1 4b 3 6 3 2b 2 1 4b 1 a a 6 8 1 1 b b 16 16 1 1 1 1 a x 8 x 8 x 8 1 1 1 1 y 16 b y 16 y 16
Vậy nếu hai đội làm một mình thì đội 1 hết 8 ngày, đội 2 hết 16 ngày là xong công việc. Trang 7
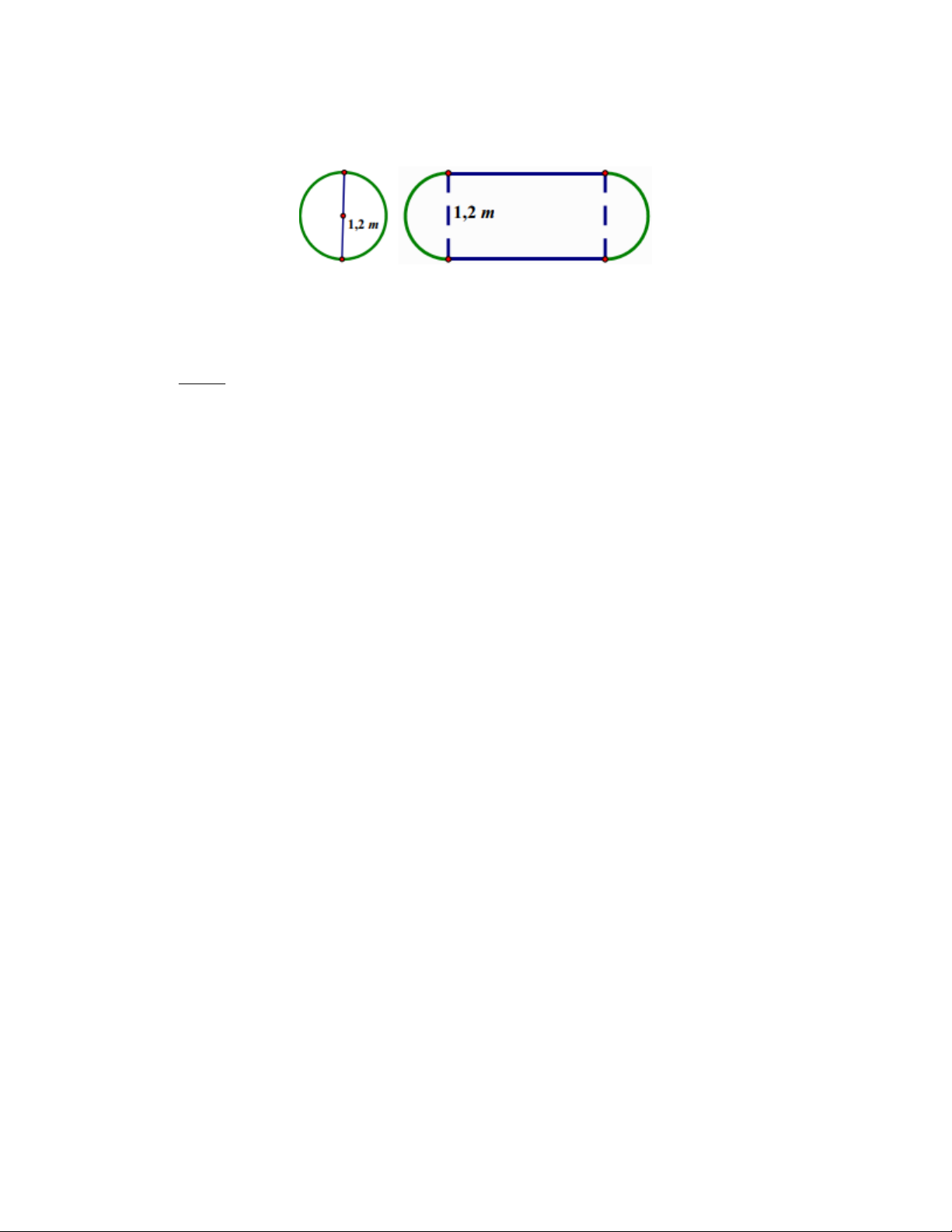
Câu 6. Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính 1, 2 m . Người ta muốn nới
rộng mặt bàn bằng cách ghép thêm vào giữa một mặt hình chữ nhật có 1 kích thước là 1, 2 m như hình vẽ dưới. Lời giải
a) Diện tích hình tròn lúc đầu 1,22 S .3,14 1,1304 2 m 2
Diện tích lúc sau gấp 3 lần: 2 1,1304.3 3,3912 m
Vậy để diện tích của bàn tăng gấp 3 lần sau khi nới thì kích thước của hình chữ nhật 1,884m
b) Chu vi hình tròn ban đầu
3,14.1, 2 3, 768m
Chu vi lúc sau tăng gấp 2 lần:
3, 768.2 7,536m
Kích thước hình chữ nhật:
(7,536 3, 768) : 2 1,884m
Vậy để chu vi mặt bàn tăng gấp đôi sau khi nới thì kích thước của hình chữ nhật là 1,884m
Câu 7. Một khối gỗ hình trụ có bán kính đáy là 3 cm , chiều cao 4 cm được đặt đứng trên mặt bàn. Một
phần của khối gỗ bị cắt rời theo các bán kính O ,
A OB và theo chiều dài thẳng đứng từ trên xuống
dưới với AOB 30 như hình vẽ bên dưới: Trang 8
a) Tính thể tích của khối gỗ còn lại sau khi bị cắt rời.
b) Diện tích toàn phần của khối gỗ còn lại sau khi đã bị cắt. Lời giải
a) Thể tích phần bị cắt là 2 .3 3 . 0 V S h 4 3 3 cm 1 quat 360
Thể tích phần còn lại là: 2
V V V .3 .4 3 33 3 cm 2 1
b) Diện tích phần còn lại của hai đầu: .9.30 33 2 .9 2 cm 360 2 Diện tích xung quanh: .3 R 0 2 Rh
h 2Rh 22 24 2 cm 180
Diện tích toàn phần là: 33 1
22 24 38 24 2 cm 2 2 Câu 8. Cho ABC
nội tiếp trong đường tròn ;
O R . Ba đường cao AD, BE,CF cắt nhau tại H .
a) Chứng minh các tứ giác AEHF, BCEF nội tiếp.
b) Kẻ đường kính AK của O . Chứng minh A . B AC 2 . R AD . Trang 9
c) Gọi M là trung điểm của BC, I là giao điểm EF và BC . Chứng minh tứ giác EFDM nội tiếp và I . B IC I . D IM . Lời giải
AFH 90(CF laø ñöôøng ca ) o
a) Xét tam tứ giác AEHF ta có
AEH 90 (BE laø ñöôøng ca ) o
mà AFH AEH 180
Tứ giác AEHF nội tiếp (2 góc đối bù nhau)
Xét tứ giác BCEF ta có BFC BEC 90
Tứ giác BCEF nội tiếp (tứ giác có 2 đỉnh liên tiếp cùng nhìn cạnh dưới hai góc bằng nhau)
b) Vì ACK là góc nội tiếp chắn nửa cung chắn nửa đường tròn O , đường kính AB ACK 90 Xét A DB và A CK 1 ABD AKC AC 2 Ta có:
ADB ACK 90 A DB ∽ A KC (g.g) AB AD (tsđd) AK AC A .
B AC AK.AD Trang 10
Mà AK 2R ( AK là đường kính) A . B AC 2 . R AD
c) Xét tứ giác BFEC ta có:
BFC CEB 90
Mà hai góc cùng nhìn cạnh BC
Tứ giác BFEC nội tiếp (tứ giác có 2 đỉnh liên tiếp cùng nhìn cạnh dưới hai góc bằng nhau)
EFC CEB (1) BFH 90
Xét tứ giác BFED ta có BDH 90
Mà BFH BDH 180
tứ giác BFED nội tiếp (2 góc đối bù nhau)
DFC EBC (2)
Từ (1), (2) EFC DFC
FC là tia phân giác góc DFE
DFC 2.EFC
Mà EMC 2.EFC
DFE EMC Xét tứ giác EFDM
Ta có DFE EMC nội tiếp (tứ giác có góc ngoài bằng góc đối trong) EIM chung Xét I FD và I ME ta có:
IDF IEM (chöùng minh treâ) n I FD∽ I ME (g.g) ID IF (tsđd) IE IM I . D IM I . E IF (3)
BFE CFE 180 BCEF noäi tieáp Ta có:
BFE IFB 0 18 Ke à buø Trang 11
BCE IFB Xét I BF và I EC có FIB: chung
IFB ICE I BF ∽ I EC (g.g) IF IB (tsđd) IC IE I .
C IB IF.IE (4)
Từ (3) và (4) I . C IB I . D IM ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN QUẬN 11
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 11 - 2
Thời gian: 120 phút (không kể thời gian phát đề) x x
Câu 1. (1,5 điểm). Cho P 2 : y
và đường thẳng d : y 2 . 4 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
x 3x 5 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2 2x 2x
hãy tính giá trị của biểu thức 1 2 A x x 2 1
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập phân,
số đo góc làm tròn đến phút.
Câu 3. (1 điểm). Quy tắc sau đây cho ta cách tính ngày cuối cùng của tháng hai trong năm 20ab là thứ mấy ?
- Lấy ab chia 12 được thương là x dư là y
- Lấy y chia 4 được thương là z
- Tính M = x + y + z
- Lấy M chia 7 được dư r
Nếu r = 0 đó là thứ 3 Trang 12
Nếu r = 1 đó là thứ 4
Nếu r = 5 đó là chủ nhật
Nếu r = 6 đó là thứ hai
Em hãy dùng quy tắc trên tính xem ngày cuối cùng của tháng hai trong năm 2024 là thứ mấy ? Từ đó
cho biết ngày 29 / 01 / 2024 là thứ mấy ?
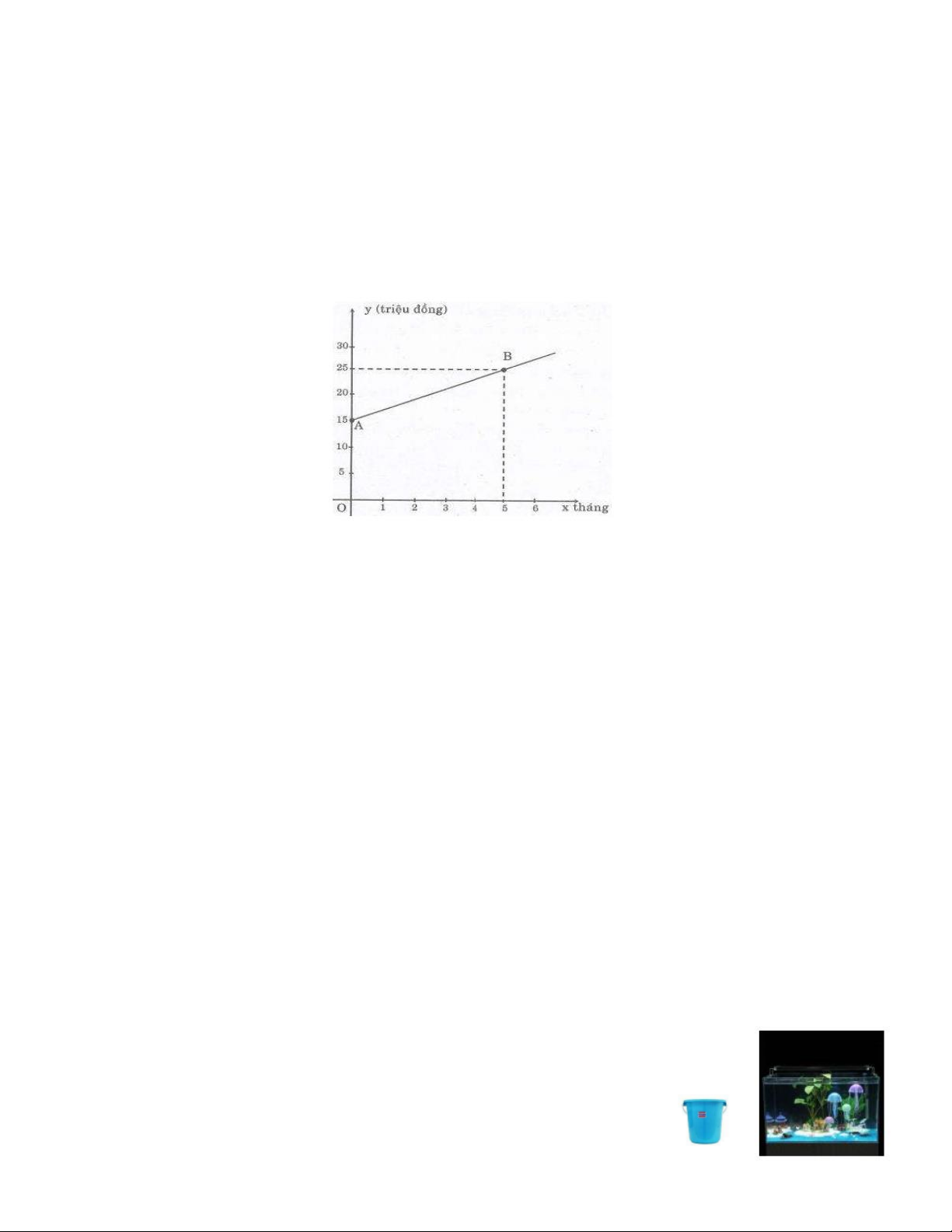
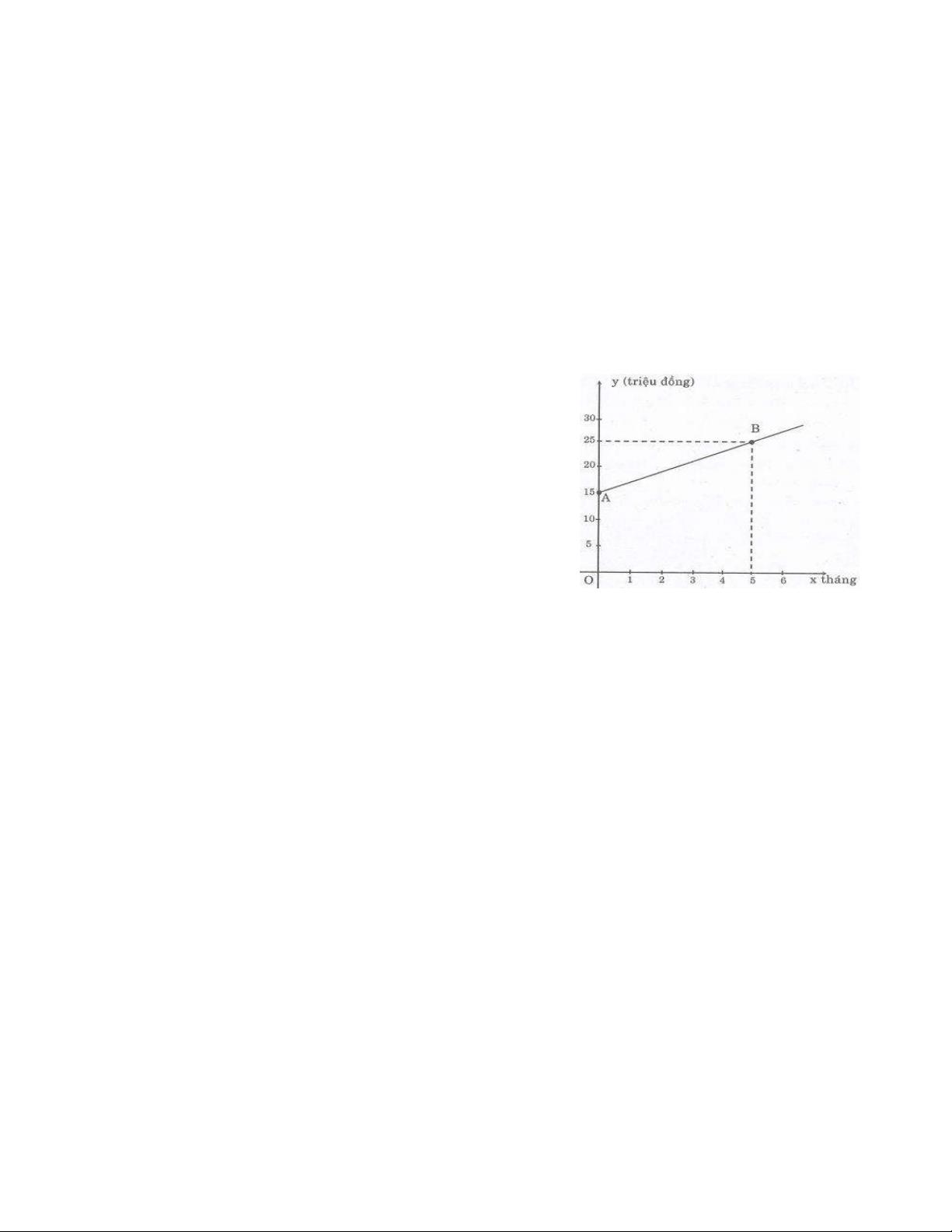
Câu 4. (0,75 điểm). Tiền vốn và lãi bán hàng của một cửa hàng kinh doanh 6 tháng đầu năm được
biểu thị bằng một doạn thẳng, với vốn ban đầu là : 15 triệu đồng ( hình vẽ ).
a) Hãy xác định hệ số a và b biết phương trình đồ thị trên là một đường thẳng có dạng
y = ax + b (a ¹ )
0 với y là số tiền vốn và lãi bán hàng; x là số tháng bán hàng.
b) Tính số tiền vốn và lãi ở tháng thứ tư ?
Câu 5. (1 điểm). Bạn Mai mua 38 cái bánh cho lớp liên hoan. Tại cửa hàng bánh A giá bánh Mai
muốn mua là 16 000 đồng/ 1 cái. Cửa hàng bánh A đang có chương trình khuyến mãi, nếu
mua hơn 10 cái sẽ được giảm giá 9%trên tổng số tiền mua bánh
a) Nếu bạn Mai mua 38 cái bánh ở cửa hàng A thì phải trả bao nhiêu tiền ?
b) Tại cửa hàng B bán cùng loại bánh nói trên ( chất lượng như nhau) đồng giá 16 000 đồng/ 1 cái,
nhưng nếu mua ba cái thì chỉ trả 43000 đồng. Bạn Mai nên mua bánh ở cửa hàng nào để có lợi hơn.
Câu 6. (1 điểm). Hôm nay, ba bạn Tuấn nhờ bạn thay dùm nước trong bể cá lòng bể là hình hộp chữ
nhật, đáy có kích thước 30cm ´ 60cm , chiều cao 40cm . Nước hiện nay chứa trong bể cách mép
trên của bể là 5cm , ba của Tuấn dặn dùng ống hút dẫn nước vào các sô tránh nước tràn nước
ra sàn nhà, kể cả hút chất bẩn dưới đáy bể, chừa lại nước cũ nửa bể, sau đó đổ nước mới vào
nếu thực hiện đung yêu cầu trên, bạn Tuấn đã rút nước từ bể cá ra ngoài bao nhiêu lít nước (
Cho biết công thức tính thể tích hình hộp chữ nhật là V = S .h , trong đó S là diện tích đáy,h
là chiều cai hình hộp và thể tích cá, rong, sỏi lót dưới đáy bể chiếm khoảng
10% thể tích bể, thể tích các chất bẩn không đáng kể, 3 1dm nước = 1 lít
nước ( làm tròn một chữ số thập phân) Trang 13
Câu 7. (1 điểm). Để hòa chung với không khí World Cup, ở một thành phố tổ chức giải bóng đá lứa
tuổi THCS bao gồm 32 đội tham gia chia thành 8 bảng. Ở vòng bảng, 2 đội có thứ hạng cao
nhất sẽ được đi tiếp vào vòng trong ( vòng loại trực tiếp). Thắng được 3 điểm, hòa được 1
điểm, thua 0 điểm. Nếu hai đội cùng điểm sẽ so hiệu số bàn thắng- thua. Ở bảng A , đội
Phượng Hoàng của bạn An nằm trong bảng hạt giống sau 2 lượt đấu số hạng như sau:
1. Đội Báo Đen: 4 điểm
2. Đội Thỏ Trắng: 2 điểm 3. Đội Sư Tử: 2 điểm
4. Đội Phượng Hoàng 1 điểm
Ở lượt đấu diễn ra song song 2 trận Báo Đen- Sư Tử và Thỏ Trắng-Phượng Hoàng. Các em hãy tính
xác suất vào vòng trong của đội Phượng Hoàng biết rằng đội Phượng Hoàng luôn có hiệu số bàn thắng
thấp nhất ? Xác suất= (số khả năng vào vòng trong): ( số khả năng xảy ra).100%
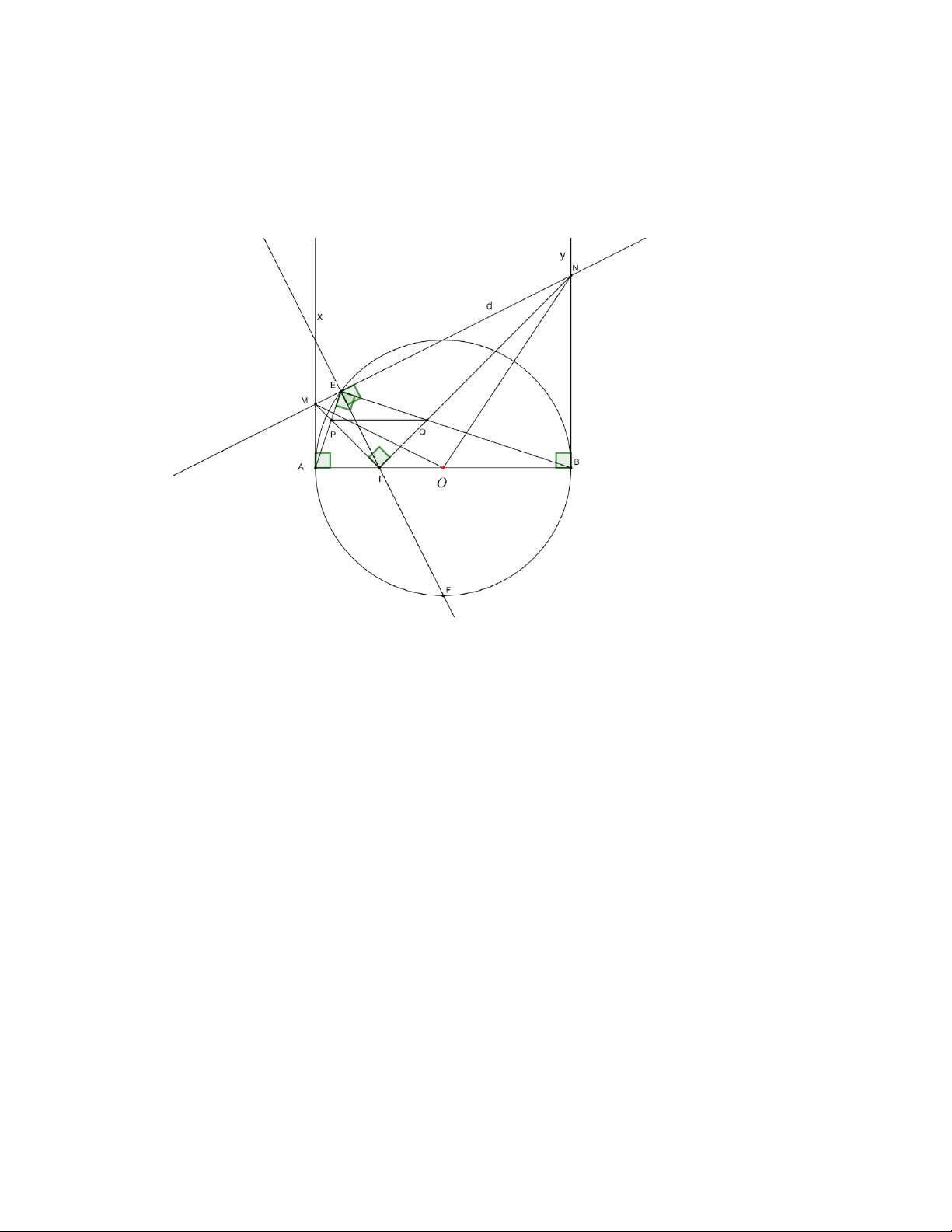
Câu 8. (3 điểm) Cho đường tròn tâm O có đường kính AB = 2R . Gọi I là trung điểm của đoạn
thẳng OA và E là điểm thuộc đường tròn tâm O ( E không trùng với A và B ). Gọi A x và B y
là các tiếp tuyến tại A và B của đương tròn (O) ( A x , By cùng thuộc một nửa mặt phẳng bờ
A B có chứa điểm E ). Qua điểm E kẻ đường thẳng d vuông góc với EI cắt A x và B y lần
lượt tại M và N .
1. Chứng minh tứ giác A MEI nội tiếp. · ·
2. Chứng minh ENI = EBI và A E .IN = BE .IM .
3. Gọi P là giao điểm của A E và MI ; Q là giao điểm của BE và N I . Chứng minh hai đường
thẳng PQ và B N vuông góc với nhau.
4. Gọi F là điểm chính giữa cung A B không chứa điểm E của đường tròn (O). Tính diện tích
tam giác OMN theo R khi ba điểm E , I , F thẳng hàng. ----HẾT--- Trang 14 HƯỚNG DẪN GIẢI x x
Câu 1. (1,5 điểm). Cho P 2 : y
và đường thẳng d : y 2 . 4 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. (1 điểm) BGT: x 4 2 0 2 4 2 x y 4 1 0 1 4 4 x 0 2 x y 2 2 1 2
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2 x x 2 4 2 1 2 1
x x 2 0 4 2 x 2 x 4 1 1
Thay x 2 vào y
x 2 , ta được: y .2 2 1 . 2 2 1 1 Thay x 4
vào y x 2 , ta được: y .( 4 ) 2 4 . 2 2 Vậy 2; 1 , 4
; 4 là hai giao điểm cần tìm. Trang 15
Câu 2. (1 điểm) Cho phương trình 2
x 3x 5 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2 2x 2x
hãy tính giá trị của biểu thức 1 2 A x x 2 1 Lời giải 2 Vì 2
b 4ac 3 4. 1 . 5 29 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b 3
S x x 3 1 2
Theo định lí Vi-et, ta có: a 1 c 5
P x .x 5 1 2 a 1 2x 2x Ta có: 1 2 A x x 2 1 x x 2 x x 2 2 2 2 2 x x x x 2 2 2 2 1 2 1 2 3 2. 5 2 2 1 2 38 1 2 A x x x x x x 5 5 1 2 1 2 1 2
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 3. (1 điểm) Quy tắc sau đây cho ta cách tính ngày cuối cùng của tháng hai trong năm 20ab là thứ mấy ?
- Lấy ab chia 12 được thương là x dư là y
- Lấy y chia 4 được thương là z
- Tính M = x + y + z
- Lấy M chia 7 được dư r
Nếu r = 0 đó là thứ 3
Nếu r = 1 đó là thứ 4 ……
Nếu r = 5 đó là chủ nhật
Nếu r = 6 đó là thứ hai
Em hãy dùng quy tắc trên tính xem ngày cuối cùng của tháng hai trong năm 2024 là thứ mấy ? Từ đó
cho biết ngày 29 / 01 / 2024 là thứ mấy ? Trang 16 Lời giải
Ta có : 2024 có 24 chia 12 được thương là 2 dư là 0
Lấy 0 chia 4 được thương là 0
Từ đó M = 2 + 0 + 0 = 2
Lấy M chia 7 dư r = 2 . Từ đó ta có ngày cuối cùng của tháng hai trong năm 2024 tính theo quy
tắc là thứ 5 . Từ 29 / 01 / 2024 đến 28 / 02 / 2024 là 31 ngày.
Ta có : 31 = 7.4 + 3 . Nên thứ 5 là 28 / 02 / 2024 lùi lại nên có 29 / 01 / 2024 là thứ 3
Câu 4. (0,75 điểm).Tiền vốn và lãi bán hàng của một cửa
hàng kinh doanh 6 tháng đầu năm được biểu thị bằng
một doạn thẳng, với vốn ban đầu là : 15 triệu đồng ( hình vẽ ).
a) Hãy xác định hệ số a và b biết phương trình đồ thị trên là
một đường thẳng có dạng y = ax + b (a ¹ )
0 với y là số tiền
vốn và lãi bán hàng; x là số tháng bán hàng.
b) Tính số tiền vốn và lãi ở tháng thứ tư ? Lời giải a)
Ta có y = ax + b
Với x = 0 và y = 15 thì 15 = .
a 0 + b Þ b = 15
Với x = 5 và y = 25 thì 25 = . a 5 + b Þ 25 = .
a 5 + 15 Þ a = 2
Từ đó ta có : y = 2x + 15 b)
Ta có: y = 2x + 15
Với x = 4 thì y = 2.4 + 15 = 23 triệu đồng.
Câu 5. (1 điểm) Bạn Mai mua 38 cái bánh cho lớp liên hoan. Tại cửa hàng bánh A giá bánh Mai
muốn mua là 16 000 đồng/ 1 cái. Cửa hàng bánh A đang có chương trình khuyến mãi, nếu
mua hơn 10 cái sẽ được giảm giá 9%trên tổng số tiền mua bánh Trang 17
a) Nếu bạn Mai mua 38 cái bánh ở cửa hàng A thì phải trả bao nhiêu tiền ?
b) Tại cửa hàng B, bán cùng loại bánh nói trên ( chất lượng như nhau) đồng giá 16 000 đồng/ 1 cái,
nhưng nếu mua ba cái thì chỉ trả 43000 đồng. Bạn Mai nên mua bánh ở cửa hàng nào để có lợi hơn. Lời giải
a) Do bạn Mai mua 38 cái bánh ở cửa hàng A nên được cửa hàng bánh giảm 9% trên tổng số tiền mua bánh.
Vậy số tiền bạn Mai phải trả là: 16 000.(100% - 9 ) % .38 = 553 280 đồng.
b) Tại cửa hàng B , nếu mua 3 cái bánh chỉ phải trả 43 000 đồng.
38 cái bánh được chia thành: 38 = 12.3 + 2 .
Để mua 38 cái bánh, số tiền bạn Mai cần trả là: 12.43 000 + 2.16 000 = 548 000 đồng.
Do 548 000 < 553280 nên bạn Mai mua bánh ở cửa hàng B thì trả tiền ít hơn.
Câu 6. (1 điểm) Hôm nay, ba bạn Tuấn nhờ bạn thay dùm nước trong bể cá lòng bể là hình hộp chữ
nhật, đáy có kích thước 30cm ´ 60cm , chiều cao 40cm . Nước hiện nay chứa trong bể cách mép
trên của bể là 5cm , ba của Tuấn dặn dùng ống hút dẫn nước vào các sô tránh nước tràn nước
ra sàn nhà, kể cả hút chất bẩn dưới đáy bể, chừa lại nước cũ nửa bể, sau đó đổ nước mới vào
nếu thực hiện đúng yêu cầu trên, bạn Tuấn đã rút nước từ bể cá ra ngoài bao nhiêu lít nước (
Cho biết công thức tính thể tích hình hộp chữ nhật là V = S .h , trong đó S là
diện tích đáy,h là chiều cao hình hộp và thể tích cá, rong, sỏi lót dưới đáy bể
chiếm khoảng 10% thể tích bể, thể tích các chất bẩn không đáng kể, 3
1dm nước = 1 lít nước ( làm tròn một chữ số thập phân) Lời giải
Ta có: Bể cá lòng bể là hình hộp chữ nhật, đáy có kích thước 30cm ´ 60cm , chiều cao 40cm . Nước hiện
nay chứa trong bể cách mép trên của bể là 5cm nên ta có chiều cao nước là 35cm .
Thể tích hồ cá khi đó là V = S h = = ( 3 cm ) = ( 3 . 30.60.35 63000 63 dm ).
Thể tích nước trong hồ cá khi đó là V = V = ( 3 90%. 56, 7 dm nuoc ) 56, 7
Ba Tuấn dặn chừa lại nước cũ nửa bể nên lượng nước bị rút ra khỏi bể là = 28, 35 » 28, 4(l) 2 Trang 18
Câu 7. (1 điểm) Để hòa chung với không khí World Cup, ở một thành phố tổ chức giải bóng đá lứa
tuổi THCS bao gồm 32 độ tham gia chia thành 8 bảng. Ở vòng bảng, 2 đội có thứ hạng cao
nhất sẽ được đi tiếp vào vòng trong ( vòng loại trực tiếp). Thắng được 3 điểm, hòa được 1
điểm, thua 0 điểm. Nếu hai đội cùng điểm sẽ so hiệu số bàn thắng- thua. Ở bảng A, đội
Phượng Hoàng của bạn An nằm trong bảng hạt giống sau 2 lượt đấu số hạng như sau:
1. Đội Báo Đen: 4 điểm
2. Đội Thỏ Trắng: 2 điểm 3. Đội Sư Tử: 2 điểm
4. Đội Phượng Hoàng 1 điểm
Ở lượt đấu diễn ra song song 2 trận Báo Đen- Sư Tử và Thỏ Trắng-Phượng Hoàng. Các em hãy tính xác
suất vào vòng trong của đội Phượng Hoàng biết rằng đội Phượng Hoàng luôn có hiệu số bàn thắng
thấp nhất ? Xác suất= (số khả năng và vòng trong): ( số khả năng xảy ra).100% Quận 7-01 Lời giải
Số khả năng xảy ra là 9 3.3 ( Trận Báo Đen- Sư Tử có 3 khả năng và trận Thỏ Trắng- Phượng Hoàng có 3 khả năng)
Số khả năng Phượng Hoàng vào là 2
TH: Báo Đen thắng Sư Tử và Thỏ Trắng thua Phượng Hoàng: Phượng Hoàng vào.
TH: Báo Đen hòa Sư Tử và Thỏ Trắng thua Phượng Hoàng: Phượng Hoàng vào. 2
Vậy xác suất để Phượng Hoàng được vào vòng trong là .100% 22,2%. 9
Câu 8. (3 điểm) Cho đường tròn tâm O có đường kính AB = 2R . Gọi I là trung điểm của đoạn
thẳng OA và E là điểm thuộc đường tròn tâm O ( E không trùng với A và B ). Gọi A x và B y
là các tiếp tuyến tại A và B của đương tròn (O) ( A x , By cùng thuộc một nửa mặt phẳng bờ
A B có chứa điểm E ). Qua điểm E kẻ đường thẳng d vuông góc với EI cắt A x và B y lần
lượt tại M và N .
1. Chứng minh tứ giác A MEI nội tiếp. · ·
2. Chứng minh ENI = EBI và A E .IN = BE .IM .
3. Gọi P là giao điểm của A E và MI ; Q là giao điểm của BE và N I . Chứng minh hai đường thẳng
PQ và B N vuông góc với nhau. Trang 19
4. Gọi F là điểm chính giữa cung A B không chứa điểm E của đường tròn (O). Tính diện tích tam giác
OMN theo R khi ba điểm E , I , F thẳng hàng. Lời giải
1) Chứng minh tứ giác A MEI nội tiếp.
Xét tứ giác AMEI , có:
MAI 90AM AB MEI 90 EM EI
MAI MEI 180
Tứ giác AMEI nội tiếp vì có hai góc đối bù nhau. · ·
2) Chứng minh ENI = EBI và A E .IN = BE .IM .
Xét tứ giác BNEI , có:
NBI 90BN AB NEI 90 EN EI
NBI NEI 180
Tứ giác BNEI nội tiếp vì có hai góc đối bù nhau. Trang 20 · ·
Þ ENI = EBI ( 2 góc có đỉnh kề nhau cùng nhìn 1 cạnh trong tứ giác nội tiếp)
Xét D A BE và D IMN , có: · · · · A BE = MNI (EBI = ENI ) · ·
BA E = IMN ( 2 góc có đỉnh kề nhau cùng nhìn cạnh EI trong tứ giác A MEI nội tiếp)
Þ DA BE DMNI (g - g)
Þ A E = BE Þ A E .NI = MI .BE MI NI
3) Gọi P là giao điểm của A E và MI ; Q là giao điểm của BE và N I . Chứng minh hai đường thẳng
PQ và B N vuông góc với nhau. Xét (O) ta có : ·
A EB là góc nội tiếp chắn nửa đường tròn · Þ A EB = ° 90 Ta có : D A B E D MNI · · Þ A EB = MIN = ° 90
Xét tứ giác EPIQ , có: PEQ 90 AEB90 PIQ 90 MIN 90
PEQ PIQ 180
Tứ giác EPIQ nội tiếp vì có hai góc đối bù nhau. · ·
Þ EQP = EIP ( vì 2 góc ở 2 đỉnh kề cùng nhìn 1 cạnh trong tứ giác nội tiếp ) Ta có: · ·
EQP = EIP (cmt ) · ·
EA M = EIM ( vì 2 góc ở 2 đỉnh kề cùng nhìn EM trong tứ giác A MEI nội tiếp ) Trang 21 · ·
EA M = EBA ( vì góc tạo bởi tiếp tuyến và dây cung EA và góc nội tiếp chắn cung EA ) · · Þ EQP = EBA · ·
Mà 2 góc EQP và EBA ở nằm vị trí đồng vị Nên PQ / / BA
Mặt khác A B ^ BN Suy ra PQ ^ BN
4) Gọi F là điểm chính giữa cung A B không chứa điểm E của đường tròn (O). Tính diện tích tam
giác OMN theo R khi ba điểm E , I , F thẳng hàng. » »
Khi E , I , F thẳng hàng thì A F = BF · · Þ A EI = IEB · · · Mà °
A EI + IEB = A EB = 90 · ·
Nên A EI = IEB = 45° Ta có : · ·
A EI = IEB = 45° · ·
A EI = A MI ( vì 2 góc ở 2 đỉnh kề cùng nhìn A I trong tứ giác A MEI nội tiếp ) · ·
BEI = BNI ( vì 2 góc ở 2 đỉnh kề cùng nhìn BI trong tứ giác BNEI nội tiếp ) · · · ·
Þ A EI = A MI = BEI = BNI = ° 45 Ta có : ·
D MA I vuông ở A và A MI = ° 45 ·
D BNI vuông ở B và B NI = 45°
Þ DMAI vuông cân ở A và DBNI vuông cân ở B ìïï R ï MA = A I = ï Þ í 2 ï ï 3R ï NB = BI = ïïî 2 Ta có : Trang 22
A B .(MA + NB ) MA.IA IB .B N S = S - S - S = - - D OMN MA B N MA I NB I 2 2 2 æ ö çR 3R ÷ ç + ÷ R R 3R 3 2 . R R ç ÷ ç ÷ è ø . . 2 2 = - 2 2 - 2 2 2 2 2 2 2 2 R 9R 3R = 2 2R - - = 8 8 4 ---HẾT---
SỞ GD $ ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 11
NĂM HỌC : 2023 - 2024 MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 11 - 3
Thời gian: 120 phút (không kể thời gian phát đề) 1 x
Câu 1. (1,5 điểm). Cho parabol 2 (P) : y
x và đường thẳng (d ) : y 2 . 4 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép toán.
Câu 2. (1 điểm). Cho phương trình 2
4x 3x 1 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A x 2x 2 1 2
Câu 3. (1 điểm). Một cửa hàng sách cũ có một chính sách như sau: Nếu khách hàng đăng ký làm hội
viên của cửa hàng sách thì mỗi năm phải đóng phí thành viên là 50000 đồng/năm. Biết rằng,
là hội viên khi thuê 2 cuốn sách thì phải trả 60000 đồng (Đã tính phí thành viên). Gọi s
(đồng), là tổng số tiền mỗi hành khách là hội viên phải trả trong mỗi năm và t là số cuốn sách
mà khách hàng thuê, biết s là hàm số bậc nhất có dạng: s at b .
a) Tìm hệ số a và b .
b) Nếu khách hàng không phải là hội viên thì sẽ thuê sách với giá 10000 đồng/ cuốn sách .
Nam là hội viên của cửa hàng sách, năm ngoái Nam đã phải trả cho cửa hàng sách tổng
cộng 90000 đồng. Hỏi nếu Nam không phải là hội viên của cửa hàng sách thì số tiền phải trả là bao nhiêu?
Câu 4. (1 điểm). Một cửa hàng điện máy nhập về một lô hàng gồm 100 chiếc điện thoại di động và
bán với giá niêm yết là 8500000 đồng. Trang 23
a) Người chủ cửa hàng cho biết mỗi điện thoại di động bán ra với giá trên đem lại lợi nhuận
70% so với giá nhập vào. Hãy cho biết giá nhập vào của lô hàng trên.
b) Sau khi bán được 60 chiếc điện thoại di động thì người chủ giảm giá 20% và bán được số
điện thoại còn lại. Hãy tính tỉ lệ phần trăm lợi nhuận mà cửa hàng đạt được của lô hàng trên.
Câu 5. (0,75 điểm). Để hưởng ứng phong trào làm lồng đèn tặng các em nhỏ vùng sâu trong dịp
Trung Thu, lớp 9A gồm 46 bạn tiến hành làm vào các ngày cuối tuần. Cô giáo đặt chỉ tiêu:
một bạn nam sẽ làm 2 cái lồng đèn còn bạn nữ thì một bạn làm ra 3 cái. Sau 2 tháng, cả lớp
làm tổng cộng được 118 cái. Hỏi lớp đó có bao nhiêu bạn học sinh nam và bao nhiêu học sinh nữ?
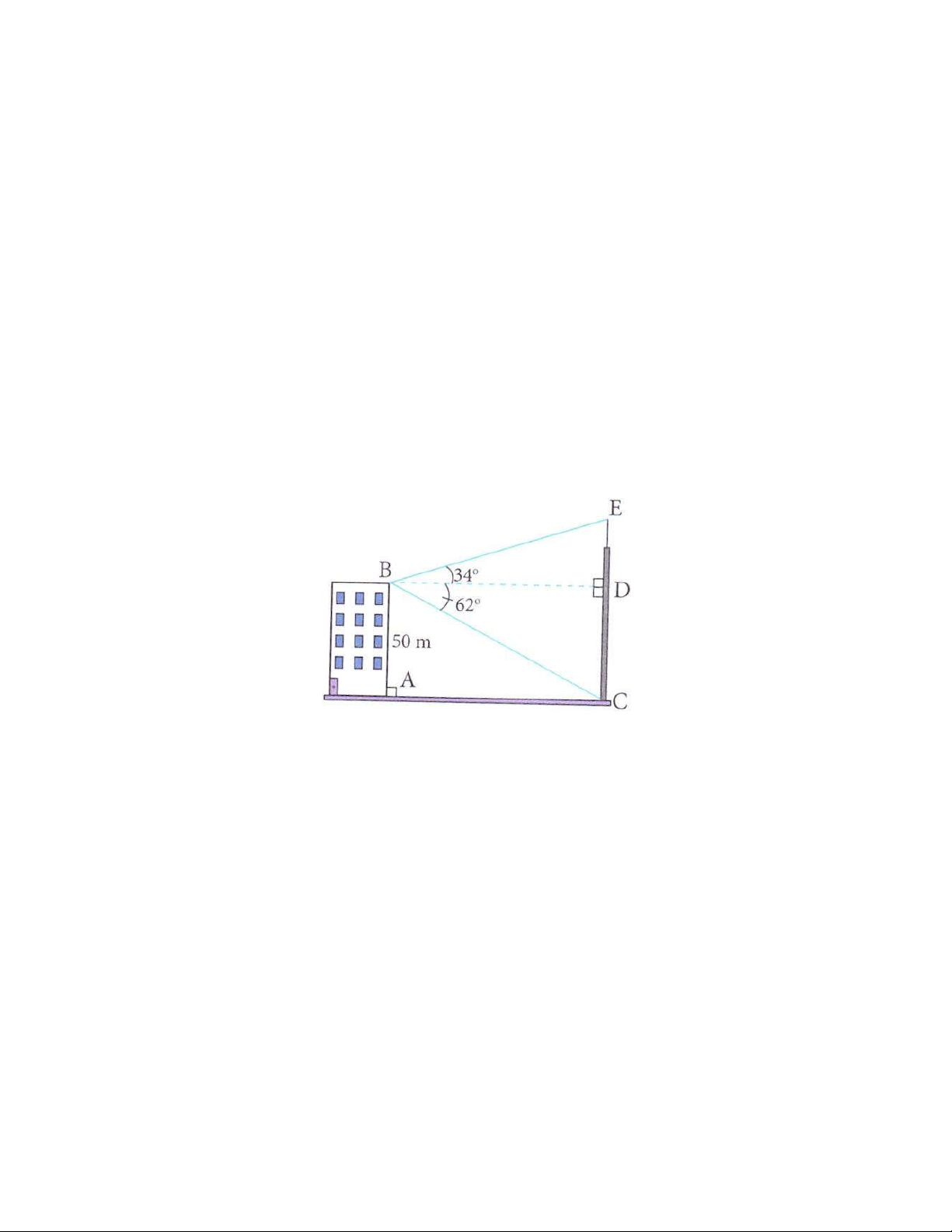
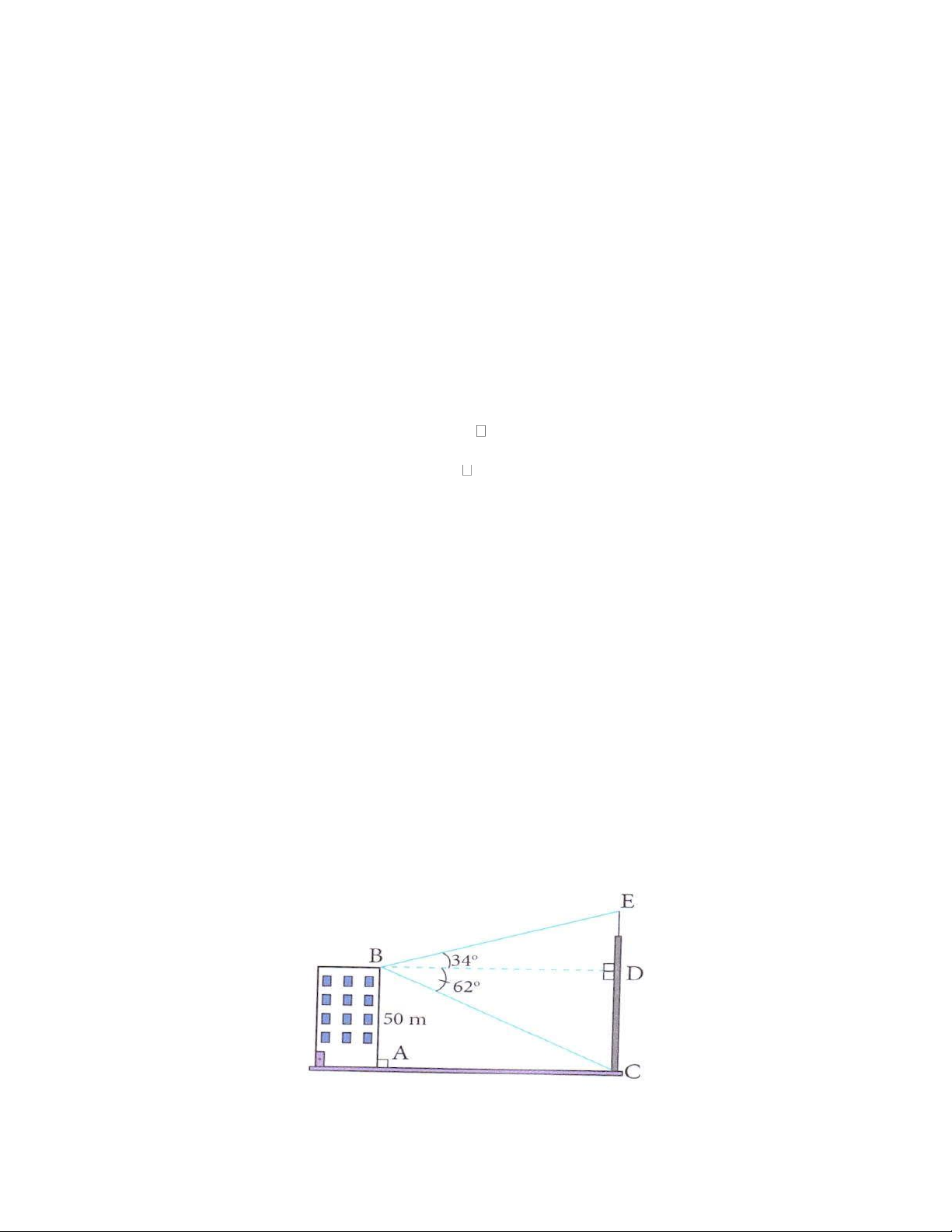
Câu 6. (0,75 điểm). Từ nóc một cao ốc cao 50m người ta nhìn thấy chân và đỉnh một cột ăng- ten với các góc
hạ và nâng lần lượt là 62 và 34 . Tính chiều cao của cột ăng- ten.
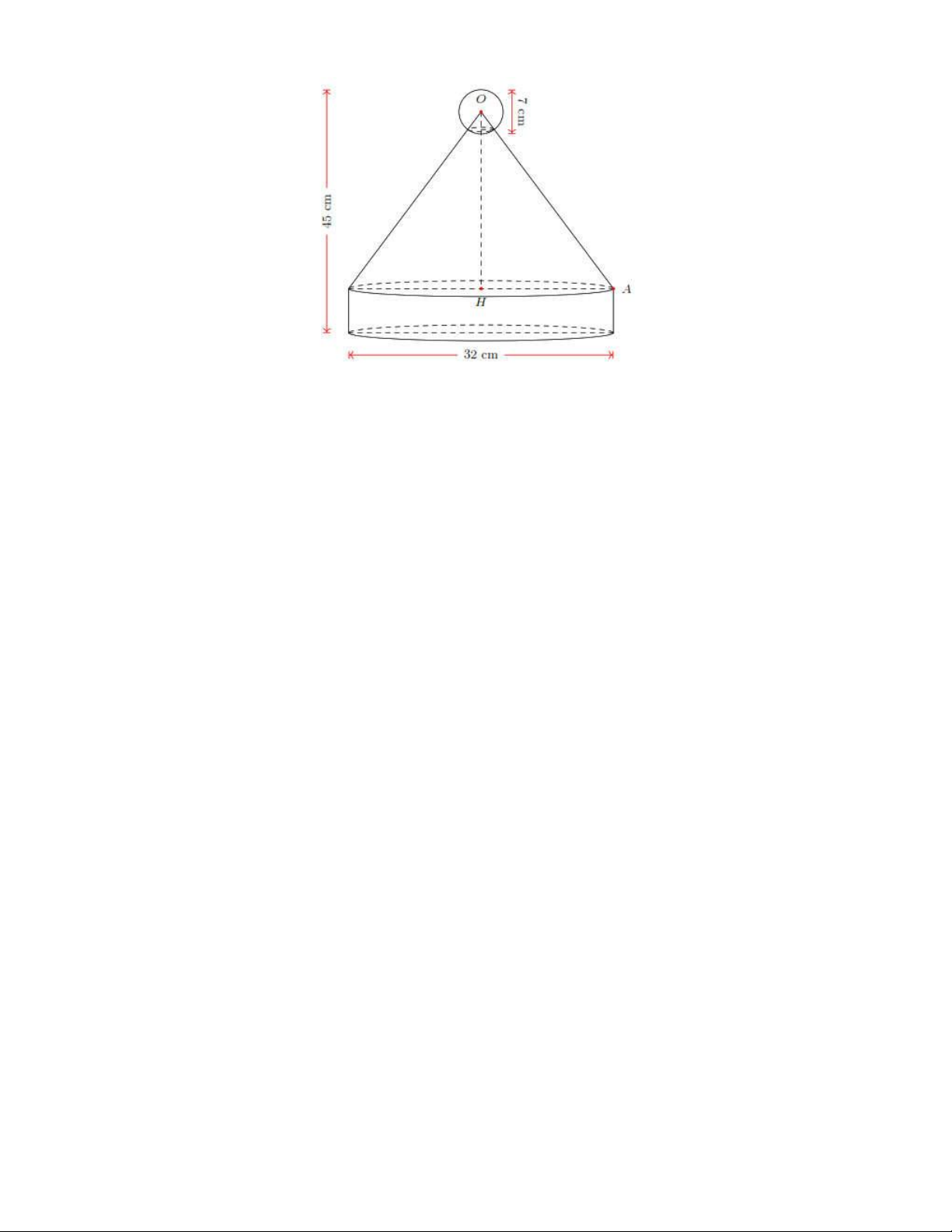
Câu 7. (1 điểm). Một chiếc nón ông già Noel thường gồm có ba phần: Hình trụ để làm đế nón, phần
mũ chính là hình nón, trên đỉnh nón là quả bóng trắng có hình cầu và có các kích thước tương
ứng như hình vẽ. Tính tổng diện tích phần vải để may nón, biết rằng chiều cao của đế nón
bằng đường kính của quả bóng (kết quả làm tròn đến hàng đơn vị). Trang 24
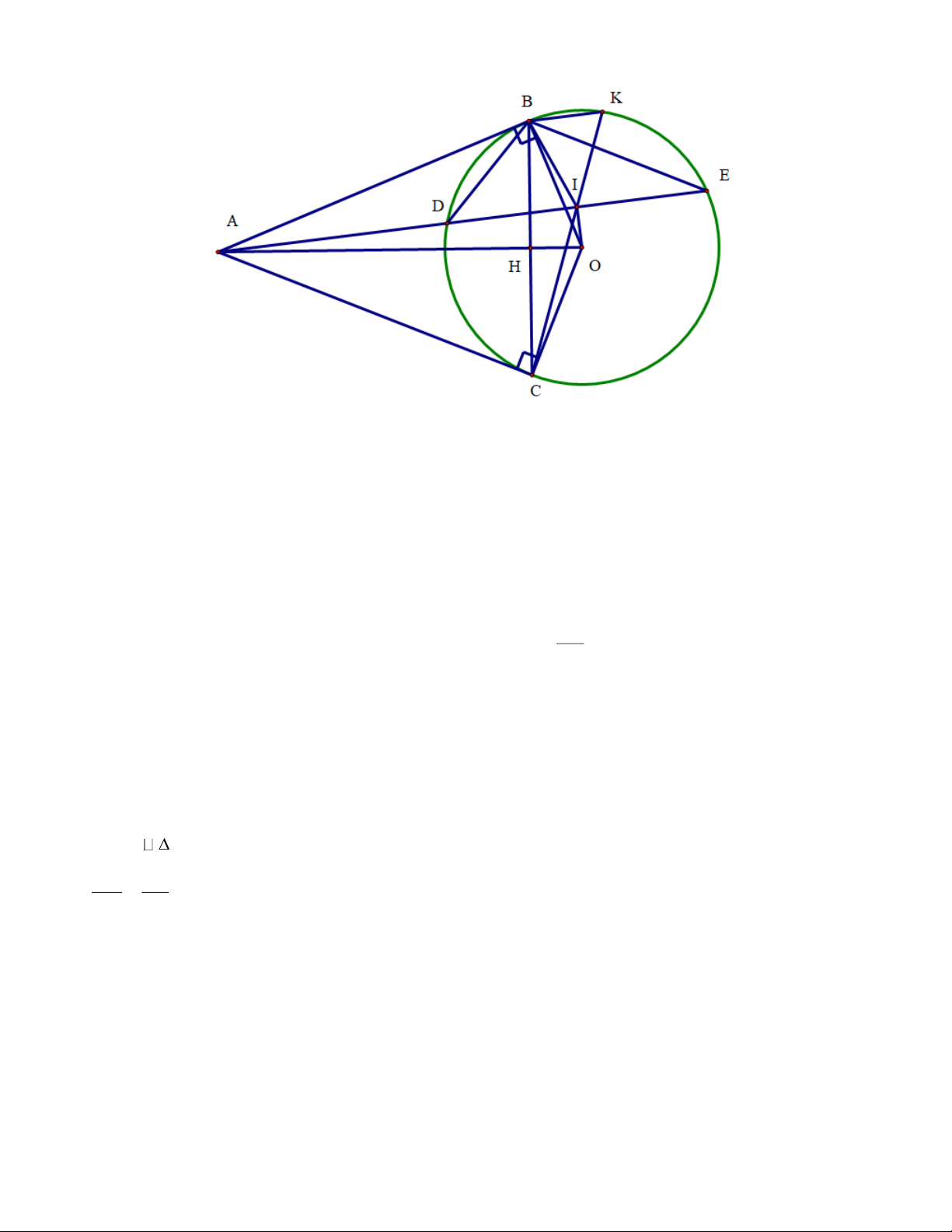
Câu 8. (3 điểm) Từ điểm A ở ngoài đường tròn ;
O R vẽ hai tiếp tuyến AB và AC và một cát tuyến
ADE không đi qua tâm O ( B,C tại là các tiếp điểm và AD AE)
a) Chứng minh tứ giác ABOC nội tiếp, xác định tâm và bán kính của đường tròn đó?.
b) Gọi H là giao điểm của OA với BC . Chứng minh AH AO AD AE 2 . . AB .
c) Gọi I là trung điểm của DE . Qua B vẽ dây BK / /DE . Chứng minh ba điểm K,I,C thẳng hàng . ----HẾT--- Trang 25 HƯỚNG DẪN GIẢI 1 x
Câu 1. (1,5 điểm) Cho 2 (P) : y
x và đường thẳng (d ) : y 2 . 4 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: x 4 2 0 2 4 y 1 2 x 4 1 0 1 4 4 x 4 0 x y 2 4 2 2
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 1 2 x x 2 4 2 1 2 x x 2 0 4 2 x 2 x 4 1 1 Thay x 4 vào y 2
x , ta được: y 2 .4 4 . 4 4 1 1
Thay x 2 vào y 2
x , ta được: y 2 .2 1 . 4 4 Trang 26 Vậy 4
; 4 , 2; 1 là hai giao điểm cần tìm.
Câu 2. (1 điểm) Cho phương trình 2
4x 3x 1 0 có 2 nghiệm là x ,x . Không giải phương trình, hãy 1 2
tính giá trị của biểu thức A x 2x 2 1 2 Lời giải Vì 2 b ac 2 4 3 4.4.(1) 25 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b
S x x 3 1 2
Theo định lí Vi-et, ta có: a 4 c
P x .x 1 1 2 a 4
Ta có: A x 2x 2 1 2
A x x 2x 2x 4 1 2 1 2
A x x 2(x x ) 4 1 2 1 2 1 3 A 2. 4 4 4 A 21 4
Câu 3. (1 điểm) Một cửa hàng sách cũ có một chính sách như sau: : Nếu khách hàng đăng ký làm hội
viên của cửa hàng sách thì mỗi năm phải đóng phí thành viên là 50000 đồng/năm. Biết rằng, là
hội viên khi thuê 2 cuốn sách thì phải trả 60000 đồng (Đã tính phí thành viên). Gọi s (đồng), là
tổng số tiền mỗi hành khách là hội viên phải trả trong mỗi năm và t là số cuốn sách mà khách
hàng thuê, biết s là hàm số bậc nhất có dạng: s at b
a) Tìm hệ số a và b
b) Nếu khách hàng không phải là hội viên thì sẽ thuê sách với giá 10000 đồng/ cuốn sách . Nam
là hội viên của cưả hàng sách, năm ngoái Nam đã phải trả cho cửa hàng sách tổng cộng 90000
đồng. Hỏi nếu Nam không phải là hội viên của cửa hàng sách thì số tiền phải trả là bao nhiêu? Lời giải
a) Xác định các hệ số a và b . Trang 27 Theo đề bài, ta có: t 0 Với
50000 0.a .1 s b 50000 t 2 Với
60000 2.a . 2 s b 60000
0a b 50000 a 5000
Từ 1 và 2 ta có hệ phương trình: .
2a b 60000 b 50000
Vậy: a 5000 , b 50000 và s 5000t 50000 .
b) Nếu khách hàng không phải là hội viên thì sẽ thuê sách với giá 10000 đồng/ cuốn sách . Nam
là hội viên của cưả hàng sách, năm ngoái Nam đã phải trả cho cửa hàng sách tổng cộng
90000 đồng. Hỏi nếu Nam không phải là hội viên của cửa hàng sách thì số tiền phải trả là bao nhiêu?
Thay s 90000 vào s 5000t 50000 ta có:
90000 5000t 50000 t 8
Vậy Nam phải trả số tiền thuê 8 cuốn sách khi không phải là hội viên là : 8.10000 80000 đồng.
Câu 4. (1 điểm). Một cửa hàng điện máy nhập về một lô hàng gồm 100 chiếc điện thoại di động và bán
với giá niêm yết là 8500000 đồng.
a) Người chủ cửa hàng cho biết mỗi điện thoại di động bán ra với giá trên đem lại lợi nhuận
70% so với giá nhập vào. Hãy cho biết giá nhập vào của lô hàng trên.
b) Sau khi bán được 60 chiếc điện thoại di động thì người chủ giảm giá 20% và bán được số
điện thoại còn lại. Hãy tính tỉ lệ phần trăm lợi nhuận mà cửa hàng đạt được của lô hàng trên. Lời giải
Giá nhập vào của một chiếc điện thoại là:
8500000 : (100% 70%) 5000000 (đồng)
Giá nhập vào của lô hàng là:
5000000.100 500000000 (đồng)
b) Số tiền thu về khi bán hết 100 chiếc điện thoại là:
60.8500000 40.8500000.80% 782000000 (đồng) Trang 28
Lợi nhuận thu được từ việc bán 100 chiếc điện thoại là:
782000000 500000000 282000000 (đồng)
Tỉ lệ phần trăm lợi nhuận mà cửa hàng đạt được của lô hàng trên là:
282000000 : 500000000.100% 56,4%
Câu 5. (0,75 điểm) Để hưởng ứng phong trào làm lồng đèn tặng các em nhỏ vùng sâu trong dịp Trung
Thu, lớp 9A gồm 46 bạn tiến hành làm vào các ngày cuối tuần. Cô giáo đặt chỉ tiêu: một bạn
nam sẽ làm 2 cái lồng đèn còn bạn nữ thì một bạn làm ra 3 cái. Sau 2 tháng, cả lớp làm tổng
cộng được 118 cái. Hỏi lớp đó có bao nhiêu bạn học sinh nam và bao nhiêu học sinh nữ? Lời giải
Gọi x (học sinh) là số học sinh Nam của lớp ( x )
Gọi y (học sinh) là số học sinh Nữ của lớp ( y )
Do lớp có 46 học sinh nên ta có phương trình: x y 46 1
Do một bạn nam sẽ làm 2 cái lồng đèn còn bạn nữ thì một bạn làm ra 3 cái mà cả lớp làm tổng cộng
được 118 cái nên ta có phương trình: 2x 3y 118 2 Từ 1 và
2 ta có hệ phương trình:
x y 46 x 20 (nhận) 2x y 3 118 y 26
Vậy lớp có 20 học sinh Nam và 26 học sinh nữ.
Câu 6. (0,75 điểm) Từ nóc một cao ốc cao 50m người ta nhìn thấy chân và đỉnh một cột ăng- ten với các
góc hạ và nâng lần lượt là 62 và 34 . Tính chiều cao của cột ăng- ten Trang 29 Lời giải
Ta có AB C D 50m
Xét DBDC vuông tại D , ta có: · DC T an DBC = (tslg) DB Þ ° = 50 T an 62 DB
Þ BD » 26, 6m
Xét D BDE vuông tại D , ta có: · DE T an DB E = (tslg) DB DE 0 Þ Tan 34 = 26, 6
Þ DE » 17, 9 m
Do đó CE = CD + DE = 50 + 17, 9 = 67, 9 m
Vậy chiều cao của cột ăng- ten là khoảng 67, 9 m .
Câu 7. (1 điểm) Một chiếc nón ông già Noel thường gồm có ba phần: Hình trụ để làm đế nón, phần mũ
chính là hình nón, trên đỉnh nón là quả bóng trắng có hình cầu và có các kích thước tương ứng
như hình vẽ. Tính tổng diện tích phần vải để may nón, biết rằng chiều cao của đế nón bằng
đường kính của quả bóng. (kết quả làm tròn đến hàng đơn vị). Trang 30 Lời giải 2 7
Diện tích vải để làm quả bóng trắng có hình cầu là: 2 4 R 4. 49 2 cm 2 2 32 2
Diện tích vải để làm đế nón hình trụ là: 2 rh 2. .7 3584 cm 2 7
Độ dài cạnh OH là: 45 7 34,5 cm 2 2 2 2 2
Độ dài cạnh OA là: OH HA 34,5 16 38 cm 32
Diện tích phần vải để làm phần mũ hình nón là: 2 rl 2 . .38 1216 2
Tổng diện tích phần vải để may nón: 49 3584 1216 15234 2 cm
Câu 8. (3 điểm) Từ điểm A ở ngoài đường tròn ;
O R vẽ hai tiếp tuyến AB và AC và một cát tuyến
ADE không đi qua tâm O ( B,C tại là các tiếp điểm và AD AE)
a) Chứng minh tứ giác ABOC nội tiếp, xác định tâm và bán kính của đường tròn đó?.
b) Gọi H là giao điểm của OA với BC . Chứng minh AH AO AD AE 2 . . AB .
c) Gọi I là trung điểm của DE . Qua B vẽ dây BK / /DE . Chứng minh ba điểm K,I,C thẳng hàng . Lời giải Trang 31
a) Chứng minh tứ giác ABOC nội tiếp, xác định tâm và bán kính của đường tròn đó?
Xét tứ giác ABOC , có: ABO ACO
90 ( AB , AC là hai tiếp tuyến của O,R
ABO ACO 180
Tứ giác ABOC nội tiếp đường tròn đường kính OA vì có hai góc đối bù nhau. OA
Tâm của đường tròn là trung điểm của OA và bán kính bằng 2
b) Gọi H là giao điểm của OA với BC . Chứng minh AH AO AD AE 2 . . AB .
Xét ABD và AEB có: BAE là góc chung
ABD AEB ( 2 gnt cùng chắn BD )
ABD AEB (g – g).
AD AB (TSĐD). AB AE AD AE 2 . AB 1 Ta có:
AB AC (tính chất hai tiếp tuyến cắt nhau)
OA OB R
OAlà đường trung trực của BC . Trang 32
OA BC tại H
Xét ABO vuông tại B , có BH là đường cao: AH AO 2 . AB (HTL) 2
Từ 1 , 2 suy ra: AH AO AD AE 2 . . AB
c) Gọi I là trung điểm của DE . Qua B vẽ dây BK / /DE . Chứng minh ba điểm K,I,C thẳng hàng .
Ta có BK / /DEgt
EKBD là hình thang
Mà EKBD là tứ giác nội tiếp (do E,K,B,D O; R )
EKBD là hình thang cân
Dễ dàng Cm: KIE BI ( D . c .
g c) IK IB
KIB cân tại I
IKB IBK
Ta có: BIA IBKSLT doBK / /ED 3 1
Lại có CKB BCA sd BC 4 2
Dễ dàng chứng minh 5 điểm A,B,C,O,I cùng thuộc một đường tròn BCA BIA 5
Từ 3 , 4 5 suy ra: IBK CKB
Mà IKB IBK (chứng minh trên)
IKB CKB
K,I,C thẳng hàng. ----HẾT--- Trang 33




