













Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT TP THUÛ ÑÖÙC
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Thủ Đức - 1
Thời gian: 120 phút (không kể thời gian phát đề) 2 x
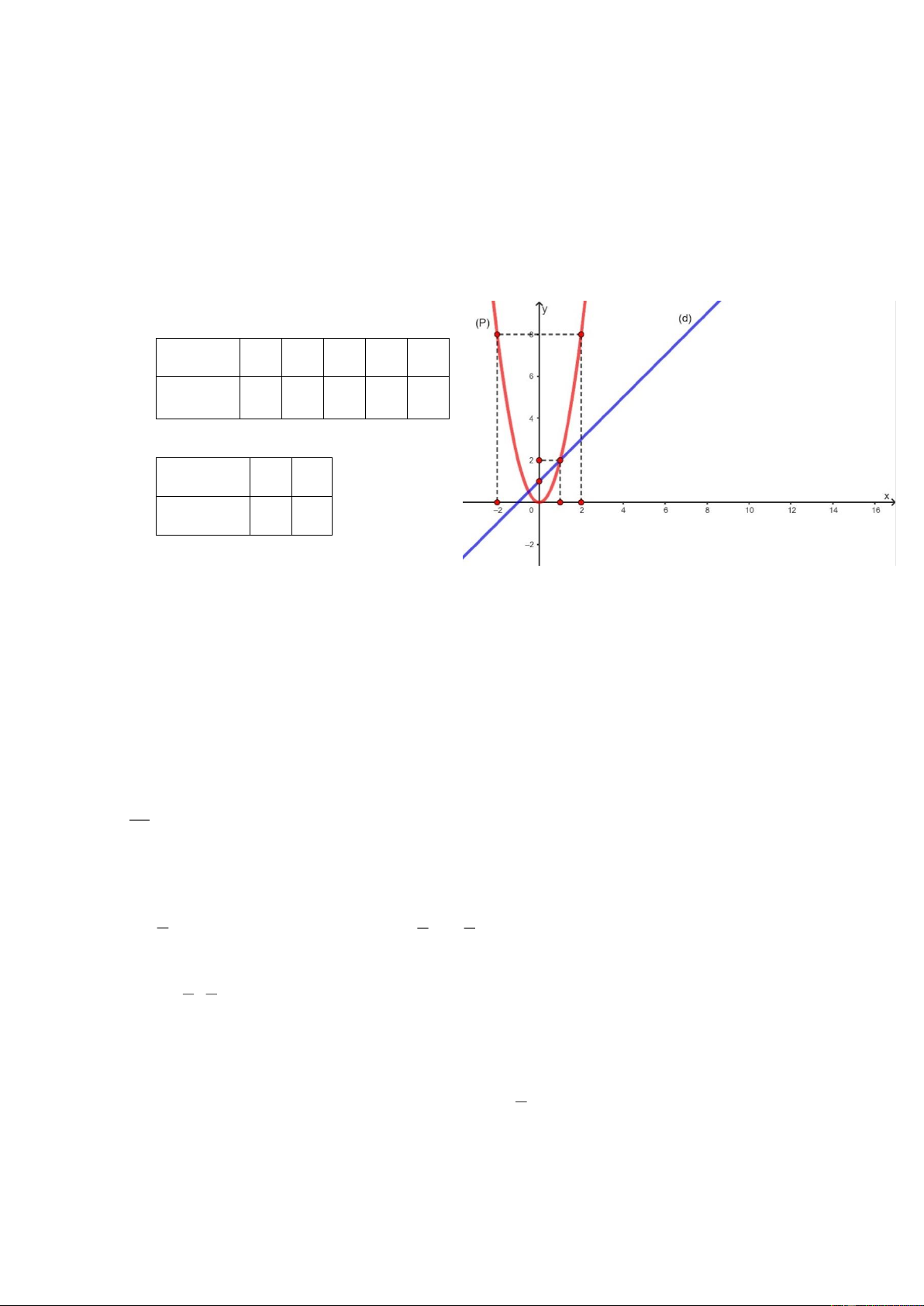
Câu 1. (1,5 điểm). Cho hàm số y
có đồ thị P và đường thẳng y x 4 có đồ thị D . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ Oxy .
b) Tìm tọa độ giao điểm của P và d bằng phép toán.
Câu 2. (1 điểm). Cho phương trình 2
2x 5x 1 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2 x x
hãy tính giá trị của biểu thức A 1 2 2022 x 1 x 1 1 2
Câu 3. (0,75 điểm). Một công ty A chuyên cung cấp dịch vụ Internet với mức phí ban đầu lắp đặt
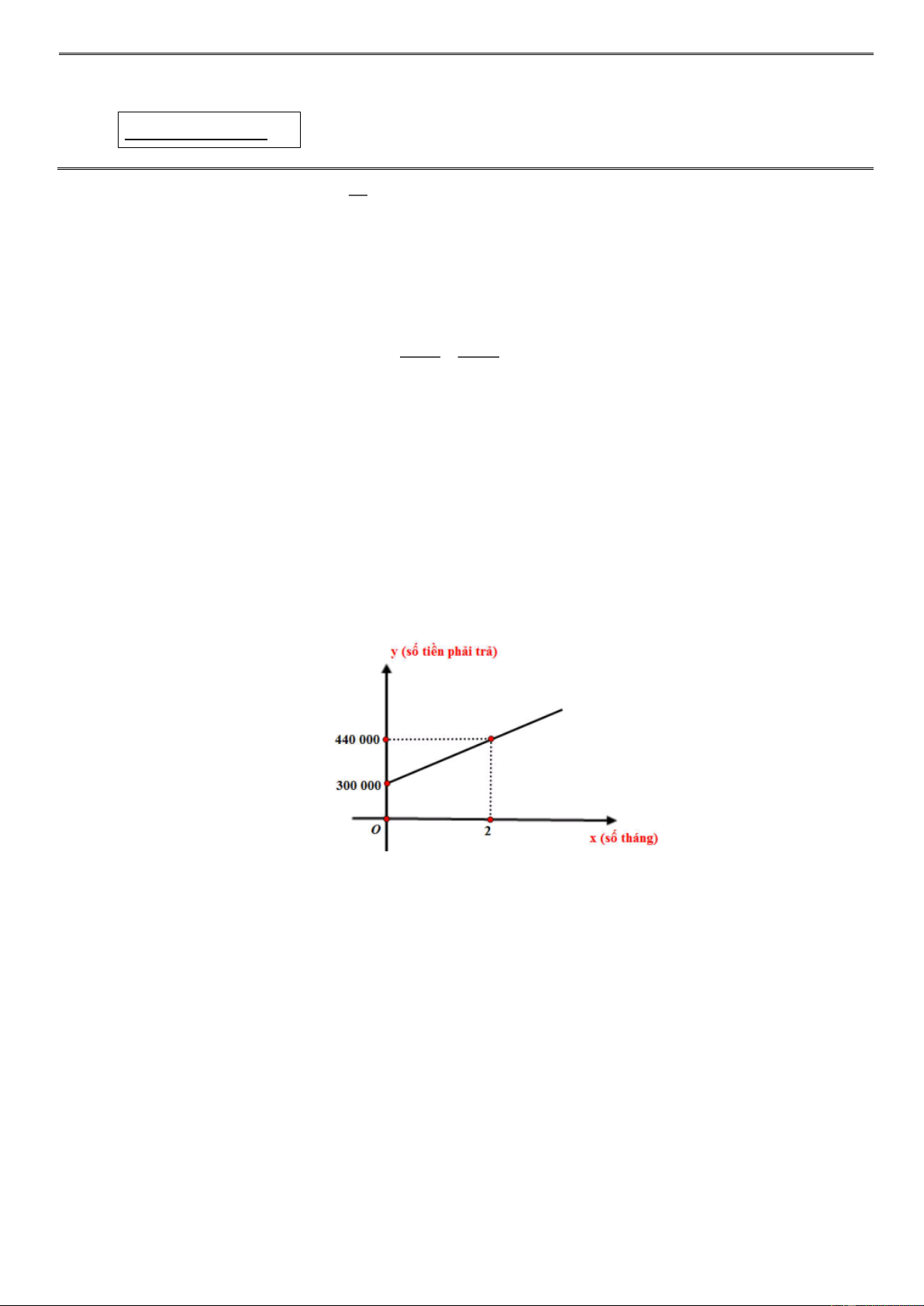
là 300000 đồng. Sau 2 tháng sử dụng thì cước phí phải trả là 440000 đồng. Cước phí y
(đồng) là số tiền mà người sử dụng Internet cần trả hàng tháng và phụ thuộc vào thời gian
sử dụng x tháng. Công thức biểu thị mối liên hệ giữa hai đại lượng này là một hàm số bậc
nhất y ax b được minh họa bởi hình vẽ bên.
a) Xác định các hệ số a và . b
b) Anh Hùng sử dụng Internet của công ty A trên thì sau nửa năm anh phải trả cước phí là bao nhiêu?
Câu 4. (1 điểm). Trong đợt lũ lụt miền Trung vừa qua đã gây thiệt hại rất lớn cho các tỉnh miền
Trung, một nhóm gồm 18 bạn lớp 9A tham gia hoạt động thiện nguyện để góp phần ủng
hộ cho một số gia đình có hoàn cảnh khó khăn. Ngoài trích từ tiền quỹ của nhóm là
500000 đồng, mỗi bạn tham gia thống nhất sẽ đóng góp 50 000 đồng. Biết các con mình
làm việc tốt, một số phụ huynh rất đồng tình ủng hộ nên đã hỗ trợ thêm các bạn tổng số
tiền là 1350 000 đồng. Các bạn dự kiến vào siêu thị mua mỗi phần quà gồm: một hộp bánh
giá 55000 , hai chai nước ngọt giá 34 000 , hai gói kẹo giá 27 000 , một túi gạo giá 90 000 ,
một hộp socola giá 45000 và một túi rau câu giá 18 000 .
a) Biết siêu thị đang có chương trình giảm giá 10% cho các mặt hàng bánh, nước ngọt,
kẹo và rau câu; giảm giá 20% cho các mặt hàng gạo và socola. Em hãy tính xem các bạn
có thể mua được bao nhiêu phần quà?
b) Nếu muốn mua đủ 14 phần quà thì các bạn cần thêm ít nhất bao nhiêu tiền? Trang 1
Câu 5. (0,75 điểm). Sau thời gian dịch bệnh kéo dài để chuẩn bị cho kỳ thi học kỳ 2 môn toán
lớp 9 vào ngày 26 / 4 / 2022 thầy giáo có giao một số bài tập toán để lớp tự ôn tập ở nhà.
Sau khi nhận bài tập xong bạn Lan lên kế hoạch cho việc ôn tập của mình như sau. Bắt đầu
từ thứ 6 ngày 11 / 02 / 2022 đến hết tháng 3 cứ những ngày chẵn sẽ làm 2 bài tập còn
những ngày lẻ thì làm 3 bài tập. Số bài còn lại là 34 bài Lan sẽ làm vào tháng 4 và sẽ hoàn thành trước ngày thi”.
a) Hỏi thầy giáo đã giao bao nhiêu bài tập toán cho Lan? biết tháng 2 / 2022 có 28 ngày
và tháng 3 / 2022 có 31 ngày.
b) Ngày thi cuối kỳ 2 là vào thứ mấy ? Tại sao?
Câu 6. (1 điểm). Để ước lượng khối lượng của cây gỗ trồng trong rừng người ta cần xác định
chiều cao h của cây (mét) và chu vi C của vòng tròn thân cây ngang tầm ngực (mét). Theo
cách đo đạc trong lâm nghiệp, độ cao ngang tầm ngực là 1,4 mét tính từ mặt đất. Từ đó
người ta có thể quấn thước dây vòng quanh thân cây ở độ cao này và ghi lại số đo chu vi C
a) Nếu một cây có chu vi C của vòng tròn thân cây ngang tầm ngực là 1,28 mét và chiều
cao là 20,4 mét thì cây có thể tích bao nhiêu (làm tròn đến chữ số thập phân thứ nhất)?
Biết công thức thể tích hình trụ V .
S h trong đó S là diện tích vòng tròn thân cây có chu vi C
nói trên và h là chiều cao của cây.
b) Biết khối lượng được tính theo công thức m .
D V (tấn). Cho biết loại cây nói trên có
khối lượng riêng là D 1,05 tấn/ 3
m . Hỏi thân cây trên nặng bao nhiêu kg ( kết quả làm tròn đến hàng trăm).
Câu 7. (1 điểm). Khi mới nhận lớp 9A , cô giáo chủ nhiệm dự định chia lớp thành 3 tổ có số học
sinh như nhau. Nhưng sau khi khai giảng xong lớp nhận thêm 4 học sinh nữa. Do đó, cô
giáo chủ nhiệm đã chia đều số học sinh của lớp thành 4 tổ. Hỏi lớp 9A hiện có bao nhiêu
học sinh, biết rằng so với phương án dự định ban đầu, số học sinh của mỗi tổ hiện nay có ít hơn 2 học sinh?
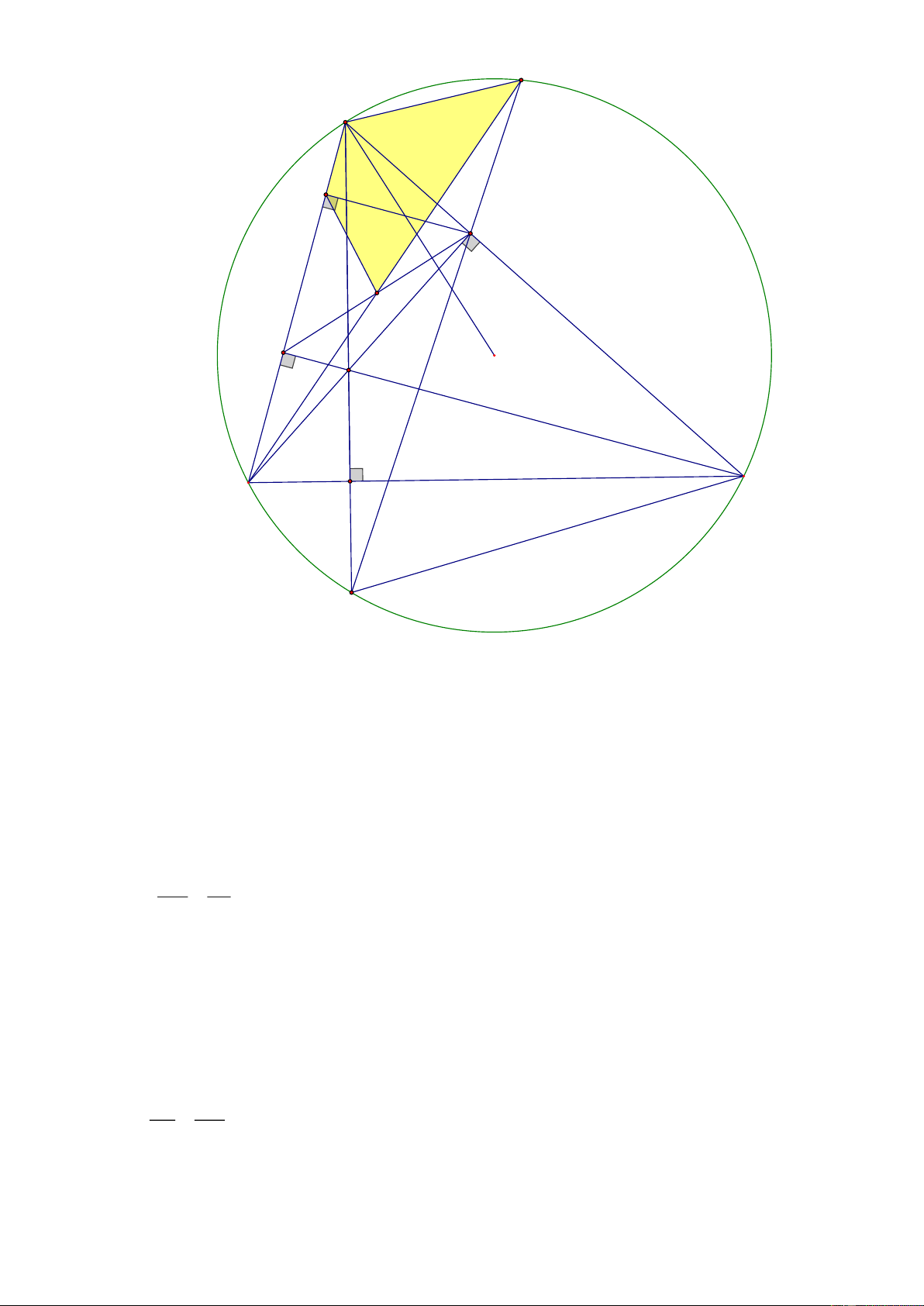
Câu 8. (3 điểm). Cho ABC nhọn, AB AC nội tiếp O . Kẻ ba đường cao AD,BE,CF cắt nhau
tại H , kéo dài AD cắt O tại K .
a) Chứng minh: Tứ giác BFEC nội tiếp và DCH DCK .
b) Tia KE cắt O tại M , BM cắt EF tại I , kẻ ES AB tại S . Chứng minh: 2
BE BI.BM
và tứ giác AMIS nội tiếp.
c) Qua điểm A kẻ tiếp tuyến xy của O , CF và CI cắt xy lần lượt tại Q và N .
Chứng minh: AQ 2FN . ----HẾT--- HƯỚNG DẪN GIẢI 2 x
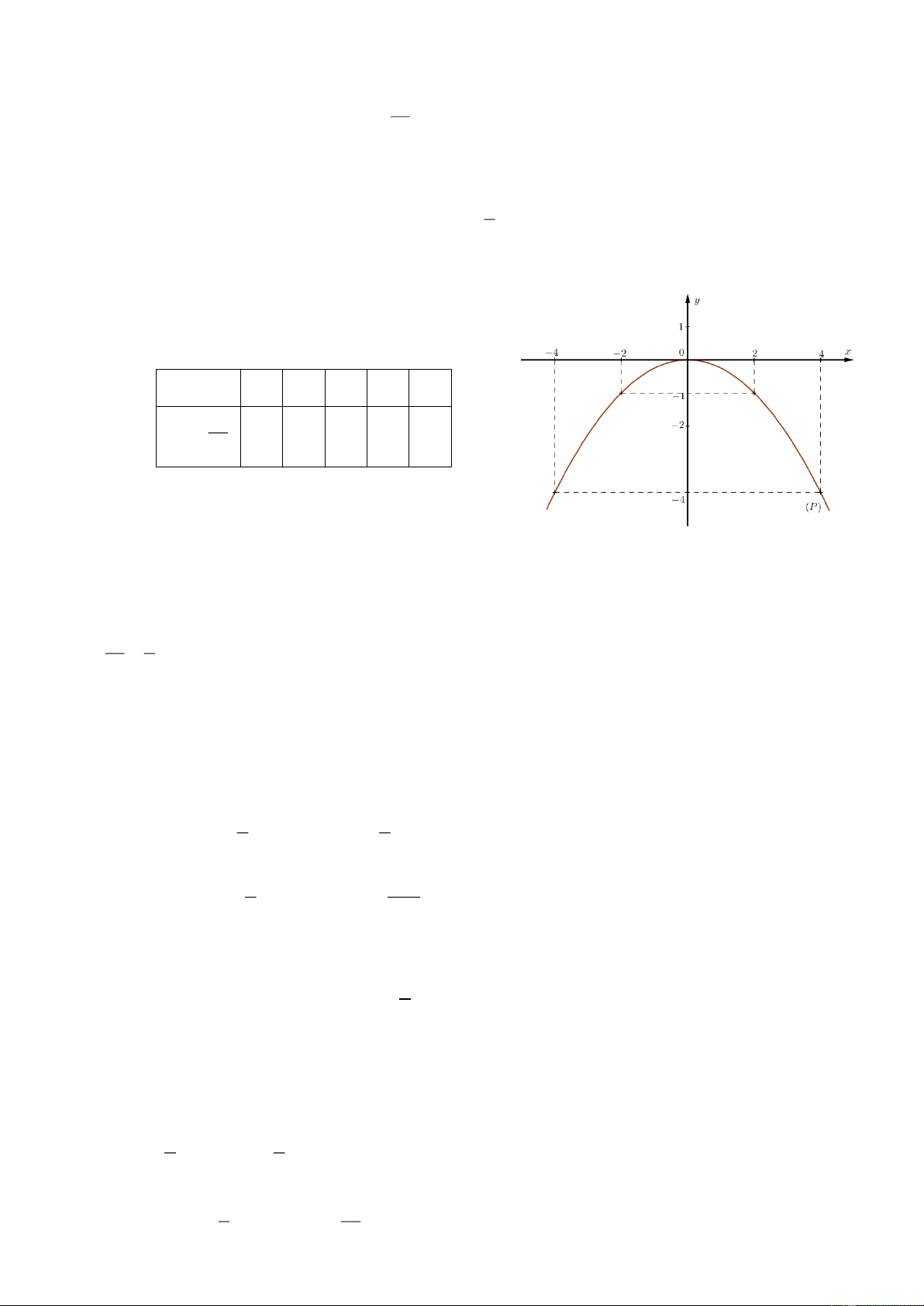
Câu 1. (1,5 điểm). Cho hàm số y
có đồ thị P và đường thẳng y x 4 có đồ thị D . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ Oxy .
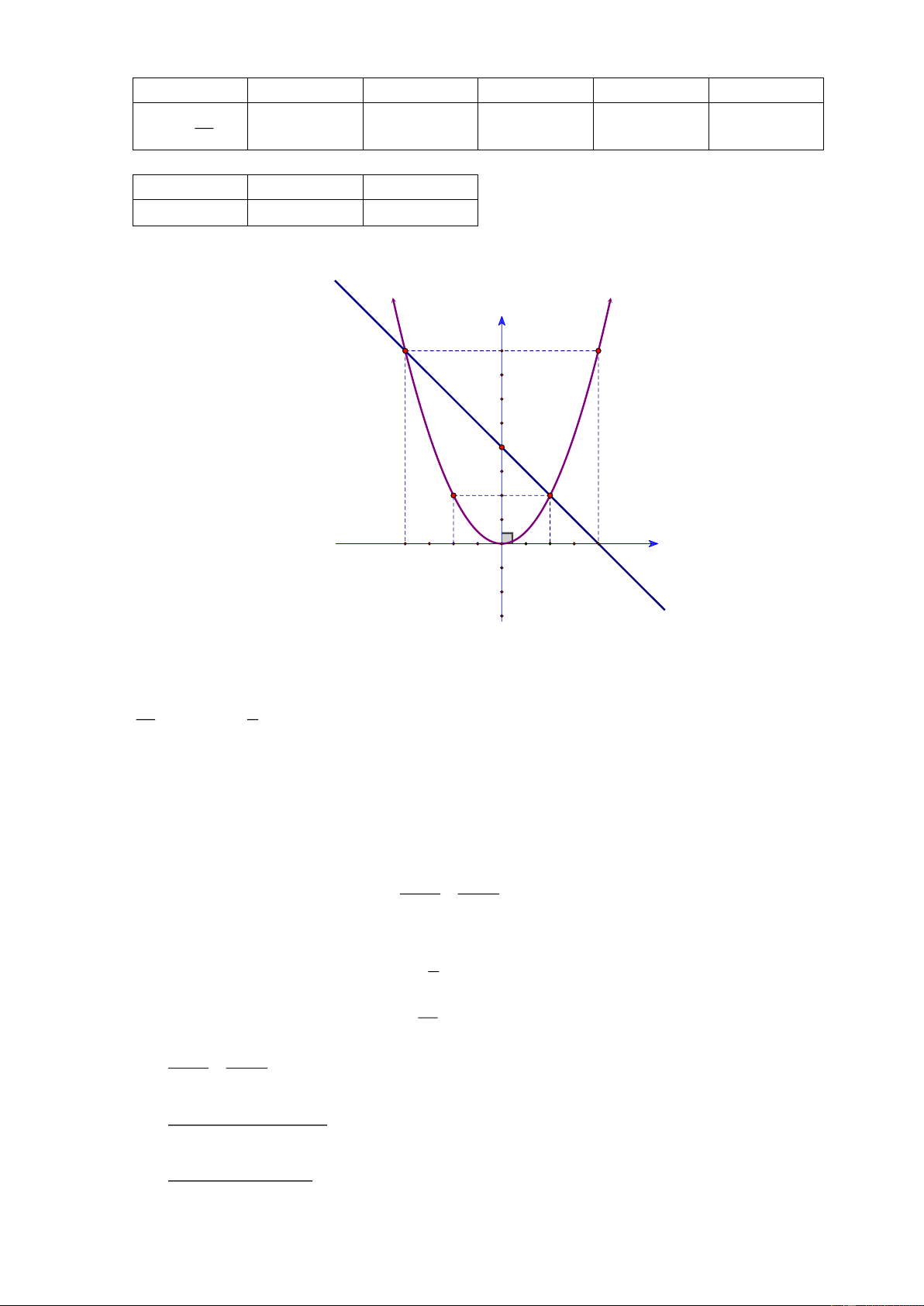
b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải Trang 2 a) Bảng giá trị: x 4 2 0 2 4 2 x y 8 2 0 2 8 2 x 0 2
y x 4 4 2 Đồ thị: y 8 7 6 5 4 3 2 1 -4 -3 -2 -1 O 1 2 3 4 x -1 -2 -3
b) Xét phương trình hoành độ giao điểm của P và D 2 x 1 x x 4 4 2
x x 4 0 2 2 x 2
Với x 4 y 4 4 8
Với x 2 y 2 4 2
Vậy toạ độ giao điểm của P và D là 4;8 và 2; 2
Câu 2. (1 điểm). Cho phương trình 2
2x 5x 1 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2 x x
hãy tính giá trị của biểu thức A 1 2 2022 x 1 x 1 1 2 Lời giải
S x x 5 1 2
Theo định lí Vi-et ta có: 2
P x .x 1 1 2 2 A x x 1 2 2022 x 1 x 1 1 2 x x 1 x x 1 1 2 2 1 A 2022 x 1 x 1 1 2
x x x x x A x 1 2 1 1 2 2 2022
x x x x 1 1 2 1 2 Trang 3 2P S A 2022 P S 1 1 5 2. A 2 2 2022 1 5 1 2 2 A 8081 4
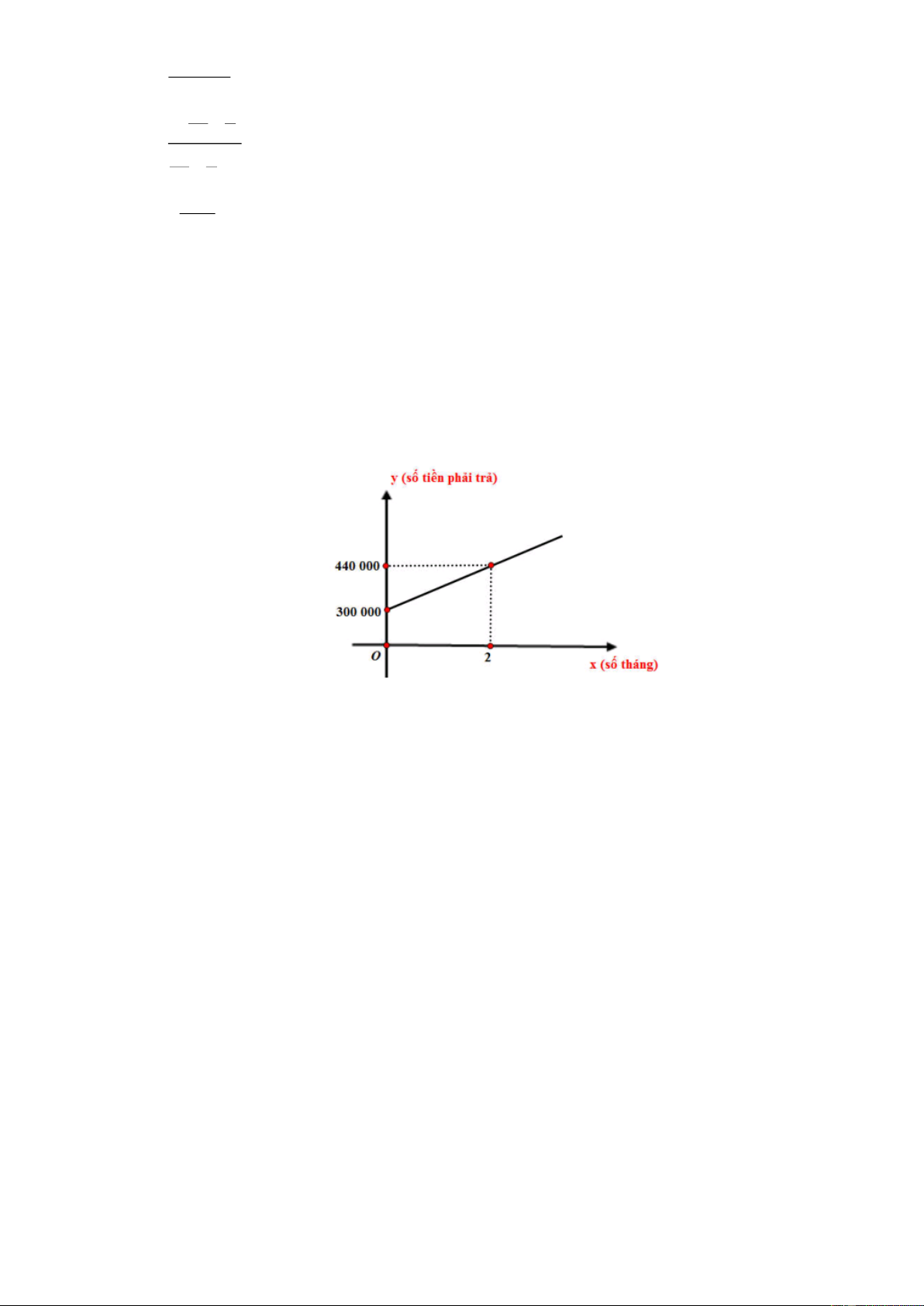
Câu 3. (0,75 điểm). Một công ty A chuyên cung cấp dịch vụ Internet với mức phí ban đầu lắp đặt
là 300000 đồng. Sau 2 tháng sử dụng thì cước phí phải trả là 440000 đồng. Cước phí y
(đồng) là số tiền mà người sử dụng Internet cần trả hàng tháng và phụ thuộc vào thời gian
sử dụng x tháng. Công thức biểu thị mối liên hệ giữa hai đại lượng này là một hàm số bậc
nhất y ax b được minh họa bởi hình vẽ bên.
a) Xác định các hệ số a và . b
b) Anh Hùng sử dụng Internet của công ty A trên thì sau nửa năm anh phải trả cước phí là bao nhiêu? Lời giải
a) Dựa vào đồ thị ta có:
x 0 tương ứng y 300000 đồng
x 2 tương ứng y 440000 đồng
Thay vào hàm số y ax b ta được hệ phương trình sau:
0.a b 330000 a 70000 2.a b 440000 b 300000
y 70000x 300000
b) Vì anh Hùng đã sử dụng nửa năm nên x 6 , thay vào công thức trên ta được:
y 70000.6 300000 720000
Vậy sau nửa năm anh Hùng trả số tiền là 720 000 đồng
Câu 4. (1 điểm). Trong đợt lũ lụt miền Trung vừa qua đã gây thiệt hại rất lớn cho các tỉnh miền
Trung, một nhóm gồm 18 bạn lớp 9A tham gia hoạt động thiện nguyện để góp phần ủng
hộ cho một số gia đình có hoàn cảnh khó khăn. Ngoài trích từ tiền quỹ của nhóm là
500000 đồng, mỗi bạn tham gia thống nhất sẽ đóng góp 50 000 đồng. Biết các con mình
làm việc tốt, một số phụ huynh rất đồng tình ủng hộ nên đã hỗ trợ thêm các bạn tổng số
tiền là 1350 000 đồng. Các bạn dự kiến vào siêu thị mua mỗi phần quà gồm: một hộp bánh
giá 55000 , hai chai nước ngọt giá 34 000 , hai gói kẹo giá 27 000 , một túi gạo giá 90 000 ,
một hộp socola giá 45000 và một túi rau câu giá 18 000 . Trang 4
a) Biết siêu thị đang có chương trình giảm giá 10% cho các mặt hàng bánh, nước ngọt,
kẹo và rau câu; giảm giá 20% cho các mặt hàng gạo và socola. Em hãy tính xem các bạn
có thể mua được bao nhiêu phần quà?
b) Nếu muốn mua đủ 14 phần quà thì các bạn cần thêm ít nhất bao nhiêu tiền? Lời giải
a) Số tiền mà nhóm bạn có được là:
500000 18.50000 1350000 2750000 đồng
Giá tiền một phần quà là:
55000340002700018000.90%9000045000.80% 228600
Số phần quà có thể mua được là:
2750000 : 228600 12 (phần quà)
b) Số tiền mua 14 phần quà là: 14.228600 3200 400 đồng
Vậy các bạn cần thêm ít nhất số tiền là: 3200 400 2750000 450 400 đồng
Câu 5. (0,75 điểm). Sau thời gian dịch bệnh kéo dài để chuẩn bị cho kỳ thi học kỳ 2 môn toán
lớp 9 vào ngày 26 / 4 / 2022 thầy giáo có giao một số bài tập toán để lớp tự ôn tập ở nhà.
Sau khi nhận bài tập xong bạn Lan lên kế hoạch cho việc ôn tập của mình như sau. Bắt đầu
từ thứ 6 ngày 11 / 02 / 2022 đến hết tháng 3 cứ những ngày chẵn sẽ làm 2 bài tập còn
những ngày lẻ thì làm 3 bài tập. Số bài còn lại là 34 bài Lan sẽ làm vào tháng 4 và sẽ hoàn thành trước ngày thi”.
a) Hỏi thầy giáo đã giao bao nhiêu bài tập toán cho Lan? biết tháng 2 / 2022 có 28 ngày
và tháng 3 / 2022 có 31 ngày.
b) Ngày thi cuối kỳ 2 là vào thứ mấy ? Tại sao? Lời giải
a) Từ 11 / 02 / 2022 đến 28 / 02 / 2022 có 9 ngày chẵn và 9 ngày lẻ (tổng là 18 ngày)
Từ 01 / 03 / 2022 đến 31 / 03 / 2022 có 15 ngày chẵn và 16 ngày lẻ (tổng là 31 ngày)
Số bài tập thầy giáo đã giao cho Lan là: 9 15.2 9 16.3 34 157 bài
b) Từ 11 / 02 / 2022 đến 26 / 4 / 2022 có tổng cộng: 18 31 26 75 ngày Ta có 75 : 7 10 (dư 5 )
Vì ngày 11 / 02 / 2022 là thứ sáu nên ngày 26 / 4 / 2022 là thứ ba.
Vậy Lan thi cuối kì 2 vào thứ ba.
Câu 6. (1 điểm). Để ước lượng khối lượng của cây gỗ trồng trong rừng người ta cần xác định
chiều cao h của cây (mét) và chu vi C của vòng tròn thân cây ngang tầm ngực (mét). Theo
cách đo đạc trong lâm nghiệp, độ cao ngang tầm ngực là 1,4 mét tính từ mặt đất. Từ đó
người ta có thể quấn thước dây vòng quanh thân cây ở độ cao này và ghi lại số đo chu vi C
a) Nếu một cây có chu vi C của vòng tròn thân cây ngang tầm ngực là 1,28 mét và chiều
cao là 20,4 mét thì cây có thể tích bao nhiêu (làm tròn đến chữ số thập phân thứ nhất)?
Biết công thức thể tích hình trụ V .
S h trong đó S là diện tích vòng tròn thân cây có chu vi C
nói trên và h là chiều cao của cây.
b) Biết khối lượng được tính theo công thức m .
D V (tấn). Cho biết loại cây nói trên có
khối lượng riêng là D 1,05 tấn/ 3
m . Hỏi thân cây trên nặng bao nhiêu kg ( kết quả làm tròn đến hàng trăm). Lời giải Trang 5 a) Ta có chu vi C R R 1,28 1,28 2 1,28 (m ) 2 1,28 2
Thể tích của cái cây là: V . S h 2 R h . .20,4 3 2,7m 2
b) Khối lượng của thân cây trên là: m .
D V 1,05.2,7 2,835 tấn 2800 kg .
Câu 7. (1 điểm). Khi mới nhận lớp 9A , cô giáo chủ nhiệm dự định chia lớp thành 3 tổ có số học
sinh như nhau. Nhưng sau khi khai giảng xong lớp nhận thêm 4 học sinh nữa. Do đó, cô
giáo chủ nhiệm đã chia đều số học sinh của lớp thành 4 tổ. Hỏi lớp 9A hiện có bao nhiêu
học sinh, biết rằng so với phương án dự định ban đầu, số học sinh của mỗi tổ hiện nay có ít hơn 2 học sinh? Lời giải
Gọi x là số học sinh đầu năm của lớp 9A * x x
Số học sinh mỗi tổ đầu năm là 3
Số học sinh sau khi khai giảng là: x 4 x 4
Số học sinh mỗi tổ sau khai giảng là: 4
Vì số học sinh của mỗi tổ hiện nay có ít hơn 2 học sinh so với ban đầu nên ta có phương x x 4 trình: 2 3 4
4x 3x 4 24
4x 3x 12 24 x 36 (nhận)
Vậy hiện tại số học sinh lớp 9A là 36 4 40 học sinh.
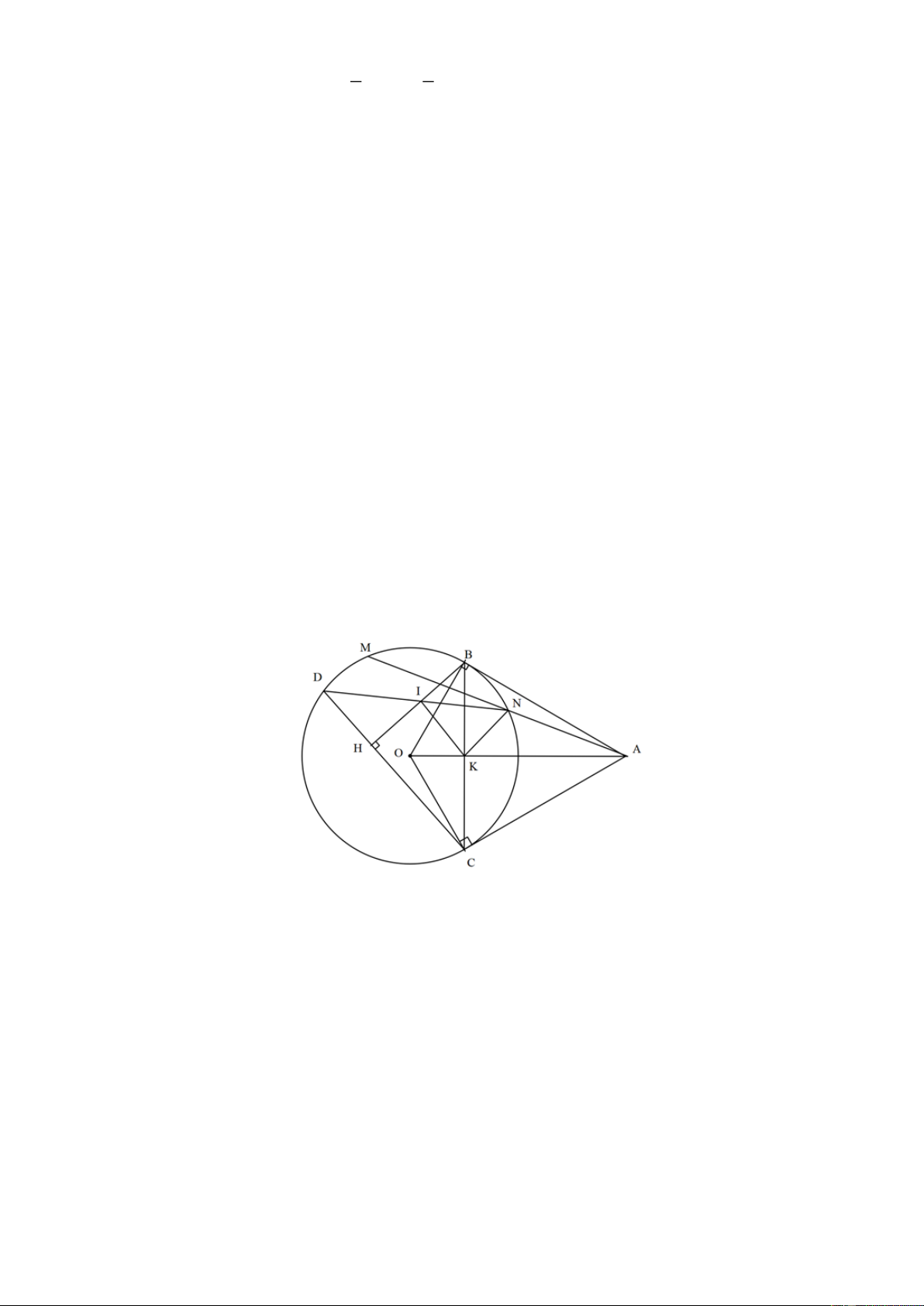
Câu 8. (3 điểm). Cho ABC nhọn, AB AC nội tiếp O . Kẻ ba đường cao AD,BE,CF cắt nhau
tại H , kéo dài AD cắt O tại K .
a) Chứng minh: Tứ giác BFEC nội tiếp và DCH DCK .
b) Tia KE cắt O tại M , BM cắt EF tại I , kẻ ES AB tại S . Chứng minh: 2
BE BI.BM
và tứ giác AMIS nội tiếp.
c) Qua điểm A kẻ tiếp tuyến xy của O , CF và CI cắt xy lần lượt tại Q và N .
Chứng minh: AQ 2FN . Lời giải
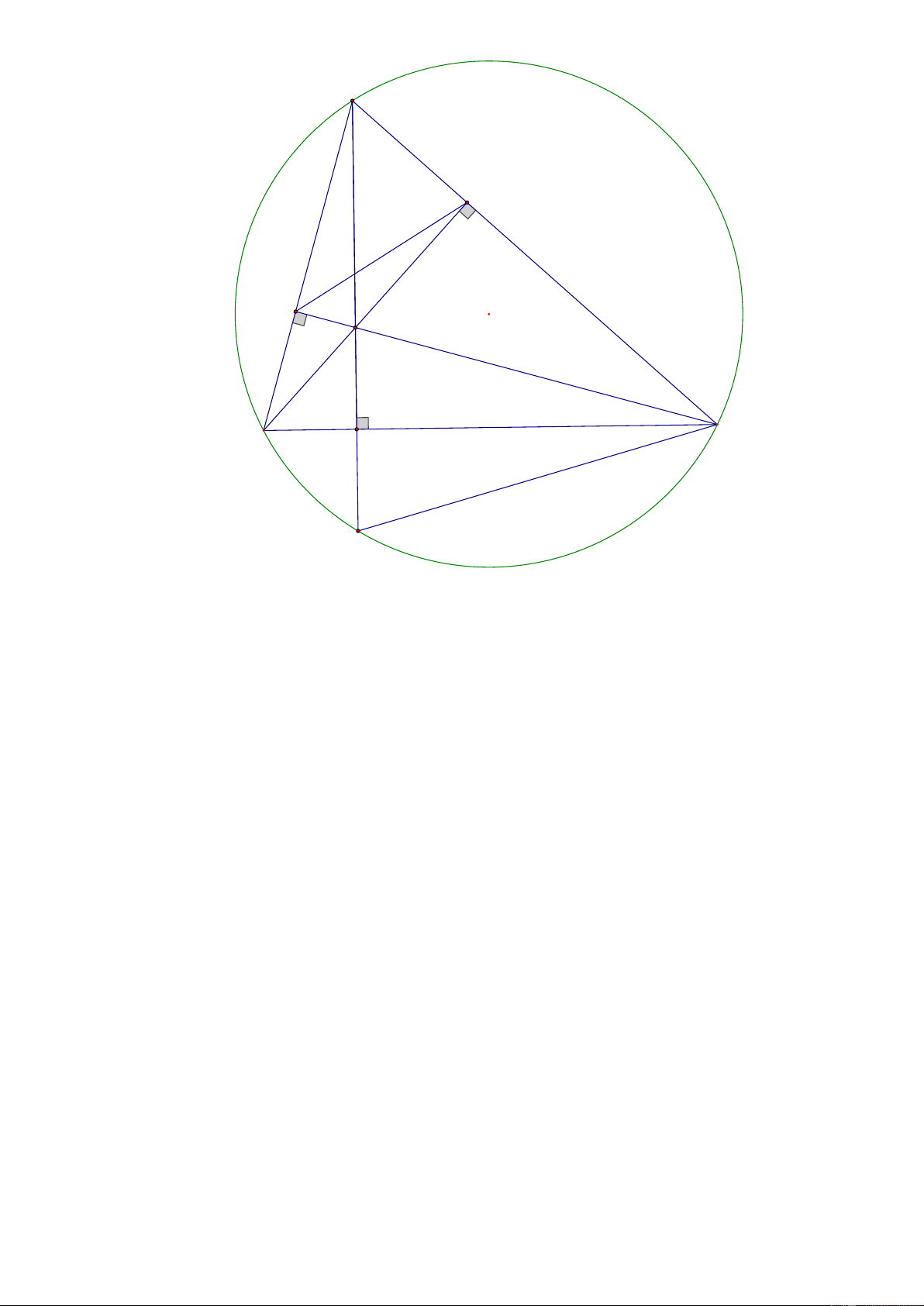
a) Chứng minh: Tứ giác BFEC nội tiếp và DCH DCK . Trang 6 A E F O H B C D K
Xét tứ giác BFEC ta có:
+ BFC BEC 90
+ Cùng nhìn cạnh BC
Tứ giác BFEC nội tiếp đường tròn đường kính BC .
Ta có DCK BAK ( 2 góc nội tiếp cùng chắn BK ) ( ) 1
Ta có BCF vuông tại F DCH phụ ABC
Ta có ABD vuông tại D BAK phụ ABC
DCH BAK (2) Từ ( )
1 và (2) suy ra DCH DCK
b) Tia KE cắt O tại M , BM cắt EF tại I , kẻ ES AB tại S . Chứng minh: 2
BE BI.BM
và tứ giác AMIS nội tiếp. Trang 7 M A S E I F O H B C D K
Ta có BME DCK ( 2 góc nội tiếp cùng chắn BK )
BME DCH
Mà tứ giác BFEC nội tiếp DCH BEI (cùng nhìn BF )
BME BEI
Xét BME và BEI + B chung
+ BME BEI (cmt)
BME” BEI gg BM BE BE BI 2
BE BI.BM ( ) 3
Xét BAE vuông tại E có ES là đường cao 2 BE .
BS BA (hệ thức lượng) (4) Từ ( )
3 và (4) suy ra BI.BM B . S BA
Xét BIS và BAM + B chung BI BS +
(vì BI.BM B . S BA ) BA BM
BIS” BAMcgc
BSI BMA (2 góc tương ứng)
AMIS nội tiếp (góc ngoài bằng góc đối trong) Trang 8
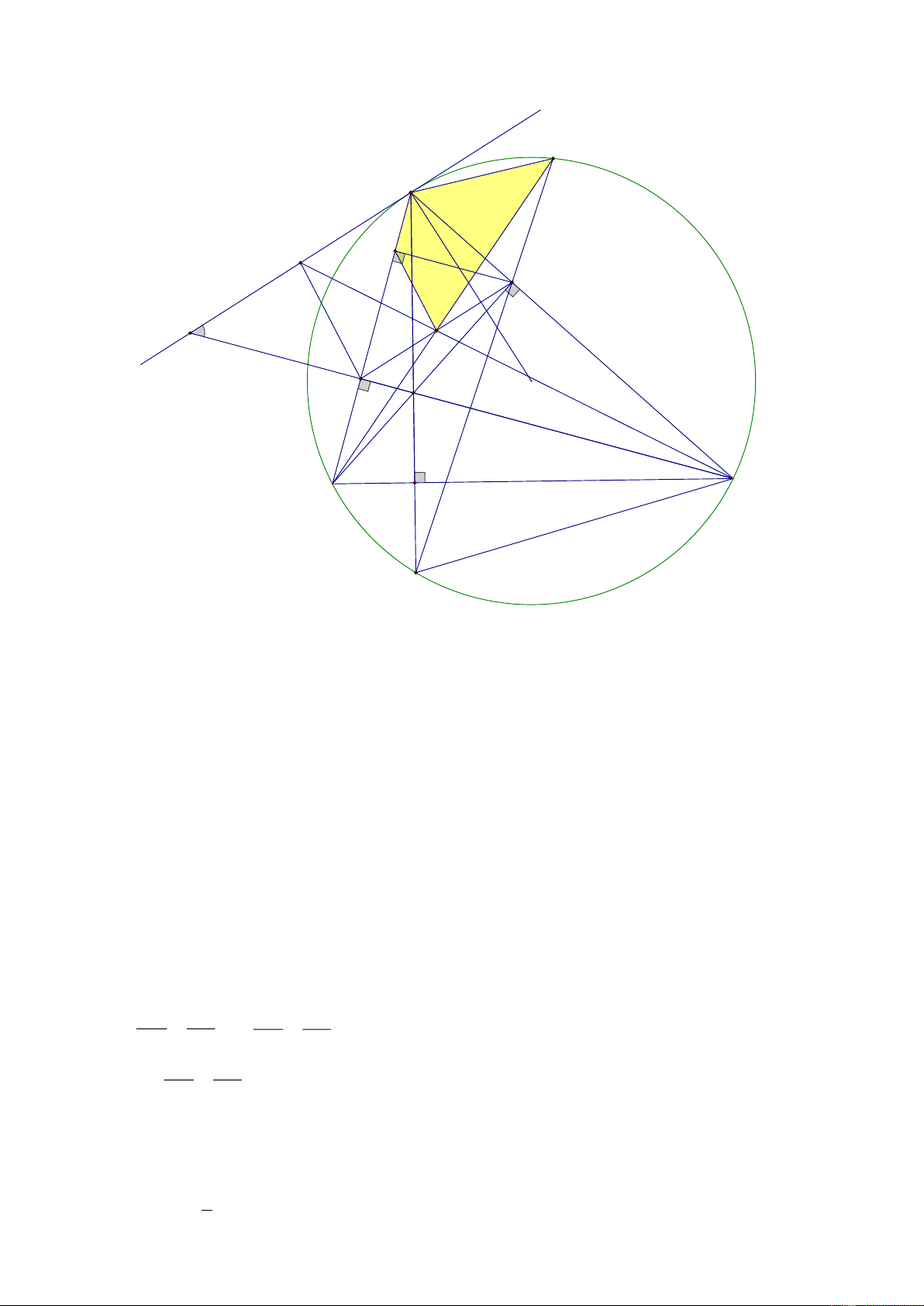
c) Qua điểm A kẻ tiếp tuyến xy của O , CF và CI cắt xy lần lượt tại Q và N .
Chứng minh: AQ 2FN . M A N S E Q x I F O H B C D K
Ta có FSI AMB (góc ngoài bằng góc đối trong)
AMB ACB ( 2 góc nội tiếp cùng chắn AB )
ACB SFI (góc ngoài bằng góc đối trong)
FSI SFI
SIF cân tại I IS IF (5)
Ta có IES ISE (cùng phụ với hai góc bằng nhau là IFS và ISF )
ISE cân tại I IS IE (6)
Từ (5) và (6) suy ra IE IF
I là trung điểm EF .
Ta có QAB ACB AFE
AQ// EF (hai góc sole trong bằng nhau)
Theo định lí Talet ta có: IF CI IE CI và NQ CN NA CN IF IE NQ NA
NQ NA (vì IE IF )
N là trung điểm AQ .
AFQ vuông tại F có FN là đường trung tuyến ứng với cạnh huyền
FN 1 AQ 2 Trang 9 AQ 2FN
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT TP THỦ ĐỨC
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: TP Thủ Đức - 4
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). Cho P y 2 :
2x và đường thẳng d : y x 1 .
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
4x 2x 1 0 có 2 nghiệm là x ,x . Không giải phương 1 2 2 1
trình, hãy tính giá trị của biểu thức A x x x x . 1 2 1 1 2
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 3. (1 điểm). Bạn An mang theo x (nghìn đồng), An mua lần lượt ba món đồ ở ba nơi khác nhau.
Món đồ thứ nhất, An trả một nửa tiền mang theo và thêm 10 000 đồng.
Món đồ thứ hai, An trả một nửa tiền còn lại sau khi mua món đồ thứ nhất và thêm 10 000 đồng.
Món đồ thứ ba, An trả một nửa tiền còn lại sau khi An mua món đồ thứ hai và thêm 10 000 đồng.
Gọi y (nghìn đồng) là số tiền còn lại sau khi An mua ba món đồ trên.
a) Viết công thức tính y theo x .
b) Sau khi mua ba món đồ trên, An còn lại 22 500 đồng. Hỏi An đã mang theo bao nhiêu
tiền và giá của mỗi món đồ trên là bao nhiêu?
Câu 4. (0,75 điểm). Giả sử giá tiền điện hàng tháng được tính theo bậc thang như sau:
Bậc 1 : Từ 1kWh đến 100kWh thì giá điện là: 1500d / kWh
Bậc 2 : Từ 101kWh đến 150kWh thì giá điện là: 2000d / kWh
Bậc 3 : Từ 151kWh trở lên thì giá điện là: 4000d / kWh
(Ví dụ: Nếu dùng 170kWh thì có 100kWh tính theo giá bậc 1 , có 50kWh tính theo giá bậc 2 và có
20kWh tính theo giá bậc 3 )
Tháng 4 năm 2022 tổng số tiền điện của nhà bạn A và bạn B là 560 000 đồng. So với tháng 4 thì
tháng 5 tiền điện của nhà bạn A tăng 30% , nhà bạn B tăng 20% , do đó tổng số tiền của cả hai nhà
trong tháng 5 là 701000 đồng. Hỏi tháng 4 nhà bạn A phải trả bao nhiêu tiền điện và dùng hết bao
nhiêu kWh ? ( biết rằng số tiền điện ở trên không tính thuế giá trị gia tăng).
Câu 5. (0,75 điểm ) Trong kết quả xét nghiệm lượng đường trong máu có bệnh viện tính theo đơn
vị là mg / dl nhưng cũng có bệnh viện tính theo đơn vị là mmol / l . Công thức chuyển đổi là
1mmol / l 18 mg / dl .Hai bạn Quý và Mão nhịn ăn sáng sau khi thử đường huyết tại nhà có
chỉ số đường huyết lần lượt là 70 mg/ dl và 90 mg/ dl . Căn cứ vào bảng sau, em hãy cho
biết tình trạng sức khỏe của hai bạn Quý và Mão. Trang 10 Chuẩn đoán Hạ đường Đường huyết Giai đoạn tiền Tên xét nghiệm bệnh tiểu huyết bình thường tiểu đường đường Đường huyết x < 4.0 4.0 £ x £ 5.6 5.6 < x < 7.0 x ³ 7.0 mmol / l lúc đói mmol / l mmol / l mmol / l
x mmol / l
Câu 6. (1 điểm). Nhân dịp năm mới, Công ty TNHH thực phẩm ORION VINA đã cho ra mắt bộ
quà Tết Orion với thiết kế đa dạng, sang trọng để phục vụ nhu cầu mua sắm, sử dụng quà
Tết cho cá nhân, gia đình và các doanh nghiệp. Bộ quà Tết Orion – Bình An I có giá
140 000 đồng. Bộ quà Tết Orion Bình An II có giá 180 000 đồng.
Bộ quà Tết Orion Bình An I
Bộ quà Tết Orion Bình An II
Để giới thiệu sâu rộng sản phẩm đến người dân, cửa hàng bác A đã quyết định giảm giá 10% bộ
quà Tết Bình An I và Bình An II . Ngoài ra nếu khách hàng mua từ 3 bộ quà của Orion trở lên thì
từ bộ thứ 3 khách hàng được giảm thêm 5%trên giá đã giảm. Chị Lan đã mua 3 bộ quà Bình An
II ở cửa hàng bác A để về biếu ông bà nội ngoại và trưng ở nhà 1 bộ. Hỏi số tiền thực tế chị phải trả là bao nhiêu?
Câu 7. (1 điểm). Trái Đất, hành tinh chúng ta đang sống, dạng hình cầu có bán kính khoảng
6370 km . Biết rằng 29% diện tích bề mặt Trái Đất không bị bao phủ bởi nước, bao gồm
núi, sa mạc, cao nguyên, đồng bằng và các địa hình khác.
a) Tính thể tích của Trái Đất?
b) Tính diện tích bề mặt Trái Đất bị bao phủ bởi nước?
(Lấy p » 3,14 , kết quả làm tròn đến chữ số hàng đơn vị.)
Câu 8. (3 điểm). Cho đường tròn ;
O R , điểm A nằm ngoài đường tròn với OA 2R , vẽ hai tiếp
tuyến A B, A C với đường tròn ( B , C là các tiếp điểm), D thuộc cung lớn BC , BD DC (
D,O, C không thẳng hàng), K là giao điểm của B C và OA .
a) Chứng minh: tứ giác AOBC nội tiếp và KB = KC . Trang 11
b) Vẽ BH vuông góc dây cung CD ( H thuộc CD ), gọi I là trung điểm của B H ; DI cắt
đường tròn O tại điểm thứ hai là N , A N cắt đường tròn O tại điểm thứ hai là M . Chứng minh: 2
AM .AN 3R và AKN ONM .
c) Chứng minh: AO là tiếp tuyến của đường tròn ngoại tiếp tam giác ABN . ----HẾT--- Trang 12 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm) Cho P y 2 :
2x và đường thẳng d : y x 1 .
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. a) BGT: x 2 1 0 1 2 y 2 2x 8 2 0 2 8 x 0 1 y x 1 1 2
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2 2x x 1 2
2x x 1 0 x 1 x 1 2
Thay x 1 vào y 2
2x , ta được: y 2 2.1 2 . 2 1 1
Thay x 1 vào y 2
2x , ta được: y 2. . 2 2 2 1 1 Vậy 1; 2 , ;
là hai giao điểm cần tìm. 2 2
Câu 2. (1 điểm) Cho phương trình 2
4x 2x 1 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2 2 1
hãy tính giá trị của biểu thức A x x x x 1 2 1 1 2 Lời giải 2 Vì 2
b 4ac 2 4.4. 1 20 0 Trang 13 x ,x
Nên phương trình có hai nghiệm phân biệt 1 2 . b S x x 2 1 1 2
Theo định lí Vi-et, ta có: a 4 2 c
P x .x 1 1 2 a 4 2 1 Ta có: A x x x x 1 2 1 1 2
A x x 2 1 x x 1 2 1 1 2 2 2
A x 2x x x x x x x 1 1 2 2 1 1 1 2 2 2
A x x x x 1 1 2 2
A x x 2 3x x 1 2 1 2 2 1 1 A 3. 2 4 A 1
Câu 3. ( 1 điểm) Bạn An mang theo x (nghìn đồng), An mua lần lượt ba món đồ ở ba nơi khác nhau.
Món đồ thứ nhất, An trả một nửa tiền mang theo và thêm 10 000 đồng.
Món đồ thứ hai, An trả một nửa tiền còn lại sau khi mua món đồ thứ nhất và thêm 10 000 đồng.
Món đồ thứ ba, An trả một nửa tiền còn lại sau khi An mua món đồ thứ hai và thêm 10 000 đồng.
Gọi y (nghìn đồng) là số tiền còn lại sau khi An mua ba món đồ trên.
a) Viết công thức tính y theo x .
Sau khi mua ba món đồ trên, An còn lại 22 500 đồng. Hỏi An đã mang theo bao nhiêu tiền và giá
của mỗi món đồ trên là bao nhiêu Lời giải
a) Viết công thức tính y theo x . x
b) Số tiền mua món hàng thứ nhất là: 10 2 x x
Số tiền còn lại sau khi mua món hàng thứ nhất là: x 10 10 2 2 x 10 x x
Số tiền mua món hàng thứ hai là: 2
10 5 10 5 2 4 4 x x x
Số tiền còn lại sau khi mua món hàng thứ hai là: 10 5 15 2 4 4 x 15 x x
Số tiền mua món hàng thứ ba là: 4
10 7,5 10 2,5 2 8 8 Trang 14 x x x
Số tiền còn lại là: y 15 2,5 17,5 4 8 8 b) Theo bài ra ta có: x 22,5 17,5 8 x 320
Vậy An mang theo 320 nghìn.
Giá của món đồ thứ nhất là: 170 nghìn
Giá của món đồ thứ hai là: 85 nghìn
Giá ccủa món đồ thứ ba là: 42, 5 nghìn
Câu 4. Giả sử giá tiền điện hàng tháng được tính theo bậc thang như sau:
Bậc 1 : Từ 1kWh đến 100kWh thì giá điện là: 1500d / kWh
Bậc 2 : Từ 101kWh đến 150kWh thì giá điện là: 2000d / kWh
Bậc 3 : Từ 151kWh trở lên thì giá điện là: 4000d / kWh
(Ví dụ: Nếu dùng 170kWh thì có 100kWh tính theo giá bậc 1 , có 50kWh tính theo giá bậc 2 và có
20kWh tính theo giá bậc 3 )
Tháng 4 năm 2022 tổng số tiền điện của nhà bạn A và bạn B là 560 000 đồng. So với tháng 4 thì
tháng 5 tiền điện của nhà bạn A tăng 30% , nhà bạn B tăng 20% , do đó tổng số tiền của cả hai nhà
trong tháng 5 là 701000 đồng. Hỏi tháng 4 nhà bạn A phải trả bao nhiêu tiền điện và dùng hết bao
nhiêu kWh ? ( biết rằng số tiền điện ở trên không tính thuế giá trị gia tăng). Lời giải
Gọi số tiền điện nhà bạn A phải trả trong tháng 4 là x x 0 (đồng)
Số tiền điện nhà bạn B phải trà trong tháng 4 là y y 0 (đồng)
Theo bài ta có tổng số tiền điện trong tháng 4 nhà bạn A và nhà bạn B phải trả là 56000 nên ta có
phương trình x y 560000 1
Số tiền điện trong tháng 5 nhà bạn A phải trả là x 30%x 1,3x (đồng)
Số tiền điện trong tháng 5 nhà bạn B phải trả là: y 20%y 1, 2y (đồng)
Theo bài ta có tổng số tiền điện trong tháng 5 nhà bạn A và nhà bạn B phải trả là 701000nên ta có
phương trình: 1,3x 1,2y 701000 2
x y 560000 x 290000
Từ 1 và 2 ta có hệ phương trình:
1,3x 1,2y 701000 y 270000
Vậy số tiền điện nhà bạn A phải trả trong tháng 4 là 290000 đồng.
Nhận thấy: 290000 100.1500 50.2000 10.4000 Trang 15
Vậy số điện nhà bạn A dùng trong tháng 4 là 100 50 10 160kWh .
Câu 5. (1 điểm) Trong kết quả xét nghiệm lượng đường trong máu có bệnh viện tính theo đơn vị là
mg / dl nhưng cũng có bệnh viện tính theo đơn vị là mmol / l . Công thức chuyển đổi là
1mmol / l 18 mg / dl .Hai bạn Quý và Mão nhịn ăn sáng sau khi thử đường huyết tại nhà có chỉ
số đường huyết lần lượt là 70 mg/ dl và 90 mg/ dl . Căn cứ vào bảng sau, em hãy cho biết tình
trạng sức khỏe của hai bạn Quý và Mão. Chuẩn đoán Hạ đường Đường huyết Giai đoạn tiền Tên xét nghiệm bệnh tiểu huyết bình thường tiểu đường đường Đường huyết x < 4.0 4.0 £ x £ 5.6 5.6 < x < 7.0 x ³ 7.0 mmol / l lúc đói mmol / l mmol / l mmol / l
x mmol / l Lời giải 1 35
Chỉ số đường huyết của Quý là 100mg / dl .70
3,9mmol / l . 18 9 1
Chỉ số đường huyết của Mão là 90mg / dl
.90 5mmol / l . 18
Căn cứ vào bảng đề bài cho, ta có thể kết luận: bạn Quý hạ đường huyết, còn bạn Mão đường huyết bình thường.
Câu 6. (1 điểm) Trái Đất, hành tinh chúng ta đang sống, dạng hình cầu có bán kính khoảng 6370 km
. Biết rằng 29% diện tích bề mặt Trái Đất không bị bao phủ bởi nước, bao gồm núi, sa mạc, cao
nguyên, đồng bằng và các địa hình khác.
c) Tính thể tích của Trái Đất?
d) Tính diện tích bề mặt Trái Đất bị bao phủ bởi nước?
(Lấy p » 3,14 , kết quả làm tròn đến chữ số hàng đơn vị.) Lời giải Trang 16 4 4
a) Thể tích của Trái Đất là: p 3 R = 3 .3,14.6370 = 3
1 082 148 051 227 (km ) 3 3 2 2 2
b) Diện tích bề mặt Trái Đất là: S = 4pR = 4.3,14.6370 = 509645864 (km )
Diện tích bề mặt Trái Đất không bị bao phủ bởi nước là: - ( 2 (100%
29%).509 645 864= 361 848 563 km ) ; O R
Câu 7. (3 điểm) Cho đường tròn
, điểm A nằm ngoài đường tròn với OA 2R , vẽ hai tiếp tuyến
A B , A C với đường tròn (B, C là các tiếp điểm), D thuộc cung lớn BC, BD DC (D, O, C không
thẳng hàng), K là giao điểm của BC và OA.
a) Chứng minh: tứ giác AOBC nội tiếp và KB = KC .
b) Vẽ BH vuông góc dây cung CD ( H thuộc CD ), gọi I là trung điểm của B H ; DI cắt O O đường tròn
tại điểm thứ hai là N , A N cắt đường tròn
tại điểm thứ hai là M . 2
Chứng minh: AM .AN
3R và AKN ONM .
c) Chứng minh: AO là tiếp tuyến của đường tròn ngoại tiếp tam giác ABN . Lời giải
a) Xét tứ giác OBAC , ta có:
OBA 90 ( AB là tiếp tuyến tại B của đường tròn O )
OCA 90 ( AC là tiếp tuyến tại C của đường tròn O )
Vậy OBA OCA 180
Do đó, tứ giác OBAC nội tiếp.
Cm: OA là trung trực của BC Suy ra: KB = KC
b) Xét tam giác OAB vuông tại B ( AB là tiếp tuyến tại B của O ) Trang 17 2 2 2
OA OB AB 2R2 2 2
R AB (1) 2 2 2
4R R AB 2 2 AB 3R Xét ABN và A MB , ta có: BAM : chung
ABN AMB (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung BN ) Suy ra: A BN A MB (g-g) AB AN Suy ra: 2
AB AM.AN (2) AM AB Từ (1) và (2) ,suy ra: 2
AM .AM 3R (đpcm) Cm: A KN A MO Cm: OMN ONM
Suy ra: AKN ONM
c) OB OC R
AB AC (Tính chất 2 tiếp tuyến cắt nhau tại A)
Suy ra: OA là đường trung trực của BC K là trung điểm của BC
Mà I là trung điểm của BH (gt)
Nên IK là đường trung bình của tam giác BHC IK // HC Suy ra: IK // HB
Vì IK // HC nên NIK NDC (hai góc đồng vị)
Mà NDC NBC (hai góc nội tiếp cùng chắn cung NC )
Nên NIK NBC .
Xét tứ giác IBNK có: NIK NBC (cmt)
Suy ra, tứ giác IBNK nội tiếp ( tứ giác có hai đỉnh I , B liên tiếp cùng nhìn KN dưới góc bằng nhau)
Trong tứ giác IBNK nội tiếp có BIK 90 , suy ra BNK 90
Ta có: NKA NBC (do cùng phụ BKN )
Mà NCA NBC (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung NC ).
Vậy NCA NKA
Xét tứ giác KNAC có: NCA NKA (cmt)
Vậy tứ giác KNAC nội tiếp ( tứ giác có hai đỉnh K,C liên tiếp cùng nhìn NA dưới góc bằng nhau)
Ta có NAO NCK (hai góc nội tiếp cùng chắn cung NK trong tứ giác NAKC nội tiếp)
Mà ABN NCK (góc nội tiếp-góc tạo bởi tia tiếp tuyến và dây cùng chắn cung BN ) Trang 18
Nên ABN NAO
Vậy AO là tiếp tuyến của đường tròn ngoại tiếp tam giác ABN . ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT THUÛ ÑÖÙC
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: TP Thủ Đức – 5
Thời gian: 120 phút (không kể thời gian phát đề) x
Câu 8. (1,5 điểm). Cho Parabol P 2 : y 4
a) Vẽ P trên mặt phẳng tọa độ Oxy .
b) Tìm tọa độ giao điểm của P và d 1 : y
x 2 bằng phép toán. 2 x
Câu 9. (1 điểm). Cho phương trình: 2 4x 1 . 2 3 3
Không giải phương trình hãy tính giá trị của biểu thức sau: T 3x 2 3x 2 . 1 2
Câu 10. Một xí nghiệp cần bán thanh lý sản phẩm.Số sản phẩm còn lại sau ngày bán được xác định
bởi hàm số: y ax b có đồ thị như sau:
a) Hãy dựa vào đồ thị hãy xác định a , b và hàm số y .
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý ?
Câu 11. Từ đài quan sát cao 15m (tính từ mực nước biển), bạn An có thể nhìn thấy hai chiếc
thuyền dưới góc hạ 400 và 100 so với phương ngang. Hãy tính khoảng cách 2 chiếc
thuyền (làm tròn đến chữ số hàng đơn vị)? Điều kiện lý tưởng: vị trí 2 chiếc thuyền và vị
trí đài quan sát thẳng hàng. ( 1 điểm).
Câu 12. Năm học 2021-2022 vừa quahai trường THCS trên địa bàn thành phố Thủ Đức có
210 học sinh thi đậu vào lớp 10 THPT, đạt tỉ lệ trúng tuyển 84% . Tính riêng thì trường Trang 19
A đậu 80% trường B đậu 90% . Em hãy tính xem mỗi trường có bao nhiêu học sinh
dự thi vào lớp 10 ; và có bao nhiêu học sinh thi đậu?
Câu 13. Một công ty du lịch dự định tổ chức một tour du lịch xuyên Việt nhân kỉ niệm ngày giải
phóng hoàn toàn miền Nam 30 – 4 . Công ty dự định nếu giá tour là 2 triệu đồng thì sẽ có
khoảng 150 người tham gia . Để kích thích mọi người tham gia, công ty sẽ quyết định giảm
giá và cứ mỗi lần giảm giá tour 100 nghìn đồng thi sẽ có thêm 20 người tham gia. Hỏi
công ty phải giảm giá tour là bao nhiêu để doanh thu từ tour xuyên Việt lả lớn nhất.
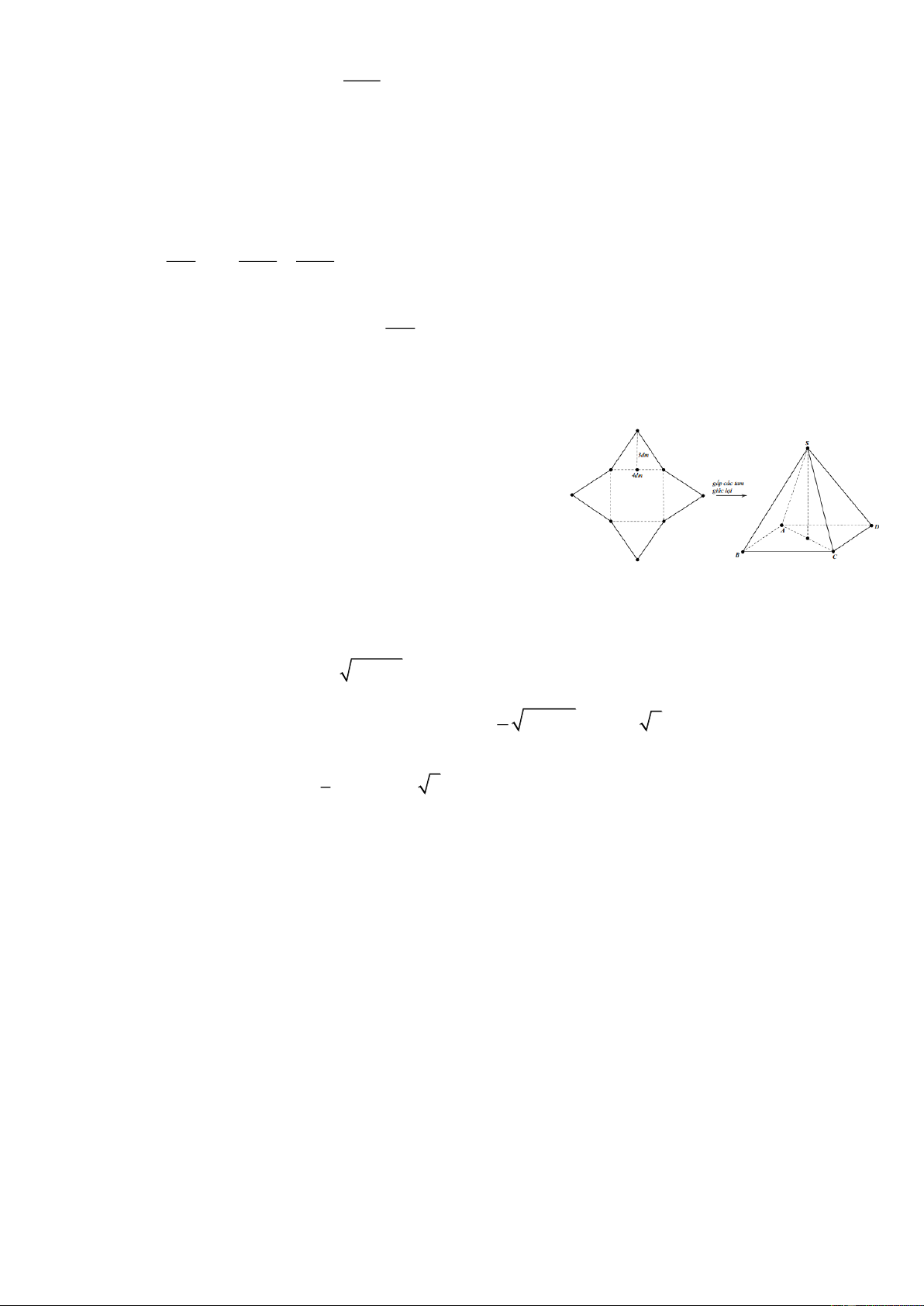
Câu 14. Để tạo một mô hình kim tự tháp (hình chóp tứ giác đều) từ tấm bìa, bạn Hạ cắt theo hình
bên (ở giữa là hình vuông cạnh 4dm, các tam giác bên ngoài là tam giác cân có chiều cao
3dm) rồi gấp 4 tam giác lại chung đỉnh. Hãy tính thể tích của mô hình được tạo thành ở
trên (làm tròn đến 1 chữ số thập phân)
Câu 15. Từ 1 điểm A ở ngoải đường tròn tâm O , vẽ 2 tiếp tuyến AB, AC với ( B,C là hai tiếp
điểm). Gọi H là giao điểm của OA và BC .
a) Chứng minh Tứ giác OBAC nội tiếp và H là trung điểm của BC .
b) Trên cung lớn BC của O lấy điểm D . Qua H vẽ dây cung DE củaO .
c) Chứng minh: BD.BE = CD.CE
d) Tia AE cắt O tại K . Chứng minh tứ giác BKDC là hình thang cân. ----HẾT--- Trang 20 HƯỚNG DẪN GIẢI 2 x
Câu 1. (1,5 điểm). Cho Parabol P : y 4
a. Vẽ P trên mặt phẳng tọa độ Oxy . 1
b. Tìm tọa độ giao điểm của P và d : y x 2 bằng phép toán. 2 Lời giải
c) Vẽ P trên mặt phẳng tọa độ Oxy . BGT: x 4 2 0 2 4 2 x y 4 1 0 1 4 4
d) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2
x 1 x 2 4 2 2 x 2x 8 2
x 2x 8 0 x 2 x 4 2 2 x 2
Thay x 2 vào y
, ta được: y 1 . 4 4 2 2 x (4) Thay x 4 vào y
, ta được: y 4 . 4 4 Vậy 2;
1 , 4; 4 là hai giao điểm cần tìm. x
Câu 2. (1 điểm) Cho phương trình: 2 4x 1 . 2 3 3
Không giải phương trình hãy tính giá trị của biểu thức sau: T 3x 2 3x 2 . 1 2 Lời giải x x Ta có: 2 2 4x
1 4x 1 0 2 2 1 2 65 Vì 2
b 4ac 4.4. 1 0 2 4 Trang 21
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 1 b S x x 1 2
Theo định lí Vi-et, ta có: 1 2 a 4 8 c
P x x 1 . 1 2 a 4 3 3
Ta có: T 3x 2 3x 2 1 2
T 3x 2 3x 2 1 3 2
T 9x x 6x 6x 43 1 2 1 2
T 9x x 3 6 x x 4 1 2 1 2 1 1 3 T 9. 6. 4 4 8 T 1
Câu 3. (1 điểm) Một xí nghiệp cần bán thanh lý sản phẩm.Số sản phẩm còn lại sau ngày bán được
xác định bởi hàm số: y ax b có đồ thị như sau:
a) Hãy dựa vào đồ thị hãy xác định a , b và hàm số y .
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý ? Lời giải
a) Hãy dựa vào đồ thị xác định a,b và hàm số y . Theo đề bài, ta có: x 0 Với
1410 0.a b 1 . y 1410 x 17 Với
900 17.a b 2 . y 900
0a b 1410 a 30
Từ 1 và 2 ta có hệ phương trình: .
17a b 900 b 1410 Vậy: a 30
, b 1410 và y 30x 1410 .
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý?
Thay y 0 vào y 30x 1410 , ta có: 0 3 0x 1410 30x 1410 x 47
Vậy cần 47 ngày để bán hết số sản phẩm cần thanh lý. Trang 22 Câu 4.
(0,75 điểm). Từ đài quan sát cao 15m (tính từ
mực nước biển), bạn An có thể nhìn thấy hai chiếc thuyền dưới góc hạ 0 40 và 0 10 so với phương ngang.
Hãy tính khoảng cách 2 chiếc thuyền (làm tròn đến
chữ số hàng đơn vị)? Điều kiện lý tưởng: vị trí 2
chiếc thuyền và vị trí đài quan sát thẳng hàng. (1 điểm). Lời giải
Ta có CD CA DA
CD AB tan CBA AB tan DBA CD 15. o 0 tan 40 tan10 CD 10m
Vậy khoảng cách 2 chiếc thuyền là 10m.
Câu 5. Năm học 2021-2022 vừa quahai trường THCS trên địa bàn thành phố Thủ Đức có 210
học sinh thi đậu vào lớp 10 THPT, đạt tỉ lệ trúng tuyển 84%. Tính riêng thì trường A
đậu 80% trường B đậu 90%. Em hãy tính xem mỗi trường có bao nhiêu học sinh dự
thi vào lớp 10 ; và có bao nhiêu học sinh thi đậu? Lời giải
Gọi x là số học sinh thi đậu trường A ( * x N ) *
Gọi y là số học sinh thi đậu trường B ( y N )
Vì hai trường THCS A và B có 210 học sinh thi đậu vào lớp 10 THPT nên ta có phương trình: x y 210 (1)
Vì trường A đậu 80% và trường B đậu 90%, cả hai trường đạt tỉ lệ trúng tuyển 84% nên ta có phương trình: x y 210 80% 90% 84% (2)
Từ (1) và (2) ta có hệ phương trình:
x y 210 x y 210 x 120 y 90 80% 90% 84% (thỏa mãn điều kiện)
Vậy trường A có 120 học sinh, trường B có 90 học sinh
Câu 6. Một công ty du lịch dự định tổ chức một tour du lịch xuyên Việt nhân kỉ niệm ngày giải
phóng hoàn toàn miền Nam 30 – 4 . Công ty dự định nếu giá tour là 2 triệu đồng thì sẽ có
khoảng 150 người tham gia . Để kích thích mọi người tham gia, công ty sẽ quyết định giảm Trang 23
giá và cứ mỗi lần giảm giá tour 100 nghìn đồng thi sẽ có thêm 20 người tham gia. Hỏi công
ty phải giảm giá tour là bao nhiêu để doanh thu từ tour xuyên Việt lả lớn nhất. Lời giải
Cách 1: Gọi số lần giảm giá 100 000 đồng thì thu được doanh thu lớn nhất là x (lần)
Sau x lần giảm thì giá của tour là:
2 000 000 100 000.x (đồng).
Vì cứ sau 1 lần giảm thì có thêm 20 người tham gia nên sau x lần giảm thì có thêm 20.x (người
tham gia) nên tổng số người tham gia sau x lần giảm giá là:
150 20.x (người )
Tổng doanh thu sau x lần giảm giá là:
S 2 000 000 100 000.x.150 20.x (đồng)
S 100 000.10.20 x.15 2x (đồng) S 2 1 000 000. 2
x 25x 300 (đồng) 25 Xét 2
2x 25x 300 2 2 x x 150 2 2 2 25 25 25 2
2 x 2. .x 150 4 4 4 2 25 3025 2 x 4 16 2 25 3025 3025 Vì : 2 x 2. 4 16 8 2 25 3025 3025
1 000 000. 2 x 1 000 000. 4 16 8 2 15 3025
1 000 000. x 378 125 000 4 16 S 378 125 000 S 378 125 000 max 25 Khi đó x 6, 25 (lần) 4
Vậy: Giá tour khi đó: 2 000 000 100 000.6, 25 1 375 000 (đồng).
Cách 2. Gọi x (đồng) là giới hạn sau khi giảm
2 x là giá được giảm. Trang 24 Khi đó, số 2 x người tham gia thêm là: .20 400 200x . 0,1
Tổng số khách tham quan khi đó là: 150 400 200x 550 200x .
Tổng doanh thu khi đó là: x 2 550 200 .x 2
00x 550x 2 2 100x 275x 2 275 3025 3025 2 10x 20 8 8 275
Vậy để doanh thu đạt lớn nhất thì 10x
0 x 1,375 (triệu đồng) 1375000 (đồng) 20
Câu 7. Để tạo một mô hình kim tự tháp (hình chóp tứ
giác đều) từ tấm bìa, bạn Hạ cắt theo hình bên (ở
giữa là hình vuông cạnh 4dm , các tam giác bên
ngoài là tam giác cân có chiều cao 3dm ) rồi gấp
4 tam giác lại chung đỉnh. Hãy tính thể tích của
mô hình được tạo thành ở trên (làm tròn đến 1
chữ số thập phân). Lời giải
Cạnh của hình chóp đều: 2 2
SA 3 4 5dm . 1
Đường cao của hình chóp đều: 2 2 2 2 2 2
SO SA AO 5
4 4 25 2 2dm . 2 1
Vậy: Thể tích hình chóp đều là: .4.4.25 2 2 3 118, 2dm . 3 Câu 16.
Từ 1 điểm A ở ngoải đường tròn tâm O , vẽ 2 tiếp tuyến AB, AC với ( B,C là
hai tiếp điểm). Gọi H là giao điểm của OA và BC .
Chứng minh Tứ giác OBAC nội tiếp và H là trung điểm của BC .
Trên cung lớn BC của O lấy điểm D . Qua H vẽ dây cung DE của O . Chứng minh: BD.BE = CD.CE
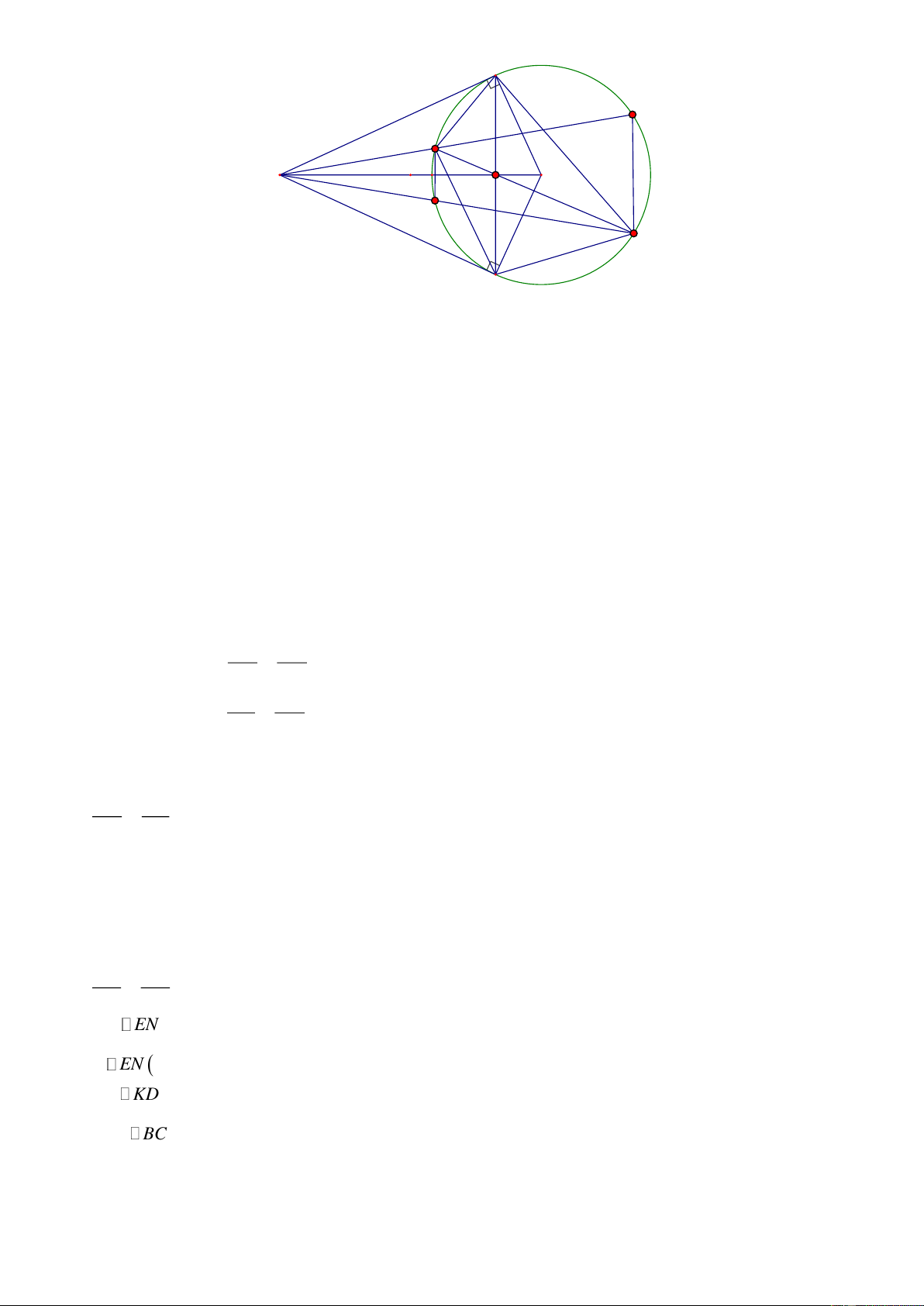
Tia AE cắt O tại K . Chứng minh tứ giác BKDC là hình thang cân. Lời giải Trang 25 B K E A H O N D C
a)Chứng minh Tứ giác OBAC nội tiếp và H là trung điểm của BC . o o o
*Ta có: ABC ACB 90 90 180
Tứ giác OBAC nội tiếp AB AC(gt) * OB OC RO
OAlà đường trung trực của BC.
OA BC tại H và H là trung điểm của BC .
b) Chứng minh: BD.BE = CD.CE ∽ BE BH BHE DHC 1 DC HD EC HC
EHC∽BHD 2 BD HD
HC HBcmt BE EC DC BD
BE.BD C . D EC
c)Chứng minh tứ giác BKDC là hình thang cân.
Ta có: AE AK AI AD 2 . . AB AE AN AD AK KD EN
*BC EN OA BC KD KD BC BKDC nôi tiêp
BKDC là hình thang cân. ----HẾT--- Trang 26




