

















Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN TAÂN
NAÊM HOÏC: 2023 - 2024 PHÚ MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
Thời gian: 120 phút (không kể thời gian phát đề)
MÃ ĐỀ: Quận Tân Phú - 1 x
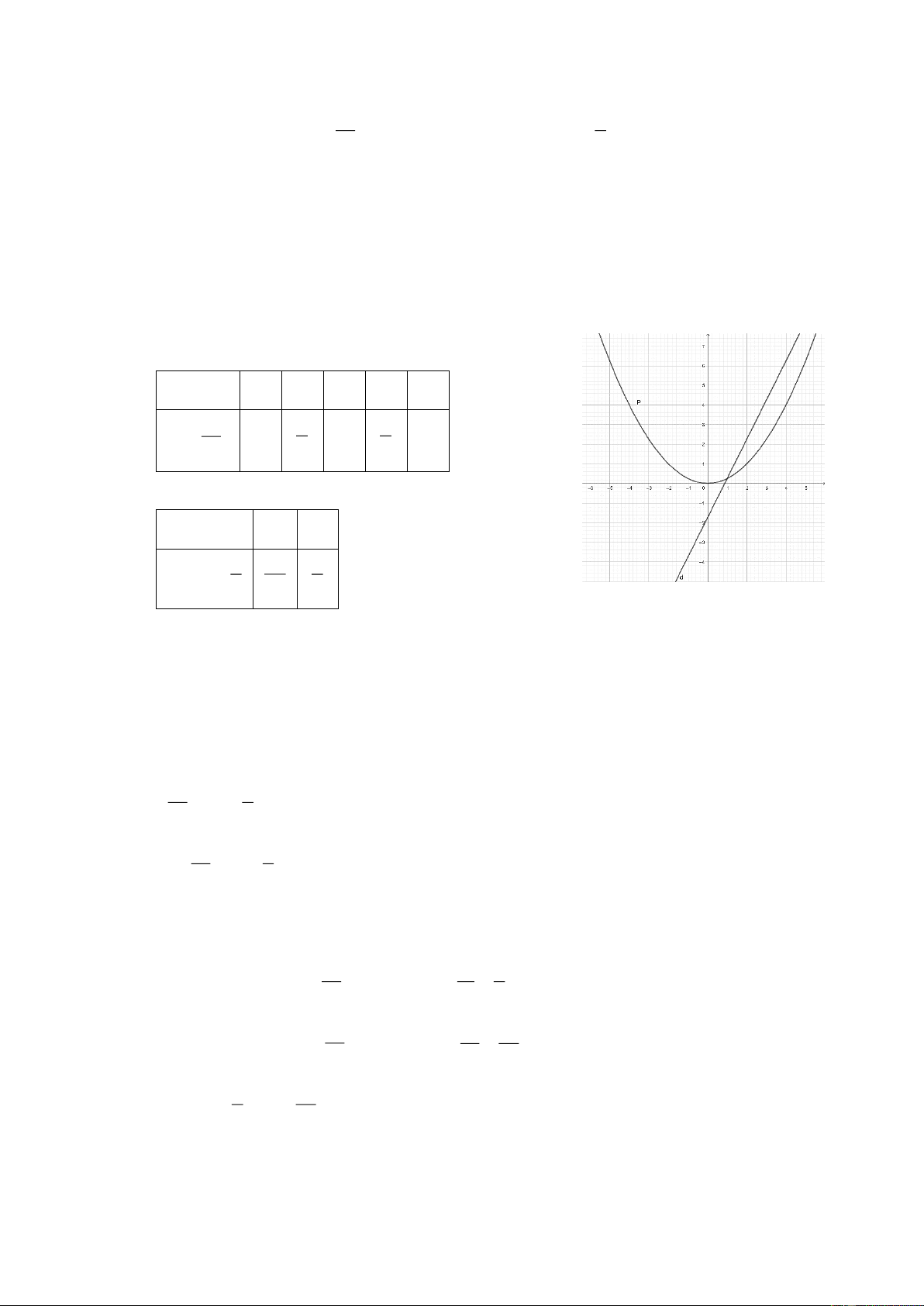
Câu 1. (1,5 điểm). Cho P 2 : y
và đường thẳng d 7
: y 2x . 4 4
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
4x 2x 5 0 có 2 nghiệm là x ,x . Không giải phương 1 2 x x
trình, hãy tính giá trị của biểu thức 1 2 B x 1 x 1 2 1
Câu 3. (1 điểm). Mỗi nơi trên thế giới có một múi giờ. Giờ mỗi ngày tại mỗi nơi được tính theo
công thức T GMT H , trong đó T là giờ tại nơi đó, GMT là giờ gốc, giờ ở múi giờ là 0 ,
H được xác định bởi bảng sau: a Múi giờ 0 1 2 3 4 5 6 7 H 0 1 2 3 4 5 6 7 Múi giờ 8 9 10 11 12 13 14 15 H H 8 9 10 11 12 11 10 9 Múi Múi giờ 16 17 18 19 20 21 22 23 H 8 7 6 5 4 3 2 1
Như vậy khi biết giờ ở một nơi có múi giờ này, ta có thể tính giờ ở nơi có múi giờ khác.
Múi giờ của một số thành phố được cho bởi bảng sau: Thành phố Hồ Chí Minh New York Moscow Los Angeles Múi giờ 7 19 3 16
Dựa vào cách tính trên em hãy tính xem:
a) Lúc 11 giờ ngày 03 / 06 ở NewYork thì ở Moscow là mấy giờ ngày nào?
b) Quỳnh đi chuyến bay từ Tp.HCM đến Moscow của hãng hàng không Aeroflot. Chuyến
bay xuất phát lúc 14 giờ 30 phút ngày 01 / 09 theo giờ tại Tp.HCM. Em hãy tính xem
chuyến bay kéo dài bao lâu biết Quỳnh đến sân bay quốc tế Sheremetyevo của Moscow lúc 21 giờ ngày 01 / 09 ?
Câu 4. (0,75 điểm). Nhân dịp kỉ niệm 1 năm thành lập, một cửa hàng thời trang đưa ra chương
trình khuyến mãi: đợt 1: Giảm 20% trên tất cả các mặt hàng từ ngày 01 / 10 / 2020 đến
05 / 10 / 2020 ; đợt 2 : giảm 5% tất cả các mặt hàng trên giá đã giảm của đợt 1 từ ngày Trang 1
06 / 10 / 2020 đến 10 / 10 / 2020 biêt giá niêm yết của áo thun là 400000 đồng/ áo, áo khoác 500 000 đồng/ áo.
a) Ngày 02 / 10 / 2020 nhóm của Lan gồm 5 người đến cửa hàng mua mỗi người 1 áo thun.
Hỏi nhóm của Lan phải trả bao nhiêu tiền?
b) Ngày 10 / 10 / 2020 Lan quay lại cửa hàng mua thêm 1 cái nón biết trước đó ngày
02 / 10 / 2020 , ngoài mua 1 áo thun, Lan đã mua thêm 1 áo khoác. Khi về đến nhà, Lan
tính tổng số tiền mua 1 áo thun, 1 áo khoác, 1 nón tổng cộng là 872000 đồng. Hỏi giá
niêm yết của 1 cái nón là bao nhiêu?
Câu 5. (1 điểm). Công ty A thực hiện một cuộc khảo sát để tìm hiểu về mối liên hệ giữa y (sản
phẩm) và số lượng sản phẩm T bán ra với x (nghìn đồng) là giá bán ra của mỗi sản phẩm
T và nhận thấy rằng y ax b ( a,b là hằng số). Biết với giá bán là 400000 (đồng)/ sản
phẩm thì số lượng sản phẩm bán ra là 1200 (sản phẩm); với giá bán là 460000 (đồng)/ sản
phẩm thì số lượng sản phẩm bán ra là 1800 (sản phẩm) a) Xác định a, . b
b) Bằng phép tính, hãy tính số lượng sản phẩm bán ra với giá bán là 440000 (đồng)/ sản phẩm?
Câu 6. (1 điểm). Một địa phương cấy 10ha giống lúa loại I và 8ha giống lúa loại II . Sau một mùa
vụ, địa phương đó thu hoạch và tính toán sản lượng thấy:
+ Tổng sản lượng của hai giống lúa thu về là 139 tấn;
+Sản lượng thu về từ 4ha giống lúa loại I nhiều hơn sản lượng thu về từ 3ha giống lúa loại
II là 6 tấn. Hãy tính năng suất lúa trung bình (đơn vị: tấn/ha) của mỗi loại giống lúa.
Câu 7. (1 điểm). Cho cốc rượu (như hình vẽ), phần phía trên là một hình nón có chiều cao 6cm và
đáy là đường tròn bán kính 3cm . Tính thể tích rượu trong ly. (Kết quả làm tròn đến chữ số thập phân thứ nhất) .
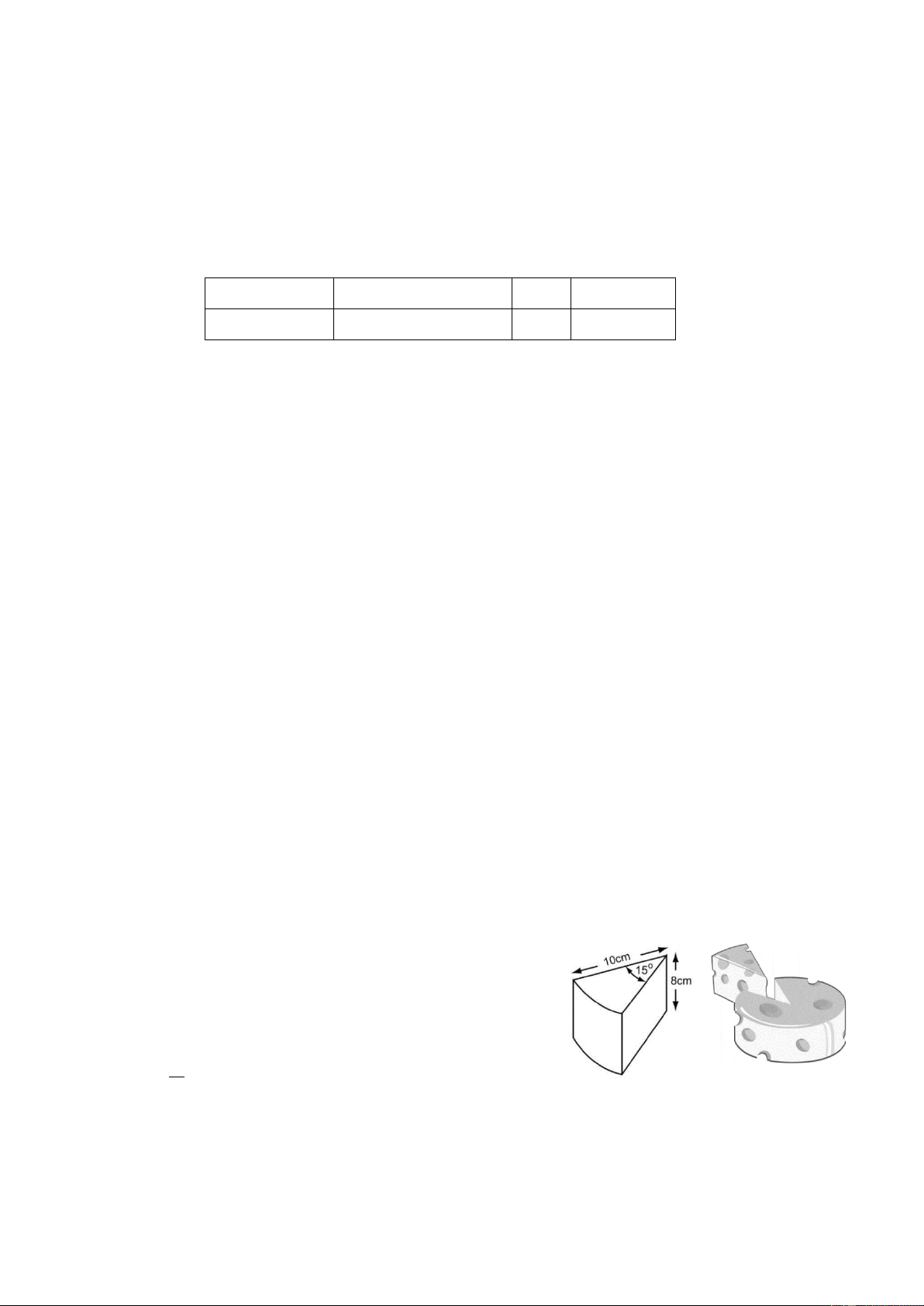
Câu 8. (3 điểm) Cho nửa đường tròn (O) , đường kính BC . Trên nửa đường tròn (O) , lấy hai điểm
A và D (theo thứ tự B, A,D,C ). Tia BA và CD cắt nhau tại S , đoạn thẳng AC cắt BD tại H.
a) Chứng minh SH BC tại E và tứ giác HECD nội tiếp.
b) Gọi T là trung điểm SH , tia AT cắt SC tại I , DE cắt HC tại K . Chứng minh:
TAH KDC . Từ đó suy ra C . K CA C . D CI Trang 2
c) Dường trung trực cả đoạn thẳng AK cắt BH tại Q . Chứng minh I
AK cân và ba điểm
A,O,Q thẳng hàng. ----HẾT--- Trang 3 HƯỚNG DẪN GIẢI 2 x Câu 1.
(1,5 điểm). Cho P : y
và đường thẳng d y x 7 : 2 . 4 4
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. a) BGT: x 2 1 0 1 2 2 x 1 1 y 1 0 1 4 4 4 x 0 1 7 1 y x 7 2 4 4 4
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2 x x 7 2 4 4 2
x x 7 2 0 4 4 x 1 x 7 2 x 2 1 1
Thay x 1 vào y , ta được: y . 4 4 4 2 x 2 7 49
Thay x 7 vào y , ta được: y . 4 4 4 1 49 Vậy 1; , 7;
là hai giao điểm cần tìm. 4 4 Trang 4 Câu 2.
(1 điểm). Cho phương trình 2
4x 2x 5 0 có 2 nghiệm là x ,x . Không giải phương 1 2 x x
trình, hãy tính giá trị của biểu thức B 1 2 x 1 x 1 2 1 Lời giải Vì 2
b ac 2 4
( 2) 4.4.(5) 64 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b S x x 1 1 2
Theo định lí Vi-et, ta có: a 2 c
P x .x 5 1 2 a 4 x x Ta có: B 1 2 x 1 x 1 2 1 B x x 1 2 x 1 x 1 2 1 x x 1 x x 1 1 1 2 2 B x 1 x 1 1 2 2 x x 2 x B x 1 1 2 2
x x x x 1 1 2 2 1 x x 2x x x x 1 2 2 1 2 1 2 B x x x x 1 1 2 1 2 1 2 5 2. 1 2 4 B 2 3 5 1 1 4 2
Câu 3. (1 điểm). Mỗi nơi trên thế giới có một múi giờ. Giờ mỗi ngày tại mỗi nơi được tính theo
công thức T = GMT + H , trong đó T là giờ tại nơi đó, GMT là giờ gốc, giờ ở múi giờ là
0 , H được xác định bởi bảng sau: a Múi giờ 0 1 2 3 4 5 6 7 H 0 1 2 3 4 5 6 7 Múi giờ 8 9 10 11 12 13 14 15 H H 8 9 10 11 12 - 11 - 10 - 9 Múi Múi giờ 16 17 18 19 20 21 22 23 H - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1
Như vậy khi biết giờ ở một nơi có múi giờ này, ta có thể tính giờ ở nơi có múi giờ khác. Trang 5
Múi giờ của một số thành phố được cho bởi bảng sau: Thành phố Hồ Chí Minh New York Moscow Los Angeles Múi giờ 7 19 3 16
Dựa vào cách tính trên em hãy tính xem:
d) Lúc 11 giờ ngày 03 / 06 ở NewYork thì ở Moscow là mấy giờ ngày nào?
e) Quỳnh đi chuyến bay từ Tp.HCM đến Moscow của hãng hàng không Aeroflot. Chuyến
bay xuất phát lúc 14 giờ 30 phút ngày 01 / 09 theo giờ tại Tp.HCM. Em hãy tính xem
chuyến bay kéo dài bao lâu biết Quỳnh đến sân bay quốc tế Sheremetyevo của Moscow lúc 21 giờ ngày 01 / 09 ? Lời giải
a) 11h ngày 03 / 06 ở NewYork T = GMT + H NY NY Þ 11 = GMT + (- 5) Þ GMT = 16
Vậy GMT là 16h ngày 03 / 06 T = GMT + H MC MC Þ T = 16 + 3 = 19 MC
Vậy ở Moscow là 19h ngày 03 / 06
b) HCM là 14h30p ngày 01 / 09 T = GMT + H HCM HCM Þ 14, 5 = GMT + 7 Þ GMT = 7, 5
Moscow là 21h ngày 01 / 09 T = GMT + H MC MC Þ 21 = GMT + 3 Þ GMT = 18
Vậy chuyến bay dài: 18 - 7, 5 = 10, 5h .
Câu 4. (0,75 điểm). Nhân dịp kỉ niệm 1 năm thành lập, một cửa hàng thời trang đưa ra chương
trình khuyến mãi: đợt 1 : Giảm 20% trên tất cả các mặt hàng từ ngày 01 / 10 / 2020 đến
05 / 10 / 2020 ; đợt 2 : giảm 5% tất cả các mặt hàng trên giá đã giảm của đợt 1 từ ngày Trang 6
06 / 10 / 2020 đến 10 / 10 / 2020 biêt giá niêm yết của áo thun là 400 000 đồng/ áo, áo khoác 500 000 đồng/ áo.
f) Ngày 02 / 10 / 2020 nhóm của Lan gồm 5 người đến cửa hàng mua mỗi người 1 áo
thun. Hỏi nhóm của Lan phải trả bao nhiêu tiền?
g) Ngày 10 / 10 / 2020 Lan quay lại cửa hàng mua thêm 1 cái nón biết trước đó ngày
02 / 10 / 2020 , ngoài mua 1 áo thun, Lan đã mua thêm 1 áo khoác. Khi về đến nhà, Lan
tính tổng số tiền mua 1 áo thun, 1 áo khoác, 1 nón tổng cộng là 872000 đồng. Hỏi giá
niêm yết của 1 cái nón là bao nhiêu? Lời giải
a) Nhóm của Lan phải trả: 5.400000.(1 - 20 ) % (1 - 5 )
% = 1600000(d)(d)
b) Gọi x là giá niêm yết của nón ((x > 0))
Số tiền Lan chi cho 3 món là: (400000 + 500000)(1 - 20 ) % + x (1 - 20 ) % (1 - 5 ) % = 872000
Þ x = 200000(N ) Þ x = 200000 (nhận)
Vậy giá niêm yết của nón là 200 000 đồng.
Câu 5. (1 điểm). Công ty ty A thực hiện một cuộc khảo sát để tìm hiểu về mối liên hệ giữa y (sản
phẩm) và số lượng sản phẩm T bán ra với x (nghìn đồng) là giá bán ra của mỗi sản phẩm
T và nhận thấy rằng y = ax + b (a,b là hằng số). Biết với giá bán là 400 000 (đồng)/ sản
phẩm thì số lượng sản phẩm bán ra là 1200 (sản phẩm); với giá bán là 460 000 (đồng)/ sản
phẩm thì số lượng sản phẩm bán ra là 1800 (sản phẩm) h) Xác định a, . b
i) Bằng phép tính, hãy tính số lượng sản phẩm bán ra với giá bán là 440 000 (đồng)/ sản phẩm? Lời giải
a) Giá bán là 400 000 (đồng)/ sản phẩm thì số lượng sản phẩm bán ra là 1200 (sản phẩm):
Thay x = 400;y = 1200 vào phương trìnhy = ax + b 1200 = . a 400 + b Trang 7
Giá bán là 460 000 (đồng)/ sản phẩm thì số lượng sản phẩm bán ra là 1800 (sản phẩm)
Thay x = 460;y = 1800 vào phương trìnhy = ax + b 1800 = . a 460 + b Ta có hệ phương trình:
ìïï1200 = a.400 + b ìï 400a + b = 1200 ìï a = 10 ï ï ï í Û í Û í
ï 1800 = a.460 + b
ï 460a + b = 1800 ï b = - 2800 ï ï ï ïî ïî î
Vậy y = 10x - 2800
b) Thay x = 440 vào phương trình y = 10x - 2800
y = 10.440 - 2800 = 1600(sp)
Câu 6. (1 điểm). Một địa phương cấy 10ha giống lúa loại I và 8ha giống lúa loại II . Sau một
mùa vụ, địa phương đó thu hoạch và tính toán sản lượng thấy:
+ Tổng sản lượng của hai giống lúa thu về là 139 tấn;
+Sản lượng thu về từ 4ha giống lúa loại I nhiều hơn sản lượng thu về từ 3ha giống lúa
loại II là 6 tấn. Hãy tính năng suất lúa trung bình (đơn vị: tấn/ha) của mỗi loại giống lúa. Lời giải
Gọi x, y lần lượt là năng suất lua trung bình của lúa loại I và lúa loại II (x,y > ) 0
Tổng sản lượng của hai giống lúa thu về là 139 tấn: 10x + 8y = 139
Sản lượng thu về từ 4ha giống lúa loại I nhiều hơn sản lượng thu về từ 3ha giống lúa
loại II là 6 tấn: 4x - 3y = 6 Ta có hệ phương trình:
ìï 10x + 8y = 139 ìï x = 7, 5 ï ï í Þ í (N ) ï 4x - 3y = 6 ï y = 8 ï ï ïî î
Năng suất lúa loại I là 7, 5 tấn/ha
Năng suất lúa loại II là 8 tấn/ha
Câu 7. (1 điểm). Cho cốc rượu (như hình vẽ), phần phía trên là một hình
nón có chiều cao 6cm và đáy là đường tròn bán kính 3cm . Tính
thể tích rượu trong ly. (Kết quả làm tròn đến chữ số thập phân thứ nhất) . Lời giải
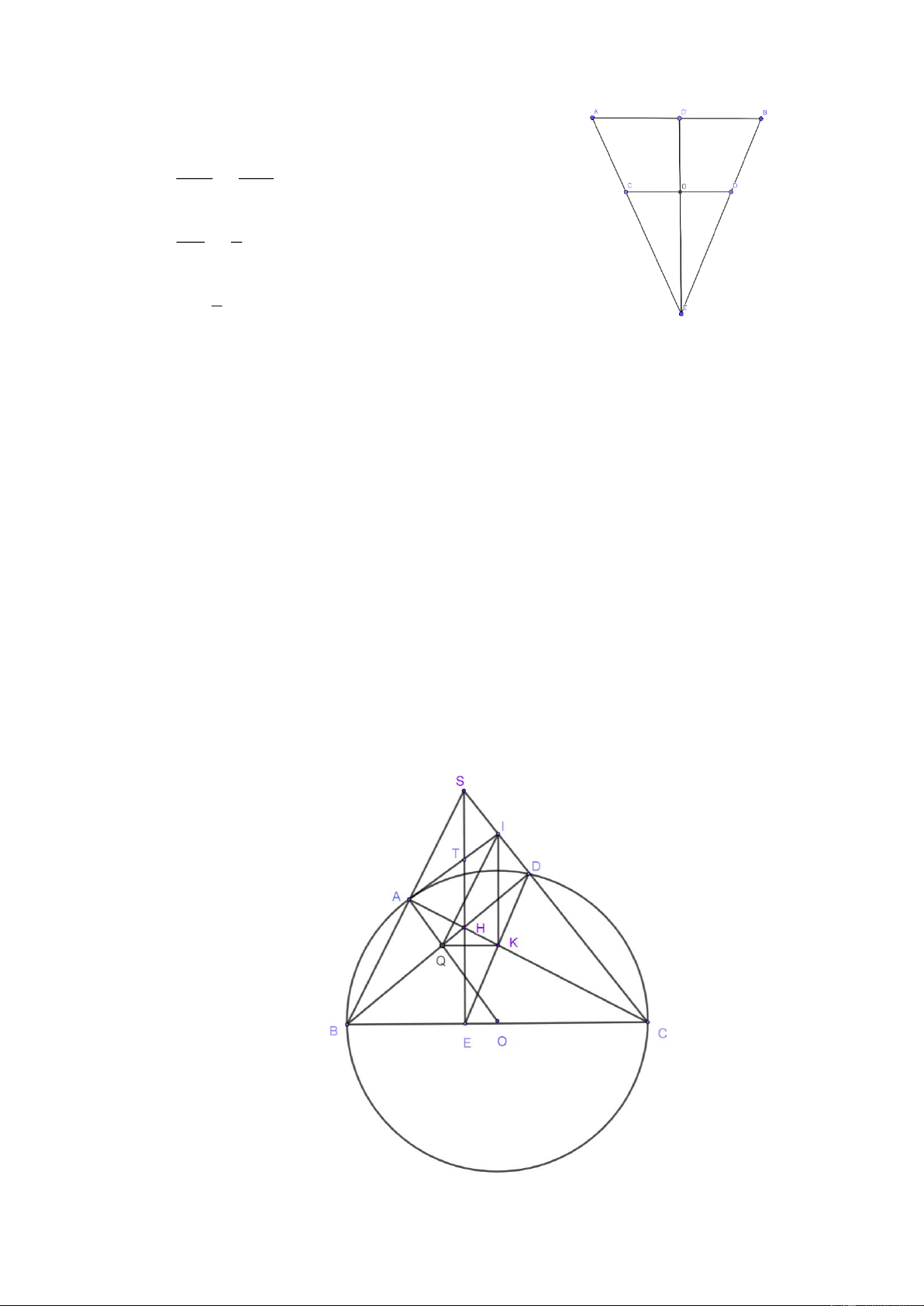
Gọi các điểm như hình vẽ Trang 8
OE = O ' E - OO ' = 6 - 2 = 4cm
Ta có: CO / / A O ' CO ' EO Þ = (Hệ quả Talet) A O ' EO ' CO 4 Þ = Þ CO = 2cm 3 6 1 2 3 V =
.p.2 .4 » 16, 8cm ruou 3
Câu 9. (3 điểm) Cho nửa đường tròn (O ) , đường kính BC . Trên nửa đường tròn (O ) , lấy hai
điểm A và D (theo thứ tự B, A, D,C ). Tia BA và CD cắt nhau tại S , đoạn thẳng A C cắt B D tại H .
a) Chứng minh SH ^ BC tại E và tứ giác HECD nội tiếp.
b) Gọi T là trung điểm SH , tia A T cắt SC tại I , DE cắt HC tại K . Chứng minh: · ·
T A H = K DC . Từ đó suy ra CK .CA = CD.CI
c) Dường trung trực cả đoạn thẳngA K cắt B H tạiQ . Chứng minh DIA K cân và ba điểm
A,O,Q thẳng hàng. Lời giải Trang 9
a) Chứng minh SH ^ BC tại E và tứ giác HECD nội tiếp. Xét (O), có:
CDB 1sñBC 90 2
BAC 1 sñBC 90 2 Xét D SBC có:
BD,CA là đường cao cắt nhau tại H
Þ H là trực tâm của DABC
Þ SH ^ BC tại E
Xét tứ giác HECD có: ìï · ï HDC = 90° ïíï · ï HEC = 90° ïî · ·
Þ HDC + HEC = 180°
Þ Tứ giác HECD nội tiếp.
b) Gọi T là trung điểm SH , tia A T cắt SC tại I , DE cắt HC tại K . Chứng minh: · ·
T A H = K DC . Từ đó suy ra CK .CA = CD.CI
Xét DSHA vuông tại A , có A I là đường trung tuyến.
Þ T A = T H = T S
Þ DT AH cân tại T · · T A H = A HT · ·
Mà A HT = EHC (đối đỉnh) · ·
Và EHC = EDC (tg EHDC nt ) · · Þ T A H = KDC
Xét DCKD và DCIA có: ìï µ ï C chung ïí ï · ·
ïT A H = KDC (cmt ) ïî Trang 10
Þ DCKD ∽ DCIA (g - g) CK CI Þ = (cctl) CD CA
Þ CK .CA = CD.CI
c) Đường trung trực cả đoạn thẳngA K cắt B H tạiQ . Chứng minh DIA K cân và ba điểm
A,O,Q thẳng hàng.
Dễ dàng Cm: Tứ giác SA HD nội tiếp.
Suy ra: HAD HSD 1 . · ·
Ta có: KDC = HA I (cmt ) Þ T g A IDK nt · ·
Þ KA D = KID ( ) 2 ( ) 1 và( ) · · 2 Þ HSD = KID
Mà 2 góc này ở vị trí đồng vị Þ IK / / SH · · Þ A HS = A KI · · Mà AHS = HAT · · Þ IKA = IA K
Þ DIAK cân tại I Ta có: ìïQA = QK ï í ï IA = IK ïî
Þ QI là đường trung trực của A K · · Þ ·
A IQ = SA I (cùng phụ IA K ) · · ·
Mà SAI = T SA = ADH · · Þ AIQ = ADQ
Þ Tứ giác A IDQ nội tiếp
Mà tứ giác A IDK nội tiếp
Þ 5 điểm A, I , D, K ,Q cùng thuộc đường tròn.
Þ Tứ giác A IKQ nội tiếp. Trang 11 · ·
Þ IA Q + IKQ = 180° · · Mà IA Q = IKQ · Þ IA Q = 90° Þ IA ^ A Q ( ) 3 Ta có: ìï · · ·
ïT A H = T HA = EHC ïïï · · í OA C = OCA ïï · ·
ïï OCA + EHC = 90° ïî · ·
Þ T A H + OA C = 90° · Þ T A O = 90° Þ T A ^ A O (4) ( )
3 và (4) Þ A,Q,O thẳng hàng. ----HẾT---
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN TÂN PHÚ
NĂM HỌC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đề thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận TP - 2
Thời gian: 120 phút (không kể thời gian phát đề) x
Câu 1. (1,5 điểm). Cho P 2
: y x và đường thẳng d : y 1,5 . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
3x 2x 6 0 có 2 nghiệm là x ,x . 1 2 x x
Không giải phương trình, hãy tính giá trị của biểu thức 1 2 M 1 .1 2x 2x 2 1
Câu 3. (0,75 điểm). Ngày n trong tháng t của năm 2021 là thứ mấy trong tuần? Có phải chủ nhật
không? Để trả lời câu hỏi này, ta áp dụng quy tắc Newday như sau:
Bước 1: Tính M như sau:
Trong trường hợp t 3 thì M (t 3).30 (n 1) N . Trong đó N là số lượng tháng có 31
ngày tính từ tháng 3 đến tháng thứ (t 1)
Trong trường hợp tháng t là tháng 1 thì M n 26 .
Trong trường hợp tháng t là tháng 2 thì M n 1 . Trang 12
Bước 2: Tìm r là dư của phép chia M cho 7 .
Nếu r 0 thì ngày n trong tháng t là thứ bảy.
Nếu r 1 thì ngày n trong tháng t là chủ nhật.
Nếu r 2 thì ngày n trong tháng t là thứ hai. …
Nếu r 6 thì ngày n trong tháng t là thứ sáu.
Biết số ngày trong tháng của năm 2021 thể hiện trong bảng sau: Tháng 1,3,5,7,8,10,12 2 4,6,9,11 Số ngày 31 28 30
a) Ngày Quốc tế Gia Đình 28 / 06 trong năm 2021 là thứ mấy? Kỷ niệm ngày thành lập
Đảng Cộng Sản 03 / 02 trong năm 2021 là thứ mấy?
b) Trên Thế Giới chọn ngày Chủ Nhật trong tuần lễ thứ hai của tháng 5 để làm “Ngày của
Mẹ”. Ngày của mẹ trong năm 2021 là ngày mấy?
Câu 4. (0,75 điểm). Cân nặng trung bình của trẻ sơ sinh đủ tháng là khoảng 3000g . Trẻ lúc 6
tháng có cân nặng gấp đôi lúc sơ sinh, 6 tháng tiếp theo mỗi tháng tăng 500g . Từ năm thứ
hai trở đi, trung bình mỗi năm tăng thêm 1,5kg . Gọi (
P kg) là cân nặng của trẻ em dưới 14
tuổi; N (tuổi) là số tuổi (dựa vào hằng số sinh học người Việt Nam năm 1975 ). Tìm cân
nặng trung bình của trẻ tròn 1 tuổi và xác định hàm số P theo N .
Câu 5. (1 điểm). Mỗi ngày, bạn An đều sử dụng điện thoại smartphone để chơi game 90 phút,
lướt facebook 30 phút, nhắn tin “chat” cùng bạn bè hết 20 phút, xem các chuyên mục giải
trí và các thông tin trên mạng hết 100 phút.
a) Thời gian bạn An sử dụng điện thoại smartphone chiếm bao nhiêu phần trăm thời gian
của một ngày ( 24 giờ)? (làm tròn kết quả đến hàng đơn vị).
b) Vì sử dụng điện thoại smartphone nhiều rất có hại cho sức khỏe, đặc biệt về trí nhớ nên
mẹ bạn An đã yêu cầu mỗi ngày bạn chỉ được phép dùng 2,5% thời gian của một ngày
để sử dụng điện thoại smartphone và 10% thời gian còn lại của ngày phải dùng vào việc
học ở nhà. Vậy mỗi ngày bạn An phải học ở nhà trong bao nhiêu phút?
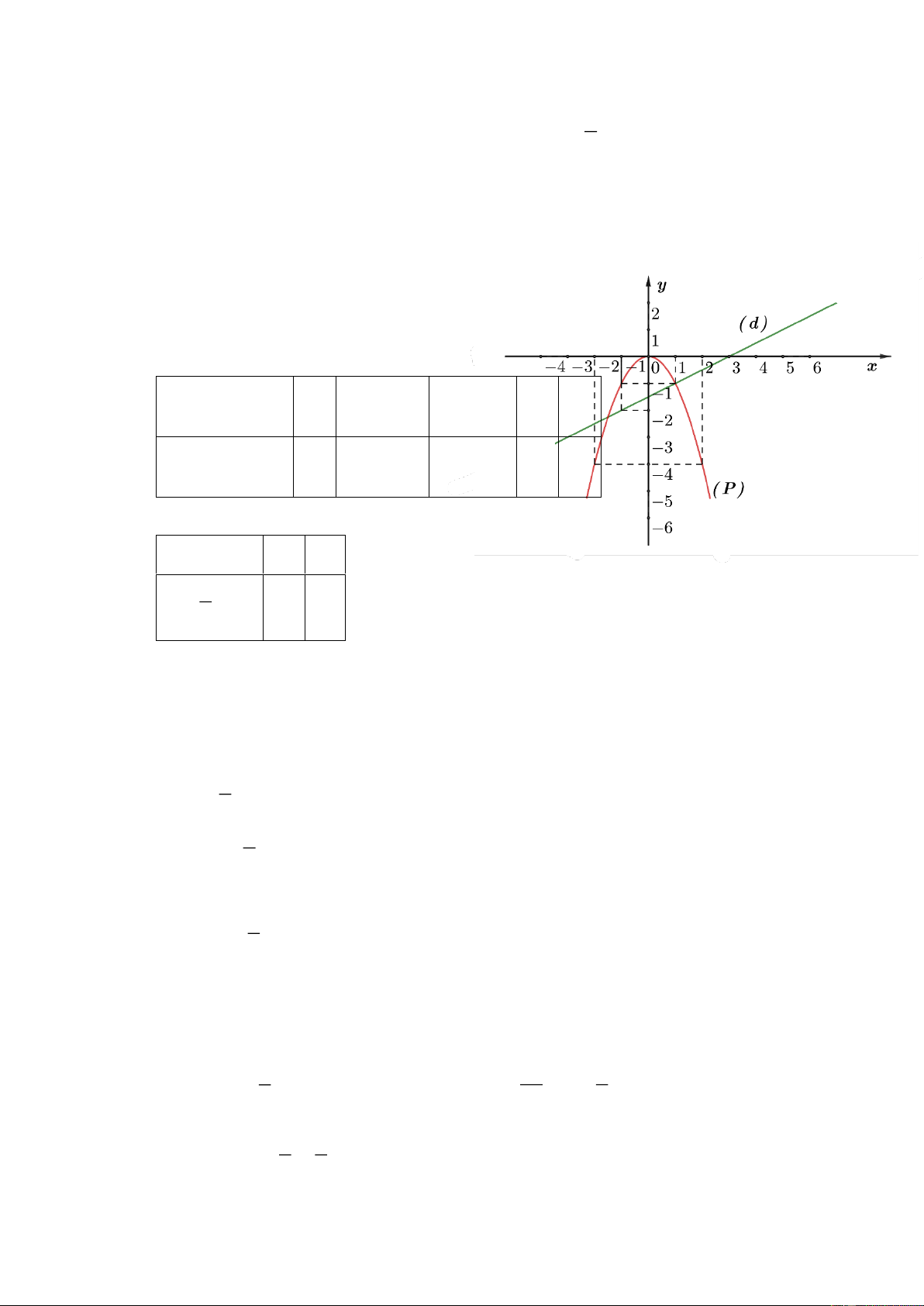
Câu 6. (1 điểm). Hình bên là một mẫu pho mát được cắt ra
từ một khối pho mát dạng hình trụ (có các kích
thước như hình vẽ). Biết khối lượng riêng của pho mát là 3
3g / cm và công thức khối lượng riêng là m D V (Trong đó D 3
g / cm là khối lượng riêng, mg là khối lượng, 3
V cm là thể tích)
a) Hãy tính diện tích 1 mặt đáy và khối lượng của mẫu pho mát trên.
Biết Thể tích hình trụ V .
S h . Trong đó S là diện tích 1 đáy và h là chiều cao của hình trụ. tru Trang 13
b) Chiếc hộp thực phẩm hình hộp chữ nhật có kích thước lần lượt là 189mm , 103mm ,
101mm có thể chứa hết phần còn lại của khối pho mát không?
Câu 7. (1 điểm). Khi thêm 200g axit vào dung dịch axit A và thu được dung dịch B có nồng độ
axit là 50% . Sau đó, ta lại thêm 300g nước vào dung dịch B và thu được dung dịch C có m
nồng độ là 40% . Tính nồng độ axit trong dung dịch A . Biết C% ct .100% , trong đó % C mdd
là nồng độ phần trăm, m là khối lượng chất tan, m là khối lượng dung dịch. ct dd
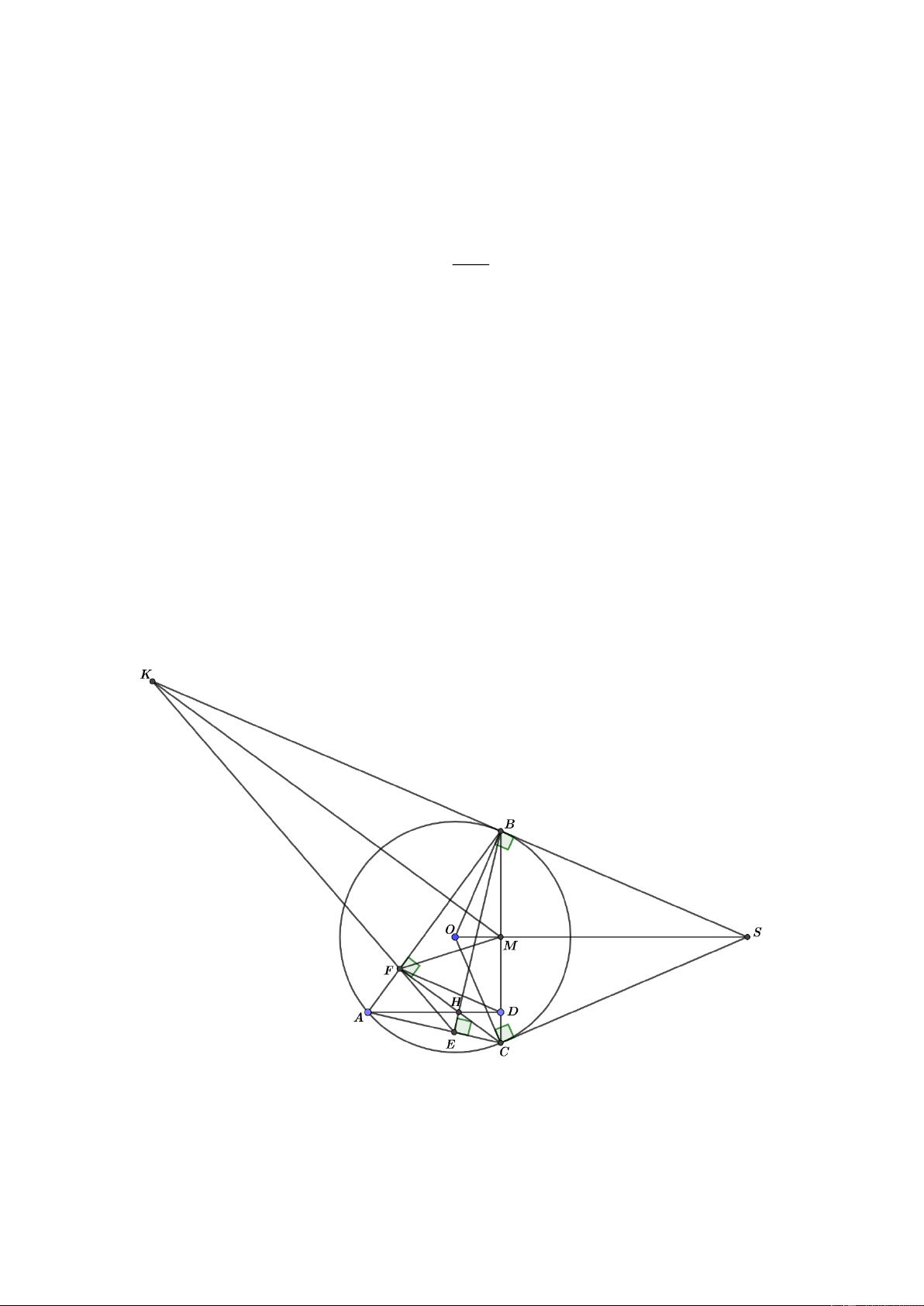
Câu 8. (3 điểm) Cho điểm S nằm ngoài đường tròn O . Kẻ SB và SC là 2 tiếp tuyến của đường
tròn ( B , C là 2 tiếp điểm). Lấy điểm A nằm trên cung lớn BC . Kẻ CF AB tại F , kẻ
BE AC tại E . Lấy M là giao điểm của OS và BC . Gọi K là giao điểm của EF với SB
và H là giao điểm của BE với CF .
a) Chứng minh: KFB ACB và BC 2.FM
b) Chứng minh: KM AB và AH BC ở D . c) Chứng minh: F
HD đồng dạng K MS . ----HẾT--- Trang 14 HƯỚNG DẪN GIẢI x
Câu 1. (1,5 điểm). Cho P 2
: y x và đường thẳng d : y 1,5 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.. Lời giải
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: 0 x 2 1 1 2 0 2
y x 4 1 1 4 x 5 3 x y 1,5 1 0 2
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : x 2 x 1,5 2 x 2
x 1,5 0 2 x 1 3 x 2 Thay x 1 vào 2
y x , ta được: 2 y 1 1 . 2 3 3 9 Thay x vào 2
y x , ta được: y . 2 2 4 3 9 Vậy 1; 1 , ;
là hai giao điểm cần tìm. 2 4
Câu 2. (1 điểm). Cho phương trình 2
3x 2x 6 0 có 2 nghiệm là x , x . 1 2 Trang 15 x x
Không giải phương trình, hãy tính giá trị của biểu thức 1 2 M 1 .1 2x 2x 2 1 Lời giải 2 Vì 2
b 4ac 2 4.3. 6 76 0
Nên phương trình có hai nghiệm phân biệt x , x . 1 2 b 2
S x x 1 2 a 3
Theo định lí Vi-et, ta có: c
P x .x 2 1 2 a Ta có: x x 1 2 M 1 .1 2x 2x 2 1
2x x 2x x 2 1 1 2 M . 2x 2x 2 1 2 2
4x x 2x 2x x x 1 2 1 2 1 2 M 4x . x 1 2 2 2 2 x x 4x x x x 1 2 1 2 1 2 M 4x . x 1 2 2
x x 2 2x x 5x x 1 2 1 2 1 2 M 4x x 1 2 2
x x 2 3x x 1 2 1 2 M 4x x 1 2 31 M 36
Câu 3. (0,75 điểm) Ngày n trong tháng t của năm 2021 là thứ mấy trong tuần? Có phải chủ
nhật không? Để trả lời câu hỏi này, ta áp dụng quy tắc Newday như sau: Bước 1: Tính M như sau:
Trong trường hợp t 3 thì M (t 3).30 (n 1) N . Trong đó N là số lượng tháng có 31
ngày tính từ tháng 3 đến tháng thứ (t 1)
Trong trường hợp tháng t là tháng 1 thì M n 26 .
Trong trường hợp tháng t là tháng 2 thì M n 1.
Bước 2: Tìm r là dư của phép chia M cho 7.
Nếu r 0 thì ngày n trong tháng t là thứ bảy. Trang 16
Nếu r 1 thì ngày n trong tháng t là chủ nhật.
Nếu r 2 thì ngày n trong tháng t là thứ hai. …
Nếu r 6 thì ngày n trong tháng t là thứ sáu.
Biết số ngày trong tháng của năm 2021 thể hiện trong bảng sau: Tháng 1,3,5,7,8,10,12 2 4,6,9,11 Số ngày 31 28 30
a) Ngày Quốc tế Gia Đình 28/06 trong năm 2021 là thứ mấy? Kỷ niệm ngày thành lập
Đảng Cộng Sản 03/02 trong năm 2021 là thứ mấy?
b) Trên Thế Giới chọn ngày Chủ Nhật trong tuần lễ thứ hai của tháng 5 để làm “Ngày
của Mẹ”. Ngày của mẹ trong năm 2021 là ngày mấy? Lời giải a) Ta có
Bước 1: Tháng 6 : t 3
M t 3.30 n 1 N
M 6 3.30 28 1 2 M 121
Bước 2: M chia 7 dư 2 vậy n là ngày thứ 2
b) Ngày Của Mẹ" được chọn vào một ngày của tháng 5 nên ta có t 5 t 1 4
Số lượng tháng có 31 ngày từ tháng 03 đến tháng 04 là 1 tháng Nên ta có N 1 Ngày 30 / 4
M t 3.30 n 1 N
M 4 3.30 30 1 1 M 62
theo quy tắc Newday ta có M 62 chia 7 dư 6 Ngày 30 / 4là thứ 6
Chủ nhật đầu tiên của tháng 5 là 2 / 5 . Vậy chủ nhật thứ hai của tháng 5 là ngày 9 / 5 .
Câu 4. (0,75 điểm). Cân nặng trung bình của trẻ sơ sinh đủ tháng là khoảng 3000g. Trẻ lúc 6
tháng có cân nặng gấp đôi lúc sơ sinh, 6 tháng tiếp theo mỗi tháng tăng 500g. Từ năm thứ
hai trở đi, trung bình mỗi năm tăng thêm 1,5kg. Gọi P (kg) là cân nặng của trẻ em dưới 14 Trang 17
tuổi; N (tuổi) là số tuổi (dựa vào hằng số sinh học người Việt Nam năm 1975). Tìm cân
nặng trung bình của trẻ tròn 1 tuổi và xác định hàm số P theo N.? Lời giải
Cân nặng trung bình của trẻ tròn 1 tuổi là: 3000.2 500.6 9000 g 9kg Ta có:
P kg cân nặng trẻ em dưới 14 tuổi N (số tuổi)
Từ đó ta có hàm số P theo N :
P 9 1, 5.N
Câu 5. (1 điểm) Mỗi ngày, bạn An đều sử dụng điện thoại smartphone để chơi game 90 phút,
lướt facebook 30 phút, nhắn tin “chat” cùng bạn bè hết 20 phút, xem các chuyên mục giải
trí và các thông tin trên mạng hết 100 phút.
a) Thời gian bạn An sử dụng điện thoại smartphone chiếm bao nhiêu phần trăm thời
gian của một ngày (24 giờ)? (làm tròn kết quả đến hàng đơn vị).
b) Vì sử dụng điện thoại smartphone nhiều rất có hại cho sức khỏe, đặc biệt về trí nhớ
nên mẹ bạn An đã yêu cầu mỗi ngày bạn chỉ được phép dùng 2,5% thời gian của một
ngày để sử dụng điện thoại smartphone và 10% thời gian còn lại của ngày phải dùng
vào việc học ở nhà. Vậy mỗi ngày bạn An phải học ở nhà trong bao nhiêu phút? Lời giải
a) Thời gian bạn An sử dụng điện thoại smartphone chiếm số phần trăm thời gian của một ngày ( 24 giờ) là:
9030 20100:60.100% 17% 24
b) Mỗi ngày bạn An phải học ở nhà số phút là:
24.1 2,5%.10%.60 140, 4 (phút)
Câu 6. (1 điểm) Hình bên là một mẫu pho mát được cắt ra từ một khối pho mát dạng hình trụ (có
các kích thước như hình vẽ). Biết khối lượng riêng của pho mát là 3
3g / cm và công thức khối m
lượng riêng là D V (Trong đó D ( 3
g / cm ) là khối lượng riêng, m (g) là khối lượng, V ( 3 cm ) là thể tích) Trang 18
a) Hãy tính diện tích 1 mặt đáy và khối lượng của mẫu pho mát trên.
Biết Thể tích hình trụ V
S.h . Trong đó S là diện tích 1 đáy và h là chiều cao của hình trụ tru
b) Chiếc hộp thực phẩm hình hộp chữ nhật có kích thước lần lượt là
189mm, 103mm, 101mm có thể chứa hết phần còn lại của khối pho mát không? Lời giải 0 2 o 2 n R 15 . .10 25
a) Diện tích 1 mặt đáy là: S 2 cm quat 0 0 360 360 6 25
Khối lượng của mẫu pho mát trên là:
.8.3 100 314,2g 6 189 103 101
b) Thể tích hình hộp là: V . . 1966, 2 cm hop 3 10 10 10
Thể tích phần còn lại của pho mát là: 25 25 2300 2 2 V .R .h .8 .10 .8 .8 2408,6 cm p at 3 ho m 6 6 3 Vì V V
nên chiếc hộp thực phẩm hình hộp chữ nhật không thể chứa hết phần hop p ho m at
còn lại của khối pho mát.
Câu 7. (1 điểm) Khi thêm 200g axit vào dung dịch axit A và thu được dung dịch B có nồng độ
axit là 50%. Sau đó, ta lại thêm 300g nước vào dung dịch B và thu được dung dịch C có m
nồng độ là 40%. Tính nồng độ axit trong dung dịch A. Biết C% ct .100% , trong đó C% mdd
là nồng độ phần trăm, m là khối lượng chất tan, m là khối lượng dung dịch. ct dd Lời giải
Gọi x g , y g lần lượt là khối lượng chất tan và khối lượng dung dịch trong dung dịch axit A ; x y 0
Vì khi thêm 200g axit vào dung dịch axit A thì thu được dung dịch axit B có nồng
độ axit là 50% nên ta có phương trình: x 200 x 200 1 .100% 50%
2.x 200 y 200 2x y 2 00 1 y 200 y 200 2
Vì sau đó thêm 300g nước vào dung dịch B thì thu được dung dịch C có nồng độ là
40% nên ta có phương trình: x 200 x 200 2 .100% 40%
5.x 200 2. y 500 5x 2y 02 y 500 y 500 5 Trang 19 Từ
1 và 2 ta có hệ phương trình:
2x y 200
5x 2y 0
x 400n y 1000 n 400
Nồng độ axit trong dung dịch A là: .100% 40% . 1000
Câu 8. (3 điểm) Cho điểm S nằm ngoài đường tròn O . Kẻ SB và SC là 2 tiếp tuyến của đường tròn
(B, C là 2 tiếp điểm). Lấy điểm A nằm trên cung lớn BC. Kẻ CF AB tại F, kẻ BE AC tại E.
Lấy M là giao điểm của OS và BC. Gọi K là giao điểm của EF với SB và H là giao điểm của BE với CF.
a) Chứng minh: KFB ACB và BC 2.FM
b) Chứng minh: KM AB và AH BC ở D. c) Chứng minh: F
HD đồng dạng K MS . Lời giải
a) Chứng minh: KFB ACB và BC 2.FM Xét tứ giác BFEC, ta có: Trang 20 BFC 90 BEC 90 BFC BEC
Tứ giác BFEC nội tiếp đường tròn
KFB ACB Xét O , ta có: SB SC OB OC
OS là đường trung trực của đoạn thẳng BC .
OS BC tại M Xét O BC , ta có:
OB OC R O
BC cân tại O Xét O
BC cân tại O , ta có:
OM là đường cao ( OM BC )
OM là đường trung tuyến.
M là trung điểm BC . Xét BFC
vuông tại F , ta có:
FM là đường trung tuyến ( M là trung điểm BC ) 1
FM BC (Hệ quả hình chữ nhật) 2
BC 2.FM
b) Chứng minh: KM AB và AH BC ở D . BC FM (cmt) 2 Ta có: BC BM MC 2
FM BM MC Ta có:
KBF ACB(gtbtt &dc gnt)
KFB ACB(cmt) KBF KFB KFB cân tại K . Trang 21 KF KB
MF MB(cmt) Ta có:
KF KB(cmt)
KM là đường trung trực của đoạn thẳng FB KM AB Xét ABC , ta có:
CF là đường cao ( CF AB)
BE là đường cao ( BE AC )
CF và BE cắt nhau tại H (gt)
H là trực tâm của ABC
AH là đường cao thứ 3
AH BC ở D . c) Chứng minh: F
HD đồng dạng K MS Xét K
FB cân tại K , ta có:
KM là đường cao ( KM AB )
KM là đường phân giác
FKM MKS Xét S
BC cân tại S , ta có:
SM là đường cao ( SM BC )
SM là đường phân giác
KSM CSM
Xét tứ giác AFHE , ta có:
AFH AEH 90 90 180
Tứ giác AFHE nội tiếp
HAE HFE 1
Xét tứ giác AEDB , ta có:
AEB ADB 90
Tứ giác AEDB nội tiếp
HAE DBE 2
Xét tứ giác BFHD , ta có: Trang 22
HFB HDB 90 90 180
HFD HBD 3
Từ 2 và 3 HFD HAE 4 Từ
1 và 4 HFD HFE KM AB Ta có: CF AB KM / /CF Ta có:
HFE FKM (KM / /CF,dongvi)
MKS FKM (cmt)
HFD HFE(cmt) HFD MKS
Xét tứ giác AFDC , ta có:
AFC ADC 90
Tứ giác AFDC nội tiếp
ACF HDF Ta có:
ACF BAC 90
KSM SBC 90
BAC SBC(gtbtt & dc gnt) ACF KSM
Mà ACF HDF(cmt)
Nên KSM HDF Xét F HD và K MS .ta có:
HDF KSM (cmt)
HFD MKS(cmt) F
HD đồng dạng K
MS (g-g) ----HẾT--- Trang 23




