Đề tham khảo vào lớp 10 môn Toán năm 2024 – 2025 sở GD&ĐT Phú Thọ

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT PHÚ THỌ NĂM HỌC 2024-2025 Môn: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian giao đề ĐỀ THAM KHẢO
(Đề tham khảo có 02 trang)
Thí sinh làm bài (cả phần trắc nghiệm khách quan và phần tự luận) vào tờ giấy thi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu 1. Giá trị của biểu thức A  4 là A. 2. B. 2  . C. 16. D. 16.
Câu 2. Trong các hàm số sau, hàm số nào là hàm số bậc nhất? 1
A. y  1 . B. y  2 x 1. C. 2
y  x 1. D. y  3  8 . x x
Câu 3. Hệ số góc của đường thẳng d  1 : y  x  3 là 2 1 3 A. 3. B. . C. . D. 2. 2 2
Câu 4. Cặp (x; y)  (1; 1) là nghiệm của hệ phương trình nào dưới đây? 2x  3y  5  3  x  2y  5 2x  3y  5 3  x  2y  5 A.  . B.  . C.  . D.  . 5  x  3y  2 5x  3y  2 5  x  3y  2 5  x  3y  2
Câu 5. Một mảnh vườn hình chữ nhật có diện tích 2
150 m . Biết rằng, chiều dài hơn chiều rộng là 5 . m
Chiều rộng mảnh vườn đó là A. 10 . m B. 15 . m C. 20 . m D. 25 . m
Câu 6. Cho điểm M x ; y thuộc đồ thị hàm số 2
y  2x có hoành độ x  2. Khi đó, y bằng M M  M M A. 4. B. 4. C. 8. D. 8.
Câu 7. Phương trình nào sau đây có tổng hai nghiệm bằng 5 ? A. 2 x  5x  6  0. B. 2 x  6x  5  0. C. 2 x  6x  5  0. D. 2 x  5x  6  0.
Câu 8. Phương trình nào dưới đây là phương trình bậc hai một ẩn? A. 2 x  2x  6  0. B. 2 3 x  x  2  0. C. 3x  5  0. D. 4 x  4  0.
Câu 9. Cho tam giác ABC vuông tại A có AB  5cm, AC  12c . m Khi đó tan C bằng 5 5 13 12 A. . B. . C. . D. . 13 12 5 5
Câu 10. Cho tam giác MNP vuông tại M , đường cao MH. Khi đó A. 2 MH  NH .H . P B. 2 MH  NH.N . P C. 2 MH  HP.PN. D. 2 MH  MN.MP.
Câu 11. Cho hai đường tròn  ;
O 2cm và I;3cm, OI  6c .
m Số tiếp tuyến chung của hai đường tròn đó là A. 1. B. 2. C. 3. D. 4. Trang 1/2
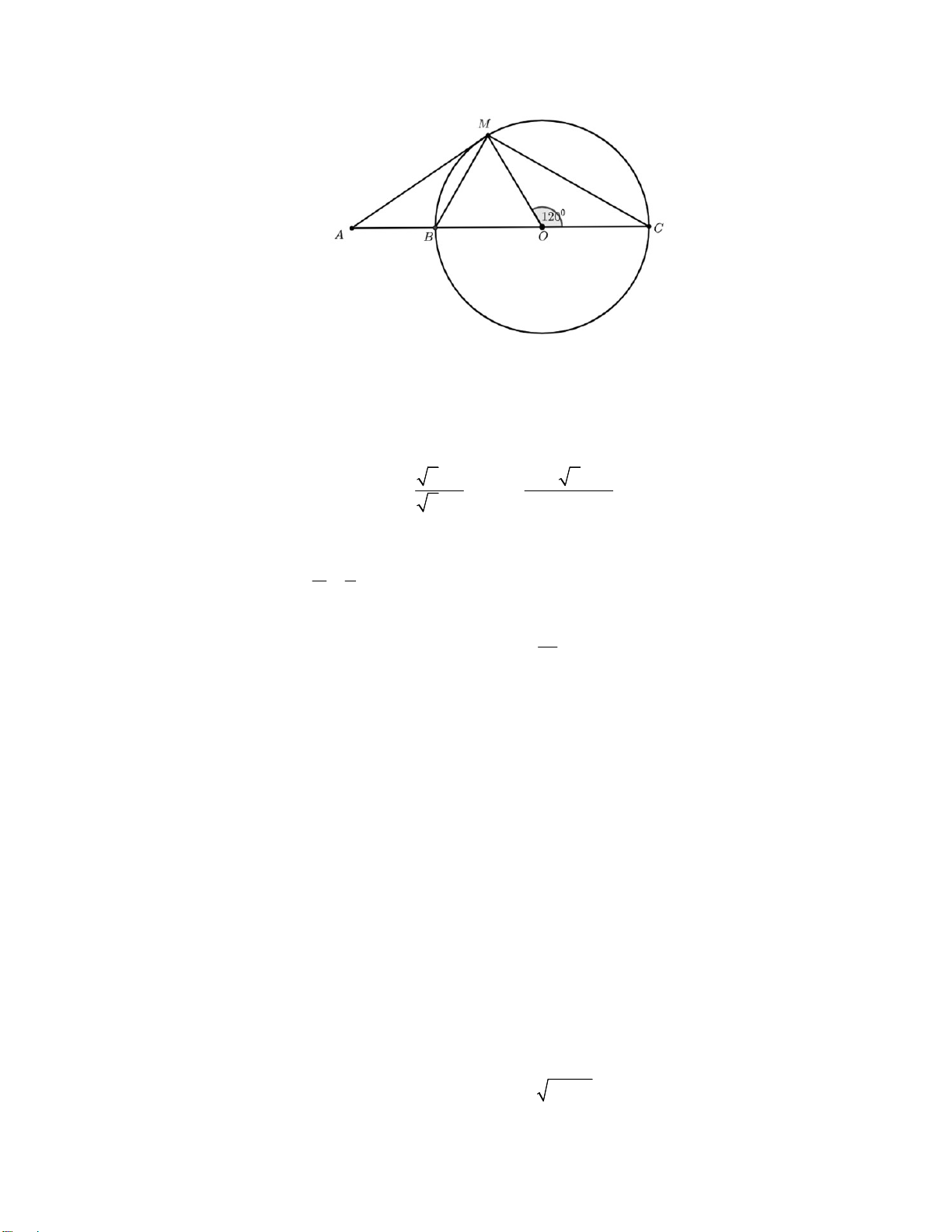
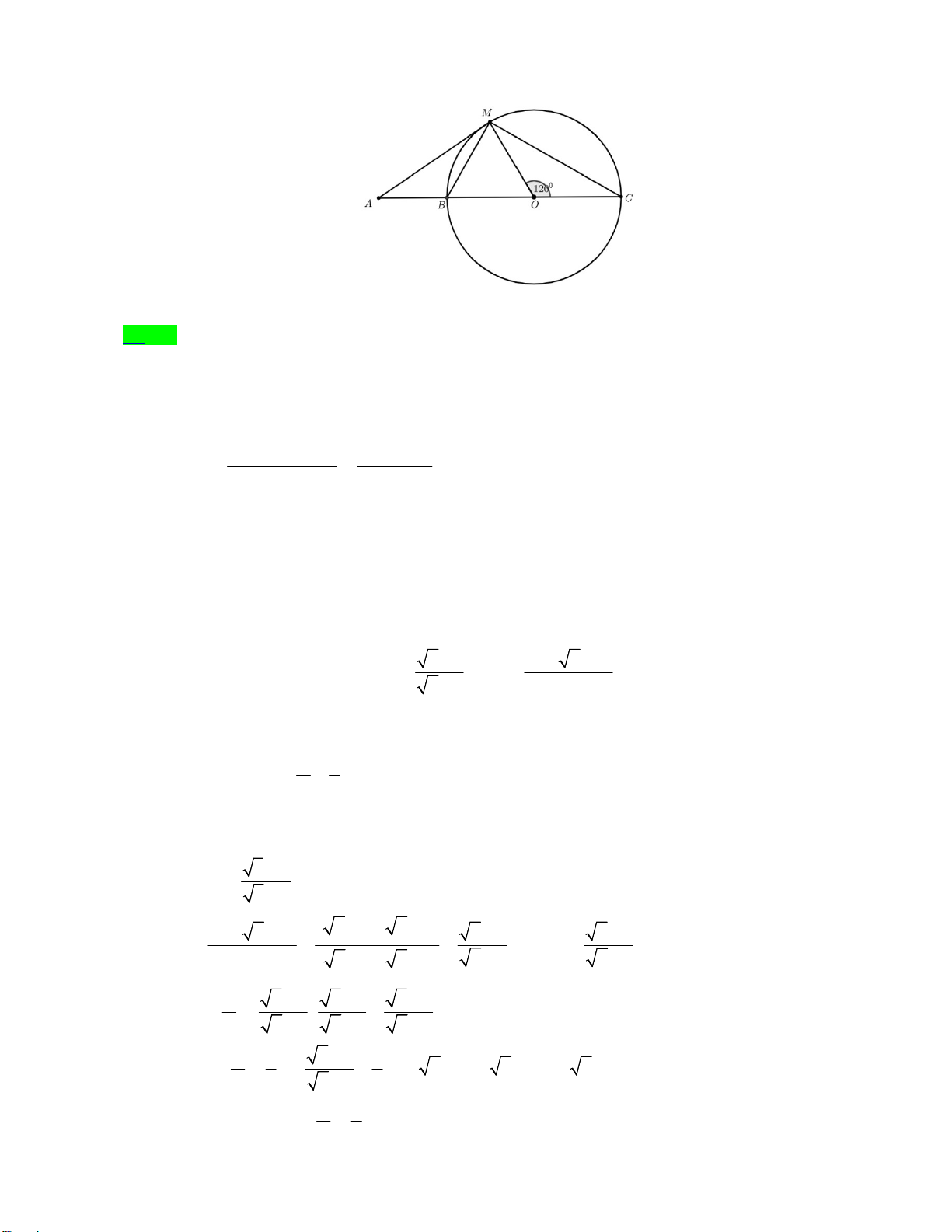
Câu 12. Cho hình vẽ bên dưới, biết rằng MA là tiếp tuyến của đường tròn O,  MOC  120 .  Số đo  MAC bằng A. 30 .  B. 90 .  C. 60 .  D. 45 . 
PHẦN II. TỰ LUẬN (7,0 điểm) x  3 x  3 x 10
Câu 1 (1,5 điểm). Cho hai biểu thức A  và B  với x  0, x  25 . x  5 x  25
a) Tính giá trị của biểu thức A khi x  9. b) Rút gọn biểu thức . B B 1 c) Tìm x biết rằng  . A 6 Câu 2 (2,0 điểm). 1 
1. Cho đường thẳng d  : y  2
 x  m và parabol P 2 : y  x . 2
a) Cho điểm C có hoành độ là 2
 thuộc parabol P. Tìm m để đường thẳng d  đi qua C.
b) Tìm m để đường thẳng d  cắt parabol P tại hai điểm phân biệt D  x ; y , E x ; y sao 1 1   2 2 cho 2 x  2y  15. 1 2 mx  3y  8
2. Cho hệ phương trình  . x  my  11
a) Giải hệ phương trình khi m  2 .
b) Tìm m để hệ phương trình có nghiệm duy nhất  ;
x y thỏa mãn x  y  5.
Câu 3 (3,0 điểm). Cho đường tròn tâm O đường kính AB, điểm C cố định trên đoạn thẳng OB (C
khác O và B ). Điểm M di động trên đường tròn O. Đường thẳng d  vuông góc với AB tại C cắt
tia AM tại E ở ngoài đường tròn, d  cắt đoạn MB ở F.
a) Chứng minh các tứ giác AMFC và BCME nội tiếp đường tròn.
b) Chứng minh BF.BM  BC.BA và AF vuông góc với E . B
c) Tia EB cắt O tại N. Chứng minh , A F, N thẳng hàng.
d) Chứng minh đường tròn ngoại tiếp tam giác AEF luôn đi qua một điểm cố định khác . A (x  4) 2 2x 16x  33  y 2 2 y   1
Câu 4 (0,5 điểm). Giải hệ phương trình  (x, y  ). 3
2xy  3x  21  3 3x  y  ____________Hết___________ Trang 2/2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT PHÚ THỌ NĂM HỌC 2024-2025 Môn: TOÁN ĐỀ THAM KHẢO
Thời gian làm bài: 120 phút, không kể thời gian giao đề
(Đề tham khảo có 02 trang)
Giải đề: Vũ Xuân Hưng – Vũ Minh Anh
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu 1. Giá trị của biểu thức A  4 là A. 2. B. 2. C. 16. D. 16. Lời giải
Ta có A  4  A  2 . Chọn A.
Câu 2. Trong các hàm số sau, hàm số nào là hàm số bậc nhất? 1
A. y 1 . B. y  2 x 1. C. 2
y  x 1. D. y  3  8 . x x Lời giải
Hàm số bậc nhất là y  3  8 . x Chọn D.
Câu 3. Hệ số góc của đường thẳng d  1 : y  x  3 là 2 1 3 A. 3. B. . C. . D. 2. 2 2 Lời giải 1
Hệ số góc của đường thẳng d  1
: y  x  3 là . Chọn B. 2 2
Câu 4. Cặp (x; y)  (1; 1) là nghiệm của hệ phương trình nào dưới đây? 2x  3y  5  3  x  2y  5 2x  3y  5 3  x  2y  5 A.  . B.  . C.  . D.  . 5  x  3y  2 5x  3y  2 5  x  3y  2 5  x  3y  2 Lời giải 2x  3y  5
Cặp (x; y)  (1; 1) là nghiệm của hệ phương trình  .Chọn C. 5  x  3y  2
Câu 5. Một mảnh vườn hình chữ nhật có diện tích 2
150 m . Biết rằng, chiều dài hơn chiều rộng là 5 .
m Chiều rộng mảnh vườn đó là A. 10 . m B. 15 . m C. 20 . m D. 25 . m Lời giải
Gọi chiều dài mảnh vườn hình chữ nhật là xm, x  5.
Chiều rộng mảnh vườn hình chữ nhật là ym,0  y  .x
Vì diện tích mảnh vườn hình chữ nhật là 2 150m nên . x y 150.  1
Vì chiều dài hơn chiều rộng 5 m nên x  y  5.2 2  .xy 150 y 
 5y150  0 y 10(TM ), y  1  5(loai) Từ (1) và (2) ta có hệ        . x   y  5 x    y  5 x   15 
Vậy chiều rộng mảnh vườn là 10 . m Chọn A. Trang 3/2
Câu 6. Cho điểm M x ; y thuộc đồ thị hàm số 2 y  2
 x có hoành độ x  2. Khi đó, y bằng M M  M M A. 4. B. 4. C. 8. D. 8. Lời giải
Vì điểm M x ; y thuộc đồ thị hàm số 2 y  2
 x có hoành độ x  2  y  2.4  8  . Chọn C. M M  M M
Câu 7. Phương trình nào sau đây có tổng hai nghiệm bằng 5 ? A. 2 x  5x  6  0. B. 2 x  6x  5  0. C. 2 x  6x  5  0. D. 2 x  5x  6  0. Lời giải b
Theo Vi – ét ta có x  x    5. Chọn D. 1 2 a
Câu 8. Biệt thức  của phương trình 2 x  3x  4  0 là A. 13. B. 25. C. 5. D. 7. Lời giải Ta có 2
  b 4ac  94.4  25.Chọn B.
Câu 9. Cho tam giác ABC vuông tại A có AB  5cm, AC  12c . m Khi đó tan C bằng 5 5 13 12 A. . B. . C. . D. . 13 12 5 5 Lời giải B 5 cm A 12 cm C AB 5 Ta có tan C   . Chọn B. AC 12
Câu 10. Cho tam giác MNP vuông tại M , đường cao MH  6cm , HP  9c .
m Độ dài đoạn thẳng NH là A. 3c . m B. 4c . m C. 5c . m D. 6c . m Lời giải N H 9 cm 6 cm M P
Theo hệ thức cạnh và đường cao trong tam giác vuông ta có 2
MH  NH.HP  NH  4 . Chọn B.
Câu 11. Cho hai đường tròn  ;
O 2cm và I;3cm, OI  6c .
m Số tiếp tuyến chung của hai đường tròn đó là A. 1. B. 2. C. 3. D. 4. Lời giải
Ta có 3 2  5  6  OI Ovà Ikhông giao nhau (ở ngoài nhau). Vậy số tiếp tuyến chung là 2 . Chọn B. Trang 4/2
Câu 12. Cho hình vẽ bên dưới, biết rằng MA là tiếp tuyến của đường tròn O,  MOC 120. Số đo  MAC bằng A. 30. B. 90. C. 60 .  D. 45 .  Lời giải Cách 1: Ta có  MOB 180  MOC  60.  sd  MC   MOC 120 , sd  MB  60. sd MC  sd MB   Ta có    120 60 MAC    30. Chọn A. 2 2
Cách 2: Ta có MA  MC  R  MOC cân tại O   OMC   OCM  30. Ta có  MCB 
 AMB  30 (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung). Ta có 
MOB  60 mà MO  OB cùng là bán kính O M  OB đều   MBA120. Xét M  BA có  AMB   MAB   ABM 180    MAB  30    MAC.
PHẦN II. TỰ LUẬN (7,0 điểm) x  3 x  3 x 10
Câu 1 (1,5 điểm). Cho hai biểu thức A  và B  với x  0, x  25 . x  5 x  25
a) Tính giá trị của biểu thức A khi x  9. b) Rút gọn biểu thức . B B 1 c) Tìm x biết rằng  . A 6 Lời giải
a) Ta có: x  9 thỏa mãn điều kiện x  0, x  25 thay x  9 vào A ta có 9 3 A 
3. Vậy khi x  9 thì A  3. 9 5 x  x   x 2 x 5 3 10  x 2 x  2 b) B    . Vậy B  với x  0, x  25 . x  25
 x 5 x 5 x 5 x  5 B x  x  x  c) Ta có  2 3 2 :  với x  0, x  25 . A x  5 x  5 x  3 B 1 x  Vì   2 1
  6 x 12  x  3  5 x  15  x  9 (TMĐK). A 6 x  3 6 B 1 Vậy x  9 thì  . A 6 Trang 5/2 Câu 2 (2,0 điểm). 1 
1. Cho đường thẳng d  : y  2
 x  m và parabol P 2 : y  x . 2
a) Cho điểm C có hoành độ là 2
 thuộc parabol P. Tìm m để đường thẳng d  đi qua C.
b) Tìm m để đường thẳng d  cắt parabol P tại hai điểm phân biệt D x ; y , E x ; y sao 1 1   2 2 cho 2 x  2y  15. 1 2 Lời giải
a) Vì C có hoành độ là 2 thuộc parabol P nên x  2   y 2  C 2  ;  2 .
Vì d  đi qua C nên 2  4  m  m  6. Vậy m  6 thì đường thẳng d  đi qua C thuộc Parabol P.
b) Xét phương trình hoành độ giao điểm của đường thẳng d  và parabol P 1 Ta có 2 2
x  2x  m  x 4x  2m  0   1 . 2
Số nghiệm của phương trình  
1 là số giao điểm của đường thẳng d  và parabol P
Ta có '  4 2m . Để đường thẳng d  cắt parabol P tại hai điểm phân biệt thì   1 phải
có hai nghiệm phân biệt  ' 0  42m  0  m  2  *
Với m  2 thì d  cắt parabol P tại hai điểm phân biệt D x ; y , E x ; y với x , x là hai 1 1   2 2 1 2  1   1 
nghiệm của phương trình  
1 . Ta có D, E P nên 2 2 Dx ; x   , Ex ; x . 1 1    2 2  2   2  x  x  4 Theo Vi – ét ta có 1 2  . x .x  2m 1 2  Theo đề bài 1 2 2 2
x  2y  15.  x  x  15   x  x
 2x x 15 16  4m  15  m  thỏa mãn 1 2 2 1 2 1 2 1 2 4   1
* . Vậy m  thì đường thẳng d  cắt parabol P tại hai điểm phân biệt 4
D  x ; y , E x ; y thỏa mãn 2 x  2y  15. 1 1   2 2 1 2 mx  3y  8
2. Cho hệ phương trình  . x   my 11
a) Giải hệ phương trình khi m  2 .
b) Tìm m để hệ phương trình có nghiệm duy nhất  ;
x y thỏa mãn x  y  5. Lời Giải  17 x   2x 3y  8    2x 3y  8   a) Với  
m  2 ta có hệ phương trình 7        . x   2y 11 2x   4y  22  30  y    7  
Vậy với m  2 thì nghiệm của hệ phương trình là x y 17 30 ;  ;   .   7 7  Trang 6/2 2 mx  3y  8 mx  3y  8 1  1m  m y  3y  8 y 2 m  3  811m b) Ta có        . x  my  11 x  11 my   x  11 my  x  11 my  Vì 2
m 3 0, m nên hệ phương trình đã cho luôn có nghiệm với mọi m .  811m  8m 33 y  x   2  2  m  3  m  3      . 8 1  1m  8 1  1m x 11 . m     y   2 2  m  3  m  3 8m33 8 1  1m
Vậy mọi m thì hệ phương trình có nghiệm  ; x y ;   . 2 2  m 3 m 3  Theo đề bài 8m  33 8 11m 2 2 x  y  5  
 5  41 3m  5m 15  5m  3m  26  0  5m 13 m  2  0 2 2    m  3 m  3 m  2    13 13 . Vậy   
m  2;m   thì hệ có nghiệm duy nhất thỏa mãn x y 5. m    5  5
Câu 3 (3,0 điểm). Cho đường tròn tâm O đường kính AB, điểm C cố định trên đoạn thẳng OB (C
khác O và B ). Điểm M di động trên đường tròn O. Đường thẳng d  vuông góc với AB tại C cắt
tia AM tại E ở ngoài đường tròn, d  cắt đoạn MB ở F.
a) Chứng minh các tứ giác AMFC và BCME nội tiếp đường tròn.
b) Chứng minh BF.BM  BC.BA và AF vuông góc với E . B
c) Tia EB cắt O tại N. Chứng minh , A F , N thẳng hàng.
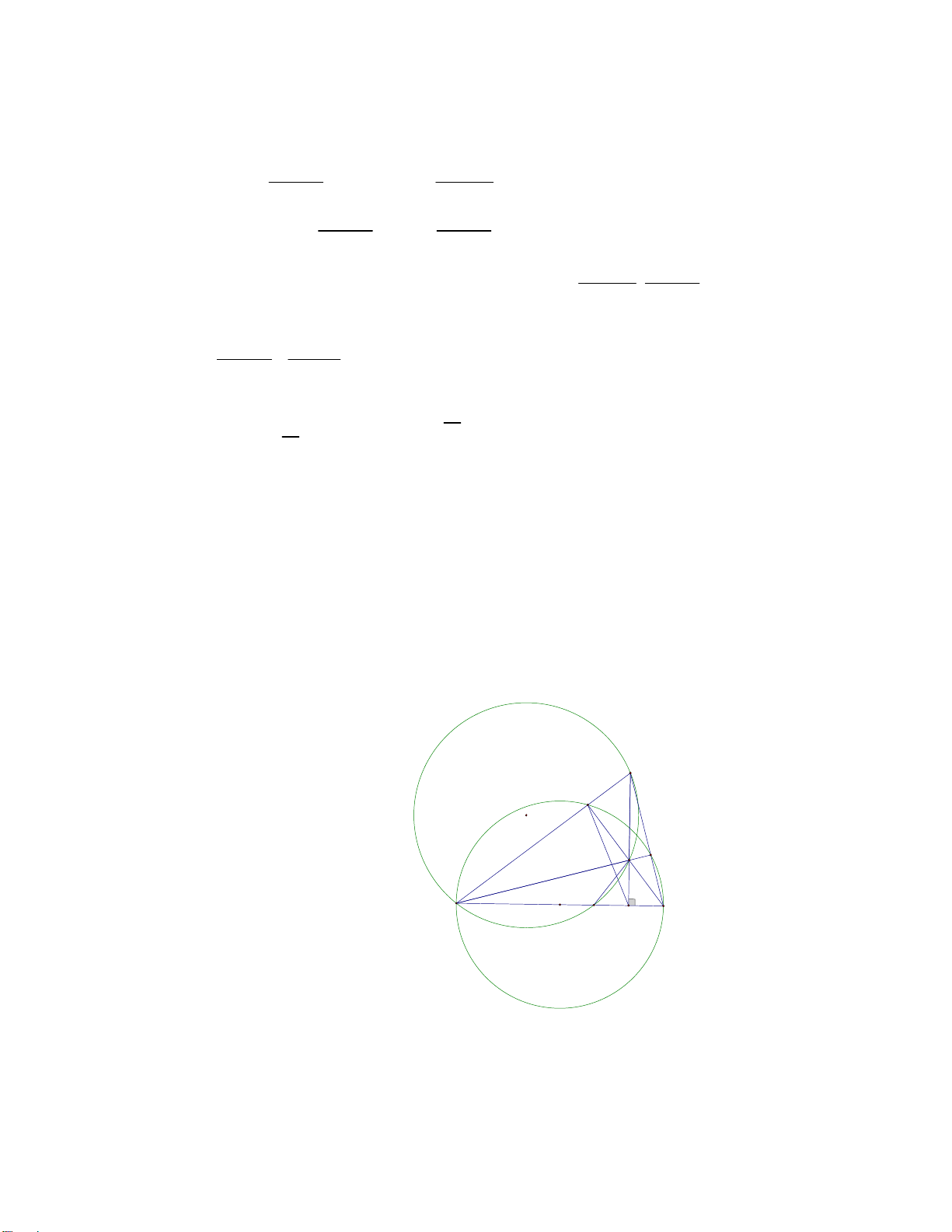
d) Chứng minh đường tròn ngoại tiếp tam giác AEF luôn đi qua một điểm cố định khác . A Lời giải E M H N F A B O I C a) Ta có 
AMB  90 (góc nội tiếp chắn nửa đường tròn), do F  MB   AMF  90.
Vì đường thẳng d vuông góc với AB tại C nên  ACF  90 . Xét tứ giác AMFC có  AMF 
 ACF  9090 180 mặt khác  AMF,  ACF là hai góc đối
nhau trong tứ giác AMFC . Do đó AMFC là tứ giác nội tiếp ■ Trang 7/2 Ta có  AMB  90 (cmt)   EMB  90 Xét tứ giác EMCB có  EMB  ECB 90  
, suy ra M ,C cùng nhìn cạnh EB dưới một góc
vuông  EMCB là tứ giác nội tiếp ■ b) Xét BFC và B  AM có  FBC 
 MBA ( có chung B ),  FCB   AMB  90
 AMB FCB (g – g). AB BM    A . B BC  BM.FB ■ FB BC Xét A
 EB có EC  AB  EC là đường cao trong A  EB .
Có MB  AE  MB là đường cao A  EB . Mà EC giao MB tại F .
 F là trực tâm tam giác AEB  AF  EB ■ c) Xét O có 
ANB  90 (góc nội tiếp chắn nửa đường tròn)  AN  EB . Mà theo b ta có AF  E . B  , A F, N thẳng hàng ■
d) Gọi I là giao điểm của đường tròn ngoại tiếp A
 EF với đường thẳng A . B
Vì AIFE là tứ giác nội tiếp nên  EAI   IFC .
Vì AMFC là tứ giác nội tiếp theo a nên  MAC 
 CFB  FC là tia phân giác  IF . B Xét I
 FB có FC  IB nên FC là đường cao trong I
 FB và FC là tia phân giác  IF . B Do đó I
 FB cân tại F  C là trung điểm IB hay I và B đối xứng qua C .
Do C, B cố định nên I cố định.
Vậy đường tròn ngoại tiếp tam giác AEF luôn đi qua một điểm I cố định khác A ■ (  x  4)   2 2x 16x 3  3  y 2 2 y  1
Câu 4 (0,5 điểm). Giải hệ phương trình (x, y   ).  3
2xy3x  21 3 3x  y  Lời Giải (  x4) 2 2x 1  6x 3 3 y 2 2 y   1  1 Ta có:  . 3
2xy3x 21 3 3x  y  2  Xét phương trình   1 x  x x
 y y  x  x 2 2 2            y 2 ( 4) 2 16 33 2 1 4 2 4 1 2 y    1    f x  4  f y. Xét f a a 2 a   3 2 1  2a  a .
Với mọi a , a  ,a  a . ta có 1 2 1 2 f a  f a  3 2a a  3 2a a  2 a a     2 2 a a .a a            a a  0 1 2 1 1 2 2 1 2 1 1 2 2   1 2   .
 f a là hàm số đồng biến  x4  y.
Thay y  x 4 vào 2 ta có phương trình 2 3 2x 1  1x21 3 4x4 2  11 21  11 47 Vì 2 2 2x 11x  21 2x   x   2x       
 0  4x4 0  x 1. 2 2   4  8 Trang 8/2    x  x 3 2x  5  3 12 3 3 4x 4   2  x  3 2x    5  3 4x42 3 2 4x4 4     x  12 3 2x5      0   3  4x42 3  2 4x4  4 x3 0  12  2x5
 0  x  3, với x  3 y  1.  3  4x42 3 2 4x4  4 
Vậy nghiệm của hệ phương trình  ; x y3;  1 . (  x4) 2 2x 1  6x 3 3 y 2 2 y   1  1 Cách 2: Ta có:  . 3
2xy3x 21 3 3x  y  2  Xét phương trình   1 x  x x
 y y  x  x 2 2 2            y 2 ( 4) 2 16 33 2 1 4 2 4 1 2 y    1  
Đặt x 4  a, y  b ta có a 2 a   b 2 b   3 3 2 1 2 1  2a  a  2b b  ab 2 2 2
a  ab b ab 0 ab 2 2 2a  2ab b   1  0 ab  0  . 2 2 2a 2abb 1 0 
Xét phương trình a  abb    a b2 2 2 2 2 2 1 0  a 1 0. a  b  2 0 Vì   ab2 2 a 1 0 vô nghiệm. 2 a  1 0 
Xét phương trình a b  0  x 4  y .
Thay y  x 4 vào 2 ta có phương trình 2 3 2x 11x 21 3 4x4 2  11 21  11 47 Vì 2 2 2x 11x  21 2x   x   2x       
 0  4x4 0  x 1. 2 2   4  8
Với x 1 theo AM – GM ta có: 3 3 3 4x 4  3 2 .x  1 .2  x 3
x  x   x   x 2 2 2 11 21 3 2
3  0 . Mặt khác x 2
3  0  x  3  y 1.
Vậy nghiệm của hệ phương trình  ; x y3;  1 . ____________Hết___________ Trang 9/2