












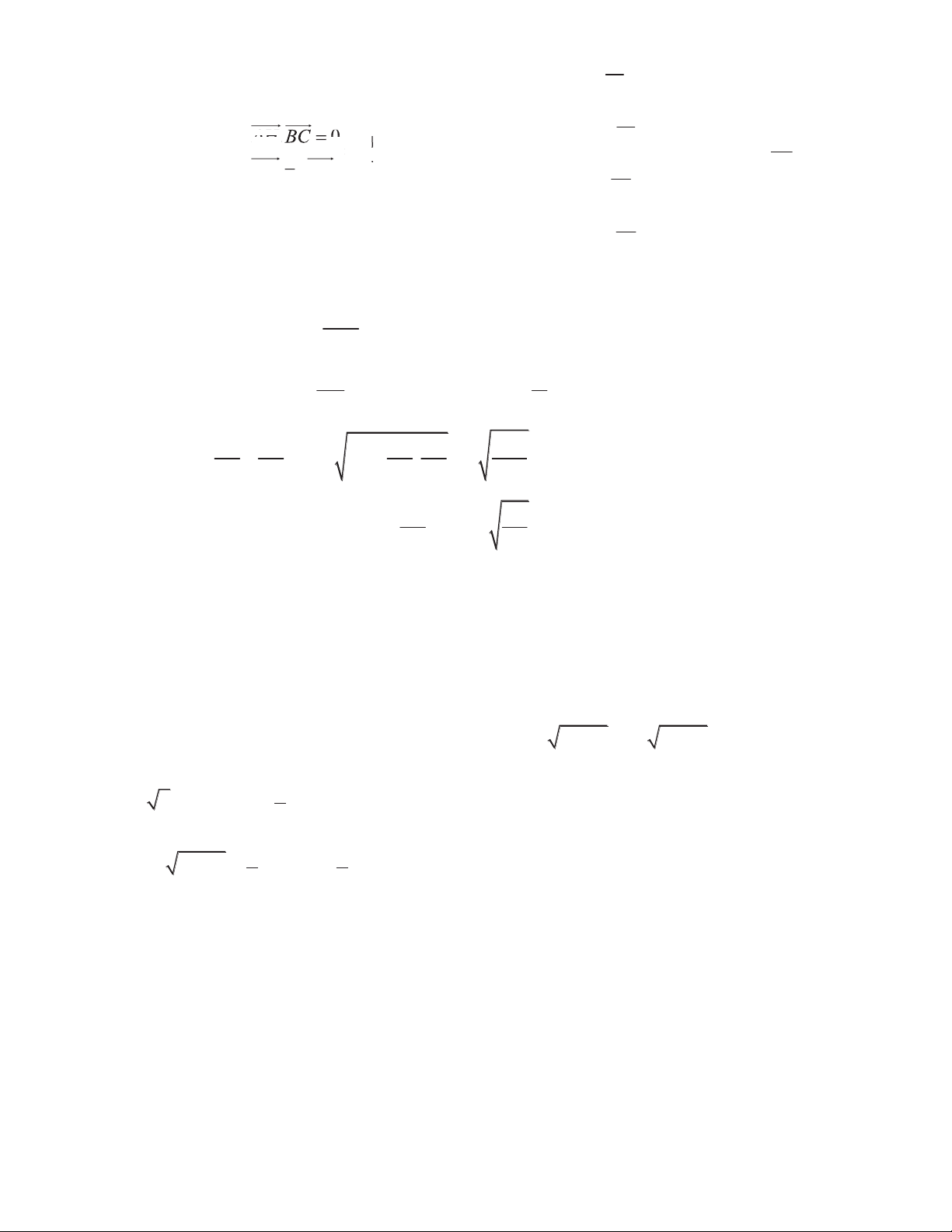

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO NAM ĐỊNH
ĐỀ THI 8 TUẦN HỌC KÌ I TRƯỜNG THPT CHUYÊN NĂM HỌC 2017 - 2018 LÊ HỒNG PHONG
Môn: Toán - Lớp: 12 THPT
Thời gian làm bài: 90 phút
Câu 1: Trong không gian với hệ tọa độ Oxyz, A 2 ;4;2,B 5 ;6;2,C 1 0;17; 7 . Viết
phương trình mặt cầu tâm C bán kính AB. 2 2 2 2 2 2 A. x 10 y 17 z 7 8 B. x 10 y 17 z 7 8 2 2 2 2 2 C. 2 x 10 y 17 8 D. x 10 y 17 z 7 8
Câu 2: F x là một nguyên hàm của hàm số 2 x
y xe . Hàm số nào sau đây không phải là Fx 1 1 1 1 A. F x 2 x e B. F x 2x e 5 C. Fx 2 x e C D. Fx 2 x 2 e 2 2 2 2 Câu 3: Biết 2x 2x 2x xe dx e be Ca,b ³ . Tính tích a.b 1 1 1 1 A. a.b B. a.b C. a.b D. a.b 4 4 8 8
Câu 4: Tìm m để đồ thị hàm số 4 2
y x 2mx 1 có ba điểm cực trị A0; 1 ,B,C thỏa mãn BC 4? A. m 2 B. m 4 C. m 4 r D. m r 2
Câu 5: Đặt a log 3,b log 3. Hãy biểu diễn log 45 theo a,b 2 5 6 a 2ab 2 2a 2ab a 2ab 2 2a 2ab A. log 45 B. log 45 C. log 45 D. log 45 6 ab b 6 ab 6 ab 6 ab b
Câu 6: Phương trình tiếp tuyến của đồ thị hàm số 3
y x 2x 3 C tại điểm M1;2 là A. y 3x 1 B. y 2x 2 C. y 2 x D. y x 1
Câu 7: Trong các mệnh đề sau, mệnh đề nào đây sai 2019 2018 § 2 · § 2 · A. 2 1 3 2 ! 2 B. ¨1 ¸ ¨1 ¸ ¨ 2 ¸ ¨ 2 ¸ © ¹ © ¹ 2017 2018 2018 2017 C. 2 1 ! 2 1 D. 3 1 ! 3 1
Câu 8: Trong các hàm số sau, hàm số nào có một nguyên hàm là hàm số Fx ln x A. f x x B. 1 f x C. 2 x f x D. f x x x 2
Câu 9: Tập xác định của hàm số y 2 lnex là A. 1;f B. 0; 1 C. 0;eº¼ D. 1;2
Câu 10: Cho f x,gx là các hàm số xác định, liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai? A. f ³ xgxdx f ³ xdx. g ³ xdx B. 2f ³ xgxdx 2 f ³ xdx C. ªf ³¬ xgxºdx f ¼ ³ xdx g ³ xdx D. ªf ³¬ xgxºdx f ¼ ³ xdx g ³ xdx
Câu 11: Trong các mệnh đề sau, mệnh đề nào sai? A. Hàm số x
y e không chẵn cũng không lẻ B. Hàm số 2
y ln x x 1 không chẵn cũng không lẻ C. Hàm số x
y e có tập xác định là 0;f D. Hàm số 2
y ln x x 1 có tập xác định là
Câu 12: Tìm họ nguyên hàm của hàm số x f x 5 A. ³ x f x dx 5 C B. ³ x f x dx 5 ln5 C C. ³ x 5 f x dx C D. ³ x 1 5 f x dx C ln5 x 1
Câu 13: Kết quả của x xe dx ³ là 2 x 2 x A. x x I xe e C B. x x I e xe C C. x I e C D. x x I e e C 2 2
Câu 14: Cho 2 hàm số y f x log x;y gx x
a . Xét các mệnh đề sau: a
I. Đồ thị của hai hàm số f x,gx luôn cắt nhau tại một điểm
II. Hàm số f x gx đồng biến khi a !1, nghịch biến khi 0 a 1
III. Đồ thị hàm số f x nhận trục Oy làm tiệm cận
IV. Chỉ có đồ thị hàm số f x có tiệm cận Số mệnh đề đúng là A. 1 B. 4 C. 2 D. 3
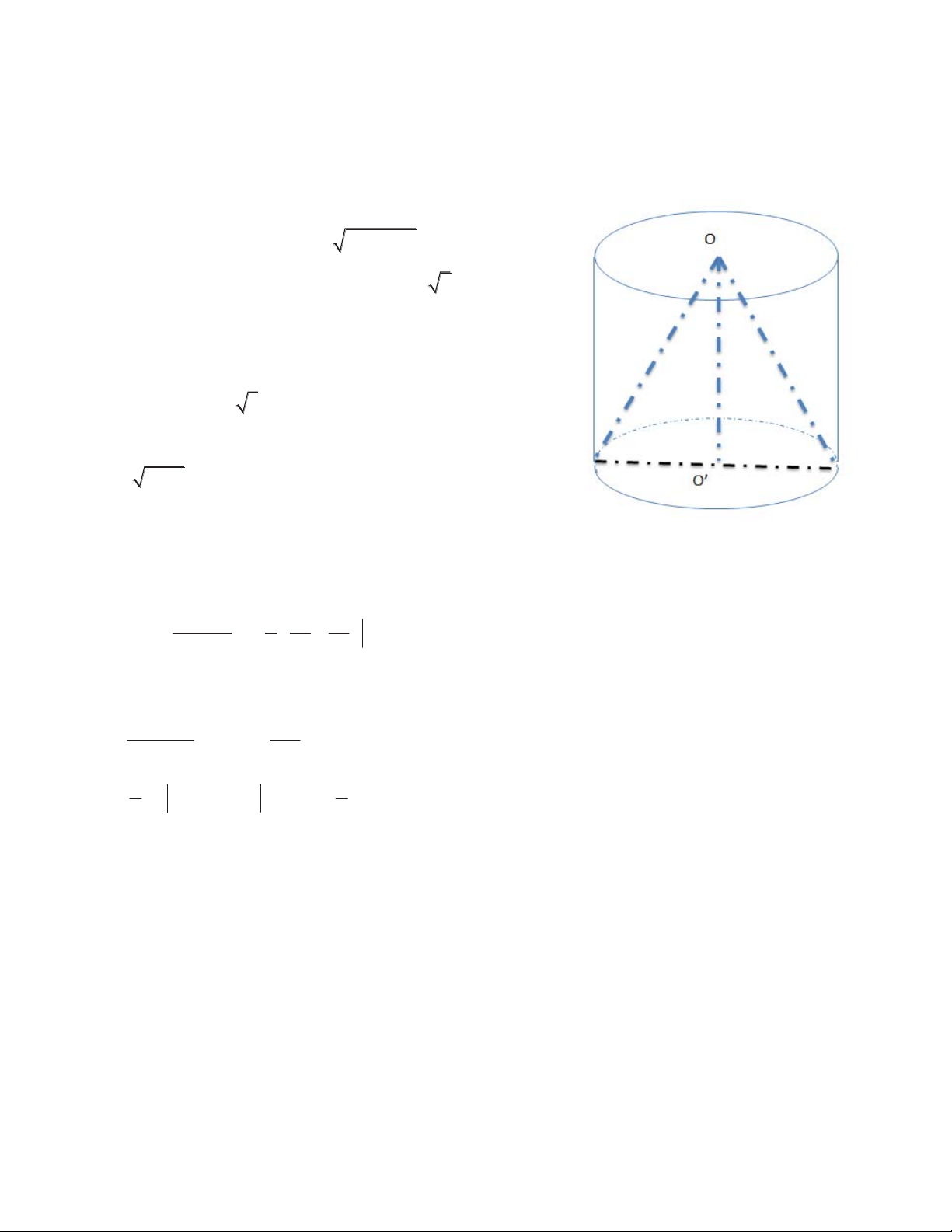
Câu 15: Cho hình trụ có hai đáy là hai hình tròn O và O' chiều cao R 3 và bán kính
đáy R. Một hình nón có đỉnh O’ và đáy là hình tròn O;R Tỷ lệ diện tích xung quanh của
hình trụ và hình nón bằng A. 3 B. 2 C. 2 D. 3 4 1 Câu 16: Cho I x 1 2xdx
Mệnh đề nào dưới đây sai? 2 ³ và u 2x 1. 0 3 1 3 A. 2 I x 2 x ³ 1dx B. 2 I u 2 u ³ 1du 2 1 1 3 5 3 1 § u u · 3 1 C. I ¨ D. 2 I u 2 u ³ 1du 2 5 3 ¸ © ¹ 2 1 1 3 2 x x 1 b Câu 17: Biết a ln , ³
với a, b là các số nguyên. Tính S a 2b. x 1 2 1 A. S 2 B. S 5 C. S 2 D. S 10
Câu 18: Trong các mệnh đề sau, mệnh đề nào sai?
A. Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp
B. Bất kì một hình tứ diện nào cũng có một mặt cầu ngoại tiếp
C. Bất kì một hình chóp đều nào cũng có một mặt cầu ngoại tiếp
D. Bất kì một hình hộp chữ nhật nào cũng có một mặt cầu ngoại tiếp
Câu 19: Cho S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA A ABCDvà
SC a 3. Tính thể tích V của khối chóp S.ABCD. 3 3a 3 a 3 a 2 3 a 3 A. V B. V C. V D. V 2 3 3 3 S 2 § S 1 ·
Câu 20: Kết quả của tích phân ³2x 1sinxdx được viết ở dạng S ¨ ¸ 1. Khẳng © a b 0 ¹
định nào sau đây là sai? A. a 2b 8 B. a b 5 C. 2a 3b 2 D. a b 2
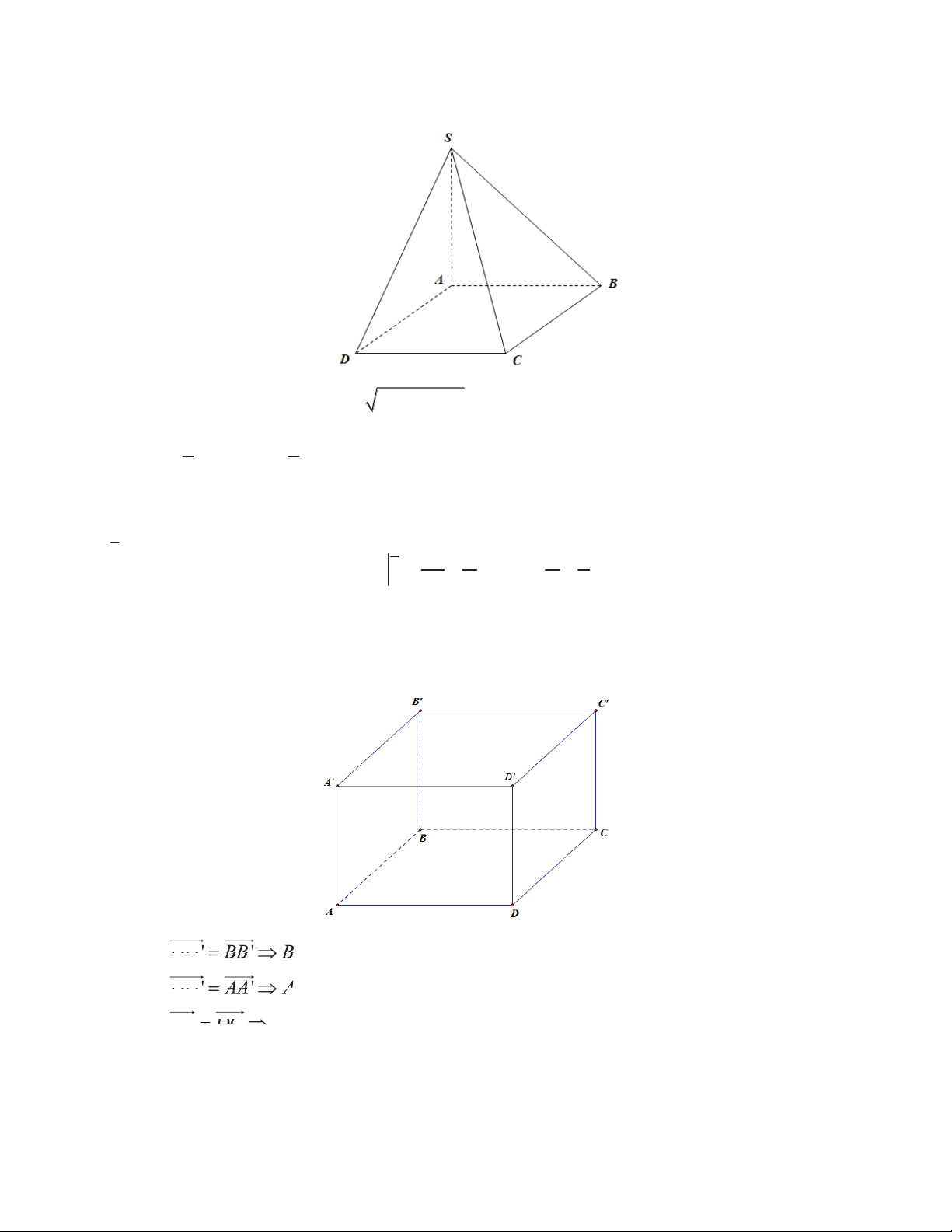
Câu 21: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’ có A0;0;0,B3;0;0,D0;3;0,D'0;3; 3
. Tọa độ trọng tâm của tam giác A’B’C’ là A. 1;1; 2 B. 2;1; 2 C. 1;2; 1 D. 2;1; 1 Câu 22: Nếu ³ 1 f x dx ln x C thì f x là x A. f x x lnx C B. 1 f x x C x 1 x 1 C. f x ln x C D. f x 2 x 2 x
Câu 23: Gọi M và m tương ứng giá trị lớn nhất và giá trị bé nhất của hàm số y 5 4x trên đoạn ª 1 ;1º. ¬ ¼ Khi đó M m bằng A. 9 B. 3 C. 1 D. 2
Câu 24: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với A0;0; 3 ,B0;0; 1 ,C1;0; 1 và D0;1;
1 . Mệnh đề nào sau đây là sai? A. AB A BD B. AB A BC C. AB A AC D. AB A CD
Câu 25: Trong các hàm số sau hàm số nào đồng biến trên . x 1 A. 2 y x x B. 4 2 y x x C. 3 y x x D. y x3
Câu 26: Trong không gian với hệ tọa độ Oxyz, Cho bốn điểm
A2;0;0,B0;2;0,C 0;0;2 và D2;2;2. Gọi M, N lần lượt là trung điểm của S và
AB. Tọa độ trung điểm I của MN là: § 1 1 · A. I1; 1 ;2 B. I1;1;0 C. I¨ ; ;1 D. I1;1 ;1 2 2 ¸ © ¹ Câu 27: Hàm số 3 x
F x e là một nguyên hàm của hàm số: 3 x e A. 3 x f x e B. 3 2 x f x 3x .e C. f x D. 3 3 x 1 f x x .e 2 3x
Câu 28: Cho hàm số y f x liên tục trên
có bảng biến thiên như hình sau: x f 1 1 2 f y’ + 0 + f 2 y 3 4
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị
B. Hàm số đạt giá trị lớn nhất bằng 2 và giá trị bé nhất bằng 3
C. Đồ thị hàm số có đúng 1 đường tiệm cận
D. Hàm số nghịch biến trên các khoảng ; f 1 .2;f e ln x Câu 29: Biết dx a e b ³ với a,b . Tính P a.b 1 x A. P 4 B. P 8 C. P 4 D. P 8 x Câu 30: Nếu f ³ x 3 x dx e C thì f x bằng 3 x x A. 2 x f x x e B. f x 4 x e C. 2 x f x 3x e D. f x 4 x e 3 12
Câu 31: Giải bất phương trình log 3x 1 ! 3 2 1 10 A. x ! 3 B. x 3 C. x 3 D. x ! 3 3
Câu 32: Tập xác định của hàm số 1 3 2 y x 27 A. D ª3;f ¬ B. D \ ^ ` 2 C. D D. D 3;f
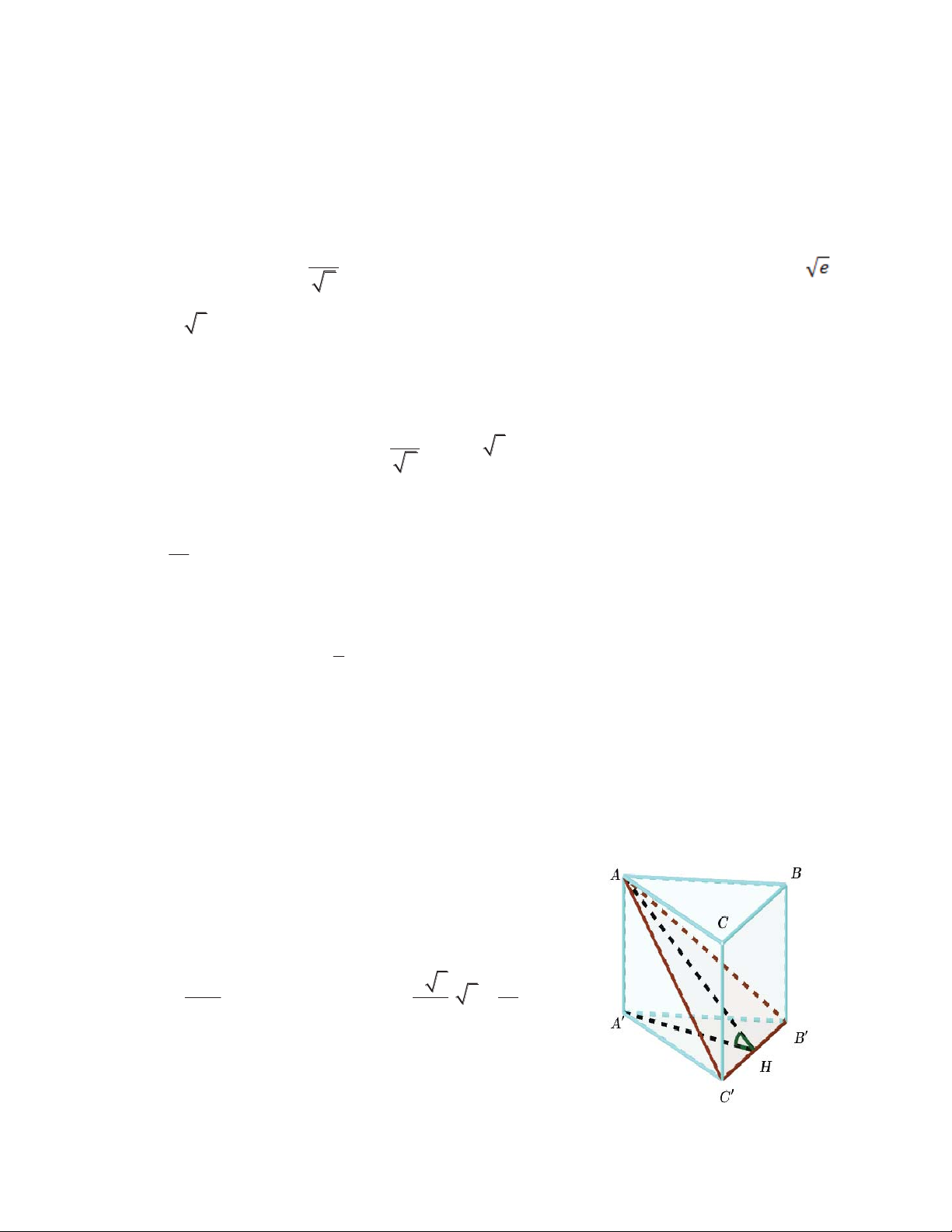
Câu 33: Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng AB'C'
tạo với mặt đáy góc 60 .
q Tính theo a thể tích lăng trụ ABC.A’B’C’ 3 3a 3 3 a 3 3 3a 3 3 a 3 A. V B. V C. V D. V 8 2 4 8 x 2
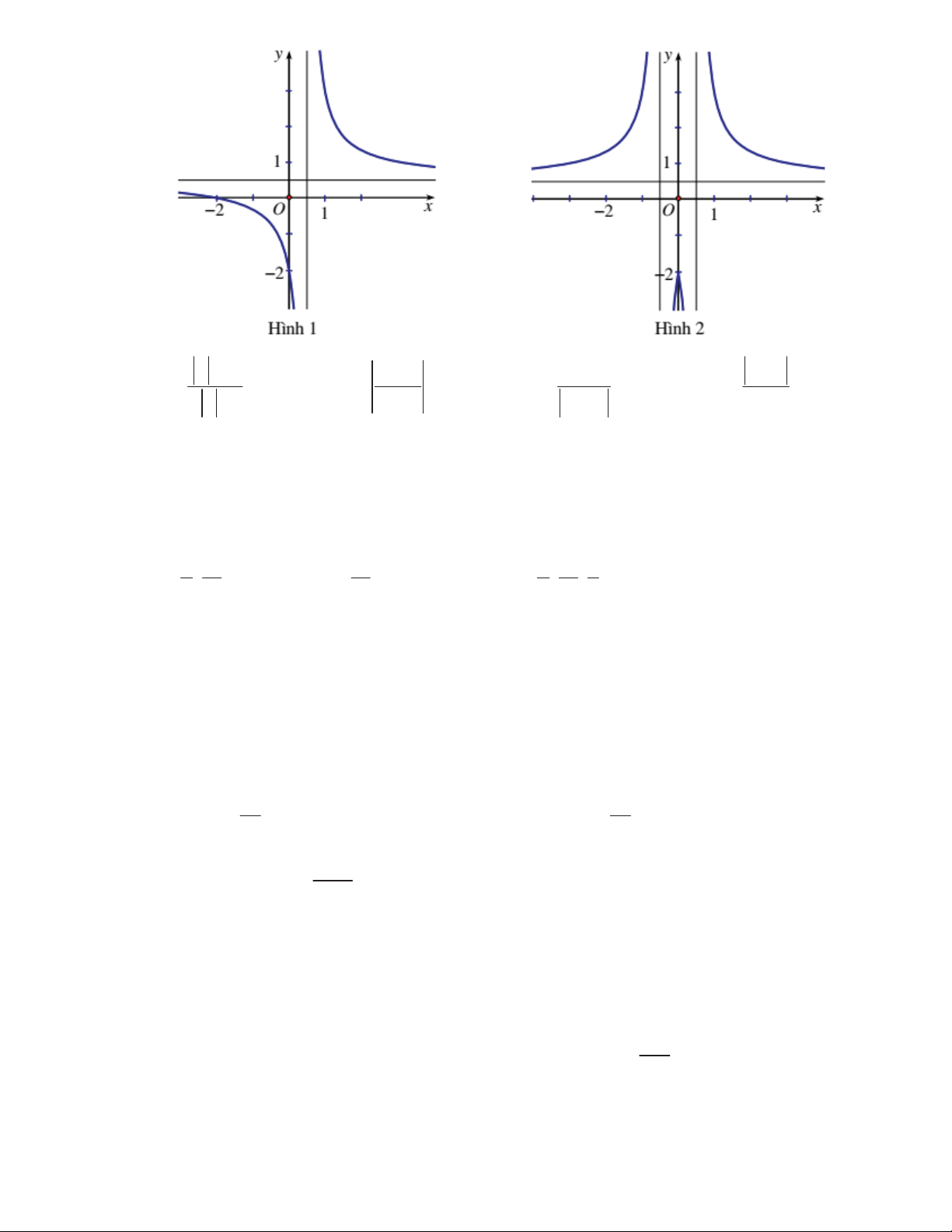
Câu 34: Cho hàm số y
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới 2x 1 đây? x 2 x 2 x 2 x 2 A. y B. y C. y D. y 2 x 1 2x 1 2x 1 2x 1
Câu 35: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A1;2; 1 ,B2; 1 ;3,C 4
;7;5. Tọa độ chân đường phân giác trong góc B của tam giác ABC là § 2 11 · §11 · § 2 11 1 · A. ¨ ; ;1 B. ; 2 ¨ ;1 C. ¨ ; ; D. 2; 11; 1 3 3 ¸ ¸ ¸ © ¹ © 3 ¹ © 3 3 3 ¹ Câu 36: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A0;1 ;1 ,B3;0; 1 ,C0;21; 1 9 2 2 1 và mặt cầu S :x 1 y 1 z 1 1 . Ma,b,c
là điểm thuộc mặt cầu S sao cho biểu thức 2 2 2
T 3MA 2MB MC đạt giá trị nhỏ nhất. Tính tổng a b c. 14 12 A. a b c B. a b c 0 C. a b c D. a b c 12 5 5 x 1
Câu 37: Cho hàm số y
Số các giá trị tham số m đêt đường thẳng y m x luôn cắt x 2
đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn 2 2 x y 3y 4 là A. 1 B. 0 C. 3 D. 2 AD
Câu 38: Cho hình thang ABCD vuông tại A và B với AB BC a. Quay hình thang 2
và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành. 3 4 a S 3 5 a S 3 7 a S A. V B. V C. 3 V a S D. V 3 3 3 Câu 39:
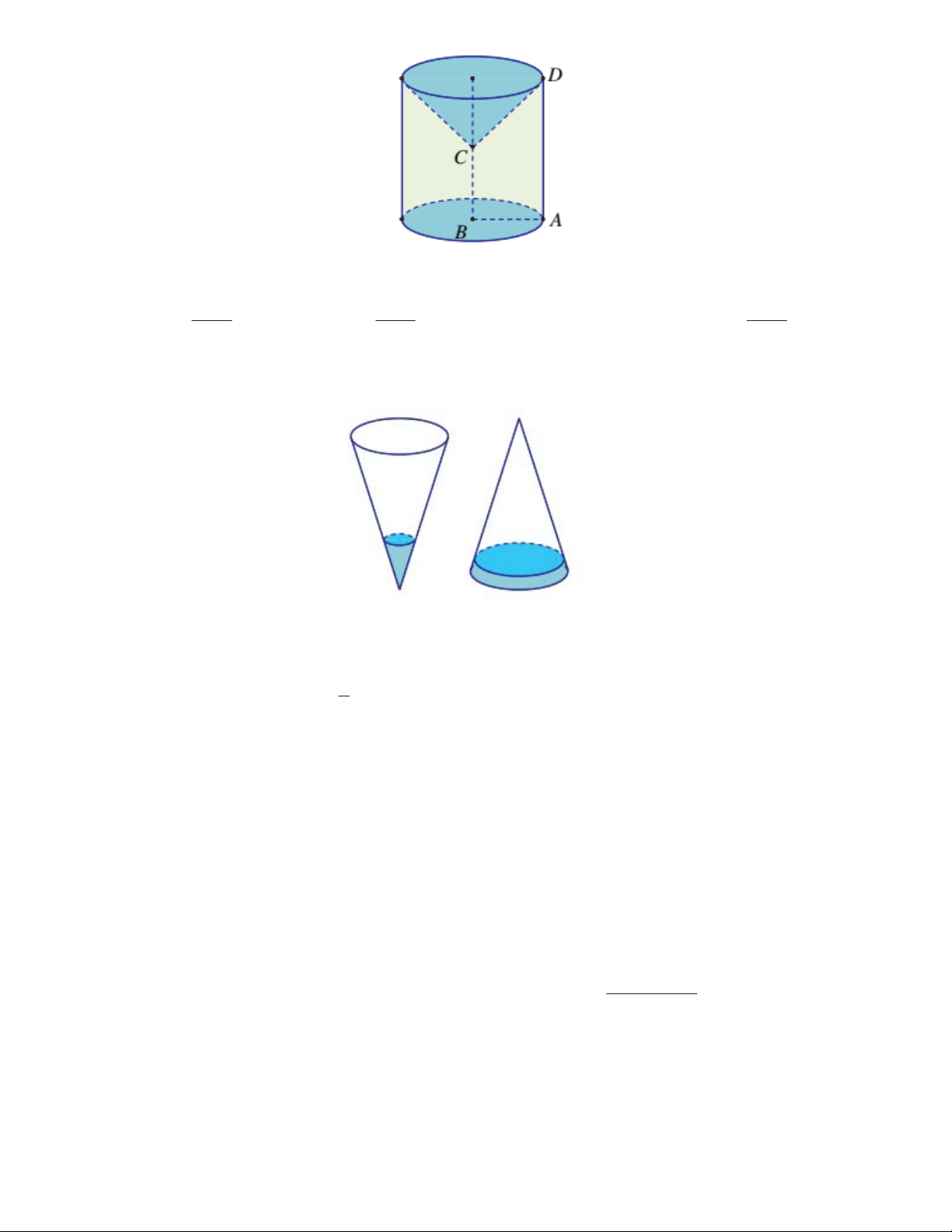
Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của 1
lượng nước trong phễu bằng
chiều cao của phễu. Hỏi nếu bịt kín miệng phễu rồi lôn ngược 3
phễu lên thì chiều cao của mực nước xấp xỉ bằng bao nhiêu? Biết rằng chiều cao của phễu là 15cm. A. 0,5cm B. 0,3cm C. 0,188cm D. 0,216cm Câu 40: Tìm giá trị nguyên của m đê phương trình 1x 1x 2x 2x 4 4
m 1 2 2 168m có nghiệm trên ª0;1º? ¬ ¼ A. 2 B. 5 C. 4 D. 3 m ln x 2
Câu 41: Tìm tất cả các giá trị thực của m để hàm số y nghịch biến trên ln x m 1 2e;f. A. m d 2 hoặc m 1 B. m 2 hoặc m 1 C. m 2 D. m 2 hoặc m !1
Câu 42: Cho khối S.ABC có góc ASB BSC CSA 60q và SA 2,SB 3,SC 4. Tính thể tích khối S.ABC. A. 2 2 B. 2 3 C. 4 3 D. 3 2
Câu 43: Gọi F x là một nguyên hàm của hàm số x f x 2 thỏa mãn 1 F 0 . Tính giá ln2 trị biểu thức T F0 F 1 F2... F2017. 2017 2 1 2017 2 1 2018 2 1 A. T 1009. B. 2017.2018 T 2 C. T D. T ln2 ln2 ln2
Câu 44: Trong không gian với hệ tọa độ Oxyz, cho ABC ' biết A2;0;0, B0;2;0, C1;1;
3 . Hx ,y ,z là chân đường vuông góc hạ từ A xuống BC. 0 0 0 Khi đó x y z bằng 0 0 0 38 34 30 11 A. B. C. D. 9 11 11 34
Câu 45: Khi thiết kế vỏ lon sữa hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí
làm vỏ lon là nhỏ nhất. Muốn thể tích khối trụ bằng V mà diện tích toàn phần của hình trụ là
nhỏ nhất thì bán kính R của mặt tròn đáy khối trụ bằng? V V V V A. B. C. 3 D. 3 S 2S S 2S
Câu 46: Xét bất phương trình 2
log 2x 2(m 1)log x 2 0. Tìm tất cả các giá trị của tham 2 2
số m để bất phương trình có nghiệm thuộc khoảng 2;f § 3 · § 3 · A. m 0;f B. m ¨ ;0 C. m ¨ ;f D. m ; f 0 4 ¸ ¸ © ¹ © 4 ¹ x 1
Câu 47: Cho hàm số y
. Tìm tất cả các giá trị của m để đồ thị hàm số có ba 2 mx 2x 3 đường tiệm cận °m z 0 °m z 0 m z 0 1 ° ° ° °m A. ®m z 1 B. ®m z 1 C. ® 1 D. ® 5 ° m 1 ° ° °¯m z 0 °m 1 °m ¯ 3 ¯ 5 ¯ 3
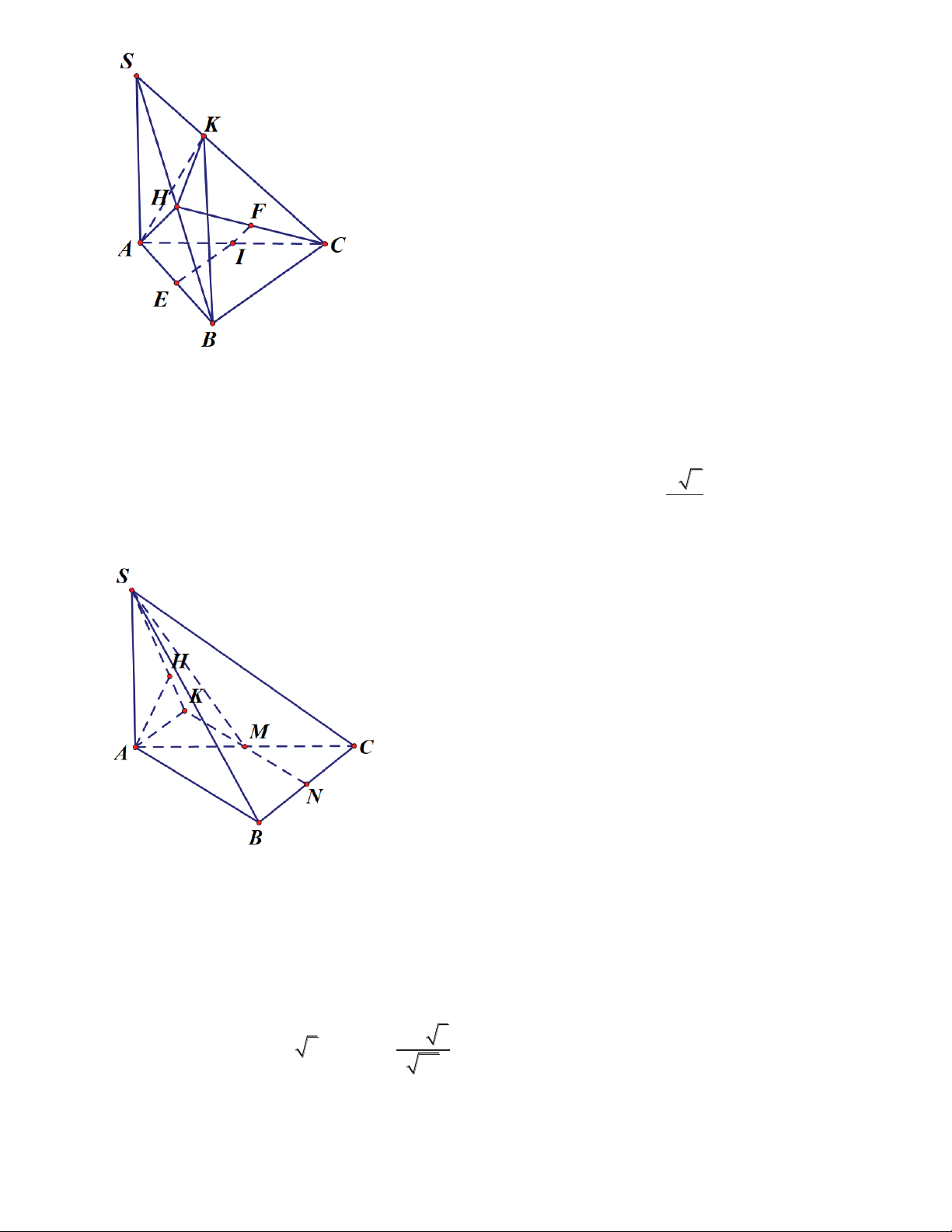
Câu 48: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC a. Cạnh
bên SA vuông góc với đáy ABC. Gọi H, K lần lượt là hình chiếu vuông góc của A lên
cạnh bên SB và SC. Tính thể tích khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKB là 3 a S 3 2 a S 3 a S A. B. C. 3 2 a S D. 2 3 6
Câu 49: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,AB 3a,BC 4a. Cạnh
bên SA vuông góc với đáy. Góc tạo bởi giữa SC với đáy bằng 60 .
q Gọi M là trung điểm AC,
tính khoảng cách giữa hai đường thẳng AB và SM 10a 3 5a A. a 3 B. C. D. 5a 3 79 2
Câu 50: Một chất điểm đang chuyển động với vận tốc v 15m / s thì tăng vận tốc với gia 0 tốc 2 2 a t t
4t m / s . Tính quảng đường chất điểm đó đi được trong khoảng thời gian 3
giây kể từ khi abwts đầu tăng vận tốc. A. 70,25m B. 68,25m C. 67,25m D. 69,75m ĐÁP ÁN 1-B 2-C 3-C 4-B 5-A 6-D 7-D 8-B 9-C 10-A 11-B 12-C 13-A 14-C 15-D 16-B 17-C 18-C 19-B 20-B 21-B 22-D 23-D 24-C 25-C 26-D 27-B 28-B 29-B 30-A 31-A 32-D 33-A 34-A 35-A 36-A 37-D 38-B 39-C 40-A 41-C 42-A 43-D 44-B 45-D 46-C 47-B 48-B 49-B 50-D
LỜI GIẢI CHI TIẾT ĐỀ Câu 1: Đáp án B Ta có AB 2; 2;0 R AB 2 2
Vậy phương trình mặt cầu tâm cần tìm là x 2 y 2 z 2 10 17 7 8 Câu 2: Đáp án C 1 c § · Ở đáp án C ta có 2 2 x x e C xe ¨ ¸
nên không phải là nguyên hàm của hàm số 2 . x y x e © 2 ¹ Câu 3: Đáp án C du dx u x ° Ta có : 2x I xe dx ³ Đặt ® ® 1 2x 2x ¯dv e v e °¯ 2 1 1 1 x 1 x 1 x 1 2 2 2 2x I xe e dx xe e C ³ Suy ra a và b . 2 2 2 4 2 4 Câu 4: Đáp án B Ta có 4 2
y x 2mx 1 TXĐ: D 3
yc 4x 4mx ªx 0 3
yc 0 4x 4mx 0 « 2 ¬x m
Đồ thị hàm số có ba điểm cực trị yc 0 có 3 nghiệm phân biệt m ! 0 . Khi ấy, ba điểm cực trị là A0; 1 , B 2
m;1 m và C 2
m;1 m . Ta có BC 2 m . Theo giả thiết:
2 m 4 m 2 m 4 (thoả) Câu 5: Đáp án A.
Sử dụng máy tính cầm tay: Nhập vào máy tính: log 3 sau đó lưu vào biến A ( SHIFT + 2
RCL + (-) ), màn hình trả kết quả log 3 o . Tương tự ta bấm log 3 o 2 A 5 B
Nhập log 45 , ta thấy log 45 |2,124538 6 6 A 2
Kiểm tra đáp án. Nhập vào máy tính
AB bấm = , ta thấy ra kết quả 2,124538 nhận A. AB B Câu 6: Đáp án D Ta có : 3 2
y x 2x 3 yc 3x 2 yc 1 1
Phương trình tiếp tuyến của đồ thị hàm số tại M 1;2 là : y 1 x 1 2 y x 1 Câu 7: Đáp án D 2018 2017
Vì 0 3 11 và 2107 < 2018 nên 3 1 3 1 Câu 8: Đáp án B 1 Ta có:
dx ln x C ³ x Câu 9: Đáp án C °2 lnex t 0 x d e Điều kiện: ® ® 0 x d e °¯ex ! 0 ¯x ! 0
Tập xác định: D 0;e@ Câu 10: Đáp án A f
³ x.gx z f ³ x. g ³ x Câu 11: Đáp án B 1 1
Ta có: ln x x2 1 ln ln 2 x x 1 ln 2 x x 1 2 x x 1 Suy ra: 2
y ln x x 1 là hàm số lẻ Câu 12: Đáp án C x 5x Ta có: 5 dx C ³ ln 5 Câu 13: Đáp án A u = x du = dx Đặt ® ® x x ¯dv=e dx ¯v=e x x x x x I e x dx = e x e dx = e x e C ³ ³ Câu 14: Đáp án C
Hàm số y log x nhận Oy làm tiệm cận đứng , đồng biến nếu a
a>1, nghịch biến nếu 0<a<1 Hàm số x
y a nhận Ox làm tiệm cận ngang, đồng biến nếu a>1,
nghịch biến nếu 0<a<1
Đồ thị hàm số y log x và đồ thị hàm số x
y a cắt nhau tại 2 điểm phân biệt hoặc không a cắt nhau nếu a>1 Vậy mệnh đề I, IV sai Mệnh đề II, III đúng Câu 15: Đáp án D
Đường sinh của hình nón là 2 2 R 3R 2R
Diện tích xung của hình trụ 2 S 2S l R =2 3S 1 R
Diện tích xung của hình nón 2 S S l= R 2S 2 R
Vậy tỷ số diện tích xung của hình trụ và diện tích xung của hình nón là 3 Câu 16: Đáp án B u= 2x+1 u du=x dx Cận u=1 khi x=0 u=3 khi x=4 2 3 u 5 3 1 1 § u u · 2 3 I u u d = ³ ¨ ¸ 1 2 2 © 5 3 1 ¹ Câu 17: Đáp án C 5 2 5 x x+1 § 1 · x= d x+ x d ³ ³¨ ¸ x+1 © x+1¹ 3 3 1 3 2 5 = x ln x+ 5 1 8 ln 3 3 2 2 Câu 18: Đáp án C
1. Ta có cách xác định mặt cầu ngoại tiếp hình chóp như sau:
Xác định trục đường tròn của mặt phẳng đáy, tức là đường thẳng đi qua tâm đường tròn ngoại
tiếp tam giác đáy. Lấy giao điểm của trục với trung trực của cạnh bên hình chóp. Vì thế với
hình tứ diện và hình chóp đều luôn có mặt cầu ngoại tiếp, nên A và B đúng.
2. Hình hộp chữ nhật luôn có tâm cách đều các đỉnh của hình hộp, do đó luôn xác định được
một mặt cầu ngoại tiếp hình hộp chữ nhật. Vậy D đúng. Chọn phương án C. Câu 19: Đáp án B Ta có 2 S a và 2 2
SA SC AC a
. Thể tích khối chóp S.ABCD là ABCD 1 1 3 V .S .SA a S . ABCD 3 ABCD 3 Câu 20: Đáp án B S 2 S ³ S S S
2x 1 sin xdx 1 2 x x cos x 2 2 1 S § · 1 ¨ ¸ 0 4 2 © 4 2 ¹ 0
a 4;b 2 a b 6 khẳng định B sai. Câu 21: Đáp án B DD DD
DD ' BB ' B '3;0; 3 °° Ta có ®DD DD
DD ' AA' A'0;0; 3
Tọa độ trọng tâm G của A
' 'B'C là G2;1; 2
°AB DC C ° 3;3;0 ¯ Câu 22: Đáp án D 1 § 1 · 1 1 1 ( )d ln ( ) ln ' x f x x x C f x x C ³ ¨ ¸ 2 2 x © x ¹ x x x Câu 23: Đáp án D § 5 º Tập xác định D ; f ¨
. Hàm số xác định và liên tục trên D nên cũng xác định và liên 4» © ¼ tục trên > 1 ; @ 1 . 2 y ' 0, x D 5 4x y 1 3 M 3 y 1 1 m 1 Vậy M m 2 Câu 24: Đáp án C Ta có: AB AB 0;0; 4 ; AC 1;0; 4
; BC 1;0;0; BD 0;1;0; CD 1 ;1;0 . AB BD . AB
0 AB A BD AB A BD .
AB BC 0 AB A BC AB A BC A . AB B AC AC 16 1 Mệnh đề C sai. Câu 25: Đáp án C Cách 1: 2 y ' 3x 1 ! 0, x
R nên HSĐB trên R
Cách 2: Bấm Mode 7 để kiểm tra tính đồng biến trên [-4; 4] với step: 0.5 Câu 26: Đáp án D x x x x x x A B x ° C D x M N x M 2 ° N ° I ° 2 ° 2 ° ° ° °
Áp dụng công thức trung điểm ta có y y y y y y A B ®y và C D ®y và M N ®y M 2 ° N 2 I ° 2 ° ° z z ° z z ° z z A B z ° C D z M N z M ¯ 2 ° N ¯ 2 ° I ¯ 2
x x x x A B C D x 1 ° I 4 ° ° Suy ra y y y y A B C D ®y 1 I I 1;1 ;1 4 ° °
z z z z A B C D z 1 ° I ¯ 4 Câu 27: Đáp án B Do 3 2 '( ) 3 x F x x e Câu 28: Đáp án B Do lim y f
nên HS không tồn tại GTLN nof Câu 29: Đáp án B e ln Cách 1: Bấm MT tính xdx 0,7025574586... ³
rồi lưu vào A. Xét hàm F(X) = A – X 1 x
(Do A a e b ) bằng cách nhập hàm trên vào Mode 7, lấy star: - 4, end: 4, step: 1. Ta sẽ X ' 2 a 2 Z thấy tại ® tức là ®
thoả mãn ycbt nên P = - 8. ¯F(X ) 4 b ¯ 4 Z e ln x a 2 Z
Cách 2: Tính tích phân từng phần dx 2 e 4 ! ³ ® nên P = - 8. x b ¯ 4 Z 1 Câu 30: Đáp án A 3 § · Ta có x x 2 x ¨
e c¸ x e f (x) © 3 ¹ Câu 31: Đáp án A 1
Điều kiện : 3x 1 ! 0 x ! 3
Bất phương trình log 3x 1 ! 3 3x 1 ! 8 x ! 3 ( nhận ) 2 Câu 32Đáp án D Hàm số xác định khi 3 x 27 ! 0 x ! 3 Vậy D 3;f Câu 33 : Đáp án A
Góc giữa AB'C' và mặt đáy là góc A AH '
Xét tam giác AIA’ vuông tại I: AA ' a 3 3a 0 0 tan 60 AA' AH.tan 60 . 3 AH 2 2 Thể tích lăng trụ 2 3 3a a 3 3a 3 V AA '.S . (dvtt) A' B 'C ' 2 4 8 Câu 34: Đáp án A
Đồ thì ở hình 2 là đồ thị của hàm số chẵn, nên đối xứng qua trục tung. Chỉ có hàm số x 2 y
là hàm số chẵn thoả mãn đề bài. 2 x 1 Câu 35: Đáp án A
Gọi D là chân đường phân giác góc B của ABC '
. Theo tính chất đường phân giác ta có : DA DC AB AB DA DA DA .DC * AB BC BC Với AB 1; 3
;4 AB 26 và BC 6 ;8;2 BC 104 AB 1 k BC 2
Từ (*) ta có, điểm D chia đoạn thẳng AC theo tỷ số k nên D có toạ độ x kx 2 A C x ° D 1 k 3 ° ° y ky 11 § 2 11 · A C ®y D ; ;1 D ¨ ¸ 1 k 3 ° © 3 3 ¹ ° z kz A C z 1 ° D ¯ 1 k Câu 36: Đáp án A
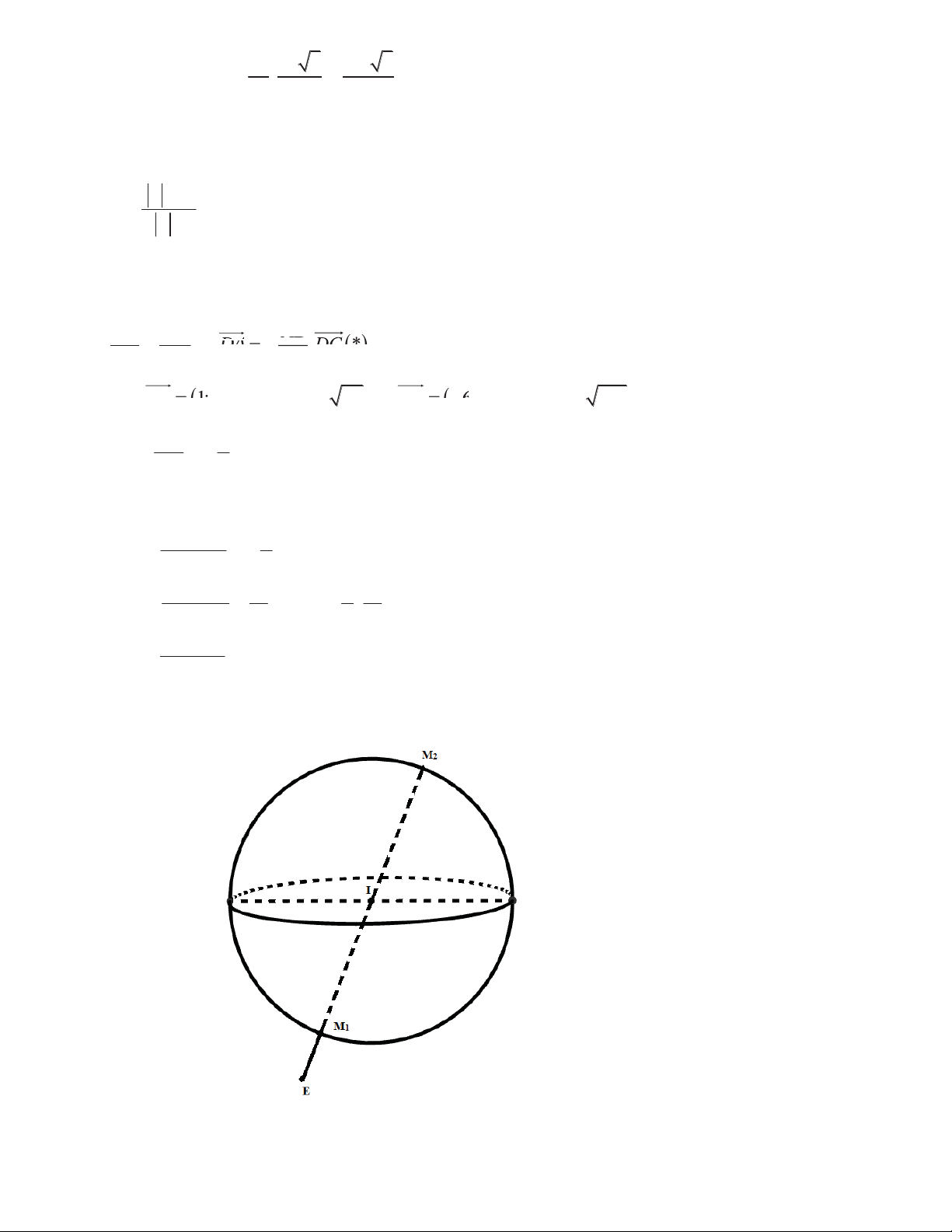
Mặt cầu (S) có tâm I(1;1;1). Gọi E là điểm thoả
3EA 2EB EC 0 E(1;4; 3) . 2 2 2 2 T 6 E M
3EA 2EB EC
T nhỏ nhất khi ME nhỏ nhất M là 1 trong 2 giao điểm của đường thẳng IE và mặt cầu (S). IE (0; (0 3; 3 4
) , EM (a 1;b 4;c 3) a 1 0 a 1 ° ° IE, ME M cùng phương EM EM EM k IE I b ® 4 3k b ® 3k 4 ° ° c 3 4 k c 4 k 3 ¯ ¯ ª 4 k « 2 2 5
M (S) (3k 3) ( 4 k 4) 1 « 6 «k «¬ 5 4 § 8 1 · 208 k M 1; ; 1 EM ¨ ¸ 1 5 © 5 5 ¹ 5 6 § 2 9 · k M 1; ; EM 6 ! (Loại) 2 ¨ ¸ 2 EM1 5 © 5 5 ¹ § 8 1 · Vậy M 1; ; ¨ ¸ © 5 5 ¹ Câu 37: Đáp án D PTHĐGĐ: 2
x (m 3)x 2m 1 0 (*) ĐK: 2
(m 3) 4(2m 1) ! 0
Gọi x1, x2 là 2 nghiệm phân biệt của (*) Ax ; x m , B x ; với S = x 1 1 2 2x m 1 + x2 = 3 – m
§ x x x x 2m · § S S 2 ·
Gọi G là trọng tâm tam giác OAB 1 2 1 2 ; ; m G G ¨ ¸ ¨ ¸ © 3 3 ¹ © 3 3 ¹ 2 2
G (C) : x y 3y 4 2 2 S (S 2 ) m 2 2 (S 2 )
m 4 S (S 2 ) m 9(S 2 ) m 36 9 9 ªm 3 ( ) n 2 2 2 (3 ) m (3 ) m 9(3 ) m 36 2m 9m 45 0 « 15 «m (n) ¬ 2 Câu 38: Đáp án B
Thể tích khối tròn xoay cần tìm = Thể tích khối trụ – Thể tích khối nón (theo hình vẽ)
Khối trụ có chiều cao AD = 2a, bán kính r = a 3 V 2Sa tru 1
Khối nón có chiều cao AD BC a , bán kính r = a 3 V S a non 3 5
Thể tích khối tròn xoay cần tìm = 3 S a 3 Câu 39: Đáp án C
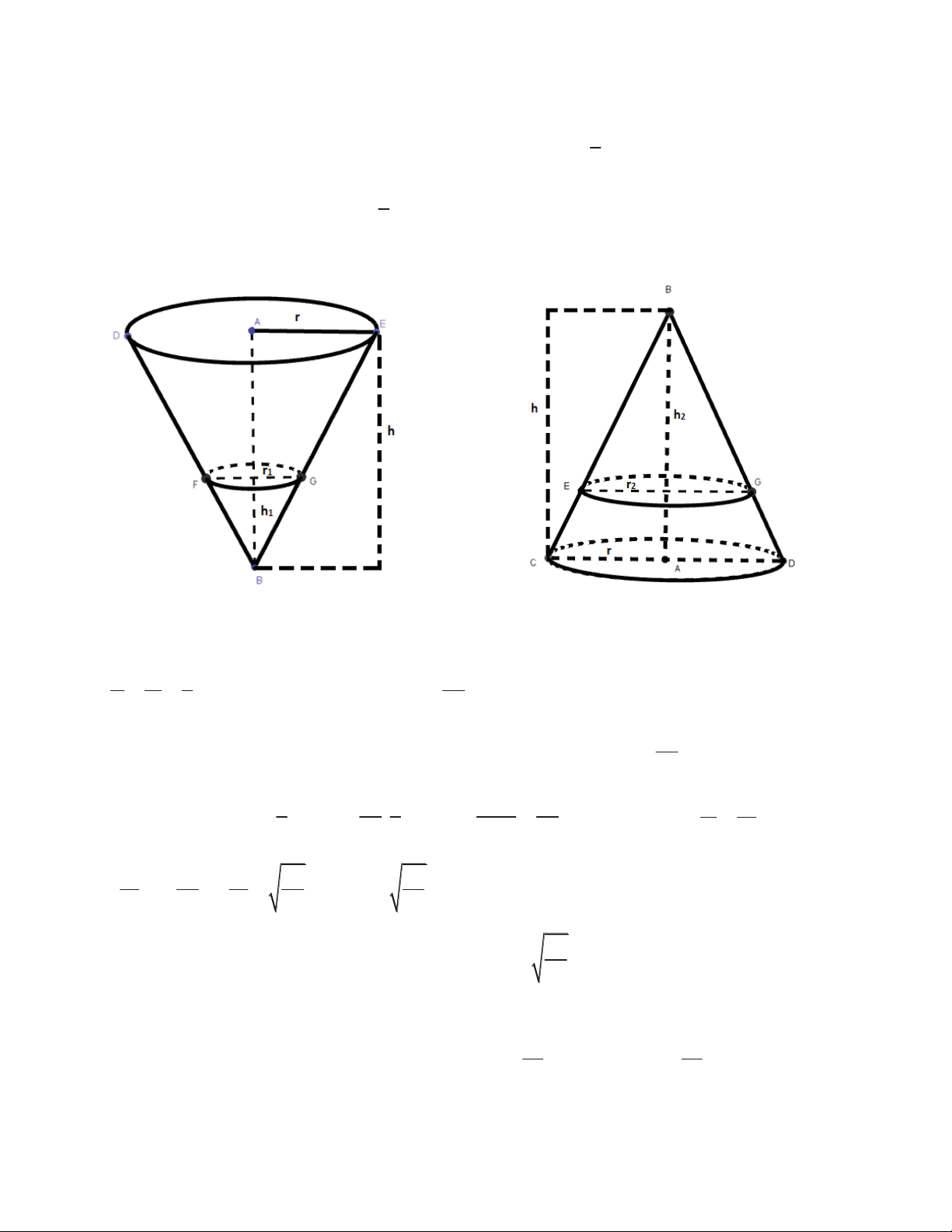
Gọi r, r1, r2, h, h1, h2 như hình vẽ.
Gọi V là thể tích khối nón ban đầu. r h 1 1 1 1
Thể tích nước đổ vào bằng V r h 3 27 26
Khi lộn ngược phễu thì thể tích phần không gian không chứa nước là V 27 2 1 26 1 r .h 26 Khi đó: 2 2 2 2 S r h r .h . S r . mà 2 2 nên 2 2 h 2 3 27 3 r .h 27 r h 3 § h · 26 h 26 26 2 2 3 3 h 15 ¨ ¸ 2 © h ¹ 27 h 27 27 26
Vậy chiều cao của nước khi lộn ngược phễu là 3 15 15 | 0,188 ( ) cm 27 Câu 40: Đáp án A 1 § · § · x 1x 2x 2 4 4 ( 1) 2 2 x m 16 x 1 x 1 8m 4 4 4(m 1) 2 16 8m ¨ ¸ ¨ ¸ © 4x ¹ © 2x ¹ x 1 x 1 Đặt t 2 với x >0; @ 1 2 4 t 2 2x 4x § · 3 x 1 t ' ln 2 2 ! 0 ¨ ¸ 0 d t d © 2x ¹ 2 ªt 2 (L) PT trở thành: 2
t (m 1)t 2 2m (t 1)(t 2) (
m t 2) «¬t m1 3 5
Yêu cầu đề 0 d m 1d 1d m d 2 2 Câu 41. Đáp án C
Đặt t ln x , vì x 2 e ; f t (2; ) f mt 2
Tìm m để hàm số y nghịch biến trên (2; ) f t m 1 Ta có 2
y ' m m 2 y ' 0 2 m m 2 0 Theo trên có ® ® m 2 ¯m 1d 2 ¯m d1 Câu 42. Đáp án A
Trên cạnh SB, SC lần lượt lấy M và N sao cho SA = SM = SN =2 2 2
Ta có SAMN là tứ diện đều cạnh 2, khi đó thể tích của tứ diện SAMN là V SAMN 3 V SA SM SN 1 Lại có SAMN . . V 3V 2 2 V SA SB SC 3 SABC SAMN SABC Câu 43. Đáp án D 1 x 2x
Ta có F(x) 2 dx C ³ , mà F(0) C 0 ln 2 ln 2 2x Vậy F(x) ln2 1 § · T 2 2 2 ...2 2017 1 2(1 2 ) 1 0 1 2 2017 1 ¨ ¸ 2018 2 1 ln 2 ln 2 © 1 2 ¹ ln 2 Câu 44. Đáp án B Có AH AH (x 2; 2 y ; z ); ) BC(1 ( ; 1 1 ; 1 3) 3 ;
) BH(x ; y 2; z ) o o o o o o 4 t ° 11 °
x 2 y 3z 0 o o o 4 ° ° °AH AH.BC . 0 xo 0 °x t ° o 11 34 Theo đề bài, có ® ® ®
x y z °¯BH y 2 t 18 o o o 11 BH t BC B ° o °y °z 3 o t ° 11 ¯ o ° 12 ° z o ¯ 11 Câu 45. Đáp án D Ta có 2 . V V V
l S R l t 2 S R 2 V 2 2 .2S 2S 2S 2S 2( V S l R R S R R S R ) t t S R R 2 S 2 V V 2 V V V 3 3 S 2(S R ) t 2.3 S R . . 6 t 2R 2R 2R 2R 4
Dấu “=” xảy ra khi và chỉ khi 2 V V 3 S R R 2R 2S Câu 46. Đáp án C 2
log 2x 2 m 1 log x 2 0 2 2
1 log x2 2 m 1 log x 2 0 2 2 Đặt t log ta được 2 x t2 m 2 t
t mt t 2 2 1 2 1 2 0 2 1 0 m m 1 ; m m 1 § · x f 1 2; t ;f ¨ ¸ © 2 ¹ 1 3 2
m m 1 ! m ! 2 4 Câu 47. Đáp án B
Đồ thị hàm số có 3 tiệm cận thì phương trình 2
mx 2x 3 0 phải có hai nghiệm phân biệt khác 1. Câu 48. Đáp án B
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC.
IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC. a 2
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB. Suy ra bán kính R 2 Câu 49. Đáp án B
Gọi N là trung điểm của BC. d A , B SM d , A SMN
Dưng đường cao AK trong tam giác AMN, dựng đường cao AH trong tam giác SAK.
Dễ dàng chứng minh được AH A SMN tại H, suy ra d A , B SM d , A SMN AH 10a 3
AK BN 2a, SA 5a 3 AH 79 Câu 50. Đáp án D 3 v t a ³ t t 2 dt 2t c 3 3 v c vt t 2 0 15 15 2t 15 3 3
Quảng đường đi được trong 3 giây: S v ³ tdt 69,75 0




