










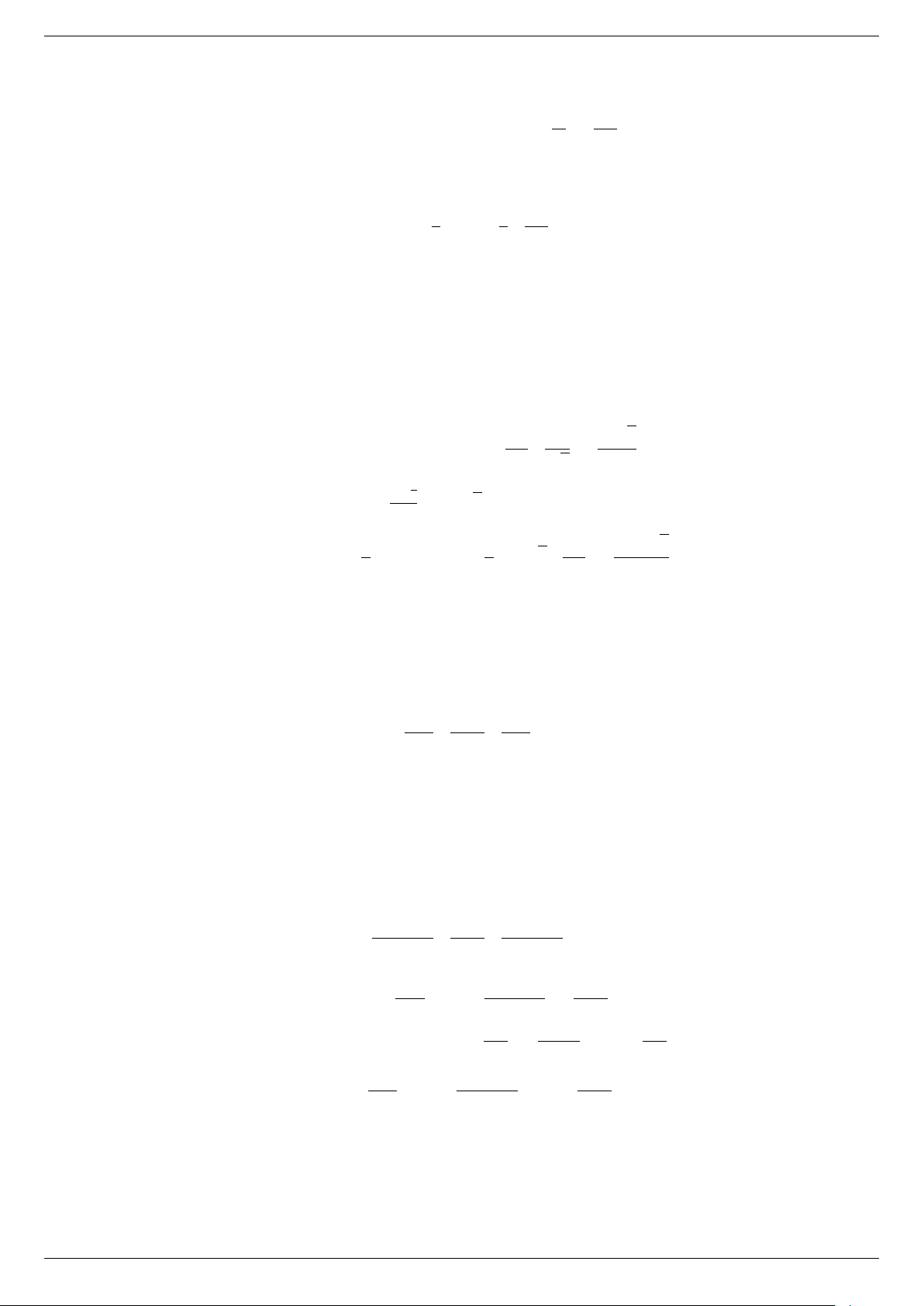


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 HÀ TĨNH NĂM HỌC 2025 - 2026 Môn thi: TOÁN ĐỀ THI C HÍNH THỨC
Thời gian làm bài: 120 phút.
(Đề thi có 2 trang, gồm 18 câu)
I. PHẦN GHI KẾT QUẢ (6.0 điểm) (Thí sinh chỉ cần ghi kết quả vào tờ giấy thi) Câu 1. 7 + 5 + 7 − 5
Rút gọn biểu thức P = − 3 − 2 2 . 7 + 2 11
Câu 2. Cho hai số dương a, b thỏa mãn điều kiện: 2 2
a + ab − 6b = 0; 3a − 4b ≠ 0; a − 4b ≠ 0 . 2025a + 2b 2026a − 2b
Giá trị của biểu thức F = + bằng bao nhiêu? 3a − 4b 4b − a
Câu 3. Cho hai đường thẳng (d ) : y = (m + 3)x + m + 2 và 3
(d ) : y = (m − 3m + 3)x + 3m − 2. 1 2
Gọi Q là tổng tất cả các giá trị của tham số m để hai đường thẳng (d ) và (d ) song song với 1 2
nhau. Giá trị của Q bằng bao nhiêu?
Câu 4. Cho các đa thức f (x) 3 2 2
= x − 6x + ax + ;
b g(x) = x − 5x + 6; h(x) = 2x − 3.
Biết f (x) chia cho g(x) dư h(x). Giá trị biểu thức T = a + 2b bằng bao nhiêu?
Câu 5. Tìm tất cả các cặp số nguyên dương x,y thoả mãn: ( 2 2
2 x + y ) − 5(x + y) = 0.
Câu 6. Tìm tất cả các số nguyên tố p để 13p + 1 là lập phương của một số tự nhiên.
Câu 7. Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên
hai con xúc xắc này trong cùng một lần gieo là một số chính phương.
Câu 8. Trên phố có hai nhà sách X, Y. Ba bạn An, Bình, Cường mỗi người vào ngẫu nhiên một
nhà sách. Tính xác suất của biến cố “Hai bạn vào nhà sách X, bạn còn lại vào nhà sách Y”.
Câu 9. Hai anh em Hùng và Lan tiết kiệm tiền để mua dụng cụ học tập giúp đỡ các bạn có
hoàn cảnh khó khăn trong đợt lũ lụt năm 2025. Trong tháng 10 có tổng số tiền tiết kiệm được
của hai anh em là 900 000 đồng. Tháng 11, số tiền tiết kiệm của Hùng, Lan lần lượt tăng 20%
và 30% so với tháng 10 nên có tổng số tiền tiết kiệm được trong tháng 11 là 1 130 000 đồng.
Hãy cho biết số tiền của Lan tiết kiệm được trong tháng 11.
Câu 10. Cho tam giác ABC vuông tại ,
A AH vuông góc với BC ( H thuộc BC ). Cho biết
AB = 21cm và HC = 4cm . Cạnh AC có độ dài bằng bao nhiêu cm ?
Câu 11. Cho hình lăng trụ đứng có đáy là tam giác đều, chiều cao bằng 4 cm và thể tích bằng 3 M
9 3 cm . Hình lăng trụ đó có diện tích xung quanh bằng bao nhiêu 2 cm ?
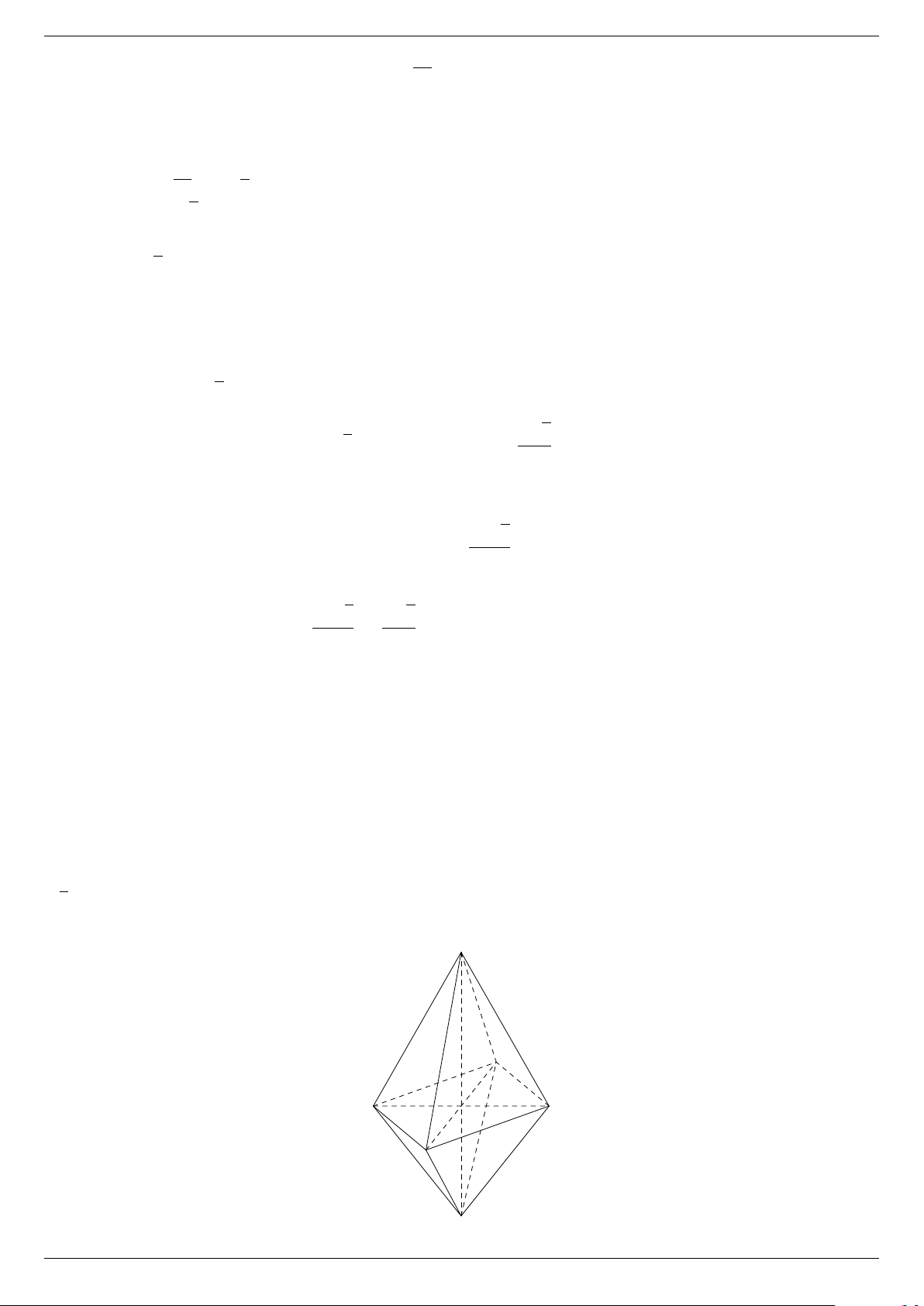
Câu 12. Một vật dụng trang trí có dạng hai hình chóp tứ giác đều M.ABCD
và N .ABCD chung đáy ABCD (Hình vẽ). Biết thể tích hình chóp B C
M.ABCD gấp hai lần thể tích hình chóp N .ABCD và độ dài cạnh đáy
ABCD bằng 2dm. Cho độ dài cạnh bên hình chóp N .ABCD bằng 6 dm. A D
Độ dài cạnh bên hình chóp M.ABCD bằng bao nhiêu dm ? N Trang 1/2
II. PHẦN TỰ LUẬN (14 điểm) (Thí sinh trình bày lời giải vào tờ giấy thi)
Câu 13. (2.0 điểm)
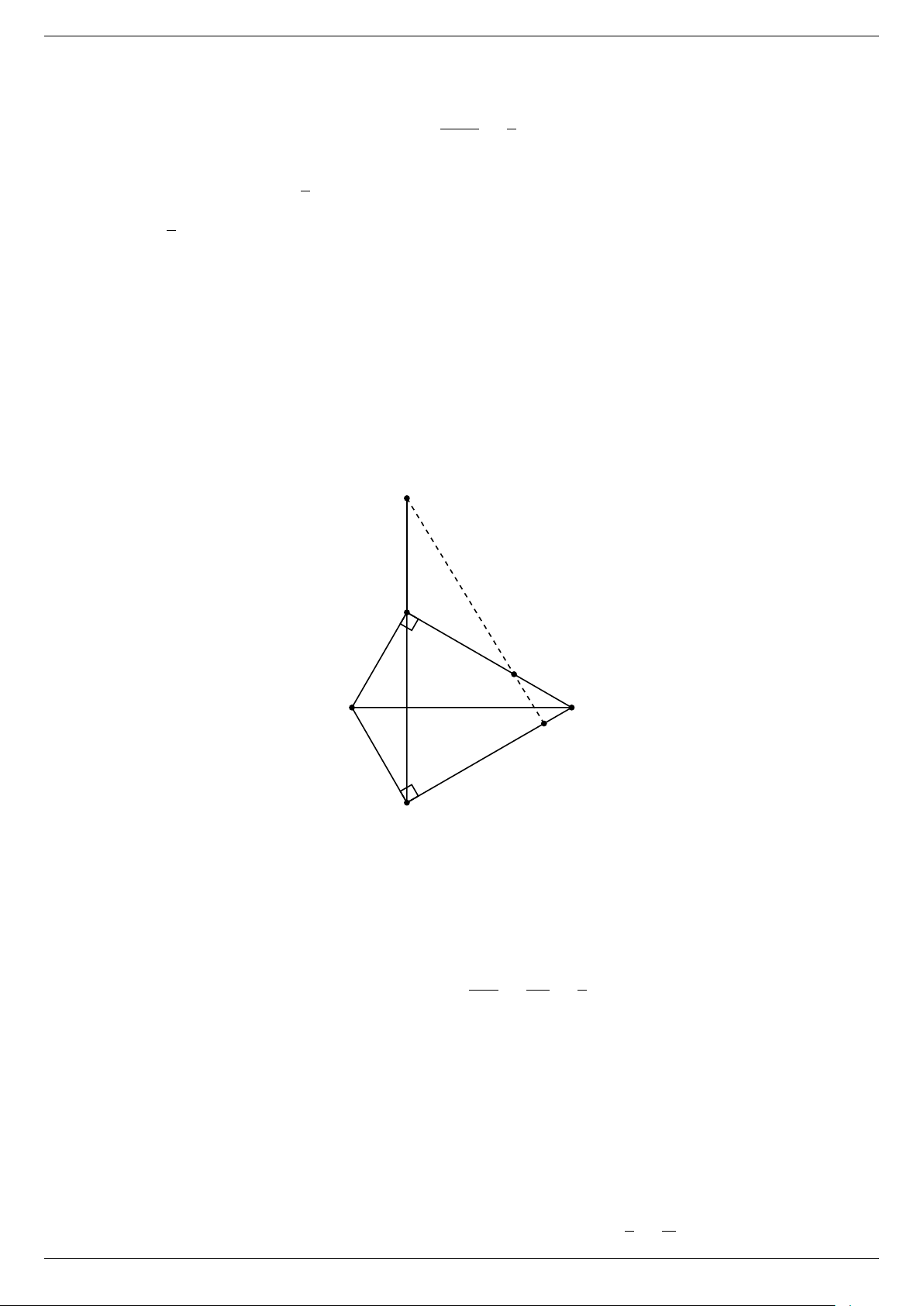
Trong một buổi trải nghiệm của đội tuyển học sinh giỏi
Toán lớp 9 trường THCS X, để đo khoảng cách từ điểm B trên
bờ hồ đến điểm A thuộc chân tháp, các bạn đó làm như sau: Tại
một điểm C nằm trên đường thẳng vuông góc với A , B dùng thước
dây đo được độ dài CB = 10m, dùng giác kế đo được góc 0
ACB = 75 (tham khảo hình vẽ). Em hãy giúp các bạn đó tính
khoảng cách từ điểm B đến điểm . A
(Yêu cầu kết quả không để dưới dạng tỉ số lượng giác của một góc).
Câu 14. (4.0 điểm) 2x + 1
a) Giải phương trình: 6x − = 1 + 3x + 1. x 3
1 − x − y y + 1 − y = x
b) Giải hệ phương trình: 2 2
x + 3 = x + y − 4.
Câu 15. (2.0 điểm) Cho các số x, ,
y z thoả mãn: x + y + z = 0 và 2 2 2 2 2 2 2 2 2
x + y ≠ z ;y + z ≠ x ;z + x ≠ y . 2 2 2 x y z
Tính giá trị của biểu thức: P = + + . 2 2 2 2 2 2 2 2 2
x − y − z
y − z − x
z − x − y
Câu 16. (3.0 điểm)
Cho đường tròn (O;R) và một điểm A sao cho OA = 2R . Qua A kẻ các tiếp tuyến A ,
B AC với đường tròn (O;R) ( ,
B C là các tiếp điểm).
a) Chứng minh rằng đường tròn (O;R) đi qua trực tâm tam giác ABC. Tính diện tích
tam giác ABC theo đại lượng . R
b) Trên tia đối của tia BC lấy điểm M bất kỳ ( M khác B ), qua M kẻ đường thẳng d
thay đổi cắt các đoạn thẳng AB, AC lần lượt tại P, Q ( d không đi qua hai điểm , A B ).
Chứng minh rằng CM.BP = CQ.BM +CQ.BP.
Câu 17. (2.0 điểm)
Với các số nguyên dương a,b sao cho 3 3
p = a + b − 3ab + 1 là số nguyên tố. Tìm số
nguyên tố p lớn nhất.
Câu 18. (1.0 điểm)
Cho các số thực a,b thỏa mãn a > b > 0 và (a −b) ab = 1. Tìm giá trị nhỏ nhất của 2 2 biểu thức 1 + 4a b 15 S = + . ab a + b ------HẾT------
- Thí sinh không được sử dụng tài liệu.
- Giám thị không giải thích gì thêm.
Họ và tên thí sinh: ................................................................ Số báo danh: ................................... Trang 2/2
TOÁN TP HÀ TĨNH TOÁN ĐIỂM 10
KỲ THI CHỌN HỌC SINH GIỎI TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO LỚP 9 HÀ TĨNH NĂM HỌC 2025 - 2026 Môn thi: TOÁN ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút.
I. PHẦN GHI KẾT QUẢ (6.0 điểm) (Thí sinh chỉ cần ghi kết quả vào tờ giấy thi) √ √ p p 7 + 5 + 7 − 5 √ p
L Câu 1. Rút gọn biểu thức P = √ − 3 − 2 2. p7 + 2 11 ✍ HƯỚNG DẪN GIẢI. √ √ Đặt p p A = 7 + 5 + 7 −
5. Vì các căn thức đều dương nên A > 0. Bình phương hai vế của A, ta có: Å» √ » √ ã2 A2 = 7 + 5 + 7 − 5 √ √ » √ √ = (7 + 5) + (7 − 5) + 2 (7 + 5)(7 − 5) » √ = 14 + 2 72 − ( 5)2 √ = 14 + 2 49 − 5 √ = 14 + 2 44 √ = 14 + 2 · 2 11 √ = 14 + 4 11 √ = 2(7 + 2 11) √ √ √ Suy ra » p A = 2(7 + 2 11) = 2 · 7 + 2 11.
Thay A vào biểu thức P , ta được phần phân thức: √ √ p A 2 · 7 + 2 11 √ √ = √ = 2 p p 7 + 2 11 7 + 2 11
Xử lý phần căn thức còn lại: » √ » √ » √ 3 − 2 2 = 2 − 2 2 · 1 + 1 = ( 2 − 1)2 √ √ √ √
Vì 2 > 1 nên 2 − 1 > 0, do đó »( 2 − 1)2 = 2 − 1.
Vậy biểu thức P trở thành: √ √ √ √ P = 2 − ( 2 − 1) = 2 − 2 + 1 = 1 Đáp án là 1
L Câu 2. Cho hai số dương a, b thỏa mãn điều kiện: a2 + ab − 6b2 = 0; 3a − 4b ̸= 0; a − 4b ̸= 0. Giá trị của biểu thức 2025a + 2b 2026a − 2b F = + bằng bao nhiêu? 3a − 4b 4b − a ✍ HƯỚNG DẪN GIẢI.
Ta phân tích điều kiện a2 + ab − 6b2 = 0 thành nhân tử: a2 + ab − 6b2 = 0 a2 − 2ab + 3ab − 6b2 = 0 a(a − 2b) + 3b(a − 2b) = 0 (a − 2b)(a + 3b) = 0 Năm 2025 Trang 1/16 TOÁN ĐIỂM 10
TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH
Vì theo đề bài a, b là hai số dương nên a > 0 và b > 0, suy ra a + 3b > 0. Do đó, để tích bằng 0 thì
thừa số còn lại phải bằng 0: a − 2b = 0 ⇔ a = 2b
Thay a = 2b vào biểu thức F , ta có: 2025(2b) + 2b 2026(2b) − 2b F = + 3(2b) − 4b 4b − (2b) 4050b + 2b 4052b − 2b = + 6b − 4b 4b − 2b 4052b 4050b = + 2b 2b = 2026 + 2025 = 4051 Đáp án là 4051
L Câu 3. Cho hai đường thẳng (d1) : y = (m + 3)x + m + 2 và (d2) : y = (m3 − 3m + 3)x + 3m − 2.
Gọi Q là tổng tất cả các giá trị của tham số m để hai đường thẳng (d1) và (d2) song song với nhau.
Giá trị của Q bằng bao nhiêu? ✍ HƯỚNG DẪN GIẢI.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song với nhau khi và chỉ khi: ®a1 = a2 b1 ̸= b2
Áp dụng vào bài toán, ta có hệ điều kiện: ®m + 3 = m3 − 3m + 3 (1) m + 2 ̸= 3m − 2 (2) Giải phương trình (1): m + 3 = m3 − 3m + 3 m3 − 4m = 0 m(m2 − 4) = 0 m(m − 2)(m + 2) = 0
Phương trình này có 3 nghiệm là m1 = 0, m2 = 2, m3 = −2. Giải điều kiện (2): m + 2 ̸= 3m − 2 −2m ̸= −4 m ̸= 2
Đối chiếu 3 nghiệm tìm được với điều kiện m ̸= 2: • Với m = 0: Thỏa mãn.
• Với m = 2: Không thỏa mãn (vì khi đó hai đường thẳng trùng nhau).
• Với m = −2: Thỏa mãn.
Vậy các giá trị của m để hai đường thẳng song song là m = 0 và m = −2. Tổng các giá trị này là: Q = 0 + (−2) = −2 Đáp án là -2 Năm 2025 Trang 2/16 TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH TOÁN ĐIỂM 10
L Câu 4. Cho các đa thức f(x) = x3 − 6x2 + ax + b; g(x) = x2 − 5x + 6; h(x) = 2x − 3. Biết f(x) chia
cho g(x) dư h(x). Giá trị biểu thức T = a + 2b bằng bao nhiêu? ✍ HƯỚNG DẪN GIẢI.
Ta phân tích đa thức chia g(x):
g(x) = x2 − 5x + 6 = x2 − 2x − 3x + 6 = x(x − 2) − 3(x − 2) = (x − 2)(x − 3)
Gọi q(x) là đa thức thương khi chia f(x) cho g(x). Vì số dư là h(x), ta có đẳng thức: f (x) = g(x) · q(x) + h(x) Hay:
f (x) = (x − 2)(x − 3) · q(x) + (2x − 3)
Đẳng thức trên đúng với mọi x. Ta lần lượt thay các nghiệm của g(x) là x = 2 và x = 3 vào để triệt tiêu q(x). • Thay x = 2:
f (2) = (2 − 2)(2 − 3) · q(2) + (2 · 2 − 3)
23 − 6(22) + a(2) + b = 0 + 1 8 − 24 + 2a + b = 1 2a + b − 16 = 1 2a + b = 17 (∗1) • Thay x = 3:
f (3) = (3 − 2)(3 − 3) · q(3) + (2 · 3 − 3)
33 − 6(32) + a(3) + b = 0 + 3 27 − 54 + 3a + b = 3 3a + b − 27 = 3 3a + b = 30 (∗2)
Từ (*1) và (*2) ta có hệ phương trình: ®2a + b = 17 3a + b = 30
Lấy phương trình dưới trừ phương trình trên theo vế:
(3a + b) − (2a + b) = 30 − 17 ⇒ a = 13
Thay a = 13 vào phương trình (*1):
2(13) + b = 17 ⇒ 26 + b = 17 ⇒ b = 17 − 26 = −9
Tính giá trị biểu thức T :
T = a + 2b = 13 + 2(−9) = 13 − 18 = −5 Đáp án là -5
L Câu 5. Tìm tất cả các cặp số nguyên dương x, y thoả mãn: 2(x2 + y2) − 5(x + y) = 0. ✍ HƯỚNG DẪN GIẢI.
Biến đổi phương trình đã cho: 2x2 + 2y2 − 5x − 5y = 0
(2x2 − 5x) + (2y2 − 5y) = 0
Xét hàm số đặc trưng f(t) = 2t2 − 5t với t là số nguyên dương (t ∈ +
Z ). Phương trình có dạng: f (x) + f (y) = 0.
Ta tính giá trị của f(t) với các số nguyên dương t = 1, 2, 3, . . . : Năm 2025 Trang 3/16 TOÁN ĐIỂM 10
TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH
• Với t = 1 ⇒ f(1) = 2(1)2 − 5(1) = −3.
• Với t = 2 ⇒ f(2) = 2(2)2 − 5(2) = 8 − 10 = −2.
• Với t = 3 ⇒ f(3) = 2(3)2 − 5(3) = 18 − 15 = 3.
• Với t = 4 ⇒ f(4) = 2(4)2 − 5(4) = 32 − 20 = 12.
Xét với t ⩾ 4, ta có t(2t − 5). Vì t ⩾ 4 nên 2t − 5 ⩾ 3, suy ra f(t) ⩾ 12 > 0 và tăng dần.
Để tổng f(x) + f(y) = 0, ta cần tìm hai giá trị sao cho chúng là số đối của nhau. Nhìn vào các
giá trị đã tính: - Các giá trị âm có thể là: −3 (tại t = 1), −2 (tại t = 2). - Các giá trị dương tương ứng phải là: 3 hoặc 2.
Ta thấy: - Tại t = 3, f(3) = 3, là số đối của f(1) = −3. Cặp này thỏa mãn. - Không có giá trị
nguyên dương nào của t để f(t) = 2 (vì 2t2 − 5t − 2 = 0 có ∆ = 25 + 16 = 41 không chính phương).
Vậy chỉ có cặp giá trị thỏa mãn là f(x) = −3, f(y) = 3 hoặc ngược lại. Điều này tương ứng với: ® ® x = 1 hoặc x = 3 y = 3 y = 1
Đáp án là (1; 3), (3; 1)
L Câu 6. Tìm tất cả các số nguyên tố p để 13p + 1 là lập phương của một số tự nhiên. ✍ HƯỚNG DẪN GIẢI.
Đặt 13p + 1 = n3 với n là số tự nhiên (n ∈ N). Do p ⩾ 2 nên 13p + 1 > 27, suy ra n > 3. Biến đổi phương trình: 13p = n3 − 1 13p = (n − 1)(n2 + n + 1)
Vì 13 và p đều là số nguyên tố, nên các ước dương của vế trái chỉ có thể là {1, 13, p, 13p}. Do n > 3
nên n − 1 > 2 và n2 + n + 1 > n − 1. Ta xét các trường hợp phân tích vế phải thành tích hai thừa số (n − 1) và (n2 + n + 1): Trường hợp 1: ®n − 1 = 13 n2 + n + 1 = p
Từ phương trình trên suy ra n = 14. Thay vào phương trình dưới:
p = 142 + 14 + 1 = 196 + 14 + 1 = 211 √
Kiểm tra 211: Vì 211 không chia hết cho các số nguyên tố nhỏ hơn 211 ≈ 14.5 (gồm 2, 3, 5, 7, 11,
13) nên 211 là số nguyên tố (Thỏa mãn). Trường hợp 2: ®n − 1 = p n2 + n + 1 = 13
Giải phương trình dưới:
n2 + n + 1 = 13 ⇔ n2 + n − 12 = 0 ⇔ (n − 3)(n + 4) = 0
Vì n là số tự nhiên nên chọn n = 3. Thay vào phương trình trên: p = n − 1 = 3 − 1 = 2
Số 2 là số nguyên tố (Thỏa mãn). Năm 2025 Trang 4/16 TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH TOÁN ĐIỂM 10 Trường hợp 3: ®n − 1 = 13p n2 + n + 1 = 1
Phương trình n2 + n + 1 = 1 ⇒ n(n + 1) = 0 ⇒ n = 0 (loại vì n3 = 13p + 1 > 1).
Vậy có hai số nguyên tố p thỏa mãn bài toán. Đáp án là 2; 211
L Câu 7. Câu 7. Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện
trên hai con xúc xắc này trong cùng một lần gieo là một số chính phương. ✍ HƯỚNG DẪN GIẢI.
Số phần tử của không gian mẫu là số kết quả có thể xảy ra khi gieo hai con xúc xắc: n(Ω) = 6 · 6 = 36
Gọi A là biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là một số chính phương”. Tổng số
chấm nhỏ nhất có thể là 1 + 1 = 2 và lớn nhất là 6 + 6 = 12. Các số chính phương nằm trong đoạn
[2; 12] là 4 và 9. Ta liệt kê các trường hợp thuận lợi cho biến cố A:
• Tổng số chấm bằng 4: (1; 3), (2; 2), (3; 1). Có 3 kết quả.
• Tổng số chấm bằng 9: (3; 6), (4; 5), (5; 4), (6; 3). Có 4 kết quả.
Số kết quả thuận lợi cho biến cố A là: n(A) = 3 + 4 = 7
Xác suất của biến cố A là: n(A) 7 P (A) = = n(Ω) 36 7 Đáp án là 36
L Câu 8. Câu 8. Trên phố có hai nhà sách X, Y. Ba bạn An, Bình, Cường mỗi người vào ngẫu
nhiên một nhà sách. Tính xác suất của biến cố “Hai bạn vào nhà sách X, bạn còn lại vào nhà sách Y”. ✍ HƯỚNG DẪN GIẢI.
Mỗi bạn có 2 lựa chọn là vào nhà sách X hoặc nhà sách Y. Vì có 3 người nên tổng số khả năng xảy
ra (số phần tử của không gian mẫu) là: n(Ω) = 2 · 2 · 2 = 8
Gọi B là biến cố “Hai bạn vào nhà sách X, bạn còn lại vào nhà sách Y”. Để chọn ra 2 người trong
số 3 người (An, Bình, Cường) vào nhà sách X, ta dùng tổ hợp chập 2 của 3: C2 = 3 (cách) 3
Người còn lại chắc chắn sẽ vào nhà sách Y (có 1 cách). Vậy số kết quả thuận lợi cho biến cố B là: n(B) = 3 · 1 = 3
Xác suất của biến cố B là: n(B) 3 P (B) = = n(Ω) 8 3 Đáp án là 8 Năm 2025 Trang 5/16 TOÁN ĐIỂM 10
TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH
L Câu 9. Câu 9. Hai anh em Hùng và Lan tiết kiệm tiền để mua dụng cụ học tập giúp đỡ các bạn
có hoàn cảnh khó khăn trong đợt lũ lụt năm 2025. Trong tháng 10 có tổng số tiền tiết kiệm được
của hai anh em là 900 000 đồng. Tháng 11, số tiền tiết kiệm của Hùng, Lan lần lượt tăng 20% và
30% so với tháng 10 nên có tổng số tiền tiết kiệm được trong tháng 11 là 1 130 000 đồng. Hãy cho
biết số tiền của Lan tiết kiệm được trong tháng 11. ✍ HƯỚNG DẪN GIẢI.
Gọi số tiền tiết kiệm được của Hùng trong tháng 10 là x (đồng) và của Lan trong tháng 10 là y
(đồng). Điều kiện: 0 < x; y < 900 000.
Theo đề bài, tổng số tiền tiết kiệm tháng 10 của hai anh em là 900 000 đồng, ta có phương trình: x + y = 900 000 (1) Trong tháng 11:
• Số tiền Hùng tiết kiệm tăng 20%, tức là bằng 100% + 20% = 120% số tiền tháng 10. Số tiền là: 1,2x (đồng).
• Số tiền Lan tiết kiệm tăng 30%, tức là bằng 100% + 30% = 130% số tiền tháng 10. Số tiền là: 1,3y (đồng).
Tổng số tiền tháng 11 là 1 130 000 đồng, ta có phương trình: 1,2x + 1,3y = 1 130 000 (2)
Từ (1) và (2) ta có hệ phương trình: ® ® x + y = 900 000 1,2x + 1,2y = 1 080 000
(Nhân hai vế pt (1) với 1,2) ⇔ 1,2x + 1,3y = 1 130 000 1,2x + 1,3y = 1 130 000
®0,1y = 50 000 (Lấy pt dưới trừ pt trên) ⇔ x = 900 000 − y ®y = 500 000 ⇔ (Thỏa mãn điều kiện) x = 400 000
Như vậy, số tiền Lan tiết kiệm được trong tháng 10 là 500 000 đồng. Số tiền Lan tiết kiệm được trong tháng 11 là:
500 000 · 1,3 = 650 000 (đồng)
Đáp án là 650 000 đồng
L Câu 10. Câu 10. Cho tam giác ABC vuông tại A, AH vuông góc với BC (H thuộc BC). Cho biết √ AB =
21 cm và HC = 4 cm. Cạnh AC có độ dài bằng bao nhiêu cm? ✍ HƯỚNG DẪN GIẢI.
Đặt độ dài đoạn thẳng BH = x (cm) (với x > 0). Áp dụng hệ thức lượng trong tam giác vuông ABC
(hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền), ta có: AB2 = BH · BC Thay số vào, ta được: √ ( 21)2 = x · (x + 4) 21 = x2 + 4x x2 + 4x − 21 = 0
Giải phương trình bậc hai ẩn x: Ta có ∆′ = 22 − 1 · (−21) = 4 + 21 = 25 > 0. Suy ra phương trình có hai nghiệm phân biệt: √ x1 = −2 + 25 = 3 (nhận) Năm 2025 Trang 6/16 TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH TOÁN ĐIỂM 10 √ x2 = −2 − 25 = −7 (loại vì x > 0)
Vậy BH = 3 cm. Suy ra cạnh huyền BC = BH + HC = 3 + 4 = 7 cm. Áp dụng hệ thức lượng để tính AC: AC2 = HC · BC = 4 · 7 = 28 √ √ Suy ra AC = 28 = 2 7 cm. √
Đáp án là 2 7 cm
L Câu 11. Câu 11. Cho hình lăng trụ đứng có đáy là tam giác đều, chiều cao bằng 4 cm và thể √
tích bằng 9 3 cm3. Hình lăng trụ đó có diện tích xung quanh bằng bao nhiêu cm2? ✍ HƯỚNG DẪN GIẢI.
Gọi Sđáy là diện tích đáy của hình lăng trụ và h là chiều cao của lăng trụ. Ta có công thức tính thể tích khối lăng trụ: V = Sđáy · h √
Theo đề bài V = 9 3 cm3 và h = 4 cm, suy ra: √ √ 9 3 9 3 = Sđáy · 4 ⇒ Sđáy = (cm2) 4
Vì đáy là tam giác đều, gọi cạnh đáy là a, ta có công thức diện tích: √ a2 3 Sđáy = 4 Suy ra: √ √ a2 3 9 3 = ⇒ a2 = 9 ⇒ a = 3 (cm) 4 4
Chu vi đáy của hình lăng trụ là: Cđáy = 3a = 3 · 3 = 9 (cm)
Diện tích xung quanh của hình lăng trụ đứng là:
Sxq = Cđáy · h = 9 · 4 = 36 (cm2)
Đáp án là 36 cm2
L Câu 12. Câu 12. Một vật dụng trang trí có dạng hai hình chóp tứ giác đều M.ABCD và N.ABCD
chung đáy ABCD (Hình vẽ). Biết thể tích hình chóp M.ABCD gấp hai lần thể tích hình chóp
N.ABCD và độ dài cạnh đáy ABCD bằng 2 dm. Cho độ dài cạnh bên hình chóp N.ABCD bằng
√6 dm. Độ dài cạnh bên hình chóp M.ABCD bằng bao nhiêu dm? M D A O C B N Năm 2025 Trang 7/16 TOÁN ĐIỂM 10
TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH ✍ HƯỚNG DẪN GIẢI.
Gọi O là giao điểm của hai đường chéo AC và BD. Vì ABCD là hình vuông cạnh 2 dm nên: √ √ √ √ AC = AB2 + BC2 = 22 + 22 = 8 = 2 2 (dm) √ √ Suy ra AC 2 2 OC = = = 2 dm. 2 2
Xét hình chóp đều N.ABCD, ta có đường cao NO vuông góc với đáy. Tam giác NOC vuông tại
O, áp dụng định lý Pytago: √ √
N O2 = N C2 − OC2 = ( 6)2 − ( 2)2 = 6 − 2 = 4 Suy ra NO = 2 dm.
Gọi V1 là thể tích của hình chóp M.ABCD và V2 là thể tích của hình chóp N.ABCD. Ta có công thức thể tích: 1 V1 = · SABCD · M O 3 1 V2 = · SABCD · N O 3
Theo đề bài, V1 = 2V2, suy ra: 1 Å 1 ã · SABCD · M O = 2 · · SABCD · N O 3 3 ⇒ M O = 2N O
Thay NO = 2 dm vào, ta được: MO = 2 · 2 = 4 dm.
Xét hình chóp đều M.ABCD, tam giác MOC vuông tại O. Áp dụng định lý Pytago để tính cạnh bên MC: √
M C2 = M O2 + OC2 = 42 + ( 2)2 = 16 + 2 = 18 √ √ Suy ra MC = 18 = 3 2 dm. √
Đáp án là 3 2 dm
L Câu 13. Trong một buổi trải nghiệm của đội tuyển học sinh giỏi Toán lớp 9 trường THCS X, để
đo khoảng cách từ điểm B trên bờ hồ đến điểm A thuộc chân tháp, các bạn đó làm như sau: Tại
một điểm C nằm trên đường thẳng vuông góc với AB, dùng thước dây đo được độ dài CB = 10 m,
dùng giác kế đo được góc ’
ACB = 75◦ (tham khảo hình vẽ). Em hãy giúp các bạn đó tính khoảng
cách từ điểm B đến điểm A. (Yêu cầu kết quả không để dưới dạng tỉ số lượng giác của một góc). A 75◦ C B 10 m Năm 2025 Trang 8/16 TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH TOÁN ĐIỂM 10 ✍ HƯỚNG DẪN GIẢI.
Xét tam giác ABC vuông tại B (do AB ⊥ BC), ta có công thức tính cạnh góc vuông: AB = BC · tan b C = 10 · tan 75◦.
Để tính giá trị chính xác của tan 75◦ mà không dùng máy tính cầm tay để ra kết quả thập phân, ta
tách 75◦ = 45◦ + 30◦. Áp dụng công thức cộng tang: tan 75◦ = tan(45◦ + 30◦) tan 45◦ + tan 30◦ = 1 − tan 45◦ · tan 30◦ √3 1 + = 3√3 1 − 1 · 3 √ 3 + 3 = 3√ 3 − 3 3√ 3 + 3 = √ . 3 − 3
Trục căn thức ở mẫu số: √ (3 + 3)2 tan 75◦ = √ √ (3 − 3)(3 + 3) √ 9 + 6 3 + 3 = 9 − 3 √ 12 + 6 3 = 6 √ = 2 + 3.
Thay giá trị vừa tìm được vào biểu thức tính AB: √ √ AB = 10 · (2 + 3) = 20 + 10 3 (m). √
Vậy khoảng cách từ điểm B đến điểm A là 20 + 10 3 mét. √
Đáp án là 20 + 10 3 m. L Câu 14. √ a) Giải phương trình: 2x + 1 6x − = 1 + 3x + 1. x √ ® √ √
b) Giải hệ phương trình: 1 − x3 − py y + 1 − y = x √ √ 2 x + 3 = x2 + y − 4 ✍ HƯỚNG DẪN GIẢI.
a) Điều kiện xác định: 1
3x + 1 ⩾ 0 và x ̸= 0 ⇔ x ⩾ − và x ̸= 0. 3
Phương trình đã cho tương đương với: 6x2 − (2x + 1) √ = 1 + 3x + 1 x √ Ä ä ⇔ 6x2 − 2x − 1 = x 1 + 3x + 1 √
⇔ 6x2 − 2x − 1 = x + x 3x + 1 √
⇔ 6x2 − 3x − 1 − x 3x + 1 = 0 (1) Năm 2025 Trang 9/16 TOÁN ĐIỂM 10
TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH √
Đặt t = 3x + 1 (với t ⩾ 0). Bình phương hai vế ta có t2 = 3x + 1 ⇒ 1 = t2 − 3x. Thay 1 = t2 − 3x
vào phương trình (1), ta được:
6x2 − 3x − (t2 − 3x) − xt = 0
⇔ 6x2 − 3x − t2 + 3x − xt = 0 ⇔ 6x2 − xt − t2 = 0
Coi đây là phương trình bậc hai ẩn t, hoặc phân tích đa thức thành nhân tử: 6x2 + 2xt − 3xt − t2 = 0
⇔ 2x(3x + t) − t(3x + t) = 0 ⇔ (2x − t)(3x + t) = 0 √
• Trường hợp 1: 2x − t = 0 ⇔ 2x = t. Thay t = 3x + 1 vào: √ ® ® x ⩾ 0 x ⩾ 0 2x = 3x + 1 ⇔ ⇔ 4x2 = 3x + 1 4x2 − 3x − 1 = 0
Giải phương trình bậc hai 1
4x2 − 3x − 1 = 0 ta có hai nghiệm là x1 = 1 và x2 = − . Đối 4
chiếu điều kiện x ⩾ 0, ta nhận nghiệm x = 1. √
• Trường hợp 2: 3x + t = 0 ⇔ t = −3x. Thay t = 3x + 1 vào: √ ®− ® 3x ⩾ 0 x ⩽ 0 −3x = 3x + 1 ⇔ ⇔ 9x2 = 3x + 1 9x2 − 3x − 1 = 0
Giải phương trình bậc hai 9x2 − 3x − 1 = 0, ta có ∆ = (−3)2 − 4 · 9 · (−1) = 9 + 36 = 45. √ √ √ Các nghiệm là 3 ± 45 3 ± 3 5 1 ± 5 x = = =
. Đối chiếu điều kiện x ⩽ 0, ta nhận √ 18 18 6 √ nghiệm 1 − 5 1 5 x =
. (Kiểm tra điều kiện ban đầu x ⩾ − : Ta có 1 − ≈ −0, 206, lớn 6 3 6 hơn −0, 333, thỏa mãn). √ √ ® ´ ® ´
Vậy tập nghiệm của phương trình là 1 − 5 1 − 5 S = 1; . Đáp án là S = 1; . 6 6 1 − x3 ⩾ 0 x ⩽ 1
b) Điều kiện xác định: y ⩾ 0 ⇔ y ⩾ 0 . x + 3 ⩾ 0 x ⩾ −3
Biến đổi phương trình thứ nhất của hệ: √ » √ √ 1 − x3 − y y + 1 − y = x √ » √ √ ⇔ 1 − x3 − x = ( y)3 + 1 + y √ Xét hàm số đặc trưng 3t2 f (t) =
t3 + 1 + t với t ⩾ −1. Đạo hàm f ′(t) = √ + 1. Với mọi 2 t3 + 1
t > −1, ta thấy f ′(t) > 0. Do đó hàm số f (t) đồng biến trên tập xác định. Phương trình trên có dạng √
f (−x) = f ( y) (chú ý: để phương trình xác định thì −x ⩾ −1 ⇔ x ⩽ 1, phù hợp với
ĐK). Vì hàm số đồng biến nên ta suy ra: √ ®x ⩽ 0 −x = y ⇔ x2 = y Năm 2025 Trang 10/16 TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH TOÁN ĐIỂM 10
Kết hợp điều kiện x ⩾ −3, ta có −3 ⩽ x ⩽ 0. Thay y = x2 và √y = −x (do x ⩽ 0) vào phương trình thứ hai của hệ: √ √ 2 x + 3 = x2 + y − 4 √ ⇔ 2 x + 3 = x2 − x − 4 √
⇔ x2 − x − 6 − 2 x + 3 + 2 = 0 √
⇔ (x2 − x − 6) − 2( x + 3 − 1) = 0 2(x + 3 − 1) ⇔ (x − 3)(x + 2) − √ = 0 x + 3 + 1 2(x + 2) ⇔ (x − 3)(x + 2) − √ = 0 x + 3 + 1 ï 2 ò ⇔ (x + 2) x − 3 − √ = 0 x + 3 + 1
• Trường hợp 1: x + 2 = 0 ⇔ x = −2. Giá trị này thỏa mãn điều kiện −3 ⩽ x ⩽ 0. Khi đó y = (−2)2 = 4. • Trường hợp 2: 2 2 x − 3 − √ = 0 ⇔ x − 3 = √
. Ta có điều kiện −3 ⩽ x ⩽ 0, x + 3 + 1 x + 3 + 1 √ √ suy ra: Vế trái: 2
x − 3 ⩽ 0 − 3 = −3. Vế phải: x + 3 ⩾ 0 ⇒ x + 3 + 1 ⩾ 1 ⇒ √ > 0. x + 3 + 1
Vế trái âm, vế phải dương nên phương trình này vô nghiệm.
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (−2; 4).
Đáp án là (x; y) = (−2; 4).
L Câu 15. Cho các số x, y, z thoả mãn: x + y + z = 0 và x2 + y2 ̸= z2; y2 + z2 ̸= x2; z2 + x2 ̸= y2.
Tính giá trị của biểu thức: x2 y2 z2 P = + + . x2 − y2 − z2 y2 − z2 − x2 z2 − x2 − y2 ✍ HƯỚNG DẪN GIẢI.
Theo giả thiết ta có x+y+z = 0, suy ra x = −(y+z). Bình phương hai vế của đẳng thức x = −(y+z), ta được:
x2 = [−(y + z)]2 = (y + z)2 = y2 + 2yz + z2.
Chuyển vế các hạng tử y2 và z2, ta có: x2 − y2 − z2 = 2yz.
Chứng minh hoàn toàn tương tự, ta cũng có:
y2 = (x + z)2 = x2 + 2xz + z2 ⇒ y2 − z2 − x2 = 2xz.
z2 = (x + y)2 = x2 + 2xy + y2 ⇒ z2 − x2 − y2 = 2xy.
Thay các kết quả trên vào biểu thức P , ta được: x2 y2 z2 P = + + 2yz 2xz 2xy x2 · x y2 · y z2 · z = + + 2xyz 2xyz 2xyz x3 + y3 + z3 = . 2xyz
Ta áp dụng hằng đẳng thức mở rộng: Nếu x + y + z = 0 thì x3 + y3 + z3 = 3xyz. Chứng minh:
x3 + y3 + z3 − 3xyz = (x + y + z)(x2 + y2 + z2 − xy − yz − zx). Năm 2025 Trang 11/16 TOÁN ĐIỂM 10
TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH
Do x + y + z = 0 nên vế phải bằng 0, suy ra x3 + y3 + z3 = 3xyz. Thay vào biểu thức P ta có: 3xyz 3 P = = . 2xyz 2
Vậy giá trị của biểu thức P là 3. 2 3 Đáp án là . 2
L Câu 16. Câu 16. (3.0 điểm) Cho đường tròn (O; R) và một điểm A sao cho OA = 2R. Qua A
kẻ các tiếp tuyến AB, AC với đường tròn (O; R) (B, C là các tiếp điểm).
a) Chứng minh rằng đường tròn (O; R) đi qua trực tâm tam giác ABC. Tính diện tích tam giác ABC theo đại lượng R.
b) Trên tia đối của tia BC lấy điểm M bất kỳ (M khác B), qua M kẻ đường thẳng d thay đổi cắt
các đoạn thẳng AB, AC lần lượt tại P, Q (d không đi qua hai điểm A, B). Chứng minh rằng
CM · BP = CQ · BM + CQ · BP . M B P O A Q C ✍ HƯỚNG DẪN GIẢI.
a) Chứng minh đường tròn (O; R) đi qua trực tâm tam giác ABC và tính diện tích.
*) Chứng minh (O; R) đi qua trực tâm: Xét tam giác OAB vuông tại B (do AB là tiếp tuyến), ta có: OB R 1 sin ’ OAB = = = . OA 2R 2 Suy ra ’
OAB = 30◦. Do tính chất hai tiếp tuyến cắt nhau, ta có AO là tia phân giác của góc ’ BAC. Suy ra ’ BAC = 2 ’
OAB = 2 · 30◦ = 60◦. Tam giác ABC cân tại A (vì AB = AC) lại có một
góc bằng 60◦ nên tam giác ABC là tam giác đều.
Vì △ABC đều nên trực tâm K cũng đồng thời là trọng tâm, tâm đường tròn ngoại tiếp và tâm
đường tròn nội tiếp tam giác. Gọi H là giao điểm của OA và BC. Do △ABC cân tại A nên
đường phân giác AO cũng là đường cao, suy ra OA ⊥ BC tại trung điểm H của BC. Trong tam giác vuông OBH, ta có: 1 R OH = OB · sin ’ OBH = OB · sin 30◦ = R · = . 2 2 Năm 2025 Trang 12/16 TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH TOÁN ĐIỂM 10 (Lưu ý: ’ OBH = ’ OBA − ’
CBA = 90◦ − 60◦ = 30◦). Ta tính được đoạn AH: R 3R AH = OA − OH = 2R − = . 2 2
Vì K là trực tâm (đồng thời là trọng tâm) nên K nằm trên đường cao AH và chia đường cao theo tỉ lệ: 2 2 3R AK = AH = · = R. 3 3 2
Ta xét khoảng cách từ tâm O đến điểm K:
OK = |OA − AK| = |2R − R| = R.
Vì khoảng cách từ O đến K bằng bán kính R, nên điểm K nằm trên đường tròn (O; R). (Điều phải chứng minh).
*) Tính diện tích tam giác ABC: Trong tam giác vuông ABH, ta có: √ 3R 1 R 3 BH = AH · tan 30◦ = · √ = . 2 3 2 √ √
Suy ra cạnh đáy BC = 2 · BH = 2 · R 3 = R 3. Diện tích tam giác ABC là: 2 √ 1 1 √ 3R 3R2 3 SABC = · BC · AH = · R 3 · = . 2 2 2 4
b) Chứng minh CM · BP = CQ · BM + CQ · BP .
Đặt cạnh của tam giác đều ABC là a (AB = AC = BC = a). Áp dụng định lý Menelaus cho
tam giác ABC với ba điểm thẳng hàng M, P, Q (cát tuyến cắt cạnh AB tại P , cạnh AC tại Q
và phần kéo dài cạnh BC tại M): P A M B QC · · = 1 P B M C QA
Theo đề bài, P nằm trên đoạn AB, Q nằm trên đoạn AC, M nằm trên tia đối của BC. Ta có các hệ thức độ dài: P A = AB − BP = a − BP QA = AC − CQ = a − CQ
Thay vào biểu thức Menelaus, ta có: a − BP M B CQ · · = 1 BP M C a − CQ a CQ M C ⇔ − 1 · = BP a − CQ M B
Ta lại có MC = MB + BC = MB + a, suy ra MC = MB+a = 1 + a . Thay vào phương trình M B M B M B trên: a CQ a − 1 · = 1 + BP a − CQ M B
Nhân cả hai vế với BP (a − CQ) · MB để khử mẫu:
M B · CQ(a − BP ) = BP (a − CQ)(M B + a) Khai triển hai vế:
Vế trái (VT) = a · MB · CQ − MB · BP · CQ Năm 2025 Trang 13/16 TOÁN ĐIỂM 10
TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH
Vế phải (VP) = (a · BP − BP · CQ)(MB + a) = a · BP · MB + a2 · BP − BP · CQ · MB − a · BP · CQ Cho VT = VP:
a · M B · CQ − M B · BP · CQ = a · BP · M B + a2 · BP − M B · BP · CQ − a · BP · CQ
Rút gọn hạng tử −MB · BP · CQ ở cả hai vế:
a · M B · CQ = a · BP · M B + a2 · BP − a · BP · CQ
Chia cả hai vế cho a (do a > 0):
M B · CQ = BP · M B + a · BP − BP · CQ
Chuyển vế hạng tử −BP · CQ sang trái:
M B · CQ + BP · CQ = BP · M B + a · BP
⇔ CQ · (M B + BP ) = BP · (M B + a)
Lại có MB + a = MB + BC = MC. Và từ biểu thức cần chứng minh, ta biến đổi ngược
lại từ dòng trên: Giữ nguyên vế trái: CQ · BM + CQ · BP . Giữ nguyên vế phải: BP · MC =
BP · (BM + BC) = BP · BM + BP · a.
Từ biểu thức đã rút gọn: MB · CQ + BP · CQ = BP · MC. Đây chính là điều phải chứng minh:
CM · BP = CQ · BM + CQ · BP .
L Câu 17. Câu 17. (2.0 điểm) Với các số nguyên dương a, b sao cho p = a3 + b3 − 3ab + 1 là số
nguyên tố. Tìm số nguyên tố p lớn nhất. ✍ HƯỚNG DẪN GIẢI.
Ta sử dụng hằng đẳng thức mở rộng:
x3 + y3 + z3 − 3xyz = (x + y + z)(x2 + y2 + z2 − xy − yz − zx)
Áp dụng hằng đẳng thức trên với x = a, y = b, z = 1, ta phân tích biểu thức p:
p = a3 + b3 + 13 − 3ab · 1 = (a + b + 1)(a2 + b2 + 12 − ab − a · 1 − b · 1)
⇒ p = (a + b + 1)(a2 + b2 + 1 − ab − a − b)
Vì a, b là các số nguyên dương (a ⩾ 1, b ⩾ 1), suy ra thừa số thứ nhất: a + b + 1 ⩾ 1 + 1 + 1 = 3
Để p là số nguyên tố, p chỉ có hai ước dương là 1 và chính nó. Do thừa số thứ nhất (a + b + 1) ⩾ 3,
nên bắt buộc thừa số thứ hai phải bằng 1. Tức là:
a2 + b2 + 1 − ab − a − b = 1 Rút gọn phương trình: a2 + b2 − ab − a − b = 0
Nhân cả hai vế của phương trình với 2:
2a2 + 2b2 − 2ab − 2a − 2b = 0
Tách các hạng tử để tạo thành hằng đẳng thức:
(a2 − 2ab + b2) + (a2 − 2a + 1) + (b2 − 2b + 1) − 2 = 0
⇔ (a − b)2 + (a − 1)2 + (b − 1)2 = 2
Vì a, b là số nguyên nên (a−b)2, (a−1)2, (b−1)2 là các số chính phương (bình phương của số nguyên).
Tổng của ba số chính phương bằng 2 chỉ có thể xảy ra trong trường hợp: Hai số bằng 1 và một số
bằng 0. Ta xét 3 trường hợp: Năm 2025 Trang 14/16 TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH TOÁN ĐIỂM 10
• Trường hợp 1: (a−1)2 = 1 và (b−1)2 = 1 và (a−b)2 = 0. Từ (a−1)2 = 1 ⇒ a = 2 (do a > 0, nếu
a = 0 loại). Từ (b − 1)2 = 1 ⇒ b = 2 (do b > 0). Kiểm tra điều kiện thứ ba: (a − b)2 = (2 − 2)2 = 0
(Thỏa mãn). Với a = 2, b = 2, ta tính giá trị của p:
p = 23 + 23 − 3 · 2 · 2 + 1 = 8 + 8 − 12 + 1 = 5
Số 5 là số nguyên tố (Thỏa mãn).
• Trường hợp 2: (a − 1)2 = 1 và (a − b)2 = 1 và (b − 1)2 = 0. Từ (b − 1)2 = 0 ⇒ b = 1. Từ
(a − 1)2 = 1 ⇒ a = 2 (do a > 0). Kiểm tra điều kiện thứ hai: (a − b)2 = (2 − 1)2 = 1 (Thỏa mãn).
Với a = 2, b = 1, ta tính giá trị của p:
p = 23 + 13 − 3 · 2 · 1 + 1 = 8 + 1 − 6 + 1 = 4
Số 4 không phải là số nguyên tố (Loại).
• Trường hợp 3: (b − 1)2 = 1 và (a − b)2 = 1 và (a − 1)2 = 0. Từ (a − 1)2 = 0 ⇒ a = 1. Từ
(b − 1)2 = 1 ⇒ b = 2 (do b > 0). Kiểm tra điều kiện thứ hai: (a − b)2 = (1 − 2)2 = 1 (Thỏa mãn).
Với a = 1, b = 2, tương tự như trên ta có p = 4 (Loại).
Vậy chỉ có cặp số (a, b) = (2, 2) thỏa mãn yêu cầu đề bài và cho ra số nguyên tố p = 5. Vì chỉ tìm
được một giá trị p thỏa mãn, nên đó cũng là giá trị lớn nhất.
Kết luận: Số nguyên tố p lớn nhất cần tìm là 5. √
L Câu 18. Câu 18. (1.0 điểm) Cho các số thực a, b thỏa mãn a > b > 0 và (a − b) ab = 1. Tìm giá
trị nhỏ nhất của biểu thức 1 + 4a2b2 15 S = + . ab a + b ✍ HƯỚNG DẪN GIẢI.
Biến đổi biểu thức S ta được: 1 4a2b2 15 1 15 S = + + = + 4ab + ab ab a + b ab a + b √
Từ giả thiết: (a − b) ab = 1. Bình phương hai vế (vì hai vế đều dương): 1
(a − b)2 · ab = 1 ⇒ (a − b)2 = ab
Ta sử dụng hằng đẳng thức (a + b)2 = (a − b)2 + 4ab. Thay thế (a − b)2 = 1 vào: ab 1 (a + b)2 = + 4ab ab
Áp dụng bất đẳng thức Cô-si (AM-GM) cho hai số dương 1 và 4ab: ab 1 … 1 √ + 4ab ⩾ 2 · 4ab = 2 4 = 4 ab ab √
Suy ra (a + b)2 ⩾ 4. Do a, b > 0 nên a + b > 0, suy ra a + b ⩾ 4 = 2.
Đặt t = a + b, điều kiện t ⩾ 2. Từ biểu thức của (a + b)2 ở trên, ta thấy S có thể viết lại như sau: Å 1 ã 15 15 S = + 4ab + = (a + b)2 + ab a + b a + b
Biểu thức trở thành hàm số theo biến t: 15 S(t) = t2 + với t ⩾ 2 t Năm 2025 Trang 15/16 TOÁN ĐIỂM 10
TOÁN ĐIỂM 10
TOÁN TP HÀ TĨNH
Ta cần tìm giá trị nhỏ nhất của S(t) trên miền t ∈ [2; +∞). Xét hiệu S(t1) − S(t2) với t1 > t2 ⩾ 2: Å 1 1 ã
S(t1) − S(t2) = (t2 − t2) + 15 − 1 2 t1 t2 Å t ã = (t 2 − t1 1 − t2)(t1 + t2) + 15 t1t2 ï 15 ò = (t1 − t2) t1 + t2 − t1t2
Vì t1 > t2 ⩾ 2 nên t1 · t2 > 4 ⇒ 15 < 15 = 3, 75. Đồng thời t t 1 + t2 > 2 + 2 = 4. Suy ra: 1t2 4 15 t1 + t2 −
> 4 − 3, 75 = 0, 25 > 0 t1t2
Vậy S(t1) − S(t2) > 0 ⇔ S(t1) > S(t2). Hàm số S(t) đồng biến trên khoảng [2; +∞). Do đó, giá trị
nhỏ nhất của S đạt được tại biên t = 2.
Thay t = 2 vào biểu thức của S: 15 Smin = 22 + = 4 + 7, 5 = 11, 5 2 ® ®
Dấu "=" xảy ra khi: a + b = 2 a + b = 2 ⇔
a, blnghimcaphngtrnh :X2 −2X +0, 5 = 1 = 4ab 4(ab)2 = 1 ⇒ ab = 0, 5 ab √ √ √ 2 + 2 2 2 0. Giải ra được a = = 1 + và b = 1 − (thỏa mãn a > b > 0). 2 2 2
Kết luận: Giá trị nhỏ nhất của biểu thức S là 11, 5 (hay 23 ). 2 Năm 2025 Trang 16/16 TOÁN ĐIỂM 10
Document Outline
- HSG TOÁN 9 nam h_c 2025-2026
- HSG 9 HÀ TĨNH 2026
- ĐÁP ÁN THAM KHẢO TĨNH HT TOÁN CHIỀU NAY



