Đề thi chọn HSG tỉnh năm học 2023-2024 môn Toán lớp 9

SỞ GD&ĐT QUẢNG BÌNH KỲ THI CHỌN HSG TỈNH NĂM HỌC 2023-2024
Khóa ngày 05 tháng 12 năm 2023 ĐỀ CHÍNH THỨC Môn thi: TOÁN LỚP 9 THCS
SỐ BÁO DANH:……………
Thời gian: 150 phút (không kể thời gian giao đề)
Đề gồm có 01 trang và 05 câu
Câu 1 (2,0 điểm). x + x + 1 1 1
a) Rút gọn biểu thức A = − +
với x ≥ 0, x ≠ 1. x + x − 2 1 − x x + 2
b) Tính giá trị biểu thức Q = 28 +12 5 + 28 −12 5 + 2 43 − 30 2 .
Câu 2 (2,0 điểm).
 y − x + x + y =
a) Giải hệ phương trình 2 3 5 
2 2y − x − 3 3x + y = 5 − 
b) Giải phương trình 2
x − 3 + 5 − x = 2x − 7x − 2. Câu 3 (1,5 điểm).
a) Cho các số thực dương x, y thỏa mãn x ≥ 0, y ≥ 0, x + y = 2..
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức A = x 2023 + y + y 2023 + x
b) Cho hai số thực dương a và b thỏa mãn các điều kiện 1012 a − a −1 = 0 và 2024 b
− b − 3a = 0. Hãy so sánh a và b.
Câu 4 (3,5 điểm).
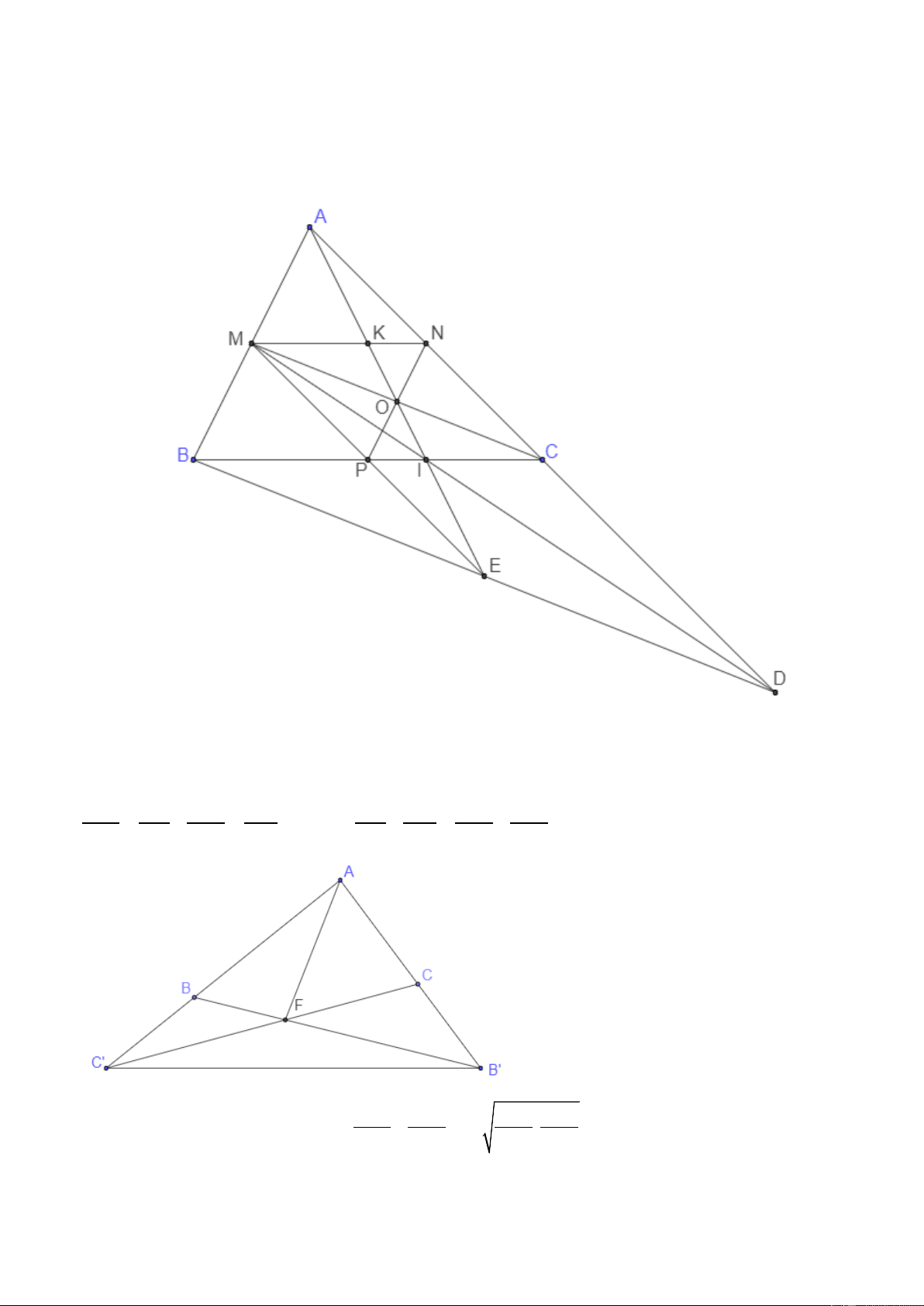
Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm các cạnh AB, AC,
BC. Gọi O là giao điểm của CM và PN, I là giao điểm của AO và BC, D là giao điểm
của MI và AC, K là giao điểm của AI và MN.
a) Chứng minh KM = 2KN.
b) Chứng minh ba đường thẳng AI, BD và và MP đồng quy.
c) Trên các tia đối của tia BA, CA lần lượt lấy các điểm C’, B’ (với C’ khác B, FB FC A . B AC
B’ khác C). Gọi F là giao điểm của BB’ và CC’. Chứng minh + ≥ 2 , FB ' FC ' Ab '.AC '
dấu bằng xảy ra khi nào? n 8
Câu 5 (1,0 điểm). Tìm tất cả các số tự nhiên n sao cho 2 + 9.2 là số chính phương.
-------------HẾT------------
Chú ý: - Cán bộ coi thi không giải thích gì thêm.
- Thí sinh không được sử dụng máy tính cầm tay. 1 HƯỚNG DẪN GIẢI Câu 1:
a) Với x ≥ 0, x ≠ 1 ta có: x + x + 1 1 1 A = − + x + x − 2 1 − x x + 2 x + x + 1 + x −1 + x + 2 =
( x −1)( x + 2) x + 3 x + 2 =
( x −1)( x + 2) ( x + 1)( x + 2) =
( x −1)( x + 2) x + 1 = x −1 b) Ta có Q =
28 +12 5 + 28 −12 5 + 2 43 − 30 2 2 2 2
= (3 2 + 10) + (3 2 − 10) + 2 (5−3 2)
= 3 2 + 10 + 3 2 − 10 + 2(5 − 3 2) = 10 Câu 2:
a) ĐK 2y − x ≥ 0,3x + y ≥ 0 Đặ a + b =
t a = 2 y − x ≥ 0,b = 3x + y ≥ 0.Ta có hệ phương trình: 5  2a − 3b = 5 −
Giải hệ ta có a = 2, b = 3 (TMĐK). 
Khi đó  2y − x = 2 
. Giải hệ ta có x = 2, y = 3 (TMĐK).  3x + y = 3 
Vậy hệ có nghiệm (x; y) = (2; 3).
b) ĐK 3 ≤ x ≤ 5 Ta có 2
x − 3 + 5 − x = 2x − 7x − 2.
⇔ ( x − 3 −1) + ( 5 − x −1) = (2x +1)(x − 4). x − 4 4 − x ⇔ +
= (2x +1)(x − 4). x − 3 +1 5 − x +1  4 − x 1 
⇔ (x − 4) 2x +1+ − = 0    5 − x +1 x − 3 +1  ⇔ 4 − x 1
x = 4 (vì 2x +1+ > 7 > ) 5 − x +1 x − 3 +1 2
Vậy phương trình có nghiệm x = 4. Câu 3: a) Ta có
A = x 2023 + y + y 2023 + x A =
x 2023x + xy +
y 2023y + xy 2 2
⇒ A = ( x 2023x + xy + y 2023y + xy)
≤ (x + y)(2023x + xy + 2023y + xy) (Bunhia copxky) = 2.(2023.2 + 2xy) 2  x + y  ≤ 4.2023 + 4.   2  = 4.2024 ⇒ A ≤ 2 2024
Vậy maxA = 2. 2024 . Đẳng thức xảy ra khi và chỉ khi x = y = 1.
Mặt khác A = x 2023 + y + y 2023 + x − (x + y) 2023 + 2 2023
= x( 2023 + y − 2023) + y( 2023 + x − 2023) + 2 2023
Vì x ≥ 0, y ≥ 0 nên A ≥ 2. 2023 .
Đẳng thức xảy ra khi và chỉ khi x = 0, y = 2 hoặc x = 2, y = 0.
Vậy min A = 2 2023 khi x = 0, y = 2 hoặc x = 2, y = 0.
b) Ta giải bài toán tổng quát sau: Cho hai số thực dương a và b thỏa mãn n
a − a −1 = 0 và 2n b
− b − 3a = 0 với n >1,n∈ N. Hãy so sánh a và b.
Do a > 0 và n
a = a +1 > 1 ⇒ a > 1. Từ đó 2n 2 a
= (a +1) > 4a . 2n Do đó 2n  b  b b + 3a b + 3a = = <   . 2n 2n  a  a a 4a 2n  b  b + 3a b + 3b b b
- Nếu a ≤ b thì < ≤ =  
, điều này vô lý vì ≥1.  a  4a 4a a a
Chứng tỏ a > b với mọi n > 1, n ∈ N.
Áp dụng bài toán tổng quát với n = 1012 ta có kết luận a > b. Câu 4:
a) Từ giả thiết, ta có MNCP là hình bình hành nên O là trung điểm NP. A
∆ MC.có hai trung tuyến MN và AO cắt nhau tại K. Suy ra K là trọng tâm A ∆ MC. Vậy MK = 2 KN.
b) Tứ giác MNCP là hình bình hành tâm O và O ∈ KI , kết hợp với MK = 2 KN nên IC = IP. MP IP 1 Vì MP //AD nên = = ⇒ CD = 2 . MP CD IC 2 3
Gọi E là giao điểm của MP và BD, khi đó E là trung điểm của BD. Mà CA = 2MP nên CD = CA. A
∆ BD có DM, BC là hai trung tuyến cắt nhau tại I nên I là trọng tâm A ∆ BD . Do đó I
nằm trên đường thẳng AE. Vậy AI, BD và MP đồng quy tại E.
c) Vì nếu hai tam giác có cùng chiều cao thì tỉ lệ diện tích giữa chúng bằng tỉ lệ giữa
hai cạnh đáy ứng với chiều cao đó. Ta có: S FB S FC FB FC S S AFB = ; AFC = . Suy ra AFB AFC + = + (1) S FB ' S FC ' FB ' FC ' S S AFB ' AFC ' AFB ' AFC ' S S S S
Theo bất đẳng thức Côsi ta có: AFB AFC + ≥ 2 AFB . AFC (2) S S S S AFB ' AFC' AFB ' AFC' 4 S S S S AB AC A . B AC
Mặt khác AFB . AFC AFB = . AFC = . = (3) S S S S AC ' AB ' AB '.AC ' AFB ' AFC ' AFC ' AFB' FB FC A . B AC Từ (1), (2), (3) ta có + = 2 FB ' FC ' AB '.AC ' S S FB FC
Dấu “=” xảy ra khi và chỉ khi AFB AFC = ⇔ = S S FB ' FC ' AFB ' AFC '
Điều đó xảy ra khi và chỉ khi BC // B’C’.
Câu 5: Giả sử n 8 2 2 + 9.2 = m , m ∈ N. Khi đó n 2 8 2 = m − 9.2 n 2 2 4 2 2 2
⇔ 2 = m − 3 .(2 ) = m − 48
⇔ 2n = (m − 48)(m + 48)
m + 48 = 2p ⇔ 
, với p, q ∈ N, p > q và p + q = . n
m − 48 = 2q Suy ra p q q p−q 5 2 − 2 = 96 ⇔ 2 (2 −1)2 .3
Nhận xét q = 0 không thỏa mãn bài toán.
Do p, q ∈ N, p > q > 0 nên 2p−q −1 là số lẻ và 2q là số chẵn.
Suy ra q = 5 và p – q = 2 nên p = 7. Khi đó n = 5 + 7 = 12. Thử lại 12 8 2 2 + 9.2 = 80 . Vây n = 12. 5