Đề thi chọn học sinh giỏi tỉnh Toán THCS năm 2021 – 2022 sở GD&ĐT Thanh Hóa

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THANH HÓA
NĂM HỌC 2021 - 2022 MÔN THI: TOÁN - THCS ĐỀ CHÍNH THỨC Ngày thi: 26/12/2021
Thời gian làm bài: 150 phút, không kể thời gian giao đề
(Đề thi có 01 trang)
Câu I (4,0 điểm).
1. Rút gọn biểu thức 3 x x − x 2 P = + ⋅ xy − 2 y x +
x − 2 xy − 2 y 1 − x x ≥ y > x ≠ y x ≠ , với 0; 0; 4 ; 1.
2. Cho a,b, c + + + =
là các số thực dương thoả mãn điều kiện a b c 2 abc 1. Tính giá trị biểu
thức Q = a(1− b)(1− c) + b(1− c)(1− a) + c(1− a)(1− b) − abc + 2020.
Câu II (4,0 điểm). 5
1. Giải phương trình 2
3x − 6x − 6 = 3 (2 − x) + (7x −19) 2 − x . 2  x 2 2 x + = 6 −   y y
2. Giải hệ phương trình  . 2  x y +1 4 2 x + 2x + = 12 − 2  y y
Câu III (4,0 điểm).
1. Tìm tất cả các cặp số nguyên dương (a,b) thỏa mãn phương trình 4 3 3 3
+ 4 − b = 4 + 4 b + b + 4 − 4 b + b. a
2. Cho ba số tự nhiên a,b,c thỏa mãn a − b là số nguyên tố và 2
ab + bc + ca = 3c .
Chứng minh 8c +1 là số chính phương.
Câu IV (6,0 điểm).
Cho nửa đường tròn (O;R) đường kính AB và C là điểm thay đổi trên nửa đường tròn đó (
C khác A và B ). Trên cùng một nửa mặt phẳng bờ AB chứa nửa đường tròn vẽ các tia tiếp tuyến
Ax và By . Tiếp tuyến tại C của nửa đường tròn cắt các tia Ax , By theo thứ tự tại D , E . Gọi I
là giao điểm của AE và BD , CI cắt AB tại H .
1. Chứng minh CH song song với BE và I là trung điểm của đoạn thẳng CH .
2. Đường tròn nội tiếp tam giác ABC tiếp xúc với cạnh AB tại K . Chứng minh rằng .
KA KB = CH .CO .
3. Qua C vẽ đường thẳng song song với AB cắt tia By tại F . Gọi M là giao điểm của
AF và BC . Xác định vị trí của điểm C trên nửa đường tròn (O; R) sao cho tam giác
ABM có diện tích lớn nhất. Tính diện tích lớn nhất đó theo R .
Câu V (2,0 điểm).
Cho a, b là các số thực dương. Chứng minh rằng a + b ab ab
a + b + 2ab + + + ≥ 3. 1 + ab 1 + a 1 + b
(1 + a)(1 + b)ab
------------- HẾT --------------
Họ và tên thí sinh:…………………………………………SBD……………
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THANH HÓA NĂM HỌC: 2021-2022 HƯỚNG DẪN CHẤM
Môn thi: TOÁN – THCS
(Hướng dẫn chấm có 06 trang) Câu NỘI DUNG Điểm I
1. Rút gọn biểu thức 4,0 3 − điểm x x x 2 x ≥ y > x ≠ y x ≠ P = + . , với 0; 0; 4 ; 1. 2,0 xy − 2 y x +
x − 2 xy − 2 y 1 − x ≥ > ≠ ≠ Với x 0; y 0; x 4 y; x 1. Ta có: x x ( x − ) 1 2 P = + 0,5
y ( x − 2 y ) ( x + )
1 ( x − 2 y ) .1− x x 2 x = − 0,5
y ( x − 2 y ) ( x − 2 y ) x − 2 xy = 0,5
y ( x − 2 y )
x ( x − 2 y ) x x = = = y ( x − y ) . 2 y y 0,5
Vậy với x ≥ 0; y > 0; x ≠ 4y; x ≠ 1 x thì P = . y
2. Cho a,b, c là các số thực dương thoả mãn điều kiện
a + b + c + 2 abc = 1. Tính giá trị biểu thức 2,0 Q =
a(1 − b)(1 − c) + b(1 − c)(1 − a) + c(1 − a)(1 − b) − abc + 2020.
Theo bài ra ta có: a + b + c + 2 abc = 1 ⇒ a + 2 abc = 1 − b − c 0,5
Do đó a(1− b)(1− c) = a(1− b − c + bc) 0,5 2
= a(a + 2 abc + bc) = (a + abc) = a + abc (vì a,b,c >0) Tương tự:
b(1 − c)(1 − a) = b + abc 0,5
c(1 − a)(1 − b) = c + abc Khi đó
Q = a + b + c + 3 abc − abc + 2020 = a + b + c + 2 abc + 2020 = 2021 0,5 Vậy Q = 2021 II 5
1. Giải phương trình 2
3x − 6x − 6 = 3 (2 − x) + (7x −19) 2 − x . 2,0 4,0 điểm 2  − − ≥
Điều kiện xác định 3x 6x 6 0  ⇔ x ≤ 1− 3 0,25 2 − x ≥ 0
Với x ≤1− 3 , phương trình đã cho tương đương với:
3x − 6x − 6 = 3(2 − x)2 2
2 − x + (7x −19) 2 − x 2 ⇔ 0,5
3x − 6x − 6 = 2 − x ( 2 3x − 5x − 7) 2
⇔ 3x − 6x − 6 − 2 − x = 2 − x ( 2 3x − 5x − 8) ( )1 2
 3x − 6x − 6 ≥ 0
Vì x ≤ 1 − 3 ⇒  2
⇒ 3x − 6x − 6 + 2 − x > 0.  2 − x > 0
Khi đó (1) tương đương với: 2 3x − 5x − 8 ⇔ = 2 − x ( 2 3x − 5x − 8) 0,5 2
3x − 6x − 6 + 2 − x 2
3x − 5x − 8 = 0 ⇔ 1= 2− x  ( 2
3x − 6x − 6 + 2 − x ) * Nếu: 2
3x − 5x − 8 = 0 ⇔ x = 1 − (thoả mãn ĐKXĐ) 0,25 hoặc: 8 x = (không thoả mãn ĐKXĐ) 3 * Nếu: = − x ( 2 1 2
3x − 6x − 6 + 2 − x ) ⇔ 1 = 2 − x + 2
3x − 6x − 6. 2 − x ⇔ x −1 = 2
3x − 6x − 6 ⋅ 2 − x (*) 0,5
Vì : x ≤ 1 − 3 nên : 2
x −1 < 0 ≤ 3x − 6x − 6. (2 − x)
Do đó phương trình (*) vô nghiệm
Vậy phương trình đã cho có nghiệm duy nhất: x = 1 − . 2  x 2 2 x + = 6 −   y y
2. Giải hệ phương trình  . 2,0 2  x y +1 4 2 x + 2x + = 12 − 2  y y + ĐKXĐ: y ≠0 0,25
+ Với y ≠ 0 hệ phương trình đã cho tương đương với hệ phương trình: 2 2  x 2  x 2 2 2 x + = 6 − x + = 6 −    y y  y y  ⇔  2  x +1 1  x + x + 2x + = 12 − (x + ) 2 2 1 1 4 2 2 1 + + = 13 2 2  y y    y y 0,5 + Đặ 1 t: 2
u = x +1;v = . y u  −1+ (u − ) 1 v = 6 − 2v u  + v + uv = 7 u  + v + uv = 7  Ta có:  ⇔  ⇔  0,5 2 2 u
 + uv + v =13 u
 + uv + v = 13 (  u + v  )2 2 2 − uv = 13 u  + v = 4 u = 1;v = 3 u  + v = − ⇒  ⇒  hoặc 5 
(hệ phương trình vô nghiệm) uv  = 3 u = 3;v = 1 uv  = 12 2 x +1 = 1  x = 0   + TH1:  1 ⇔  1 = (thoả mãn) 3 y =   0,25  y  3 2 x +1 = 3  x = ± 2 + TH2:  1 ⇔  = (thoả mãn). 0,25 1   y =1  y  1  
* Vậy hệ phương trình có nghiệm: ( ; x y ) ∈  0; ,   ( 2 ) ;1 ,(− 2 ) ;1  .   0,25 3   III
1. Tìm tất cả các cặp số nguyên dương (a,b) thỏa mãn phương trình 4,0 điểm 4 2,0 3 3 3
+ 4 − b = 4 + 4 b + b + 4 − 4 b + b (1) a
Phương trình (1) tương đương với phương trình: 4 0,25 3
+ 4 − b = ( 2+ b )2 +( 2− b )2 3 3 (2) a Đặ 3 3 = + > = − ⇒ + = t: 3 3 x 2 b 0; y 2 b x y 4 . 3 3 Phương tr x + y ình (2) trở thành: 2 2
+ xy = x + y a (x + y)( 2 2
x − xy + y ) 0,5 2 2 ⇔
= x + y − xy ⇔ ( 2 2
x + y − xy )( x + y − a) = 0 a 2 2 ⇔  x  3x x + y = a 2 2 + − = − + > ∀ > ∈ (vì x y xy y 0, x 0, y R   )  2  4 3 3  a − 4  3 3 3 3
⇒ 2 + b + 2 − b = a ⇔ 4 + 3a 4 − b = a ⇔ 4 − b =   (3) 0,5 3a   Vì a,b +
∈  nên từ (3) suy ra: 3
a − 43a ⇒ 4a ⇒ a ∈{1;2; } 4 (4) 0,5
Thay trực tiếp các giá trị của a từ (4) vào (3) ta được duy nhất một cặp số nguyên
dương (a,b) thỏa mãn: (a,b) = (1;5) . 0,25
2. Cho ba số tự nhiên a,b,c thỏa mãn a − b là số nguyên tố và 2 2,0
ab + bc + ca = 3c . Chứng minh 8c +1 là số chính phương. 2 2 2
Ta có: ab + bc + ca = 3c ⇔ 4c = c + ab + bc + ca = (a + c)(b + c) d =
Đặt (a + c,b + c) = d ⇒ (a + c) − (b + c)d ⇔ a − b 1 d ⇒  0,5
d = a − b
(vì a − b là số nguyên tố)
TH1: Xét d = a − b . a + c = 
(a −b).m
Vì (a + c,b + c) = d nên đặt:  (với , m n ∈ N ) b  + c = 
(a −b).n
⇒ a − b = (a − b)(m − n) 0,5
Mà a − b nguyên tố nên: a − b >
⇒ m − n = ⇒ m = n + ⇔ c = (a − b)2 2 0 1 1 4 (n + )1n Mà 2 4c và ( − )2 a b
là các số chính phương. Suy ra n(n + ) 1 là số chính phương.
Vì n ∈ N nên n ≤ n + n < n + n + ⇒ n ≤ n + n < (n + )2 2 2 2 2 2 2 1 1 . Mà 2 n + n là số chính phương. Suy ra 2 2 2 + = ⇒ = ⇒ = ⇒ = ⇔ + = 0,25 n n n n 0 4c 0 c 0 8c 1 1 là số chính phương. (1) TH2: Xét d = 1.
Vì (a + c, b + c) =1 mà (a + c)(b + c) 2
= 4c là số chính phương nên: 2
a + c = x 
(x, y∈ N ) 2 2
⇔ a − b = x − y ⇔ a − b = (x − y)(x + y) ⇒ x − y > 0 2 b  + c = y 0,5 x − y =
Mà 0 < x − y ≤ x + y và a − b nguyên tố nên suy ra 1  ⇒ x = y +1  + = − x y a b ⇒ c = ( y + )2 2 2 4
1 ⋅ y ⇔ c =  y ( y + ) 2 2 4 1  
 mà c, y ≥ 0 ⇒ 2c = y( y + ) 1 2
⇔ 8c +1 = 4y + 4y +1 ⇔ c + = ( y + )2 8 1 2
1 là số chính phương. (2) 0,25
Từ (1) và (2) suy ra điều phải chứng minh. IV
Cho nửa đường tròn (O;R) đường kính AB và C là điểm thay đổi trên 6,0
điểm nửa đường tròn đó (C khác A và B ). Trên cùng một nửa mặt phẳng bờ 6,0
AB chứa nửa đường tròn vẽ các tia tiếp tuyến Ax và By . Tiếp tuyến tại C
của nửa đường tròn cắt các tia Ax , By theo thứ tự tại D , E . Gọi I là giao
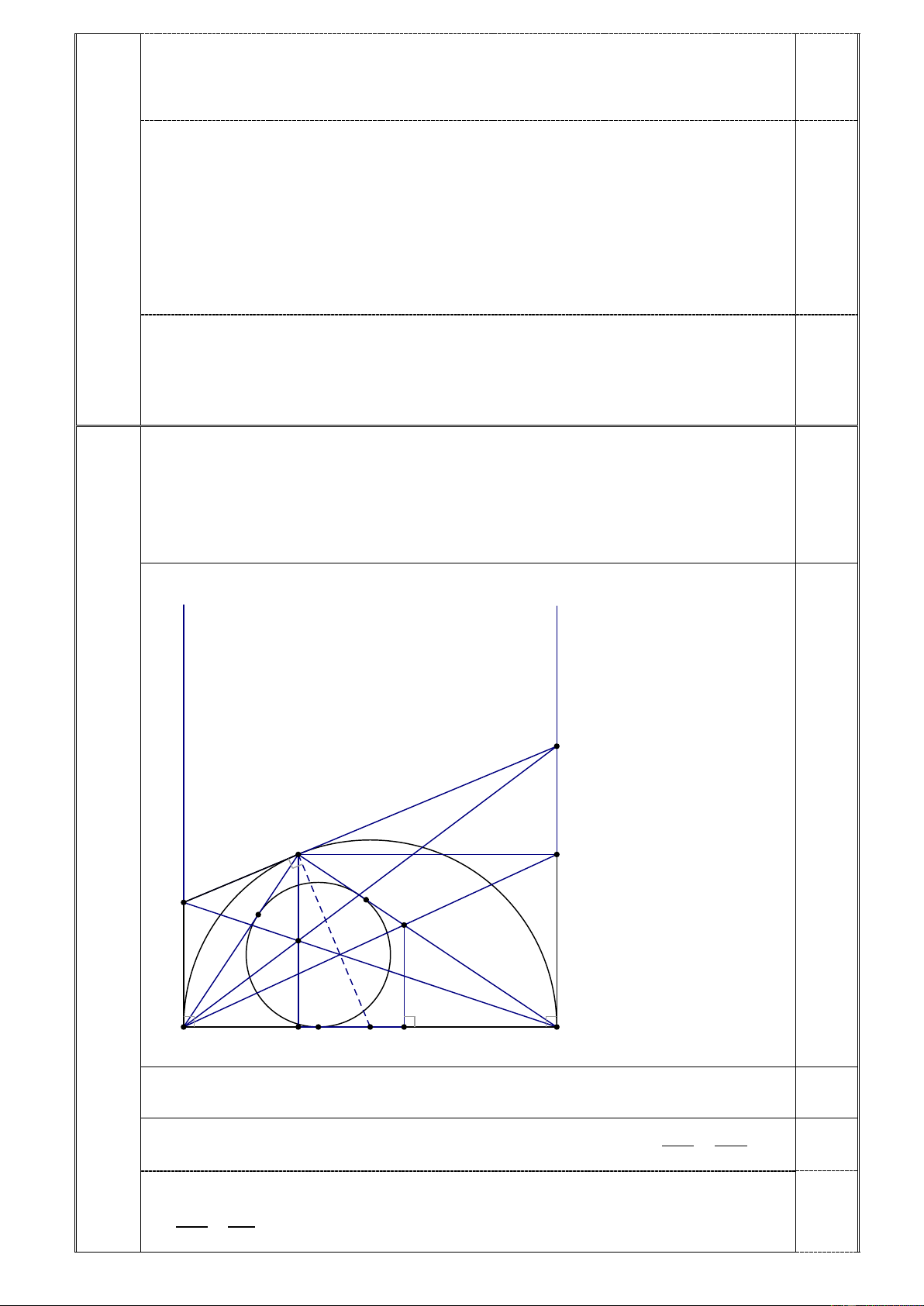
điểm của AE và BD , CI cắt AB tại H . x y E C F D P Q M I A x H K O N B
1. Chứng minh CH song song với BE và I là trung điểm của đoạn thẳng CH . 2,0
Theo tính chất hai tiếp tuyến cắt nhau : AD DC
AD = DC, BE = CE ⇒ = . (1) 0,25 BE CE
Vì Ax, By là các tia tiếp tuyến của (O) nên Ax ⊥ AB, By ⊥ AB ⇒ Ax / /By AD DI ⇒ = 0,25 (2) BE IB Từ ( ) DC DI 1 và (2) suy ra: =
⇒ CI / /BE (Định lí Talét đảo) hay CH / /BE. 0,5 CE IB IH BI
Xét tam giác ABD có IH / / AD ⇒ =
(3) (Hệ quả của định lí Talét) AD BD IC CD IC BE CE BI 0,5
Xét tam giác BDE có IC / / BE ⇒ = ⇒ = = = (4) BE DE CD DE DE BD
(Hệ quả của định lí Talét và BE = CE ) IH IC Từ (3) và (4) suy ra: =
. Mà DA = DC ⇒ IH = IC AD CD 0,5
Vậy I là trung điểm của CH.
2. Đường tròn nội tiếp tam giác ABC tiếp xúc với cạnh AB tại K . 2,0 Chứng minh rằng: .
KA KB = CH .CO .
Trước hết ta chứng minh đẳng thức quen thuộc như SGK Toán 9:
2 AK = AB + AC − BC .
Gọi P,Q lần lượt là tiếp điểm của ,
CA CB với đường tròn nội tiếp ABC ∆
Theo tính chất của hai tiếp tuyến cắt nhau, ta có: 0,25
AK = AP, BK = BQ, CP = C . Q
⇒ 2 AK = AP + AK = ( AC − CP) + ( AB − BK ) = ( AC + AB) − (CP + BK )
= (AC + AB) − (CQ + BQ) = AC + AB − BC (5) . 0,5
Tương tự: 2BK = BA + BC − AC (6)
Vì điểm C thuộc đường tròn đường kính AB nên ABC ∆ vuông tại C . 0,25
Từ (5),(6) kết hợp với 2 2 2
AB = AC + BC (định lí Pitago), suy ra :
4 AK.BK = ( AB + AC − BC )( AB + BC − AC ) 0,5
= AB − ( AC − BC)2 2 = 2AC.BC (7)
Áp dụng các hệ thức về cạnh và đường cao trong tam giác ABC vuông tại C ,
đường cao CH ta có: AC.BC = CH.AB = CH.(2R) = 2CH.CO (8) . 0,5 Từ (7) và (8) suy ra: .
KA KB = CH.CO .
3. Qua C vẽ đường thẳng song song với AB cắt tia By tại F . Gọi M là
giao điểm của AF và BC . Xác định vị trí của điểm C trên nửa đường
tròn (O;R) sao cho tam giác ABM có diện tích lớn nhất. Tính diện tích 2,0
lớn nhất đó theo R .
Kẻ đường cao MN của tam giác ABM . Vì CH / /BF,CF / /HB nên tứ giác
BHCF là hình bình hành. Mà  0
HBF = 90 nên BHCF là hình chữ nhật.
Suy ra: CH = BF , CF = . HB 0,5 Đặt:
x = AH (0 < x < 2R). ⇒ CF = HB = 2R − x, BF = CH = . HA HB =
x(2R − x)
Áp dụng định lí Talét và hệ quả, ta có: FB FA FM + MA FM CF 2R − x 4R − x = = = +1 = +1 = +1 = . MN MA MA MA AB 2R 2R 0,5 2 2 . R FB
2R x(2R − x) MN.AB 2R
x(2R − x) ⇒ MN = = ⇒ S = = (9) 4R − x 4 ABM R − x 2 4R − x
Áp dụng bất đẳng thức Cosi:
2 x(4R − 2x)
x + 4R − 2x 4R − x 0,5
x(2R − x) = ≤ = (10) 2 2 2 2 2 2 2 2 2 2R
x(2R − x)
2R .(4R − x) R
Từ (9), (10) suy ra : S = ≤ = ABM 4R − x (4R − x).2 2 2 4R
Dấu “=” xảy ra ⇔ x = 4R − 2x ⇔ x = 3 4R 2 6
⇔ AC = AH.AB = .2R = R 0,5 3 3   Điể 2 6
m C là giao điểm của đường tròn  ; A
R  với nửa đường tròn ( ; O R) . 3   V
Cho các số thực dương a,b . Chứng minh rằng: 2,0 điểm a + b ab ab
a + b + 2ab 2,0 + + + ≥ 3 1 + ab 1 + a 1 + b
(1 + a)(1 + b)ab
Đặt vế trái của bất đẳng thức là M . 2 2 ab ab
a + b + 2ab
(2 + a + b)a b + a + b + 2ab Ta có: + + = . 1 + a 1 + b
(1 + a)(1 + b)ab
(1 + a)(1 + b)ab (vì 2 2
a b +1≥ 2ab với mọi a,b ). 0,25 2 2
(a + b)(a b +1) + 2ab(ab +1)
2ab(a + b) + 2ab(ab +1) = ≥
(1 + a)(1 + b)ab
(1 + a)(1 + b)ab 0,5
2ab(1 + a)(1 + b) = = 2
(1 + a)(1 + b)ab
Như vậy nếu a + b ≥1 thì M ≥3, bất đẳng thức được chứng minh (1) 1 + ab 2 2  = 0,25
Đẳng thức xảy khi và chỉ khi a b 1  ⇔ a = b = 1
a + b = 1+ ab
Ta xét trường hợp a + b <1 ⇔ a +b<1+ ab ⇔ ab+ a +b+1< 2 + 2ab 1 + ab 0,25
⇔ (1+ a)(1+ b) < 2(1+ ab). Khi đó: a + b
(2 + a + b)ab
a + b + 2ab M = + + 1 + ab (1 + a)(1 + b)
(1 + a)(1 + b)ab a + b
(2 + a + b)ab
a + b + 2ab > + + 1 + ab 2(1 + ab) 2(1 + ab)ab 0,5 2 2
2ab(a + b) + (a + b)a b + (a + b) + 2ab(1 + ab) 2 + + = (a b)(ab 1) = +1 2(1 + ab)ab 2(1 + ab)ab 2
(a + b)(ab +1) (a + b) = +1 >
+1 ≥ 3 (vì (a +b)2 ≥4ab ) 2ab 2ab
Vậy với a + b <1 thì M >3 (2) 1 + ab 0,25
Từ (1) và (2) suy ra M ≥3 với mọi số thực a,b . Đẳng thức xảy ra khi và chỉ khi a = b =1.
----------- Hết ----------- Chú ý:
- Các cách làm khác nếu đúng vẫn cho điểm tối đa, điểm thành phần giám khảo tự phân chia
trên cơ sở tham khảo điểm thành phần của đáp án.
- Các trường hợp khác tổ chấm thống nhất phương án chấm.