Đề thi chọn học sinh giỏi Toán 9 năm 2016 – 2017 sở GD&ĐT Ninh Bình

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi chọn học sinh giỏi môn Toán năm 2016 – 2017 sở GD&ĐT Ninh Bình giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

7 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH NINH BÌNH
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
NĂM HỌC 2016 - 2017
Môn: TOÁN
Ngày thi: 21/02/2017
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Đề thi gồm 05 câu, trong 01 trang
Câu 1 (4,0 điểm):
Cho biểu thức:
2x 16 x 4 2x 1
M
x 6x 8 2 x x 4
− ++
= ++
−+ − −
với
x 0; x 4; x 16≥≠≠
a) Rút gọn biểu thức M
b) Tìm x để
M6=
c) Tìm các số nguyên x để M là số nguyên
Câu 2 (6,0 điểm): Giải các phương trình, hệ phương trình sau:
a)
432 2
x 2x 2x 2x x 2x 10 2+ + ++ ++=
b)
32
4 x 8 x x 10+= ++
c)
22
x 2y 2xy4x3y20+ + − − −=
, trong đó
là các số nguyên dương
d)
1
4 x 2 (1 ) 3
x y1
1
4y 2 (1 ) 1
x y1
++ =
++
+− =
++
Câu 3 (2,0 điểm): Cho phương trình:
22
x 2( m 1) x m 2m 1 0
+ −+++=
(
x
là ẩn;
m
là tham số
khác 0). Tìm
m
để phương trình có hai nghiệm phân biệt
12
x ;x
thỏa mãn:
22
1 2 12
2 1 10
0
x x x x 9m
+ +=
+
Câu 4 (6,0 điểm): Cho đường tròn tâm O, bán kính R có đường kính AB cố định. C là một
điểm thay đổi trên đường tròn (C khác A và B). Gọi H là hình chiếu của C trên AB, I là
trung điểm của AC. Đường thẳng OI cắt tiếp tuyến tại A của đường tròn (O; R) tại M, đường
thẳng MB cắt đường thẳng CH tại K.
a) Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn
b) Chứng minh MC là tiếp tuyến của đường tròn (O;R)
c) Chứng minh IK song song với AB
d) Xác định vị trí của điểm C để chu vi tam giác ABC đạt giá trị lớn nhất? Tìm giá trị
lớn nhất đó.
Câu 5 (2,0 điểm): Cho
a, b, c
là các số thực không âm thỏa mãn
abc3++=
. Tìm giá trị
nhỏ nhất của biểu thức
3 33
Qa b c=++
------HẾT-----
Họ và tên thí sinh :..................................................... Số báo danh:…………….........................
Họ và tên, chữ ký:
Giám thị 1:.................................................................................................
Giám thị 2:.................................................................................................
ĐỀ THI CHÍNH THỨC
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH NINH BÌNH
HƯỚNG DẪN CHẤM
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
NĂM HỌC 2016-2017
Môn: TOÁN - Ngày thi 21/2/2017
(Hướng dẫn chấm này gồm 06 trang)
I. Hướng dẫn chung
1. Bài làm của học sinh đúng đến đâu cho điểm đến đó.
2. Học sinh có thể sử dụng kết quả câu trước làm câu sau.
3. Đối với bài hình, nếu vẽ sai hình hoặc không vẽ hình thì không cho điểm.
4. Nếu thí sinh làm bài không theo cách nêu trong đáp án mà đúng vẫn cho điểm đủ từng
phần như hướng dẫn, thang điểm chi tiết do tổ chấm thống nhất.
5. Việc chi tiết hoá thang điểm (nếu có) so với thang điểm trong hướng dẫn phải đảm bảo
không sai lệch và đảm bảo thống nhất thực hiện trong toàn hội đồng chấm.
6. Điểm toàn bài thi lẻ đến 0,25.
II. Hướng dẫn chi tiết
Câu
Đáp án
Điểm
Câu
1(4đ)
Cho biểu thức
2x 16 x 4 2x 1
M
x 6x 8 2 x x 4
− ++
= ++
−+ − −
với
0; 4; 16≥≠≠xx x
a) Rút gọn biểu thức M (1,25 điểm)
- Ta có
2x 16 x 4 2x 1
M
(x2)(x4) x2 x4
− ++
= −+
−− − −
0.25
2 x 16 ( x 4)( x 4) (2 x 1)( x 2)
( x 2)( x 4)
−− + −+ + −
=
−−
0.25
x x2
( x 2)( x 4)
−−
=
−−
0.25
(x 2)(x 1)
( x 2)( x 4)
−+
=
−−
0.25
x1
x4
+
=
−
0.25
b) Tìm x để M = 6 (1,25 điểm)
Ta có:
x1
M6 6
x4
+
=↔=
−
0.5
x 1 6( x 4)↔ += −
0.25
x5↔=
0.25
x 25↔=
0.25
c) Tìm các số x nguyên để M là số nguyên (1,5 điểm)
Ta có:
x 45 5
M1
x4 x4
−+
= = +
−−
0.5
Để M là số nguyên thì
5
Z
x4
∈
−
( x 4)↔−
là ước của 5
0.25
{ } { }
( x 4) 5;5; 1;1 x 1;9;3;5↔ − ∈− − ↔ ∈−
0.25
Suy ra:
{ }
x 9; 25; 81∈
0.25
Vậy:
{ }
x 9; 25; 81∈
thì
∈
MZ
0.25
2
Câu
2
(6đ)
Giải các phương trình, hệ phương trình sau
a) GPT:
432 2
2 2 2 2 10 2+ + ++ ++=xxxxxx
(1,5 điểm)
- Điều kiện
∈
xR
(hoặc
2
2 10 0++≥xx
)
0.25
- Phương trình
4 32 2 2
( 2 )( 21) 2103↔ + + + +++ ++=
xxx xx xx
0.25
22 2 2
( ) ( 1) ( 1) 9 3↔ + +++ ++=xx x x
0.25
Do
22
2 22 2 2
2
( )0
: ( 1) 0 ( ) ( 1) ( 1) 9 3
( 1) 9 3
+≥
∀∈ +≥ → + +++ ++≥
+ +≥
xx
xR x x x x x
x
0.25
Dấu bằng xẩy ra
22
2
2
( )0
( 1) 0 1
( 1) 9 3
+=
+ = ↔=−
+ +=
xx
xx
x
(tmđk)
0.25
Vậy phương trình ban đầu có nghiệm x = -1.
0.25
b) GPT:
32
4 x 8 x x 10+= ++
(1,5 điểm)
- Điều kiện
2≥−x
- Phương trình:
22
4 ( 2)( 2 4) 2 4 3( 2)↔ + −+=−++ +x xx xx x
0.25
22
2 3( 2)
41
24 24
++
↔=+
−+ −+
xx
xx xx
0.25
Đặt
2
2
( 0)
24
+
= ≥
−+
x
tt
xx
, khi đó ta có
2
1
4 13
1
3
=
=+↔
=
t
tt
t
0.25
+) TH1:
{ }
22
1 2 2 4 3 2 0 1; 2 ( : 2)=→+= − +↔ − +=↔∈ ≥−
t x x x x x x tm x
0.25
+) TH2:
22
11 177
( : 2)
1
2
9( 2) 2 4 11 14 0
3
11 177
( : 2)
2
+
= ≥−
=→ + = − +↔ − − =↔
−
= ≥−
x tm x
t x xx x x
x tm x
0.25
- Vậy tập nghiệm của pt:
11 177 11 177
1; 2; ;
22

+−

=



S
0.25
*Cách khác:
- Điều kiện
2≥−x
- Phương trình
22
4 ( 2)( 2 4) ( 2 4) 3( 2)↔ + −+= −++ +x xx xx x
0.25
Đặt
2
2 4; 2;; 0, 0= −+ = + ≥ ≥ux xvx uv
. Khi đó ta có
22
43= +uv u v
0.25
Học sinh lập luận ra
3
=
=
uv
uv
0.25
+) TH1:
{ }
22
2 4 2 3 2 0 1; 2 ( : 2)=↔ − +=+↔ − +=↔∈ ≥−u v x x x x x x tm x
0.25
+) TH2:
22
11 177 11 177
3 2 4 9( 2) 11 14 0 ;
22

+−

= → − += + ↔ − − =↔∈



uvx x x x x x
0.25
- Vậy tập nghiệm của pt:
11 177 11 177
1; 2; ;
22

+−

=



S
0.25
3
c) GPT:
22
2 2 4 3 20+ + −−−=x y xy x y
, trong đó x, y là các số nguyên dương (1,5 điểm)
Viết lại pt dưới dạng:
22
2 ( 2) 2 3 2 0 (*)+ − + − −=
x xy y y
0.25
Coi (*) là pt bậc hai ẩn x. Pt (*) có nghiệm nên
' 22 2
0 ( 2) (2 3 2) 0 6 0 3 2∆≥↔ − − − − ≥↔ +−≤↔−≤≤y y y yy y
0.25
Do y là số nguyên dương nên
{ }
1; 2∈y
0.25
+) TH1:
2
1
1 2 30
3
= −
=→ − −=⇔
=
x
y xx
x
Cặp số x = 3; y = 1 thỏa mãn pt ban đầu
0.25
+) TH2:
2
2 0 0 ( : 0)
=→ =↔= >
y x x ktm x
0.25
- Vậy nghiệm của pt:
( ; ) (3, 1)=
xy
0.25
d) GHPT:
1
4 2 (1 ) 3
1
1
4 2 (1 ) 1
1
x
xy
y
xy
++ =
++
+− =
++
(1.5 điểm)
- Điều kiện:
11
; ; 10
22
x y xy≥− ≥− + + ≠
Từ hệ phương trình suy ra
11
x ;y
22
>− >−
0.25
- Hệ phương trình
13
1 ()
1
42
11
1 ()
1
42
a
xy
x
b
xy
y
+=
++
+
↔
−=
++
+
0.25
Cộng vế theo vế của pt (a) và pt (b), ta được:
31
2 (1)
42 42xy
= +
++
0.25
Trừ vế theo vế của pt (a) cho pt (b), ta được:
2 31
(2)
1
42 42
xy
xy
= −
++
++
Nhân tương ứng hai vế của (1) và (2):
4 91
14 24 2xy x y
= −
++ + +
0.25
22
4(4 2)(4 2) ( 1)( 4 36 16)
8 9 5( ) 0 ( )( 9 5) 0
x y xy x y
x xy y xy xyx y
↔ + +=++−+ +
↔+ − + −=↔− + +=
+) TH1:
=xy
Thay vào (a):
1
4y 2 1 y
13
4
1 (4y 2) 2 3 4y 2
1
2y 1
4y 2
4y 2 2 y
2
+=↔=−
+ = ↔ + += +↔
+
+
+=↔=
1 1 111 1 11
y x (tm : x ;y ); y x (tm : x ;y )
4 4 22 2 2 22
−− −−
=−→=− > > =→= > >
0.25
+) TH2:
9 50xy+ +=
loại do
11
x ;y
22
>− >−
0.25
- Vậy nghiệm của hệ là:
1 111
( ; ) ( , );( , )
4 4 22
−−

=


xy
4
Câu
3(2đ)
Cho phương trình
22
2( 1) 2 1 0
x m xm m+ − + + +=
( x là ẩn; m là tham số khác 0). Tìm m để
phương trình có hai nghiệm phân biệt
12
;xx
thỏa mãn:
22
1 2 12
2 1 10
0
9
x x xx m
+ +=
+
(2 điểm)
Phương trình phải có 2 nghiệm phân biệt
12
;xx
22
' 0 ( 1) ( 2 1) 0 4 0 0m mm m m
↔∆>↔ − − + +>↔− >↔ <
0.25
Theo Viet:
2
1 2 12
2( 1); 2 1x x m xx m m+=− − = + +
0.25
Để tồn tại đẳng thức
22
1 2 12
2 1 10
0
9x x xx m
+ +=
+
thì
2
12
0 2 10 1
≠↔ + +≠↔ ≠−
xx m m m
(Học sinh không lập luận phần này vẫn cho điểm)
Ta có:
22 2
1 2 12 1 2 12 12
2 1 10 2 1 10
00
x x xx 9m (x x) 2xx xx 9m
+ +=↔ + +=
+ +−
0.25
22 2 2 2
2 1 10 1 1 10
00
4(m 1) 2(m 2m 1) m 2m 1 9m m 6m 1 m 2m 1 9m
↔ + +=↔ + +=
−− ++ ++ −+ ++
0.25
1 1 1 10 1 1 10
( )0 0
11 11
m9 9
m6 m2 m6 m2
mm mm
↔ ++=↔++=
−+ ++ −+ ++
0.25
Đặt
1
tm
m
= +
. Do
0; 1mm< ≠−
nên
0; 2tt< ≠−
. Khi đó ta có phương trình
2
t 3 (tm : t 0;t 2)
1 1 10
0 10t 22t 156 0
26
t6 t2 9
t (ktm: t 0;t 2)
5
=− < ≠−
+ +=↔ − − =↔
−+
= < ≠−
0.25
Với
2
1 3 53 5
t 3 m 3 m 3m 1 0 m ;
m 22

−− −+

=−→ + =−↔ + += ↔ ∈



0.25
Vậy
3 53 5
;
22
m

−− −+

∈



là giá trị cần tìm
0.25
Câu
4(6đ)
Cho đường tròn tâm O, bán kính R có đường kính AB cố định. C là một điểm thay đổi trên
đường tròn (C khác A và B). Gọi H là hình chiếu của C trên AB, I là trung điểm của AC.
Đường thẳng OI cắt tiếp tuyến tại A của đường tròn (O; R) tại M, đường thẳng MB cắt đường
thẳng CH tại K.
K
M
I
C
O
H
B
A
5
a) Chứng minh 4 điểm C, I, O, H cùng thuộc một đường tròn (1,5 điểm)
+)
0
90⊥→ =CH AB CHO
nên H thuộc đường tròn đường kính CO
0.5
+)
;
= = →OA OC IA IC
∆AOC
cân tại O có trung tuyến OI nên
0
90⊥→ =OI AC OIC
→
I
thuộc đường tròn đường kính CO
0.5
Vậy: 4 điểm O, I, C, H cùng thuộc một đường tròn đường kính CO
0.5
b) Chứng minh MC là tiếp tuyến của của (O; R) (1,5 điểm)
Tam giác OAC cân tại O, có OI là đường trung tuyến nên OI là đường trung trực
Mà
∈→ =M OI MA MC
0.5
Xét hai tam giác AMO và CMO có
(..)
=
→∆ =∆
=
OA OC
OM chung OAM OCM c c c
MA MC
0.5
Vì
00
90 90=→=MAO MCO
→⊥MC CO
, hay MC là tiếp tuyến của (O;R)
0.5
c) Chứng minh IK song song với AB (1,5 điểm)
Ta có
⊥
→
⊥
CH AB
MA AB
/ / (1)
2
⇒==
KH BH BH
KH MA
MA AB R
0.25
Do
0
90 / /=→⊥→
ACB BC AC BC OM
Xét hai tam giác BCH và OMA có
(2)
=
→∆ ∆ → = =
=
BHC OAM
CH BH BH
BCH OMA
MA OA R
CBH MOA
0.25
0.25
Từ (1) và (2) suy ra
2= →CH KH K
là trung điểm của CH
0.25
∆CAH
có:
=
→
=
IC IA
IK
KC KH
là đường trung bình của
// //∆→ →CAH IK AH IK AB
0.5
d) Xác định vị trí của điểm C để chu vi tam giác ABC đạt giá trị lớn nhất? Tìm giá trị lớn nhất
đó. (1,5 điểm)
Chu vi tam giác ABC là
(2 ) 2 ( )= ++=+ +P AB BC CA R CB CA
0.25
Mặt khác ta có
2 2222 22
( ) ( )(1 1 ) 2 8CB CA CB CA AB R+ ≤ + += =
22CA CB R
→+≤
0.25
0.25
Suy ra
(2 ) 2 2 2 (2 2 2)≤+ =+
PR R R
Dấu “=” xảy ra
↔=↔CA CB
C là điểm chính giữa cung AB
0.25
0.25
Vậy:
ax(2 ) 2(1 2 )
=+↔MP R
C là điểm chính giữa cung AB
0.25
Câu
5(2đ)
Cho a, b, c là các số thực không âm thỏa mãn
3++=abc
. Tìm giá trị nhỏ nhất của biểu thức
333
=++Qabc
(2,0 điểm)
Do
,, 0
0 ,, 3
3
≥
→≤ ≤
++=
abc
abc
abc
0.25
Ta có
33 3 3
( ) 3 ( ) (3 ) 3( 3)+=+ − +=− + −b c b c bc b c a a bc
0.25
Do
23
22
30
33
3( 3) ( 3)(3 ) (3 )
1
44
( ) (3 )
24
−≤
→− ≥ − −=− −
+
≤=−
a
a bc a a a
bc
bc a
0.25
Suy ra
33 3 3 2 3
31
(3 ) (3 ) (27 27 9 )
44
+≥−−−= −+−bc a a a aa
0.25
Khi đó
333 3 2 3 3 2
13
(27 27 9 ) ( 3 9 9)
44
=++≥+ − + − = + −+Qabca a aa a a a
0.25
6
32 2
33
4 ( 3 9 5) 4 ( 1) ( 5) 3
44

= + + −+ = +− + ≥

aaa a a
0.25
Dấu bằng xẩy ra
30
10
1
1
10
3
φ
−=
−=
∈
↔ ↔===
=
= = =

−=
++=
a
a
a
abc
bc
abc
a
abc
0.25
Vậy giá trị nhỏ nhất của Q là 3 khi a = b = c = 1
0.25
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS TỈNH NINH BÌNH NĂM HỌC 2016 - 2017 Môn: TOÁN
ĐỀ THI CHÍNH THỨC Ngày thi: 21 /02/2017
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Đề thi gồm 05 câu, trong 01 trang Câu 1 (4,0 điểm): Cho biểu thức: 2 x −16 x + 4 2 x +1 M = + +
với x ≥ 0; x ≠ 4; x ≠ 16 x − 6 x + 8 2 − x x − 4 a) Rút gọn biểu thức M b) Tìm x để M = 6
c) Tìm các số nguyên x để M là số nguyên
Câu 2 (6,0 điểm): Giải các phương trình, hệ phương trình sau: a) 4 3 2 2
x + 2x + 2x + 2x + x + 2x +10 = 2 b) 3 2 4 x + 8 = x + x +10 c) 2 2
x + 2y + 2xy − 4x − 3y − 2 = 0 , trong đó x, y là các số nguyên dương  1 4x + 2 (1+ ) = 3  x + y +1 d)  1  4y + 2 (1− ) =1  x + y +1
Câu 3 (2,0 điểm): Cho phương trình: 2 2
x + 2(m −1)x + m + 2m +1 = 0 (x là ẩn; m là tham số
khác 0). Tìm m để phương trình có hai nghiệm phân biệt x ;x thỏa mãn: 1 2 2 1 10 + + = 0 2 2 x + x x x 9m 1 2 1 2
Câu 4 (6,0 điểm): Cho đường tròn tâm O, bán kính R có đường kính AB cố định. C là một
điểm thay đổi trên đường tròn (C khác A và B). Gọi H là hình chiếu của C trên AB, I là
trung điểm của AC. Đường thẳng OI cắt tiếp tuyến tại A của đường tròn (O; R) tại M, đường
thẳng MB cắt đường thẳng CH tại K.
a) Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn
b) Chứng minh MC là tiếp tuyến của đường tròn (O;R)
c) Chứng minh IK song song với AB
d) Xác định vị trí của điểm C để chu vi tam giác ABC đạt giá trị lớn nhất? Tìm giá trị lớn nhất đó.
Câu 5 (2,0 điểm): Cho a, b, c là các số thực không âm thỏa mãn a + b + c = 3. Tìm giá trị
nhỏ nhất của biểu thức 3 3 3 Q = a + b + c ------HẾT-----
Họ và tên thí sinh :..................................................... Số báo danh:…………….........................
Họ và tên, chữ ký: Giám thị 1:.................................................................................................
Giám thị 2:.................................................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM TỈNH NINH BÌNH
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS NĂM HỌC 2016-2017
Môn: TOÁN - Ngày thi 21/2/2017
(Hướng dẫn chấm này gồm 06 trang)
I. Hướng dẫn chung
1. Bài làm của học sinh đúng đến đâu cho điểm đến đó.
2. Học sinh có thể sử dụng kết quả câu trước làm câu sau.
3. Đối với bài hình, nếu vẽ sai hình hoặc không vẽ hình thì không cho điểm.
4. Nếu thí sinh làm bài không theo cách nêu trong đáp án mà đúng vẫn cho điểm đủ từng
phần như hướng dẫn, thang điểm chi tiết do tổ chấm thống nhất.
5. Việc chi tiết hoá thang điểm (nếu có) so với thang điểm trong hướng dẫn phải đảm bảo
không sai lệch và đảm bảo thống nhất thực hiện trong toàn hội đồng chấm.
6. Điểm toàn bài thi lẻ đến 0,25.
II. Hướng dẫn chi tiết Câu Đáp án Điểm Cho biểu thức 2 x −16 x + 4 2 x +1 M = + +
với x ≥ 0; x ≠ 4; x ≠ 16 x − 6 x + 8 2 − x x − 4
a) Rút gọn biểu thức M (1,25 điểm) - Ta có 2 x −16 x + 4 2 x +1 M = − + 0.25 ( x − 2)( x − 4) x − 2 x − 4
2 x −16 − ( x + 4)( x − 4) + (2 x +1)( x − 2) = 0.25 ( x − 2)( x − 4) x − x − 2 = 0.25 ( x − 2)( x − 4) ( x − 2)( x +1) = 0.25 ( x − 2)( x − 4) x +1 = 0.25 x − 4 Câu
1(4đ) b) Tìm x để M = 6 (1,25 điểm) Ta có: x +1 M = 6 ↔ = 6 0.5 x − 4 ↔ x +1 = 6( x − 4) 0.25 ↔ x = 5 0.25 ↔ x = 25 0.25
c) Tìm các số x nguyên để M là số nguyên (1,5 điểm) Ta có: x − 4 + 5 5 M = = 1+ 0.5 x − 4 x − 4
Để M là số nguyên thì 5 ∈ Z ↔ ( x − 4) là ước của 5 0.25 x − 4 ↔ ( x − 4)∈{ 5 − ;5; 1 − ; } 1 ↔ x ∈{ 1 − ;9;3; } 5 0.25 Suy ra: x ∈{9; 25; } 81 0.25 Vậy: x ∈{9; 25; }
81 thì M ∈ Z 0.25 1
Giải các phương trình, hệ phương trình sau a) GPT: 4 3 2 2
x + 2x + 2x + 2x + x + 2x +10 = 2 (1,5 điểm)
- Điều kiện x∈ R (hoặc 2
x + 2x +10 ≥ 0 ) 0.25 - Phương trình 4 3 2 2 2
↔ (x + 2x + x ) + (x + 2x +1) + x + 2x +10 = 3 0.25 2 2 2 2
↔ (x + x) + (x +1) + (x +1) + 9 = 3 0.25 2 2 (x + x) ≥ 0  Do 2 2 2 2 2
∀x ∈ R : (x +1) ≥ 0
→ (x + x) + (x +1) + (x +1) + 9 ≥ 3 0.25  2  (x +1) + 9 ≥ 3 2 2 (x + x) = 0 Câu  Dấu bằng xẩy ra  2 (x +1) = 0 ↔ x = 1 − (tmđk) 0.25 2 (6đ) 2  (x +1) + 9 = 3
Vậy phương trình ban đầu có nghiệm x = -1. 0.25 b) GPT: 3 2
4 x + 8 = x + x +10 (1,5 điểm)
- Điều kiện x ≥ 2 − - Phương trình: 2 2
↔ 4 (x + 2)(x − 2x + 4) = x − 2x + 4 + 3(x + 2) 0.25 x + 2 3(x + 2) ↔ 4 = 1+ 0.25 2 2 x − 2x + 4 x − 2x + 4 t =1 Đặt x + 2 t =
(t ≥ 0) , khi đó ta có 2 4t 1 3  = + t ↔ 2 0.25 x − 2x + 4 1 t =  3 +) TH1: 2 2
t =1→ x + 2 = x − 2x + 4 ↔ x − 3x + 2 = 0 ↔ x ∈{1; } 2 (tm : x ≥ 2 − ) 0.25  11+ 177 x = (tm : x ≥ 2) − +) TH2: 1 2 2 2
t = → 9(x + 2) = x − 2x + 4 ↔ x −11x −14 = 0 ↔  0.25 3  11− 177 x = (tm : x ≥ 2) −  2  + − 
- Vậy tập nghiệm của pt: 11 177 11 177 S 1; 2; ;  =  0.25 2 2    *Cách khác:
- Điều kiện x ≥ 2 − - Phương trình 2 2
↔ 4 (x + 2)(x − 2x + 4) = (x − 2x + 4) + 3(x + 2) 0.25 Đặt 2
u = x − 2x + 4;v = x + 2;; u ≥ 0,v ≥ 0 . Khi đó ta có 2 2
4uv = u + 3v 0.25
Học sinh lập luận ra u = v  0.25 u = 3v +) TH1: 2 2
u = v ↔ x − 2x + 4 = x + 2 ↔ x − 3x + 2 = 0 ↔ x ∈{1; } 2 (tm : x ≥ 2 − ) 0.25  + −  +) TH2: 2 2 11 177 11 177 u 3v
x 2x 4 9(x 2) x 11x 14 0 x ;  = → − + = + ↔ − − = ↔ ∈  2 2  0.25    + − 
- Vậy tập nghiệm của pt: 11 177 11 177 S 1; 2; ;  =  2 2  0.25   2 c) GPT: 2 2
x + 2y + 2xy − 4x − 3y − 2 = 0, trong đó x, y là các số nguyên dương (1,5 điểm)
Viết lại pt dưới dạng: 2 2
x + 2x(y − 2) + 2y − 3y − 2 = 0 (*) 0.25
Coi (*) là pt bậc hai ẩn x. Pt (*) có nghiệm nên ' 2 2 2
∆ ≥ 0 ↔ (y − 2) − (2y − 3y − 2) ≥ 0 ↔ y + y − 6 ≤ 0 ↔ 3 − ≤ y ≤ 2 0.25
Do y là số nguyên dương nên y ∈{1; } 2 0.25 +) TH1: x = 1 − 2
y =1→ x − 2x − 3 = 0 ⇔  x = 3 0.25
Cặp số x = 3; y = 1 thỏa mãn pt ban đầu +) TH2: 2
y = 2 → x = 0 ↔ x = 0 (ktm : x > 0) 0.25
- Vậy nghiệm của pt: ( ;x y) = (3, 1) 0.25  1 4x + 2(1+ ) = 3  x + y +1 d) GHPT: (1.5 điểm) 1  4y + 2(1− ) =1  x + y +1 - Điều kiện: 1 1
x ≥ − ; y ≥ − ; x + y +1 ≠ 0 2 2 0.25
Từ hệ phương trình suy ra 1 1 x > − ; y > − 2 2  1 3 1+ = (a)  x+ y +1 - Hệ phương trình 4x + 2 ↔  1 1 0.25 1  − = (b)  x + y +1 4y +  2
Cộng vế theo vế của pt (a) và pt (b), ta được: 3 1 2 = + (1) 4x + 2 4y + 2 0.25
Trừ vế theo vế của pt (a) cho pt (b), ta được: 2 3 1 = − (2) x + y +1 4x + 2 4y + 2
Nhân tương ứng hai vế của (1) và (2): 4 9 1 = −
x + y +1 4x + 2 4y + 2 0.25
↔ 4(4x + 2)(4y + 2) = (x + y +1)( 4 − x + 36y +16) 2 2
↔ x + 8xy − 9y + 5(x − y) = 0 ↔ (x − y)(x + 9y + 5) = 0
+) TH1: x = y Thay vào (a):  1 4y + 2 =1 ↔ y = − 1 3  4 1+ =
↔ (4y + 2) + 2 = 3 4y + 2 ↔  2y +1 4y + 2  1 0.25 4y + 2 = 2 ↔ y =  2 1 1 1 − 1 − 1 1 1 − 1 y x (tm : x ; y ); y x (tm : x ; y − = − → = − > > = → = > > ) 4 4 2 2 2 2 2 2
+) TH2: x + 9y + 5 = 0 loại do 1 1 x > − ; y > − 0.25 2 2
- Vậy nghiệm của hệ là:  1 − 1 − 1 1 ( ; x y) ( , );( , ) =  4 4 2 2    3 Cho phương trình 2 2
x + 2(m −1)x + m + 2m +1 = 0 ( x là ẩn; m là tham số khác 0). Tìm m để
phương trình có hai nghiệm phân biệt x ; x thỏa mãn: 2 1 10 + + = (2 điểm) 1 2 0 2 2 x + x x x 9m 1 2 1 2
Phương trình phải có 2 nghiệm phân biệt x ; x 1 2 2 2
↔ ∆ ' > 0 ↔ (m −1) − (m + 2m +1) > 0 ↔ 4
− m > 0 ↔ m < 0 0.25 Theo Viet: 2 x + x = 2
− (m −1); x x = m + 2m +1 1 2 1 2 0.25
Để tồn tại đẳng thức 2 1 10 + + = 0 thì 2
x x ≠ 0 ↔ m + 2m +1 ≠ 0 ↔ m ≠ 1 − 2 2 x + x x x 9m 1 2 1 2 1 2
(Học sinh không lập luận phần này vẫn cho điểm) Ta có: 2 1 10 2 1 10 + + = 0 ↔ + + = 0 0.25 2 2 2 x + x x x 9m (x + x ) − 2x x x x 9m 1 2 1 2 1 2 1 2 1 2 Câu 2 1 10 1 1 10 ↔ + + = 0 ↔ + + = 0 3 0.25 (2đ) 2 2 2 2 2
4(m −1) − 2(m + 2m +1) m + 2m +1 9m m − 6m +1 m + 2m +1 9m 1 1 1 10 1 1 10 ↔ ( + + ) = 0 ↔ + + = 0 m 1 1 9 1 1 9 m − 6 + m + 2 + m − 6 + m + 2 + 0.25 m m m m Đặt 1
t = m + . Do m < 0;m ≠ 1
− nên t < 0;t ≠ 2
− . Khi đó ta có phương trình m t = 3 − (tm : t < 0;t ≠ 2) − 1 1 10 0.25 2 0 10t 22t 156 0  + + = ↔ − − = ↔ 26 t − 6 t + 2 9 t = (ktm: t < 0;t ≠ 2) −  5 − − − +  Với 1 2 3 5 3 5 t 3 m 3 m 3m 1 0 m  ;  = − → + = − ↔ + + = ↔ ∈ 0.25 m 2 2    − − − +  Vậy 3 5 3 5 m ;  ∈  là giá trị cần tìm 0.25 2 2   
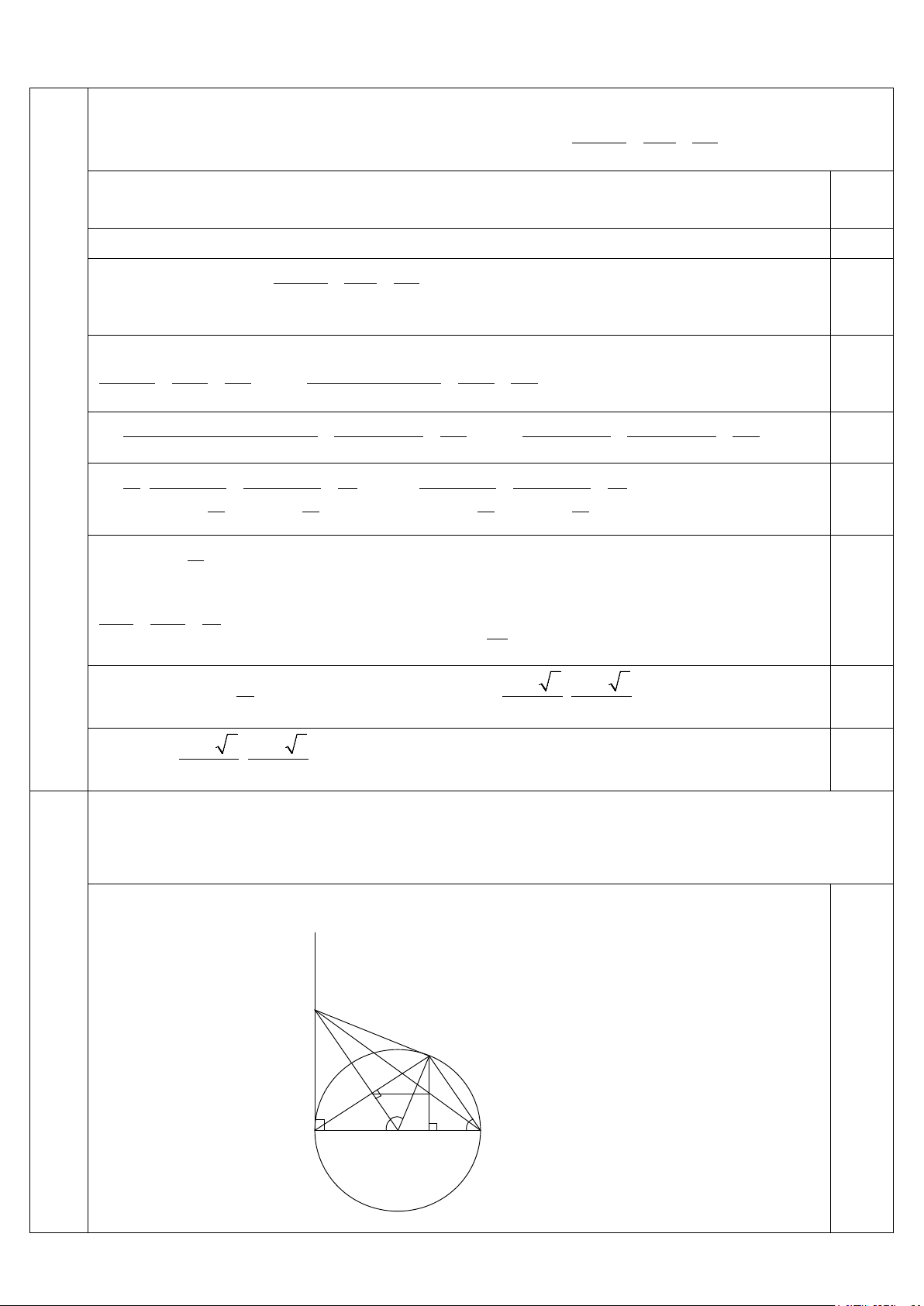
Cho đường tròn tâm O, bán kính R có đường kính AB cố định. C là một điểm thay đổi trên
đường tròn (C khác A và B). Gọi H là hình chiếu của C trên AB, I là trung điểm của AC.
Đường thẳng OI cắt tiếp tuyến tại A của đường tròn (O; R) tại M, đường thẳng MB cắt đường
thẳng CH tại K. Câu 4(6đ) M C I K A B O H 4
a) Chứng minh 4 điểm C, I, O, H cùng thuộc một đường tròn (1,5 điểm)
+) CH ⊥ AB →  0
CHO = 90 nên H thuộc đường tròn đường kính CO 0.5
+) OA = OC; IA = IC → ∆AOC cân tại O có trung tuyến OI nên OI ⊥ AC →  0 OIC = 90 0.5
→ I thuộc đường tròn đường kính CO
Vậy: 4 điểm O, I, C, H cùng thuộc một đường tròn đường kính CO 0.5
b) Chứng minh MC là tiếp tuyến của của (O; R) (1,5 điểm)
Tam giác OAC cân tại O, có OI là đường trung tuyến nên OI là đường trung trực
Mà M ∈OI → MA = MC 0.5 OA = OC
Xét hai tam giác AMO và CMO có OM chung → ∆OAM = ∆OCM ( .c .cc) 0.5 MA =  MC Vì  0 MAO = →  0 90
MCO = 90 → MC ⊥ CO , hay MC là tiếp tuyến của (O;R) 0.5
c) Chứng minh IK song song với AB (1,5 điểm)
Ta có CH ⊥ AB KH BH BH  → KH / /MA ⇒ = = (1) 0.25 MA ⊥ AB MA AB 2R Do  0
ACB = 90 → BC ⊥ AC → BC / /OM 0.25
Xét hai tam giác BCH và OMA có  BHC =  OAM CH BH BH
→ ∆BCH  ∆OMA → = = (2)   0.25 CBH =  MOA MA OA R
Từ (1) và (2) suy ra CH = 2KH → K là trung điểm của CH 0.25 IC IA ∆CAH có: = 
→ IK là đường trung bình của ∆CAH → IK / / AH → IK / / AB 0.5 KC = KH
d) Xác định vị trí của điểm C để chu vi tam giác ABC đạt giá trị lớn nhất? Tìm giá trị lớn nhất
đó. (1,5 điểm)
Chu vi tam giác ABC là (2P) = AB + BC + CA = 2R + (CB + ) CA 0.25 Mặt khác ta có 2 2 2 2 2 2 2 (CB + )
CA ≤ (CB + CA )(1 +1 ) = 2AB = 8R 0.25
→ CA+ CB ≤ 2 2R 0.25
Suy ra (2P) ≤ 2R + 2 2R = (2 + 2 2)R 0.25
Dấu “=” xảy ra ↔ CA = CB ↔ C là điểm chính giữa cung AB 0.25 Vậy: a
M x(2P) = 2(1+ 2)R ↔ C là điểm chính giữa cung AB 0.25
Cho a, b, c là các số thực không âm thỏa mãn a + b + c = 3. Tìm giá trị nhỏ nhất của biểu thức 3 3 3
Q = a + b + c (2,0 điểm) a b c ≥ Do , , 0 
→ 0 ≤ a,b,c ≤ 3 0.25
a + b + c = 3 Ta có 3 3 3 3
b + c = (b + c) − 3bc(b + c) = (3− a) + 3(a − 3)bc 0.25 a − 3 ≤ 0 Do  3 2 3 3  b + c 1
→ 3(a − 3)bc ≥ (a − 3)(3− a) = − (3− a) 0.25 2 2 bc ≤ ( ) = (3−  a) 4 4  2 4 Câu 3 1 5(2đ) Suy ra 3 3 3 3 2 3
b + c ≥ (3− a) − (3− a) = (27 − 27a + 9a − a ) 0.25 4 4 Khi đó 3 3 3 3 1 2 3 3 3 2
Q = a + b + c ≥ a + (27 − 27a + 9a − a ) = (a + 3a − 9a + 9) 0.25 4 4 5 3 3 2 3 2
= 4 + (a + 3a − 9a + 5) = 4 + (a −1) (a + 5) ≥ 3 0.25 4   4   a − 3 = 0  a −1 = 0 a ∈φ
Dấu bằng xẩy ra b = c ↔
↔ a = b = c =  1 0.25 
a = b = c = 1 a −1 = 0
a +b+c =  3
Vậy giá trị nhỏ nhất của Q là 3 khi a = b = c = 1 0.25 6
Document Outline

  • DE-TOAN-HSG9-2016-2017
  • HDC-TOAN-HSG9-2016-2017