Đề thi chọn HSG lý 10 Sở GD Hải Dương 2022-2023 có đáp án

UBND TỈNH HẢI DƯƠNG
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 10 THPT
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022-2023 Môn thi: Vật Lý
Thời gian làm bài 180 phút, không tính thời gian phát đề ĐỀ CHÍN H THỨC
Ngày thi: 10 tháng 04 năm 2023
Đề thi có 02 trang Câu 1: (2 điểm)
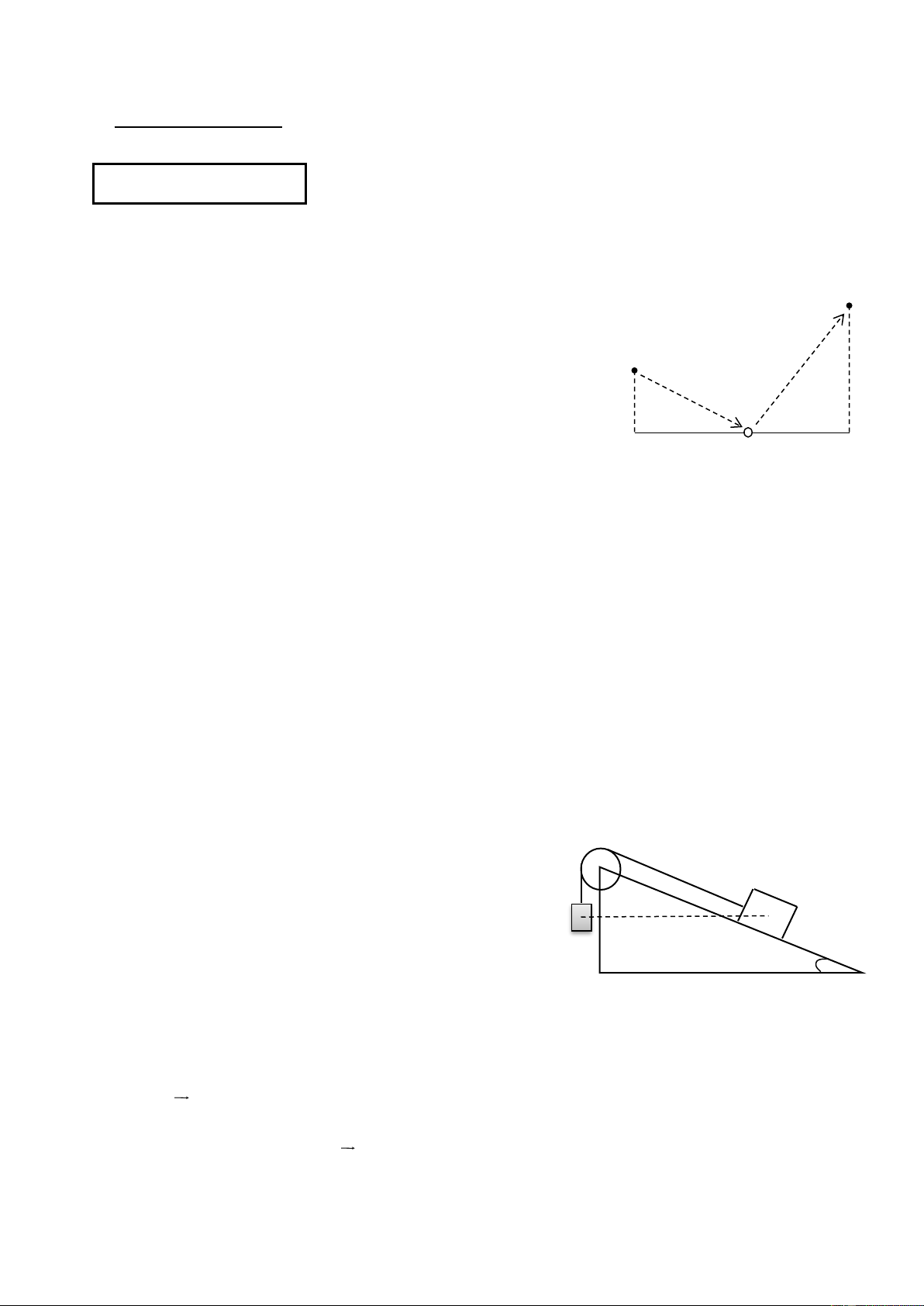
1. Trong một trò chơi Team Building với luật chơi như sau: B
Người chơi thứ nhất xuất phát từ điểm A chạy tới đường MN
nhặt bóng sau đó mang về đích tại B, khi người chơi thứ nhất
đến B thì các người chơi tiếp theo mới tiếp tục được xuất A
phát từ A và lặp lại quá trình như người thứ nhất cho tới khi
hết thời gian quy định. Điểm A cách đường đặt bóng một
khoảng AM = 4(m); điểm B cách đường đặt bóng một M
khoảng BN = 8(m); khoảng cách MN = 16(m). Từ A tới bất N
kì điểm nào trên đường MN đều có thể nhặt được bóng (hình
vẽ), coi các người chơi chạy với tốc độ không đổi.
a. Muốn quãng đường di chuyển là ngắn nhất thì người chơi phải chạy đi theo đường
như thế nào? Tính chiều dài quãng đường ấy?.
b. Giả sử người chơi chạy đều với tốc độ v = 4 m/s (bỏ qua thời gian nhặt và thả bóng,
số lượng bóng không giới hạn), tổng thời gian của một đội chơi là 3 phút. Tính số bóng tối đa
mà một đội chơi có thể mang về đích.
2. Một xe ôtô chuyển động thẳng đều trên đường với vận tốc v1 = 16m/s. Một người đứng
cách đường một đoạn a= 60m. Người này nhìn thấy xe ôtô ở trên vào thời điểm xe cách
người một khoảng b = 400m.
a. Hỏi người phải chạy theo hướng nào để tới được đường cùng lúc hoặc trước khi xe
ôtô tới đó, biết người chạy thẳng đều với vận tốc v2 = 4m/s.
b. Nếu người đó muốn gặp xe với tốc độ nhỏ nhất thì người đó phải chạy theo hướng
nào và tốc độ nhỏ nhất là bao nhiêu?. Câu 2: (2,5 điểm)
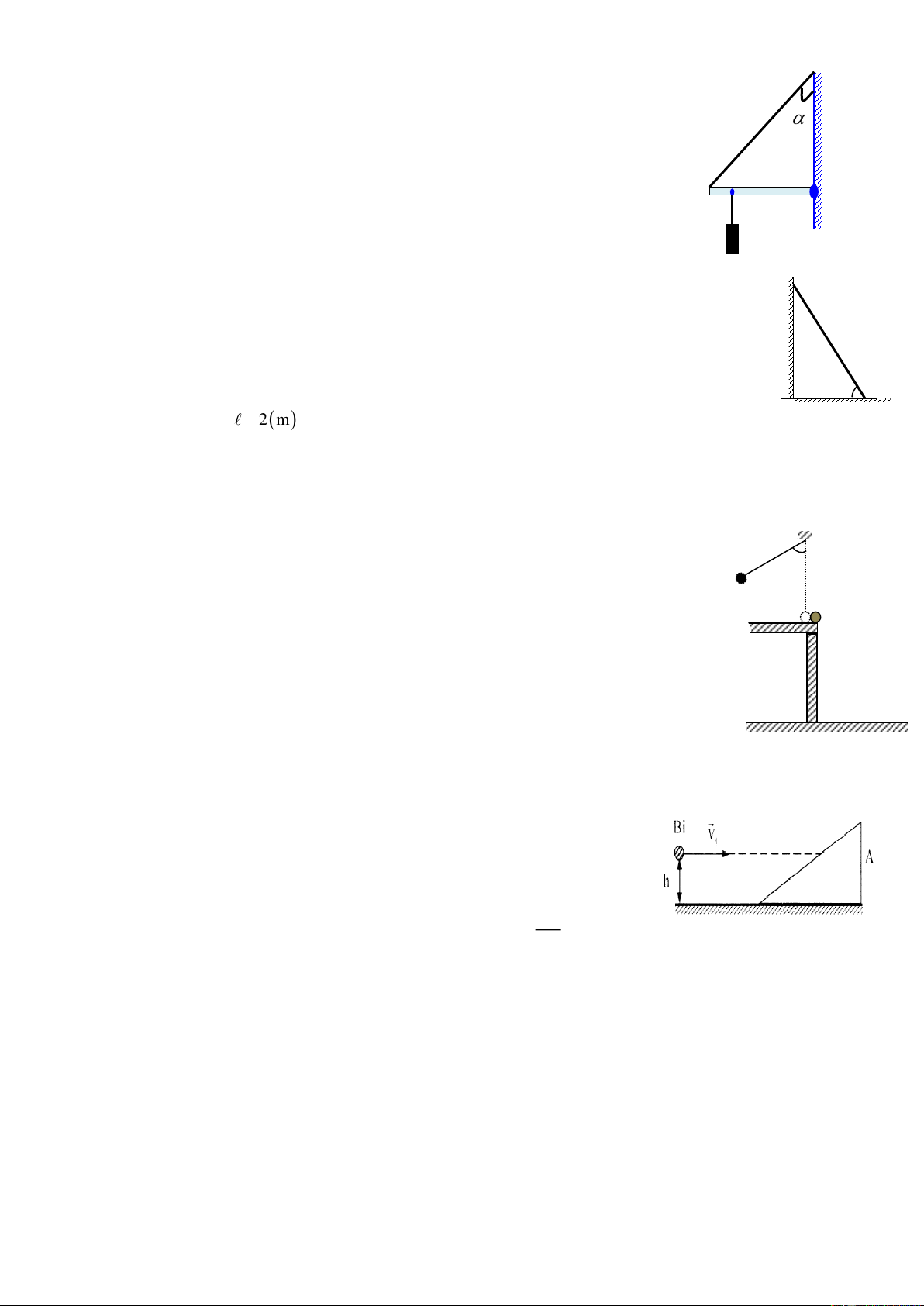
1. Hai vật A và B có khối lượng lần lượt là m1 = 3kg và m2 = 2kg nối với nhau bằng một sợi dây
không dãn vắt qua ròng rọc gắn ở đỉnh mặt phẳng
nghiêng nhẵn cố định, đủ dài với góc nghiêng α = 300
như hình vẽ. Ban đầu A được giữ ở vị trí ngang với B,
thả cho hai vật chuyển động. Lấy g = 10 m/s2 A . B
a. Hai vật chuyển động theo chiều nào?
b. Tính lực căng của dây và lực nén lên trục α
ròng rọc. Bỏ qua ma sát, khối lượng ròng rọc và dây.
c. Tại thời điểm vật nọ thấp hơn vật kia một
đoạn bằng 0,75 m thì dây nối hai vật bị đứt. Tính
hiệu độ cao giữa hai vật sau khi dây đứt 0,8s. Biết B có độ cao đủ lớn.
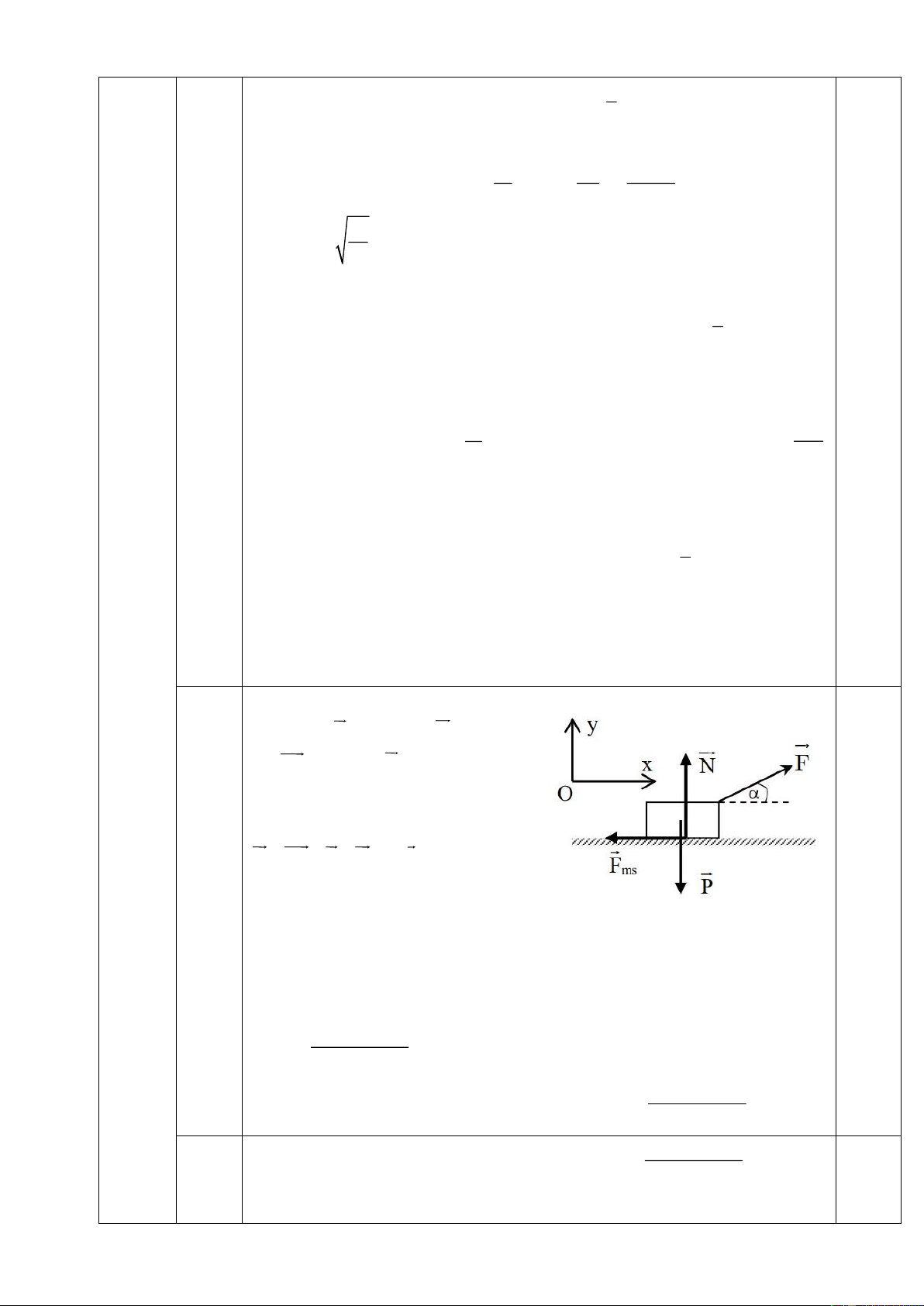
2. Một khúc gỗ khối lượng m = 0,5kg đặt trên mặt sàn nằm ngang. Người ta kéo khúc gỗ
một lực F hướng lên trên và hợp với phương nằm ngang một góc α = 600. Biết hệ số ma sát
trượt giữa gỗ và sàn nhà là µ = 0,2, lấy g =9,8m/s2.
a. Tính độ lớn của lực F để khúc gỗ chuyển động với gia tốc a =1m/s2
b. Để kéo khúc gỗ trượt đều với lực kéo nhỏ nhất thì góc α bằng bao nhiêu. Tính lực kéo nhỏ nhất khi đó? D Câu 3: (2 điểm)
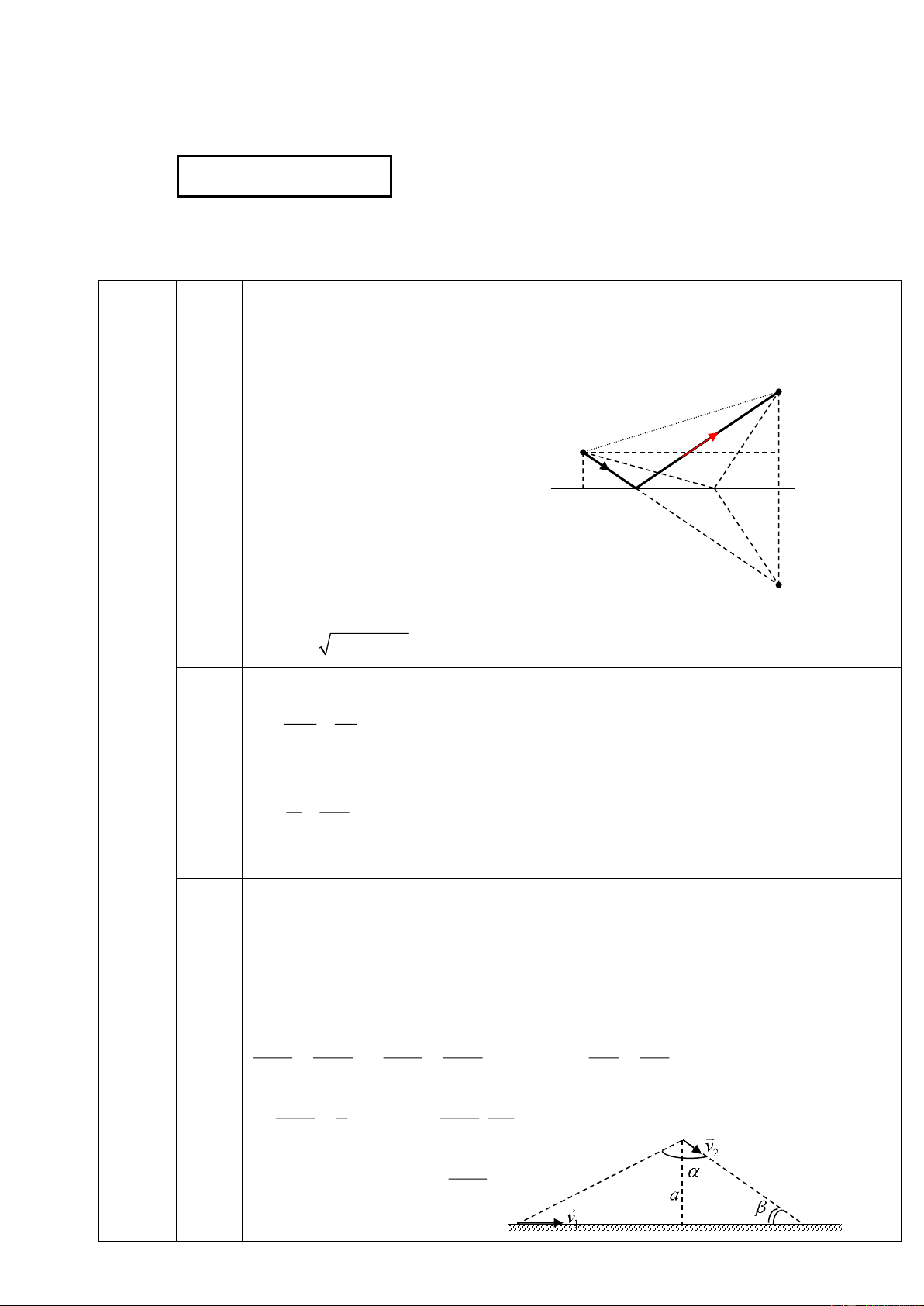
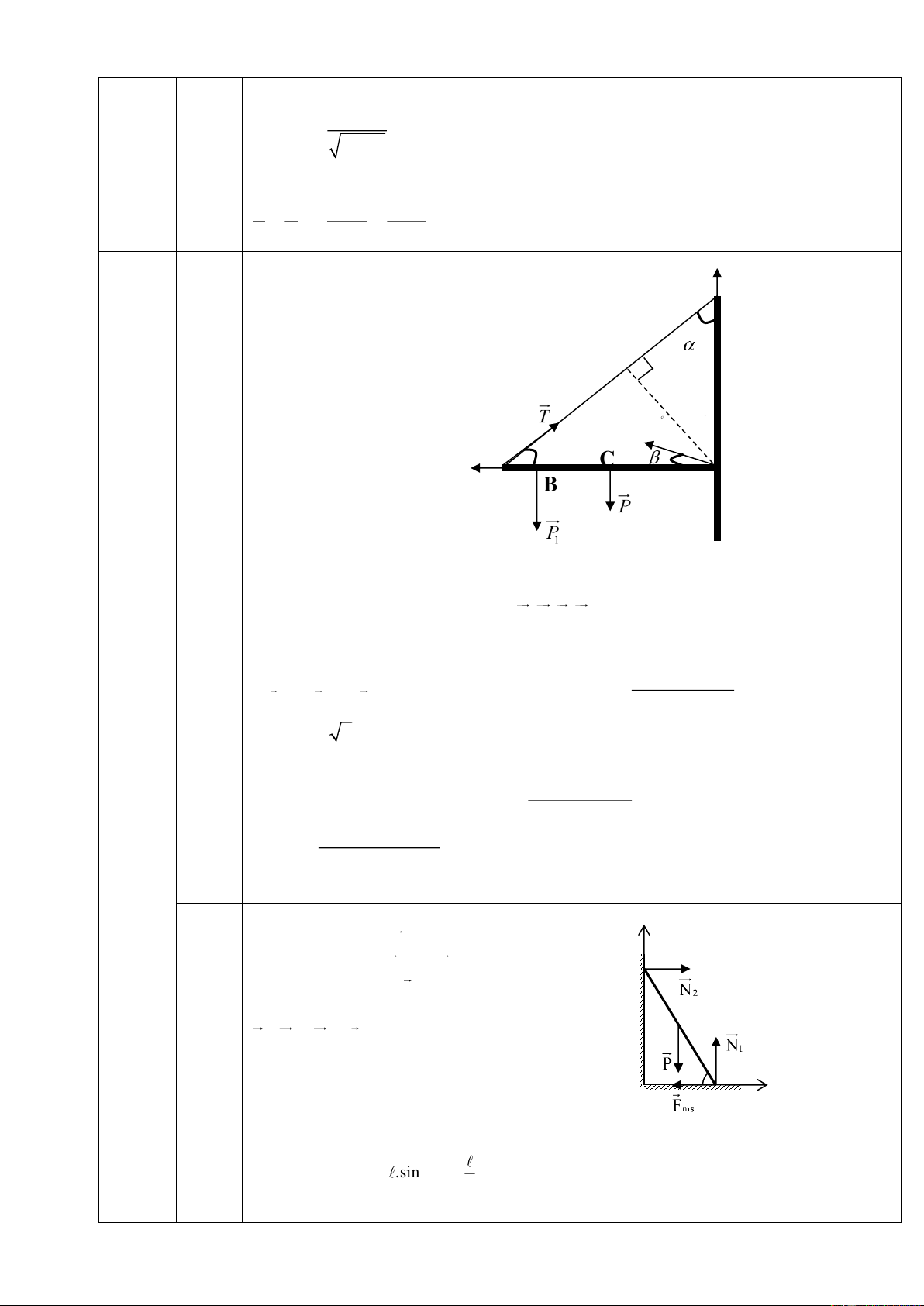
1. Thanh OA đồng chất, tiết diện đều dài l=1m, khối lượng
M=0,5kg, thanh có thể quay trong mặt phẳng thẳng đứng xung quanh
bản lề O gắn vào tường. Để thanh nằm ngang thì đầu A của thanh
được giữ bởi dây DA hợp với tường góc  = 45o như hình vẽ. A B Tại B treo vật O
có khối lượng m = 1kg, biết OB = 60cm, lấy g=10m/s2.
a. Tính lực căng dây AD. m
b. Dây chỉ chịu được lực căng tối đa Tmax= 11,314N. Tìm vị trí
treo vật m trên thanh để dây không đứt.
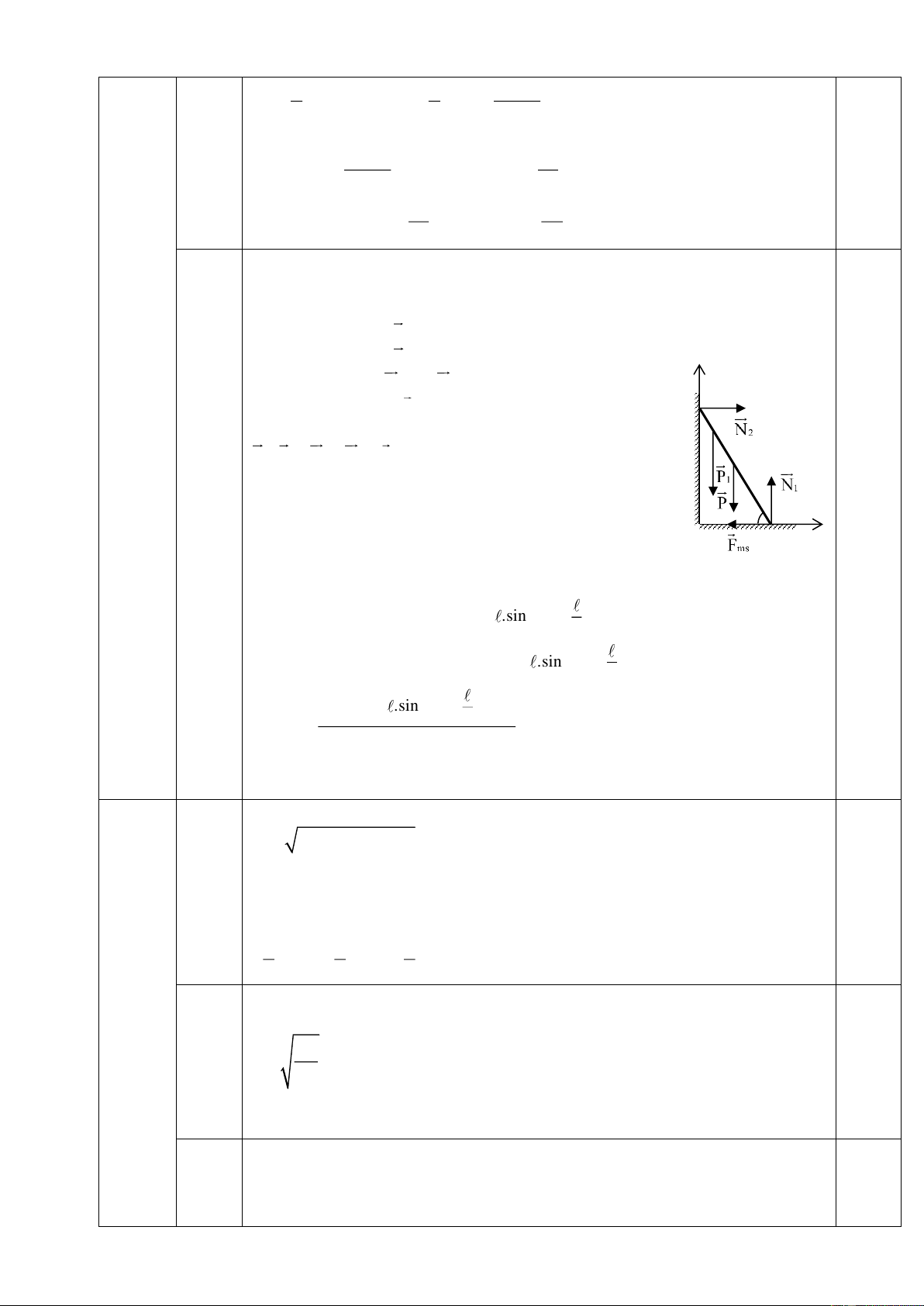
2. Thang có khối lượng m = 30kg được dựa vào tường trơn nhẵn với góc nghiêng
 như hình vẽ. Hệ số ma sát giữa thang và sàn là  = 0,6. Lấy g = 10 m/s2.
a. Tìm các giá trị của  để thang đứng yên không trượt trên sàn.
b. Một người có khối lượng m1 = 60kg leo lên thang khi  = 45o. Hỏi 
người này lên đến vị trí M nào trên thang (so với chân thang) thì thang sẽ bị trượt. Chiều dài thang = 2(m) . Câu 4: (2,5 điểm)
1. Một hòn bi A khối lượng m1 = 3m được treo vào một sợi dây không giãn, khối lượng
không đáng kể, dài 40 cm. Kéo hòn bi A lệch khỏi phương thẳng đứng một góc αo = 60o rồi
thả không vận tốc đầu. Khi đến vị trí cân bằng, hòn bi A va chạm đàn hồi, xuyên tâm với hòn
bi B có khối lượng m2 = m đang đứng yên ở mép một cái bàn cao 80 cm so 
với sàn nhà (hình vẽ). Lấy g = 10 m/s2. Bỏ qua lực cản không khí. A 1.1. Tính:
a. Tốc độ của hai hòn bi ngay sau khi chúng va chạm với nhau. B
b. Thời gian từ khi bi B rời bàn đến khi nó va chạm với sàn nhà lần
đầu, điểm va chạm cách chân bàn O bao nhiêu?
1.2. Biết va chạm giữa hòn bi B và sàn nhà không tuyệt đối đàn hồi, cơ
năng của bi B sau va chạm bằng 80% cơ năng của nó trước va chạm. Giả O
sử va chạm có hướng của véctơ vận tốc tuân theo quy tắc phản xạ gương.
a. Tính độ cao cực đại của hòn bi B so với mặt sàn sau lần va chạm thứ nhất với sàn nhà.
b. Hòn bi B va chạm với sàn nhà lần thứ hai cách chân bàn O một khoảng bao nhiêu?
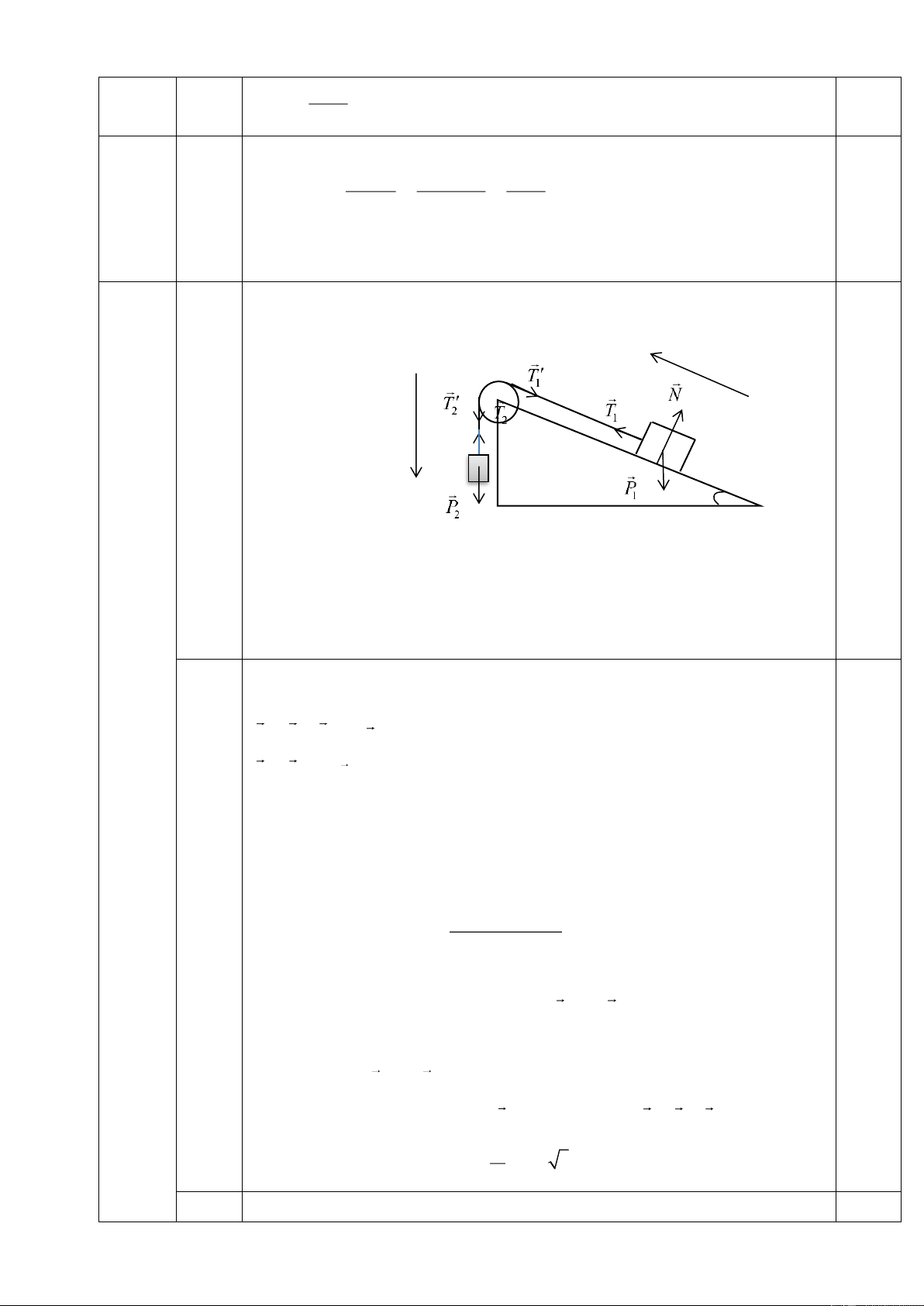
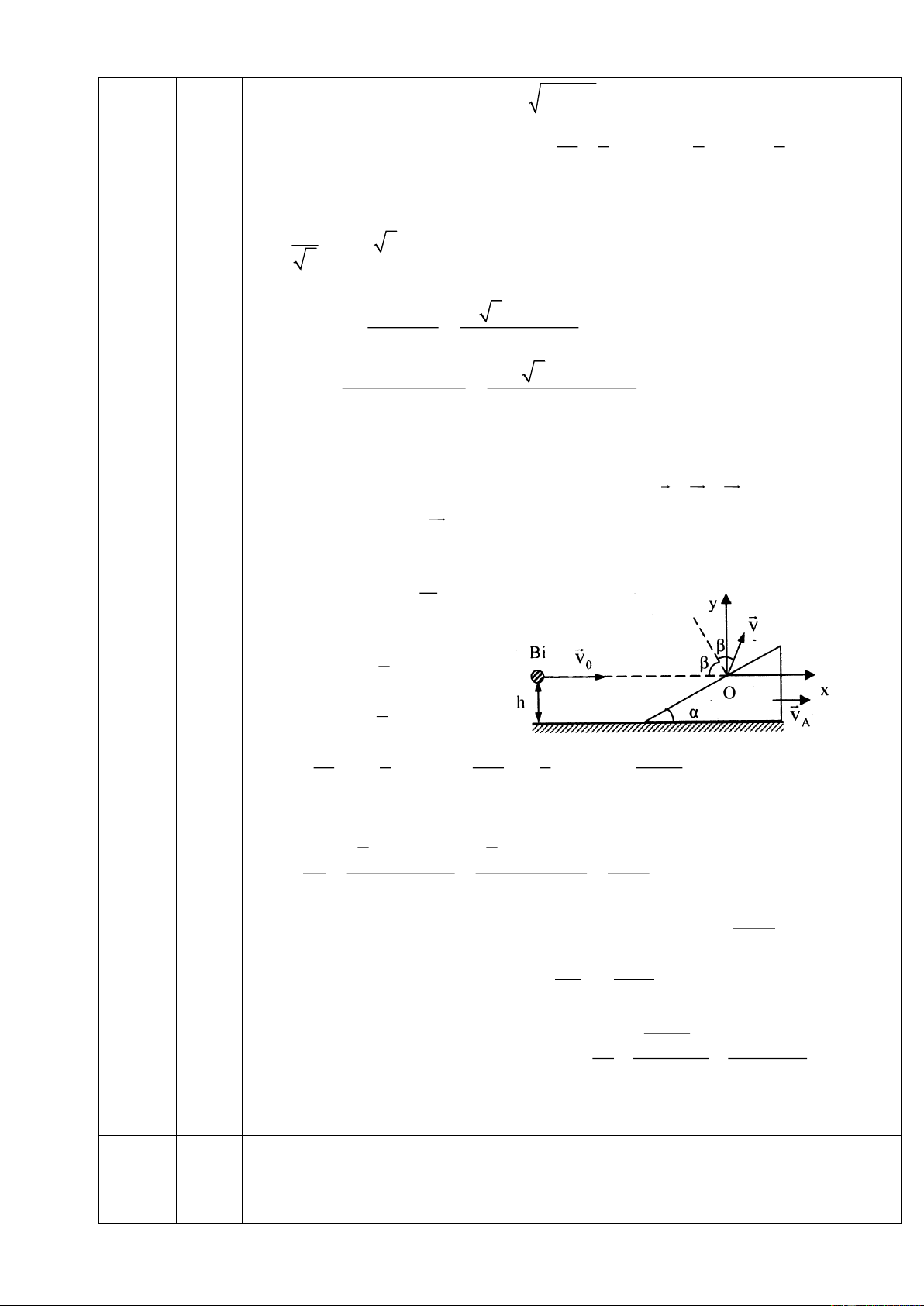
2. Một nêm A có khối lượng M đặt trên mặt sàn nằm ngang. Cho
hệ số ma sát giữa nêm và mặt sàn là µ, góc nghiêng của nêm
 = 30 (hình vẽ). Một viên bi khối lượng m đang bay theo
phương ngang với tốc độ v (ở độ cao h so với sàn) đến chạm vào 0
mặt nghiêng của nêm. Va chạm của bi vào nêm tuân theo định luật 7v
phản xạ gương và vận tốc bi sau va chạm có độ lớn 0 . Hỏi sau 9
khi va chạm viên bi lên tới độ cao tối đa là bao nhiêu (so với mặt sàn) và nêm dịch trên sàn
theo phương ngang được một đoạn bao nhiêu? Câu 5: (1,0 điểm)
1. Cho các dụng cụ sau: Một vật nặng, một đồng hồ bấm giây. Hãy đưa ra phương án thí
nghiệm xác định chiều cao từ tầng 2 của trường học em?
2. Cho các dụng cụ sau: Cốc hình trụ, thước kẹp, đồng hồ bấm giây. Hãy đưa ra phương án
thí nghiệm xác định vận tốc chảy của nước ra khỏi vòi nước?
--------------Hết-------------
(Thí sinh không sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh:……………………….……Số báo danh:………………Phòng thi:……….
Cán bộ coi thi số 1:………………………………Cán bộ coi thi số 2:……………………….
SỞ GIÁO DỤC & ĐÀO TẠO HƯỚNG DẪN CHẤM HẢI DƯƠNG
BÀI THI CHỌN HỌC SINH GIỎI CẤP TỈNH NĂM HỌC 2022-2023 DỰ THẢO
MÔN THI: VẬT LÝ- LỚP 10
Ngày thi: 10 tháng 04 năm 2023
Hướng dẫn chấm gồm 06 trang Câu Ý Đáp án Biểu điểm
+ Giả sử người chơi đi theo đường AIB. Gọi B/ là điểm đối xứng của B qua MN. B
+ Ta có: AIB = AI + IB = AI + IB/ = AIB/ A P 1.a
+ Để AIB ngắn nhất thì 3 điểm A, M J I N I, B/ thẳng hàng. 0,25
+ Dựa vào hình vẽ ta có: AP = MN = 16 m B/ B/P = B/N + NP = 12 m ' 2 2 0,25 AB = AP +B'P = 20 m
Thời gian ngắn nhất khi đi từ A đến lấy bóng mang đến B là: AB' 20 t = = = 5 s 1 v 4 0,25 1 1.b
Trong thời gian chơi t’= 3 phút = 180 s số lần chơi chọn vẹn : (2 t' 180 điểm) N = = = 36 t 5 1
Tổng số bóng tối đa lấy được là : 36 0,25
Ban đầu người ở B thấy xe ở A. C là điểm người đón xe ở trên đường.
Gọi  = góc(ABC);  =góc(ACB) (hình vẽ).
Thời gian xe từ A đến C là t
1,người từ B đến C là t2.
Để người đến C trước xe: t  t . 1 2
Áp dụng định lí hàm sin cho tam giác ABC, ta có: AC AB v t b BH a 2.a 1 1 =  = ; với sin  = = sin  sin  sin  sin  BC v t 2 2 v t b v t a 1 1 1 1  = v t  t = . (1) 2 2 2 0,25 sin a sin bv B 2 0, 6t b Thay số ta được: 1  t = . 2 sin Đề
người đến C trước xe: t  t 1 2A H C 0, 6t 1  t 
 sin  0,6  143,13o    36,87o 1 sin 0,25
Để người gặp được xe với vận tốc nhỏ nhất thì: t1 = t2 v a 16.60 2, 4 Từ (1) 1 v = = =  sin = 1  = 90o   2 2.b b sin 400sin sin  v = v = 2, 4m / s 2 2 min 0,25 0,25
Hai vật chuyển động theo chiều nào + + A 1.a B α
Chỉ ra các lực tác dụng lên các vật trong hệ như hình vẽ
Với: P2 = m2g = 20 (N); P1sinα = m1gsinα = 15 (N). 0,25
Ta thấy P2> P1sinα. ⟹ vật B sẽ đi xuống, còn vật A đi lên 0,25
Tính lực căng dây, lực nén lên trục ròng rọc
Theo định luật II Niu tơn ta có 2
P + N + T = m a (1) 1 1 1 1 (2,5 điể + = m) P T m a (2) 2 2 2 2
Chiếu (1) và (2) theo thứ tự lên hướng chuyển động của A và B ta có: -P1sinα + T1 = m1a1 (3) P2 – T2 = = m2a2 (4)
Ta có a1 = a2 = a; T1 = T2 = T 1.b − 
từ(3)và (4)ta suy ra a = (m m .sin ) 2 1 g = 1 (m/s2); m + m 1 2 T = m2 (g – a) = 18 (N) 0,25
Dây sẽ nén lên ròng rọc hai lực căng T  và T  1 2
với T  = T  =T 1 2 1 = T2 = 18 (N).
Góc hợp bởi T  và T  là: β = 900 – α = 600. 1 2
Do đó lực nén lên ròng rọc là
F được xác định: F = T + T  1 2 
và có độ lớn bằng: F = 2Tcos =18 3  31,2 (N) 0,25 2 1.c
Tại thời điểm vật nọ ở thấp hơn vật kia một đoạn bằng 0,75 m
Quãng đường mỗi vật đã đi là: s 1 1 = s2 = s = at2 2
Khoảng cách giữa hai vật theo phương thẳng đứng là: s 2d 2.0, 75 d = s 2 + s1sinα = s(1+ sinα) = 3 ⟹ s = = = 0,5 (m) 2 3 3 Do đó: t= 2s =1s a
Thời điểm dây đứt hai vật có cùng vận tốc v0= a.t= 1m/s 0,25
Vật B coi như được ném thẳng đứng xuống : S 1 B = v0.t1 + g. 2 t = 4m 2 1 Vật A:
Giai đoạn 1: Đi lên chậm dần với gia tốc a1= -g.sin =-5m/s2 2 Thời gian A dừng lại t v vo 2= -
0 = 0,2s và đi lên được quãng đường - a 2.a 1 1 =0,1m
Giai đoạn 2: Đi xuống nhanh dần với gia tốc a2= g.sin =5m/s2
Quãng đường A đi xuống được trong 0,6s còn lại là 1 a.  2 t = 0,9m 2
Vậy sau 0,8s kể từ khi dây đứt A ở dưới vị trí ban đầu đoạn : SA= 0,9 - 0,1= 0,8m
Hiệu độ cao giữa hai vật lúc này: h= SB +0,75 - SA .sin = 4,35 m 0,25
Các lực tác dụng lên vật gồm:
trọng lực P , phản lực N , lực ma
sát F , lực kéo F biểu diễn như ms hình vẽ
Áp dụng định luật II Niu tơn:
F + F + P + N = . m a (1) ms
Chọn hệ trục 0xy như hình vẽ 2.a
Chiếu (1) lên trục 0y: N – P + Fsinα = 0 → N = P + Fsinα
→ Fms = µN = µ(P – Fsinα)
Chiếu (1) lên 0x: - Fms + Fcosα = ma
↔ - µ(P – Fsinα) + Fcosα = ma ↔ Fcosα + µFsinα = µP + ma  + → P ma F = 0,25 cos +sin  P + ma
khi vật chuyển động với gia tốc a = 1m/s2 thì F = = 2,198 N 0,25 cos +sin P
khi vật chuyển động thẳng đều thì a = 0 nên F = 2.b cos +sin
Theo bất đẳng thức Bunhia ta có: (a.c + b.d) ≤ ( a2 + b2)(c2 + d2)
↔ (1.cosα + µsinα) ≤ ( 1 + µ2)( cos2α + sin2α) = 1 + µ2  → P F =  0,96 N min 2 1+  0,25
Dấu = xảy ra khi và chỉ khi: a b 1  0 =  =
→ tan =  →   11,31 c d cos sin 0,25 y D H x C O A B 1.a
Lực căng dây AD, giá và độ lớn phản lực của thanh OA lên bản lề
Các lực tác dụng vào thanh OA: ,
P P ,T ,Q như hình vẽ 1
Đối với trục quay qua bản lề O : .
P OC + P.OB
M = M + M  T.OH= P.OC+P1.OB 1  T = (1) T P P 3 1 OH 0,25 (2,0
 T = 8,5 2N 12,02N 0,25 điểm) Vị trí treo m .
P OC + P.OB
Từ (1) để dây không đứt 1  T =  T 0,25 ax m OH 1.b T .OH − . P OC max  OB 
= 0,55m = 55cm P 1 0,25
Vậy treo vật trong đoạn OB =55cm thì dây không đứt
Các lực tác dụng lên thang gồm: ▪ Trọng lực y P của thang ▪ Phản lực 1
N và N2 của sàn và tường B
▪ Lực ma sát Fms giữa thang và sàn
+ Điều kiện cân bằng về lực: P + + + = 1 N N2 Fms 0 (1) 2.a
+ Chiếu (1) lên Ox, Oy ta có:  Ox: N − F = 0  N = F (2) 2 ms 2 ms O A x
Oy: N − P = 0  N = P = mg = 300 N (3) 1 1 ( )
+ Điều kiện cân bằng về momen với trục quay qua A: M(
= M  N . .sin  = P. .cos N P 2 2 ) ( ) 2 0,25 P (2) P P N = cot  ⎯⎯→ F = cot  = 2 ms 2 2 2 tan 
+ Điều kiện để thang không trượt: Fms≤ 𝜇. 𝑁 P (3) 1 F  N    N  ⎯⎯→tan   ms 1 1 2 tan  2  1   1  0,25  o   arctan    arctan = 39,8      2  1,2 
Giả sử khi người lên đến M có độ cao h so với đất thì thang bắt đầu trượt
+ Các lực tác dụng lên thang gồm: ▪ Trọng lực P của thang ▪ Trọng lực 1 P của người ▪ y Phản lực 1
N và N2 của sàn và tường
▪ Lực ma sát Fms giữa thang và sàn B
+ Điều kiện cân bằng về lực: M P + + + + = 1 P 1 N N2 Fms 0
+ Chiếu (1) lên Ox, Oy ta có: Ox: N − F = 0  N = F 2 ms 2 ms  2.b
Oy: N − P − P = 0  N = P + P 1 1 1 1 O A x + Vì thang trượt nên: F = N  =  P + P ms 1 ( 1 )
+ Điều kiện cân bằng về momen với trục quay qua A: M 0,25 ( = M + M
 N . .sin  = P. .cos + P .MA.cos N P P 2 1 2 ) ( ) ( 1) 2
+ Vì N2 = Fms nên suy ra: (P + P . .sin  = P. .cos  + P .MA.cos 1 ) 1 2 (
P + P . .sin  − P. .cos  1 )  2 MA = =1,3(m) P .cos  1
+ Vậy người này lên đến điểm M trên thang cách chân thang một đoạn 0,25 1,3 m
Vận tốc của hòn bi A trước khi va chạm v = 2gl(1 − cos ) = 2 m/s O 0,25
Áp dụng định luật bảo toàn động lượng và định luật bảo toàn cơ năng 1.1.a ta có m v = m v + m v 1 1 1 2 2  0,25 1 1 1
suy ra: v1 = 1 m/s; v2 = 3 m/s 2 2 2 m v = m v + m v  1 1 1 2 2 2 2 2 4
Sau va chạm với hòn bi A, bi B chuyển động ném ngang đến va chạm (2,0
với sàn. Thời gian từ khi bi rời bàn đến khi va chạm lần đầu với sàn điểm) 2h 1.1.b t = =0,4 s 0,25 g
Khoảng cách từ điểm va chạm đến O 0,25 x1 = v2t = 1,2 m
Vận tốc của vật trước khi va chạm với sàn 1.2.a 2 2 v = v + v = 5(m / s) x y v = v = 3(m / s)   x 0  →  vy 4 4 3 v = g.t =10.0,4 = 4(m / s)  y tan  = = → sin  = ,cos = v 3 5 5  x
Sau khi va chạm với sàn vì WS = 0,8WT do đó 0,25 2 v = v = 2 5(m / s)  s T 5
và hợp với phương ngang một góc hướng 0,25 lên 2 2 2 2 v sin  (2 5) .(4 / 5) s H = = = 0,64(m) Ta có: max 2g 2.10 2 2 2.v .sin .
 cos 2.(2 5) .4 / 5.3 / 5 Ta có: s L = = = 1,92(m) 2g 2.10 0,25 1.2.b
Khoảng cách từ điểm va chạm lần 2 tới chân bàn O là: 1,2 + 1,92 = 3,12 (m) 0,25
Gọi O là điểm va chạm, hệ trục Oxy như hinh vẽ; v = v + v là vận tốc x y
bi ngay sau va chạm; v là vận tốc nêm ngay sau va chạm A
Theo phương ngang, động lượng của hệ "bi + nêm" được bảo toàn nên: m
mv + Mv = mv  v = v − v x A 0 A ( 0 x ) M với:  7 v = v cos 2 = v cos 2  x 0  9  7  v = v sin 2 = v sin 2 y 0  9 m  7  mv  7  11mv 0 0  v = v − cos 2 = 1 − cos 60 = A  0    M  9  M  9  18M 2
Độ lên cao tối đa của bi kể từ chỗ chạm với mặt nêm là: 2 2  7   7    2 v sin 2 v sin 60  0   0  2 vy  9   9  49v0 h = = = = max 2g 2g 2g 216g 2 Độ 49v
lên cao tối đa của bi so với mặt bàn là: 0 H = h + h = + h 0,25 max max 216g F Mg
Gia tốc trượt ngang của nêm là: ms a = − = − = −g M M 2 11mv  0 2   2 2 Quãng đường trượ v  18M  121m v t ngang của nêm là: A 0 s = = = 2 2a 2 g 648M  g 0,25
(Lưu ý: Nếu học sinh tính được ra hmax thì vẫn cho 0,25 điểm)
Phương án thí nghiệm : Thả vật nặng rơi từ tầng 2 xuống mặt đất đồng a
thời bấm đồng hồ để đo thời gian vật rơi xuống mặt đất. Lấy g= 9,8 0,25 𝑚/𝑠2 1
Sử dụng công thức : ℎ = 𝑔𝑡2 2
Ta tính được chiều cao từ tầng 2 trường học 0,25 5
+ Dùng đồng hồ bấm giây đo thời gian t nước chảy đầy cốc, sau đó
dùng thước kẹp đo chiều cao cốc h và đường kính trong của đáy cốc d1 
+.Tính thể tích cốc và cũng chính là thể tích nước: d . 2 V 1 = h 4 b
+.Đo đường kính trong tiết diện vòi nước máy d2 và tính tiết diện vòi: . 2 d 0,25 2 S = 4 2
+ Xác định vận tốc nước chảy V d h . v 1 = = S t . d 2 t . 0,25 2
Học sinh làm theo cách khác cho kết quả đúng vẫn cho điểm tối đa.