Đề thi chọn HSG Toán 9 cấp tỉnh năm 2020 – 2021 sở GD&ĐT Thanh Hóa

SỞ GIÁO DỤC & ĐÀO TẠO
KÌ THI CHỌN HSG MÔN VĂN HÓA CẤP TỈNH THANH HÓA NĂM HỌC 2020-2021 ĐỀCHÍNH THỨC
Môn thi: TOÁN – Lớp 9 THCS
Ngày thi: 16 tháng 12 năm 2020
Thời gian: 150 phút (khô ng kể thời gian giao đề)
( Đề gồm có 05 câu, gồm 01 trang) Câu I:(4,0 điểm)  x  3 x   3  x x  2 9  x 
1.Rút gọn biểu thức P  1  :     
với x  0; x  4; x  9 x 9   x 2 3 x x x 6          
2. Cho a, b,c là các số thực đôi một khác nhau thỏa mãn 3 3 3 a 1  3 ; a b 1  3 ; b c 1  3c . Tính giá trị biểu thức : 2 2 2 Q  a  b  c Câu II: ( 4,0 điểm) 1. Giải phương trình :  3 2 x  x  x   2x   4 15 2 4 5 2 x  4. 2 2
x  xy  y  4y 1  0 
2. Giải hệ phương trình:  2 x   1x y2  y Câu III: ( 4,0 điểm)
1. Tìm tất cả các cặp số nguyên dương (x,y) thỏa mãn phương trình: x 2 2 2 x  9y 12 y 19
2. Cho x,y là hai số nguyên dương thỏa mãn 2 2
x  y  58 chia hết cho xy. 2 2 x  y  58 Chứng minh: chia hết cho 12. xy Câu IV:( 6,0 điểm).
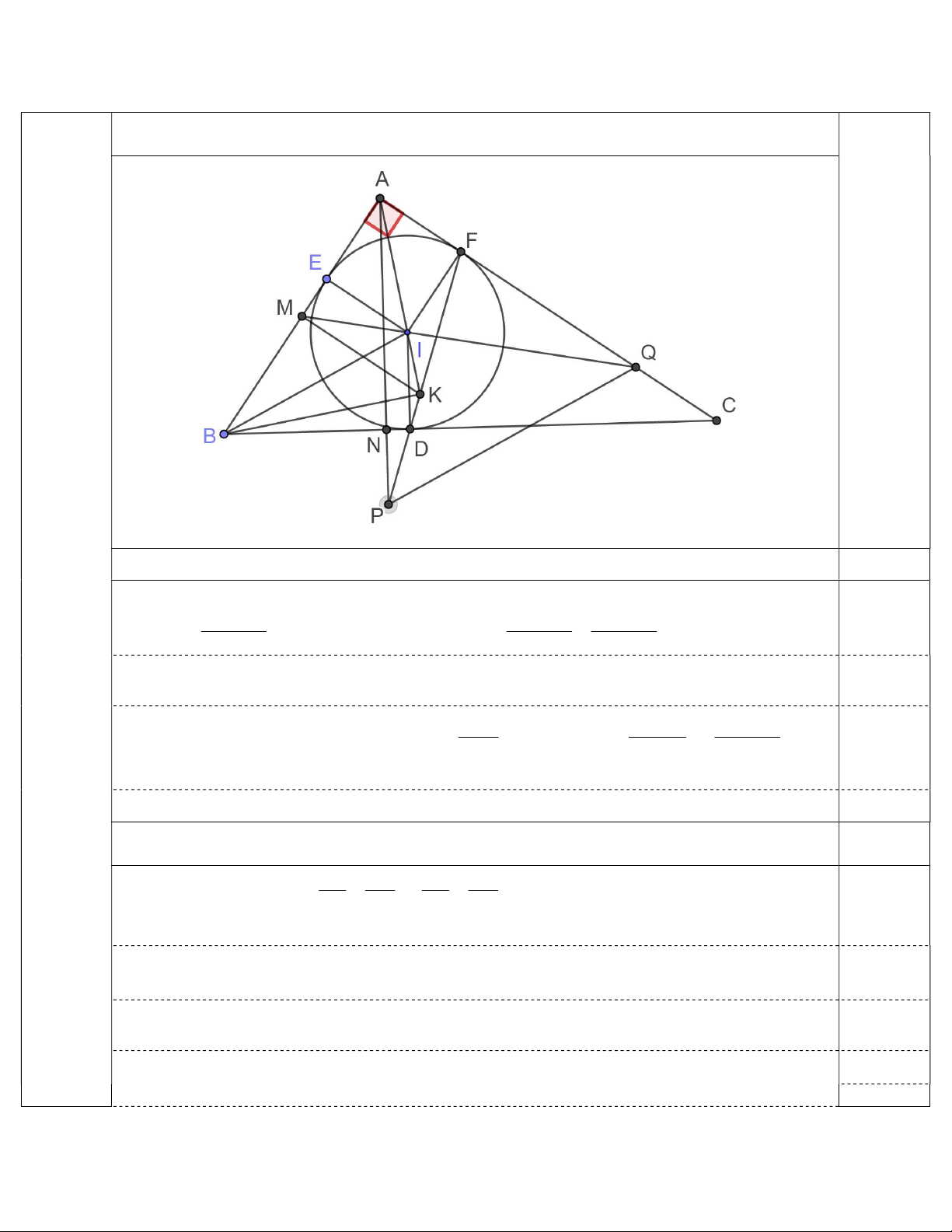
Cho đường tròn (I. r) có hai bán kính IE, IF vuông góc với nhau . Kẻ hai tiếp tuyến với
đường tròn(I) tại E và F, cắt nhau tại A. Trên tia đối của tia EA lấy điểm B sao cho EB > r, qua
B kẻ tiếp tuyến thứ hai với đường tròn (I). D là tiếp điểm, BD cắt tia AF tại C. Gọi K là giao điểm của AI với FD.
1) Chứng minh hai tam giác IAB và FAK đồng dạng.
2) Qua A kẻ đường thẳng vuông góc với BC, cắt FD tại P. Gọi M là trung điểm của
AB, MI cắt AC tại Q. Chứng minh tam giác APQ là tam giác cân.
3)Xác định vị trí của điểm B để chu vi tam giác AMQ đạt giá trị nhỏ nhất. Tính giá
trị nhỏ nhất đó theo r. Câu V: ( 2,0 điểm).
Cho các số thực dương x, y, z thỏa mãn 2 2
x  y  4xyz  2xy  yz  zx . Tính giá trị lớn
nhất của biểu thức P  x1 y1 z. Hết
Thí sinh không được sử dụng tài liệu, giám thị không giải thích thêm.
Họ và tên thí sinh:…………………………………………………………….
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM (Gồm có 07 trang) Câu NỘI DUNG Điểm I  x  3 x   3  x x  2 9  x  4,0
1.Rút gọn biểu thức P  1  :         với  2,0 điểm x 9 x  2 3  x x  x  6     x  0, x  4, x  9
Với điều kiện x  0, x  4, x  9 , ta có:    x  3 x  3  x x  2 9  x P 1  :        0,25
x  3   x  2 3  x   
 x 3 x 2  x  x     
    x   x   x  2 3 3 3 2  9  x  1    0,5     x   x   : 3 3  
  x  2 x  3  x  2 x  3  x  23 x         x 9  x x  4 x  4 9  x 1          0,5 x  : 3
   x 2 x 3  x 23 x  x 23 x             
 3 x  x  9  x  x  4 x  4  9  x x  4 x  4   :      3  x       x 2 x 3
 x 23 x 3 x x 2 3  3  .  0,75 3  x  x  2 x  2 2 3 Vậy P  (x  0, x  4; x  9) x  2
2. Cho a, b,c là các số thực đôi một khác nhau thỏa mãn 3 3 3 a 1  3 ; a b 1  3 ;
b c 1  3c . Tính giá trị biểu thức : 2 2 2 Q  a  b  c 2,0 Từ giả thiết : 3 3 3 a 1  3a;b 1  3 ; b c 1  3c ta có, 0,5 3 3  a  b  3a  b 2 2 a  ab  b  3 (1)   3 3 b   c  3b  c 2 2  b   bc  c  3 (2)
( vì a, b,c đôi một khác nhau)   3 3 c  a  3  c  a 2 2 c  ca  a  3 (3)  Từ (1) và (2) suy ra: 2 2
a  c  ab  bc  0  a ca b  c  0  a b  c  0 0,5
(vì a, b, c đôi một khác nhau)
Cộng (1); (2) ;(3) vế với vế ta có 0,5 2 2 2
2a  2b  2c  ab  bc  ca  9
 a b  c   ab  bc  ca   a b  c  a  b  c2 2 2 2 2 2 2 4 2 2 2 18 3 18.   2 2 2
3. a  b  c   0  18 0,5 Vậy Q = 6. II 1. Giải phương trình :  3 2 x  x  x   2x   4 15 2 4 5 2 x  4. 2,0 4,0 điểm Điều kiện x  R. 15x  2 x  x  2  4 5  2 x  2 4
Phương trình tương đương: x  4 2  1  7 7 0,5 2 2 4 Vì x  x  2  x 
   0; x  2  0; x  4  0    2  4 4 với mọi x  R. Suy ra x >0
Chia cả hai vế của phương trình cho 2 x ta được: 2  2   1   2  15 x  1  4 x x  x   4        x   2   x  0,5 2
Đặt t  x  , vì x > 0 suy ra t  2 2 x Phương trình : t   2 15 1  4 5t t  4 2  t t   t  t    t  2 4 5 4 20 5 15 0 4
t  4  5  5t 3  0 4 5t  2t 9  t t   
 5t 3  0  t 3 4 5  3   5  0 2 2 t  4  5  t  4  5  0,5 4 5t t  3  t 3  0 hoặc  5  0 2 t  4  5
Th1: Với t  3  0  t  3 ( thỏa mãn đk t  2 2 ). Khi đó: 2 x  1 2 0,25
x   3  x  3x  2  0   x   1  x  2  0  thỏa mãn x >0. x  x  2 4 5t t  3   Th 2: 5 0 (1) 2 t  4  5 4 5t t  3 Vì t  2 2 
 0  VT(1)> 5 > 0. Do đó pt (1) vô nghiệm. 0,25 2 t  4  5
Vậy phương trình đã cho có hai nghiệm : x=1; x=2
Lưu ý : Nếu không xét dấu của x trước khi chia x cho tối đa 1,0 điểm. 2 2
x  xy  y  4y 1  0 
2. Giải hệ phương trình:  2 x  2,0  1x y2  y 2 2 2
x  xy  y  4y 1  0 x 1 y   x  y  4y Ta có :    0,25 2 x   1x y2  y  2x   1x y2  y
Với y = 0, phương trình thứ nhất vô nghiệm nên hpt vô nghiệm.
Với y  0, chia từng vế của mỗi phương trình cho y ta được. 2  x 1   x  y  2  2  y 0,5 Hệ phương trình   2  x 1   x  y  2  1  y   2  x 1   m Đặt  y
hệ phương trình trở thành:  x  y  2  n 0,5 m  n  2 n  2  m n  2  m   m 1         . m n  1 m  2  m  1   m   2 1  0 n  1 2 2  x 1  y  x 1 2 2   1 y  x 1 y  x 1  Suy ra :  y      x 1 2 0,5  x  x  2  0   x   1x  2  0 x  y  2  1  x  2 x  1 x  2
Vậy nghiệm của hệ phương trình là:  và  0,25  y  2  y  5 III
1. Tìm tất cả các cặp số nguyên dương (x,y) thỏa mãn phương trình: 4,0 x 2 2 2 x  9y 12 y 19 2,0 điểm Ta có : x x x  y  y   x   y  2 2 2 2 2 9 12 19 2 3 2 15 0,25 x  2k 1  +) Nếu x lẻ thì ( k N). 2 2 1  2 2  x  x  x    k x k k 2 2 2 2 . 4 .2 3 1 .2x  2x 2 x  0;1(mod 3) ( mod 3). Mà k 2  2.4 .x  0;2(mod 3) 0,25 .  y  2 3 2  1(mod 3) Mặt khác :
Vậy x không thể là số lẻ * x  2k(k  N ) +)Nếu x chẵn thì 0,5 Ta có phương trình: k    2 2 2 2 .4 3
2  15  2k.2 3  2.2k y k y .2k  3y  2 15 (*) Vì *
k, y  N nên 2k.2  3  2  2k k y .2k  3y  2. 0,5
và 2k.2k  3y  2  0 nên 2k.2k  3y  2  0 2k.2k  3y  2 15 2k.2k  3y  2  5 Do đó (*)   hoặc   0,25 2k.2k  3y  2 1 2k.2k  3y  2  3 2k.2k  3y  2 15 2k.2k  8 Trường hợp 1:     ( vô nghiệm) 0,25 2k.2k  3y  2 1  y  3 2k.2k  3y  2  5 2k.2k  4 k 1 x  2 Trường hợp 2:         0,25 2k.2k  3y  2  3 y 1 y 1 y  1
Vậy nghiệm nguyên dương của phương trình là ( x, y) = (2; 1) 0,25
2. Cho x,y là hai số nguyên dương thỏa mãn 2 2
x  y  58 chia hết cho xy. Chứng minh: 2 2 x  y  58 2,0 chia hết cho 12. xy 2 2 x  y  58 k3 Đặt k= , k * N 2 2
 kxy  x  y  58. Ta chứng minh k 1  2   0,25 xy k4
+ Nếu trong hai số x,y có một số chí hết cho 3.
Do vai trò x, y bình đẳng , giả sử x3  xy3 Ta có: 2 2 2 2 2 2
x  y  58xy  x  y  583  y 13  y  2(mod3) Vô lí vì 2 y là số chính phương 0,5
Vì vậy cả x, y đều không chia hết cho 3 mà 3 là nguyên tố.  x , y  3 1 và 2 2 2 2
x  1(mod 3); y  1(mod 3)  x  y  58  111  0(mod 3)  2 2 2 2
x  y  583  kxy  x  y  58 mà  xy,3 1 k3 (1)
+ Nếu trong hai số x, y có một số chia hết cho 2.
Do vai trò x, y như nhau, không mất tính tổng quát giả sử x2  xy2 Ta có: 2 2 2 2
x  y  58xy  x  y  582 mà 2
x2,582  y 2  y2  xy4 0,5 2 2
 x  y  584 vô lí vì x4, y4 do x2, y2 mà 58 không chia hết cho 4.
Vì vây cả x, y đều không chia hết cho 2.  ,
x y đều lẻ  x 1, x 1, y 1, y 1 đều chia hết cho 2. 2  x 1 x   1  x   1 và 2 y 1   y   1  y   1 đều chia hết cho 4. 0,5 2 2 2 2 2 2
 x  y  58  x 1 y 1 604  kxy  x  y  584
Mà (xy,4) = 1 do x, y lẻ  k4 (2)
Từ (1) và (2) kết hợp với (3,4) = 1  k 1  2 (đpcm) 0,25
IV Cho đường tròn (I,r) có hai bán kính IE, IF vuông góc với nhau. Kẻ hai tiếp tuyến với
6,0 đư đường tròn (I) tại E và F , cắt nhau tại A. Trên tia đối của tia EA lấy điểm B sao cho
điểm E EB >r, qua B kẻ tiếp tuyến thứ hai với đường tròn (I), D là tiếp điểm, BD cắt tia À tại
G . Gọi K là giao điểm của AI với FD.
1. Chứng minh hai tam giác IAB và FAK đồng dạng.
2. Qua A kẻ đường thẳng vuông góc với BC , cắt FD tại P. Gọi M là trung điểm của
AB,MI cắt AC tại Q. Chứng minh tam giác APQ là tam giác cân.
3. Xác định vị trí của điểm B để chu vi tam giác AMQ đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất theo r.
1. Chứng minh hai tam giác IAB và FAK đồng dạng. 2,0
Theo tính chất hai tiếp tuyến cắt nhau, ta có: CD  CF  C  DF cân tại C.  0 180   C    0,5 CFD    180 C 180 C 0 AFK  180   0  0  0 CFK  180   (1) 2 2 2
Tứ giác AEIF có ba góc vuông nên là hình chữ nhật > Hình chữ nhật AEIF có IE= IF nên 0,5 là hình vuông. Suy ra  IAB   0 FAK  45    ABC   90  C  180  C 0 AIB  180   IAB    ABI   0  0  0 0 0 0  180   45    180   45     2   2  2     0,5 (2) Từ (1) và (2) suy ra :  ABI   AFK kết hợp với  IAB  
AFK   IAB  FAK (g.g) 0,5
2. Qua A kẻ đường thẳng vuông góc với BC, cắt FD tại P. Gọi M là trung điểm của AB, 2,5
MI cắt AC tại G. Chứng minh tam giác APQ cân. IA FA IA EA Vì  IAB  F  AK nên   
( vì FA = EA). Đẳng thức này kết hợp AB AK AB AK 0,5 với điều kiện 
IAE chung, suy ra:  AKB  AEI (c.g.c)
AEI vuông cân tại E nên AKB vuông tại K. Suy ra đường trung tuyến KM cũng là đường cao nên KM  A . B 0,5
Ta có: KM  AB, IE  AB, AC  AB  KM / /IE / / AC.  0,5
ID  BC, AP  BC  ID / / AP.
Áp dụng định lí Talet và hệ quả Talet, kết hợp ID = IE. 0,5 ID KI ME IE     AP  AQ  A  PQ Ap KA MA AQ cân tại A.
3. Xác định vị trí điểm B để chu vi tam giác APQ đạt giá trị nhỏ nhất. Tính giá trị nhỏ 1,5 nhất đó theo R.
Đặt : ME  x, PQ  y với x > 0, y > 0   ME EI x r MEI  IFQ (g.g) 2      xy  r (2) 0,5 IF FQ r y Chu vi của AMQ là : 2 2 C
 AM  AQ  MQ  AM  AQ AMQ 0,5 C
 r  x  r  y  r  x2  r  y2  r  x  y   2 2
x  y   r x  y 2 2 2  2r AMQ
Áp dụng bất đẳng thức cói cho hai số thực dương x, y ta có: r   x  y   2 2
x  y   r x  y 2 2 2 2 2 2
 2r  2r  2 xy  2 x y  2r.2 xy  2r (2) 0,5 Từ (1) và (2) suy ra: 2 2 2 C
 2r  2r  2r  2r.2r  2r  4r  8r  4  2 2.r AMQ
Dấu (=) xảy ra  x = y = r  EB  3r.
Vậy khi EB = 3r thì chu vi tam giác AMQ nhỏ nhất. Giá trị nhỏ nhất bằng 4  2 2.r 0,5 V
cho các số thực dương x, y, z thỏa mãn 2 2
x  y  4xyz  2xy  yz  zx . Tính giá trị 2,0 2,0 điểm
n lớn nhất của biểu thức P  x1 y1 z. 2  y  z 
+ Ta có P  x    y  z      p      y  z 2 1 4 2  4      0,5 + Từ giả thiết ta có 2 2 2
x  y  2xy  z  4xyz  2x y  z  4yz  x   y  z2 2
 2x  y  z  1 x4yz.
+ Nhận thấy x   y  z2  x  y  z   x  y  z2 2 2  0 nên x 1
+ Vì vậy x   y  z2 2
 2x  y  z  1 x4yz
 x   y  z2  x y  z    x y  z2 2 2 1 0,5
 x  x  y  z  x y  z2  x   y  z   y  z2 2 2 2
 x   y  z 2    y  z.
+ Suy ra P   y  z    y  z 2 4 2   
x   y  z2   y  z   
Đặt 2   y  z  t ; ta có x  0
 2   y  z  0  0  t  2 (*) 0,5  y  z  0  4
 6  3t  t  t  t  81 27
Khi đó ta có 4P  2  t 3
t  12P  6  3t.t.t.t    P     4  16 64 3
Dấu “=” xảy ra khi 6  3t  t  t  thỏa mãn (*) 2 y  z  27  3 3 1 Vậy max P 
khi và chỉ khi 2   y  x   x  ; y  z  0,5 64 2 4 4  
x   y  z 2   y  z   
Chú ý:- Các cách làm khác nếu đúng vẫn cho điểm tối đa, điểm thành phần giám khảo tự
phân chia trên cơ sở tham khảo điểm thành phần của đáp án.
- Đối với Câu IV (Hình học): Không vẽ hình, hoặc vẽ hình sai cơ bản thì không chấm.
- Các trường hợp khác tổ chấm thống nhất phương án chấm.