











Preview text:
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐỀ THI CUỐI KỲ HỌC KỲ 2 NĂM HỌC 2017- THÀNH PHỐ HỒ CHÍ MINH 2018
KHOA ĐÀO TẠO CHẤT LƯỢNG CAO
Môn: Toán Ứng Dụng Cho Kỹ Sư Điện – Điện Tử
NGÀNH CÔNG NGHỆ KỸ THUẬT ĐIỆN – Mã môn học: AMEE331944
Đề số/Mã đề: 1/1A. Đề thi có 2 trang. ĐIỆN TỬ Thời gian: 90 phút.
-------------------------
Được phép sử dụng tài liệu. Câu 1: ( 2,5 điểm)
Cho mạch điện gồm có R = 5, L = 1H nối tiếp với nhau và được nối vào nguồn điện áp u(t) có giá trị như (*) : 10sin2t khi t 0 u(t) (*) 0 khi t 0
Biết rằng i(0) = 0. Anh (Chị) thực hiện các yêu cầu sau :
a. Viết phương trình vi phân mô tả mạch điện.
b. Tìm thành phần xác lập iXL của dòng điện i.
c. Tìm thành phần quá độ iQĐ (hay thành phần tự do iTD) của dòng điện i.
d. Viết biểu thức dòng điện i. Câu 2: (3 điểm)
Cho mạch điện như hình 1. Trong hình vẽ, i1 là dòng điện qua L và i2 là dòng điện qua C.
Biết rằng L = 8H, R = 20, C = 0,05F, i1(0) = 0 và i2(0) = 2A. Hình 1
Và nguồn v(t) xác định theo (**). 10V khi t 0 v(t) (**) 0 khi t 0 Anh (Chị) hãy :
a. Viết hệ phương trình vi phân mô tả mạch điện theo i1 và i2.
b. Biến đổi Laplace hệ phương trình vi phân ở câu a.
c. Dùng công thức Cramer giải hệ phương trình Laplace ở câu b. d. Tìm i1 và i2. Câu 3: (2,5 điểm)
Cho tín hiệu tuần hoàn f(t) được xác định trong 1 chu kỳ theo (***)
2 khi 4 t 2
f (t) 6 khi 2 t 0 (***)
0 khi 0 t 2 Anh (Chị) hãy :
a. Tìm tần số cơ bản và các hệ số khai triển fourier lượng giác a0, an, bn của hàm f(t).
b. Viết biểu thức khai triển fourier của f(t) với n 4.
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1 Câu 4: (1,5 điểm) z2 1
a. Tìm f '(z) tại z = 1 + j với f (z) . z 2
b. Hãy tìm hàm giải tích f(z) = u(x,y) + jv(x,y) với u(x,y) = 2xy + y2.
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 2.4]: Có khả năng ứng dụng giải phương trình vi Câu 1
phân vào các bài toán kỹ thuật điện.
[CĐR 2.3]: Có khả năng ứng dụng phép biến đổi Laplace, Câu 2
biến đổi Laplace ngược và định thức để phân tích các bài toán kỹ thuật điện.
[CĐR 1.4]: Có khả năng phân tích tín hiệu tuần hoàn theo Câu 3
chuỗi fourier lượng giác.
[CĐR 1.3]: Có khả năng tính toán số phức và hàm phức. Câu 4 Ngày tháng năm 20
Thông qua Trưởng ngành
(ký và ghi rõ họ tên)
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐÁP ÁN ĐỀ THI CUỐI KỲ HỌC KỲ 2 NĂM THÀNH PHỐ HỒ CHÍ MINH HỌC 2017-2018
KHOA ĐÀO TẠO CHẤT LƯỢNG CAO
Môn: Toán Ứng Dụng Cho Kỹ Sư Điện – Điện Tử
NGÀNH CÔNG NGHỆ KỸ THUẬT ĐIỆN – Mã môn học: AMEE331944
Đề số/Mã đề: 1/1A. Đề thi có 2 trang. ĐIỆN TỬ Thời gian: 90 phút.
-------------------------
Được phép sử dụng tài liệu. Câu 1: (3 điểm)
a. Viết phương trình vi phân mô tả mạch điện.
5i i' 10sin 2t (0,25đ)
b. Tìm thành phần xác lập iXL của dòng điện i.
5Im sin(2t ) 2Im cos(2t ) 10sin2t (0,5đ)
29Im sin(2t 21,80) 10sin2t (0,5đ) Im 1,857
(0,25đ) i 1,857sin(2t 21,80) (0,25đ) XL 21,80
c. Tìm thành phần quá độ iQĐ (hay thành phần tự do iTD) của dòng điện i. 5 + s = 0 s = - 5 (0,25đ) iQĐ = Ke-5t (0,25đ)
d. Viết biểu thức dòng điện i.
i Ke5t 1,857sin(2t 21,80)
(0,25đ) i(0) 0 K 0,69 (0,25đ)
i 0,69e5t 1,875sin(2t 21,80) (0,25đ) Câu 2: (3 điểm)
a. Viết hệ phương trình vi phân mô tả mạch điện theo i1 và i2.
8i' 20(i i ) 10 ' 1 1 2 8i 1 20(i1 i2) 10 u C 20(i1 i2) 0 (0,5đ) ' ' (0,25đ) 20i 2 20i1 20i2 0
i2 0,05u'C
b. Biến đổi Laplace hệ phương trình vi phân ở câu a.
8[sI i (0)] 20(I I ) 10
(8s 20)I 20I 10 1 1 1 2 s (0,5đ) 1 2 s (0,25đ) 20I 2
20[sI1 i1(0)] 20[sI2 i2(0)] 0
20sI1 (20 20s)I2 40
c. Dùng công thức Cramer giải hệ phương trình Laplace ở câu b.
10 (20 20s) 4020 103 I s s 200 1
(8s 20)(20 20s) 20(20s) 160s(s2 s 2,5) (0,25đ) I
40(8s 20) 2010 320s 1000 (0,25đ) 2
(8s 20)(20 20s) 20(20s)
160(s2 s 2,5) d. Tìm i1 và i2.
I 0,5 0,25 2 j 0,25 2 j 1 s
s 0,5 1,5 j s 0,5 1,5 j
0,5 0,5s 5,75 0,5 0,5(s 0,5) 6 (0,25đ) s (s 0,5)2 2,25 s
(s 0,5)2 2,25 (s 0,5)2 2,25 i 1
0,5 0,5e0,5t cos1,5t 4e0,5t sin1,5t (0,25đ)
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1 I 2(s 0,5) 3,51,5 (0,25đ) 2
(s 0,5)2 1,52 (s 0,5)2 1,52 i 2
2e0,5t cos1,5t 3,5e0,5t sin1,5t (0,25đ) Câu 3: (2,5 điểm)
a. Tìm tần số cơ bản và các hệ số khai triển fourier lượng giác a0, an, bn của hàm f(t). 1 2 1 0 8 T 6 3 (0,25đ) a 0 (0,25đ) 6 2dt 4 6 6dt 2 3 1 2 1 0 a n
3 2 cosntdt 3 6 cosntdt 4 2
2 [sin(2n) sin(4n)] 2 [sin(0) sin(2n)] 3n n (0,25đ)
2 (2sin2n sin4n) 2 sinn 2 (0,25đ) 3n 3n 3 3 n 1,4,. . n 3 n 2,5,. . (0,25đ) n 0 n 3,6,. .
b 2 [cos(2n) cos(4n)] 2 [cos(0) cos(2n)] (0,25đ) n 3n n 2 (cos2n 1) (0,25đ) n 9 n 1,2,4,5,. . n (0,25đ) 0 n 3,6,. .
b. Viết biểu thức khai triển fourier của f(t) với n 4. 8 9 9 3 3
f (t) ( cosn t sinn t) ( cosn t sinn t) 3 n 3 n 3 n2,5 n 3 n 3 (0,25đ) n1,4 8 3 9 3 2 9 2 3 4 9 4
cos t sin t cos t sin t cos t sin t 3 3 3 2 3 2 3 4 3 4 3 (0,25đ) Câu 4: (1,5 điểm) z2 1
a. Tìm f '(z) tại z = 1 + j với f (z) . z 2
2z(z 2) (z2 1) f '(z) z2 4z 1 (0,25đ) (z 2)2 (z 2)2
f '(1 j) (1 j)2 4(1 j) 1 0,6 0,3 j (0,25đ) (1 j 2)2
b. Hãy tìm hàm giải tích f(z) = u(x,y) + jv(x,y) với u(x,y) = 2xy + y2.
u'x 2y v'y Số hiệ v 'u: BM1/QT-PĐB' CL-RĐTV
2ydy y2 w(x) Trang: 1/1
u y 2x 2y v x
Downloaded by Nguyen Linh (vjt65@gmail.com) (0,25đ) (0,25đ)
v'x w' 2x 2 y w (2x 2y)dx x2 2xy C (0,25đ)
Do v = y2 – x2 – 2xy + C nên không tồn tại hàm giải tích f(z) thỏa điều kiện bài toán. (0,25đ)
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 2.4]: Có khả năng ứng dụng giải phương trình vi Câu 1
phân vào các bài toán kỹ thuật điện.
[CĐR 2.3]: Có khả năng ứng dụng phép biến đổi Laplace, Câu 2
biến đổi Laplace ngược và định thức để phân tích các bài toán kỹ thuật điện.
[CĐR 1.4]: Có khả năng phân tích tín hiệu tuần hoàn theo Câu 3
chuỗi fourier lượng giác.
[CĐR 1.3]: Có khả năng tính toán số phức và hàm phức. Câu 4 Ngày tháng năm 20
Thông qua Trưởng ngành
(ký và ghi rõ họ tên)
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐỀ THI CUỐI KỲ HỌC KỲ 1 NĂM HỌC 2018- THÀNH PHỐ HỒ CHÍ MINH 2019
KHOA ĐÀO TẠO CHẤT LƯỢNG CAO
Môn: Toán Ứng Dụng Cho Kỹ Sư Điện – Điện Tử
NGÀNH CÔNG NGHỆ KỸ THUẬT ĐIỆN – Mã môn học: AMEE331944
Đề số/Mã đề: 1/1A. Đề thi có 2 trang. ĐIỆN TỬ Thời gian: 90 phút.
-------------------------
Được phép sử dụng tài liệu. Câu 1 : (2,0 điểm)
Cho 2 ma trận A và B như sau : 2 5 4 6 A B 1 3 2 1
a. Giải phương trình AX = B để tìm ma trận X.
b. Tìm ma trận nghịch đảo của ma trận A. Câu 2 : ( 2,0 điểm)
Dùng phép biến đổi Laplace giải hệ phương trình vi phân với giả thiết y1(0) = 1, y2(0) = 0 :
y' y 0 1 2
y1 y' 2cost 2 Câu 3 : (3,0 điểm)
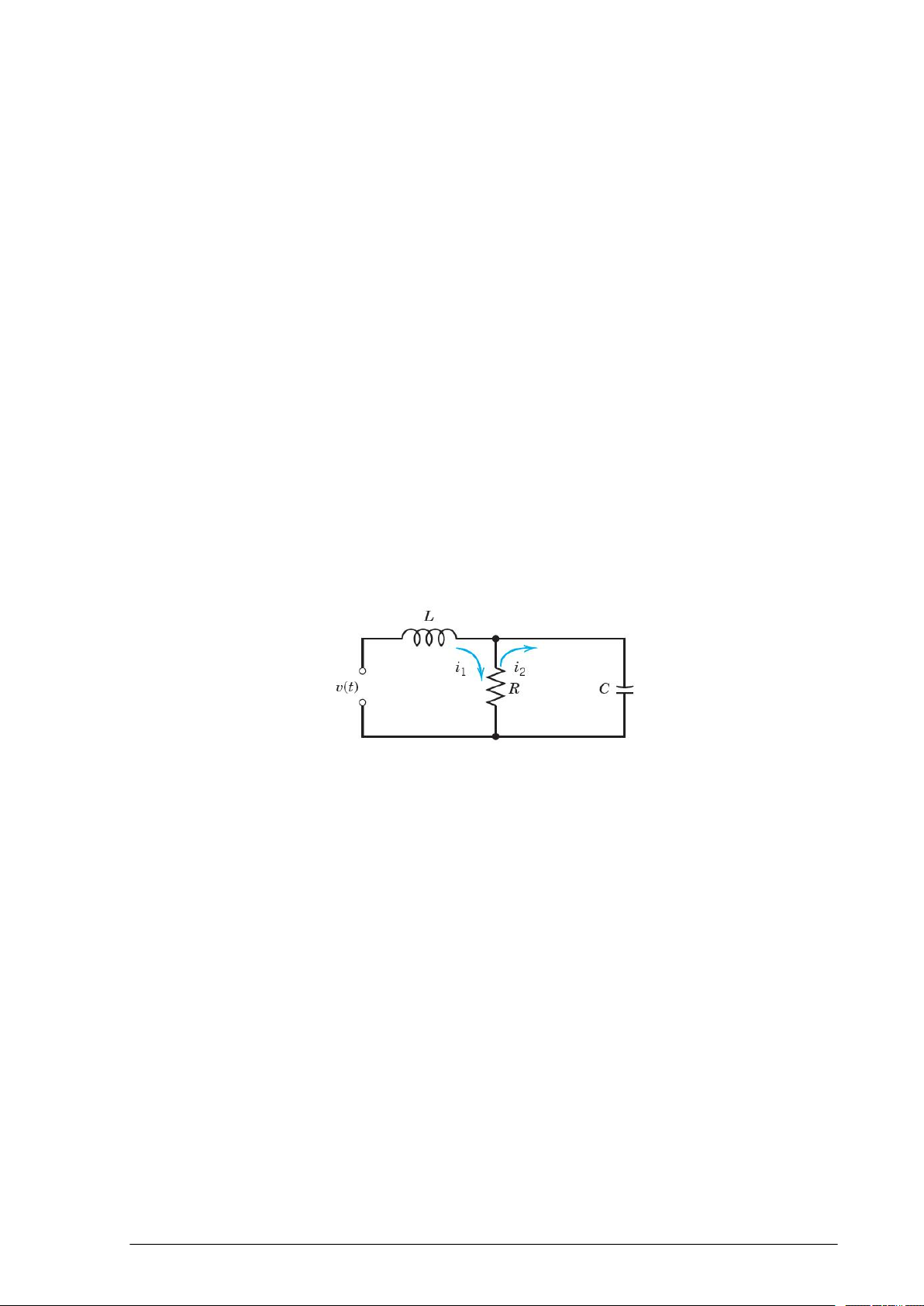
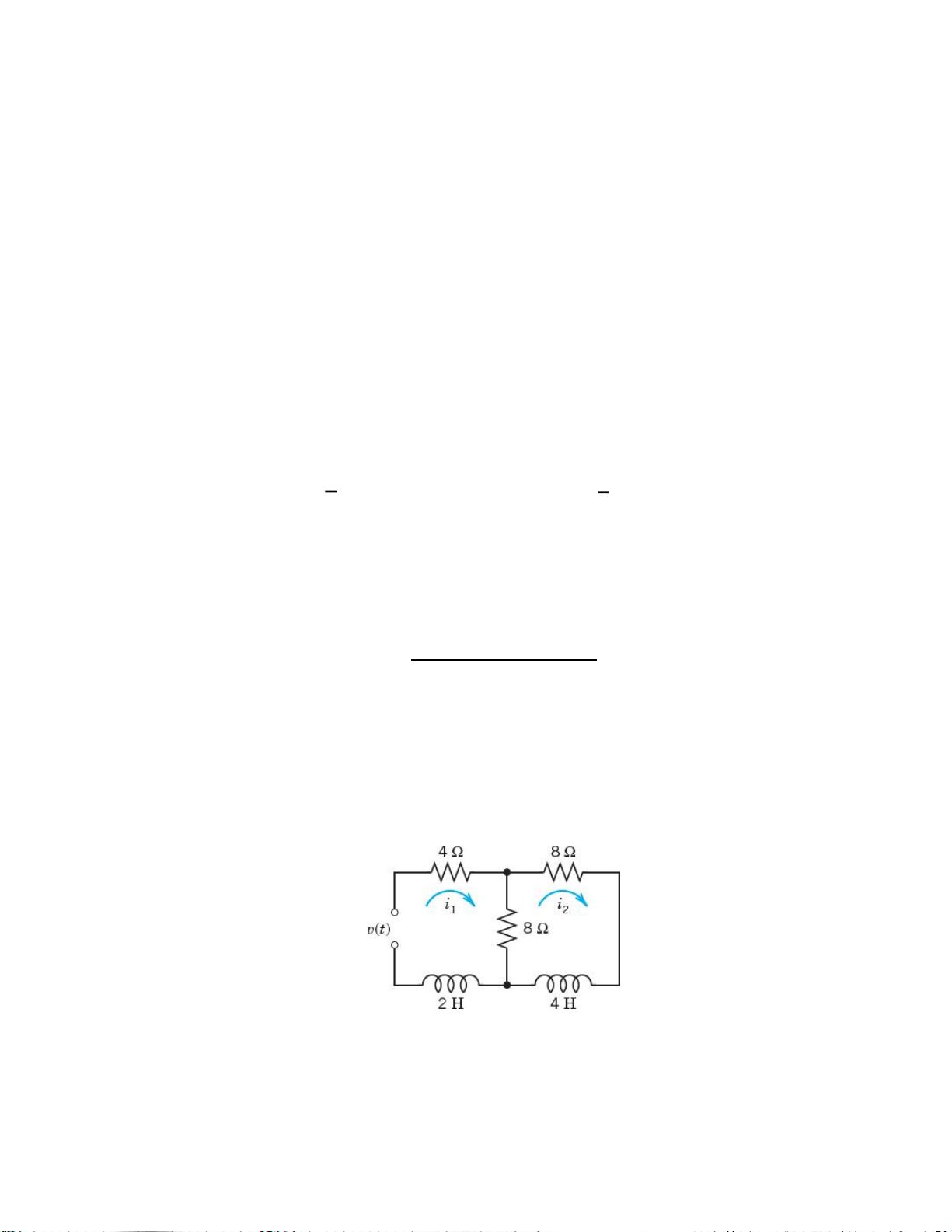
Cho mạch điện như hình 1. Biết rằng L = 1H, R = 6, C = 1/9F, iL(0) = 0, uC(0) = 2V.
Nguồn v(t) = 2cos(t) V nếu 0 < t < và v(t) = 0 nếu t > Hình 1 a. Tìm V(s) và IL(s)
b. Suy ra iL(t) khi t > 0. Câu 4: (2,0 điểm)
Cho tín hiệu tuần hoàn f(t) được xác định trong 1 chu kỳ như hình 2 Hình 2
Hãy tìm các hệ số a0, an, bn và chuỗi fourier của f(t). Câu 5: (1,0 điểm)
Hãy tìm phần thực và phần ảo của hàm f(z) = e1/z.
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang 1/2
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 2.4]: Có khả năng thực hiện các phép toán với ma Câu 1 trận.
[CĐR 2.3]: Sử dụng được phép biến đổi Laplace và Câu 2
Laplace ngược để giải hệ phương trình vi phân.
[CĐR 2.1; 2.3]: Có khả năng mô hình hóa bài toán mạch Câu 3
điện bằng phương trình vi phân. Ứng dụng biến đổi
Laplace, biến đổi Laplace ngược để phân tích bài toán mạch điện.
[CĐR 1.4]: Có khả năng phân tích tín hiệu tuần hoàn theo Câu 4 chuỗi fourier.
[CĐR 1.3]: Có khả năng tính toán số phức, hàm phức. Câu 5 Ngày 28 tháng 12 năm 2018
Thông qua Trưởng ngành
(ký và ghi rõ họ tên)
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang 2/2
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐỀ THI CUỐI KỲ HỌC KỲ 2 NĂM HỌC 2018- THÀNH PHỐ HỒ CHÍ MINH 2019
KHOA ĐÀO TẠO CHẤT LƯỢNG CAO
Môn: Toán Ứng Dụng Cho Kỹ Sư Điện – Điện Tử
NGÀNH CÔNG NGHỆ KỸ THUẬT ĐIỆN – Mã môn học: AMEE341944
Đề số/Mã đề: 1/1A. Đề thi có 2 trang. ĐIỆN TỬ) Thời gian: 90 phút.
-------------------------
Được phép sử dụng tài liệu. Câu 1: (2,0 điểm)
Cho 3 ma trận A, B và C như sau : 1 A 2 0 4 4 5 , , C 2 B 1 1 2 1 8
Hãy trình bày chi tiết cách của bạn để:
a. Tìm ma trận X thỏa mãn phương trình AX + B = C
b. Tìm hạng của ma trận A. Câu 2: (2,5 điểm) Bạn hãy:
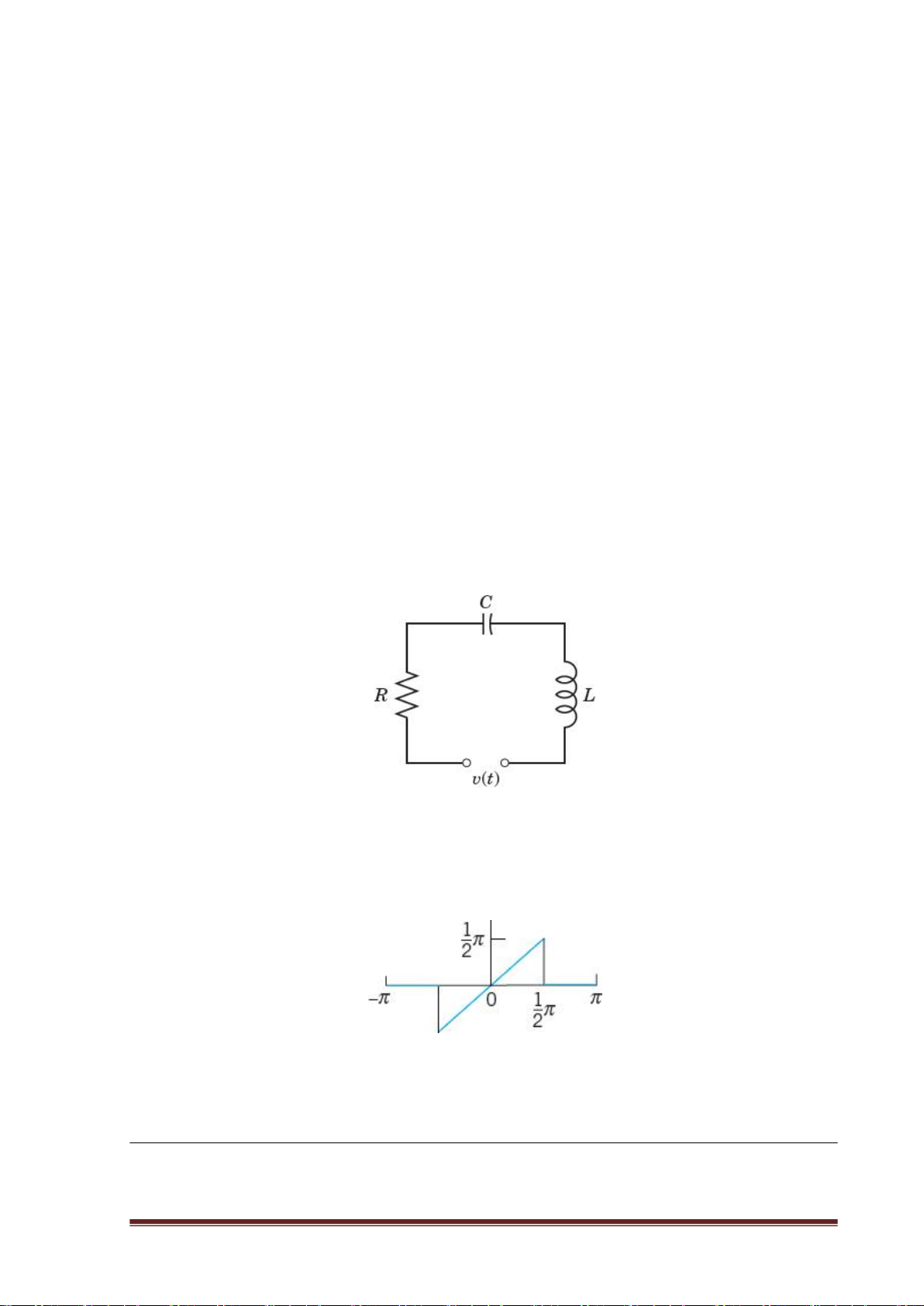
a. Tìm hàm f(z) giải tích với v = – e-2x sin 2y
b. Tìm các nghiệm của phương trình cosh z = – 1. Câu 3: (3,5 điểm)
Cho mạch điện như hình 1. Biết rằng i1(0) = 0 và i2(0) = 1A. Hình 1
Và nguồn v(t) được xác định theo (**) 10V v(t )
khi 0 t 2 (**) 0 khi t 2 Anh (Chị) hãy :
a. Viết hệ phương trình vi phân theo i1 và i2 trong hình 1.
b. Viết biểu thức nguồn v(t) theo (**) và tìm V(s).
c. Biến đổi Laplace hệ phương trình vi phân ở câu a.
d. Tìm I1(s), I2(s) và i1(t), i2(t). Câu 4: (2,0 điểm)
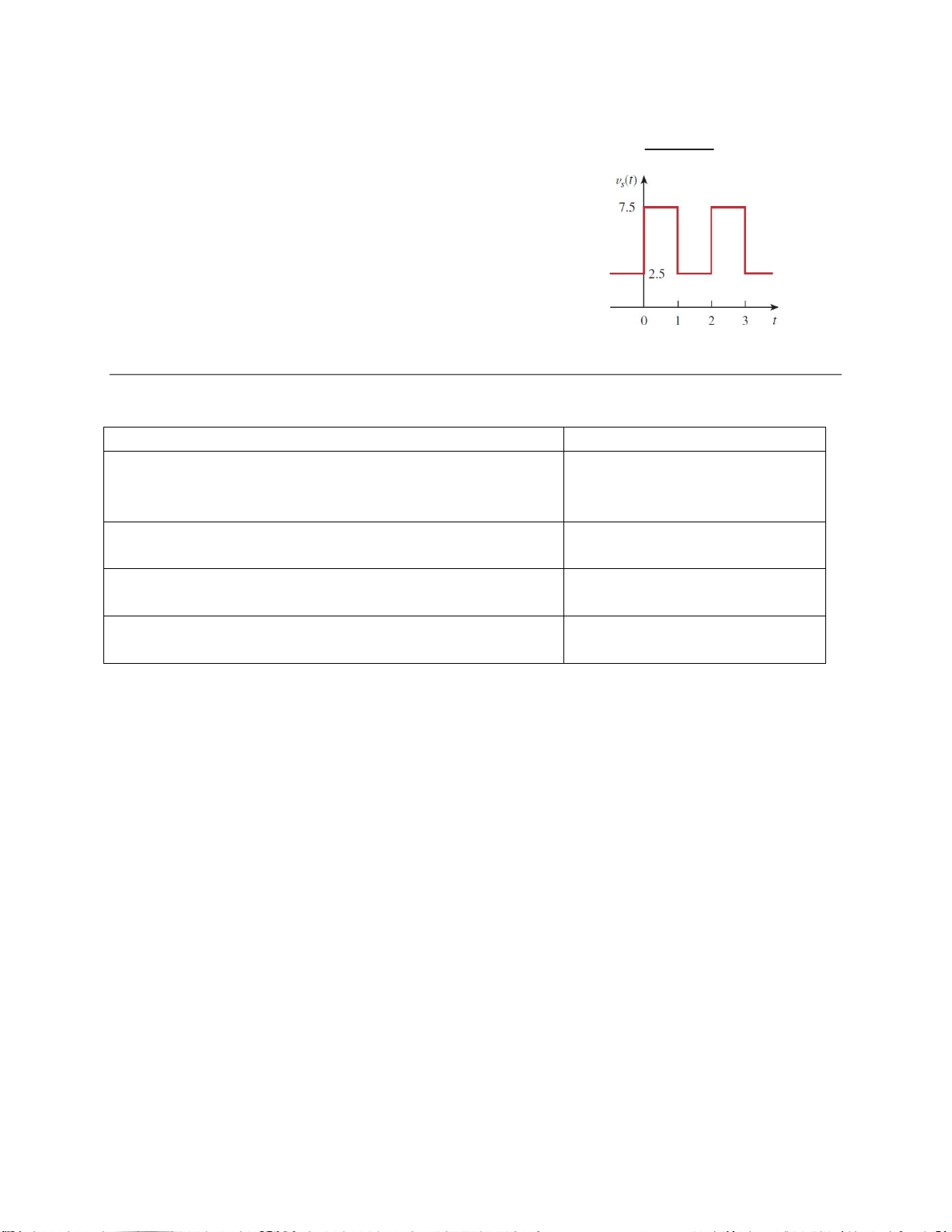
Cho tín hiệu tuần hoàn f(t) được xác định như hình 2. Anh (Chị) hãy:
a. Tìm các hệ số khai triển fourier lượng giác a0, an, bn của hàm f(t).
b. Viết biểu thức khai triển fourier lượng giác của f(t) với n 6.
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1 Hình 2
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 2.4]: Có khả năng ứng dụng giải phương trình vi Câu 3
phân vào các bài toán kỹ thuật điện.
[CĐR 2.3]: Có khả năng tính toán ma trận và định thức. Câu 1
[CĐR 1.4]: Có khả năng phân tích tín hiệu tuần hoàn theo Câu 4
chuỗi fourier lượng giác.
[CĐR 1.3]: Có khả năng tính toán số phức và hàm phức. Câu 2 Ngày 23 tháng 5 năm 2019
Thông qua Trưởng ngành
(ký và ghi rõ họ tên)
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐỀ THI CUỐI KỲ HỌC KỲ 2 NĂM HỌC 2018-2019 THÀNH PHỐ HỒ CHÍ MINH
Môn: Toán Ứng Dụng Cho Kỹ Sư Điện – Điện Tử
KHOA ĐIỆN – ĐIỆN TỬ Mã môn học: AMEE341944
Đề số/Mã đề: 1/1A. Đề thi có 2 trang.
------------------------- Thời gian: 90 phút.
Được phép sử dụng tài liệu. Câu 1 (2 điểm): Cho 2 ma trận A, B 0 2 4 0 5
a. Trình bày chi tiết cách tìm ma trận A C = A×B. 6 5 5 B 5 3
b. Trình bày chi tiết cách tìm ma trận 1 0 3 2 4 A-1. Câu 2 (2,5 điểm):
a. Tìm hàm f(t) biết 2 + 1 �(�) = ln (� − 1)2
b. Một mạch điện được mô tả bởi phương trình vi phân (1) theo điện áp u trên tụ điện C
2�′′ + 4�′ + 6,5� = 10 sin 1,5� V (1)
Biết �(0) = 0 và �′(0) = 0
Tìm các thành phần nghiệm uh, up và u của phương trình vi phân (1). Câu 3 (3,5 điểm):
Cho mạch điện như hình 1. Biết
rằng R = 4 , L = 1 H, C = 0,05 F.
Dòng điện iL qua cuộn cảm L có iL(0) =
0 và điện áp v0 trên tụ có v0(0) = 0. Hình 1
10V khi 0 t 4 Và nguồn v
s(t) được xác định theo (**) v( t ) 5V (**) khi t 4
a. Viết hệ phương trình vi phân theo iL và v0.
b. Viết biểu thức nguồn v(t) và tìm V(s).
c. Biến đổi Laplace hệ phương trình vi phân ở câu a.
d. Tìm IL(s), V0(s) theo công thức Cramer.
e. Viết biểu thức của iL(t) và v0(t).
Downloaded by Nguyen Linh (vjt65@gmail.com) Câu 4 (2 điểm):
a. Tính các giá trị của z và biểu diễn z dưới dạng đại số � = 3√−4 + 3j
b. Tìm các hệ số khai triển fourier
lượng giác của vs(t) có dạng sóng tuần hoàn như hình 2 Hình 2
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 2.4]: Có khả năng ứng dụng giải phương trình Câu 2, 3
vi phân vào các bài toán kỹ thuật điện và sử dụng
phép biến đổi Laplace để giải phương trình vi phân.
[CĐR 2.3]: Có khả năng tính toán ma trận và định Câu 1 thức.
[CĐR 1.4]: Có khả năng phân tích tín hiệu tuần hoàn Câu 4b
theo chuỗi fourier lượng giác.
[CĐR 1.3]: Có khả năng tính toán số phức và hàm Câu 4a phức. Ngày 31 tháng 5 năm 2019
Thông qua Trưởng Bộ môn
(ký và ghi rõ họ tên)
Downloaded by Nguyen Linh (vjt65@gmail.com)
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐỀ THI CUỐI KỲ HỌC KỲ 1 NĂM HỌC 2019- THÀNH PHỐ HỒ CHÍ MINH 2020
KHOA ĐIỆN – ĐIỆN TỬ
Môn: Toán Ứng Dụng Cho Kỹ Sư Điện – Điện Tử
------------------------- Mã môn học: AMEE142044.
Đề số/Mã đề: 1/1A. Đề thi có 2 trang. Thời gian: 90 phút.
Được phép sử dụng tài liệu. Câu 1 (1,5 điểm): Cho ma trận A 1 5 � = [−2 1 −4] 3 1 2
Xác định giá trị của � để rank � = 2 và tìm ma trận nghịch đảo �−1 với giá trị � đó. Câu 2 (2 điểm):
a. Cho � = −4 + j4√2. Hãy tìm tất cả các giá trị của 3√�.
b. Tìm giá trị của số phức � thỏa mãn phương trình �2 + (2 + j)� − 1 + 7j = 0. Câu 3 (2,0 điểm):
a. Tìm hàm �(�) biết hàm 2 + 4 ( ) = · (� + 1)(� − 3)(� + 4)
b. Tìm hàm �(�) nếu hàm
�(�) = ��−� + 2 sin � − 3 cosh �. Câu 4 (3,0 điểm):
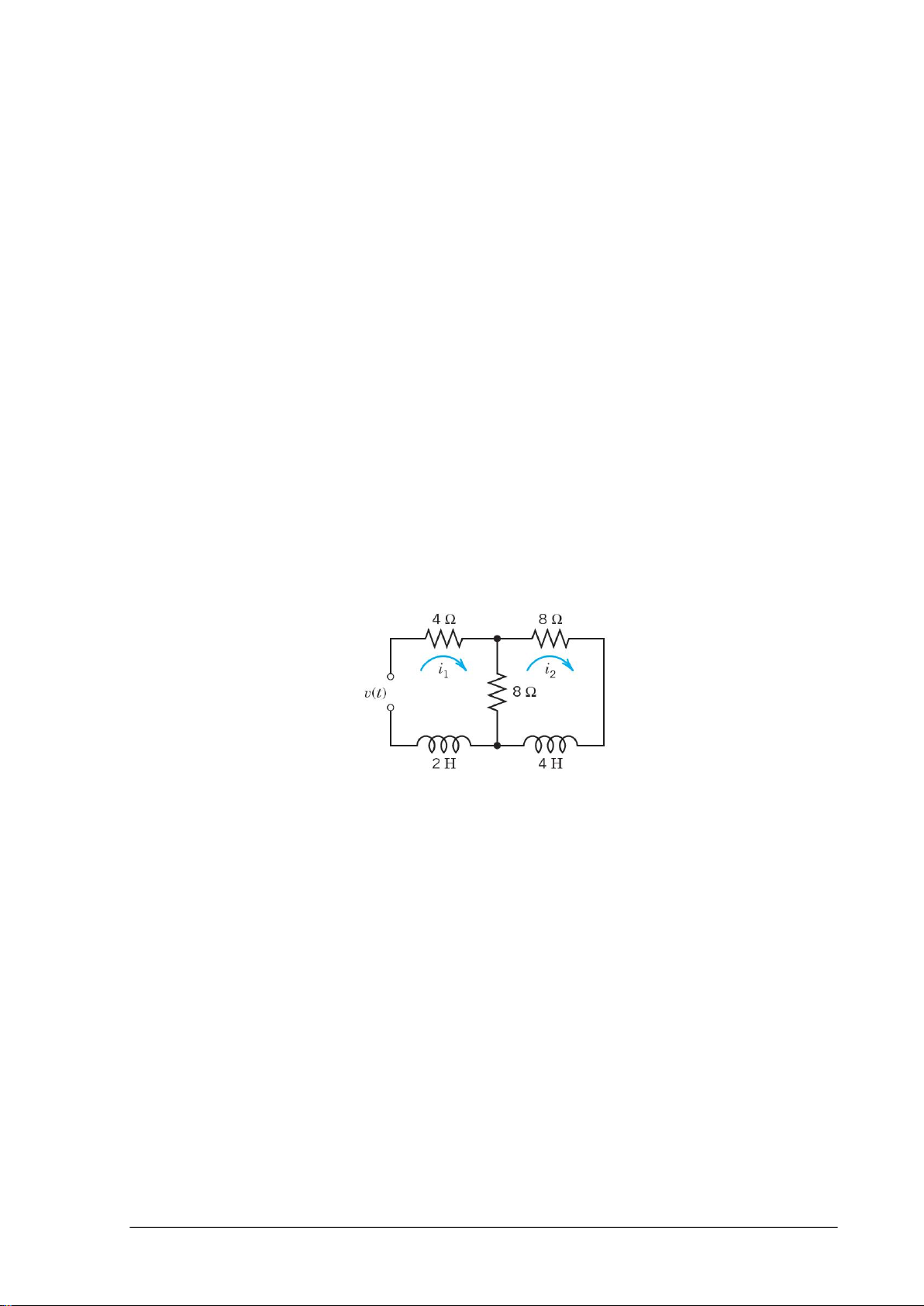
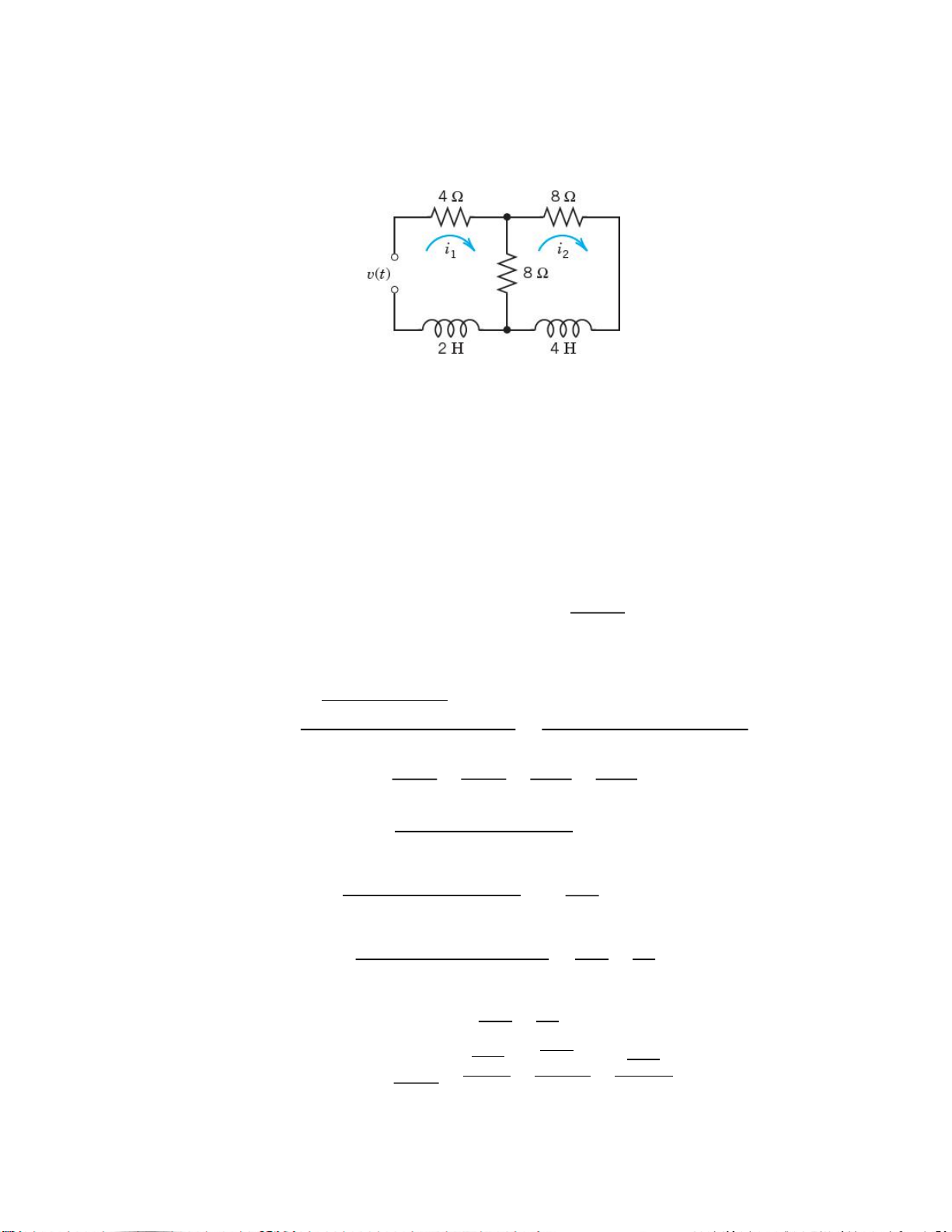
Cho mạch điện như hình 1. Hình 1
a. Viết hệ phương trình vi phân mô tả mạch điện theo các dòng điện �1 và �2 như hình vẽ.
Downloaded by Nguyen Linh (vjt65@gmail.com)
b. Dùng phép biến đổi laplace tìm dòng điện �1 và �2 biết rằng �1 = 0, �2 = 1� và ( ) = 220 cos .
c. Tìm giá trị � ′1 tại � = 1�. Câu 5 (1,5 điểm):
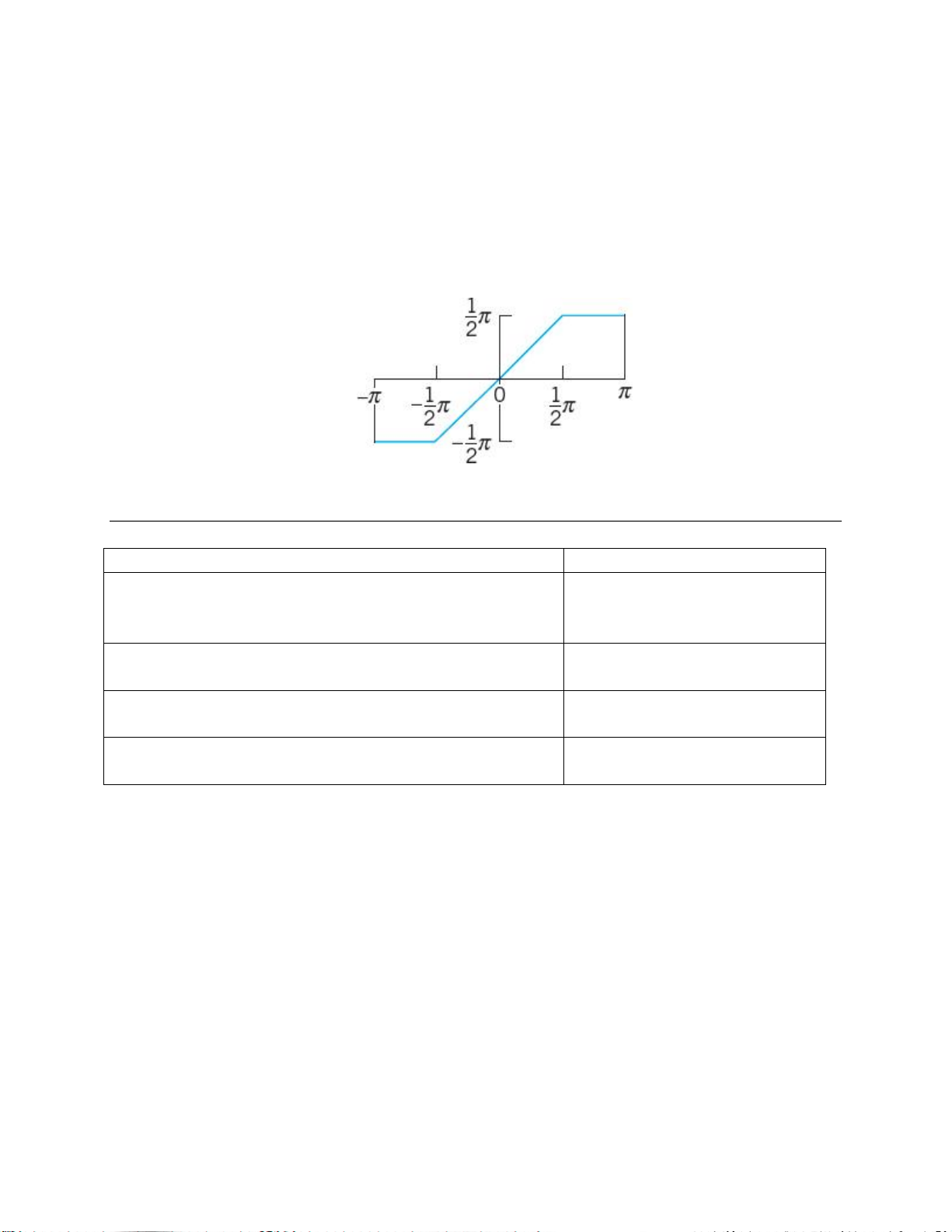
Cho hàm tuần hoàn �(�) có dạng sóng trong 1 chu kỳ như hình 2. Hãy xác định các
hệ số khai triển fourier lượng giác của hàm �(�). Hình 2
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 2.4]: Có khả năng ứng dụng giải phương trình Câu 3, 4
vi phân vào các bài toán kỹ thuật điện và sử dụng
phép biến đổi Laplace để giải phương trình vi phân.
[CĐR 2.3]: Có khả năng tính toán ma trận và định Câu 1 thức.
[CĐR 1.3]: Có khả năng tính toán số phức và hàm Câu 2 phức.
[CĐR 1.4]: Có khả năng phân tích tín hiệu tuần hoàn Câu 5
theo chuỗi fourier lượng giác. Ngày 10 tháng 12 năm 2019
Thông qua Trưởng Bộ môn
(ký và ghi rõ họ tên)
Downloaded by Nguyen Linh (vjt65@gmail.com)
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐÁP ÁN THI CUỐI KỲ HỌC KỲ 1 NĂM HỌC THÀNH PHỐ HỒ CHÍ MINH 2019-2020
KHOA ĐIỆN – ĐIỆN TỬ
Môn: Toán Ứng Dụng Cho Kỹ Sư Điện – Điện Tử
------------------------- Mã môn học: AMEE142044.
Đề số/Mã đề: 1/1A. Đề thi có 2 trang. Thời gian: 90 phút.
Được phép sử dụng tài liệu. Câu 1 (1,5 điểm):
Xác định giá trị của � để rank � = 2 và tìm ma trận nghịch đảo �−1 với giá trị � đó. 1 5 1 5 1 5
� = [−2 1 −4] → [0 1 + 2� 6 ] → [0 1 + 2� 6] 3 1 2 0 1 − 3� −13
0 (1 − 3�) + 13(1 + 2�)/6 0 Để rank � = 2 thì 13(1 + 2 ) 19 (1 − 3�) +
= 0 ⇔ 6 − 18� + 13 + 26� = 0 ⇔ � = − 6 8 Và
(1 + 2�) − 1,2� ≠ 0 ⇔ � ≠ −1.25
Vậy � = − 19 thì rank � = 2. 8
Vì det � = 0 nên không tồn tại ma trận nghịch đảo �−1. Câu 2 (2 điểm):
a. Cho � = −4 + �4√2. Hãy tìm tất cả các giá trị của 3√�.
� = −4 + �4√2 = 4√3∠125,260 3 3 125,260 + 3600 125,260 + 3600 √� = √4√3(cos + ) 3 sin 3 Với � = 0 thì 3√� = Với � = 1 thì 3√� = Với � = 2 thì 3√� =
b. Tìm giá trị của số phức � thỏa mãn phương trình �2 + (2 + �)� − 1 + 7� = 0.
Giả sử � = � + �� với �, � là số thực.
�2 + j2xy − y2 + 2x + j2y + jx − y − 1 + 7j = 0
�2 − y2 + 2x − y − 1 = 0 { 2xy + 2y + x + 7 = 0
Downloaded by Nguyen Linh (vjt65@gmail.com) 7 + 2y x = − 2y + 1 7 + 2y 2 7 + 2y (− ) − y2 − 2 ( ) − y − 1 = 0 2y + 1 2y + 1
(7 + 2y)2 − y2(2y + 1)2 − 2(7 + 2y)(2y + 1) − (y + 1)(2y + 1)2 = 0
49 + 28� + 4�2 − 4y4 − 4y3 − y2 − 32y − 8y2 − 14 − 4y3 − 8y2 − 5� − 1 = 0
4y4 + 8y3 + 13y2 + 9� − 34 = 0 � = −2 và � = 1 � = 1 và � = −3
Vậy � = 1 − 2� và � = −3 + �. Câu 3 (2,0 điểm):
a. Tìm hàm �(�) biết hàm �(�) 2 + 4 ( ) = = + + (� + 1)(� − 3)(� + 4) + 1 � − 3 + 4 2 = lim + 4 5 = −
�→−1 (� − 3)(� + 4) 12 2 + 4 13 = lim = �→3 (� + 1)(� + 4) 28 2 + 4 20 = lim =
�→−4 (� + 1)(� − 3) 21 5 13 20 �(�) = − 12 + 28 + 21 � + 1 � − 3 � + 4 5 �(�) = − 13 20 �−� + �3� + �−4� 12 28 21
b. Tìm hàm �(�) nếu hàm �(�) �� + �−�
�(�) = ��−� + 2 sin � − 3 cosh � = ��−� + 2 sin � − 3 2
= ��−� + 2 sin � − 1,5�� − 1,5�−� 1 2 1,5 1,5 1 2 3 �(�) = + − − = + −
(� + 1)2 �2 + 1 � − 1 � + 1 (� + 1)2 �2 + 1 �2 − 1
Downloaded by Nguyen Linh (vjt65@gmail.com) Câu 4 (3,0 điểm):
Cho mạch điện như hình 1. Hình 1
a. Viết hệ phương trình vi phân mô tả mạch điện theo các dòng điện �1 và �2 như hình vẽ. 12� ′ 1 + 2�1 − 8�2 = �(�) { −8� ′ 1 + + = 0 16 2 4 2
b. Dùng phép biến đổi laplace tìm dòng điện �1 và �2 biết rằng �1(0) = 0, �2(0) =
1� và �(�) = 220 cos � �.
(12 + 2�)�1 − 8�2 = 220 2 { + 1 −8�1 + (16 + 4s)�2 = 4 220 (16 + 4s) 2 + 32 + 1 912 2 + 3520 + 32 �1 = ( =
12 + 2�)(16 + 4�) − 64 8(� + 2)(� + 8)(�2 + 1) = + + + + 2 + 8 � − � + = lim 912 2 + 3520 + 32 2 = −14 �→−2 8( + 8)( + 1) = lim 912 2 + 3520 + 32 126 2 = − = −9,692 �→−8 8( + 2)( + 1) 13 = lim 912 2 + 3520 + 32 154 55 = − �
�→� 8(� + 2)(� + 8)(� + �) 13 13 154 55 = + 13 13 126 14 308 110 �1 = − − 13 + 13 + 13 + 2 + 8 2 + 1 2 + 1
Downloaded by Nguyen Linh (vjt65@gmail.com)


