ÑEÀ THI MOÂN VI TÍCH PHAÂN B2 Naêm 2016-2017
(Ñeà coù 2 maët. Thôøi gian 120 phuùt. Khoâng duøng ña phöông tieän, taøi lieäu) ÑAÏO HAØM- VI PHAÂN
Baøi 1. [1ñ] Cho haøm soá f ñònh bôûi 4 ( , ) y f x y x e .
a) Giaûi thích vì sao haøm f khaû vi taïi (8; 0) vaø vieát phöông trình maët phaúng tieáp xuùc
vôùi ñoà thò cuûa f taïi (8; 0).
b) Duøng pheùp xaáp xæ tuyeán tính ñeå xaáp xæ giaù trò cuûa f (8, 02; 0, 05).
Baøi 2. [1ñ] Giaû söû f laø moät haøm soá khaû vi vaø u f ( , x ) y . Giaû söû 2 2 2 2 s u u u u cos , s x e t y e sin . t Chöùng minh 2s e . x y s t
Baøi 3. [1ñ] Giaû söû moät ñóa phaúng kim loaïi coù taâm ñaët taïi ñieåm (0,0) vôùi nhieät ñoä T
(ñôn vò oC) taïi ñieåm ( , x ) y
(0, 0) treân maët ñóa ñöôïc cho bôûi coâng thöùc 125 T T( , x ) y 2 2 x y
a) Haõy tính toác ñoä bieán thieân nhieät töø ñieåm (3,4) höôùng ñeán ñieåm (1,1) (ghi roõ ñôn vò tính).
b) Xeùt taïi ñieåm (x,y) baát kyø khaùc taâm ñóa, chöùng minh raèng höôùng maø theo ñoù nhieät
ñoä taêng nhanh nhaát laø höôùng ñeán taâm ñóa; vaø haõy cho bieát toác ñoä taêng nhieät theo
höôùng ñoù laø bao nhieâu?
Baøi 4. [1ñ] Cho haøm soá f ñònh bôûi 3 2 2 2 f ( , x ) y 2x xy 5x
y . Chöùng minh f ñaït
cöïc tieåu taïi moät ñieåm, ñaït cöïc ñaïi taïi moät ñieåm vaø f coù hai ñieåm yeân ngöïa. TÍCH PHAÂN
Baøi 5. [1ñ] Cho f laø haøm soá lieân tuïc xaùc ñònh treân mieàn
phaúng D naèm trong goùc phaàn tö thöù nhaát vaø bò bao y
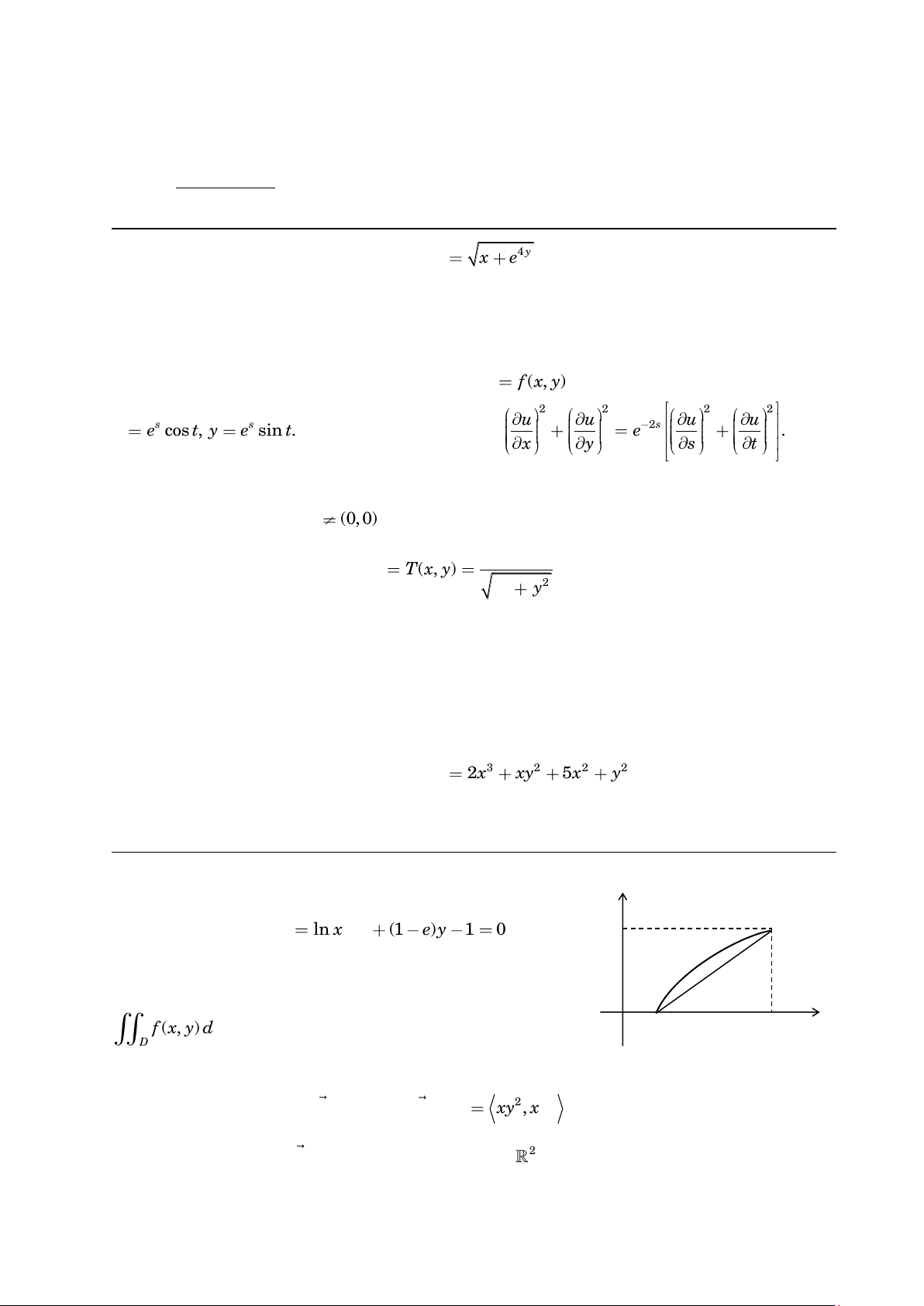
quanh bôûi hai ñöôøng y ln x ; x (1 ) e y 1 0 (e laø 1
haèng soá Neùpere). Phaùc hoïa cuûa D nhö hình beân.
Duøng ñònh lyù Fubini, vieát coâng thöùc tính tích phaân keùp x f ( , x )
y dA theo hai tích phaân laëp vôùi thöù töï laáy tích O 1 e D phaân khaùc nhau.
Baøi 6. Cho tröôøng vectô F ñònh bôûi 2 2 F( , x ) y xy , x y .
a) [0.5ñ] Chöùng minh F laø tröôøng baûo toaøn treân 2 . 1
b) [0.5ñ] Tìm haøm theá f cuûa F vaø tính
F dr vôùi C laø ñöôøng cong cho bôûi C 1 1 C : r( ) t t sin ,t t cos t , 0 t 1. 2 2
Baøi 7. Xeùt tích phaân ñöôøng x dx
y dy , vôùi C goàm ñoaïn thaúng höôùng töø (0,1) ñeán C
(0,0); ñoaïn thaúng höôùng töø (0,0) ñeán (1,0) vaø parabol 2
y 1 x höôùng töø (1,0) ñeán
(0,1). Haõy tính tích phaân treân theo hai caùch:
(a) [1ñ] Tính tröïc tieáp
(b) [0.5ñ] Duøng ñònh lyù Green. PHÖÔNG TRÌNH VI PHAÂN
Baøi 8. Giaûi caùc phöông trình vi phaân sau a) [0.5ñ] 3 xy 2y x , x 0, ( y 1) 0 b) [1ñ] y 2y 3y x 2
Baøi 9. [1ñ] Chöùng minh haøm soá 3 f ( , x ) y
xy coù caùc ñaïo haøm rieâng taïi (0,0), nhöng
khoâng taïi ñoù khoâng toàn taïi ñaïo haøm theo baát cöù höôùng naøo khaùc vôùi i vaø j . HEÁT 2