Câu 1:
Đáp ứng xung là đầu ra của hệ khi đầu vào là xung đơn vị, nên: ℎ( ) = − ℎ( − 1) + ( ) + ( − 1)
Suy ra: ℎ(0) = − ℎ(−1) + (0) +
(−1) = (do ℎ(−1) = (−1) = 0) ⇒ = 1 ( )
Biến đổi Z 2 vế, ta được: ( ) = − ( ) + ( ) + ( ) ⇒ ( ) = = ( )
Khi z = 1 thì H(z) = 4 nên: 1 + = 4(1 + ) ⇒ = 3 + 4 Khi tín hiệu vào là cos thì tín hiệu ra là: ( ) = cos + arg 3
Biên độ của tín hiệu hình sin ở đầu ra bằng 2 nên ta có: = 2 Có: 1 + 1 + = = 1 + 1 + Mà: √3 √3 1 + = 1 + cos − sin = 1 + − ⇒ 1 + = 1 + + = + + 1 3 3 2 2 2 2 Tương tự: 1 + = √ + + 1 Suy ra: √ + + 1 = = 2 ⇒ + + 1 = 4( + + 1) √ + + 1 ⇒ 16 + 24 + 9 + 3 + 4 + 1 = 4 + 4 + 4 ⇒ 4 + 8 + 3 = 0 1 3 ⇒ = − ∪ = − 2 2 ( ) Có hàm truyền đạt ( ) = = =
. Điểm cực z = -c, cần chọn c sao cho hệ ổn định và nhân quả => điểm ( )
cực nằm trong đường tròn đơn vị, hay c = -1/2. Giá trị c = -3/2 bị loại. Khi c = -1/2 thì b = 1 Vậy a=b=1, c = -1/2. Câu 2:
a) Xác định PTSP: ( ) = ( ) +
( − 1) + ( − 2) = ( ) − ( − 1) + ( − 2)
Đáp ứng xung của hệ là đầu ra của hệ khi đầu vào là xung đơn vị, do đó:
ℎ( ) = ( ) − ( − 1) + ( − 2) b) Xác định và vẽ
. Nhận xét ứng dụng bộ lọc. Ta có: = ℎ( ) = 1 − + = 1 − (cos
− sin ) + (cos 2 − sin 2 ) = (1 − cos + cos 2 ) + (sin − sin 2 ) Suy ra: = 1 − cos + 2 cos − 1 = cos (2 cos − 1) = sin − 2 sin cos = sin (1 − 2 cos ) ⇒ = ( ) + ( ) = |1 − 2 cos | Vẽ đáp ứng biên độ:
Nhận xét: đây là bộ lọc thông thấp. Câu 3:
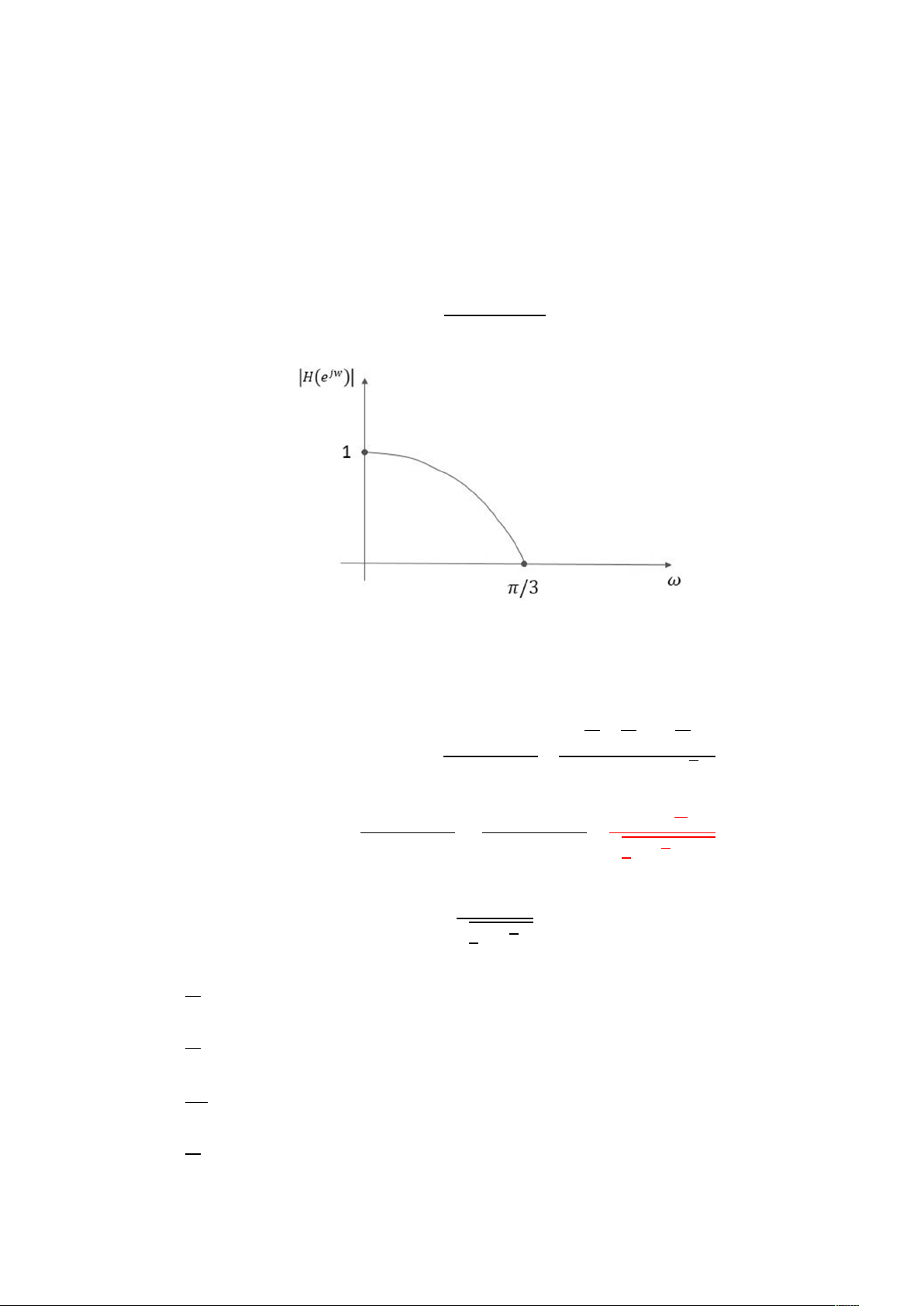
a) Ta có đáp ứng tần số: + 1 + = ( )| = = − 0,7071 cos + − √2/2 Đáp ứng biên độ: + 1 | + 1| 2 cos = = = 2 − 0,7071 | − 0,7071| 3 − 2 √2. cos
+ Tại thành phần một chiều:
= 0, ta có đáp ứng biên độ là: 2.1 . = ≈ 6,82827 3 2 − √2. 1 Tần số góc lấy mẫu: = + Tại = = /4: . / ≈ 2,61313 + Tại = = /2: . / ≈ 1,1547 + Tại = = 3 /4: . / ≈ 0,48406 + Tại = = : . = 0
b) Vẽ đáp ứng biên độ trong đoạn [0; ] Theo định lí Shannon,
≤ , với Fs là tần số lấy mẫu, fMax là tần số lớn nhất của tín hiệu
Do đó ta xét trong khoảng [0; fMax], nhận thấy đáp ứng biên độ giảm -> Lọc thông thấp Câu 4:
a) Khi ( ) = − ( ) + ( − 1) thì ( ) = ( ) + ( − 1) − ( − 2) − ( − 3) =
( )ℎ( − ) = (0)ℎ( − 0) + (1)ℎ( − 1) = −ℎ( ) + ℎ( − 1)
Khi ( ) = ( ) − ( − 5) thì ( ) = ∑
( )ℎ( − ) = (0)ℎ( ) + (5)ℎ( − 5) = ℎ( ) − ℎ( − 5) Ta có:
ℎ( ) − ℎ( − 1) = − ( ) − ( − 1) + ( − 2) + ( − 3)
ℎ( − 1) − ℎ( − 2) = − ( − 1) − ( − 2) + ( − 3) + ( − 4)
ℎ( − 2) − ℎ( − 3) = − ( − 2) − ( − 3) + ( − 4) + ( − 5)
ℎ( − 3) − ℎ( − 4) = − ( − 3) − ( − 4) + ( − 5) + ( − 6)
ℎ( − 4) − ℎ( − 5) = − ( − 4) − ( − 5) + ( − 6) + ( − 7) Cộng từng vế được:
( ) = ℎ( ) − ℎ( − 5) = − ( ) − 2 ( − 2) − ( − 2) + ( − 5) + 2 ( − 6) + ( − 7) Vẽ y2(n):
b) Xác định và vẽ h(n): Ta có: ( ) = ( ) ∗ ℎ( ) =
( )ℎ( − ) = (0)ℎ( ) + (1)ℎ( − 1) = −ℎ( ) + ℎ( − 1) Từ đồ thị, ta có:
(0) = 1 ⇒ −ℎ(0) + ℎ(−1) = 1 ⇒ ℎ(0) = ℎ(−1) − 1 = 0 − 1 = −1
(1) = 1 ⇒ −ℎ(1) + ℎ(0) = 1 ⇒ ℎ(1) = ℎ(0) − 1 = −2
(2) = −1 ⇒ −ℎ(2) + ℎ(1) = −1 ⇒ ℎ(2) = ℎ(1) + 1 = −1
(3) = −1 ⇒ −ℎ(3) + ℎ(2) = −1 ⇒ ℎ(3) = ℎ(2) + 1 = 0 ( ) = 0, ≥ 4 ⇒ −ℎ( ) + ℎ( − 1) = 0 ⇒ ℎ( ) = 0, ≥ 3
Từ đây có đồ thị của đáp ứng xung h(n):