Bộ môn
ĐỀ THI XỬ LÝ TÍN HIỆU SỐ KTMT
Thời gian 90 phút. Không sử dụng tài liệu và thiết bị nghe nhìn. Sinh A
viên đề nghị cán bộ coi thi và ký vào bài làm đề A hoặc B. Nếu không
bài thi sẽ không điểm. Nộp lại đề cùng bài làm.
Câu 1: a) Có 3 hệ mắc nối tiếp nhau và đáp ứng xung lần lượt của 3 hệ là ℎ ( ) = ( ) − ( −
1), ℎ ( ) = ℎ( ), ℎ ( ) = ( ). Không dùng biến đổi Z, hãy tính toán trong miền thời gian để xác định
đáp ứng xung của toàn hệ ℎ ( ). b) Cho ( ) = ( + 4). Hãy tính .
Câu 2: Cho hàm truyền đạt của 2 bộ lọc như sau: 1 − 1 − 1 + ( ) = , ( ) = . 1 − 2 1 − a) Hãy tính , . b) Giả thiết = 0,8 và = = . Tính và . Nếu > ta nói rằng bộ lọc
thứ nhất có dải thông lớn hơn bộ lọc thứ hai, còn nếu <
thì bộ lọc thứ hai có dải thông lớn hơn. Vậy
so sánh dải thông của 2 bộ lọc trong trường hợp này như thế nào? Câu 3: Cho PT-SP ( ) = ( − 1) + ( ) với =
. Giả thiết ( ) là thực. Như vậy ( ) sẽ là
phức và được biểu diễn theo phần thực và phần ảo như sau: ( ) = ( ) + ( ).
a) Xác định phương trình mô tả hệ với một đầu vào ( ) và 2 đầu ra ( ) và ( ).
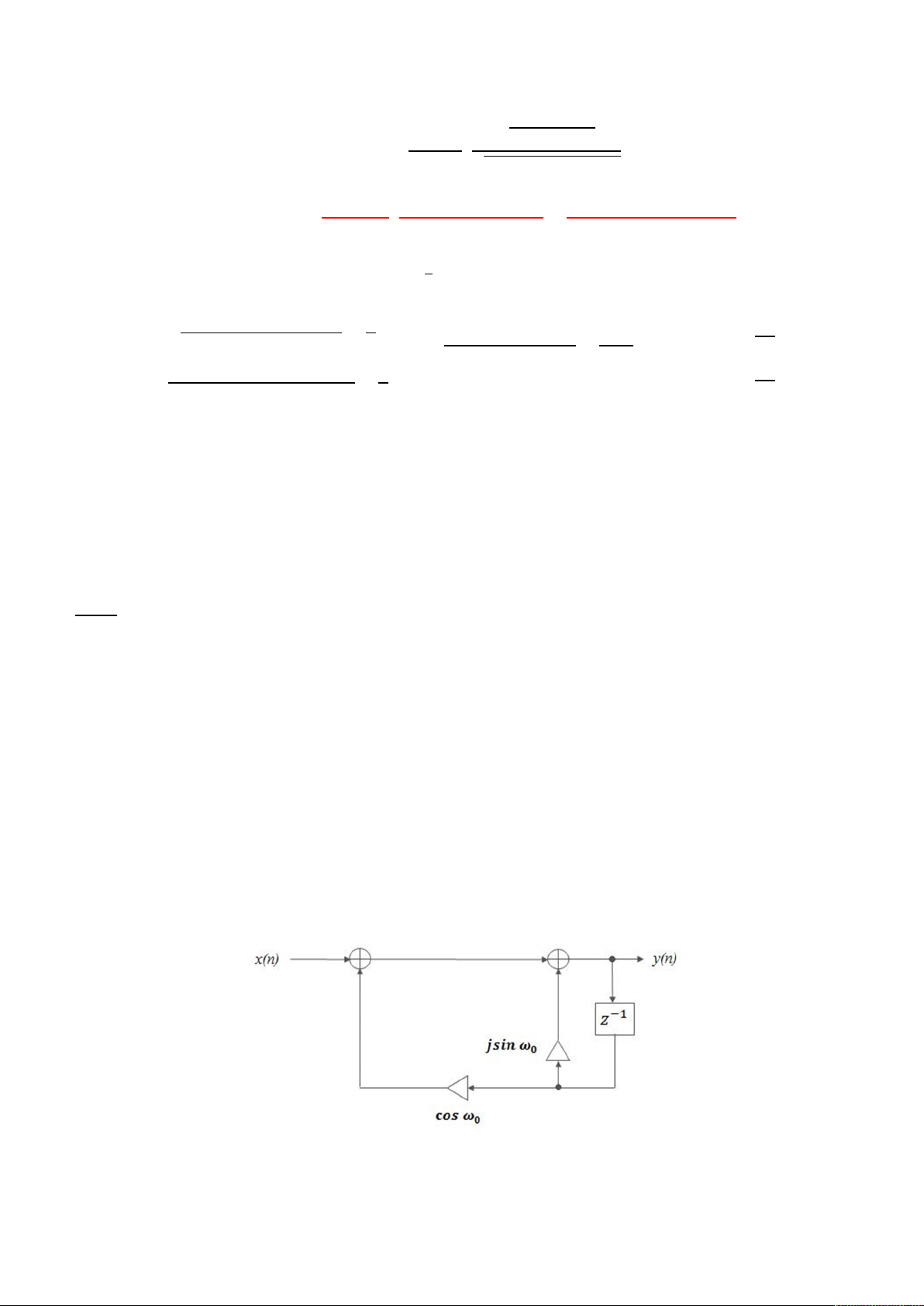
b) Vẽ sơ đồ khối thực hiện hệ.
c) Chứng minh rằng nếu ( ) = ( ) thì ( ) = (cos ) ( ), ( ) = (sin ) ( )
d) Hệ này có thể được sử dụng để làm gì?
Câu 4: Cho PT-SP ( ) = ( ) + ( − 10)
a) Xác định và vẽ đáp ứng biên độ của hệ
b) Tính tín hiệu ra ( ) nếu ( ) = cos + 3 sin + , −∞ < < ∞
Câu 5: Xét bộ lọc có quan hệ vào-ra ( ) = 0,9 ( − 1) + 0,1 ( )
a) Xác định tần số sao cho = 1/√2
b) Đây là bộ lọc thông thấp hay thông cao? Vì sao? HƯỚNG DẪN GIẢI Câu 1:
a) Do 3 hệ mắc nối tiếp nhau nên đáp ứng xung toàn hệ là:
ℎ ( ) = ℎ ( ) ∗ ℎ ( ) ∗ ℎ ( ) = ℎ ( ) ∗ [ℎ ( ) ∗ ℎ ( )] Ta có: ℎ ( ) ∗ ℎ ( ) = ℎ ( ). ℎ ( − ) 1, = 0
Do ℎ ( ) = ( ) − ( − 1) = −1, = 1 , nên ta có: 0, còn lại
ℎ ( ) ∗ ℎ ( ) = ℎ (0). ℎ ( − 0) + ℎ (1). ℎ ( − 1) = ℎ ( ) − ℎ ( − 1) = ( ) − ( − 1) 1, ≥ 0 1, ≥ 1 Lại vì ( ) = ; ( − 1) = nên ta có: 0, < 0 0, < 1 1, = 0 ℎ ( ) ∗ ℎ ( ) = = ( ) 0, ≠ 0
Vì vậy: ℎ ( ) = ℎ ( ) ∗ ( ) = ℎ ( ) = ℎ( )
Kết luận: đáp ứng xung toàn hệ là ( ) = ( ) b) Ta có ( ) = ( + 4). 1, ≥ −4 , ≥ 4 Vì ( + 3) = nên ( ) = 0, < −4 0, < 4
Từ đây có biến đổi Fourier của tín hiệu x(n) là: 1 1 = ( ) = = (∗) 4 3 Do
= < 1 nên chuỗi (*) hội tụ, vì thế tồn tại biến đổi Fourier. Ta có: 1 1 256 = 4 = 4 1 1 1 − 1 − 4 4 Kết luận: ( ) = − Câu 2: a) Ta có: 1 − 1 − 1 + ( ) = , ( ) = . 1 − 2 1 − Suy ra: 1 − = ( )| = , 1 − 1 − 1 + = ( )| = . 2 1 − Từ đây có: 1 − |1 − | = = 1 − |1 − | 1 − 1 + |1 − | 1 + = . = . 2 1 − 2 |1 − | Ta có: 1 + = 1 + cos − sin ⇒ 1 + =
(1 + cos ) + (− sin ) = √2 + 2 cos 1 − = 1 − (cos − sin ) = 1 − cos + sin ⇒ 1 − = (1 − cos ) + ( sin ) = 1 + − 2 cos Vì thế: |1 − | = √1 + − 2 cos ( − ) ⇒ ( ) = + − |1 − | √2 + 2 cos = . 2 √1 + − 2 cos ( − ) + ( − ) ( + ) ⇒ ( ) = . = + − ( + − ) b) Với = 0,8; = = , ta có: ⎧ (1 − 0,8) 1 39 ⎪ = 1 + cos 1 1 + 0,8 − 1,6 cos 2 cos = = ⇔ 40 1,64 − 1,6 cos 0,04 ⇔ ⎨ (1 − 0,8) (1 + cos ) 1 40 ⎪ = 1,64 − 1,6 cos = 0,08 cos = ⎩2(1 + 0,8 − 1,6 cos ) 2 41 ≈ 0,2241 + 2 ⇔ ( ∈ ) ≈ 0,2213 + 2
Ta chỉ xét trong đoạn [0; 2 ], do đó ≈ 0,2241; ≈ 0,2213. Dễ thấy >
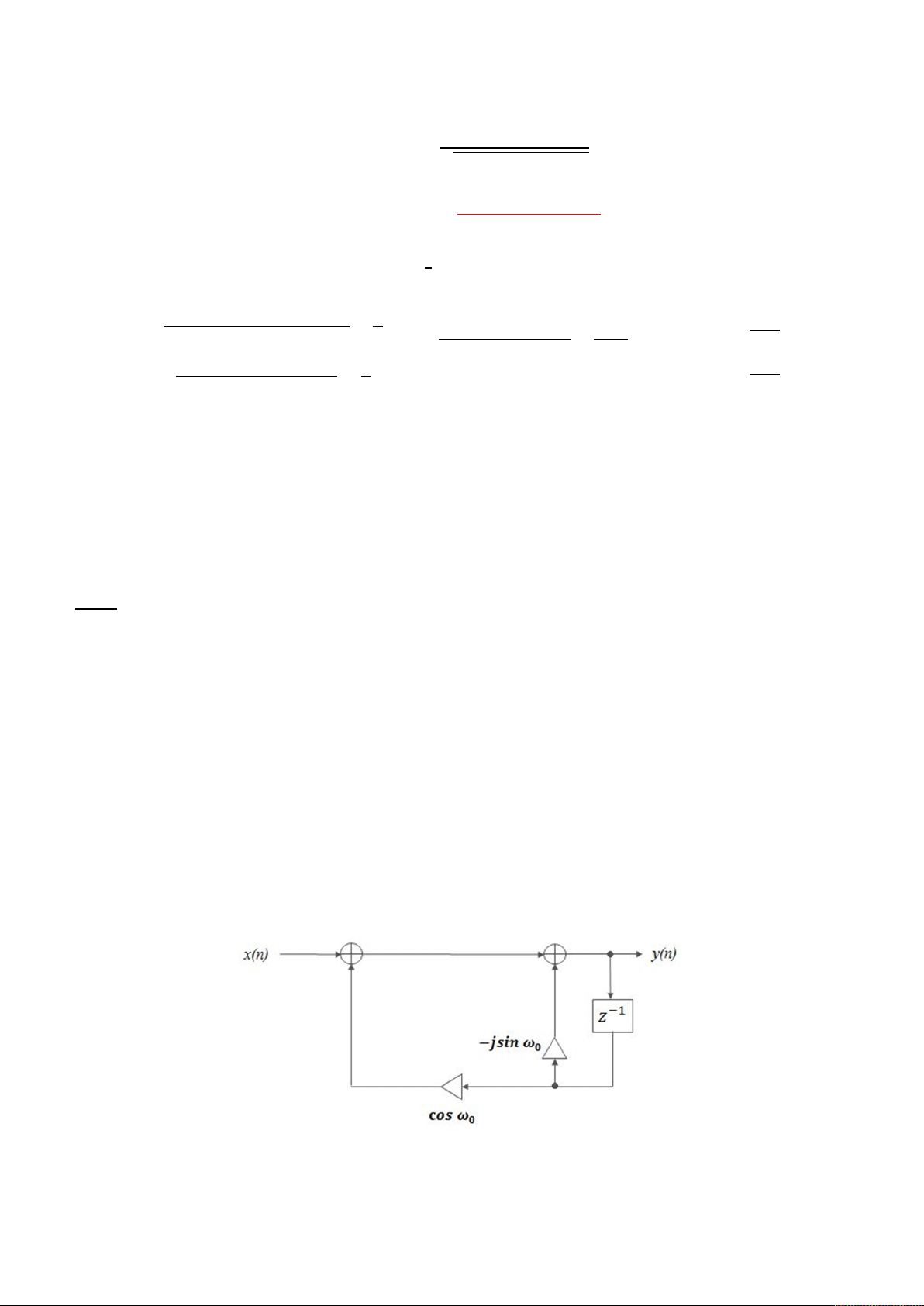
Kết luận: Bộ lọc thứ nhất có dải thông lớn hơn. Câu 3: a) Ta có: ( ) = ( − 1) + ( ); = , do đó: ( ) = ( − 1) + ( ) Theo công thức Euler: = cos + sin , nên: ( ) = (cos + sin ) ( − 1) + ( ) = ( ) + cos ( − 1) + sin ( − 1) Từ đây ta có: ( ) = ( ) + ( ) với ( ) = ( ) + cos ( − 1) ( ) = sin ( − 1)
b) Vẽ sơ đồ khối thực hiện hệ c) Chứng minh …
d) Hệ này được dùng để:
Câu 4: PT-SP: ( ) = ( ) + ( − 10)
a) Thực hiện biến đổi Fourier cả 2 vế của PT-SP ta được: = + ⇒ = 1 + Đáp ứng tần số: = = 1 + = + = 2 cos(5 ) ( )
Từ đây suy ra đáp ứng biên độ: ( ) = | ( )| Vẽ đáp ứng biên độ: b) Ta có: ( ) = cos + 3sin + 10 3 10
Mà theo giả thiết: ( ) = ( ) + ( − 10), do đó tín hiệu ra y(n) là: ( ) = cos + 3sin + + cos ( − 10) + 3sin ( − 10) + 10 3 10 10 3 10 10 = cos + 3sin + + cos − + 3sin − + 10 3 10 10 3 3 10 = cos + 3sin + − cos 10 3 10 10 10 10 + 3 sin + . cos − cos + . sin 3 10 3 3 10 3 3 3√3 = 3sin + − . sin + − cos + 3 10 2 3 10 2 3 10 3 3√3 7 = sin + − cos + = 3 sin + − = 3 sin − 2 3 10 2 3 10 3 10 3 3 30
Kết luận: Tín hiệu ra y(n) là: ( ) = −
Câu 5: Bộ lọc có quan hệ vào-ra: ( ) = 0,9 ( − 1) + 0,1 ( )
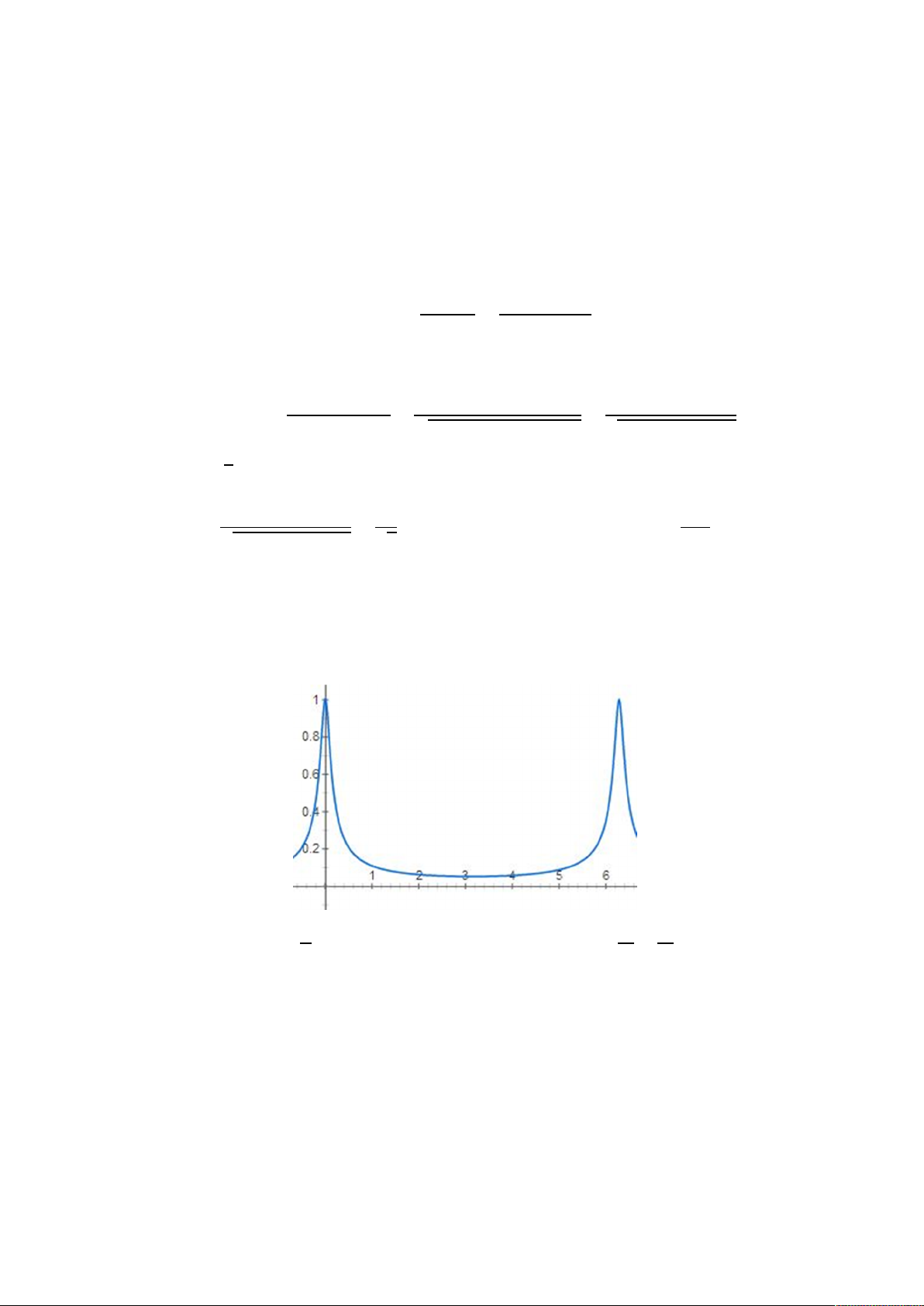
a) Thực hiện biến đổi Fourier cả 2 vế của phương trình sai phân: = 0,9 + 0,1 ⇒ 1 − 0,9 = 0,1 Đáp ứng tần số: 0,1 = = ( ) 1 − 0,9 Đáp ứng biên độ: 0,1 0,1 0,1 = = = |1 + 0,9 | 1 + 0,9 − 1,8 cos √1,81 − 1,8 Để = 1/√2 thì: 0,1 1 179 = ⇔ 181 − 180 cos = 2 ⇔ cos = √1,81 − 1,8 √2 180 ⇔ ≈ , + ( ∈ )
b) Xác định tính chất bộ lọc Vẽ đáp ứng biên độ: Theo định lí Shannon:
≤ , với là tần số lấy mẫu, suy ra: ≤ = =
Do đó ta chỉ xét đáp ứng biên độ trong đoạn [0; ]
Dễ dàng thấy được từ 0 đến pi thì đáp ứng biên độ giảm, nên đây là bộ lọc thông thấp
Kết luận: Bộ lọc thông thấp Bộ môn
ĐỀ THI XỬ LÝ TÍN HIỆU SỐ KTMT
Thời gian 90 phút. Không sử dụng tài liệu và thiết bị nghe nhìn. Sinh B
viên đề nghị cán bộ coi thi và ký vào bài làm đề A hoặc B. Nếu không
bài thi sẽ không điểm. Nộp lại đề cùng bài làm.
Câu 1: a) Có 3 hệ mắc nối tiếp nhau và đáp ứng xung lần lượt của 3 hệ là ℎ ( ) = ℎ( ), ℎ ( ) =
( ), ℎ ( ) = ( ) − ( − 1). Không dùng biến đổi Z, hãy tính toán trong miền thời gian để xác định
đáp ứng xung của toàn hệ ℎ ( ). b) Cho ( ) = ( + 3). Hãy tính .
Câu 2: Cho hàm truyền đạt của 2 bộ lọc như sau: 1 − 1 + 1 − ( ) = . , ( ) = 2 1 − 1 − a) Hãy tính , . b) Giả thiết = 0,7 và = = . Tính và . Nếu > ta nói rằng bộ lọc
thứ nhất có dải thông lớn hơn bộ lọc thứ hai, còn nếu <
thì bộ lọc thứ hai có dải thông lớn hơn. Vậy
so sánh dải thông của 2 bộ lọc trong trường hợp này như thế nào? Câu 3: Cho PT-SP ( ) = ( − 1) + ( ) với =
. Giả thiết ( ) là thực. Như vậy ( ) sẽ là
phức và được biểu diễn theo phần thực và phần ảo như sau: ( ) = ( ) + ( ).
a) Xác định phương trình mô tả hệ với một đầu vào ( ) và 2 đầu ra ( ) và ( ).
b) Vẽ sơ đồ khối thực hiện hệ.
c) Chứng minh rằng nếu ( ) = ( ) thì ( ) = (cos ) ( ), ( ) = (sin ) ( )
d) Hệ này có thể được sử dụng để làm gì?
Câu 4: Cho PT-SP ( ) = ( ) + ( − 4)
a) Xác định và vẽ đáp ứng biên độ của hệ
b) Tính tín hiệu ra ( ) nếu ( ) = cos + + cos , −∞ < < ∞
Câu 5: Xét bộ lọc có quan hệ vào-ra ( ) = −0,9 ( − 1) + 0,1 ( )
a) Xác định tần số sao cho = 1/√2
b) Đây là bộ lọc thông thấp hay thông cao? Vì sao? HƯỚNG DẪN GIẢI Câu 1:
a) Do 3 hệ mắc nối tiếp nhau nên đáp ứng xung toàn hệ là:
ℎ ( ) = ℎ ( ) ∗ ℎ ( ) ∗ ℎ ( ) = ℎ ( ) ∗ [ℎ ( ) ∗ ℎ ( )] Ta có: ℎ ( ) ∗ ℎ ( ) = ℎ ( ). ℎ ( − ) 1, = 0
Do ℎ ( ) = ( ) − ( − 1) = −1, = 1 , nên ta có: 0, còn lại
ℎ ( ) ∗ ℎ ( ) = ℎ (0). ℎ ( − 0) + ℎ (1). ℎ ( − 1) = ℎ ( ) − ℎ ( − 1) = ( ) − ( − 1) 1, ≥ 0 1, ≥ 1 Lại vì ( ) = ; ( − 1) = nên ta có: 0, < 0 0, < 1 1, = 0 ℎ ( ) ∗ ℎ ( ) = = ( ) 0, ≠ 0
Vì vậy: ℎ ( ) = ℎ ( ) ∗ ( ) = ℎ ( ) = ℎ( )
Kết luận: đáp ứng xung toàn hệ là ( ) = ( ) b) Ta có ( ) = ( + 3). 1, ≥ −3 , ≥ 3 Vì ( + 3) = nên ( ) = 0, < −3 0, < 3
Từ đây có biến đổi Fourier của tín hiệu x(n) là: 1 1 = ( ) = = (∗) 3 3 Do
= < 1 nên chuỗi (*) hội tụ, vì thế tồn tại biến đổi Fourier. Ta có: 1 1 27 = 3 = 3 1 1 1 − 1 − 3 3 Kết luận: ( ) = − Câu 2: a) Ta có: 1 − 1 + 1 − ( ) = . , ( ) = 2 1 − 1 − Suy ra: 1 − 1 + = ( )| = . , 2 1 − 1 − = ( )| = 1 − Từ đây có: 1 − 1 + |1 − | 1 + = . = . 2 1 − 2 |1 − | 1 − |1 − | = = 1 − |1 − | Ta có: 1 + = 1 + cos − sin ⇒ 1 + =
(1 + cos ) + (− sin ) = √2 + 2 cos 1 − = 1 − (cos − sin ) = 1 − cos + sin ⇒ 1 − = (1 − cos ) + ( sin ) = 1 + − 2 cos Vì thế: |1 − | √2 + 2 cos = . 2 √1 + − 2 cos ( − ) + ( − ) ( + ) ⇒ ( ) = . = + − ( + − ) |1 − | = √1 + − 2 cos ( − ) ⇒ ( ) = + − b) Với = 0,7; = = , ta có: ⎧ (1 − 0,7) (1 + cos ) 1 140 ⎪ = 1 + cos 1 2(1 + 0,7 − 1,4 cos ) 2 cos = = ⇔ 149 1,49 − 1,4 cos 0,09 ⇔ ⎨ (1 − 0,7) 1 131 ⎪ = 1,49 − 1,4 cos = 0,18 cos = ⎩ 1 + 0,7 − 1,4 cos 2 140 ≈ 0,3493 + 2 ⇔ ( ∈ ) ≈ 0,3605 + 2
Ta chỉ xét trong đoạn [0; 2 ], do đó ≈ 0,3493; ≈ 0,3605. Dễ thấy <
Kết luận: Bộ lọc thứ hai có dải thông lớn hơn. Câu 3: a) Ta có: ( ) = ( − 1) + ( ); = , do đó: ( ) = ( − 1) + ( ) Theo công thức Euler: = cos − sin , nên: ( ) = (cos − sin ) ( − 1) + ( ) = ( ) + cos ( − 1) − sin ( − 1) Từ đây ta có: ( ) = ( ) + ( ) với ( ) = ( ) + cos ( − 1) ( ) = − sin ( − 1)
b) Vẽ sơ đồ khối thực hiện hệ c) Chứng minh …
d) Hệ này được dùng để:
Câu 4: PT-SP: ( ) = ( ) + ( − 4)
a) Thực hiện biến đổi Fourier cả 2 vế của PT-SP ta được: = + ⇒ = 1 + Đáp ứng tần số: = = 1 + = + = 2 cos(2 ) ( )
Từ đây suy ra đáp ứng biên độ: ( ) = | ( )| Vẽ đáp ứng biên độ: b) Ta có: ( ) = cos + + cos 2 7 4
Mà theo giả thiết: ( ) = ( ) + ( − 4), do đó tín hiệu ra y(n) là: ( ) = cos + + cos + cos ( − 4) + + cos ( − 4) 2 7 4 2 7 4 = cos + + cos + cos + − 2 + cos − 2 7 4 2 7 4 = cos + + cos + cos + − cos = 2 cos + 2 7 4 2 7 4 2 7
Kết luận: Tín hiệu ra y(n) là: ( ) = +
Câu 5: Bộ lọc có quan hệ vào-ra: ( ) = −0,9 ( − 1) + 0,1 ( )
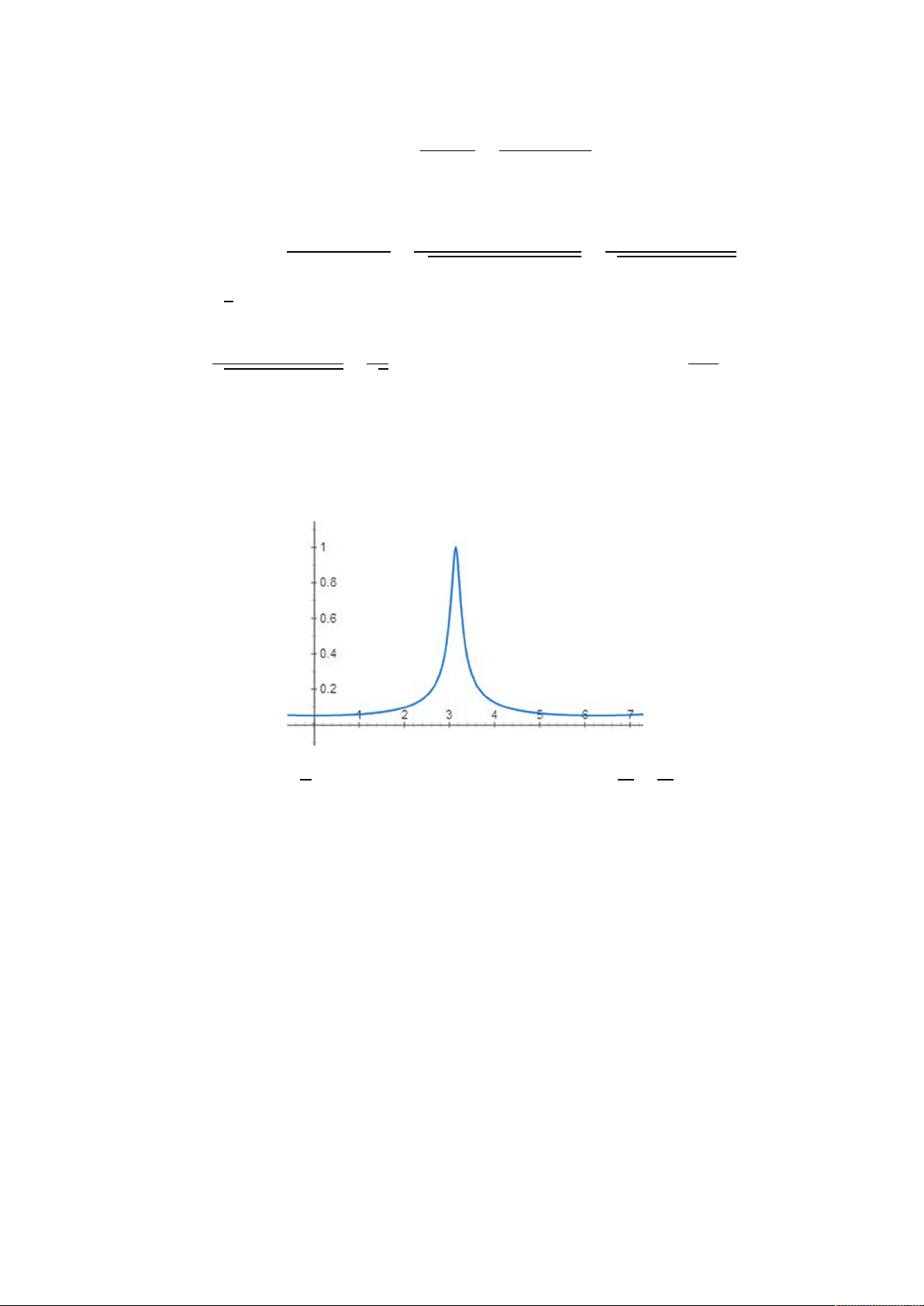
a) Thực hiện biến đổi Fourier cả 2 vế của phương trình sai phân: = −0,9 + 0,1 ⇒ 1 + 0,9 = 0,1 Đáp ứng tần số: 0,1 = = ( ) 1 + 0,9 Đáp ứng biên độ: 0,1 0,1 0,1 = = = |1 + 0,9 | 1 + 0,9 + 1,8 cos √1,81 + 1,8 Để = 1/√2 thì: 0,1 1 179 = ⇔ 181 + 180 cos = 2 ⇔ cos = − √1,81 + 1,8 √2 180 ⇔ ≈ , + ( ∈ )
b) Xác định tính chất bộ lọc Vẽ đáp ứng biên độ: Theo định lí Shannon:
≤ , với là tần số lấy mẫu, suy ra: ≤ = =
Do đó ta chỉ xét đáp ứng biên độ trong đoạn [0; ]
Dễ dàng thấy được từ 0 đến pi thì đáp ứng biên độ tăng, nên đây là bộ lọc thông cao
Kết luận: Bộ lọc thông cao